Геометрия на клетчатой бумаге | Образовательная социальная сеть
Тема работы: Геометрия на клетчатой бумаге
Обычный листок в клетку… Каждый из нас имел дело с ним с первых дней изучения математики, а может быть, и раньше. Клеточка как наглядный инструмент, помогает лучше изучить свойства геометрических фигур и открывает для нас достаточно оригинальные и интересные задачи. Это задачи на клетчатой бумаге.
Эти задачи отличаются от обычных задач из действующих учебников геометрии, и в то же время они не требуют дополнительных сведений, они направлены на обобщающее повторение основного курса геометрии 7 – 9 классов, на его более глубокое освоение и понимание, выработку необходимых компетенций.
Проанализировав школьные учебники математики, научно – популярную и занимательную литературу, интернет-ресурсы, я нашел разные задачи, которые решаются на клетчатой бумаге.
У меня возникли вопросы: в чём заключается особенность таких задач, существуют ли специальные методы и приёмы решения задач на клетчатой бумаге. Тем более что с задачами на клетчатой бумаге я столкнулся при подготовке к ОГЭ (основному государственному экзамену), также они присутствуют и в контрольно-измерительных материалах ЕГЭ. А значит, для меня важно, научиться решать такие задачи.
Тем более что с задачами на клетчатой бумаге я столкнулся при подготовке к ОГЭ (основному государственному экзамену), также они присутствуют и в контрольно-измерительных материалах ЕГЭ. А значит, для меня важно, научиться решать такие задачи.
Чёткой классификации и структурирования задач на клетчатой бумаге по методам и способам решения я не встретил. Возможно, потому, что большинство таких задач считается «занимательными», и для них нет общего правила решения, конкретных способов и приёмов. Вот это их свойство обуславливает их ценность для развития не конкретного учебного умения или навыка, а вообще умения думать, размышлять, анализировать, искать аналогии, то есть, эти задачи развивают мыслительные навыки в самом широком их понимании.
Я определил:
Объект исследования: задачи на клетчатой бумаге
Предмет исследования: многообразие задач на клетчатой бумаге, методы и приёмы их решения.
Методы исследования: изучение литературных и Интернет-ресурсов, анализ и классификация информации, обобщение.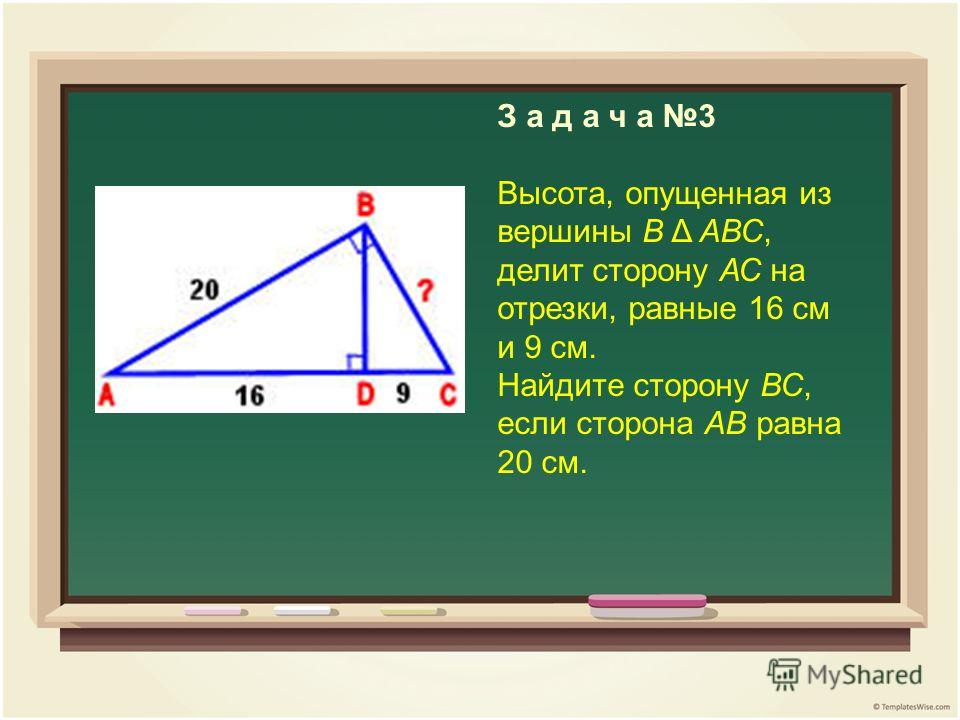
Цель исследования — расширение знаний о многообразии задач на клетчатой бумаге, о приёмах и методах решения этих задач.
Задачи:
- Подобрать необходимую литературу;
- Отобрать материал для исследования, проанализировать и систематизировать полученную информацию;
- Найти различные методы и приёмы решения задач на клетчатой бумаге;
- Классифицировать исследуемые задачи;
- Оформить работу в виде буклета;
- Создать электронную презентацию работы для представления собранного материала одноклассникам.
Глава 1. Задачи на нахождение геометрических величин (длин, углов, площадей)
Среди многообразия задач на клетчатой бумаге я обратил свое внимание на те задачи, которые нашел в контрольно-измерительных материалах ОГЭ и ЕГЭ, так как на сегодняшний момент они актуальны для меня и моих одноклассников. Я попытался их классифицировать для себя и определил три группы:
1.Задачи на нахождение длин
Задача 1. На клетчатой бумаге с размером клетки 1×1 отмечены точки A и B. Найдите длину отрезка AB.
Найдите длину отрезка AB.
Решение
Расстояние между точками A и B равно длине гипотенузы треугольника ABC, катеты которого равны 15 и 8. Поэтому искомая длина AB равна 17.
Задача 2. На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его высоты, опущенной на сторону AB.
Решение.
Из точки С можно опустить перпендикуляр к прямой, содержащей сторону АВ. Этот перпендикуляр будет являться высотой треугольника АВС, его длина равна 3.
Задача 3. На клетчатой бумаге с размером клетки 1×1 изображён равнобедренный прямоугольный треугольник. Найдите длину его медианы, проведённой к гипотенузе.
Решение
Медиана, проведённая к гипотенузе, равна её половине. Поэтому она равна 4,5.
Задача 4. На клетчатой бумаге с размером клетки 1×1 отмечены точки A, B и C. Найдите расстояние от точки A до прямой BC.
Решение
Расстояние от точки до прямой равно длине перпендикуляра, опущенного из этой точки на данную прямую. Тем самым, искомое расстояние равно 4.
Тем самым, искомое расстояние равно 4.
Задача 5. Найдите биссектрису треугольника ABC, проведенную из вершины B, если стороны квадратных клеток равны 1.
.
Решение
По рисунку видно, что АВ=ВС, значит, биссектриса, проведенная из вершины В, также будет делить основание АС пополам. Построим отрезок ВК. Видно, что он равен 4.
Задача 6. Найдите медиану треугольника АВС, проведенную из вершины С, если стороны квадратных клеток равны 1.
Решение
Медиана проведенная из вершины С, будет делить основание АВ пополам. Построим отрезок СК. Видно, что он равен 3.
Задача 7. На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AB.
Решение
Средняя линия треугольника равна половине той стороны, которой она параллельна. Длина стороны АВ равна 4, поэтому искомая длина средней линии равна 2.
Задача 8. Найдите периметр четырехугольника ABCD, если стороны квадратных клеток равны .
Найдите периметр четырехугольника ABCD, если стороны квадратных клеток равны .
Задача 9. Найдите среднюю линию трапеции ABCD, если стороны квадратных клеток равны .
Задача 10. На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите радиус описанной около него окружности.
Решение
Изображенная на рисунке окружность вписана в квадрат со стороной 5, поэтому радиус этой окружности равен 2,5.
2.Задачи на нахождение углов
Задача 11. Найдите тангенс угла .
Решение
Проведем высоту BK из точки B на сторону OA. Тогда, принимая во внимание, что BK = OK, получим:
Задача 12. Найдите тангенс угла .
Решение.
Достроим угол до треугольника OBA, OB=BA. BK делит основание OA пополам, значит, – высота. Из рисунка находим ОК=ВК =.
Задача 13. На клетчатой бумаге с размером клетки изображён угол. Найдите его градусную величину.
Решение
Изображённый на рисунке угол равен сумме прямого угла и угла 45°, поэтому он равен 135°.
Задача 14. Найдите величину угла АВС. Ответ дайте в градусах.
3.Задачи на нахождение площадей
Задача 15. Найдите площадь трапеции, изображенной на клетчатой
бумаге с размером клетки 1 см × 1 см (см. рис.).
Ответ дайте в квадратных сантиметрах.
Я приведу три решения этой задачи.
I решение предполагает, что я хорошо знаю формулу площади трапеции.
ABCD — трапеция, т.е. четырёхугольник, у которого две противолежащие стороны параллельны. На рисунке параллельны стороны ВС и AD, они проходят по вертикальным линиям сетки, значит они являются основаниями трапеции. Площадь трапеции равна полусумме оснований, умноженной на высоту (обозначим её — h). Длину оснований определяем простым подсчётом клеточек на рисунке. ВС = 2, AD = 4. Как определить h? Вспомним, что высота трапеции это расстояние между параллельными прямыми, на которых лежат основания. Обычно, для определения этого расстояния, нужно из какой-либо вершины трапеции опустить перпендикуляр на противолежащую параллельную прямую, но здесь у нас такие перпендикуляры уже есть — это горизонтальные линии сетки. Возьмем, например, линию, на которой находятся точки А и С, на ней укладывается ровно 4 клеточки. Следовательно, h = 4. Подставляем значения в формулу:
Обычно, для определения этого расстояния, нужно из какой-либо вершины трапеции опустить перпендикуляр на противолежащую параллельную прямую, но здесь у нас такие перпендикуляры уже есть — это горизонтальные линии сетки. Возьмем, например, линию, на которой находятся точки А и С, на ней укладывается ровно 4 клеточки. Следовательно, h = 4. Подставляем значения в формулу:
S = h = 4= 12.
II решение предполагает, что я знаю самые простые формулы площади: площадь прямоугольника и площадь прямоугольного треугольника.
Провожу дополнительную линию AC, которая «разрезает» нашу трапецию на два прямоугольных треугольника. Первый с катетами AC = 4 и BC = 2, его площадь S1 = 4×2/2 = 4. Второй с катетами AC = 4 и AD = 4, его площадь S2 = 4×4/2 = 8. Площадь трапеции равна сумме площадей треугольников ACB и DAC.
S = S1 + S2 = 4 + 8 = 12.
III решение требует тех же знаний, что и второе решение.
Только теперь я буду не «разрезать» нашу трапецию на части, а «вырезать» её из прямоугольника, стороны которого проходят по линиям сетки через вершины заданной трапеции.
Провожу горизонтальные линии через вершины В и D, продолжаем вертикальные линии AD и ВС до пересечения с горизонтальными. Точки пересечения обозначаю точками E и F. Получил прямоугольник DEBF со сторонами DE = 6 и DF = 4, его площадь 6×4 = 24. Чтобы получить искомую площадь трапеции, нужно из площади этого прямоугольника вычесть площади (зелёных) треугольников AEB и DFC.
SAEB = AE·EB/2 = 2·4/2 = 4 и SDFC = DF·FC/2 = 4·4/2 = 8
Следовательно, площадь трапеции равна
S = 24 − 4 − 8 = 12.
И, наконец, еще одно IV решение пригодится, если я не знаю формул из предыдущих решений, но знаком лишь с одной формулой, которую подарил нам австрийский математик Георг Александр Пик (1859 – 1942).
Глава 2. Формула Пика
Георга, который был одарённым ребёнком, обучал отец, возглавлявший частный институт. В 16 лет Георг закончил школу и поступил в Венский университет. В 20 лет получил право преподавать физику и математику. Шестнадцатого апреля 1880 года Пик защитил докторскую диссертацию «О классе абелевых интегралов» В Немецком университете в Праге в 1888 году Пик получил место экстраординарного профессора математики, затем в 1892-м стал ординарным профессором. В 1900—1901 годах занимал пост декана философского факультета.
В 1900—1901 годах занимал пост декана философского факультета.
В 1910 году Георг Пик был в комитете, созданном Немецким университетом Праги для рассмотрения вопроса о принятии Альберта Эйнштейна профессором в университет. Пик и физик Антон Лампа были главными инициаторами этого назначения, и благодаря их усилиям Эйнштейн, с которым Пик впоследствии сдружился, в 1911 году возглавил кафедру теоретической физики в Немецком университете в Праге.
Пик и Эйнштейн не только имели общие научные интересы, но и страстно увлекались музыкой. Пик, игравший в квартете, который состоял из университетских профессоров, ввёл Эйнштейна в научное и музыкальное общества Праги. Широкую известность получила открытая им в 1899 году теорема Пика для расчёта площади многоугольника. В Германии эта теорема включена в школьные учебники.
Я считаю настоящей находкой моего исследования формулу Пика!
Сюжет будет разворачиваться на обычном листке клетчатой бумаги.[2] Линии, идущие по сторонам клеток, образуют сетку, а вершины клеток – узлы этой сетки. Нарисуем на листе многоугольник с вершинами в узлах
Нарисуем на листе многоугольник с вершинами в узлах
Рис. 1 (рис. 1) и найдем его площадь.
Оказывается, площади многоугольников, вершины которых расположены в узлах сетки, можно вычислять гораздо проще: есть формула, связывающая их площадь с количеством узлов, лежащих внутри и на границе многоугольника. Эта замечательная и простая формула называется формулой Пика.
Рис. 2 Пусть АВСD – прямоугольник с вершинами в узлах и сторонами, идущими по линиям сетки (рис. 2).
Обозначим через В количество узлов, лежащих внутри прямоугольника, а через Г – количество узлов на его границе. Сместим сетку на полклетки вправо и полклетки вниз. Тогда территорию прямоугольника можно «распределить» между узлами следующим образом: каждый из В узлов «контролирует» целую клетку смещённой сетки, а каждый из Г узлов – 4 граничных не угловых узла – половину клетки, а каждая из угловых точек – четверть клетки. Поэтому площадь прямоугольника S равна
S = В + + 4 · = В + — 1 .
Итак, для прямоугольников с вершинами в узлах и сторонами, идущими по линиям сетки, мы установили формулу S = В + — 1 .
Оказывается, эта формула верна не только для прямоугольников, но и для произвольных многоугольников с вершинами в узлах сетки!
Это и есть формула Пика.
Использую формулу Пика в нашем IV решении
В = 7, Г = 12. По формуле Пика: S = В + — 1 .
S = 7 + 12/2 – 1 = 12.
Помогает нам формула Пика и для решения геометрических задач с практическим содержанием.
Задача. Найдите площадь лесного массива (в м²), изображённого на плане с квадратной сеткой 1 × 1(см) в масштабе 1 см – 200 м
Решение. Найдём S площадь четырёхугольника, изображённого на клетчатой бумаге по формуле Пика: S = В + — 1
В = 8, Г = 7. S = 8 + 7/2 – 1 = 10,5 (см²)
1 см² — 200² м²; S = 40000 · 10,5 = 420 000 (м²)
Ответ: 420 000 м²
Заключение
В процессе работы над данной темой я изучил учебное издание «Геометрия на клетчатой бумаге» Смирновой И. М., тематические статьи из газеты «Математика» ИД «Первое сентября», просмотрел сайты ФИПИ, открытого банка заданий ЕГЭ и ОГЭ. Я думаю, что задачи на клетчатой плоскости не являются несерьёзными или бесполезными, они не так уж и далеки от серьёзных математических задач. Каждая задача на клетчатой бумаге требует применения геометрических знаний в необычной ситуации, что позволяет проверить качество освоения геометрического материала, готовность ученика использовать полученные знания и умения для решения нестандартных и исследовательских задач.
М., тематические статьи из газеты «Математика» ИД «Первое сентября», просмотрел сайты ФИПИ, открытого банка заданий ЕГЭ и ОГЭ. Я думаю, что задачи на клетчатой плоскости не являются несерьёзными или бесполезными, они не так уж и далеки от серьёзных математических задач. Каждая задача на клетчатой бумаге требует применения геометрических знаний в необычной ситуации, что позволяет проверить качество освоения геометрического материала, готовность ученика использовать полученные знания и умения для решения нестандартных и исследовательских задач.
Работа по данной теме позволила мне преодолеть психологический барьер и поверить в свои силы, что является важнейшим фактором успешного решения олимпиадных и экзаменационных задач, выступления перед аудиторией с теоретическим материалом по данной теме.
В результате работы я прорешал немало задач, расширил свои знания о решении задач на клетчатой бумаге, определил для себя классификацию исследуемых задач, убедился в их многообразии.
И я думаю, что решение этих задач рассмотренными способами превратится в интересное занятие, итогом, которого будет не только прекрасное настроение, но и высокий тестовый балл.
Литература
- Жарковская Н. М., Рисс Е. А. Геометрия клетчатой бумаги. Формула Пика // Математика, 2009, № 17, с. 24-25.
- Математика – газета ИД «Первое сентября», № 23/2009г.
- Погорелов А.В. Геометрия: учебник для 7-9кл.общеобразовательных учреждений.- М.: Просвещение, 2007.
- Смирнова И.М., Смирнов В.А. Геометрия на клетчатой бумаге. — М.: Чистые пруды, 2009.
Интернет – ресурсы:
- Открытый банк задач ЕГЭ по математике: www.mathege.ru
- Федеральный институт педагогических измерений: fipi.ru
- ЕГЭ 2015: решение задачи по планиметрии: mathematichka.ru/ege/problems/problem_B3P1.html
Диагностическая работа по математике в форме ЕГЭ профильного уровня.
Вариант 1
Система навигации, встроенная в спинку самолетного кресла, информирует пассажира о том, что полет проходит на высоте 21 910 футов. Выразите высоту полета в метрах.
 Считайте, что 1 фут равен 30,5 см.
Считайте, что 1 фут равен 30,5 см.
На графике показано изменение температуры в процессе разогрева двигателя легкового автомобиля. На горизонтальной оси отмечено время в минутах ,прошедшее с момента запуска двигателя, на вертикальной оси — температура двигателя в градусах Цельсия. Определите по графику, до скольких градусов Цельсия двигатель нагрелся за первые 3 минуты с момента запуска.
Найдите высоту параллелограмма ABCD, опущенную на сторону AB, если стороны квадратных клеток равны 1.
Вероятность того, что в случайный момент времени температура тела здорового человека окажется ниже чем 36,8С, равна 0,88. Найдите вероятность того, что в случайный момент времени у здорового человека температура окажется 36,8С или выше.
Решите уравнение .

Площадь ромба равна 52. Одна из его диагоналей равна 4. Найдите другую диагональ.
На рисунке изображён график производной функции и восемь точек на оси абсцисс: , , , , . В скольких из этих точек функция убывает?
Даны два шара. Диаметр первого шара в 8 раз больше диаметра второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
Найдите значение выражения .
Автомобиль разгоняется на прямолинейном участке шоссе с постоянным ускорением . Скорость (в км/ч) вычисляется по формуле где — пройденный автомобилем путь (в км). Найдите, сколько километров проедет автомобиль к моменту, когда он разгонится до скорости 70 км/ч.
Первая труба наполняет резервуар на 6 минут дольше, чем вторая.
 Обе трубы наполняют этот же резервуар за 4 минуты. За сколько минут наполняет этот резервуар одна вторая труба?
Обе трубы наполняют этот же резервуар за 4 минуты. За сколько минут наполняет этот резервуар одна вторая труба?
Найдите точку максимума функции принадлежащую промежутку.
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Дана правильная треугольная призма АВСА1В1С1, все рёбра которой равны 4. Через точки A, С1 и середину T ребра А1В1 проведена плоскость.
а) Докажите, что сечение призмы указанной плоскостью является прямоугольным треугольником.
б) Найдите угол между плоскостью сечения и плоскостью ABC.
Решите неравенство:
Стороны KN и LM трапеции KLMN параллельны, прямые LM и MN — касательные к окружности, описанной около треугольника KLN .

а) Докажите, что треугольники LMN и KLN подобны.
б) Найдите площадь треугольника KLN , если известно, что KN = 3 , а угол LMN =120 градусов.
Вклад планируется открыть на четыре года. Первоначальный вклад составляет целое число миллионов рублей. В конце каждого года вклад увеличивается на 10% по сравнению с его размером в начале года, а, кроме этого, в начале третьего и четвёртого годов вклад ежегодно пополняется на 3 млн рублей. Найдите наибольший размер первоначального вклада, при котором через четыре года вклад будет меньше 25 млн рублей.
Найдите все положительные значения а, при каждом из которых система имеет единственное решение.
Вариант 2
Система навигации, встроенная в спинку самолетного кресла, информирует пассажира о том, что полет проходит на высоте 17850 футов.
 Выразите высоту полета в метрах. Считайте, что 1 фут равен 30,5 см.
Выразите высоту полета в метрах. Считайте, что 1 фут равен 30,5 см.
На графике показано изменение температуры двигателя в процессе разогрева двигателя легкового автомобиля. На оси абсцисс откладывается время в минутах, прошедшее от запуска двигателя, на оси ординат — температура двигателя в градусах Цельсия. Определите по графику, на сколько градусов нагреется двигатель с третьей по восьмую минуту разогрева.
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AB.
Даша, Оля, Дима и Денис бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должна будет девочка.
Найдите корень уравнения
Площадь ромба равна 27.
 Одна из его диагоналей равна 6. Найдите другую диагональ.
Одна из его диагоналей равна 6. Найдите другую диагональ.
На рисунке изображён график производной функции и девять точек на оси абсцисс: , , , , . В скольких из этих точек функция возрастает?
Даны два шара. Радиус первого шара в 3 раза больше радиуса второго. Во сколько раз объем первого шара больше объема второго?
Найдите значение выражения
Расстояние от наблюдателя, находящегося на небольшой высоте километров над землёй, до наблюдаемой им линии горизонта вычисляется по формуле , где км — радиус Земли. С какой высоты горизонт виден на расстоянии 48 километров? Ответ выразите в километрах.
Первая труба наполняет резервуар на 24 минуты дольше, чем вторая.
 Обе трубы наполняют этот же резервуар за 5 минут. За сколько минут наполняет этот резервуар одна вторая труба?
Обе трубы наполняют этот же резервуар за 5 минут. За сколько минут наполняет этот резервуар одна вторая труба?
Найдите точку максимума функции принадлежащую промежутку .
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Дана правильная треугольная призма АВСА1В1С1, все рёбра которой равны 6. Через точки A, С1 и середину T ребра А1В1 проведена плоскость.
а) Докажите, что сечение призмы указанной плоскостью является прямоугольным треугольником.
б) Найдите угол между плоскостью сечения и плоскостью ABC.
Решите неравенство
Первая окружность с центром O, вписанная в равнобедренный треугольник KLM, касается боковой стороны KL в точке B, а основания ML — в точке A.
 Вторая окружность с центром O1 касается основания ML и продолжений боковых сторон.
Вторая окружность с центром O1 касается основания ML и продолжений боковых сторон.
а) Докажите, что треугольник OLO1 прямоугольный.
б) Найдите радиус второй окружности, если известно, что радиус первой равен 6 и AK = 16.
По вкладу «А» банк в течение трёх лет в конце каждого года увеличивает на 20 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивает на 21 % в течение каждого из первых двух лет. Найдите наименьшее целое число процентов за третий год по вкладу «Б», при котором за все три года этот вклад всё ещё останется выгоднее вклада «А».
Найдите все положительные значения , при каждом из которых система уравнений
имеет единственное решение.
Вариант 3
Система навигации, встроенная в спинку самолетного кресла, информирует пассажира о том, что полет проходит на высоте 30870 футов.
 Выразите высоту полета в метрах. Считайте, что 1 фут равен 30,5 см.
Выразите высоту полета в метрах. Считайте, что 1 фут равен 30,5 см.
На графике показано изменение температуры двигателя в процессе разогрева двигателя легкового автомобиля. На оси абсцисс откладывается время в минутах, прошедшее от запуска двигателя, на оси ординат — температура двигателя в градусах Цельсия. Определите по графику, на сколько градусов нагреется двигатель со второй по пятую минуту разогрева.
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его высоты, опущенной на сторону AB.
Вика, Рита, Ульяна и Боря бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должен будет мальчик.
Решите уравнение .
Площадь ромба равна 18.
 Одна из его диагоналей равна 12. Найдите другую диагональ.
Одна из его диагоналей равна 12. Найдите другую диагональ.
На рисунке изображён график — производной функции На оси абсцисс отмечено девять точек: Сколько из этих точек принадлежит промежуткам убывания функции
Даны два шара. Диаметр первого шара в 7 раз больше диаметра второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
Найдите значение выражения .
Автомобиль разгоняется на прямолинейном участке шоссе с постоянным ускорением Скорость (в км/ч) вычисляется по формуле где — пройденный автомобилем путь (в км). Найдите, сколько километров проедет автомобиль к моменту, когда он разгонится до скорости 90 км/ч.
Первая труба наполняет резервуар на 12 минут дольше, чем вторая. Обе трубы наполняют этот же резервуар за 8 минут.
 За сколько минут наполняет этот резервуар одна вторая труба?
За сколько минут наполняет этот резервуар одна вторая труба?
Найдите точку максимума функции на промежутке
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Дана правильная треугольная призма АВСА1В1С1, все рёбра которой равны 4. Через точки A, С1 и середину T ребра А1В1 проведена плоскость.
а) Докажите, что сечение призмы указанной плоскостью является прямоугольным треугольником.
б) Найдите угол между плоскостью сечения и плоскостью ABC.
Решите неравенство:
Стороны KN и LM трапеции KLMN параллельны, прямые LM и MN — касательные к окружности, описанной около треугольника KLN .

а) Докажите, что треугольники LMN и KLN подобны.
б) Найдите площадь треугольника KLN , если известно, что KN = 3 , а угол LMN =120 градусов.
Вклад планируется открыть на четыре года. Первоначальный вклад составляет целое число миллионов рублей. В конце каждого года вклад увеличивается на 10% по сравнению с его размером в начале года, а, кроме этого, в начале третьего и четвёртого годов вклад ежегодно пополняется на 3 млн рублей. Найдите наибольший размер первоначального вклада, при котором через четыре года вклад будет меньше 25 млн рублей.
Найдите все положительные значения а, при каждом из которых система имеет единственное решение.
Вариант 4
Система навигации, встроенная в спинку самолетного кресла, информирует пассажира о том, что полет проходит на высоте 20370 футов.
 Выразите высоту полета в метрах. Считайте, что 1 фут равен 30,5 см.
Выразите высоту полета в метрах. Считайте, что 1 фут равен 30,5 см.
На графике показано изменение температуры в процессе разогрева двигателя легкового автомобиля. На горизонтальной оси отмечено время в минутах ,прошедшее с момента запуска двигателя, на вертикальной оси — температура двигателя в градусах Цельсия. Определите по графику, до скольких градусов Цельсия двигатель нагрелся за первые 3 минуты с момента запуска.
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его высоты, опущенной на сторону AB.
Вероятность того, что в случайный момент времени температура тела здорового человека окажется ниже чем 36,8 °С, равна 0,81. Найдите вероятность того, что в случайный момент времени у здорового человека температура окажется 36,8 °С или выше.

Найдите корень уравнения
Площадь ромба равна 60. Одна из его диагоналей равна 6. Найдите другую диагональ.
На рисунке изображён график производной функции и шесть точек на оси абсцисс: , , , , . В скольких из этих точек функция возрастает?
Даны два шара. Радиус первого шара в 5 раз больше радиуса второго. Во сколько раз объем первого шара больше объема второго?
Найдите значение выражения .
Расстояние от наблюдателя, находящегося на небольшой высоте километров над землёй, до наблюдаемой им линии горизонта вычисляется по формуле , где км — радиус Земли. С какой высоты горизонт виден на расстоянии 32 километра? Ответ выразите в километрах.
Первая труба наполняет резервуар на 16 минут дольше, чем вторая.
 Обе трубы наполняют этот же резервуар за 6 минут. За сколько минут наполняет этот резервуар одна вторая труба?
Обе трубы наполняют этот же резервуар за 6 минут. За сколько минут наполняет этот резервуар одна вторая труба?
Найдите точку максимума функции принадлежащую промежутку .
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Дана правильная треугольная призма АВСА1В1С1, все рёбра которой равны 6. Через точки A, С1 и середину T ребра А1В1 проведена плоскость.
а) Докажите, что сечение призмы указанной плоскостью является прямоугольным треугольником.
б) Найдите угол между плоскостью сечения и плоскостью ABC.
Решите неравенство
Первая окружность с центром O, вписанная в равнобедренный треугольник KLM, касается боковой стороны KL в точке B, а основания ML — в точке A.
 Вторая окружность с центром O1 касается основания ML и продолжений боковых сторон.
Вторая окружность с центром O1 касается основания ML и продолжений боковых сторон.
а) Докажите, что треугольник OLO1 прямоугольный.
б) Найдите радиус второй окружности, если известно, что радиус первой равен 6 и AK = 16.
По вкладу «А» банк в течение трёх лет в конце каждого года увеличивает на 20 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивает на 21 % в течение каждого из первых двух лет. Найдите наименьшее целое число процентов за третий год по вкладу «Б», при котором за все три года этот вклад всё ещё останется выгоднее вклада «А».
Найдите все положительные значения , при каждом из которых система уравнений
имеет единственное решение.
Ответы
1 | 2 | 3 | 4 | |
1 | 6682,55 | 5444,25 | 6212,85 | 9415,35 |
2 | 40 | 50 | 40 | 30 |
3 | 4 | 2 | 5 | 3 |
4 | 0,12 | 0,5 | 0,19 | 0,25 |
5 | 5 | -4 | 1 | 6 |
6 | 26 | 9 | 20 | 3 |
7 | 4 | 3 | 2 | 3 |
8 | 64 | 27 | 125 | 49 |
9 | 4 | 7 | 81 | 4 |
10 | 0,7 | 0,18 | 0,08 | 0,9 |
11 | 6 | 6 | 8 | 6 |
12 | 0,5 | 1,5 | 1,5 | 1,5 |
13 | ||||
14 | ||||
15 | (-∞; -5)U(1; +∞) | (-∞; 6)U(11; +∞) | (-∞; 6)U(11; +∞) | (-∞; -5)U(1; +∞) |
16 | 24 | 24 | ||
17 | 12 | 19 | 19 | 12 |
18 | 3; +2 | 16; -3 | 16; -3 | 3; +2 |
Страница не найдена — Фонд Наффилда
Страница не найдена — Фонд Наффилда Страница, которую вы ищете, не может быть найдена. Пожалуйста, попробуйте использовать либо главное меню, либо поиск по сайту.
Пожалуйста, попробуйте использовать либо главное меню, либо поиск по сайту.
Поиск проектов, новостей, событий, событий
Поиск
Образование 655 Когнитивные и некогнитивные навыки 33 Учебная программа и выбор предметов 31 Ранние годы 166 Педагогические кадры 75 Оценка образования 29 Высшее образование 92 Язык и грамотность 79 Обучение на протяжении всей жизни 15Nuffield Research Placement 23Анализ математических наук 84Воспитание детей 75Педагогика 20После 16 лет образование и навыки 95Начальное образование 134Q-Step 26Эффективность школы 45Среднее образование 156Специальные образовательные потребности и инвалидность 57Системные проблемы образования 98Правосудие 235Доступ к правосудию 39Административное правосудие 26Гражданское правосудие 22Судебный опыт и доказательства 21Уголовное правосудие 24Домашнее насилие 5Равенство и права человека 17Семейное правосудие 134Частное право юридическое право 3Социальное право 12Юстиция по делам несовершеннолетних 23Социальное право 771Искусственное интеллект 3Вспомогательная смерть 1Дополненная реальность 0Преимущества 52Обязанности по уходу 27Сообщества и социальная сплоченность 63Стоимость жизни 21Страна рождения 24COVID-19327Прогнозирование преступности 2Данные для общественного блага 29Цифровой вред и дезинформация 33Цифровая интеграция и исключение 14Цифровые навыки 16Цифровое общество 48Инвалидность 14Экономика, государственные расходы и услуги 182Этническая принадлежность 48Семья и семейная динамика 117Гендер 43Глобальное неравенство в отношении здоровья 11Жилье 24Доход и богатство 116Неравенство и социальная мобильность 211Вопросы поколений 35Рынок труда 109Присмотр за детьми и нуждающиеся дети 74Психическое здоровье 91Нарушения опорно-двигательного аппарата 18Пенсии 16Физическое здоровье 50Бедность и уровень жизни 109Производительность и инновации.
Ознакомьтесь с нашими проектами
Правосудие | 2023 – 2025
Физические наказания и последствия для детей в Великобритании
Посмотреть проект
В процессе
Образование | 2023 – 2025
Целенаправленная и эффективная практическая работа по естествознанию начальных классов
Посмотреть проект
Благосостояние | 2023 – 2026
Широкие плечи: повышение налогов наверху
Посмотреть проект
Новый
Благосостояние | 2023 – 2025
Испытание PAW: осуществимость и приемлемость набора инструментов Pain-at-Work Toolkit
Посмотреть проект
В процессе
Образование | 2023 – 2024
Оптимизация и осуществимость родительской программы Triple P для дистанционного обучения
Новый
Благосостояние | 2023 – 2026
Продление трудовой жизни людям с заболеваниями опорно-двигательного аппарата
Посмотреть проект
Новый
Благосостояние | 2023 – 2025
Ювенильные ревматические заболевания: образование, профессиональная подготовка и трудоустройство
Посмотреть проект
Новый
Правосудие | 2023 – 2023
Создание и использование более качественных данных о правосудии
Посмотреть проект
Новый
Благосостояние | 2023 – 2025
Психологические, социальные и экономические последствия заболеваний опорно-двигательного аппарата
Посмотреть проект
Новый
Образование | 2023 – 2023
Кризис стоимости жизни: влияние на школы
Посмотреть проект
Благосостояние | 2023 – 2026
Широкие плечи: повышение налогов наверху
Образование | 2023 – 2024
Приоритеты образования на следующих всеобщих выборах
Посмотреть проект
Правосудие | 2023 – 2025
Физические наказания и последствия для детей в Великобритании
Посмотреть проект
В процессе
Образование | 2023 – 2024
Оптимизация и осуществимость родительской программы Triple P для дистанционного обучения
Посмотреть проект
В процессе
Образование | 2022 – 2024
Понимание использования прав на дошкольное образование
Посмотреть проект
Образование | 2023 – 2026
Переосмысление особых образовательных потребностей
Посмотреть проект
Новый
Благосостояние | 2023 – 2026
Артрит, работа и благополучие: исследование смешанных методов с рекомендациями по политике
Новый
Благосостояние | 2023 – 2025
Испытание PAW: осуществимость и приемлемость набора инструментов Pain-at-Work Toolkit
Посмотреть проект
В процессе
Образование | 2022 – 2024
Работа или учеба? Пол и переход от учебы к работе
Посмотреть проект
В процессе
Благосостояние | 2023 – 2025
Региональный индекс регенерации для отслеживания социально-экономического «повышения уровня»
Посмотреть проект
В процессе
Образование | 2019 – 2024
Пути развития после 16 лет: роль сверстников, семейное положение и ожидания
Посмотреть проект
В процессе
Благосостояние | 2023 – 2024
Разработка инклюзивной удаленной и гибридной работы для поддержки работников с ограниченными возможностями
Посмотреть проект
В процессе
Образование | 2023 – 2024
Влияние выявления потребностей в дополнительном обучении в Уэльсе
Посмотреть проект
В процессе
Образование | 2022 – 2024
Сравнение неравенства и результатов в образовании после 16 лет в Великобритании
Посмотреть проект
В процессе
Правосудие | 2022 – 2025
Изучение расового неравенства при отвлечении от системы ювенальной юстиции
Посмотреть проект
В процессе
Благосостояние | 2022 – 2024
Жизнь детей в переменчивых местах
Посмотреть проект
В процессе
Правосудие | 2022 – 2024
Административная справедливость в цифровом государстве всеобщего благосостояния
Посмотреть проект
Новый
Благосостояние | 2023 – 2025
Дистанционное наставничество по остеоартриту для малообеспеченных людей
Новый
Благосостояние | 2023 – 2025
Ювенильные ревматические заболевания: образование, профессиональная подготовка и трудоустройство
Посмотреть проект
Новый
Благосостояние | 2023 – 2026
Продление трудовой жизни людям с заболеваниями опорно-двигательного аппарата
Посмотреть проект
Новый
Образование | Благосостояние | 2022 – 2024
Изменение выбора школы для более справедливого обучения в Англии
Посмотреть проект
Новый
Образование | 2022 – 2023
Среднесрочное влияние пандемии COVID-19 на учащихся с SEND
Посмотреть проект
Сообщено
Правосудие | 2019 – 2021
Личное представление свидетельских показаний адвокатами и сторонами в процессе
Посмотреть проект
Сообщено
Образование | 2020 – 2022
COVID-19 и уход за детьми: местные последствия в Англии
Посмотреть проект
Сообщено
Правосудие | 2020 – 2022
Когда свадьба не брак? Изучение не имеющих юридической силы церемоний
Посмотреть проект
Сообщено
Образование | 2020 – 2022
Этические принципы, лежащие в основе совместного производства с молодежью
Посмотреть проект
Сообщено
Образование | 2020 – 2021
Меры по смягчению последствий COVID-19: предоставление образования и доступ к специальным школам
Посмотреть проект
Сообщено
Образование | 2020 – 2022
Могут ли математические приложения повысить ценность обучения?
Посмотреть проект
Сообщено
Благосостояние | 2020 – 2021
Как кризис COVID-19 влияет на продовольственную безопасность
Посмотреть проект
Сообщено
Образование | 2020 – 2021
Влияние COVID-19 на общеобразовательные школы Англии
Посмотреть проект
Сообщено
Образование | Благосостояние | 2020 – 2022
Взросление в условиях COVID-19
Посмотреть проект
Увидеть всеПоследние
Последние
Неправильные треугольники: закон косинусов
Цели обучения
В этом разделе вы:
- Используйте закон косинусов для решения косоугольных треугольников.

- Решение прикладных задач с использованием закона косинусов.
- Используйте формулу Герона, чтобы найти площадь треугольника.
Предположим, что лодка выходит из порта, проходит 10 миль, поворачивает на 20 градусов и проходит еще 8 миль, как показано на (рис.). Как далеко от порта лодка?
. -сторона) треугольника, или, когда известны все три стороны, но не известны углы, треугольник SSS (сторона-сторона-сторона). В этом разделе мы исследуем еще один инструмент для решения косоугольных треугольников, описываемых этими двумя последними случаями.
Использование закона косинусов для решения косоугольных треугольников
Инструмент, который нам понадобится для решения проблемы расстояния лодки от порта, — это Закон косинусов , который определяет взаимосвязь между измерениями углов и длинами сторон в косоугольных треугольниках. Три формулы составляют закон косинусов. На первый взгляд формулы могут показаться сложными, поскольку они включают много переменных. Однако, как только закономерность понята, с законом косинусов работать легче, чем с большинством формул на этом математическом уровне.
Однако, как только закономерность понята, с законом косинусов работать легче, чем с большинством формул на этом математическом уровне.
Понимание того, как выводится закон косинусов, будет полезно при использовании формул. Вывод начинается с обобщенной теоремы Пифагора, которая является расширением теоремы Пифагора на непрямоугольные треугольники. Вот как это работает: произвольный непрямоугольный треугольник[латекс]\,ABC\,[/латекс] помещается в координатную плоскость с вершиной[латекс]\,А\,[/латекс] в начале координат, сторона[ латекс]\,с\,[/латекс], нарисованный вдоль оси x , и вершина [латекс]\,С\,[/латекс], расположенная в некоторой точке[латекс]\,\слева(х,у\ справа)\,[/latex] в плоскости, как показано на (рис.). Как правило, треугольники существуют где угодно на плоскости, но для этого объяснения мы поместим треугольник, как указано выше.
Рисунок 2.
Мы можем опустить перпендикуляр из [латекс]\,С\,[/латекс] на ось x- (это высота или высота). Вспоминая основные тригонометрические тождества, мы знаем, что
Вспоминая основные тригонометрические тождества, мы знаем, что
[латекс]\mathrm{cos}\,\theta =\frac{x\text{(смежный)}}{b\text{(гипотенуза)}}\text{ и }\mathrm{sin}\,\theta =\frac{y\text{(наоборот)}}{b\text{(гипотенуза)}}[/latex]
С точки зрения[latex]\,\theta , \text{ }x=b\mathrm{cos}\,\theta \,[/latex]and[latex]y=b\mathrm{sin}\,\theta .\text{ }[/latex]The[latex] ]\,\left(x,y\right)\,[/latex]точка, расположенная в [latex]\,C\,[/latex]имеет координаты [latex]\,\left(b\mathrm{cos}\ ,\theta ,\,\,b\mathrm{sin}\,\theta \right).\,[/latex]Используя сторону[latex]\,\left(x-c\right)\,[/latex] как один катет прямоугольного треугольника и [латекс]\,y\,[/латекс]в качестве второго катета, мы можем найти длину гипотенузы[латекс]\,а\,[/латекс]используя теорему Пифагора. Таким образом, 9{2}-2bc\mathrm{cos}\,\theta \hfill & \hfill & \hfill & \hfill & \hfill & \hfill \end{array}[/latex]
Полученная формула является одной из трех уравнения закона косинусов. Аналогично находятся остальные уравнения.
Имейте в виду, что всегда полезно делать набросок треугольника при вычислении углов или сторон. В реальном сценарии попробуйте нарисовать схему ситуации. По мере появления дополнительной информации диаграмму, возможно, придется изменить. Внесите эти изменения в диаграмму, и, в конце концов, проблему будет легче решить.
Закон косинусов
Закон косинусов гласит, что квадрат любой стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение двух других сторон и косинуса прилежащего угла . Для треугольников, обозначенных как на (Рисунок), с углами [латекс]\,\альфа,\бета,[/латекс] и [латекс]\,\гамма,[/латекс] и противоположными соответствующими сторонами [латекс]\,а, b,[/latex] и[latex]\,c,\,[/latex] соответственно, закон косинусов задается в виде трех уравнений. 9{2}}{2ab}\hfill \end{array}\hfill \end{array}[/latex]
Имея две стороны и угол между ними (SAS), найдите размеры оставшейся стороны и углы треугольник.
- Нарисуйте треугольник.
 Найдите величины известных сторон и углов. Используйте переменные для представления мер неизвестных сторон и углов.
Найдите величины известных сторон и углов. Используйте переменные для представления мер неизвестных сторон и углов. - Примените закон косинусов, чтобы найти длину неизвестной стороны или угла.
- Примените закон синусов или косинусов, чтобы найти величину второго угла.
- Вычислите величину остаточного угла.
Нахождение неизвестной стороны и углов треугольника SAS
Найдите неизвестную сторону и углы треугольника на (рис.).
Рис. 4.
Показать решение
Попробуйте
Найдите недостающую сторону и углы данного треугольника:[латекс]\,\альфа =30°,\,\,b=12,\,\,с=24.[/латекс]
Показать решение
Нахождение угла SSS-треугольника
Найти угол[латекс]\,\альфа \,[/латекс]для заданного треугольника, если сторона[латекс]\,а=20,\,[/латекс]сторона [латекс]\,b=25,\,[/латекс]и сторона[латекс]\,с=18.[/латекс]
Показать решение
Анализ
Поскольку арккосинус может возвращать любой угол от 0 до 180 градусов, при использовании этого метода не будет неоднозначных случаев.
Попробуйте
Учитывая [латекс]\,a=5,b=7,\,[/латекс] и [латекс]\,с=10,\,[/латекс] найдите недостающие углы.
Показать решение
Решение прикладных задач с использованием закона косинусов
Точно так же, как закон синусов обеспечивает соответствующие уравнения для решения ряда приложений, закон косинусов применим к ситуациям, в которых данные соответствуют косинусным моделям. Мы можем увидеть их в области навигации, геодезии, астрономии и геометрии, и это лишь некоторые из них.
Использование закона косинусов для решения задачи связи
На многих сотовых телефонах с GPS приблизительное местоположение может быть указано до получения сигнала GPS. Это достигается с помощью процесса, называемого триангуляцией, который работает с использованием расстояний от двух известных точек. Предположим, что в радиусе действия сотового телефона есть две вышки сотовой связи. Две башни расположены на расстоянии 6000 футов друг от друга вдоль прямого шоссе, идущего с востока на запад, а сотовый телефон находится к северу от шоссе. Основываясь на задержке сигнала, можно определить, что сигнал находится на расстоянии 5050 футов от первой башни и 2420 футов от второй башни. Определите положение сотового телефона к северу и востоку от первой башни и определите, насколько далеко он находится от шоссе.
Основываясь на задержке сигнала, можно определить, что сигнал находится на расстоянии 5050 футов от первой башни и 2420 футов от второй башни. Определите положение сотового телефона к северу и востоку от первой башни и определите, насколько далеко он находится от шоссе.
Показать решение
Расчет пройденного расстояния с использованием треугольника SAS
Возвращаясь к нашей задаче в начале этого раздела, предположим, что лодка выходит из порта, проходит 10 миль, поворачивает на 20 градусов и проходит еще 8 миль. Как далеко от порта лодка? Диаграмма повторяется здесь на (Рисунок).
Рис. 8.
Показать решение
Использование формулы Герона для нахождения площади треугольника
Мы уже научились находить площадь косоугольного треугольника, зная две стороны и угол. Мы также знаем формулу нахождения площади треугольника через основание и высоту. Однако, когда мы знаем три стороны, мы можем использовать формулу Герона вместо нахождения высоты. Герон Александрийский был геометром, жившим в первом веке нашей эры. Он открыл формулу для нахождения площади косоугольного треугольника, когда известны три стороны.
Герон Александрийский был геометром, жившим в первом веке нашей эры. Он открыл формулу для нахождения площади косоугольного треугольника, когда известны три стороны.
Формула Герона
Формула Герона находит площадь косоугольного треугольника, в котором стороны [латекс]\,а,б\текст{,}[/латекс]и[латекс]\,с\,[/латекс]известны.
[латекс]\текст{Область}=\sqrt{s\left(s-a\right)\left(s-b\right)\left(s-c\right)}[/latex]
где [латекс]\,s =\frac{\left(a+b+c\right)}{2}\,[/latex] — половина периметра треугольника, иногда называемого полупериметром.
Использование формулы Герона для нахождения площади заданного треугольника
Найдите площадь треугольника на (рис.) с помощью формулы Герона.
Рис. 9.
Показать решение
Попробуйте
Используйте формулу Герона, чтобы найти площадь треугольника со сторонами длиной [латекс]\,a=29,7\,\text{ft},b=42,3\,\text{ft},\,[ /latex]and[latex]\,c=38. 4\,\text{ft}.[/latex]
4\,\text{ft}.[/latex]
Показать решение
Применение формулы Герона к реальной задаче
Городской застройщик из Чикаго хочет построить здание, состоящее из лофтов для художников, на треугольном участке, граничащем с Раш-стрит, Вабаш-авеню и Пирсон-стрит. Фасад по Раш-стрит составляет примерно 62,4 метра, по Вабаш-авеню — примерно 43,5 метра, а по Пирсон-стрит — примерно 34,1 метра. Сколько квадратных метров доступно застройщику? См. (Рисунок) вид на городскую собственность.
Рисунок 10.
Показать решение
Попробуйте
Найдите площадь заданного треугольника[латекс]\,а=4,38\,\текст{фут}\,b=3,79\,\текст{фут,}\,[/латекс]и[ латекс]\,c=5.22\,\text{ft}\text{.}[/latex]
Показать решение
Доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с законом косинусов.
- Закон косинусов
- Закон косинусов: приложения
- Закон косинусов: Приложения 2 9{2}-2abcos\,\gamma\hfill\end{массив}[/latex]
- Закон косинусов определяет взаимосвязь между измерениями углов и длинами сторон в косоугольных треугольниках.

- Обобщенная теорема Пифагора — это закон косинусов для двух случаев косоугольных треугольников: SAS и SSS. Отбрасывание воображаемого перпендикуляра разбивает косой треугольник на два прямоугольных треугольника или образует один прямоугольный треугольник, что позволяет связать стороны и вычислить измерения. См. (Рисунок) и (Рисунок).
- Закон косинусов полезен для многих типов прикладных задач. Первым шагом в решении таких задач обычно является набросок представленной проблемы. Если предоставленная информация соответствует одной из трех моделей (трем уравнениям), примените закон косинусов, чтобы найти решение. См. (Рисунок) и (Рисунок).
- Формула Герона позволяет вычислить площадь в косоугольных треугольниках. Все три стороны должны быть известны, чтобы применить формулу Герона. См. (Рисунок) и См. (Рисунок).
Ключевые понятия
Упражнения по разделам
Вербальные
Если вы ищете недостающую сторону треугольника, что вам нужно знать при использовании закона косинусов?
Показать решение
Если вы ищете недостающий угол треугольника, что вам нужно знать при использовании закона косинусов?
Объясните, что представляет собой [латекс]\,s\,[/латекс] в формуле Герона.
Показать решение
Объясните связь между теоремой Пифагора и законом косинусов.
Когда следует использовать закон косинусов вместо теоремы Пифагора?
Показать решение
Алгебраический
Для следующих упражнений предположим, что [латекс]\,\альфа \,[/латекс] является противоположной стороной [латекс]\,а,\бета \,[/латекс] является противоположной стороной [латекс]\, b,\,[/latex] и [латекс]\,\gamma \,[/latex] является противоположной стороной[латекс]\,c.\,[/latex]Если возможно, решите каждый треугольник относительно неизвестной стороны. Округлите до десятых.
[латекс]\gamma =41,2°,a=2,49,b=3,13[/латекс]
[латекс]\альфа =120°,b=6,c=7[/латекс]
Показать решение
[латекс]\бета=58,7°,а=10,6,с=15,7[/латекс]
[латекс]\гамма=115°,а=18,b=23[/латекс]
Показать решение
[латекс]\alpha =119°,a=26,b=14[/латекс]
[латекс]\gamma =113°,b=10,c=32[/латекс]
Показать решение
[латекс]\бета =67°,а=49,b=38[/латекс]
[латекс]\альфа =43,1°,а=184,2,b=242,8[/латекс]
Показать решение
[латекс]\альфа =36,6°,а=186,2,b=242,2[/латекс] 9{}[/latex]
Показать решение
В следующих упражнениях используйте закон косинусов, чтобы найти недостающий угол косоугольного треугольника. Округлите до десятых.
Округлите до десятых.
[латекс]\,a=42,b=19,c=30;\,[/latex]найти угол[латекс]\,A.[/latex]
[латекс]\,a=14,\ text{ }b=13,\text{ }c=20;\,[/latex]найти угол[latex]\,C.[/latex]
Показать решение
[латекс]\,a=16,b=31,c=20;\,[/latex]найти угол[латекс]\,B.[/latex]
[латекс]\,a=13,\ ,b=22,\,c=28;\,[/latex]найти угол[latex]\,A.[/latex]
Показать решение
[латекс]a=108,\,b=132,\,c=160;\,[/латекс]найти угол[латекс]\,C.\,[/латекс]
Для следующих упражнений решите треугольник. Округлите до десятых.
[латекс]A=35°,b=8,c=11[/латекс]
Показать решение
[латекс]B=88°,a=4,4,c=5,2[/латекс]
[латекс]C=121°,a=21,b=37[/латекс]
Показать решение
[латекс]a=13,b=11,c=15[/латекс]
[латекс]a=3.1,b=3.5,c=5[/латекс]
Показать решение
[латекс]a=51,b=25,c=29[/латекс]
В следующих упражнениях используйте формулу Герона, чтобы найти площадь треугольника.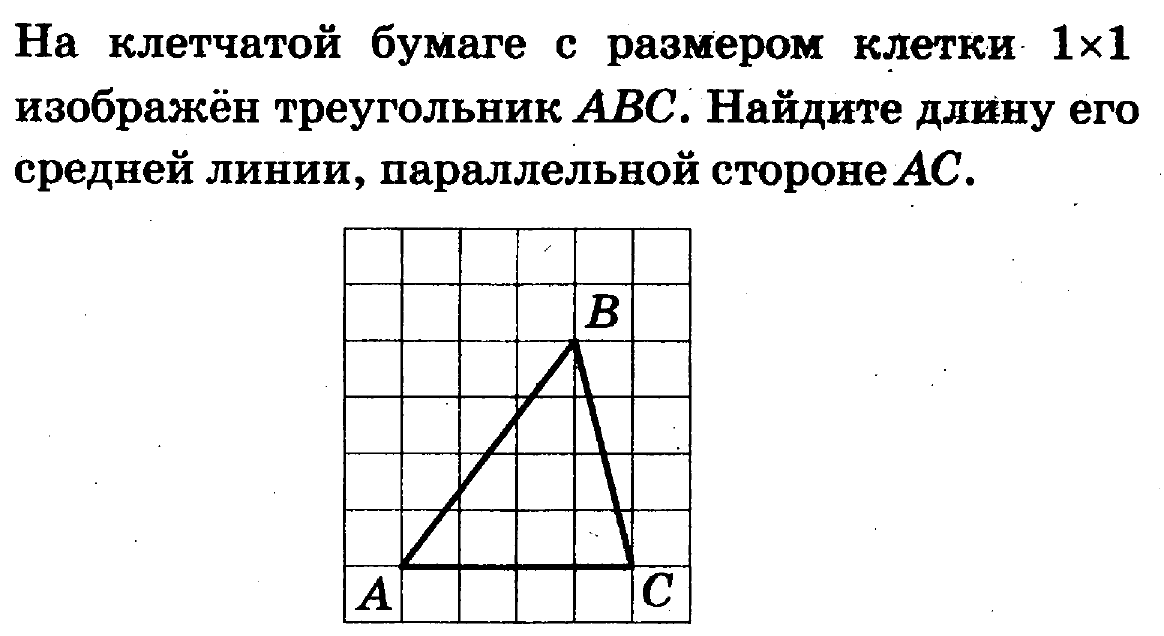 Округлить до сотых.
Округлить до сотых.
Найдите площадь треугольника со сторонами 18 дюймов, 21 дюйм и 32 дюйма. Округлите до десятых.
Показать решение
Найдите площадь треугольника со сторонами 20 см, 26 см и 37 см. Округлите до десятых.
[латекс]a=\frac{1}{2}\,\text{m},b=\frac{1}{3}\,\text{m},c=\frac{1}{4 }\,\текст{м}[/латекс]
Показать решение
[латекс]a=12,4\текст{ футов},\текст{ }b=13,7\текст{ футов},\текст{ }c=20,2\текст{ футов}[/латекс]
[латекс]a= 1.6\text{ yd},\text{ }b=2.6\text{ yd},\text{ }c=4.1\text{ yd}[/latex]
Показать решение
Графический
Для следующих упражнений найдите длину стороны [латекс]х.[/латекс] Округлите до десятых.
Показать решение
Показать решение
Показать решение
Для следующих упражнений найдите измерение угла[латекс]\,А. [/латекс]
[/латекс]
Показать решение
Показать решение
Найдите величину каждого угла в треугольнике, показанном на (рис.). Округлите до десятых.
Рис. 11.
В следующих упражнениях найдите неизвестную сторону. Округлите до десятых.
Показать решение
Показать решение
Для следующих упражнений найдите площадь треугольника. Округлить до сотых.
Показать решение
Показать решение
Показать решение
Удлинители
Параллелограмм имеет длину сторон 16 единиц и 10 единиц. Меньшая диагональ равна 12 единицам. Найдите длину большей диагонали.
Стороны параллелограмма 11 футов и 17 футов. Большая диагональ составляет 22 фута. Найдите длину меньшей диагонали.
Показать решение
Стороны параллелограмма равны 28 см и 40 см. Размер большего угла равен 100°. Найдите длину меньшей диагонали. 9{2}=25+36-60\mathrm{cos}\left(52\right)\,[/latex] представляет отношение трех сторон треугольника и косинуса угла.
Нарисуйте треугольник.
Показать решение
Найдите длину третьей стороны.
Для следующих упражнений найдите площадь треугольника.
Показать решение
Показать решение
Реальные приложения
Геодезист провел измерения, показанные на (Рисунок). Найдите расстояние через озеро. Ответы округлить до десятых.
Рисунок 14.
Спутник вычисляет расстояния и углы, показанные на (Рисунок) (не в масштабе). Найдите расстояние между двумя городами. Ответы округлить до десятых.
Рис. 15.
Показать решение
Самолет пролетает 220 миль с курсом 40°, а затем пролетает 180 миль с курсом 170°. На каком расстоянии находится самолет от начальной точки и по какому курсу? Ответы округлить до десятых.
На каком расстоянии находится самолет от начальной точки и по какому курсу? Ответы округлить до десятых.
113-футовая башня расположена на холме под углом 34° к горизонтали, как показано на (Рисунок). Растяжка должна быть прикреплена к вершине башни и закреплена в точке 9.8 футов в гору от основания башни. Найдите необходимую длину провода.
Рис. 16.
Показать решение
Два корабля вышли из порта одновременно. Один корабль шел со скоростью 18 миль в час при курсе 320°. Другой корабль двигался со скоростью 22 мили в час под курсом 194°. Найдите расстояние между двумя кораблями через 10 часов пути.
На графике (рисунок) показаны две лодки, отходящие в одно и то же время от одного и того же причала. Первая лодка движется со скоростью 18 миль в час при курсе 327°, а вторая лодка — со скоростью 4 мили в час при курсе 60°. Найдите расстояние между двумя лодками через 2 часа.
Рис. 17.
Показать решение
Треугольный бассейн имеет длину 40 футов с одной стороны и 65 футов с другой стороны. Эти стороны образуют угол, равный 50°. Какова длина третьей стороны (с точностью до десятых)?
Эти стороны образуют угол, равный 50°. Какова длина третьей стороны (с точностью до десятых)?
Пилот летит по прямой 1 час 30 мин. Затем он корректирует курс, направляясь на 10° вправо от своего первоначального курса, и летит 2 часа в новом направлении. Если она поддерживает постоянную скорость 680 миль в час, как далеко она находится от своего начального положения?
Показать решение
Лос-Анджелес находится в 1744 милях от Чикаго, Чикаго — в 714 милях от Нью-Йорка, а Нью-Йорк — в 2451 миле от Лос-Анджелеса. Нарисуйте треугольник, соединяющий эти три города, и найдите углы треугольника.
Филадельфия находится в 140 милях от Вашингтона, округ Колумбия, Вашингтон, округ Колумбия, — в 442 милях от Бостона, а Бостон — в 315 милях от Филадельфии. Нарисуйте треугольник, соединяющий эти три города, и найдите углы треугольника.
Показать решение
Два самолета вылетели из одного аэропорта в одно и то же время. Один летит на 20° к востоку от севера со скоростью 500 миль в час. Второй летит под углом 30° к востоку от юга со скоростью 600 миль в час. На каком расстоянии будут самолеты через 2 часа?
Один летит на 20° к востоку от севера со скоростью 500 миль в час. Второй летит под углом 30° к востоку от юга со скоростью 600 миль в час. На каком расстоянии будут самолеты через 2 часа?
Два самолета взлетают в разные стороны. Один движется со скоростью 300 миль в час строго на запад, а другой — на 25° к северу от запада со скоростью 420 миль в час. Через 90 минут на каком расстоянии они будут друг от друга, если предположить, что летят на одной высоте?
Показать решение
Параллелограмм имеет стороны длины 15,4 единицы и 9.8 единиц. Его площадь составляет 72,9 кв. Найдите длину большей диагонали.
Четыре последовательные стороны четырехугольника имеют длину 4,5 см, 7,9 см, 9,4 см и 12,9 см. Угол между двумя наименьшими сторонами равен 117°. Чему равна площадь этого четырехугольника?
Показать решение
Четыре последовательные стороны четырехугольника имеют длину 5,7 см, 7,2 см, 9,4 см и 12,8 см.

 Считайте, что 1 фут равен 30,5 см.
Считайте, что 1 фут равен 30,5 см.
 Обе трубы наполняют этот же резервуар за 4 минуты. За сколько минут наполняет этот резервуар одна вторая труба?
Обе трубы наполняют этот же резервуар за 4 минуты. За сколько минут наполняет этот резервуар одна вторая труба?
 Выразите высоту полета в метрах. Считайте, что 1 фут равен 30,5 см.
Выразите высоту полета в метрах. Считайте, что 1 фут равен 30,5 см. Одна из его диагоналей равна 6. Найдите другую диагональ.
Одна из его диагоналей равна 6. Найдите другую диагональ. Обе трубы наполняют этот же резервуар за 5 минут. За сколько минут наполняет этот резервуар одна вторая труба?
Обе трубы наполняют этот же резервуар за 5 минут. За сколько минут наполняет этот резервуар одна вторая труба? Вторая окружность с центром O1 касается основания ML и продолжений боковых сторон.
Вторая окружность с центром O1 касается основания ML и продолжений боковых сторон. Выразите высоту полета в метрах. Считайте, что 1 фут равен 30,5 см.
Выразите высоту полета в метрах. Считайте, что 1 фут равен 30,5 см. Одна из его диагоналей равна 12. Найдите другую диагональ.
Одна из его диагоналей равна 12. Найдите другую диагональ. За сколько минут наполняет этот резервуар одна вторая труба?
За сколько минут наполняет этот резервуар одна вторая труба?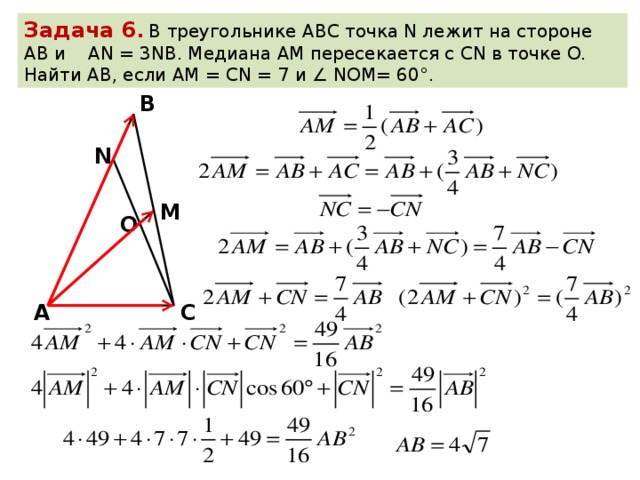
 Выразите высоту полета в метрах. Считайте, что 1 фут равен 30,5 см.
Выразите высоту полета в метрах. Считайте, что 1 фут равен 30,5 см.
 Обе трубы наполняют этот же резервуар за 6 минут. За сколько минут наполняет этот резервуар одна вторая труба?
Обе трубы наполняют этот же резервуар за 6 минут. За сколько минут наполняет этот резервуар одна вторая труба? Вторая окружность с центром O1 касается основания ML и продолжений боковых сторон.
Вторая окружность с центром O1 касается основания ML и продолжений боковых сторон.
 Найдите величины известных сторон и углов. Используйте переменные для представления мер неизвестных сторон и углов.
Найдите величины известных сторон и углов. Используйте переменные для представления мер неизвестных сторон и углов.
Leave A Comment