19. Найдите четырёхзначное число, которое в 11 раз меньше куба некоторого натурального… Ященко И. В. ЕГЭ-2017 Математика ГДЗ. Вариант 7.
19. Найдите четырёхзначное число, которое в 11 раз меньше куба некоторого натурального… Ященко И. В. ЕГЭ-2017 Математика ГДЗ. Вариант 7. – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
19.
Найдите четырёхзначное число, которое в 11 раз меньше куба некоторого натурального числа. В ответе укажите какое-нибудь одно такое число.
ответы
ответ
3267; 7744
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
ГИА
ОГЭ
Экзамены
Выпускной
похожие вопросы 5
ГДЗ. Математика. Базовый уровень ЕГЭ — 2017. Вар.№22. Зад.№1.Под руководством Ященко. Помогите найти значение выражения.
Здравствуйте! Помогите найти значение выражения:
(Подробнее…)
ГДЗЭкзаменыМатематикаЯщенко И.В.
Определите расстояние № 23 ГДЗ Математика 6 класс Никольский С.М.
Расстояние между двумя городами равно 200 км. Определите
расстояние между изображениями этих городов на карте, (Подробнее. ..)
..)
ГДЗМатематика6 классНикольский С.М.
Определите длину № 25 ГДЗ Математика 6 класс Никольский С.М.
План комнаты имеет вид прямоугольника со сторонами 40 мм
и 31 мм. Определите длину и ширину комнаты, если численный
ГДЗМатематика6 классНикольский С.М.
Подскажите, могу ли я рассчитывать на пересдачу, если не смогла сдать ЕГЭ по математике профильного уровня?
Если я не сдала ЕГЭ по математике профильного уровня, будет ли пересдача? (Подробнее…)
ШколаЕГЭНовостиЭкзамены
Задание 8 Текст. Текст и его план. Русский язык.4 класс. Канакина В.П., Горецкий В.Г. ГДЗ
Приветствую, как ответить на вопросы к заданию?
Прочитайте.
Первая вахта (Подробнее…)
ГДЗРусский языкКанакина В.П.Горецкий В.Г.4 класс
Задание №19 (1-30) из ЕГЭ по математике базовый уровень с решением (2022)
 Найдите семизначное натуральное число, которое записывается только цифрами 1 и 2 и делится на 72. В ответе укажите какое-нибудь такое число.
Найдите семизначное натуральное число, которое записывается только цифрами 1 и 2 и делится на 72. В ответе укажите какое-нибудь такое число.2. Найдите четырёхзначное число, которое в 4 раза меньше четвёртой степени некоторого натурального числа. В ответе укажите какое–нибудь одно такое число.
3. Найдите трёхзначное число А, обладающее двумя свойствами:
1) сумма цифр числа А делится на 10;
2) сумма цифр числа (А + 8) делится на 10.
В ответе укажите ровно одно такое число.
4. Найдите четырёхзначное число, большее 6000, но меньшее 8000, которое делится на 18 и каждая следующая цифра которого меньше предыдущей.
В ответе укажите какое-нибудь такое число.
5. Найдите четырёхзначное число, кратное 125, все цифры которого различны и нечётны. В ответе укажите какое-нибудь одно такое число.
6. Найдите четырехзначное число кратное 55 все цифры которого различны и четны. В ответе укажите какое-нибудь такое число
7. Найдите трёхзначное натуральное число, которое при делении на 8 и на 10 даёт равные ненулевые остатки и первая цифра справа в записи которого является суммой двух других цифр. В ответе укажите какое-нибудь такое число.
В ответе укажите какое-нибудь такое число.
8. Найдите трехзначное число, кратное 70, все цифры которого различны, а сумма квадратов цифр делится на 5, но не делится на 25. В ответе укажите какое-нибудь одно такое число.
9. Найдите трехзначное число, кратное 40, все цифры которого различны, а сумма квадратов цифр делится на 4, но не делится на 16. В ответе укажите какое-нибудь одно такое число.
10. Найдите трехзначное число, кратное 25, все цифры которого различны, а сумма квадратов цифр делится на 3, но не делится на 9. В ответе укажите какое-нибудь одно такое число.
11. Найдите трёхзначное число А, обладающее двумя свойствами:
1) сумма цифр числа А делится на 11;
2) сумма цифр числа (А + 7) делится на 11.
В ответе укажите какое-нибудь одно такое число.
12. Найдите трёхзначное число А, обладающее тремя свойствами:
1) сумма цифр числа А делится на 5;
2) сумма цифр числа (А +3) делится на 5;
3) число А больше 700 и меньше 900
В ответе укажите какое-нибудь одно такое число.
13. Найдите четырёхзначное число, большее 6000, но меньшее 7000, которое делится на 12 и каждая следующая цифра которого меньше предыдущей.
В ответе укажите какое-нибудь такое число.
14. Найдите трёхзначное натуральное число, большее 500, которое при делении на 8 и на 5 даёт равные ненулевые остатки и средняя цифра которого является средним арифметическим крайних цифр. В ответе укажите какое-нибудь одно такое число.
15. Найдите трёхзначное натуральное число, которое при делении на 4 и на 15 даёт равные ненулевые остатки и первая цифра справа в записи которого является средним арифметическим двух других цифр. В ответе укажите какое-нибудь одно такое число.
16. Найдите трёхзначное натуральное число, меньшее 500, которое при делении на 5 и на 6 даёт равные ненулевые остатки и первая цифра справа в записи которого является средним арифметическим двух других цифр. В ответе укажите какое-нибудь одно такое число.
17. Найдите трёхзначное натуральное число, большее 400, которое при делении и на 6, и на 5 даёт равные ненулевые остатки и первая цифра в записи которого является средним арифметическим двух других цифр.
18. На 6 карточках написаны цифры 1; 2; 2; 3; 5; 7 (по одной цифре на каждой карточке). В выражении □ + □□ + □□□ вместо каждого квадратика положили карточку из набора. Оказалось, что полученная сумма делится на 20. Найдите эту сумму. В ответе укажите какое-нибудь одно такое число.
19. Найдите четырёхзначное число, которое в 11 раз меньше куба некоторого натурального числа. В ответе укажите какое–нибудь одно такое число.
20. На 6 карточках написаны цифры 1; 2; 3; 3; 4; 7 (по одной цифре на каждой карточке). В выражении □ + □□ + □□□ вместо каждого квадратика положили карточку из набора. Оказалось, что полученная сумма делится на 20. Найдите эту сумму. В ответе укажите какое-нибудь одно такое число.
21. Найдите четырёхзначное число, которое в 3 раза меньше четвертой степени некоторого натурального числа. В ответе укажите какое–нибудь одно такое число.
22. Найдите четырёхзначное натуральное число, большее 3000, но меньшее 3200, которое делится на каждую свою цифру и все цифры которого различны и не равны 0.
23. Найдите трехзначное натуральное число, большее 400, но меньшее 650, которое делится на каждую свою цифру, и все цифры которого различны и не равны нулю. В ответе укажите какое-нибудь одно такое число.
24. Найдите четырёхзначное натуральное число, большее 3850 но меньшее 4150, которое делится на каждую свою цифру и все цифры которого различны и не равны 0. В ответе укажите какое–нибудь одно такое число.
25. Найдите трехзначное натуральное число, большее 800, которое делится на каждую свою цифру, и все цифры которого различны и не равны нулю. В ответе укажите какое-нибудь одно такое число.
26. Найдите трехзначное натуральное число, большее 1640, но меньшее 1930, которое делится на каждую свою цифру, и все цифры которого различны и не равны нулю. В ответе укажите какое-нибудь одно такое число.
27. Цифры нечетного четырехзначного числа ,кратного 5,записали в обратном порядке и получили второе четырехзначное число. Затем из первого числа вычли второе и получили 1638.Приведите ровно один пример такого числа.
Затем из первого числа вычли второе и получили 1638.Приведите ровно один пример такого числа.
28. Четырехзначное число А состоит из цифр 0; 1; 5; 6, а четырехзначное число В – из цифр 0; 1; 2; 3. Известно, что число В вдвое больше числа А. Найдите число А. В ответе укажите какое-нибудь такое число.
29. Найдите четырехзначное число, кратное 33, все цифры которого различны и нечетны. В ответе укажите какое-нибудь такое число.
30. Четырехзначное число А состоит из цифр 1; 2; 6; 7, а четырехзначное число В – из цифр 2; 3; 4; 5. Известно, что число В вдвое больше числа А. Найдите число А. В ответе укажите какое-нибудь такое число, большее 1500.
Math Tricks — Behavioral Sciences Research Core
Page MenuЭта веб-страница посвящена
невероятно умной
идее о том, что математика может быть интересной!
Попробуйте эти трюки:
- Easy Magic Addition
- Магический квадрат #15
- Магический квадрат #34
- Создайте свой собственный магический квадрат
- Перевернутый магический квадрат
- Антимагический квадрат
- Выиграйте ставки с этим квадратом
- Магический фокус с картами
- Калькулятор молний
- Таблицы забавных чисел
- Знаете ли вы.
 ..?
..? - Уловка на этот год
- Где нить?
- Огромный магический квадрат
Вот несколько интересных ссылок:
- Список книг по хитрой математике для чтения, большинство из которых я использовал для этого сайта.
- Узнайте об оригинальном компьютере: The Abacus (http://www.ee.ryerson.ca:8080/~elf/abacus/)
- Сыграйте в математическую игру (http://dev.eyecon.com/marcia) — для одного или двух игроков. (Если вы используете Netscape, Не прокручивать страницу вниз, пока загружается .
- Играйте в Shoot Balls (http://www.fi.uu.nl/wisweb/en/applets/bollen/Welcome.html).
- Играйте в Flippo 24 (http://www.fi.uu.nl/wisweb/en/applets/bollen/Welcome.html).
- Проверьте свои знания таблицы умножения (http://www.fi.uu.nl/wisweb/en/applets/tafels/Welcome.html)
- Попробуйте свои силы в оценке (http://www.fi.uu.nl/wisweb/en/applets/bollen/Welcome.html).
- Исследуйте геометрию в увлекательной интерактивной форме.

- Попробуйте загадку «Ханойская башня» (http://www.eng.auburn.edu/~fwushan/Hanoi1.html).
- Посмотрите, что такое Spriographis (http://www.mainstrike.com/mstservices/handy/Spiro/).
- Посмотрите, что такое набор Мандельброта (http://www.franceway.com/java/fractale/mandel_b.htm).
- Если вы хотите больше задач по математике , попробуйте новый сайт PBS MATHLINE MATH CHALLENGES. Попробуйте, вам понравится. (Но помните, что мы были первыми.)
Волшебный трюк №1
Удивите пеонов этим. Все просто. Это эффективно. Он получает их каждый раз.
- Спросите свою оценку выберите три (3) разных номеров от 1 до 9.
- Скажите ему или ей (или ей или ему) записать три числа рядом друг с другом, самое большое в начале и наименьшее в конце, чтобы сформировать одно трехзначное число. Скажите ему/ей, чтобы он не говорил вам, что это за цифры.
- Затем попросите ее или его составить новое трехзначное число, переставив цифры местами, поставив наименьшее первым, а самое большое последним.
 И напишите это число прямо под первым числом.
И напишите это число прямо под первым числом. - Теперь попросите его или ее вычесть меньшее (и меньшее) трехзначное число из старшего (и большего) трехзначного числа. Скажи им, чтобы они не говорили тебе, каков результат.
- Теперь у вас есть выбор оберток:
- Попросите вашего друга сложить три цифры числа, которое получается в результате вычитания меньшего из большего трехзначного числа. Затем удивите его или ее, сказав, какова сумма этих трех чисел. Сумма трехзначного ответа всегда будет 18!
- Скажите своему другу, что если он или она скажет вам, какая первая ИЛИ последняя цифра ответа, вы скажете ей или ему, какие две другие цифры. Это возможно, потому что средняя цифра всегда будет 9, а сумма двух других цифр всегда будет 9! Таким образом, чтобы получить цифру, отличную от средней (которая равна 9) и отличную от цифры, которую сказал вам ваш друг, просто вычтите цифру, которую ваш друг сказал вам, из 9, и это будет неизвестная цифра.

Вернуться к началу
Магический квадрат #15
Каждая строка и столбец в этом магическом квадрате в сумме дают 15. Так сделайте обе диагонали!
| 8 | 3 | 4 |
| 1 | 5 | 9 |
| 6 | 7 | 2 |
Вернуться к началу
Магический квадрат #34
Каждая строка и столбец в этом магическом квадрате в сумме дают 34. Так сделайте обе диагонали!
| 1 | 15 | 14 | 4 |
| 12 | 6 | 7 | 9 |
| 8 | 10 | 11 | 5 |
| 13 | 3 | 2 | 16 |
Вернуться к началу
Рецепт собственного магического квадрата 3 X 3
Вот рецепт изготовления собственного магического квадрата 3 X 3. Этот рецепт и оба вышеупомянутых магических квадрата взяты из одной чертовски замечательной книги под названием 9.0004 Математика для миллиона , Ланселот Хогбен, опубликовано Norton and Company. Я очень рекомендую это. Вам совсем не нужно много математики, чтобы погрузиться в приключения чисел, описанные в этой классической книге.
Этот рецепт и оба вышеупомянутых магических квадрата взяты из одной чертовски замечательной книги под названием 9.0004 Математика для миллиона , Ланселот Хогбен, опубликовано Norton and Company. Я очень рекомендую это. Вам совсем не нужно много математики, чтобы погрузиться в приключения чисел, описанные в этой классической книге.
Некоторые необходимые правила и определения:
- Пусть буквы a , b и c обозначают целые числа (то есть целые числа).
- Всегда выбирайте a так, чтобы оно было больше суммы b и c . То есть a > b + c . Это гарантирует отсутствие записи в магический квадрат отрицательного числа.
- Не допускайте 2 X b = c . Это гарантирует, что вы не получите одно и то же число в разных ячейках.
- Используя формулы, приведенные в таблице ниже, вы можете составить магический квадрат, в котором сумма строк, столбцов и диагоналей равна 3 X независимо от числа или .

Чтобы создать первый магический квадрат #15 выше, пусть a будет равно 5, пусть b будет равно 3, и пусть c будет равно 1. Вот некоторые другие:
- а = 6, б = 3, в = 2
- а = 6, б = 3, в = 1
- а = 7, б = 3, в = 2
- а = 7, б = 4, в = 2
- а = 8, б = 6, в = 1
- а = 8, б = 5, в = 2
- а = 8, б = 4, в = 3
Попробуйте придумать что-нибудь свое.
Вернуться к началу
Перевернутый магический квадрат
Вот магический квадрат, который не только дает в сумме 264 по всем направлениям, но и делает это, даже когда он перевернут! Если не веришь мне, посмотри на это, стоя на голове! (Или просто скопируйте его и переверните вверх ногами.)
| 96 | 11 | 89 | 68 |
| 88 | 69 | 91 | 16 |
| 61 | 86 | 18 | 99 |
| 19 | 98 | 66 | 81 |
Вернуться к началу
Антимагический квадрат
Вот магический квадрат с максимально возможным количеством различных сумм .
| 5 | 1 | 3 |
| 4 | 2 | 6 |
| 8 | 7 | 9 |
Эта таблица дает 8 разных итого.
Вернуться к началу
Выиграть ставки с помощью магического квадрата
Итак, вот отличный способ выиграть ставки с помощью магического квадрата. Позвоните другу по телефону. Пусть он или она возьмет карандаш и бумагу и поднесет их к телефону, чтобы он или она могли записать цифры от 1 до 9. Скажите своему другу, что вы будете по очереди называть цифры от 1 до 9. Никто из вас не может повторить номер, который называет другой. Затем вы оба запишите числа от 1 до 9.. Затем, когда ваш друг называет одно из чисел, он обводит это число кружком, и вы тоже. Когда вы называете число, вы рисуете квадрат вокруг этого числа, и ваш друг делает то же самое. Выигрывает тот, кто первым наберет три числа, сумма которых точно равна 15.
Допустим, вы идете первым и называете 8. Ваш друг может назвать 6. Затем вы называете 2. Ваш друг называет 5, и вы называете 4. Ваш друг называет 7, а вы называете 3. Затем вы говорите своему другу, что вы только что выиграли, потому что назвали 8, 3 и 4, что в сумме дает 15.
Ваш друг снова захочет поиграть. Так что на этот раз вы можете поспорить с ним, что выиграете, с условием, что в случае ничьей (когда вы используете числа от 1 до 9, но ни один из вас не получает в сумме 15) никто ничего не должен.
Если вы знаете хитрость, вы никогда не проиграете, и, вероятно, проиграете в большинстве случаев.
Фокусы На самом деле фокус основан как на крестиках-ноликах, так и на магическом квадрате. Магический квадрат выглядит так:
| 8 | 1 | 6 |
| 3 | 5 | 7 |
| 4 | 9 | 2 |
Поскольку это магический квадрат, каждая строка, каждый столбец и каждая диагональ в сумме дают 15. Поэтому, если этот квадрат находится перед вами с вашим другом по телефону, вы можете поставить крестик рядом с ним. квадраты числа, которое вы называете, и O в квадратах чисел, которые называет ваш друг. Затем, как и в крестиках-ноликах, вы пытаетесь поставить три крестика подряд, потому что в сумме это всегда будет 15.
Затем, как и в крестиках-ноликах, вы пытаетесь поставить три крестика подряд, потому что в сумме это всегда будет 15.
Итак, в приведенном выше примере, когда вы называете 8, вы ставите X в верхнем левом углу. Когда ваш друг говорит 6, вы ставите ) в правом верхнем углу. И так далее.
Наверх
Математический фокус с картами
Для этого задания вам понадобится обычная колода карт. Никаких причудливых перетасовок не требуется. Просто следуйте этим простым шагам:
- Перемешайте карты, чтобы тщательно их перемешать.
- Разложите 36 карт стопкой.
- Попросите друга выбрать одну из 36 карт, посмотреть на нее и запомнить, а затем положить ее обратно в стопку, не показывая ее вам.
- Перемешайте 36 карт.
- Разложите 36 карт в 6 рядов по 6 карт в каждом. Обязательно сдавайте верхний ряд слева направо. Затем нанесите второй ряд под ним слева направо. И так далее, каждый последующий ряд кладется под предыдущий.
- Попросите друга посмотреть на карточки и сказать, в каком ряду находится выбранная карточка.
 Запомните, под каким номером находится ряд.
Запомните, под каким номером находится ряд. - Аккуратно поднимите карты в том же порядке, в котором вы их положили . Таким образом, первая карта слева в верхнем ряду находится наверху стопки, а последняя карта справа в нижнем ряду — внизу стопки.
- Теперь разложите карты в 6 рядов по 6 карт в каждом, но на этот раз разложите карты по одному столбцу за раз . Вместо того, чтобы переходить от одной строки к другой, переходите от одного столбца к другому. Разложите первые шесть карт в столбце сверху вниз в крайний левый угол. Затем выложите следующие шесть карт во второй столбец из шести карт справа от первого столбца из шести карт. Продолжайте делать это, пока у вас не будет 6 столбцов по 6 карт в каждом (что выглядит так же, как 6 рядов по 6 карт в каждом, потому что это 9).0004 это то же самое).
- Еще раз спросите у друга, в каком ряду находится выбранная карта.
- Когда ваш друг говорит вам, в каком ряду находится карта, вы можете сказать, какая именно выбранная карта.
 Как? Если ваш друг сказал, что карта была в строке 2 в первый раз, а в строке 5 во второй раз, то выбранная карта — это карта во втором столбце пятой строки. Это связано с тем, что при расположении карточек то, что в первый раз было строками, во второй раз становится столбцами.
Как? Если ваш друг сказал, что карта была в строке 2 в первый раз, а в строке 5 во второй раз, то выбранная карта — это карта во втором столбце пятой строки. Это связано с тем, что при расположении карточек то, что в первый раз было строками, во второй раз становится столбцами.
Вернуться к началу
Калькулятор молний
Вот уловка, чтобы удивлять их каждый раз! Попросите кого-нибудь записать свой номер социального страхования. Затем попросите их переписать его так, чтобы все было перемешано. (Если у них нет номера социального страхования, попросите их записать любые 9 цифр от 1 до 9.) Если есть нули, попросите заменить их на любую другую цифру от 1 до 9. Затем попросите их скопировать свои девять цифр. числа в том же порядке рядом с исходными девятью числами. Это даст им число с 18 цифрами, первая половина которого такая же, как вторая половина. Далее измените вторую цифру на 7, и измените одиннадцатую цифру (это будет то же число, что и вторая цифра, но во вторых девяти цифрах) также на 7. Тогда поспорьте с ними, что вы сможете сказать им, что останется после деления числа на 7, быстрее, чем они сообразят это вручную. Ответ: 0 — 7 делится на это новое число ровно без остатка!
Тогда поспорьте с ними, что вы сможете сказать им, что останется после деления числа на 7, быстрее, чем они сообразят это вручную. Ответ: 0 — 7 делится на это новое число ровно без остатка!
Вернуться к началу
Таблицы забавных чисел
Следующие забавные таблицы взяты из одной из моих любимых книг всех времен, Recreations in the Theory of Numbers , Альберт Х. Бейлер, опубликовано Dover Publications. Эта книга на самом деле объясняет математические причины, по которым эти трюки работают.
 111111 x 111111 = 12345654321
111111 x 111111 = 12345654321
.
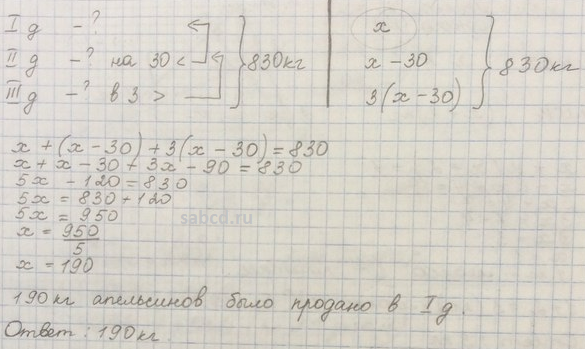 5 = 98765
5 = 98765
Наверх
Знаете ли вы.
 ..?
..?Каждое двузначное число, оканчивающееся на 9, представляет собой сумму, кратную двум цифрам, плюс сумму двух цифр. Так, например, 29 = (2 х 9) + (2 + 9). 2 X 9 = 18. 2 + 9 = 11. 18 + 11 = 29.
40 — уникальное число, потому что, когда оно записано как «сорок», это единственное число, буквы которого расположены в алфавитном порядке.
А премьер число — это целое число больше 1, которое не делится без остатка ни на какое другое целое число, кроме самого себя (и 1). 2, 3, 5, 7, 11, 13 и 17 являются примерами простых чисел.
139 и 149 — первые последовательные простые числа, отличающиеся на 10.
69 — единственное число, в квадрате и кубе которого между ними используются все цифры от 0 до 9 по одному разу:
69 2 = 4761 и 69 3 = 328 509.
Один фунт железа содержит примерно 4 891 500 000 000 000 000 000 000 атомов.
Существует около 318 979 564 000 возможных способов сыграть первые четыре хода с каждой стороны в игре в шахматы.
Земля проходит более полутора миллионов миль каждый день.
В Эйфелевой башне 2 500 000 заклепок.
Если бы все кровеносные сосуды в человеческом теле были сложены встык, они растянулись бы на 100 000 миль.
Вернуться к началу
Математический трюк для этого года
Предполагается, что этот трюк будет работать только в 1998 году, но на самом деле одно изменение позволит ему работать в течение любого года.
1. Выберите количество дней в неделю, когда вы хотели бы выходить на улицу (1-7).
2. Умножьте это число на 2.
3. Прибавьте 5.
4. Умножьте полученную сумму на 50.
5. В 1998 году, если у вас уже был день рождения в этом году, прибавьте 1748. Если нет , добавьте 1747. В 1999 году просто добавьте 1 к этим двум числам (поэтому добавьте 1749, если у вас уже был день рождения, и добавьте 1748, если нет). В 2000 году номер меняется на 1749 и 1748. И так далее.
6. Вычтите из четырех цифр год вашего рождения (19ХХ).
Результаты:
У вас должно быть трехзначное число.
Первая цифра этого номера — это количество дней, в течение которых вы хотите выходить на улицу каждую неделю (1–7).
Последние две цифры — ваш возраст.
(Спасибо, что передали мне это, Джуди.)
Вернуться к началу
Где нить?
В следующий раз, когда вы будете с группой людей и захотите произвести на них впечатление своими экстрасенсорными способностями, попробуйте это. Пронумеруйте всех в группе от 1 до любого числа. Возьмите кусок веревки и скажите, чтобы он привязал ее кому-нибудь к пальцу, пока вы выходите из комнаты или поворачиваетесь спиной. Затем скажите, что вы можете сказать им не только, у кого он есть, но и на какой руке и на каком пальце он находится, если они просто посчитают за вас и дадут вам ответы. Затем попросите одного из них ответить на следующие вопросы:
1. Умножьте номер человека со строкой на 2.
2. Прибавьте 3.
3. Умножьте результат на 5.
4. Если строка справа, добавьте 8.
Если струна находится на левой руке, добавьте 9.
5. Умножьте на 10.
6. Добавьте номер пальца (большой палец = 1).
7. Добавить 2.
Попросите их сказать вам ответ. Затем мысленно вычтите 222. Остаток дает ответ, начиная с правой цифры ответа.
Например, предположим, что струна находится на безымянном пальце левой руки Игрока №6:
1. Умножить на 2 = 12.
2. Прибавить 3 = 15.
3. Умножить на 5 = 75
4. Поскольку струна находится на левой руке, прибавьте 9 = 84.
5. Умножьте на 10 = 840.
6. Прибавьте номер пальца (3) = 843.
7. Прибавьте 2 = 845.
Теперь мысленно вычтите 222 = 623. Цифра справа (3) говорит о том, что струна находится на безымянном пальце. Средняя цифра говорит о том, что он находится на левой руке (правая рука = 1). Цифра слева говорит о том, что строка принадлежит Игроку №6.
Кстати, когда номер человека больше 9, вы получите ЧЕТЫРЕХзначное число, а ДВЕ левые цифры будут номером Игрока.
В чем секрет?
(Это из замечательной книги под названием Giant Book of Puzzles & Games, Шейлы Энн Бэрри. Опубликовано Sterling Publishing Co., Inc., Нью-Йорк, 1978 г., недавно переиздано в мягкой обложке.)
Оставайтесь с нами. больше математических трюков. Они будут добавляться время от времени, так что не забудьте проверить снова.
Комбинаторика— неубывающие цифры спросил
Изменено 3 года, 7 месяцев назад
Просмотрено 11 тысяч раз
$\begingroup$
Говорят, что число состоит из неубывающих цифр, если все цифры слева от любой цифры меньше или равны этой цифре.
Например, четырехзначное число $1234$ состоит из неубывающих цифр. Некоторые другие четырехзначные числа, состоящие из неубывающих цифр: $0011$, $1111$, $1112$, $1122$, $2223$.
Некоторые другие четырехзначные числа, состоящие из неубывающих цифр: $0011$, $1111$, $1112$, $1122$, $2223$.
Обратите внимание, что начальные нули обязательны: $0000$, $0001$, $0002$ — все допустимые четырехзначные числа с неубывающими цифрами.
Вопрос
Сколько четырехзначных чисел неубывающих?
- комбинаторика 99 \binom{l+3}{3}$$ $$= \binom{9+4}{4} = 715$$
$\endgroup$
5
$\begingroup$
Пусть четыре цифры будут $d_1,d_2,d_3$ и $d_4$ слева направо. Пусть $a_1=d_1,a_2=d_2-d_1,a_3=d_3-d_2$, $a_4=d_4-d_3$ и $a_5=9-d_4$. Обратите внимание, что каждое неубывающее четырехзначное число соответствует уникальному $5$-набору $\langle a_1,a_2,a_3,a_4,a_5\rangle$ целых неотрицательных чисел, такому что $a_1+a_2+a_3+a_4+a_5 =9$ и наоборот: по такому $5$-кортежу мы можем восстановить число, потому что $d_1=a_1,d_2=a_1+a_2$, $d_3=a_1+a_2+a_3$ и $d_4=a_1+a_2+a_3 +а_4$.
 (Пятое число, $a_5$, просто служит для того, чтобы гарантировать, что общее число известно.)
(Пятое число, $a_5$, просто служит для того, чтобы гарантировать, что общее число известно.)Задача подсчета неотрицательных целочисленных решений — это стандартная задача со звездочками и решетками. Статья в Википедии дает достойное объяснение приведенных рассуждений; ответ $$\binom{9+5-1}{5-1}=\binom{13}4=715\;.$$
$\endgroup$
3
$\begingroup$
Есть 10!/(4!*6!) = 210, чтобы получить 4 разных числа
Есть 3* [10!/(3!*7!)] =3*120 =360, чтобы получить 3 разных числа с 1 повторяющимся
Есть 10!/(2!*8!) = 45, чтобы получить 2 разных числа с каждым повторяющимся
Есть 2* [10!/(2!*8!) ] = 2*45 = 90, чтобы получить 2 разных числа, 1 из которых повторяется 3 раза
Есть 10 способов получить 1 число, повторяющееся 4 раза
210 +360 +45 +90 +10 = 715
$\endgroup$
1
$\begingroup$
Мое решение немного отличается от ответа Брайана, хотя я использую ту же технику «звезды и полосы».
 Пусть $d_1d_2d_3d_4$ будет одним таким числом, а диапазон значений для каждой цифры $d_i$ будет [0-9]. Для любой заданной комбинации из 4 цифр у нас всегда есть ровно одно неубывающее число. например: 2,5,2,4 имеет только одну комбинацию неубывающих чисел, то есть 2245. Таким образом, наша проблема сводится к простому нахождению «общего количества комбинаций, где 4 цифры должны быть выбраны из набора 10 цифр ( 0-9цифры), где каждая цифра может повторяться». Для каждой комбинации у нас есть ровно одно неубывающее число. Таким образом, в основном нам нужно найти неотрицательные интегральные решения уравнения $x_0 + x_1 + … +x_{9} = 4$, что оказывается $\binom{10+4-1}{10-1}=\binom{13}4=715\;.$
Пусть $d_1d_2d_3d_4$ будет одним таким числом, а диапазон значений для каждой цифры $d_i$ будет [0-9]. Для любой заданной комбинации из 4 цифр у нас всегда есть ровно одно неубывающее число. например: 2,5,2,4 имеет только одну комбинацию неубывающих чисел, то есть 2245. Таким образом, наша проблема сводится к простому нахождению «общего количества комбинаций, где 4 цифры должны быть выбраны из набора 10 цифр ( 0-9цифры), где каждая цифра может повторяться». Для каждой комбинации у нас есть ровно одно неубывающее число. Таким образом, в основном нам нужно найти неотрицательные интегральные решения уравнения $x_0 + x_1 + … +x_{9} = 4$, что оказывается $\binom{10+4-1}{10-1}=\binom{13}4=715\;.$$\endgroup$
$\begingroup$
Вот простое решение.
Легко заметить, что существует только одна перестановка любого набора из 4 цифр, образующая неубывающую последовательность. Таким образом, между нахождением количества искомых последовательностей и количеством набора $4$ цифр (разрешено повторение) существует однозначное соответствие, т.


 ..?
..?
 И напишите это число прямо под первым числом.
И напишите это число прямо под первым числом.

 Запомните, под каким номером находится ряд.
Запомните, под каким номером находится ряд. Как? Если ваш друг сказал, что карта была в строке 2 в первый раз, а в строке 5 во второй раз, то выбранная карта — это карта во втором столбце пятой строки. Это связано с тем, что при расположении карточек то, что в первый раз было строками, во второй раз становится столбцами.
Как? Если ваш друг сказал, что карта была в строке 2 в первый раз, а в строке 5 во второй раз, то выбранная карта — это карта во втором столбце пятой строки. Это связано с тем, что при расположении карточек то, что в первый раз было строками, во второй раз становится столбцами.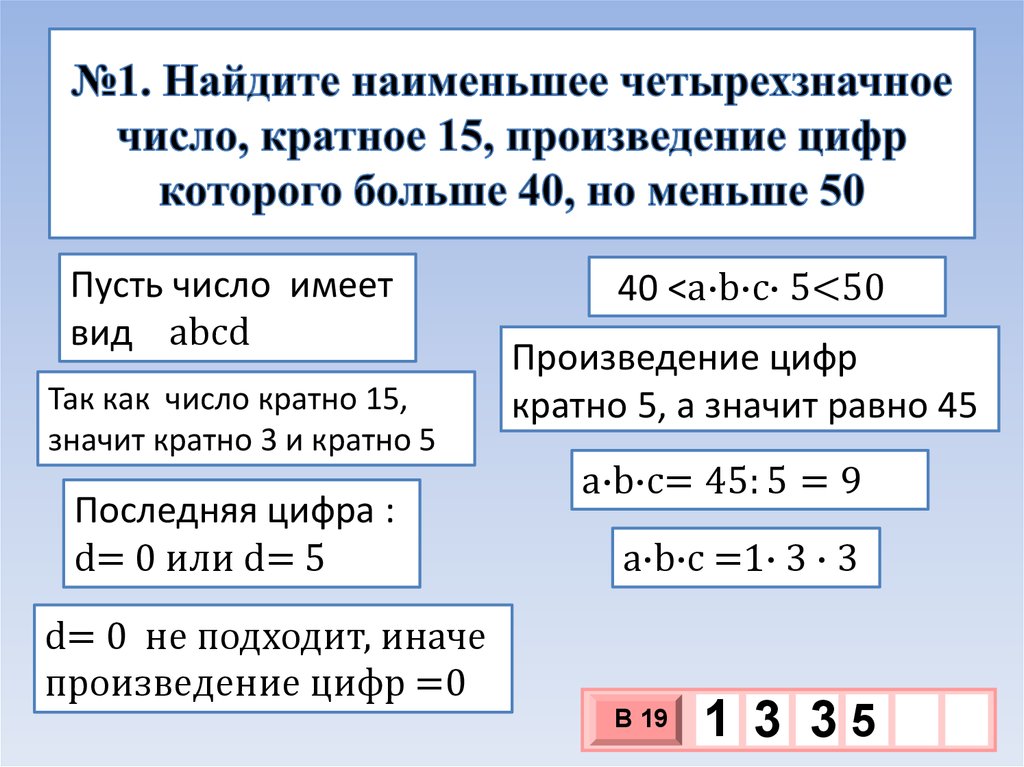 (Пятое число, $a_5$, просто служит для того, чтобы гарантировать, что общее число известно.)
(Пятое число, $a_5$, просто служит для того, чтобы гарантировать, что общее число известно.) Пусть $d_1d_2d_3d_4$ будет одним таким числом, а диапазон значений для каждой цифры $d_i$ будет [0-9]. Для любой заданной комбинации из 4 цифр у нас всегда есть ровно одно неубывающее число. например: 2,5,2,4 имеет только одну комбинацию неубывающих чисел, то есть 2245. Таким образом, наша проблема сводится к простому нахождению «общего количества комбинаций, где 4 цифры должны быть выбраны из набора 10 цифр ( 0-9цифры), где каждая цифра может повторяться». Для каждой комбинации у нас есть ровно одно неубывающее число. Таким образом, в основном нам нужно найти неотрицательные интегральные решения уравнения $x_0 + x_1 + … +x_{9} = 4$, что оказывается $\binom{10+4-1}{10-1}=\binom{13}4=715\;.$
Пусть $d_1d_2d_3d_4$ будет одним таким числом, а диапазон значений для каждой цифры $d_i$ будет [0-9]. Для любой заданной комбинации из 4 цифр у нас всегда есть ровно одно неубывающее число. например: 2,5,2,4 имеет только одну комбинацию неубывающих чисел, то есть 2245. Таким образом, наша проблема сводится к простому нахождению «общего количества комбинаций, где 4 цифры должны быть выбраны из набора 10 цифр ( 0-9цифры), где каждая цифра может повторяться». Для каждой комбинации у нас есть ровно одно неубывающее число. Таким образом, в основном нам нужно найти неотрицательные интегральные решения уравнения $x_0 + x_1 + … +x_{9} = 4$, что оказывается $\binom{10+4-1}{10-1}=\binom{13}4=715\;.$
Leave A Comment