Microsoft Word — геометрия-1.doc
%PDF-1.6 % 955 0 obj > endobj 952 0 obj >stream 2009-08-03T12:57:02ZMicrosoft Word — геометрия-1.doc2009-08-12T12:51:21+04:002009-08-12T12:51:21+04:00application/pdf
|
|
|
содержание .. 48 49 50 51 ..
Задание №1817 Площадь параллелограмма ABCD равна 118. Середина стороны CD — точка E. Вычислите площадь треугольника ADE Решение
Разобьём параллеаграмм ABCD на равные треугольники (как на рисунке) — всего их 4, треугольник ADE, состоит из одного такого треугольника, значит его площадь равна 1/4 от площади параллеаграмма ABCD По найденной формуле вычисляем, что площадь треугольника ADE=29,5
Задание №4231
Даны два угла вписанного в окружность четырехугольника.  Они равны 38° и 148°.
Найдите больший из оставшихся углов. Ответ дайте в градусах. Они равны 38° и 148°.
Найдите больший из оставшихся углов. Ответ дайте в градусах.Решение По теореме Птолемея — сумма противоположных углов в четырехугольнике, вписанном в окружность равна 180 градусов угол противоположный углу 38 градусов равен 180-38=142 градусов угол противоположный углу 148 градусов равен 180-148=32 градусов Больший из неизвестных углов 142 градусов
Задание №2308 Угол между соседними двумя сторонами правильного многоугольника, вписанного в окружность, равен 140°. Найдите число вершин многоугольника Решение Каждый угол правильного многоугольника равен 180° * (n – 2) / n , где n – число его углов (вершин) Составляем уравнение: 180 * ( n – 2 ) / n=140 180*n – 360 = 140 * n n=9 Ответ: 9
Задание №1206 Дан параллелограмм ABCD. Его площадь равна 110. Точка E – середина стороны BC.  Решение
Разобьём параллеаграмм ABCD на равные треугольники (как на рисунке) — всего их 4, трапеция ADEB, состоит из трёх таких треугольников, значит площадь трапеции ADEB равна 3/4 от площади параллеаграмма ABCD По найденной формуле вычисляем, что площадь трапеции ADEB=82,5 Ответ: 82,5
Задание №4313
В четырехугольник ABCD вписана окружность, AB= 29, BC=8, CD=60. Найдите четвертую сторону четырехугольника В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда AB+CD=BC+AD Сторона AD=AB+CD-BC=29+60-8=81 Ответ: 81
Задание №2671 Площадь треугольника АВС равна 129. DE – средняя линия, параллельная стороне AB. Рассчитайте площадь трапеции ABED Решение
Площадь трапеции ABED можно найти как разность площадей двух треугольников: Площадь треугольника CED будет в 4 раза меньше площади треугольника ABC, так как линейные размеры треугольника CED в 2 раза меньше соответствующих размеров треугольника ABC
Задание №3973
Катеты равнобедренного прямоугольного треугольника равны 30+15√2 .  Рассчитайте радиус окружности, вписанной в этот треугольник Рассчитайте радиус окружности, вписанной в этот треугольникРешение Пусть катеты прямоугольного треугольника равны a, тогда гипотенуза AB, равна: Радиус вписанной в прямоугольный треугольник окружности равен половине разности суммы катетов и гипотенузы:
Задание №1336
У прямоугольной трапеции, описанной около окружности, периметр равен 109, ее большая боковая сторона равна 48 . Найдите радиус окружности Решение Сторона AD равна диаметру окружности, значит R=AD/2 В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда AB+CD=BC+AD R = 3,25 Ответ: 3,25
Задание №3732
Основания равнобедренной трапеции равны 60 и 32.  Решение Проведем высоту KH через центр окружности O Из рисунка видно, что треугольники DOC и AOB – равнобедренные и их высоты KO и HO делят стороны DC и AB пополам. Найдем эти высоты из прямоугольных треугольников DKO и AOH по теореме Пифагора, имеем: Подставим известные значения в формулы и вычислим KO и HO KO=30 HO=16 Следовательно, высота трапеции равна KH=KO+HO=30+16=46 Примечание: Если бы большее основание трапеции лежало выше центра окружности (то есть оба основания располагались по одну сторону от центра окружности) длина высоты равнялась бы не сумме, а разности найденных отрезков. Решая данную задачу необходимо принимать во внимание рисунок, данный в условии
Задание №3121
Дана трапеция, описанная около окружности.  Боковые стороны трапеции, равны 18 и 30 .
Рассчитайте среднюю линию трапеции Боковые стороны трапеции, равны 18 и 30 .
Рассчитайте среднюю линию трапецииРешение В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда AB+CD=BC+AD Средняя линия MK = (DC+AB) / 2 = (AD+BC) / 2 = 48 / 2 = 24 Ответ: 24
Задание №3472
Дан правильный шестиугольник. Его периметр равен 432. Найдите диаметр описанной окружности Решение
Периметр (P) — это сумма длин всех сторон, поэтому: AB / 6 = P / 6 =432 / 6 = 72 Рассмотрим угол AOB. Он равен 60°, т.к. вся окружность 360°, а треугольников 6 (360°/6=60°) Рассмотрим треугольник AOB. Он равносторонний, т.к. AO=OB=R и угол AOB=60° и тогда Диаметр D=2R=2AB=2*72=144 Ответ: 144
Задание №5515
В треугольнике ABC BC=80, AC=18, угол C равен 90° . Рассчитайте радиус окружности, вписанной в этот треугольник Решение Радиус вписанной в прямоугольный треугольник окружности равен половине разности суммы катетов и гипотенузы: Подставим в формулу вместо значение AC и BC и решим уравнение Радиус r=8 Ответ: 8
Задание №5439
Дана окружность, вписанная в треугольник ABC, к которой проведены три касательные.  Периметры отсеченных треугольников равны 17, 41, 66.
Вычислите периметр данного треугольника
Периметры отсеченных треугольников равны 17, 41, 66.
Вычислите периметр данного треугольникаРешение
EF и ED — отрезки касательных, проведенных из одной точки Е. Они по свойству касательных равны. Аналогично, GF = GH. То есть, GE = GH + ED, а периметр треугольника AGE запишется как =17+41+66=124 Ответ: 124
Задание №1328
Дан равнобедренный треугольник. Боковые стороны равны 100, основание равно 120 . Найдите радиус окружности, вписанной в этот треугольник Решение Радиус вписанной окружности равен отношению площади к полупериметру. Для нахождения площади, воспользуемся формулой Герона:
Подставим значения сторон треугольника и найдём площадь. Она равна S=4800 Подствавим значения и найдём полупериметр P=160 Тогда: Подствавим значения и найдём радиус r=4800/160=30 Ответ: 30
Задание №1228
Окружность вписана в четырёхугольник ABCD, сторона AB= 67, CD= 50 .  Найдите периметр четырёхугольника ABCD Найдите периметр четырёхугольника ABCDРешение В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда AB+CD=BC+AD Периметр (P) четырехугольника – это сумма длин всех его сторон, то есть P=AB+BC+AD+CD= 2*(AB+CD) P = 234 Ответ: 234
Задание №4693
Дан равнобедренный треугольник. Окружность, вписанная в треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 44 и 17, считая от вершины, противолежащей основанию. Найдите периметр треугольника Решение
Пусть точки H и K являются точками касания окружности и сторон AB и СВ соответственно. Треугольники KOH и KOB равны, т.к. являются прямоугольными с общей гипотенузой и равными катетами, значит, HB=KB=17 Периметр треугольника равен P=AC+CB+AH+HB=2CB+2HB=122+34=156 Ответ: 156
Задание №4452 Основания равнобедренной трапеции равны 18 и 108.  Синус острого угла трапеции равен 0,8.
Вычислите боковую сторону
Синус острого угла трапеции равен 0,8.
Вычислите боковую сторону
Решение Треугольники ADH и BKC равны (так как AD=CD и DH=CK), значит, AH=KB Треугольник ADH прямой, поэтому гипотенуза AD = AH / cos(a) По найденной формуле вычисляем, что AD=75 Ответ: 75
Задание №1601
Дана трапеция, описанная около окружности. Периметр трапеции равен 57. Рассчитайте длину средней линии трапеции Решение Периметр (Р) — сумма всех сторон трапеции В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда AB+CD=BC+AD
Средняя линия MK = 57 / 4 = 14,25 Ответ: 14,25
Задание №4237 Площадь параллелограмма ABCD равна 136. Середины его сторон — это вершины параллелаграмма A′B′C′D′. Найдите площадь параллелограмма A′B′C′D′ Решение
Разобьём параллеаграмм ABCD на равные треугольники (как на рисунке) — всего их 8, параллелограмм A′B′C′D′ состоит из четырёх таких треугольников, значит, его площадь равна 1/2 от площади параллеаграмма ABCD По найденной формуле вычисляем, что площадь параллелограмма A′B′C′D′=68 Ответ: 68
Задание №2532
В четырёхугольник ABCD вписана окружность, периметр = 191, стророна AB= 45 .  Вычислите длину стороны CD Вычислите длину стороны CDРешение В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда AB+CD=BC+AD Значит P / 2 = AB + CD CD = P/2-AB=50,5 Ответ: 50,5
содержание .. 48 49 50 51 ..
|
|
«Начальные геометрические сведения». Вариант 2!
М А Т Е М А Т И К А В Ш К О Л Е
Самостоятельная работа 1 на тему: «Прямая, отрезок, луч, угол» 1.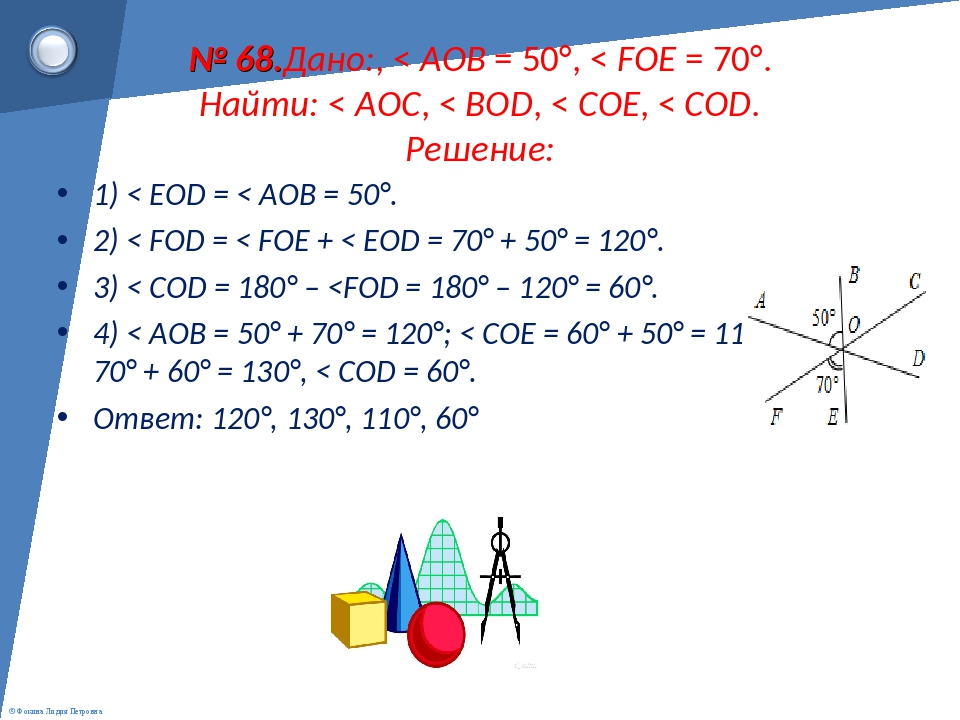 На прямой отмечены точки E, F, G и H. Какие точки принадлежат отрезку FH? Отметьте на отрезке EG такую точку, которая не принадлежит FG.
На прямой отмечены точки E, F, G и H. Какие точки принадлежат отрезку FH? Отметьте на отрезке EG такую точку, которая не принадлежит FG.
Часть І. Самостоятельные работы
Часть І. Самостоятельные работы Блок 1. Геометрические фигуры. Точка, прямая, луч, отрезок Самостоятельная работа 1 (на чертежах) 1. Какие из точек A, B, C, D (рис. 1) лежат на прямой a, а какие не лежат?
Подробнее1 Точки, отрезки, прямые,
1 Точки, отрезки, прямые, лучи 1 Самостоятельная работа (теоретическая) 1 1. На прямой MN отмечена точка K. Принадлежит ли точка N прямой MK? 2. Верно ли утверждение: если точка C лежит на прямой AB, то
ПодробнееКонтрольная работа 1 (7 класс)
Контрольная работа 1 (7 класс) по теме «Начальные геометрические сведения» (глава I, п. п. 1-13) 1. Три точки В, С, и D лежат на одной прямой а. Известно, что ВD = 17 см, DC = 25 см. Какой может быть длина
п. 1-13) 1. Три точки В, С, и D лежат на одной прямой а. Известно, что ВD = 17 см, DC = 25 см. Какой может быть длина
10.Окружность, круг и их элементы
10.Окружность, круг и их элементы Касательная, хорда, секущая, радиус 1. Радиус OB окружности с центром в точке O пересекает хорду AC в точке D и перпендикулярен ей. Найдите длину хорды AC, если BD = 1
ПодробнееБилеты промежуточной аттестации 7 класс.
Билеты промежуточной аттестации 7 класс. (к учебникам А.В. Погорелова и Л.С. Атанасяна, геометрия 7кл) БИЛЕТ 1. 1. Сформулируйте определение равнобедренного треугольника. Назовите элементы равнобедренного
ПодробнееГеометрия
Геометрия 1. Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65 и 50. Найдите меньший угол параллелограмма. 2. Разность углов, прилежащих к одной стороне параллелограмма, равна
2. Разность углов, прилежащих к одной стороне параллелограмма, равна
Многоугольники и их свойства
Задание 19 Планиметрические задачи Многоугольники и их свойства 1. На стороне CD квадрата ABCD построен равносторонний треугольник CPD. Найдите высоту треугольника ADP, проведённую из вершины D, если известно,
ПодробнееСОГЛАСОВАНО зам. директора. Юхнова Л.М.
Муниципальное автономное общеобразовательное учреждение «Средняя общеобразовательная школа 20» городского округа город Стерлитамак Республики Башкортостан РАССМОТРЕНО на заседании МО учителей естественноматематических
ПодробнееОСНОВНЫЕ ЭЛЕМЕНТЫ ОКРУЖНОСТИ
УГЛЫ В ОКРУЖНОСТИ ОСНОВНЫЕ ЭЛЕМЕНТЫ ОКРУЖНОСТИ Диаметр в 2 раза больше радиуса.!!! Это очень важно знать для выполнения данного задания: ЦЕНТРАЛЬНЫЙ УГОЛ Центральный угол равен дуге, на которую он опирается
ПодробнееТренировочные задачи
И. В. Яковлев Материалы по математике MathUs.ru Тренировочные задачи Окружность. Свойства окружности. Если хорда не является диаметром, то диаметр, проходящий через середину этой хорды, перпендикулярен
В. Яковлев Материалы по математике MathUs.ru Тренировочные задачи Окружность. Свойства окружности. Если хорда не является диаметром, то диаметр, проходящий через середину этой хорды, перпендикулярен
Зачеты по геометрии за курс 7-8 класс
МУНИЦИПАЛЬНОЕ АВТОНОМНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА 28 г.томска Зачеты по геометрии за курс 7-8 класс Составила Смолякова Оксана Геннадьевна учитель математики МАОУ
ПодробнееОкружность, круг и их элементы
Окружность, круг и их элементы 1. B 7 90. Центральный угол AOB опирается на хорду AB длиной 6. При этом угол OAB равен 60. Найдите радиус окружности. О т в ет: 6 2. B 7 116. В окружности с центром в точке
ПодробнееПояснительная записка.
Пояснительная записка. Рабочая программа по геометрии разработана для обучающихся 7 классов муниципального бюджетного общеобразовательного учреждения «Кряш- Сердинская основная общеобразовательная школа»
Рабочая программа по геометрии разработана для обучающихся 7 классов муниципального бюджетного общеобразовательного учреждения «Кряш- Сердинская основная общеобразовательная школа»
Планиметрия на ЕГЭ по математике
И. В. Яковлев Материалы по математике MathUs.ru Планиметрия на ЕГЭ по математике Здесь приведены задачи по планиметрии, которые предлагались на ЕГЭ по математике (профильный уровень, сложная часть), а
ПодробнееСредняя линия треугольника
И. В. Яковлев Материалы по математике MathUs.ru Средняя линия треугольника Средняя линия треугольника это отрезок, соединяющий середины двух сторон треугольника. Говоря о средней линии, третью сторону
ПодробнееЛуч: чертеж, определение, построение на прямой, обозначение; Угол: определение, обозначение, построение, виды, области угла;
Вопросы к экзамену по геометрии 7 класс. . (по учебнику: Геометрия 7-9 класс, Л. С. Анатосян) Свойство прямой, обозначение; Отрезок: чертеж, определение; Луч: чертеж, определение, построение на прямой,
. (по учебнику: Геометрия 7-9 класс, Л. С. Анатосян) Свойство прямой, обозначение; Отрезок: чертеж, определение; Луч: чертеж, определение, построение на прямой,
ГЕОМЕТРИЯ: ПЛАНИМЕТРИЯ
ГЕОМЕТРИЯ: ПЛАНИМЕТРИЯ I Группа 1.01 Разность двух углов, получившихся при пересечении двух прямых, равна 20. Найти больший из этих углов. 1.02 Углы треугольника пропорциональны числам 3:7:8. Найти наибольший
ПодробнееТреугольники
А.С. Крутицких и Н.С. Крутицких. Подготовка к ЕГЭ по математике. http://matematikalegko.ru Открытый банк заданий ЕГЭ по математике http://mathege.ru Треугольники 27284. В треугольнике ABC,. Найдите AB.
ПодробнееБилеты по геометрии 7 класс. Билет 5
Билеты по геометрии 7 класс Билет 1 1. Сформулируйте признаки параллельности двух прямых. 2. Смежные углы (определение). Теорема о сумме смежных углов. 3. Задача по теме «Признаки равенства треугольников»..
2. Смежные углы (определение). Теорема о сумме смежных углов. 3. Задача по теме «Признаки равенства треугольников»..
В.А. Смирнов ГЕОМЕТРИЯ УГЛЫ
В.А. Смирнов ГЕОМЕТРИЯ УГЛЫ 2011 ВВЕДЕНИЕ Выработка умений находить величины углов относится к основным целям обучения геометрии в школе. Задачи на нахождение углов входят в содержание ГИА и ЕГЭ по математике.
Подробнее3. В прямоугольном треугольнике ABC С = 90, AB = 5, BC = 3, АC = 4. Найдите tg B. 4. В параллелограмме ABCD диагонали пересекаются в точке О,
ГЕОМЕТРИЯ, 8 класс Вариант 1, Апрель 2011 ГЕОМЕТРИЯ, 8 класс Вариант 1, Апрель 2011 2. В треугольнике MNK сторона MK равна 19 см. Найдите длину средней линии треугольника, параллельной MK. 8 см 8, см )
ПодробнееТренировочные задачи
И. В. Яковлев Материалы по математике MathUs.ru Тренировочные задачи Параллелограмм. Периметр параллелограмма равен, а одна из его сторон вдвое больше другой. Найдите стороны параллелограмма. и 4. Найдите
В. Яковлев Материалы по математике MathUs.ru Тренировочные задачи Параллелограмм. Периметр параллелограмма равен, а одна из его сторон вдвое больше другой. Найдите стороны параллелограмма. и 4. Найдите
Планиметрия на ЕГЭ по математике
И. В. Яковлев Материалы по математике MathUs.ru Планиметрия на ЕГЭ по математике Здесь приведены задачи по планиметрии, которые предлагались на ЕГЭ по математике (профильный уровень, сложная часть), а
ПодробнееПрототипы задания В6-2 (2013)
Прототипы задания В6-2 (2013) ( 27742) Один острый угол прямоугольного треугольника на больше другого. Найдите больший острый угол. Ответ дайте в градусах. ( 27743) В треугольнике ABC угол A равен, внешний
ПодробнееID_5695 1/8 neznaika.pro
Планиметрическая задача Ответами к заданиям являются слово, словосочетание, число или последовательность слов, чисел. Запишите ответ без пробелов, запятых и других дополнительных символов. 1 В треугольнике
Запишите ответ без пробелов, запятых и других дополнительных символов. 1 В треугольнике
ТЕМА 3Г. ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ
ТЕМА 3Г. ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ Определение Две прямые на плоскости называются параллельными, если они не пересекаются. Теорема Две прямые, перпендикулярные к третьей, параллельны. Следствие Если прямая перпендикулярна
Подробнее«ПАРАЛЛЕЛОГРАММ И ТРАПЕЦИЯ»
МЕТОДИЧЕСКОЕ ПОСОБИЕ ПО ГЕОМЕТРИИ ДЛЯ 8 КЛАССА ТЕМАТИЧЕСКОЕ ТЕСТИРОВАНИЕ «ПАРАЛЛЕЛОГРАММ И ТРАПЕЦИЯ» Амосова Галина Владимировна, учитель математики и информатики ГБОУ СОШ 2 Василеостровского района г.
ПодробнееЗадания В6. . Найдите AB.
Задания В6 1. В треугольнике ABC угол C равен 90, тангенс внешнего угла при вершине A равен -0,1. Найдите tga. 2. Угол A четырехугольника ABCD, вписанного в окружность, равен 52. Найдите угол C этого 3.
Найдите угол C этого 3.
Перпендикулярность прямых и плоскостей
Глава 1 Перпендикулярность прямых и плоскостей Основные факты и понятия Прямая a, пересекающая плоскость α в точке A, перпендикулярна плоскости α, если она перпендикулярна любой прямой, лежащей в этой
ПодробнееВсе прототипы заданий В года
1. Прототип задания B5 ( 27450) Найдите тангенс угла AOB. Все прототипы заданий В5 2014 года 2. Прототип задания B5 ( 27456) Найдите тангенс угла AOB. 7. Прототип задания B5 ( 27547) Найдите площадь треугольника,
ПодробнееТреугольники общего вида
Треугольники общего вида 1. Найдите площадь треугольника, две стороны которого равны 8 и 12, а угол между ними равен 30. Площадь треугольника равна половине произведения его сторон на синус угла между
ПодробнееMAO = NAO.
 Таким образом, если из Рис. 1
Таким образом, если из Рис. 1005-006 уч. год. 6, 9 кл. Математика. Планиметрия (часть II). Вторая часть по планиметрии содержит три параграфа. В 1 подробно обсуждаются свойства касательных, хорд и секущих, доказывается теорема о касательной
Подробнее7 sin A. Найдите AB. 25
Прототипы задания 6 1. В треугольнике ABC угол C равен 90 0, AC = 4,8, 25. В треугольнике ABC AC = BC, AB = 8, 33 tga. 7 4 33 sin A. Найдите AB. 25 Найдите AC. 2. В треугольнике ABC угол C равен 90 0,
ПодробнееУ р о к 1 ПРЯМАЯ И ОТРЕЗОК
У р о к 1 ПРЯМАЯ И ОТРЕЗОК Ц е л и : познакомить учащихся с тем, что изучает геометрия, какой раздел геометрии называется планиметрией, какие фигуры в планиметрии называются основными; систематизировать
ПодробнееID_9151 1/10 neznaika.
 pro
proУглы и расстояния в пространстве Ответами к заданиям являются слово, словосочетание, число или последовательность слов, чисел. Запишите ответ без пробелов, запятых и других дополнительных символов. В основание
ПодробнееПланиметрия на олимпиаде «Физтех»
И. В. Яковлев Материалы по математике MathUs.ru Планиметрия на олимпиаде «Физтех» 1. («Физтех», 017, 9 ) В треугольник ABC вписаны два равных прямоугольника P QRS и P 1 Q 1 R 1 S 1 (при этом точки P и
ПодробнееГеометрия Атанасян Задачи к Главе 1
Практические задания и задачи из учебника геометрии для 7 класса к Главе 1 «Начальные геометрические сведения» (УМК Атанасян и др.) Ознакомительная версия перед покупкой книги. Цитаты из учебника представлены в учебных целях. Геометрия Атанасян Задачи к Главе 1.
Вернуться в Оглавление учебника по геометрии.
Геометрия 7 класс (УМК Атанасян)
Практические задания и задачи к Главе 1«Начальные геометрические сведения»
Практические задания к § 1 «Прямая и отрезок» (упр.№№ 1-7)
- Проведите прямую, обозначьте её буквой а и отметьте точки А и В, лежащие на этой прямой, и точки Р, Q и R, не лежащие на ней. Опишите взаимное расположение точек А, В, Р, Q, R и прямой а, используя символы ∈ и ∉.
- □ Отметьте три точки А, В и С, не лежащие на одной прямой, и проведите прямые АВ, ВС и СА.
- Проведите три прямые так, чтобы каждые две из них пересекались. Обозначьте все точки пересечения этих прямых. Сколько получилось точек? Рассмотрите все возможные случаи.
- Отметьте точки А, В, С, D так, чтобы точки А, В, С лежали на одной прямой, а точка D не лежала на ней. Через каждые две точки проведите прямую. Сколько получилось прямых?
- Проведите прямую а и отметьте на ней точки А и В.
 Отметьте: а) точки М и N, лежащие на отрезке АВ; б) точки Р и Q, лежащие на прямой а, но не лежащие на отрезке АВ; в) точки R и S, не лежащие на прямой а.
Отметьте: а) точки М и N, лежащие на отрезке АВ; б) точки Р и Q, лежащие на прямой а, но не лежащие на отрезке АВ; в) точки R и S, не лежащие на прямой а. - Проведите прямую и отметьте на ней три точки. Сколько отрезков получилось на прямой?
- □ На рисунке 10 изображена прямая, на ней отмечены точки А, В, С и D. Назовите все отрезки: а) на которых лежит точка С; б) на которых не лежит точка В.
Практические задания к § 2 «Луч и угол» (упр.№№ 8-17)
- Проведите прямую, отметьте на ней точки А и В и на отрезке АВ отметьте точку С. а) Среди лучей АВ, ВС, СА, АС и ВА назовите совпадающие лучи; б) назовите луч, который является продолжением луча СА.
- Начертите три неразвёрнутых угла и обозначьте их так: ∠AOB, ∠hk, ∠M.
- Начертите два развёрнутых угла и обозначьте их буквами.
- Начертите три луча h, k и I с общим началом. Назовите все углы, образованные данными лучами.

- Начертите неразвёрнутый угол hk. Отметьте две точки внутри этого угла, две точки вне этого угла и две точки на сторонах угла.
- Начертите неразвёрнутый угол. Отметьте точки А, В, М и N так, чтобы все точки отрезка АВ лежали внутри угла, а все точки отрезка MN лежали вне угла.
- Начертите неразвёрнутый угол АОВ и проведите: а) луч ОС, который делит угол АОВ на два угла; б) луч OD, который не делит угол АОС на два угла.
- □ Сколько неразвёрнутых углов образуется при пересечении двух прямых?
- □ Какие из точек, изображённых на рисунке 17, лежат внутри угла hk, а какие — вне этого угла?
- Какие из лучей, изображённых на рисунке 18, делят угол АОВ на два угла?
- 18. На луче с началом О отмечены точки А, В и С так, что точка В лежит между точками О и А, а точка А — между точками О и С. Сравните отрезки ОВ и ОА, ОС и О А, ОВ и ОС.
- 19.
 Точка О является серединой отрезка АВ. Можно ли совместить наложением отрезки: а) ОА и ОВ; б) ОА и АВ?
Точка О является серединой отрезка АВ. Можно ли совместить наложением отрезки: а) ОА и ОВ; б) ОА и АВ? - 20. □ На рисунке 25 отрезки АВ, ВС, CD и DE равны. Укажите: а) середины отрезков АС, АЕ и СЕ; б) отрезок, серединой которого является точка D; в) отрезки, серединой которых является точка С.
- 21. Луч ОС делит угол АОВ на два угла. Сравните углы АОВ и АОС.
- 22. □ Луч l — биссектриса угла hk. Можно ли наложением совместить углы: a) hl и lk; б) hl и hk?
- 23. □ На рисунке 26 углы, обозначенные цифрами, равны. Укажите: а) биссектрису каждого из углов АОС, BOF, АОЕ; б) все углы, биссектрисой которых является луч ОС.
- 24. Измерьте ширину и длину учебника геометрии и выразите их в сантиметрах и в миллиметрах.
- 25.
 Измерив толщину учебника геометрии без обложки, найдите толщину одного листа.
Измерив толщину учебника геометрии без обложки, найдите толщину одного листа. - 26. □ Найдите длины всех отрезков, изображённых на рисунке 31, если за единицу измерения принят отрезок: a) KL; б) АВ.
- 27. □ Начертите отрезок АВ и луч h. Пользуясь масштабной линейкой, отложите на луче h от его начала отрезки, длины которых равны 2АВ, 1/2АВ и 1/4АВ.
- 28. Начертите прямую и отметьте на ней точки А и В. С помощью масштабной линейки отметьте точки С и D так, чтобы точка В была серединой отрезка АС, а точка D — серединой отрезка ВС.
- 29. Начертите прямую АВ. С помощью масштабной линейки отметьте на этой прямой точку С, такую, что АС = 2 см. Сколько таких точек можно отметить на прямой АВ?
- 30. □ Точка В делит отрезок АС на два отрезка. Найдите длину отрезка АС, если АВ = 7,8 см, ВС = 25 мм.
- 31. □ Точка В делит отрезок АС на два отрезка. Найдите длину отрезка ВС, если: а) АВ = 3,7 см, АС = 7,2 см; б) АВ = 4 мм, АС = 4 см.

- 32. Точки А, В и С лежат на одной прямой. Известно, что АВ = 12 см, ВС = 13,5 см. Какой может быть длина отрезка АС?
- 33. □ Точки В, D и М лежат на одной прямой. Известно, что BD = 7 см, MD = 16 см. Каким может быть расстояние ВМ?
- 34. Точка С — середина отрезка АВ, равного 64 см. На луче С А отмечена точка D так, что СD = 15см. Найдите длины отрезков BD и DA.
- 35. Расстояние между Москвой и С.-Петербургом равно 650 км. Город Тверь находится между Москвой и С.-Петербургом в 170 км от Москвы. Найдите расстояние между Тверью и С.-Петербургом, считая, что все три города расположены на одной прямой.
- 36. Лежат ли точки А, Б и С на одной прямой, если АС = 5 см, АВ = 3 см, ВС = 4 см?
Решение.
Если точки А, В и С лежат на одной прямой, то больший из отрезков АВ, ВС и АС равен сумме двух других. По условию больший из данных отрезков (отрезок АС) равен 5 см, а сумма двух других (АВ + ВС) равна 7 см. Поэтому точки А, B и С не лежат на одной прямой.
Поэтому точки А, B и С не лежат на одной прямой. - 37. Точка С — середина отрезка АВ, точка О — середина отрезка АС. Найдите: а) АС, СВ, АО и ОВ, если АВ = 2 см; б) АВ, АС, АО и OB, если СB = 3,2 м.
- 38. □ На прямой отмечены точки О, А и В так, что ОА = 12 см, ОB = 9 см. Найдите расстояние между серединами отрезков ОА и ОB, если точка О: а) лежит на отрезке АВ; б) не лежит на отрезке АВ.
- 39. Отрезок, длина которого равна а, разделён произвольной точкой на два отрезка. Найдите расстояние между серединами этих отрезков.
- 40. □ Отрезок, равный 28 см, разделён на три неравных отрезка. Расстояние между серединами крайних отрезков 16 см. Найдите длину среднего отрезка.
- 41. Начертите три неразвёрнутых угла и один развёрнутый угол и обозначьте их так: ∠AOB, ∠CDE, ∠hk и ∠ С помощью транспортира измерьте углы и запишите результаты измерений.

- 42. Начертите луч ОА и с помощью транспортира отложите от луча ОА углы АОВ, АОС и AOD так, чтобы ∠AOB = 23°, ∠AOC = 67°, ∠AOD = 138°.
- 43. Начертите угол, равный 70°, и с помощью транспортира проведите его биссектрису.
- 44. Начертите угол АОВ и с помощью транспортира проведите луч ОС так, чтобы луч ОА являлся биссектрисой угла ВОС. Всегда ли это выполнимо?
- 45. □ Градусные меры двух углов равны. Равны ли сами углы?
- 46. На рисунке 37 изображены лучи с общим началом О.
а) Найдите градусные меры углов АОХ, BOX, АОВ, СОВ, DOX; б) назовите углы, равные 20°; в) назовите равные углы; г) назовите все углы со стороной ОА и найдите их градусные меры. - 47. □ Луч ОЕ делит угол АОВ на два угла. Найдите ∠AOB, если:
а) ∠AOE = 44°, ∠EOB = 77°; б) ∠AOE = 12°37′, ∠EOB = 108°25′. - 48. Луч ОС делит угол АОВ на два угла. Найдите угол СОВ, если ∠AOB = 78°, а угол АОС на 18° меньше угла ВОС.

- 49. Луч ОС делит угол АОВ на два угла. Найдите угол АОС, если ∠AOB = 155°, а угол АОС на 15° больше угла СОВ.
- 50. □ Угол АОВ является частью угла АОС. Известно, что ∠AOC= 108°, ∠AOB = 3∠ Найдите угол АОВ.
- 51. □ На рисунке 38 угол AOD — прямой, ∠AOB = ∠BOC = ∠ Найдите угол, образованный биссектрисами углов АОВ и COD.
- 52. На рисунке 39 луч OV является биссектрисой угла ZOY, а луч OU — биссектрисой угла XOY. Найдите угол XOZ, если ∠UOV = 80°.
- 53. Луч l является биссектрисой неразвёрнутого угла hk. Может ли угол hl быть прямым или тупым?
- 58. □ Найдите угол, смежный с углом АВС, если: a) ∠ABC = 111°; б) ∠ABC = 90°; в) ∠ABC = 15°.
- 59. □ Один из смежных углов прямой. Каким (острым, прямым, тупым) является другой угол?
- 60.
 □ Верно ли утверждение: если смежные углы равны, то они прямые?
□ Верно ли утверждение: если смежные углы равны, то они прямые? - 61. Найдите смежные углы hk и kl, если: а) ∠hk меньше ∠kl на 40°; б) ∠hk больше ∠kl на 120°; в) ∠hk больше ∠kl на 47°18′; г) ∠hk = 3∠kl; д) ∠hk : ∠kl = 5:4.
- 62. На рисунке 46 углы BOD и COD равны. Найдите угол AOD, если ∠COB = 148°.
- 63. Даны два равных угла. Равны ли смежные с ними углы?
- 64. □ Найдите изображённые на рисунке 41 углы: а) 1, 3, 4, если ∠2 = 117°; б) 1, 2, 4, если ∠3 = 43°27′.
- 65. □ Найдите неразвёрнутые углы, образованные при пересечении двух прямых, если: а) сумма двух из них равна 114°; б) сумма трёх углов равна 220°.
- 66. □ На рисунке 41 найдите углы 1, 2, 3, 4, если: а) ∠2 + ∠4 = 220°; б) 3 (∠1 +∠3) = ∠2 + ∠4; в) ∠2 – ∠1 = 30°.
- 67. □ На рисунке 47 изображены три прямые, пересекающиеся в точке О. Найдите сумму углов: ∠1 + ∠2 + ∠
- 68.
 На рисунке 48 ∠AOB = 50°, ∠FOE = 70°. Найдите углы АОС, BOD, СОЕ и COD.
На рисунке 48 ∠AOB = 50°, ∠FOE = 70°. Найдите углы АОС, BOD, СОЕ и COD. - 69. □ Прямая а пересекает стороны угла А в точках Р и Q. Могут ли обе прямые АР и AQ быть перпендикулярными к прямой а?
- 70. □ Через точку А, не лежащую на прямой а, проведены три прямые, пересекающие прямую а. Докажите, что по крайней мере две из них не перпендикулярны к прямой а.
- 1. Сколько прямых можно провести через две точки?
- 2. Сколько общих точек могут иметь две прямые?
- 3. Объясните, что такое отрезок.
- 4. Объясните, что такое луч. Как обозначаются лучи?
- 5. Какая фигура называется углом? Объясните, что такое вершина и стороны угла.
- 6. Какой угол называется развёрнутым?
- 7. Какие фигуры называются равными?
- 8.
 Объясните, как сравнить два отрезка.
Объясните, как сравнить два отрезка. - 9. Какая точка называется серединой отрезка?
- 10. Объясните, как сравнить два угла.
- 11. Какой луч называется биссектрисой угла?
- 12. Точка С делит отрезок АВ на два отрезка. Как найти длину отрезка АВ, если известны длины отрезков АС и СВ?
- 13. Какими инструментами пользуются для измерения расстояний?
- 14. Что такое градусная мера угла?
- 15. Луч ОС делит угол АОВ на два угла. Как найти градусную меру угла АОВ, если известны градусные меры углов АОС и СОВ?
- 16. Какой угол называется острым? прямым? тупым?
- 17. Какие углы называются смежными? Чему равна сумма смежных углов?
- 18. Какие углы называются вертикальными? Каким свойством обладают вертикальные углы?
- 19. Какие прямые называются перпендикулярными?
- 20.
 Объясните, почему две прямые, перпендикулярные к третьей, не пересекаются.
Объясните, почему две прямые, перпендикулярные к третьей, не пересекаются. - 21. Какие приборы применяют для построения прямых углов на местности?
Дополнительные задачи (упр.№№ 71-86)
- 71. Отметьте четыре точки так, чтобы никакие три не лежали на одной прямой. Через каждую пару точек проведите прямую. Сколько получилось прямых?
- 72. Даны четыре прямые, каждые две из которых пересекаются. Сколько точек пересечения имеют эти прямые, если через каждую точку пересечения проходят только две прямые?
- 73. Сколько неразвёрнутых углов образуется при пересечении трёх прямых, проходящих через одну точку?
- 74. Точка N лежит на отрезке МР. Расстояние между точками М и Р равно 24 см, а расстояние между точками N и М в два раза больше расстояния между точками N и Р. Найдите расстояние: а) между точками N и Р; б) между точками N и М.
- 75.
 Три точки К, L, М лежат на одной прямой, КL = 6 см, LM = 10 см. Каким может быть расстояние КМ? Для каждого из возможных случаев сделайте чертёж.
Три точки К, L, М лежат на одной прямой, КL = 6 см, LM = 10 см. Каким может быть расстояние КМ? Для каждого из возможных случаев сделайте чертёж. - 76. Отрезок АВ длины а разделён точками Р и Q на три отрезка АР, PQ и QB так, что АР = 2PQ = 2QB. Найдите расстояние между: а) точкой А и серединой отрезка QB; б) серединами отрезков АР и QB.
- 77. Отрезок длины m разделён: а) на три равные части; б) на пять равных частей. Найдите расстояние между серединами крайних частей.
- 78. Отрезок в 36 см разделён на четыре не равные друг другу части. Расстояние между серединами крайних частей равно 30 см. Найдите расстояние между серединами средних частей.
- 79* □ Точки А, В и С лежат на одной прямой, точки М и N — середины отрезков АВ и АС. Докажите, что BC = 2MN.
- 80. Известно, что ∠AOB = 35°, ∠BOC = 50°. Найдите угол АОС. Для каждого из возможных случаев сделайте чертёж с помощью линейки и транспортира.

- 81. Угол hk равен 120°, а угол hm равен 150°. Найдите угол km. Для каждого из возможных случаев сделайте чертёж.
- 82. Найдите смежные углы, если: а) один из них на 45° больше другого; б) их разность равна 35°.
- 83. Найдите угол, образованный биссектрисами двух смежных углов.
- 84. Докажите, что биссектрисы вертикальных углов лежат на одной прямой.
- 85* □ Докажите, что если биссектрисы углов АВС и CBD перпендикулярны, то точки А, В и D лежат на одной прямой.
- 86. □ Даны две пересекающиеся прямые а и b и точка А, не лежащая на этих прямых. Через точку А проведены прямые m и n так, что m ⊥ а, n ⊥ Докажите, что прямые m и n не совпадают.
Вы смотрели: Практические задания и задачи из учебника геометрии для 7 класса к Главе 1 «Начальные геометрические сведения» (УМК Атанасян и др.) Ознакомительная версия перед покупкой книги. Цитаты из учебника представлены в учебных целях.
Цитаты из учебника представлены в учебных целях.
Вернуться к Оглавлению учебника по геометрии (Атанасян).
Разработка и внедрение экологически чистых гидроэнергетических турбин: предварительное проектирование и испытания модели Alden Turbine (технический отчет)
Фауст, Дж., Хекер, Г., Ли, С., и Аллен, Г. Разработка и внедрение экологически безопасных гидроэнергетических турбин: предварительное проектирование и испытания модели турбины Олдена . США: Н. п., 2011.
Интернет. DOI: 10,2172 / 1050066.
Фуст, Дж., Хеккер, Г., Ли, С., и Аллен, Г. Разработка и внедрение экологически безопасных гидроэнергетических турбин: предварительное проектирование и испытания модели турбины Олдена . Соединенные Штаты. https://doi.org/10.2172/1050066
Foust, J. , Hecker, G., Li, S., and Allen, G. Sat.
«Разработка и внедрение экологически чистых гидроэнергетических турбин: предварительное проектирование и испытания модели Alden Turbine».Соединенные Штаты. https://doi.org/10.2172/1050066. https://www.osti.gov/servlets/purl/1050066.
, Hecker, G., Li, S., and Allen, G. Sat.
«Разработка и внедрение экологически чистых гидроэнергетических турбин: предварительное проектирование и испытания модели Alden Turbine».Соединенные Штаты. https://doi.org/10.2172/1050066. https://www.osti.gov/servlets/purl/1050066.
@article {osti_1050066,
title = {Разработка и внедрение экологически чистых гидроэнергетических турбин: предварительное проектирование и испытания модели Alden Turbine},
author = {Фуст, Дж., Хеккер, Г., Ли, С. и Аллен, Г.},
abstractNote = {Турбина Олдена была разработана U.S. Бывшая программа передовых гидротурбинных систем Министерства энергетики (DOE) (1994-2006), а в последнее время - через Исследовательский институт электроэнергетики (EPRI) и программу DOE по ветро- и водной энергии. Основная цель описанного здесь технического исследования состояла в том, чтобы предоставить коммерчески конкурентоспособную конструкцию турбины, которая обеспечила бы выживаемость рыбы при пролете, сравнимую или превышающую выживаемость при обходе или проливании потока. Хотя конструкция турбины была выполнена для условий площадки, соответствующих чистому напору 92 футов (28 м) и расходу 1500 кубических футов в секунду (42.5 см), конструкция может быть изменена для дополнительных площадок с различными условиями эксплуатации. Во время разработки турбины были внесены изменения в конструкцию спирального корпуса, распределителя (упорные лопатки и калитки), рабочего колеса и отсасывающей трубы для улучшения характеристик турбины при сохранении характеристик, обеспечивающих высокую выживаемость прохода рыбы. Результаты расчета скоростей изменения давления и сдвига в проходе рабочего колеса были аналогичными для исходной и конечной геометрий турбины, в то время как прогнозируемые минимальные давления были выше для последней турбины.Ожидается, что окончательная геометрия турбины и результирующая среда потока дополнительно улучшат характеристики прохождения рыбы в турбине. Результаты расчетов для окончательного проекта показали, что КПД турбины повысился более чем на 6% в выбранных условиях эксплуатации по сравнению с исходной концепцией.
Хотя конструкция турбины была выполнена для условий площадки, соответствующих чистому напору 92 футов (28 м) и расходу 1500 кубических футов в секунду (42.5 см), конструкция может быть изменена для дополнительных площадок с различными условиями эксплуатации. Во время разработки турбины были внесены изменения в конструкцию спирального корпуса, распределителя (упорные лопатки и калитки), рабочего колеса и отсасывающей трубы для улучшения характеристик турбины при сохранении характеристик, обеспечивающих высокую выживаемость прохода рыбы. Результаты расчета скоростей изменения давления и сдвига в проходе рабочего колеса были аналогичными для исходной и конечной геометрий турбины, в то время как прогнозируемые минимальные давления были выше для последней турбины.Ожидается, что окончательная геометрия турбины и результирующая среда потока дополнительно улучшат характеристики прохождения рыбы в турбине. Результаты расчетов для окончательного проекта показали, что КПД турбины повысился более чем на 6% в выбранных условиях эксплуатации по сравнению с исходной концепцией. Перед выпуском гидравлических компонентов для изготовления модели были проведены расчеты методом конечных элементов для упорных лопаток, ворот калитки и рабочего колеса, чтобы убедиться, что критерии проектирования конструкции для напряжений и прогибов были выполнены.Физическая модель турбины была изготовлена и испытана с использованием собранных данных о мощности и КПД, пределах кавитации, скорости разгона, осевой и радиальной осевой нагрузке, пульсации давления и крутящем моменте калитки. Было замечено, что все параметры находятся в пределах ожидаемых для обычных машин с радиальным потоком. На основе этих измерений ожидаемый пик эффективности для прототипа составляет 93,64%. Эти данные были использованы в окончательной проклейке опорного механического и баланса заводского оборудования.Предварительная стоимость оборудования по проектной документации составляет 1450 долларов США / кВт при общем графике поставки 28 месяцев. Поставка оборудования включает турбину, генератор, средства управления агрегатом, ограниченный баланс заводского оборудования, монтаж на месте и ввод в эксплуатацию.
Перед выпуском гидравлических компонентов для изготовления модели были проведены расчеты методом конечных элементов для упорных лопаток, ворот калитки и рабочего колеса, чтобы убедиться, что критерии проектирования конструкции для напряжений и прогибов были выполнены.Физическая модель турбины была изготовлена и испытана с использованием собранных данных о мощности и КПД, пределах кавитации, скорости разгона, осевой и радиальной осевой нагрузке, пульсации давления и крутящем моменте калитки. Было замечено, что все параметры находятся в пределах ожидаемых для обычных машин с радиальным потоком. На основе этих измерений ожидаемый пик эффективности для прототипа составляет 93,64%. Эти данные были использованы в окончательной проклейке опорного механического и баланса заводского оборудования.Предварительная стоимость оборудования по проектной документации составляет 1450 долларов США / кВт при общем графике поставки 28 месяцев. Поставка оборудования включает турбину, генератор, средства управления агрегатом, ограниченный баланс заводского оборудования, монтаж на месте и ввод в эксплуатацию. Основываясь на выбранных расчетных условиях напора и потока, выживаемость рыбы при прохождении через последнюю турбину оценивается примерно в 98% для рыбы диаметром 7,9 дюйма (200 мм), а прогнозируемая выживаемость достигает 100% для рыбы размером 3,9 дюйма (100 мм). и меньше по длине.Обратите внимание, что рыба длиной до 7,9 дюймов (200 мм) составляет более 90% рыбы, уловленной на гидроэлектростанциях в США. Завершение этих усилий обеспечивает механическую и электрическую конструкцию, которая может быть легко адаптирована к условиям конкретной площадки с дополнительными инженерными разработками, сопоставимыми с затратами, связанными с традиционными конструкциями турбин.},
Основываясь на выбранных расчетных условиях напора и потока, выживаемость рыбы при прохождении через последнюю турбину оценивается примерно в 98% для рыбы диаметром 7,9 дюйма (200 мм), а прогнозируемая выживаемость достигает 100% для рыбы размером 3,9 дюйма (100 мм). и меньше по длине.Обратите внимание, что рыба длиной до 7,9 дюймов (200 мм) составляет более 90% рыбы, уловленной на гидроэлектростанциях в США. Завершение этих усилий обеспечивает механическую и электрическую конструкцию, которая может быть легко адаптирована к условиям конкретной площадки с дополнительными инженерными разработками, сопоставимыми с затратами, связанными с традиционными конструкциями турбин.},
doi = {10.2172 / 1050066},
url = {https://www.osti.gov/biblio/1050066},
журнал = {},
номер =,
объем =,
place = {United States},
год = {2011},
месяц = {10}
}
р.D. Sharma Solutions Class 9
Вопрос: 1 На рисунке О — центр круга. Если ∠APB = 50 °, найдите AOB и ∠OAB.
Если ∠APB = 50 °, найдите AOB и ∠OAB.
∠APB = 50 °
По теореме о степени меры
∠AOB = 2∠APB
⇒ ∠APB = 2 × 50 ° = 100 °, так как OA = OB [радиус круга]
Тогда ∠OAB = ∠OBA [Углы напротив равных]
Пусть ∠OAB = x
In ΔOAB, по свойству суммы углов
∠OAB + ∠OBA + ∠AOB = 180 °
⟹ x + x + 100 ° = 180 °
⟹ 2x = 180 ° -100 °
⟹ 2x = 80 °
⟹ x = 40 °
∠OAB = ∠OBA = 40 °
Вопрос: 2На рисунке показано, что O является центром круга и ∠AOC = 150 °.Найдите ∠ABC.
Решение:∠AOC = 150 °
∴ ∠AOC + рефлекс ∠AOC = 360 ° [Комплексный угол]
⇒ 150 ° + рефлекс ∠AOC = 360 °
⇒ рефлекс ∠AOC = 360 ° — 150 °
⇒ рефлекс ∠AOC = 210 °
⇒ 2∠ABC = 210 ° [По теореме о степени меры]
⇒ ABC = 210 ° / 2 = 105 °
Вопрос: 3 На рисунке О — центр круга. Найдите ∠BAC.
Найдите ∠BAC.
Имеем ∠AOB = 80 °
А AOC = 110 °
Следовательно, AOB + ∠AOC + ∠BOC = 360 ° [Полный угол]
⇒ 80 ° + 100 ° + ∠BOC = 360 °
⇒ ∠BOC = 360 ° — 80 ° — 110 °
⇒ ∠BOC = 170 °
По теореме о степени меры
∠BOC = 2∠BAC
⇒ 170 ° = 2∠BAC
⇒ ∠BAC = 170 ° / 2 = 85 °
Вопрос: 4Если O — центр круга, найдите значение x на каждом из следующих рисунков.
Решение:(i) AOC = 135 °
∴ ∠AOC + ∠BOC = 180 ° [Пара линейных углов]
⇒ 135 ° + ∠BOC = 180 °
⇒ ∠BOC = 180 ° — 135 °
⇒ ∠BOC = 45 °
По теореме о степени меры
∠BOC = 2∠CPB
⇒ 45 ° = 2x
⇒ x = 45 ° / 2 = 22½ °
(ii) Имеем ∠ABC = 40 °
∠ACB = 90 ° [Угол в полукруге]
В ΔABC, по свойству суммы углов
∠CAB + ∠ACB + ∠ABC = 180 °
⇒ ∠КАБИНА + 90 ° + 40 ° = 180 °
⇒ ∠CAB = 180 ° — 90 ° — 40 °
⇒ ∠CAB = 50 °
Теперь ∠CDB = ∠CAB [Угол в сегменте такой же]
⇒ x = 50 °
(iii) У нас
∠AOC = 120 ° По теореме о степени меры.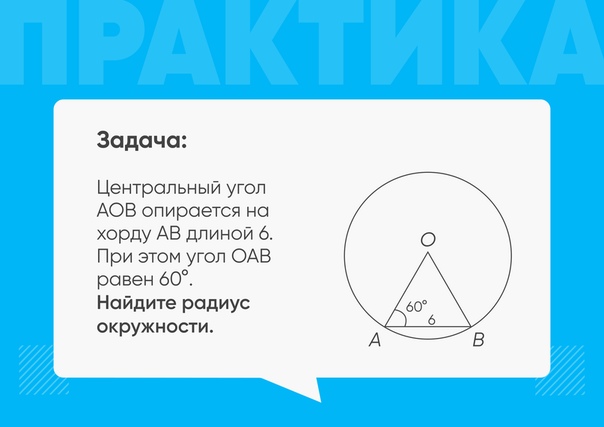
∠AOC = 2∠APC
⇒ 120 ° = 2∠APC
⇒ ∠APC = 120 ° / 2 = 60 °
∠APC + ∠ABC = 180 ° [Противоположные углы вписанных четырехугольников]
⇒ 60 ° + ∠ABC = 180 °
⇒ ABC = 180 ° — 60 °
⇒ ∠ABC = 120 °
∴ ∠ABC + ∠DBC = 180 ° [Линейная пара углов]
⇒ 120 + x = 180 °
⇒ x = 180 ° — 120 ° = 60 °
(iv) У нас
∠CBD = 65 °
∴ ∠ABC + ∠CBD = 180 ° [Линейная пара углов]
⇒ ABC = 65 ° = 180 °
⇒ ABC = 180 ° — 65 ° = 115 °
∴ рефлекс ∠AOC = 2∠ABC [По теореме о степени меры]
⇒ x = 2 × 115 °
⇒ x = 230 °
(v) У нас
∠OAB = 35 ° Тогда
∠OBA = ∠OAB = 35 ° [Углы, противоположные равным радиусам]
In ΔAOB, по свойству суммы углов
⇒ AOB + ∠OAB + ∠OBA = 180 °
⇒ ∠AOB + 35 ° + 35 ° = 180 °
⇒ AOB = 180 ° −35 ° — 35 ° = 110 °
∴ ∠AOB + рефлекс ∠AOB = 360 ° [Комплексный угол]
⇒ 110 ° + рефлекс ∠AOB = 360 °
⇒ рефлекс ∠AOB = 360 ° — 110 ° = 250 °
По теореме о степени меры reflex
∠AOB = 2∠ACB
⇒ 250 ° = 2x
⇒ x = 250 ° / 2 = 125 °
(vi) У нас
∠AOB = 60 ° По теореме о градусной мере reflex
∠AOB = 2∠ACB
⇒ 60 ° = 2∠ACB
⇒ ∠ACB = 60 ° / 2 = 30 ° [углы, противоположные равным радиусам]
⇒ x = 30 °.
(vii) У нас
∠BAC = 50 ° и ∠DBC = 70 °
∴ ∠BDC = ∠BAC = 50 ° [Угол в том же сегменте]
В ΔBDC, по свойству суммы углов
∠BDC + ∠BCD + ∠DBC = 180 °
⇒ 50 ° + x + 70 ° = 180 °
⇒ x = 180 ° — 50 ° — 70 ° = 60 °
(viii) У нас
∠DBO = 40 ° и ∠DBC = 90 ° [Угол в полукруге]
⇒ DBO + ∠OBC = 90 °
⇒ 40 ° + ∠OBC = 90 °
⇒ OBC = 90 ° — 40 ° = 50 ° Теорема о градусной мере
∠AOC = 2∠OBC
⇒ x = 2 × 50 ° = 100 °
(ix) В ΔDAB, по свойству суммы углов
∠ADB + ∠DAB + ∠ABD = 180 °
⇒ 32 ° + ∠DAB + 50 ° = 180 °
⇒ ∠DAB = 180 ° — 32 ° — 50 °
⇒ ∠DAB = 98 °
Итак, ∠OAB + ∠DCB = 180 ° [Противоположные углы циклического четырехугольника]
⇒ 98 ° + x = 180 °
⇒ x = 180 ° — 98 ° = 82 °
(x) Имеем,
∠BAC = 35 °
∠BDC = ∠BAC = 35 ° [Угол в том же сегменте]
В ΔBCD, по свойству суммы углов
∠BDC + ∠BCD + ∠DBC = 180 °
⇒ 35 ° + x + 65 ° = 180 °
⇒ x = 180 ° — 35 ° — 65 ° = 80 °
(xi) У нас
∠ABD = 40 °
∠ACD = ∠ABD = 40 ° [Угол в том же сегменте]
В ΔPCD, по свойству суммы углов
∠PCD + ∠CPO + ∠PDC = 180 °
⇒ 40 ° + 110 ° + x = 180 °
⇒ x = 180 ° — 150 °
⇒ x = 30 °
(xii) Учитывая это,
∠BAC = 52 °
Тогда ∠BDC = ∠BAC = 52 ° [Угол в том же сегменте]
Так как OD = OC
Тогда ∠ODC = ∠OCD [Противоположный угол равным радиусам]
⇒ x = 52 °
Вопрос: 5 O — длина окружности треугольника ABC, OD перпендикулярен BC. Докажите, что ∠BOD = ∠A.
Докажите, что ∠BOD = ∠A.
Дана O — центр описанной окружности треугольника ABC и OD⊥BC
.Доказать ∠BOD = 2∠A
Проба:
In ΔOBD и ΔOCD
ODB = ∠ODC [каждые 90 °]
OB = OC [Радиус круга]
OD = OD [Обычный]
Тогда ΔOBD ≅ ΔOCD [по условию RHS].
∴ ∠BOD = ∠COD …. (i) [PCT].
По теореме о степени меры
∠BOC = 2∠BAC
⇒ 2∠BOD = 2∠BAC [Используя (i)]
⇒ BOD = ∠BAC.
Вопрос: 6На рисунке O — центр окружности, BO — биссектриса ∠ABC. Покажем, что AB = AC.
Решение:Учитывая, что BO является биссектрисой ∠ABC
Доказать, что AB = BC
Проба:
Так как BO — биссектриса ABC.
Тогда ∠ABO = ∠CBO … (i)
Поскольку, OB = OA [Радиус окружности]
Тогда ∠ABO = ∠DAB… (ii) [противоположные углы к равным сторонам]
Так как OB = OC [Радиус окружности]
Тогда ∠OAB = ∠OCB . .. (iii) [противоположные углы к равным сторонам]
.. (iii) [противоположные углы к равным сторонам]
Сравните уравнения (i), (ii) и (iii)
∠OAB = OCB … (iv)
In ΔOAB и ΔOCB
∠OAB = ∠OCB Из (iv)]
∠OBA = ∠OBC [дано]
OB = OB [общий]
Тогда ΔOAB ≅ ΔOCB [По условию AAS]
∴ AB = BC [CPCT]
Вопрос: 7На рисунке O — центр круга, затем докажите, что ∠x = ∠y + ∠z.
Решение:У нас,
∠3 = ∠4 [Углы в одном сегменте]
∴ ∠x = 2∠3 [По теореме о степени меры]
⇒ ∠x = ∠3 + ∠3
⇒ ∠x = ∠3 + ∠4 … (i) [∠3 = угол 4]
Но ∠y = ∠3 + ∠1 [По свойству внешнего угла]
⇒ ∠3 = ∠y — ∠1 …. (ii)
из пунктов (i) и (ii)
∠x = ∠y — ∠1 + ∠4
⇒ ∠x = ∠y + ∠4 — ∠1
⇒ ∠x = ∠y + ∠z + ∠1 — ∠1 [По свойству внешнего угла]
⇒ ∠x = ∠y + ∠z
Вопрос: 8 На рисунке O и O ‘- центры двух окружностей, пересекающихся в точках B и C. ACD — прямая линия, найдите x.
ACD — прямая линия, найдите x.
По теореме о степени меры
∠AOB = 2∠ACB
⇒ 130 ° = 2∠ACB
⇒ ∠ACB = 130 ° / 2 = 65 °
∴ ∠ACB + ∠BCD = 180 ° [Облицовка пары углов]
⇒ 65 ° + ∠BCD = 180 °
⇒ ∠BCD = 180 ° — 65 ° = 115 ° По теореме о градусной мере reflex
∠BOD = 2∠BCD
⇒ рефлекс ∠BOD = 2 × 115 ° = 230 °
Теперь рефлекс ∠BOD + ∠BO′D = 360 ° [Комплексный угол]
⇒ 230 ° + x = 360 °
⇒ x = 360 ° — 230 °
∴ х = 130 °
Вопрос: 9На рисунке O — центр круга, а PQ — диаметр.Если
∠ROS = 40 °, найти ∠RTS.
Решение:Поскольку PQ имеет диаметр
Затем,
∠PRQ = 90 ° [Угол в полукруге]
∴ ∠PRQ + ∠TRQ = 180 ° [Пара линейных углов]
900 + ∠TRQ = 180 °
∠TRQ = 180 ° — 90 ° = 90 °.
По теореме о степени меры
∠ROS = 2∠RQS
⇒ 40 ° = 2∠RQS
⇒ ∠RQS = 40 ° / 2 = 20 °
В ΔRQT, по свойству Сумма углов
∠RQT + ∠QRT + ∠RTS = 180 °
⇒ 20 ° + 90 ° + ∠RTS = 180 °
⇒ ∠RTS = 180 ° — 20 ° — 90 ° = 70 °
Вопрос: 10На рисунке, если ACB = 40 °, ∠DPB = 120 °, найдите ∠CBD.
Решение:У нас,
∠ACB = 40 °; ∠DPB = 120 °
∴ ∠APB = ∠DCB = 40 ° [Угол в том же сегменте]
В ΔPOB, по свойству суммы углов
∠PDB + ∠PBD + ∠BPD = 180 °
⇒ 40 ° + ∠PBD + 120 ° = 180 °
⇒ ∠PBD = 180 ° — 40 ° — 120 °
⇒ ∠PBD = 20 °
∴ ∠CBD = 20 °
Вопрос: 11Хорда круга равна радиусу круга.Найдите угол, образуемый хордой в точке на малой дуге, а также в точке на большой дуге.
Решение:У нас,
Радиус OA = Хорда AB
⟹ OA = OB = AB
Тогда треугольник OAB — равносторонний треугольник.
∴ ∠AOB = 60 ° [один угол равностороннего треугольника]
По теореме о степени меры
∠AOB = 2∠APB
⇒ 60 ° = 2∠APB
⇒ ∠APB = 60 ° / 2 = 30 °
Теперь ∠APB + ∠AQB = 180 ° [противоположные углы циклического четырехугольника]
⇒ 300 + ∠AQB = 180 °
⇒ ∠AQB = 180 ° — 30 ° = 150 °.
Следовательно, Угол по хорде AB при малой дуге = 150 °
Угол по хорде AB при большой дуге = 30 °
рупий Aggarwal 2018 для класса 7 по математике Глава 14
Страница № 177:
Вопрос 1:
На данном рисунке л || м и т поперечный.
Если ∠5 = 70 °, найдите размер каждого из углов
∠1, ∠3, ∠4 и ∠8.
Ответ:
Дано: l∥mt — поперечное сечение. 5 = 70 ° ∠5 = ∠3 = 70 ° (альтернативные внутренние углы) ∠5 + ∠8 = 180 ° (линейная пара) или 70 ° + ∠8 = 180 ° ∠ 8 = 110 ° 1 = ∠3 = 70 ° (вертикально противоположные углы) ∠3 + ∠4 = 180 ° (линейная пара) или ∠4 = 180-∠3 = 180-70 = 110 °
Страница № 178:
Вопрос 2:
На данном рисунке л || м и т поперечный. Если ∠1 и ∠2 находятся в соотношении 5: 7, найдите размер каждого из углов
Если ∠1 и ∠2 находятся в соотношении 5: 7, найдите размер каждого из углов
∠1, ∠2, ∠3 и ∠8.
Ответ:
Дано: l∥mt — трансверсаль. 1: ∠2 = 5: 7 Пусть углы составляют 5x и 7x. ∠1 + ∠2 = 180 ° (линейная пара) ∴ 5x + 7x = 180 или 12x = 180 или x = 15 ∠1 = 5x = 5 (15) = 75 ° и ∠2 = 7x = 7 (15) = 105 ° ∠2 + ∠3 = 180 ° (линейная пара) ∠3 = 180-105 = 75 ° ∠3 + ∠6 = 180 (внутренние углы на одной стороне поперечины являются дополнительными) ∠6 = 180-3 = 105 ° и ∠6 = ∠8 = 105 ° (вертикально противоположные углы) ∴ ∠1 = 75 ° ∠2 = 105 ° ∠3 = 75 ° ∠8 = 105 °
Страница № 178:
Вопрос 3:
Две параллельные линии l и m , разрезанные поперечно t .Если внутренние углы одной и той же стороны t равны (2 x — 8) ° и (3 x — 7) °, найдите размер каждого из этих углов.
Ответ:
Дано: l∥mt является поперечной. Пусть: ∠1 = (2x-8) ° ∠2 = (3x-7) ° Мы знаем, что следующие друг за другом внутренние углы являются дополнительными. 1 + ∠2 = 180 ° или (2x-8) + (3x-7) = 180 или 5x -15 = 180 или 5x = 195 или x = 39∠1 = (2x-8) = (2 × 39-8) = 70 ° ∠2 = (3x-7 ) = (3 × 39-7) = 110 °
Страница № 178:
Вопрос 4:
На данном рисунке л || м .Если s и t должны быть поперечными, так что s не параллельна t . найдите значения x и y .
Ответ:
Из данного рисунка:
∠ 1 = ∠3 = 50 ° (соответствующие углы) и ∠ 1 + x ° = 180 ° (линейная пара) или x ° = 180 ° — 50 ° = 130 ° или x = 130∠ 2 = ∠4 = 65 ° (соответствующие углы) и ∠ 2 + y ° = 180 ° (линейная пара) или y ° = 180 ° — 65 ° = 115 ° или y = 115
Страница № 178:
Вопрос 5:
На данном рисунке B = 65 ° и ∠ C = 45 ° в ∆ ABC и DAE || г. до н.э. .Если ∠ DAB = x ° и ∠ EAC = y ° , найдите значения x и y .
до н.э. .Если ∠ DAB = x ° и ∠ EAC = y ° , найдите значения x и y .
Ответ:
Дано: ∠B = 65 ° ∠C = 45 ° DAE∥ BC Указанные прямые параллельны. ∴ x ° = ∠B = 65 ° (чередующиеся углы, когда AB принимается за поперечное) y ° = ∠C = 45 ° (чередующиеся углы, когда AC принимается в качестве поперечного) ∴ x = 65 y = 45
Страница № 178:
Вопрос 6:
На следующем рисунке указано, что CE || BA , ∠ BAC = 80 ° и ∠ EC D = 35 °.
Найдите (i) ACE , (ii) ∠ ACB , (iii) ABC .
Ответ:
Дано: CE BA BAC = 80 °, ∠ECD = 35 ° (i) ∠BAC = ∠ACE = 80 ° (чередующиеся углы с AC в качестве поперечного) (ii) ∠ACB + ∠ACD = 180 ° (линейный пара) или ACB + ∠ACE + ∠ECD = 180 ° или ACB + 80 ° + 35 ° = 180 ° или ∠ACB = 65 ° (iii) в ∆ABC: BAC + ∠ACB + ∠ABC = 180 ° (свойство суммы углов) 80 ° + 65 ° + ABC = 180 ° ∠ABC = 35 °
Страница № 178:
Вопрос 7:
На следующем рисунке указано, что AO || CD, OB || CE и AOB = 50 °
Найдите размер ∠ ECD .
Ответ:
Дано: AO∥ CD OB ∥CE ∠AOB = 50 ° ∠AOD = ∠CDB = 50 ° (когда AO∥ CD и OB являются поперечными) ∠ECD + ∠CDB = 180 ° (последовательные внутренние углы являются дополнительными, DB ∥ CE и CD — поперечные) ∠ECD = 180 ° -50 ° = 130 °
Страница № 178:
Вопрос 8:
На следующем рисунке указано, что AB || CD, ∠ AOB = 50 ° и ∠CDO = 40 °.
Найдите размер ∠ BOD .
Ответ:
Дано: AB∥ CD ∠ABO = 50 ° ∠CDO = 40 ° Конструкция: Через точку O проведите EOF∥AB. ABO = ∠BOF = 50 ° (чередующиеся углы, когда AB∥EF и OB являются поперечными) ∠FOD = ∠ODC = 40 ° (чередующиеся углы, когда CD∥EF и OD являются поперечными) ∠BOD = ∠BOF + ∠FOD∠BOD = 50 ° + 40 ° = 90 °
Страница № 178:
Вопрос 9:
На данном рисунке AB || CD и поперечный EF разрезают их на G и H соответственно.
Если GL и HM являются биссектрисами альтернативных углов ∠ AGH и ∠ GHD соответственно, докажите, что GL || НМ .
Ответ:
Дано: AB ∥CD GL и HM — биссектрисы углов ∠AGH и ∠GHD соответственно. AGH = ∠GHD (альтернативные углы) или 12 ∠AGH = 12∠GHD или ∠LGH = ∠GHM (дано) Следовательно, GL ∥ HM, как мы знаем, что если углы любой пары альтернативных внутренних углов равны, то прямые параллельны.
Страница № 179:
Вопрос 10:
На данном рисунке AB || CD ,
∠ ABE = 120 °, ∠ ECD = 100 ° и ∠ BEC = x °
Найдите значение x .
Ответ:
Дано: AB ∥CD ∠ABE = 120 ° ∠ECD = 100 ° ∠BEC = x ° Конструкция: FEG ∥AB Теперь, поскольку AB∥FEG и AB∥CD, FEG∥CD∴ EFG∥AB∥CD∠ABE = ∠BEG = 120 ° (альтернативные углы) или x ° + y ° = 120 °. … (i) ∠DCE = ∠CEF = 100 ° (альтернативные углы) или x ° + z ° = 100 ° ….. (ii) Кроме того, x ° + y ° + z ° = 180 ° (FEG является прямой линией) … (iii) Складываем (i) и (ii): 2x ° + y ° + z ° = 220 ° или, x ° + 180 ° = 220 ° (заменяя (iii)) x ° = 40 ° ∴ x = 40
… (i) ∠DCE = ∠CEF = 100 ° (альтернативные углы) или x ° + z ° = 100 ° ….. (ii) Кроме того, x ° + y ° + z ° = 180 ° (FEG является прямой линией) … (iii) Складываем (i) и (ii): 2x ° + y ° + z ° = 220 ° или, x ° + 180 ° = 220 ° (заменяя (iii)) x ° = 40 ° ∴ x = 40
Страница № 179:
Вопрос 11:
На данном рисунке ABCD представляет собой четырехугольник, в котором AB || DC и AD || г. до н.э. .
Докажите, что ∠ ADC = ∠ ABC .
Ответ:
Дано: AB∥ CD AD∥ BC∠1 + ∠2 = 180 ° (AB∥CD и AD — трансверсаль) … (i) ∠2 + ∠3 = 180 ° (AD∥BC и AB — трансверсаль ) … (ii) Из (i) и (ii): ∠1 + ∠2 = 180 ° = ∠2 + ∠3 ∠1 = ∠3∠ADC = ∠ABC
Страница № 179:
Вопрос 12:
На данном рисунке л || м и p || q .
Найдите размер каждого из углов ∠ a , ∠ b , ∠ c и ∠ d .
Ответ:
Дано: l∥m p∥q ∠1 = 65 ° ∴∠1 = ∠a = 65 ° (вертикально противоположные углы) ∠a + ∠d = 180 ° (следующие друг за другом внутренние углы на одной и той же стороне трансверсали являются дополнительными) или ∠d = 180 ° -65 ° = 115 ° ∠c + ∠d = 180 ° (последовательные внутренние углы на одной и той же стороне поперечного сечения являются дополнительными) или ∠c = 180 ° -115 ° = 65 ° ∠c + ∠b = 180 ° (последовательные внутренние углы на одной и той же стороне поперечного являются дополнительными) или ∠b = 180 ° -65 ° = 115 ° ∴ ∠a = 65 ° ∠b = 115 ° ∠c = 65 ° ∠d = 115 °
Страница № 179:
Вопрос 13:
На данном рисунке AB || DC и AD || BC, и AC — диагональ.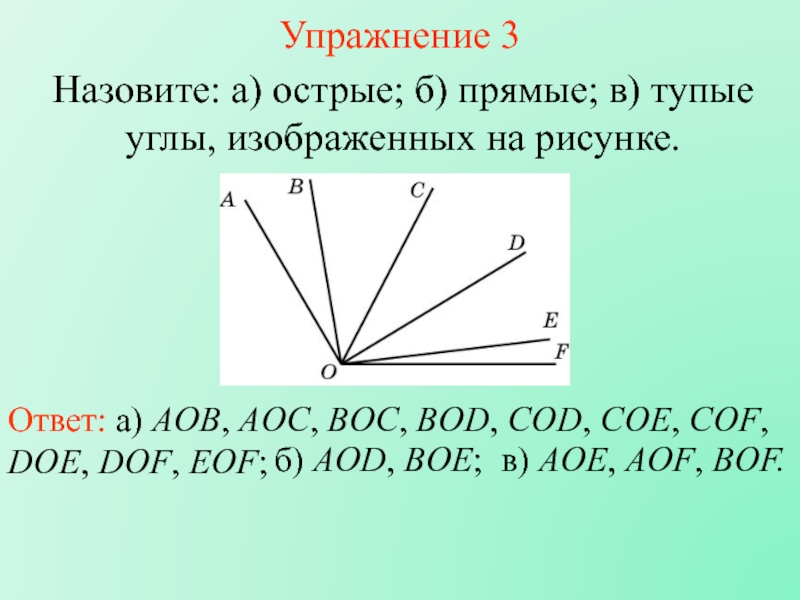 Если ∠ BAC = 35 °, ∠ CAD = 40 °, ∠ACB = x ° и ∠ ACD = y °, найдите значение x и y
Если ∠ BAC = 35 °, ∠ CAD = 40 °, ∠ACB = x ° и ∠ ACD = y °, найдите значение x и y
Ответ:
Дано: AB∥ DCAD∥BC∠BAC = 35 ° ∠CAD = 40 ° ∴ ∠BAC = y = 35 ° (чередующиеся углы при AB∥DC) ∠CAD = x = 40 ° (чередующиеся углы при AD∥BC) ∴ х = 40 у = 35
Страница № 179:
Вопрос 14:
На данном рисунке AB || CD и CA были произведены по E , так что ∠ BAE = 125 °.
Если ∠ BAC = x °, ∠ ABD = x °, ∠ BDC = y ° и ∠ ACD = z °, найдите значения x , у, z .
Ответ:
Дано: AB ∥CD ∠BAE = 125 ° ∠CAB + ∠BAE = 180 ° или 125 ° + x ° = 180 ° или x = 55x + z = 180 ° (последовательные внутренние углы на одной и той же стороне поперечного сечения являются дополнительными) z = 180-x = 180-55 = 125y + x = 180 ° (последовательные внутренние углы на одной стороне поперечного являются дополнительными) y = 180- x = 180-55 = 125
Страница № 179:
Вопрос 15:
На каждом из приведенных рисунков две линии l и m прорезаны трансеврсалом t .
Найти ли л || м .
Ответ:
(i) ∠1 + ∠2 = 180 (линейная пара) или 130 ° + ∠2 = 180 ° или ∠2 = 50 ° ≠ 40 ° = ∠3∴ l∦m (ii) ∠2 + ∠3 = 180 ° (линейная пара) 35 ° + ∠3 = 180 ° ∠3 = 145 ° = 145 ° = ∠1 ∴ l∥m (iii) ∠2 + ∠3 = 180 (линейная пара) ∠3 = 180 ° — 125 ° = 55 ° ∠3 = 55 ° ≠ 60 ° = ∠1∴ л∦м
Просмотреть решения NCERT для всех глав класса 7
важных вопросов для кружков по математике класса 9 CBSE
важных вопросов по математике класса 9 CBSE, глава 4 кружков
Темы и подтемы в Учебнике математики NCERT для класса 9 Глава 10 Круги:
- Круги
- Введение
- Круги и связанные с ним термины: обзор
- Угол, образованный хордой в точке
- Перпендикуляр от центра к хорде
- Обведите три точки
- Равные аккорды и их расстояние от центра
- Угол, образованный дугой окружности
- Циклические четырехугольники
- Сводка
ОЧЕНЬ КОРОТКИЙ ОТВЕТ НА ВОПРОСЫ
1. На данном рисунке O — центр круга, хорды AP и BP соединены с R и Q соответственно. Если ∠QPR = 35 °, найдите меру ∠AOB. [CBSE-14-17DIG1U]
На данном рисунке O — центр круга, хорды AP и BP соединены с R и Q соответственно. Если ∠QPR = 35 °, найдите меру ∠AOB. [CBSE-14-17DIG1U]
Ответ.
2. Какова мера угла x на данном рисунке?
Ответ. Мы знаем, что внешний угол вписанного четырехугольника равен внутреннему противоположному углу.
.-. ∠ CBE = ∠ ADC
=> x = 120 °
Дополнительные ресурсы для CBSE Class 9
3.На данном рисунке, если O — центр круга и POQ = 110 °, то найти ∠PRQ
Ответ. Мы знаем, что угол, образованный дугой в центре, в два раза больше угла, образованного ею в оставшейся части круга.
∠PRQ = 1/2 ∠POQ
= 1/2 x 110 °
= 55 °
4. На данном рисунке ΔABC — равносторонний треугольник, а ABDC — вписанный четырехугольник, затем найдите меру ∠BDC.
Ответ.
5. На данном рисунке О — центр круга. PQ — это хорда окружности, а R — любая точка на окружности. Если ∠PRQ = l и ∠OPQ = m, найти l + m.
Ответ.
6. На данном рисунке показан круг с центром O, в котором диаметр AB делит пополам хорду PQ в точке R. Если PR = RQ = 8 см и RB = 4 см, найдите радиус круга.
Ответ.
7. На данном рисунке ABCD представляет собой вписанный четырехугольник, такой что ∠ADB = 40 ° и ∠DCA = 70 °, затем найдите меру ∠DAB.
Ответ.
8. На рисунке «O» — центр круга, ABO = 20 ° и ∠ACO = 30 °, где A, B, C — точки на окружности. Какое значение x?
Ответ.
9. На данном рисунке, если O — центр круга.Хорда AB равна радиусу окружности, затем найти ∠ACB.
На данном рисунке, если O — центр круга.Хорда AB равна радиусу окружности, затем найти ∠ACB.
Ответ.
10. Если на данном рисунке ∠OAB = 40 °, то найдите меру ∠ACB. [Проблема с образцом NCERT]
Ответ.
11. На данном рисунке О — центр круга. Если BOC = 120 °, найдите значение x.
Ответ.
12.На данном рисунке O — центр круга, затем сравните хорды.
Ответ. В аккордах AB и CD AB проходит через центр круга. AB — диаметр круга. Таким образом, AB> CD [v диаметр — самая большая хорда]
13. На данном рисунке ∠ACP = 40 ° и ∠BPD = 120 °, затем найдите ∠CBD.
Ответ.
14. На данном рисунке, если ∠SEC = 120 °, ∠DCE = 25 °, найти BAC.
Ответ.
15. AD — диаметр окружности, а AB — хорда. Если AD = 34 см, AB = 30 см, то найдите расстояние AB от центра круга. [CBSE, март 2012 г.]
Ответ.
16. На данном рисунке, если ∠DAB = 60 °, ∠ABD = 50 °, найти ∠ACB. [Проблема с образцом NCERT]
Ответ.
17.На данном рисунке AB || ОКРУГ КОЛУМБИЯ. Если ∠A = 50 °, найти меру ABC. [Проблема с образцом NCERT]
Ответ.
КРАТКИЕ ВОПРОСЫ ТИП-I
18. Равные хорды окружности образуют равные углы в центре. [CBSE, март 2012 г.]
Ответ.
19. Если углы, образуемые хордами окружности в центре, равны, то хорды равны. [CBSE, март 2012 г.]
Ответ.
20. На рисунке O — центр окружности, ∠ABC = 45 °. Покажи, что OA⊥OC [/ latex]. [CBSE, март 2013 г.]
Ответ. Поскольку угол, образованный дугой в центре окружности, в два раза больше угла, образованного ею в любой точке оставшейся части окружности.
21. На данном рисунке ∠PQR = 100 °, где P, Q и R — точки на окружности с центром O. Найдите ∠OPR. [CBSE, март 2012 г.]
Ответ.
22. На рисунке ABCD представляет собой вписанный четырехугольник, в котором AB продолжается до F и BE || ОКРУГ КОЛУМБИЯ. Если ∠FBE = 20 ° и ∠DAB = 95 °, найдите ADC. [CBSE, март 2012 г.]
Ответ.
23. На рисунке хорда AB окружности с центром O переходит в точку C, так что BC = OB. CO соединяется и создается так, чтобы пересечь круг в D. Если ∠ACD = y и ∠AOD = x, покажите, что x = 3y. [CBSE, март 2011 г.]
[CBSE, март 2011 г.]
Ответ.
24. Если прямая пересекает две концентрические окружности (окружности с одинаковым центром) с центром O в точках A, B, C и D, докажите, что AB = CD (см. Рис.). [CBSE, март 2013 г.]
Ответ. Нарисуйте OM⊥ l
Так как перпендикуляр от центра окружности к хорде окружности делит хорду пополам.
BM = CM… (i)
и AM = DM… (ii)
Вычитая (i) из (ii), мы получаем
AM — BM = DM — CM
AB = CD
25.На данном рисунке P — центр круга. Докажите, что: ∠ XPZ = 2 (∠ XZY + ∠ YXZ)
Ответ.
26. Два круга пересекаются в двух точках B и C. Через B два отрезка ABD и PBQ пересекаются с кругами в точках A, D и P, Q соответственно (см. Рис.). Докажите, что ∠ ACP = ∠ QCD.
Ответ.
27. Если диагонали вписанного четырехугольника являются диаметрами окружности, проходящей через противоположные вершины четырехугольника.Докажите, что четырехугольник — прямоугольник. [CBSE-14-GDQNI3W]
Ответ.
КОРОТКИЙ ОТВЕТ НА ВОПРОСЫ ТИП-II
28. Если непараллельные стороны трапеции равны, докажите, что она циклична. [CBSE, март 2013 г.]
Ответ.
29. ABCD — параллелограмм. Окружность, проходящая через A, B и C, пересекается (при необходимости произведите) в E. Докажите, что AE = AD.
Ответ.
30.ABCD — это вписанный четырехугольник, в котором AB и CD при образовании встречаются в E и EA = ED. Докажите, что: (i) AD \\ BC (ii) EB = EC
Ответ.
31. Если две равные хорды окружности пересекаются внутри окружности, докажите, что отрезок прямой, соединяющий точку пересечения с центром, образует равные углы с хордами. [CBSE-15-NS72LP7]
[CBSE-15-NS72LP7]
Ответ.
32. Две окружности с центрами O и O ‘пересекаются в точке P.Через P проведена линия, параллельная OO ’, пересекающая окружности в точках C и D, как показано на рисунке. Докажите, что CD = 200 ′. [CBSE-15-6DWMW5A] [CBSE-14-ERFKZ8H]
Ответ.
33. Если ABC — равносторонний треугольник, вписанный в окружность, а P — любая точка на малой дуге BC, которая не совпадает с B или C, докажите, что PA является биссектрисой угла ∠BPC. [Проблема с образцом NCERT]
Ответ.
34.На данном рисунке AB и CD — две равные хорды окружности с центром O. OP и OQ — перпендикуляры на хордах AB и CD соответственно. Если ∠ POQ = 120 °, найдите APQ. [CBSE-14-ERFKZ8H]
Ответ.
ДЛИННЫЙ ТИП ОТВЕТА НА ВОПРОСЫ
35. Покажите, что четырехугольник, образованный биссектрисами циклического четырехугольника, также является вписанным. [CBSE, март 2012 г.]
Покажите, что четырехугольник, образованный биссектрисами циклического четырехугольника, также является вписанным. [CBSE, март 2012 г.]
Ответ.
36.Докажите, что угол, образованный дугой в центре, в два раза больше угла, образуемого ею в любой точке оставшейся части круга. [CBSE, март 2012 г.]
Ответ.
37. Докажите, что биссектрисы угла, образованного противоположными сторонами циклического четырехугольника (при условии, что они не параллельны), пересекаются под прямым углом.
Ответ.
38. Биссектрисы углов A, B и C треугольника ABC пересекают его описанную окружность в точках D, E и F соответственно.Докажите, что углы ΔDEF равны 90 ° -∠ A / 2, 90 ° — ∠ B / 2 и 90 ° — ∠ C / 2 соответственно.
Ответ.
39. На данном рисунке O — центр окружности радиуса r см, OP и OQ перпендикуляры к AB и CD соответственно и PQ = 1 см. Если AB II CD, AB = 6 см и CD = 8 см, определитель. [CBSE-15-6DWMW5A]
Если AB II CD, AB = 6 см и CD = 8 см, определитель. [CBSE-15-6DWMW5A]
Ответ. Так как перпендикуляр, проведенный от центра окружности к хорде, делит хорду пополам.Следовательно, P и Q являются серединами AB и CD соответственно.
40. Если две хорды AB и CD окружности AYDZBWCX пересекаются под прямым углом (см. Рис.), Докажите, что дуга CXA + дуга DZB = дуга AYD + дуга BWC = полукруг. [Проблема с образцом NCERT]
Ответ. Даны две хорды AB и CD окружности, пересекающиеся под прямым углом. Пусть P — точка пересечения хорды, а O — центр окружности AYDZBWCX.
41.На данном рисунке AC — это диаметр окружности с центром O. Хорда BD перпендикулярна AC. Запишите меры углов a, b, c и d через x. [CBSE-15-NS72LP7]
Ответ.
42. Биссектриса \ (\ angle B \) равнобедренного треугольника ABC с AB = AC пересекает описанную окружность ΔABC в точке P, как показано на данном рисунке. Если AP и BC встречаются в Q, докажите, что CQ = CA. [CBSE-14-GDQNI3W]
Если AP и BC встречаются в Q, докажите, что CQ = CA. [CBSE-14-GDQNI3W]
Ответ.
Вопросы, основанные на ценностях
1. Небольшая надомная промышленность, в которой работают люди из близлежащих трущоб, изготавливает скатерти для круглых столов с шестью одинаковыми рисунками в шести сегментах, образованных равными поясами AB, BC, CD, DE, EF и FA. Если O — центр круглой скатерти (см. Рисунок). Найдите \ (\ angle AOB \), \ (\ angle AEB \) и \ (\ angle AFB \). Какое значение отображается в этом вопросе? [CBSE-14-17DJG1U]
Ответ.
Изображенная ценность: Нанимая людей из района трущоб для изготовления скатертей для круглых столов, осознайте их социальную ответственность за работу по оказанию помощи нуждающимся.
2. Трое студентов Приянка, Сания и Дэвид протестуют против убийства невинных животных в коммерческих целях в круглом парке радиусом 20 метров. Они стоят на равных расстояниях на его границе, держа в руках знамена.
Они стоят на равных расстояниях на его границе, держа в руках знамена.
(i) Найдите расстояние между ними.
(ii) Какое математическое понятие используется в нем?
(iii) Как подобный поступок отражает их отношение к обществу?
Ответ.
3. Круглый парк радиусом 10 м расположен в колонии. Трое учеников Ашок, Раман и Канаихья стоят на равных расстояниях по его окружности, каждый с игрушечным телефоном в руках, чтобы разговаривать друг с другом о Честности, Мире и Дисциплине.
(i) Найдите длину строки каждого телефона.
(ii) Напишите роль дисциплины в жизни студентов.
Ответ. Предположим, A, B и C — положение трех учеников Ашока, Рамана и Канаихья соответственно на окружности кругового парка с центром O и радиусом 10 м.Поскольку центр окружности совпадает с центром тяжести равностороннего элемента ΔABC.

 Задания №1 с ответами, профильные
Задания №1 с ответами, профильные Отметьте: а) точки М и N, лежащие на отрезке АВ; б) точки Р и Q, лежащие на прямой а, но не лежащие на отрезке АВ; в) точки R и S, не лежащие на прямой а.
Отметьте: а) точки М и N, лежащие на отрезке АВ; б) точки Р и Q, лежащие на прямой а, но не лежащие на отрезке АВ; в) точки R и S, не лежащие на прямой а.
 Точка О является серединой отрезка АВ. Можно ли совместить наложением отрезки: а) ОА и ОВ; б) ОА и АВ?
Точка О является серединой отрезка АВ. Можно ли совместить наложением отрезки: а) ОА и ОВ; б) ОА и АВ? Измерив толщину учебника геометрии без обложки, найдите толщину одного листа.
Измерив толщину учебника геометрии без обложки, найдите толщину одного листа.
 Поэтому точки А, B и С не лежат на одной прямой.
Поэтому точки А, B и С не лежат на одной прямой.

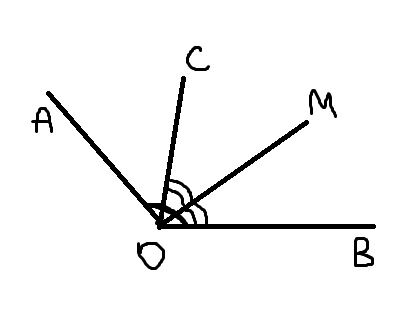 □ Верно ли утверждение: если смежные углы равны, то они прямые?
□ Верно ли утверждение: если смежные углы равны, то они прямые?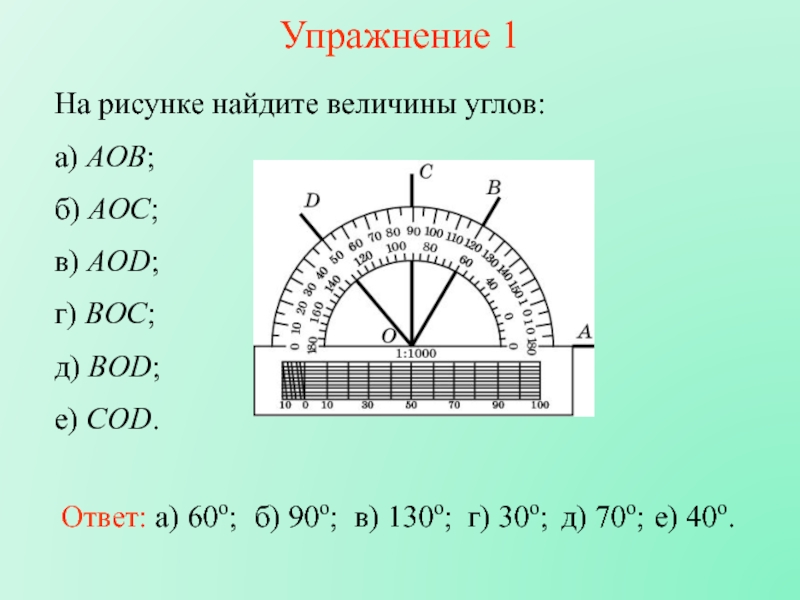 На рисунке 48 ∠AOB = 50°, ∠FOE = 70°. Найдите углы АОС, BOD, СОЕ и COD.
На рисунке 48 ∠AOB = 50°, ∠FOE = 70°. Найдите углы АОС, BOD, СОЕ и COD. Объясните, почему две прямые, перпендикулярные к третьей, не пересекаются.
Объясните, почему две прямые, перпендикулярные к третьей, не пересекаются. Три точки К, L, М лежат на одной прямой, КL = 6 см, LM = 10 см. Каким может быть расстояние КМ? Для каждого из возможных случаев сделайте чертёж.
Три точки К, L, М лежат на одной прямой, КL = 6 см, LM = 10 см. Каким может быть расстояние КМ? Для каждого из возможных случаев сделайте чертёж.
Leave A Comment