Общая физика. Оптика / Шпоргалки / 15-16
15. Поток магнитной индукции. Теорема о циркуляции
магнитной индукции
Сначала
рассмотрим магнитное поле, созданное
одиночным проводником с током. Линии
магнитной индукции поля такого проводника
представляют собой окружности, центры
которых расположены на проводнике. На
рис. 5.11 одна из них показана штриховой
линией, а сам проводник с током
перпендикулярен плоскости рисунка.
Модуль магнитной индукции в каждой
точке окружности радиуса r определяется
по (5.12):
.
Направление при выбранном направлении тока в
проводнике указано на рис. 5.11 в соответствии
с правилом буравчика. Выберем нарисованную
окружность радиуса r в качестве произвольного контура для
расчета циркуляции магнитной индукции,
причем направление обхода контура
согласуем с направлением линии магнитной
индукции по правилу правого винта. Тогда
элемент окружности – вектор
–
совпадает в каждой точке по направлению
с вектором
.
,
где – угол, под которым элемент виден из центра окружности. Циркуляция по всему замкнутому контуру будет определяться так:
. (5.21)
Таким образом, в отличие от циркуляции напряженности электростатического поля, циркуляция магнитной индукции по замкнутому контуру не равна нулю, следовательно, магнитное поле не является потенциальным.
Если в качестве замкнутого контура интегрирования выбрана не окружность, совпадающая с линией магнитной индукции, а произвольная кривая (рис. 5.12), то
.
Таким образом, все равно циркуляция магнитной индукции по произвольному замкнутому контуру отлична от нуля:
.
Отметим,
что в случаях, изображенных на рис.5.11 и
5.12, контуры интегрирования “охватывали”
проводник с током, т.е. проводник с током
пересекал поверхность, ограниченную
контуром L. Такой проводник (или ток) называют проводником (током), сцепленным
с контуром.
Рассмотрим, чему будет равна циркуляция
магнитной индукции по произвольному
замкнутому контуру, не охватывающему
ток. В этом случае (рис.5.13) весь контур
Такой проводник (или ток) называют проводником (током), сцепленным
с контуром.
Рассмотрим, чему будет равна циркуляция
магнитной индукции по произвольному
замкнутому контуру, не охватывающему
ток. В этом случае (рис.5.13) весь контур
. (5.22)
Итак, если ток не сцеплен с контуром интегрирования, то циркуляция магнитной индукции по такому контуру равна нулю.
Если магнитное поле создается системой токов, то применим принцип суперпозиции магнитных полей. Однако необходимо учитывать согласование направления обхода контура интегрирования и направления токов. В примере, изображенном на рис. 5.14, мы получим
, , , , ,
где
–
магнитная индукция поля, созданного
проводником с током силой
.
. (5.23)
Объединяя все выводы (5.21)–(5.23) в один, можно сформулировать общее правило: циркуляция вектора магнитной индукции по произвольному замкнутому контуру прямо пропорциональна алгебраической сумме токов, сцепленных с этим контуром, причем направление обхода контура и направление тока связаны правилом буравчика. Этот вывод называется теоремой о циркуляции магнитной индукции:
. (5.24)
Еще раз подчеркнем, что, поскольку циркуляция магнитной индукции по произвольному зам
кнутому контуру в общем случае отлична от нуля, то магнитное поле не является потенциальным. Оно относится к вихревым физическим полям. Вихревой характер поля означает, что его линии индукции замкнуты сами на себя, а неподвижные “магнитные заряды”, создающие такое поле, в природе отсутствуют.
Очень
часто теорему о циркуляции магнитной
индукции называют законом
полного тока,
поскольку в правой части выражения
(5. 24) записана алгебраическая сумма токов
(полный ток), сцепленных с контуром
24) записана алгебраическая сумма токов
(полный ток), сцепленных с контуром
1. Исходя из симметрии распределения заданной системы токов в пространстве необходимо построить линии магнитной индукции поля, т.е. определить направление вектора в любой точке пространства.
2. Выбрать “удобный” замкнутый контур интегрирования, отвечающий следующим требованиям:
а) он должен проходить через исследуемую точку;
б) длина контура должна быть известна;
в) модуль индукции поля должен быть постоянен в точках всего контура или хотя бы его части;
г)
угол между и касательной к контуру должен быть
известен в любой точке контура (это
обеспечивается выполнением п. 1).
1).
3. Определить циркуляцию магнитной индукции по выбранному замкнутому контуру. Если выполнено условие п.2в, то
,
где – постоянный модуль магнитной индукции во всех точках части контура .
4. Определить алгебраическую сумму токов, сцепленных с контуром L.
5. Применить теорему, т.е. приравнять результаты, полученные в пп.3 и 4 с учетом коэффициента пропорциональности.
Пример.
Определим магнитную индукцию поля бесконечно
длинного соленоида.
Таким термином называется катушка,
образованная одинаковыми плотно
прилегающими друг к другу витками
(рис.5.15), причем длина катушки существенно
больше ее диаметра. В этом случае
суперпозиция полей каждого витка (см.
рис. 5.8) приводит к образованию внутри
соленоида однородного магнитного поля,
кривизной линий индукции которого
вблизи центра соленоида можно пренебречь.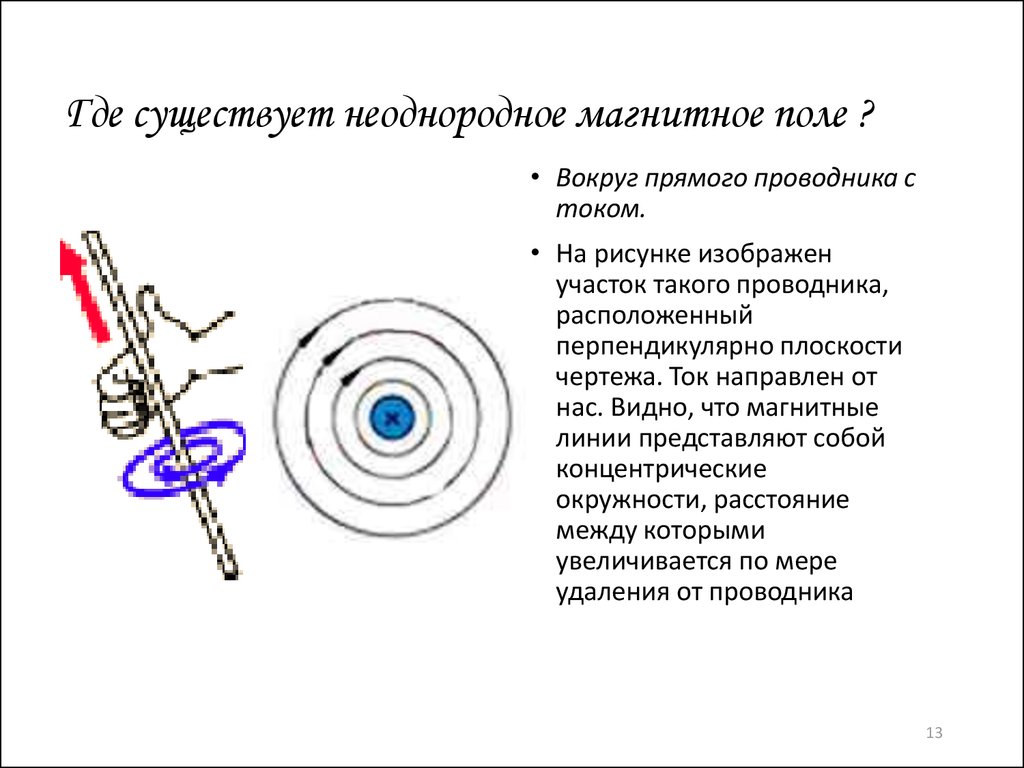
.
Если , то модуль магнитной индукции в точках дальней от соленоида стороны контура стремится к нулю, поэтому
. (5.25)
Алгебраическая сумма токов, сцепленных с контуром L, определится числом витков соленоида, расположенных на длине отрезка :
. (5.26)
Применим
закон полного тока, приравняв выражения
(5.
.
Тогда модуль магнитной индукции в центре бесконечно длинного соленоида (на его оси) выражается так:
. (5.27)
Модуль на краю бесконечно длинного соленоида (на его оси) можно найти следующим образом. Поскольку любой бесконечно длинный соленоид можно представить в виде последовательно соединенных двух бесконечно длинных соленоидов (рис. 5.17), то , где . Тогда
. (5.28)
16. Движение зарядов в магнитном и электрическом полях.
Эффект Холла
Экспериментально
обнаружен факт, что магнитное поле
действует на движущиеся в нем частицы,
имеющие электрические заряд (см. п.5.1).
В соответствии с (5.1), магнитная индукция
численно равна максимальной силе,
действующей со стороны магнитного поля
на заряженную частицу, движущуюся в
поле с единичной скоростью, отнесенной
к величине заряда частицы.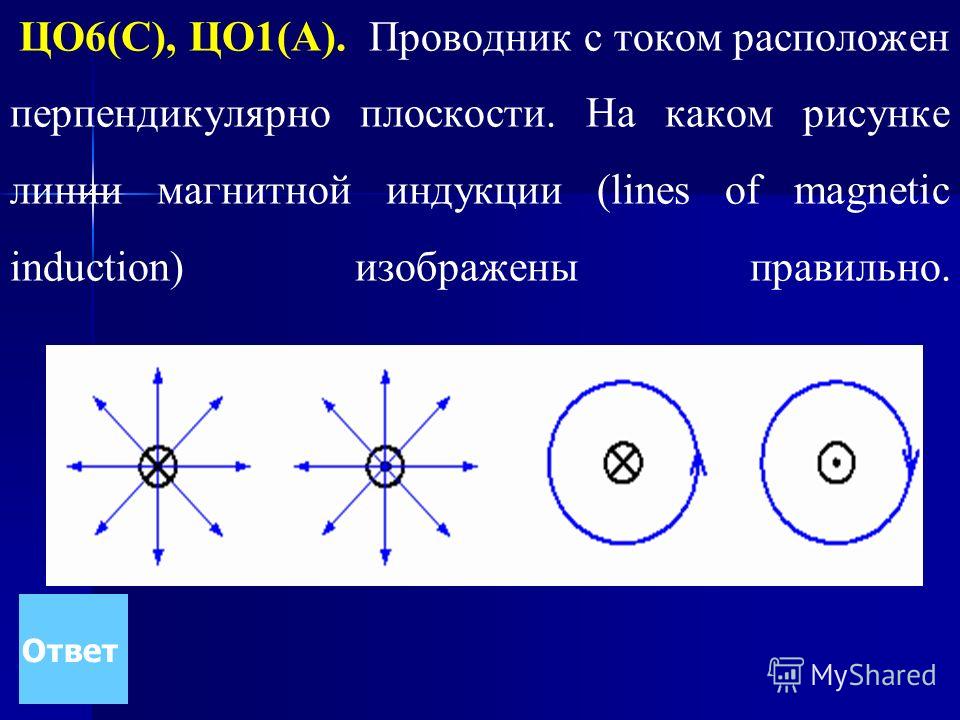 Если заряженная
частица влетает в магнитное поле со
скоростью (рис.5.18), то действующая со стороны поля
сила оказывается перпендикулярной и скорости
частицы, и магнитной индукции. Направление
вектора таково, что выполняется соотношение
Если заряженная
частица влетает в магнитное поле со
скоростью (рис.5.18), то действующая со стороны поля
сила оказывается перпендикулярной и скорости
частицы, и магнитной индукции. Направление
вектора таково, что выполняется соотношение
(5.29)
Таким образом, при и при . Оба этих случая изображены на рис. 5.18. Поскольку сила, действующая на частицу, перпендикулярна ее скорости, то ускорение, сообщаемое этой силой, тоже перпендикулярно скорости частицы, т.е. оно является нормальным ускорением. Следовательно, прямолинейная траектория полета частицы будет искривляться при ее попадании в магнитное поле.
Так как , то при , т.е. магнитное поле не действует на электрически заряженную частицу, влетающую в поле вдоль линий магнитной индукции.
Если
же частица влетает в поле перпендикулярно
линиям магнитной индукции, то из (5.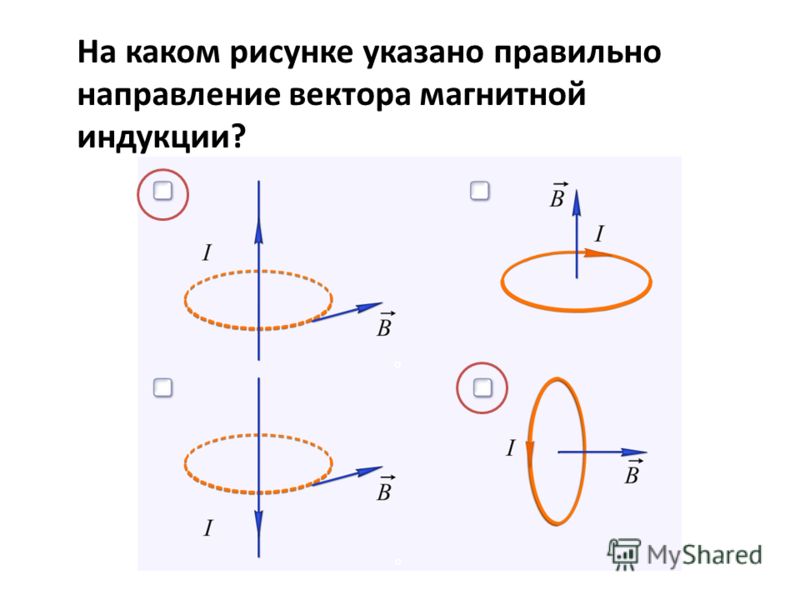 29)
следует, что
.
Тогда можно записать второй закон
Ньютона:
29)
следует, что
.
Тогда можно записать второй закон
Ньютона:
, или ,
где m – масса частицы, а R – радиус кривизны траектории. Получаем, что в однородном поле () частица будет двигаться по окружности радиуса
. (5.30)
Период обращения частицы по этой окружности не зависит от скорости частицы. Действительно,
.
Следует отметить, что при любом попадании частицы в магнитное поле, частица не будет менять свою кинетическую энергию. Т.к. , то сила перпендикулярна перемещению частицы в любой точке траектории, а, следовательно, сила со стороны магнитного поля не совершает работы по перемещению свободно двигающейся частицы.
Направление
силы
,
согласно (5.29), можно определить по правилу
“левой руки”: если
расположить ладонь левой руки так, чтобы
четыре пальца показывали направление
скорости частицы, а линии магнитной
индукции входили в раскрытую ладонь,
то отогнутый под прямым углом большой
палец покажет направление силы,
действующей на положительно заряженную
частицу. Если заряд частицы отрицателен, то
направление силы будет противоположным.
Если заряд частицы отрицателен, то
направление силы будет противоположным.
Если же заряженная частица попадает в область совместного действия электрического и магнитного полей, то, в соответствии с (1.5) и (5.29), на нее действует сила
. (5.31)
Сила, определяемая соотношением (5.31), называется силой Лоренца (в честь голландского физика Х.-А. Лоренца, получившего в 1902 г. Нобелевскую премию за описание поведения заряженных частиц в электромагнитном поле). Первое слагаемое (5.31) определяет электрическую компоненту силы Лоренца, а второе – магнитную.
Рассмотрим
некоторые примеры практического
использования воздействия магнитного
и электрического полей на заряженные
частицы. На рис. 5.19 показана схема работы
селектора частиц, т.е. устройства,
разделяющего пучок частиц по их скоростям
или энергиям. В таком устройстве
существует область, в которой созданы
однородные электрическое и магнитное
поля. Векторы напряженности и индукции
этих полей взаимно перпендикулярны. На
рисунке вектор магнитной индукции
направлен “на нас”, а вектор напряженности
электрического поля вправо. Пусть в
селектор влетает пучок одинаковых
положительно заряженных частиц, имеющих
разные скорости. Тогда, если частицы
движутся так, что и
,
то электрическая и магнитная компоненты
силы Лоренца направлены в противоположные
стороны. При определенном значении
модуля скорости эти компоненты равны:
Векторы напряженности и индукции
этих полей взаимно перпендикулярны. На
рисунке вектор магнитной индукции
направлен “на нас”, а вектор напряженности
электрического поля вправо. Пусть в
селектор влетает пучок одинаковых
положительно заряженных частиц, имеющих
разные скорости. Тогда, если частицы
движутся так, что и
,
то электрическая и магнитная компоненты
силы Лоренца направлены в противоположные
стороны. При определенном значении
модуля скорости эти компоненты равны:
, т.е. .
Это
означает, что все частицы пучка, модули
скоростей которых равны
,
пролетят селектор, в соответствии с
первым законом Ньютона, не отклоняясь
от своего первоначального направления.
Частицы пучка, модули скоростей которых
больше, чем
,
отклонятся влево. Для них
,
т.е. магнитная компонента силы Лоренца
превосходит электрическую. Остальные
частицы отклонятся вправо, т.к. для них
.
Таким образом, на выходе из селектора
будет получен моноэнергетический пучок частиц, т. е. пучок частиц, обладающих
одинаковой кинетической энергией.
е. пучок частиц, обладающих
одинаковой кинетической энергией.
Если пучок образован частицами разных масс, то дальнейшее воздействие магнитного поля на него способно разделить частицы по массе. На этом основано действие масс-спектрометра (рис.5.20). Пусть пучок частиц, прошедших селектор, попадает в однородное магнитное поле, индукция которого перпендикулярна скорости частиц. Тогда частицы пучка, масса которых равна , будут, согласно (5.30), в дальнейшем двигаться по окружности радиусом . Соответственно, чем больше удельный заряд частицы (отношение ее заряда к массе), тем меньше радиус траектории ее движения. Экспериментально выяснено, что в природе нет различных элементарных частиц с одинаковым удельным зарядом. Таким образом, масс-спектрометр позволяет установить состав исследуемого пучка частиц.
Воздействие
магнитного поля на пучки движущихся
частиц приводит иногда к неожиданным
экспериментальным результатам. В 1879 г.
американский физик Э. Г. Холл обнаружил
эффект, названный впоследствии его
именем. Эффект
Холла заключается в возникновении в проводнике
с током, помещен-ном в магнитное поле,
разности потенциалов в направлении,
перпендикулярном плотности тока и
магнитной индукции.
Г. Холл обнаружил
эффект, названный впоследствии его
именем. Эффект
Холла заключается в возникновении в проводнике
с током, помещен-ном в магнитное поле,
разности потенциалов в направлении,
перпендикулярном плотности тока и
магнитной индукции.
Р
ассмотрим
фрагмент плоского металлического
проводника толщиной b,
в котором электрическим полем с
напряженностью создан электрический ток плотностью
(рис.
5.21, а).
В отсутствие магнитного поля свободные
электроны металла упорядоченно движутся
со скоростью
,
направленной противоположно вектору
.
Если проводник поместить в магнитное
поле так, что
,
то на электроны будет действовать
магнитная компонента силы Лоренца
,
направление которой показано на рисунке.
Ее действие приведет к поперечному
смещению электронов, в результате чего
между верхней и нижней поверхностями
проводника появится электрическое поле
разделенных зарядов. Если проводник
достаточно тонкий, то напряженность
этого поля
можно
считать постоянной. Процесс смещения
электронов прекратится, когда
скомпенсируются силы, действующие на
них со стороны магнитного и электрического
полей:
.
В проводнике установится суммарное
электрическое поле с напряженностью (рис.5.21, б).
Изменение направления суммарного
электрического поля в проводнике
приведет к изменению положения
эквипотенциальных плоскостей, т.к. они
должны быть перпендикулярны
.
Раньше такая плоскость проходила через
точки M и N проводника (рис.5.21, в).
Теперь она пройдет через точки
и N.
Поэтому между точками M и N возникнет разность потенциалов. Для
однородного электрического поля будет
справедливо (см.(1.19)) соотношение
.
Поскольку
,
где п – концентрация свободных электронов
в металле, то
Процесс смещения
электронов прекратится, когда
скомпенсируются силы, действующие на
них со стороны магнитного и электрического
полей:
.
В проводнике установится суммарное
электрическое поле с напряженностью (рис.5.21, б).
Изменение направления суммарного
электрического поля в проводнике
приведет к изменению положения
эквипотенциальных плоскостей, т.к. они
должны быть перпендикулярны
.
Раньше такая плоскость проходила через
точки M и N проводника (рис.5.21, в).
Теперь она пройдет через точки
и N.
Поэтому между точками M и N возникнет разность потенциалов. Для
однородного электрического поля будет
справедливо (см.(1.19)) соотношение
.
Поскольку
,
где п – концентрация свободных электронов
в металле, то
.
Полученное
выражение называется “холловской
разностью потенциалов”,
ее экспериментальное измерение при
заданных размерах проводника и силе
тока в нем позволяет определить магнитную
индукцию поля, в которое помещен холловский
датчик. Это – один из основных методов измерения
магнитной индукции постоянных магнитных
полей.
Это – один из основных методов измерения
магнитной индукции постоянных магнитных
полей.
Глава 22. Магнитные взаимодействия. Магнитная индукция.Силы Лоренца и Ампера
Если заряд движется, то наряду с электрическим полем он создает еще одно поле — магнитное, которое действует на другие движущиеся заряды. В результате возникает дополнительное (наряду с кулоновским) взаимодействие движущихся электрических зарядов, которое называется магнитным. В результате магнитного взаимодействия возникает взаимодействие проводников с током.
В 1820 г. датский физик Х. Эрстед обнаружил, что проводник с током действует на магнитную стрелку. После этого стало ясно, что магнитное взаимодействие движущихся электрических зарядов и токов и взаимодействие постоянных магнитов имеют одну и ту же природу. На основании подробных исследований А. Ампер установил, что взаимодействие постоянных магнитов между собой и с токами можно объяснить, если предположить, что внутри магнитов есть электрические токи (в настоящее время известно, что эти токи имеют внутримолекулярную природу).
Для характеристики магнитного поля вводится векторная величина, которая называется индукцией магнитного поля и которая позволяет найти силы, действующие со стороны магнитного поля на движущиеся заряды. Как правило, эту величину обозначают буквой . Для нахождения индукции в каждой точке магнитного поля, созданного проводником с током, используется закон Био-Савара-Лапласа и принцип суперпозиции. Закон Био-Савара-Лапласа позволяет найти поле , созданное бесконечно малым элементом проводника, а принцип суперпозиции требует сложить векторы индукции, созданные всеми элементами проводников. Закон Био-Савара-Лапласа в школьный курс физики, однако, не входит. В задачи ЕГЭ входят только вопросы, связанные с направлением вектора магнитной индукции (но не с величиной). Существует несколько вариантов правила нахождения направления вектора . Наиболее удобным является правило буравчика — оно более универсально, чем правило левой руки. Правило буравчика утверждает, что если вкручивать правыйбуравчик1 по току в проводнике, то направление движения ручки в каждой точке пространства покажет направление вектора индукции магнитного поля в этой точке. Относительно величины достаточно помнить, что чем дальше от проводника, тем меньше индукция, и что внутри бесконечной катушки (бесконечного соленоида) магнитное поле направлено вдоль оси катушки и однородно.
Относительно величины достаточно помнить, что чем дальше от проводника, тем меньше индукция, и что внутри бесконечной катушки (бесконечного соленоида) магнитное поле направлено вдоль оси катушки и однородно.
Магнитное поле можно изобразить графически с помощью линий магнитной индукции. Линии магнитной индукции — воображаемые линии, касательные к которым в каждой точке совпадают с направлением вектора в этой точке. Линии магнитной индукции проводят так, что их густота в каждой области пространства пропорциональна величине индукции в этой области. В отличие от силовых линий электрического поля линии магнитной индукции всегда являются замкнутыми.
На электрический заряд величиной , движущийся со скоростью в магнитном поле с индукцией , со стороны магнитного поля действует сила, которая называется силой Лоренца
(22.1) |
где — угол между скоростью и вектором индукции. Направление силы Лоренца определяется следующим образом (см. рисунок).
рисунок).
1. Сила Лоренца перпендикулярна плоскости, в которой лежат векторы скорости заряда и индукции магнитного поля (на рисунке эта плоскость показана тонким пунктиром).
2. Выбор между двумя перпендикулярными направлениями осуществляется с помощью правила буравчика (или правила левой руки): если вращать правый буравчик так, что его ручка движется от вектора к вектору , то направление его вкручивания указывает направление силы Лоренца, действующей на положительный заряд (траектория ручки буравчика показана на рисунке изогнутой стрелкой).
3. Для отрицательного заряда направление силы Лоренца противоположно.
Можно также определять направление силы Лоренца по правилу левой руки: левую руку нужно расположить так, чтобы вектор входил в ладонь, направление четырех пальцев совпадало с направлением вектора скорости заряда, тогда направление отогнутого под прямым углом к четырем пальцам большого пальца покажет направление силы, действующей на положительный заряд (на отрицательный заряд действует сила противоположного направления).
Поскольку магнитное поле действует на движущиеся заряды, то магнитное поле действует и на проводник, по которому течет электрический ток. Если в магнитном поле с индукцией находится проводник длиной , по которому течет ток , то на этот проводник действует сила
(22.2) |
где — угол между током и вектором индукции. Направлен вектор силы (22.2) перпендикулярно плоскости, в которой лежат вектор и проводник, причем в таком направлении, что если поставить правый буравчик перпендикулярно указанной плоскости и вращать его так, что ручка вращается от тока к вектору , то направление его вкручивания покажет направление силы (см. рисунок; плоскость в которой лежат проводник и вектор индукции обозначена тонким пунктиром, движение ручки буравчика — изогнутой стрелкой). Также для нахождения направления силы можно использовать правило левой руки. Сила (22.2), действующая со стороны магнитного поля на проводник с током, называется силой Ампера.
Рассмотрим теперь задачи.
Правильный ответ в задаче 22.1.1 — 4 (магнитное поле создается движущимися заряженными телами), в задаче 22.1.2 — 2 (в магнитном веществе есть незатухающие электрические токи). Что же касается того, заряжен магнит или нет, то от этого существование магнитного поля (если магнит покоится) не зависит.
В задаче 22.1.3 следует воспользоваться правилом буравчика. Если вкручивать буравчик по направлению тока в проводнике, то в точке его ручка будет двигаться за чертеж. Следовательно, за чертеж направлен в точке и вектор индукции магнитного поля (ответ 1).
Если вкручивать буравчик по току в кольце (в любой точке кольца), то ручка буравчика в центре кольца будет двигаться за чертеж. Поэтому правильный ответ в задаче 22.1.4 — 3.
Поскольку угол между скоростью заряда и вектором магнитной индукции равен нулю (задача 22.1.5), то согласно формуле (22.1) сила Лоренца, действующая на этот заряд, равна нулю (ответ 4).
Применим к проводнику с током из задачи 22.1.6 формулу (22.2) для силы Ампера. Имеем (ответ 2).
Как следует из формулы (22.2) сила Ампера равна нулю, если угол между током и индукцией равен нулю или 180°. Из приведенных на рисунке в задаче 22.1.7 проводников, таковым является только проводник 1. Поэтому на него магнитное поле не действует (ответ 1).
Применяем к частице из задачи 22.1.8 (см. рисунок) правила нахождения направления силы Лоренца (пункты 1-3 после формулы (22.1)). Во-первых, сила Лоренца направлена перпендикулярно плоскости, в которой лежат векторы скорости заряда и индукции магнитного поля — т.е. либо за чертеж, либо на нас. Во-вторых, при вращении ручки буравчика, поставленного на чертеж в ту точку, где находится заряд, от вектора к вектору (в направлении меньшего угла между ними), буравчик будет «выкручиваться» из чертежа. А по-скольку частица заряжена положительно, сила Лоренца направлена «на нас» (ответ 1).
|
Используя правила для силы Ампера (формула (22.2) и текст после нее), найдем, что сила Ампера, действующая со стороны магнитного поля на проводник с током в задаче 22.1.9, направлена «от нас» (ответ 3). |
В задаче 22.1.10 следует сначала найти направление вектора магнитной индукции поля провода в той точке, где находится заряд, а затем использовать правила для силы Лоренца (формула (22.1) и текст за ней). Согласно результатам задачи 22.1.3, вектор в той точке, где находится заряд, направлен за чертеж (см. рисунок).
Вектор силы Лоренца направлен перпендикулярно плоскости, в которой лежат векторы и , т.е. либо к проводу, либо от него. Ставим буравчик перпендикулярно этой плоскости и вращаем его так, что ручка движется от вектора к вектору (см. рисунок; буравчик нужно вращать по часовой стрелке, если смотреть снизу). При таком вращении буравчик будет вкручиваться вверх. А поскольку электрон заряжен отрицательно, то действующая на него сила направлена противоположно, т. е. от провода (ответ 2).
е. от провода (ответ 2).
В задаче 22.2.1 используем принцип суперпозиции. Ток в горизонтальном кольце создает поле в его центре с индукцией, направленной вверх, ток в вертикальном кольце — с индукцией, направленной вправо (см. задачу 22.1.4.). Результат сложения этих векторов — индукция суммарного магнитного поля — направлена на «северо-восток» (ответ 1).
Ток в верхнем проводе (задача 22.2.2) создает поле с индукцией, направленной «за чертеж», ток в нижнем — «на нас». Результат их сложения зависит от величин этих векторов. Поскольку поле нижнего провода в точке больше поля верхнего (меньше расстояние), то вектор суммы направлен «на нас» (ответ 1).
Сила Лоренца в любой момент времени перпендикулярна скорости частицы. Поэтому угол между бесконечно малым перемещением частицы в любой момент времени и силой Лоренца, действующей на частицу в этот момент времени, — прямой. А поскольку в формулу для работы силы на бесконечно малом участке перемещения входит косинус угла между силой и перемещением, то работа силы Лоренца равна нулю (задача 22. 2.3 — ответ 3). Из этих рассуждений и теоремы об изменении кинетической энергии следует, что заряженная частица, движущаяся под действием магнитного поля, изменяет направление, но не величину своей скорости.
2.3 — ответ 3). Из этих рассуждений и теоремы об изменении кинетической энергии следует, что заряженная частица, движущаяся под действием магнитного поля, изменяет направление, но не величину своей скорости.
Если заряженная частица влетает в однородное магнитное поле перпендикулярно линиям магнитной индукции, то она движется по окружности, причем эта окружность лежит в плоскости, перпендикулярной линиям магнитной индукции. Радиус окружности можно найти из второго закона Ньютона для этой частицы
(22.3) |
где и — масса частицы и ее заряд, — ускорение, — скорость, которая не изменяется по величине (см. предыдущую задачу), — индукция магнитного поля. В формуле (22.3) использовано известное выражение для центростремительного ускорения . Из формулы (22.3) получаем для радиуса окружности
(22.4) |
Применяя формулу (22. 4) к задаче 22.2.4 находим отношение радиусов окружности первой и второй частиц
4) к задаче 22.2.4 находим отношение радиусов окружности первой и второй частиц
(ответ 2).
Найдем сначала скорости протона и -частицы, ускоренных одним и тем же напряжением (задача 22.2.5). По теореме об изменении кинетической энергии имеем
где и — масса частицы и ее заряд, — скорость, которую частица приобретает после разгона (здесь предполагается, что начальная скорость частицы равна нулю). Из этой формулы находим отношение скоростей протона и -частицы , ускоренных одним и тем же напряжением
Поскольку заряд протона вдвое меньше заряда -частицы, а масса вчетверо меньше, то . Теперь из формулы (22.4) находим отношение радиусов окружности протона и -частицы, ускоренных одним и тем же электрическим напряжением и движущихся в одном и том же магнитном поле
(ответ 4).
Период обращения заряженной частицы в магнитном поле (задача 22.2.6) можно найти из следующих соображений. В однородном магнитном поле частица движется по окружности и за период проходит путь, равный длине этой окружности , где — ее радиус. Используя формулу (22.4) для радиуса траектории, получим для периода обращения
где — скорость частицы, — ее масса, — заряд, — индукция магнитного поля. Отсюда заключаем, что период обращения заряженной частицы в магнитном поле не зависит от ее скорости (ответ 3).
Индукция магнитного поля в задаче 22.2.7 должна быть направлена так, чтобы сила Лоренца, действующая на электрон, была направлена к центру окружности, по которой он движется (см. рисунок). А поскольку сила Лоренца перпендикулярна скорости и индукции, то вектор индукции может быть направлен в этой ситуации только «за чертеж» или «на нас». Воспользуемся далее правилом буравчика (см. текст после формулы (22.1)): если вращать буравчик так, что его ручка будет вращаться от скорости заряда к индукции магнитного поля , то направление его вкручивания указывает направление силы Лоренца, действующей на положительный заряд. Для электрона ( < 0) направление силы противоположно. Непосредственной проверкой убеждаемся, что вектор индукции направлен «за чертеж» (ответ 4).
текст после формулы (22.1)): если вращать буравчик так, что его ручка будет вращаться от скорости заряда к индукции магнитного поля , то направление его вкручивания указывает направление силы Лоренца, действующей на положительный заряд. Для электрона ( < 0) направление силы противоположно. Непосредственной проверкой убеждаемся, что вектор индукции направлен «за чертеж» (ответ 4).
В области среднего провода (задача 22.2.8) ток в верхнем проводе создает магнитное поле с индукцией, направленной «от нас», ток в нижнем — «на нас» (см. задачу 22.1.3). Но ток в нижнем проводе вдвое меньше тока в верхнем, а индукция поля — пропорциональна току. Поэтому индукция суммарного поля верхнего и нижнего проводов в области среднего провода направлена «от нас». Согласно правилам нахождения направления силы Ампера (см. текст после формулы (22.2)) находим, что сила, действующая на средний провод со стороны магнитного поля верхнего и нижнего проводов, направлена вверх (ответ 1). Отметим, что из приведенных рассуждений также следует, что два параллельных провода, по которым текут токи одинакового направления притягиваются, противоположного — отталкиваются.
Отметим, что из приведенных рассуждений также следует, что два параллельных провода, по которым текут токи одинакового направления притягиваются, противоположного — отталкиваются.
В задаче 22.2.9 магнитное поле действует на рамку следующим образом. На стороны и , которые параллельны линиям индукции, поле не действует. На стороны и действуют силы Ампера, равные по величине , где — ток в рамке, — индукция магнитного поля, — длина стороны. Сила, действующая на сторону , направлена «на нас», на сторону — «от нас». Поскольку суммарная сила, действующая на рамку, равна нулю, как целое рамка перемещаться в пространстве не будет, а будет вращаться вокруг оси, показанной на рисунке пунктиром (ответ 4).
Задача 22.2.10 по формуле (22.2) находим силы Ампера, действующие на стороны треугольника
где — ток в контуре, и — длины сторон и , — индукция магнитного поля (последняя из приведенных формул следует из того, что сторона параллельна линиям индукции). Из теоремы синусов для треугольника
Из теоремы синусов для треугольника
заключаем, что , а из правил для направления силы Ампера — что один из векторов или направлен «за чертеж», один — «на нас» (в зависимости от направления тока в контуре). Поэтому правильный ответ в задаче — 3.
12.4 Магнитное поле токовой петли – University Physics Volume 2
Глава 12. Источники магнитных полей
Цели обучения
К концу этого раздела вы сможете:
- Объяснять, как закон Био-Савара используется для определения магнитного поля, вызванного током в проволочной петле в точке вдоль линии перпендикулярно плоскости петли.
- Определить магнитное поле дуги тока.
Круговая петля на рис. 12.11 имеет радиус R , по ней течет ток I , и она лежит в плоскости xz . Чему равно магнитное поле, обусловленное током в произвольной точке P по оси петли?
Рисунок 12. 11 Определение магнитного поля в точке P вдоль оси проволочного контура с током.
11 Определение магнитного поля в точке P вдоль оси проволочного контура с током.Мы можем использовать закон Био-Савара, чтобы найти магнитное поле, вызванное током. Сначала мы рассмотрим произвольные сегменты на противоположных сторонах петли, чтобы качественно показать векторными результатами, что чистое направление магнитного поля находится вдоль центральной оси петли. Отсюда мы можем использовать закон Био-Савара, чтобы получить выражение для магнитного поля.
Пусть P будет расстоянием y от центра петли. Согласно правилу правой руки, магнитное поле [латекс]d\stackrel{\to }{\textbf{B}}[/latex] при P , создаваемое токоведущим элементом [латекс]I\фантом{\правило {0.2em}{0ex}}d\stackrel{\to }{\textbf{l}},[/latex] направлен под углом [latex]\theta[/latex] над осью y , как показано . Поскольку [latex]d\stackrel{\to }{\textbf{l}}[/latex] параллелен вдоль оси x , а [latex]\hat{\textbf{r}}[/latex] находится в 9{\prime}[/latex], перпендикулярные оси y , поэтому сокращаются, и при расчете чистого магнитного поля необходимо учитывать только компоненты вдоль оси y . {3}}.[/латекс] 9{3}}.[/латекс]
{3}}.[/латекс] 9{3}}.[/латекс]
Расчет магнитного поля из-за круговой токовой петли в точках вне оси требует довольно сложной математики, поэтому мы просто посмотрим на результаты. Линии магнитного поля имеют форму, показанную на рис. 12.12. Обратите внимание, что одна линия поля следует за осью петли. Это линия поля, которую мы только что нашли. Кроме того, в непосредственной близости от провода линии поля почти круглые, как линии длинного прямого провода.
Рисунок 12.12 Эскиз силовых линий магнитного поля круглой петли с током.Пример
Магнитное поле между двумя контурами
Два контура провода пропускают один и тот же ток 10 мА, но текут в противоположных направлениях, как показано на Рис. 12.13. Одна петля имеет радиус [латекс]R=50\phantom{\rule{0.2em}{0ex}}\text{см}[/латекс], а другая петля имеет радиус [латекс]2R= 100\phantom{\rule{0.2em}{0ex}}\text{см}.[/latex] Расстояние от первого контура до точки, где измеряется магнитное поле, равно 0,25 м, а расстояние от этой точки до вторая петля 0,75 м. Какова величина чистого магнитного поля в точке 9?0017 Р ?
Какова величина чистого магнитного поля в точке 9?0017 Р ?
Стратегия
Магнитное поле в точке P было определено по уравнению 12.15. Поскольку токи текут в противоположных направлениях, чистое магнитное поле представляет собой разницу между двумя полями, создаваемыми катушками. Затем, используя заданные в задаче величины, рассчитывается суммарное магнитное поле. 9{\text{−9}}\text{T}\phantom{\rule{0.2em}{0ex}}\text{вправо}.\hfill \end{массив}[/latex]
Значение
Катушки Гельмгольца обычно имеют петли одинакового радиуса с током, текущим в одном направлении, чтобы иметь сильное однородное поле в средней точке между петлями. Аналогичное применение распределения магнитного поля, создаваемого катушками Гельмгольца, можно найти в магнитной бутылке, которая может временно улавливать заряженные частицы. См. Магнитные силы и поля для обсуждения этого.
См. Магнитные силы и поля для обсуждения этого.
Проверьте свое понимание
Используя пример 12.5, на какое расстояние вам придется переместить первую катушку, чтобы иметь нулевое измеряемое магнитное поле в точке P ?
Show Solution0,608 метра
Резюме
- Напряженность магнитного поля в центре круглой петли определяется выражением [латекс]B=\frac{{\mu }_{0}I}{2R}\phantom{\rule{0.2em}{ 0ex}}\text{(в центре петли)},[/latex] где R — радиус петли. РХР-2 дает направление поля вокруг петли.
Концептуальные вопросы
Является ли магнитное поле токовой петли однородным?
Что происходит с длиной подвешенной пружины, когда через нее проходит ток?
Показать решениеДлина пружины уменьшается, так как каждая катушка имеет магнитное поле, создаваемое северным полюсом, рядом с южным полюсом следующей катушки.
По двум концентрическим круглым проводам разного диаметра текут токи в одном направлении. Опишите силу, действующую на внутреннюю проволоку. 9{\text{−5}}\text{T}[/латекс]
Опишите силу, действующую на внутреннюю проволоку. 9{\text{−5}}\text{T}[/латекс]
По круговой петле радиусом R течет ток I . На каком расстоянии вдоль оси петли магнитное поле составляет половину своего значения в центре петли?
Две плоские круглые катушки, каждая с радиусом R и намотанные на N витков, установлены вдоль одной оси так, чтобы они были параллельны на расстоянии d друг от друга. Каково магнитное поле в середине общей оси, если ток 9{3\текст{/}2}}[/латекс]
Для катушек в предыдущей задаче, каково магнитное поле в центре каждой катушки?
Лицензии и атрибуты Магнитное поле токовой петли. Автор: : Колледж OpenStax. Расположен по адресу : https://openstax.org/books/university-physics-volume-2/pages/12-4-magnet-field-of-current-loop. Лицензия : CC BY: Attribution . Условия лицензии : Скачать бесплатно на https://openstax. org/books/university-physics-volume-2/pages/1-introduction
org/books/university-physics-volume-2/pages/1-introduction
Объяснение урока: Магнитные поля, создаваемые электрическими токами
В этом объяснении мы научимся описывать магнитное поле, которое производится проводом, по которому течет электрический ток.
Если по проводу протекает поток заряда, то в проводе есть ток. На приведенной ниже схеме показан длинный прямой провод, по которому течет ток.
Ток создает вокруг себя магнитное поле. Линии поля, показанные внизу сформируйте круги вокруг проволоки.
Магнитное поле, образованное током, существует повсюду вокруг провода. Вокруг него формируются круговые силовые линии, простирающиеся на любое расстояние от проволока.
Если мы изменим нашу перспективу и посмотрим на провод с одного конца, ток может указывать прямо на нас, как показано ниже. С этой точки зрения мы говорим, текущие точки «за пределами экрана» или «за пределами экрана».
На этом рисунке показан символ, указывающий ток за пределы экрана: круг.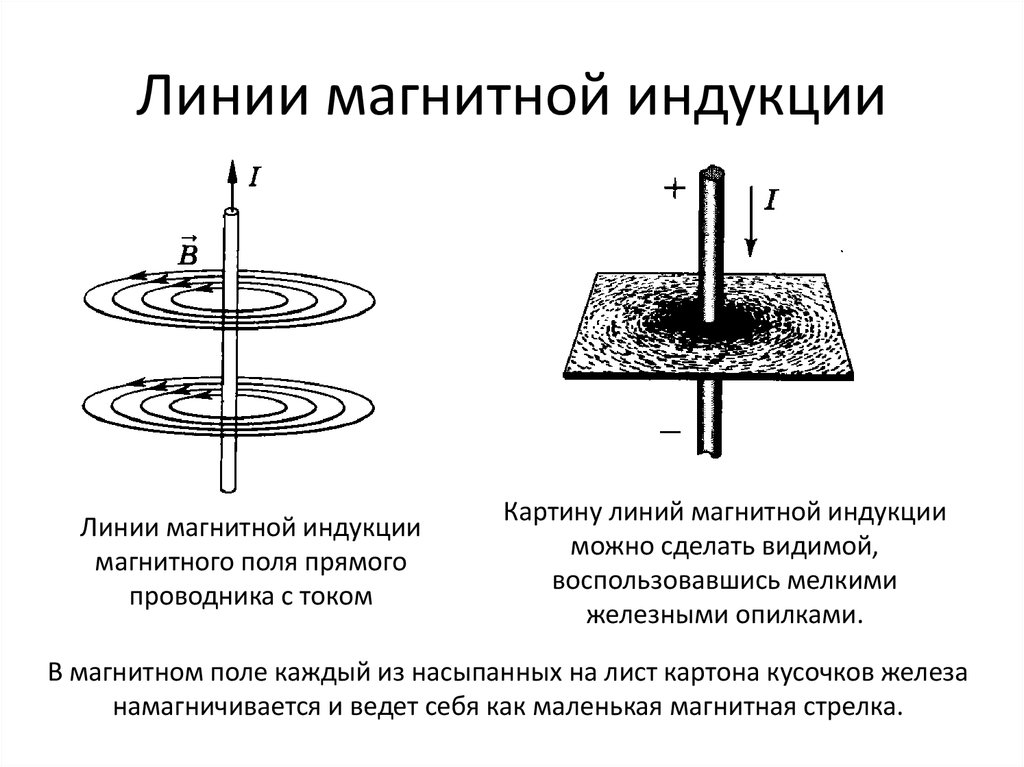 с точкой в центре. Он также показывает, что силовые линии магнитного поля при разных
расстояния от проволоки образуют концентрические окружности.
с точкой в центре. Он также показывает, что силовые линии магнитного поля при разных
расстояния от проволоки образуют концентрические окружности.
По мере увеличения расстояния от провода круги отдаляются друг от друга. Этот указывает на уменьшение напряженности магнитного поля.
Вместо того, чтобы смотреть на ток, указывающий на нас с экрана, он можно смотреть в противоположном направлении: «в экран». Ток в это направление обозначено кружком вокруг буквы X, как показано ниже.
Обратите внимание, что магнитное поле на этом рисунке направлено вокруг провода по часовой стрелке. а поле на рисунке с направленным током из экрана указывает против часовой стрелки.
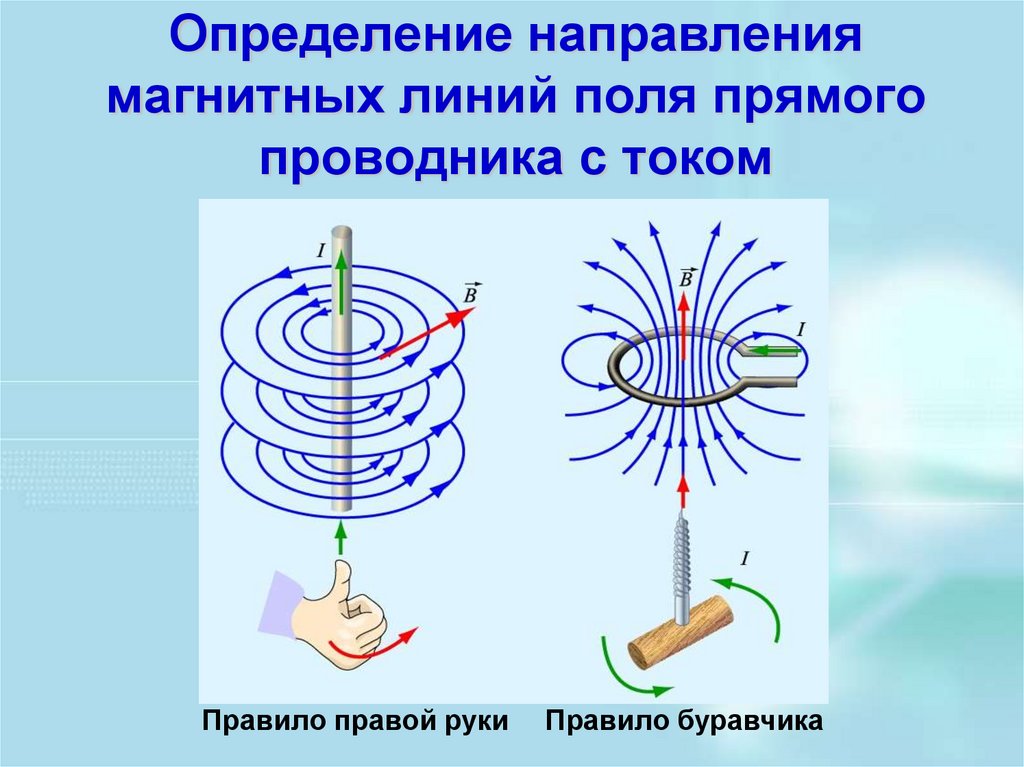
Для определения направления магнитного поля вокруг проводящего ток
проволоки, мы используем так называемое «правило правой руки». Это правило гласит, что если
мы указываем большим пальцем правой руки в направлении тока в
прямой провод, направление, в котором сгибаются наши пальцы (скажем, чтобы схватить что-то) является
направление магнитного поля вокруг этого провода.
Этот метод применяется для проводов, по которым ток поступает на экран и выходит из него, как показано ниже.
В обоих случаях, когда мы указываем большим пальцем правой руки в направлении текущей в проводе наши пальцы сгибаются в направлении создаваемого магнитного поля по течению.
Пример 1: Понимание магнитного поля, создаваемого проводом с током
На какой из четырех диаграмм правильно показаны силовые линии магнитного поля, создаваемого вокруг провода с током?
Ответ
Чтобы ответить на этот вопрос, воспользуемся так называемым «правым хватом». правило». Это правило гласит, что направление магнитного поля, образованного электрический ток задается направлением, в котором сгибаются наши пальцы, когда большой палец нашей правой руки указывает в том же направлении, что и ток.
Мы можем применить это правило к четырем случаям (A), (B), (C) и (D) по порядку.
Для сценария (А) мы указываем большим пальцем правой руки на экран с момента
текущие точки в этом направлении. Сгибая пальцы, мы обнаруживаем, что они двигаются
по дуге по часовой стрелке. Это идет против указанного против часовой стрелки
направление магнитного поля. Следовательно, диаграмма (А) неправильно показывает
силовые линии магнитного поля вокруг проводника с током.
Сгибая пальцы, мы обнаруживаем, что они двигаются
по дуге по часовой стрелке. Это идет против указанного против часовой стрелки
направление магнитного поля. Следовательно, диаграмма (А) неправильно показывает
силовые линии магнитного поля вокруг проводника с током.
В сценарии (B) ток направлен за пределы экрана. Когда большой палец наша правая рука указывает туда, наши пальцы сгибаются против часовой стрелки направление. Это идет против указанного магнитного поля по часовой стрелке. направление на схеме. Диаграмма (B) также неправильно показывает магнитное поле, создаваемое вокруг провода с током.
Сценарий (C) имеет ток, направленный на экран, и направленный по часовой стрелке.
направление поля. Проверяя это с помощью нашего правила хвата правой рукой, мы обнаруживаем, что
действительно, наши пальцы сгибаются по часовой стрелке, когда большой палец правой руки указывает на
экран. Схема (С) верна!
Схема (С) верна!
Рассматривая сценарий (D), мы видим, что часть магнитного поля указывает против часовой стрелки и часть по часовой стрелке. Это физически невозможно, поэтому мы знаем, что диаграмма (D) не является правильным изображением магнитного поля вокруг провод с током.
Наш последний вариант — диаграмма (С).
Мы отметили, что напряженность магнитного поля, создаваемого проводник с током становится слабее по мере увеличения расстояния от провода.
Другим фактором, влияющим на напряженность поля, является величина текущее его создание. Чем сильнее течение (больше его величина), тем сильнее магнитное поле.
Пример 2: понимание магнитных полей, создаваемых электрическими токами
Для магнитного поля, создаваемого вокруг провода с током, ток, магнитное поле.
- больше, слабее
- меньше, сильнее
- больше, сильнее
Ответ
Существует прямая зависимость между величиной электрического
ток, создающий магнитное поле, и величина самого поля.
Таким образом, мы можем сказать, что чем больше ток, тем сильнее поля, и чем меньше ток, тем слабее поле.
Оба этих описания правильно заполняют пробелы в предложение, но только одно из них предлагается в качестве опции. Вариант (С), «больше, сильнее» приведет к предложению, которое гласит: «Для магнитное поле, создаваемое вокруг провода с током, тем больше ток, тем сильнее магнитное поле». Это правильно завершает предложение, поэтому наш последний вариант — вариант (C).
Провод, по которому течет ток, может быть прямым, как мы рассматривали до сих пор, но он также может быть расположен в виде катушки, как показано на следующем рисунке.
Такая катушка проволоки называется соленоидом. Как и любая другая форма провод, когда соленоид пропускает ток, он создает магнитное поле вокруг себя.
Интересно, что магнитное поле соленоида очень похоже на
магнитное поле, создаваемое стержневым магнитом.
Когда по соленоиду течет ток, магнитное поле внутри его катушек равно достаточно сильное, а внешнее поле относительно слабое.
Можно усилить магнитное поле внутри соленоида путем поместить материал, который может намагничиваться, в сердечник соленоида.
Намагничиваемый материал – это такой материал, который при помещении в магнитное поле сам становится магнитом и создает собственное магнитное поле.
Примером такого материала является железо. Если поставить железный цилиндр внутри соленоида, как показано ниже, поле соленоида намагничивает железо, которое затем создает собственное магнитное поле, которое в очередь усиливает поле соленоида.
Пример 3: Идентификация соленоида
На каждой из следующих диаграмм изображен объект, сделанный из меди. Какой объект является соленоидом?
Ответ
Соленоид сделан из проволоки, которая может проводить ток. Важно отметить, что
провод в соленоиде непрерывен, то есть заряд может течь с одного конца
соленоида к другому.
Провод в соленоиде также скрученный, чтобы создать множество витков, которые параллельно друг другу.
Варианты (A) и (B) показывают отсоединенные петли проводов. Так как они не непрерывный, ни один из этих вариантов не показывает соленоид.
Вариант (C) показывает петли, соединенные вместе. Петли не расположены параллельно друг другу, поэтому мы не будем выбирать вариант (C) или.
Вариант (Е) изображает полый цилиндр. Поскольку это не построено из одного отрезка провода, это не соленоид.
Зная, что соленоид сделан из непрерывной проволоки расположенные в параллельных петлях, исключают все варианты, кроме варианта (D).
Пример 4: Знание ключевых терминов, связанных с электромагнетизмом
Что из следующего является правильным описанием соленоида?
- Соленоид представляет собой один прямой кусок провода. Пропуская по ней электрический ток, вокруг нее создается магнитное поле.

- Соленоид представляет собой одиночный контур изолированного провода. Пропуская через него электрический ток, создается магнитное поле похоже на стержневой магнит.
- Соленоид представляет собой длинную катушку изолированного провода. Прохождение электрического ток через него создает магнитное поле, подобное стержню магнит.
Ответ
Рассматривая эти три описания кандидатов, мы видим, что они различаются в первую очередь из-за формы провода, из которого состоит соленоид.
Соленоид — это не прямой кусок проволоки; состоит из ряда петель называется катушкой. Чем больше петель в катушке, тем сильнее магнитное поле. это создает.
Когда электрический заряд проходит через соленоид, он создает сильное поле подобно магнитному полю из-за стержневого магнита.
Это описание соответствует опции (C).
Пример 5: Знакомство с соленоидами
Какие два из следующих способов позволяют повысить прочность магнитное поле, создаваемое соленоидом?
- Увеличение ширины соленоида
- Уменьшение длины соленоида
- Увеличение тока через соленоид
- Уменьшение числа витков соленоида
- Добавление железного сердечника к соленоиду
Ответ
Напомним, что соленоид представляет собой катушку провода с множеством витков.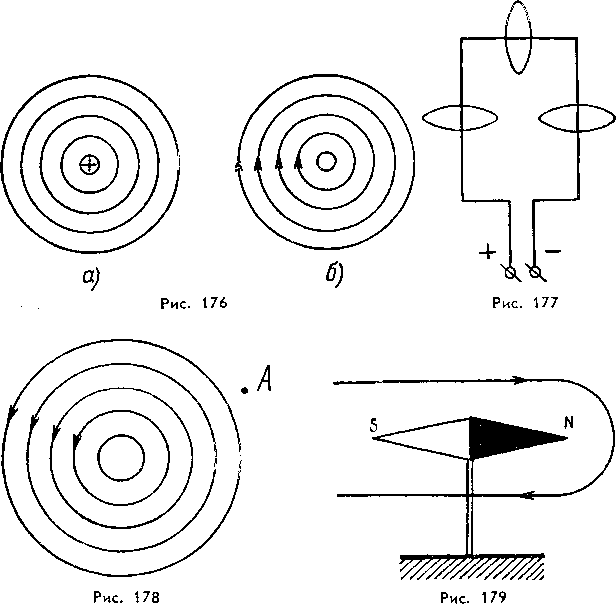
Магнитное поле, создаваемое соленоидом, фактически является суммой магнитные поля, создаваемые каждой отдельной петлей. Чем больше там петель равны, тем больше будет эта сумма и тем сильнее будет общее поле.
Следовательно, вариант (D) «Уменьшение числа витков в соленоид», не может быть правильным. Уменьшение количества витков соленоида фактически ослабит общее магнитное поле.
Аналогично вариант (B) «Уменьшение длины соленоида» не не описывает способ усиления магнитного поля соленоида. Уменьшение длины соленоида эффективно удаляет витки из катушки, снова ослабляя общее поле.
Вариант (A) утверждает, что увеличение ширины соленоида увеличивает его напряженность магнитного поля. Однако именно количество петель, а не их диаметр, что влияет на напряженность магнитного поля в соленоид.
Что касается способов увеличения напряженности поля соленоида, один подход
который работает для токонесущих проводов любой формы, заключается в увеличении
ток в проводе.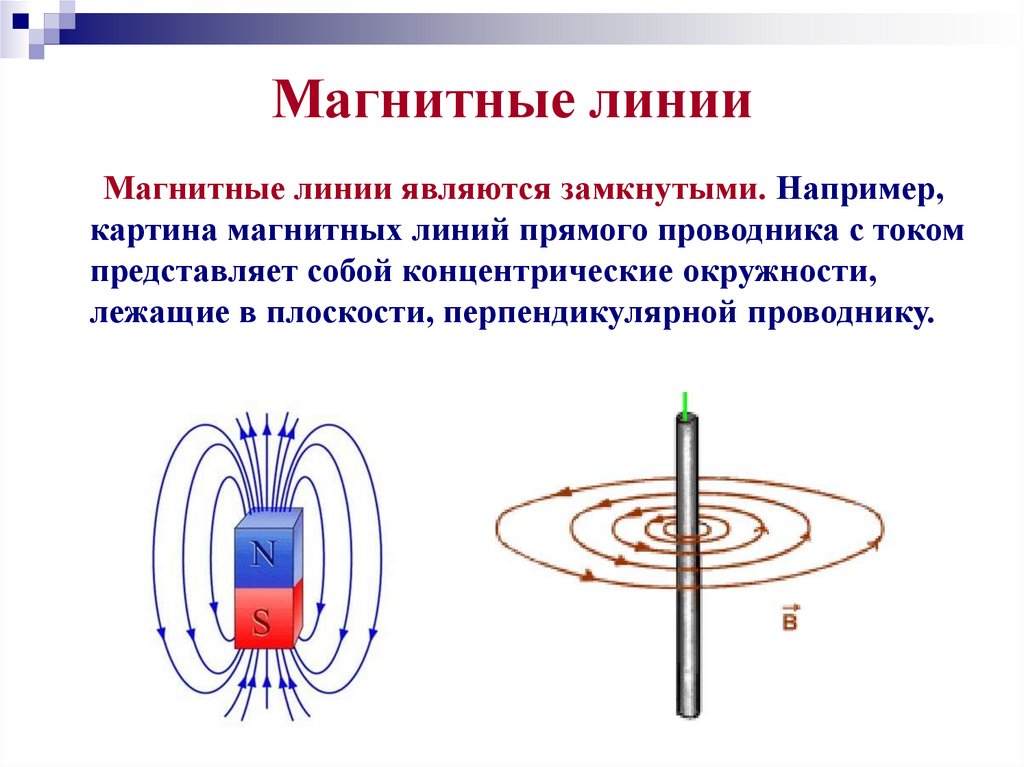

Leave A Comment