Задание № 7. Производная функции. ЕГЭ . Математика. 3
ПОДГОТОВКА К ЕГЭ ПО МАТЕМАТИКЕ
1. Планиметрия
2. Стереометрия
3. Начала теории вероятностей
4. Теория вероятностей
5. Простейшие уравнения
6. Преобразование выражений
7. Производная функции
8. Практические задачи
9. Текствые задачи
10. Графики функций
11. Исследование функций
12. Уравнения
13. Стереометрия с доказ-вом
14. Неравенства
15. Финансовая математика
16. Планиметрия с доказ-вом
17. Задачи с параметром
18. Задачи на логику
БАЗА ЗАДАНИЙ
Задание № 7.
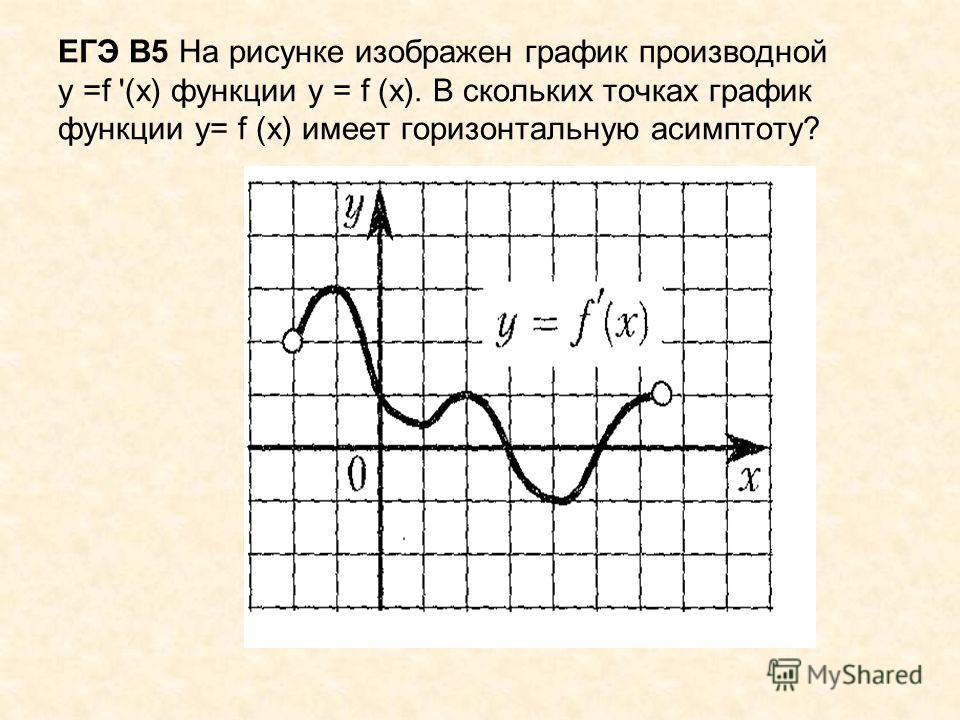
51. На рисунке изображён график y=f '(x) — производной функции f(x), определённой на интервале (− 4; 6). Найдите абсциссу точки, в которой касательная к графику функции y=f(x) параллельна прямой y = 3x или совпадает с ней.
Ответ: 5
52. На рисунке изображён график y=F(x) одной из первообразных некоторой функции f(x) и отмечены десять точек на оси абсцисс. В скольких из этих точек функция f(x) положительна?
Ответ: 7
53. На рисунке изображён график 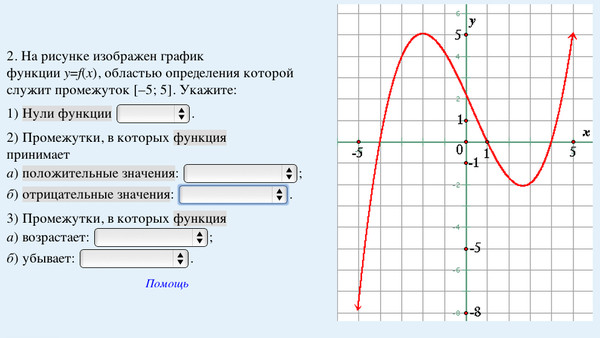 В скольких из этих точек функция f(x) отрицательна?
В скольких из этих точек функция f(x) отрицательна?
Ответ: 3
54. На рисунке изображён график y=F(x) одной из первообразных некоторой функции f(x) и отмечены десять точек на оси абсцисс. В скольких из этих точек функция
Ответ: 6
55. На рисунке изображён график y=F(x) одной из первообразных некоторой функции f(x), определённой на интервале (− 7; 5). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [− 5; 2].
Ответ: 3
56. На рисунке изображён график y=F(x) одной из первообразных некоторой функции f(x), определённой на интервале (− 8; 7). Пользуясь рисунком, определите количество решений уравнения 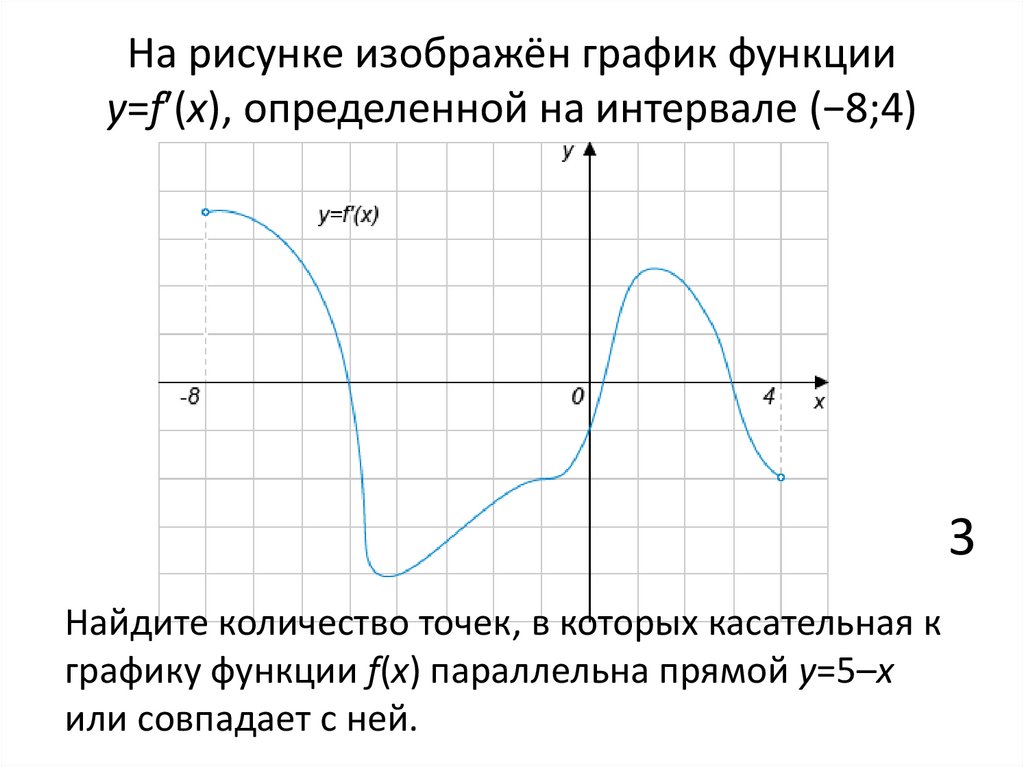
Ответ: 4
57. На рисунке изображён график y=F(x) одной из первообразных некоторой функции f(x), определённой на интервале (1;13). Пользуясь рисунком, определите количество решений уравнения f (x)=0 на отрезке [2;11].
Ответ: 4
58. На рисунке изображён график некоторой функции
Ответ: 20
59. На рисунке изображён график некоторой функции y=f(x) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(−1)−F(−9), где F(x) — одна из первообразных функции f(x).
Ответ: 24
60. На рисунке изображён график некоторой функции y=f(x). Функция
— одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.
Ответ: 6
61. На рисунке изображён график некоторой функции y=f(x). Функция
— одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.
Ответ: 14,5
62. Прямая y=7x-5 параллельна касательной к графику функции y=x2+6x-8. Найдите абсциссу точки касания.
Ответ: 0,5
63. Прямая y=—4x-11 является касательной к графику функции y=x3+7x2+7x-6. Найдите абсциссу точки касания.
Найдите абсциссу точки касания.
Ответ: -1
64. Прямая y=-3x-5 является касательной к графику функции y=x2+7x+c. Найдите c.
Ответ: 20
65. Прямая y=3x+1 является касательной к графику функции y=ax2+2x+3. Найдите a.
Ответ: 0,125
66. Прямая y=-5x+8 является касательной к графику функции y=28x2+bx+15. Найдите b, учитывая, что абсцисса точки касания больше 0.
Ответ: -33
67. Материальная точка движется прямолинейно по закону
где x — расстояние от точки отсчёта в метрах, t — время в секундах, измеренное с момента начала движения. В какой момент времени (в секундах) её скорость была равна 96 м/с?
В какой момент времени (в секундах) её скорость была равна 96 м/с?
Ответ: 18
68. Материальная точка движется прямолинейно по закону
где x — расстояние от точки отсчёта в метрах, t — время в секундах, измеренное с момента начала движения. В какой момент времени (в секундах) её скорость была равна 48 м/с?
Ответ: 9
69. Материальная точка движется прямолинейно по закону
где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в м/с) в момент времени t=6 с.
Ответ: 20
70. Материальная точка движется прямолинейно по закону
где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в м/с) в момент времени t=3 с.
Ответ: 59
Главная
@ 2017- 2023
База заданий сформирована из Официального Банка заданий ФИПИ,
Открытого банка заданий ЕГЭ, а также из реальных вариантов ЕГЭ прошлых лет.
Репетитор
по математике
WhatsApp: 8-913-866-07-50
Производная — «Математика ЕГЭ ПрофилЬ»
Категория: Производная
323080. На рисунке изображён график некоторой функции y = f(x). Функция F(x) = –x3–27×2–240x–8 — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.
Дата: 2015-08-03
14749
Комментировать
Категория: Производная
Метка: ЕГЭ-№7
Далее
323080. На рисунке изображён график некоторой функции y = f(…
323079. На рисунке изображён график некоторой функции y = f(x). Функция F(x) = x3+30×2+302x–1,875 — одна из первообразных функции y = f(x). Найдите площадь закрашенной фигуры.
Функция F(x) = x3+30×2+302x–1,875 — одна из первообразных функции y = f(x). Найдите площадь закрашенной фигуры.
Дата: 2015-08-03
2946
Комментировать
Категория: Производная
Метка: ЕГЭ-№7
Далее
323079. На рисунке изображён график некоторой функции y = f(…
323078. На рисунке изображён график некоторой функции y = f(x) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8)–F(2), где F(x) — одна из первообразных функции f(x).
Дата: 2015-08-03
7515
Комментировать
Категория: Производная
Метка: ЕГЭ-№7
Далее
323078. На рисунке изображён график некоторой функции y = f(…
323077. На рисунке изображён график функции y=F(x) — одной из первообразных некоторой функции f(x), определённой на интервале (–3;5). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [–2;4].
Дата: 2015-08-03
2602
Комментировать
Категория: Производная
Метка: ЕГЭ-№7
Далее
323077. На рисунке изображён график функции y=F(x) — одной и…
На рисунке изображён график функции y=F(x) — одной и…
119979. Материальная точка движется прямолинейно по закону где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 2 м/с?
Дата: 2015-08-03
2139
Комментировать
Категория: Производная
Метка: ЕГЭ-№7
Далее
119979. Материальная точка движется прямолинейно по закону …
119978. Материальная точка движется прямолинейно по закону где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 3 м/с?
Дата: 2015-08-02
826
Комментировать
Категория: Производная
Метка: ЕГЭ-№7
Далее
119978. Материальная точка движется прямолинейно по закону …
119977. Материальная точка движется прямолинейно по закону где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t=3с.
Найдите ее скорость (в метрах в секунду) в момент времени t=3с.
Дата: 2015-08-02
510
Комментировать
Категория: Производная
Метка: ЕГЭ-№7
Далее
119977. Материальная точка движется прямолинейно по закону …
119976. Материальная точка движется прямолинейно по закону где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t=6с.
Дата: 2015-08-02
1796
Комментировать
Категория: Производная
Метка: ЕГЭ-№7
Далее
119976. Материальная точка движется прямолинейно по закону …
119975. Материальная точка движется прямолинейно по закону где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t=9с.
Дата: 2015-08-02
704
Комментировать
Категория: Производная
Метка: ЕГЭ-№7
Далее
119975. Материальная точка движется прямолинейно по закону
…
Материальная точка движется прямолинейно по закону
…
119974. Прямая у=3х+4 является касательной к графику функции 3х2–3х+с. Найдите c.
Дата: 2015-08-02
12099
Комментировать
Категория: Производная
Метка: ЕГЭ-№7
Далее
119974. Прямая у=3х+4 является касательной к графику функции…
Следующая страница »
↑
Используя этот сайт, Вы соглашаетесь с тем, что мы сохраняем и используем файлы cookies, а также используем похожие технологии для улучшения работы сайта.
Ok
На рисунке показан график зависимости x-координаты частицы, движущейся по оси x, от времени. Найдите а) среднюю скорость за время от 0 до 10 с. (б) мгновенная скорость 2, 5, 8 и 12 сек.(А) (а)1Мм/сек, (б) 20м/сек, ноль, 20м/сек, -20м/сек.(Б) (а)20м/сек с, (b) 15 м/с, ноль, -10 м/с, 15 м/с. (C) (a) 15 м/с, (b) 15 м/с, 10 м/с, -15 м/с, 20 м/с. (D) (a) 25 м/сек, (b) 10 м/сек, -10 м/сек, ноль, 20 м/сек.
Дата последнего обновления: 04 марта 2023 г.
•
Всего просмотров: 255,6 тыс.
•
Просмотров сегодня: 4.40k
Ответить
Проверено
255.6k+ просмотров
Подсказка Сначала посчитаем смещение объекта от 0 до 10 секунд. Затем вычислим среднюю скорость, используя значение смещения по формуле $\bar \vee = \dfrac{{dx}}{{dt}}$ .
\[{V_{inst}} = \] наклон графика используется для расчета мгновенной скорости.
Полное пошаговое решение:
Средняя скорость: определяется как скорость изменения скорости объекта. Он говорит нам, какое смещение совершает объект в определенном временном диапазоне. 9{} \dfrac{{\Delta x}}{{\Delta t}}$ используется в численных расчетах.
При 2 с = наклон (1) $ = \dfrac{{50 — 0}}{{2,5 — 0}}$
= 20 м/с
При 5 с = наклон (2) $ = \dfrac{{ 50–50}}{{7,5–2,5}}$
= ноль
В 8 с = наклон (3) $ = \dfrac{{100–50}}{{10,5–7,5}}$
$ = \dfrac {{50}}{{2,5}}$
= 20 м/с
В 12 с = наклон (4) $ = \dfrac{{0 — 100}}{{15 — 10}}$
$ = \dfrac {{ — 100}}{5}$
= -20 м/сек
, поэтому у нас остался только один правильный вариант, т. е. (Отдельно. 9{} \dfrac{{\Delta x}}{{\Delta t}}$ для расчета мгновенной скорости. Так как мы получаем среднюю скорость как 10 м/с
е. (Отдельно. 9{} \dfrac{{\Delta x}}{{\Delta t}}$ для расчета мгновенной скорости. Так как мы получаем среднюю скорость как 10 м/с
Недавно обновленные страницы
Рассчитайте изменение энтропии, связанное с преобразованием химии класса 11 JEE_Main
Закон, сформулированный доктором Нернстом, является первым законом термодинамики 11 класса химии JEE_Main
Для реакции при rm0rm0rmC и нормальном давлении A химический класс 11 JEE_Main
Двигатель, работающий между rm15rm0rm0rmC и rm2rm5rm0rmC химический класс 11 JEE_Main
Для реакции rm2Clg в rmCrmlrm2rmg знаки химического класса 11 JEE_Main
Изменение энтальпии перехода жидкой воды в химический класс 11 JEE_Main
Рассчитайте изменение энтропии, связанное с преобразованием химического класса 11 JEE_Main
Закон, сформулированный Д-р Нернст — это Первый закон термодинамики. Химический класс 11 JEE_Main
Для реакции при rm0rm0rmC и нормальном давлении.0003
Для реакции rm2Clg в rmCrmlrm2rmg признаки 11-го класса химии JEE_Main
Изменение энтальпии перехода жидкой воды 11-го класса химии JEE_Main
Трендовые сомнения Что такое линейная функция? — Уравнение, график, определение
Линейная функция — это функция, представляющая прямую линию на координатной плоскости.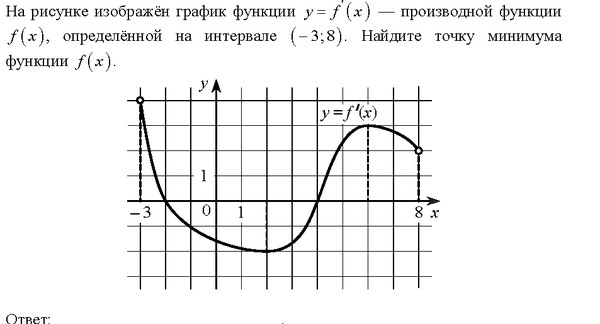 Например, y = 3x — 2 представляет собой прямую линию на координатной плоскости и, следовательно, представляет собой линейную функцию. Поскольку y можно заменить на f(x), эту функцию можно записать в виде f(x) = 3x — 2,9.0003
Например, y = 3x — 2 представляет собой прямую линию на координатной плоскости и, следовательно, представляет собой линейную функцию. Поскольку y можно заменить на f(x), эту функцию можно записать в виде f(x) = 3x — 2,9.0003
В этой статье мы изучим определение линейной функции, а также ее график, область определения и диапазон. Мы также узнаем, как идентифицировать линейную функцию и как найти ее обратную.
| 1. | Что такое линейная функция? |
| 2. | Уравнение линейной функции |
| 3. | Определение линейной функции |
| 4. | График линейной функции |
| 5. | Область и диапазон линейной функции |
| 6. | Обратная линейная функция |
| 7. | Кусочно-линейная функция |
| 8. | Часто задаваемые вопросы о линейной функции |
Что такое линейная функция?
Линейная функция имеет вид f(x) = mx + b, где m и b — действительные числа. Разве это не похоже на форму пересечения наклона линии, которая выражается как y = mx + b? Да, это потому, что линейная функция представляет собой линию, т. е. ее график является линией. Здесь
Разве это не похоже на форму пересечения наклона линии, которая выражается как y = mx + b? Да, это потому, что линейная функция представляет собой линию, т. е. ее график является линией. Здесь
- ‘м’ — это наклон линии .
- ‘b’ — точка пересечения по оси y линии .
- ‘x’ — независимая переменная
- ‘y’ (или f(x)) — зависимая переменная
Линейная функция — это алгебраическая функция. Это потому, что он включает только алгебраические операции.
Уравнение линейной функции
Родительская линейная функция f(x) = x, которая представляет собой прямую, проходящую через начало координат. В общем случае уравнение линейной функции имеет вид f(x) = mx + b, и вот несколько примеров.
- f(x) = 3x — 2
- f(x) = -5x — 0,5
- f(x) = 3
Реальный пример линейной функции
Вот несколько примеров практического применения линейной функции.
- Служба потоковой передачи фильмов взимает ежемесячную плату в размере 4,50 доллара США и дополнительную плату в размере 0,35 доллара США за каждый загруженный фильм.
 Теперь общая ежемесячная плата представлена линейной функцией f(x) = 0,35x + 4,50, где x — количество фильмов, скачанных за месяц.
Теперь общая ежемесячная плата представлена линейной функцией f(x) = 0,35x + 4,50, где x — количество фильмов, скачанных за месяц. - Компания по производству футболок взимает единовременную плату в размере 50 и 7 долларов США за каждую футболку за печать логотипов на футболках. Таким образом, общий сбор выражается линейной функцией f(x) = 7x + 50, где x — количество футболок.
- Линейная функция используется для представления целевой функции в задачах линейного программирования, чтобы помочь минимизировать закрытие или максимизировать прибыль.
Как найти линейную функцию?
Мы используем форму пересечения наклона или форму точки-наклона, чтобы найти линейную функцию. Процесс нахождения линейной функции аналогичен процессу нахождения уравнения прямой и объясняется на примере.
Пример: Найдите линейную функцию, на которой есть две точки (-1, 15) и (2, 27).
Решение:
Даны точки (x 1 , y 1 ) = (-1, 15) и (x₂, y₂) = (2, 27).
Шаг 1: Найдите наклон функции по формуле: -1)) = 12/3 = 4.
Шаг 2: Найдите уравнение линейной функции, используя форму точечного наклона.
у — у 1 = м (х — х 1 )
у — 15 = 4 (х — (-1))
у — 15 = 4 (х + 1)
у — 15 = 4х + 4
у = 4х + 19
Следовательно, уравнение линейная функция: f(x) = 4x + 19,
Определение линейной функции
Если информация о функции представлена в виде графика, то она является линейной, если график представляет собой линию. Если информация о функции дана в алгебраической форме, то она линейна, если имеет вид f(x) = mx + b. Но чтобы увидеть, представляют ли данные в табличном формате линейную функцию:
- Вычислить разницу в значениях x.
- Вычислить разницу значений y
- Проверьте, всегда ли постоянно отношение разницы значений y к разнице значений x.
Пример: Определите, представляют ли следующие данные из следующей таблицы линейную функцию.
| х | г |
|---|---|
| 3 | 15 |
| 5 | 23 |
| 7 | 31 |
| 11 | 47 |
| 13 | 55 |
Решение:
Мы каждый раз будем вычислять разность значений x, разность значений y и отношение (разность y)/(разница x) и смотреть, является ли это отношение константой.
Поскольку все числа в последнем столбце равны константе, данные в данной таблице представляют собой линейную функцию.
График линейной функции
Мы знаем, что для построения линии нам нужны только две точки на ней. Если мы найдем две точки, то мы можем просто соединить их линией и продолжить ее в обе стороны. График линейной функции f(x) = mx + b
- является возрастающей линией при m > 0
- убывающая линия, когда m < 0
- горизонтальная линия при m = 0
Есть два способа построить график линейной функции.
- Найдя на нем две точки.
- Используя наклон и точку пересечения по оси Y.
Построение графика линейной функции путем нахождения двух точек
Чтобы найти любые две точки на линейной функции (линии) f(x) = mx + b, мы просто принимаем некоторые случайные значения для ‘x’ и подставляем эти значения в функцию найти соответствующие значения для y. Процесс объясняется на примере, где мы собираемся построить график функции f(x) = 3x + 5,9.0003
- Шаг 1: Найдите две точки на прямой, взяв несколько случайных значений.
Будем считать, что x = -1 и x = 0, - Шаг 2: Подставьте каждое из этих значений в функцию, чтобы найти соответствующие значения y.
Вот таблица линейной функции y = 3x + 5.
Следовательно, две точки на прямой — это (-1, 2) и (0, 5).х г -1 3(-1)+5 = 2 0 3(0)+5 = 5 
- Шаг 3: Нанесите точки на график и соедините их линией. Также продлите линию с обеих сторон.
График линейной функции с использованием наклона и точки пересечения с осью y
Чтобы построить график линейной функции f(x) = mx + b, мы можем использовать ее наклон ‘m’ и точку пересечения с осью y ‘b’. Процесс снова объясняется путем построения графика той же линейной функции f (x) = 3x + 5. Ее наклон равен m = 3, а ее точка пересечения по оси y равна (0, b) = (0, 5).
- Шаг 1: Постройте точку пересечения по оси y (0, b).
Здесь мы наносим точку (0, 5). - Шаг 2: Запишите наклон в виде доли подъема/набега и определите «нарастание» и «набег».
Здесь наклон = 3 = 3/1 = подъем/разбег.
Итак, подъем = 3 и бег = 1. - Шаг 3: Поднимите точку пересечения по вертикали с помощью «подъема», а затем пройдите горизонтально с помощью «бег».
 Это приводит к новой точке.
Это приводит к новой точке.
(Обратите внимание, что если «подъем» положительный, мы идем вверх, а если «подъем» отрицательный, мы идем вниз. Кроме того, если «бег» положительный, мы идем вправо, а если «бег» отрицательный, мы идем влево. )
Здесь мы поднимаемся на 3 единицы вверх от точки пересечения y и, таким образом, идем вправо на 1 единицу. - Шаг 4: Соедините точки Шаг 1 и Шаг 2 линией и продолжите линию с обеих сторон.
Область и диапазон линейной функции
Область определения линейной функции — это множество всех действительных чисел, а диапазон линейной функции — это также множество всех действительных чисел. На следующем рисунке показано, как f(x) = 2x + 3 и g(x) = 4−x отложены на одних и тех же осях.
Обратите внимание, что обе функции принимают действительные значения для всех значений x, а это означает, что областью определения каждой функции является множество всех действительных чисел (R). Посмотрите вдоль оси X, чтобы убедиться в этом. Для каждого значения x у нас есть точка на графике.
Посмотрите вдоль оси X, чтобы убедиться в этом. Для каждого значения x у нас есть точка на графике.
Кроме того, выходной сигнал для каждой функции постоянно находится в диапазоне от отрицательной бесконечности до положительной бесконечности, что означает, что диапазон любой функции также равен R. Это можно подтвердить, посмотрев вдоль оси Y, которая ясно показывает, что существует точка на каждом графике для каждого значения y. Таким образом, при наклоне m ≠ 0,
- Область определения линейной функции = R
- Диапазон линейной функции = R
Примечание:
(i) Область определения и область значений линейной функции равна R, если в задаче не упоминается какая-либо конкретная область или область значений.
(ii) Когда наклон m = 0, то линейная функция f(x) = b является горизонтальной линией, и в этом случае домен = R, а диапазон = {b}.
Обратная линейная функция
Обратная линейная функция f(x) = ax + b представлена функцией f -1 (x) такой, что f(f -1 (x)) = f -1 (f (х)) = х. Процесс поиска обратной линейной функции объясняется на примере, где мы собираемся найти обратную функцию f(x) = 3x + 5.
Процесс поиска обратной линейной функции объясняется на примере, где мы собираемся найти обратную функцию f(x) = 3x + 5.
- Шаг 1: Напишите y вместо f(x ).
Тогда приведенное выше уравнение принимает вид y = 3x + 5, . - Шаг 2: Поменять местами переменные x и y.
Тогда мы получаем x = 3y + 5, - Шаг 3: Решите приведенное выше уравнение для y.
х — 5 = 3 года
у = (х — 5)/3 - Шаг 4: Замените y на f -1 (x), и это будет функция, обратная f(x).
f -1 (х) = (х — 5)/3
Обратите внимание, что f(x) и f -1 (x) всегда симметричны относительно прямой y = x. Построим линейную функцию f(x) = 3x + 5 и обратную ей f -1 (x) = (x — 5)/3 и посмотреть, симметричны ли они относительно y = x. Кроме того, когда (x, y) лежит на f(x), то (y, x) лежит на f -1 (x). Например, на следующем графике (-1, 2) лежит на f(x), тогда как (2, -1) лежит на f -1 (x).
Кусочно-линейная функция
Иногда линейная функция не может быть определена единообразно во всей области определения. Он может быть определен двумя или более способами, поскольку его домен разделен на две или более частей. В таких случаях это называется кусочно-линейная функция. Вот пример.
Пример: Постройте график следующей кусочно-линейной функции.
\(f(x)=\left\{\begin{массив}{ll}
х+2, & х \in[-2,1) \\
2 x-3 и x \in[1,2]
\end{array}\right.\)
Решение:
Эта кусочная функция линейна в обеих указанных частях своей области определения. Найдем концы прямой в каждом случае.
Когда x ∈ [-2, 1):
| x | г |
|---|---|
| -2 | -2 + 2 = 0 |
| 1 (дырка в данном случае как 1 ∉ [-2, 1)) | 1 + 2 = 3 |
При x ∈ [1, 2]:
| x | г |
|---|---|
| 1 | 2(1) — 3 = -1 |
| 2 | 2(2) — 3 = 1 |
Соответствующий график показан ниже:
Важные замечания о линейных функциях:
- Линейная функция имеет форму f(x) = mx + b, поэтому ее график представляет собой линию.

- Линейная функция f(x) = mx + b представляет собой горизонтальную линию, когда ее наклон равен 0, и в этом случае она известна как постоянная функция.
- Область определения и область значений линейной функции f(x) = ax + b равна R (все действительные числа), тогда как область значений постоянной функции f(x) = b равна {b}.
- Эти линейные функции полезны для представления целевой функции в линейном программировании.
- Постоянная функция не имеет обратной, поскольку она НЕ является однозначной функцией.
- Две линейные функции параллельны, если их наклоны равны.
- Две линейные функции перпендикулярны, если произведение их наклонов равно -1.
- Вертикальная линия НЕ является линейной функцией, так как она не проходит тест вертикальной линии.
☛ Связанные темы:
- Калькулятор линейных функций
- Формула линейной функции
- Квадратичная функция
- Графические функции
Часто задаваемые вопросы о линейной функции
Что такое определение линейной функции?
Линейная функция — это функция, график которой представляет собой линию. Таким образом, оно имеет вид f(x) = mx + b, где m и b — действительные числа. Здесь «m» — это наклон, а «b» — точка пересечения с осью y линейной функции.
Таким образом, оно имеет вид f(x) = mx + b, где m и b — действительные числа. Здесь «m» — это наклон, а «b» — точка пересечения с осью y линейной функции.
По какой формуле найти линейную функцию?
Поскольку линейная функция представляет собой прямую, все формулы, используемые для нахождения уравнения прямой, можно использовать для нахождения уравнения линейной функции. Таким образом, формулы линейной функции:
- Стандартная форма: ax + by + c = 0
- Форма пересечения наклона: y = mx + b
- Форма вершины-наклона: y — y 1 = m (x — x 1 )
- Форма перехвата: x/a + y/b = 1
Обратите внимание, что y можно заменить на f(x) во всех этих формулах.
Что такое таблица линейных функций?
Иногда данные, представляющие линейную функцию, представляются в виде таблицы с двумя столбцами, где первый столбец содержит данные независимой переменной, а второй столбец — соответствующие данные зависимой переменной. Это называется таблицей линейных функций.
Это называется таблицей линейных функций.
В чем разница между линейной функцией и нелинейной функцией?
График линейной функции представляет собой линию, тогда как график нелинейной функции НЕ является линией. Уравнение линейной функции имеет вид f(x) = ax + b (т. е. является линейным выражением), тогда как уравнение нелинейной функции может быть любого другого вида, кроме ax + b.
Как построить график линейной функции?
Чтобы построить график линейной функции, найдите на ней любые две точки, приняв несколько случайных чисел либо за зависимую, либо за независимую переменную, и найдите соответствующие значения другой переменной. Просто нанесите эти две точки и соедините их прямой линией, продлив линию с обеих сторон.
Что такое область определения и область значений линейной функции?
Область определения и область значений линейной функции f(x) = ax + b, где a ≠ 0 — множество всех действительных чисел. Если a = 0, домен по-прежнему является набором всех действительных чисел, но диапазоном является набор {b}.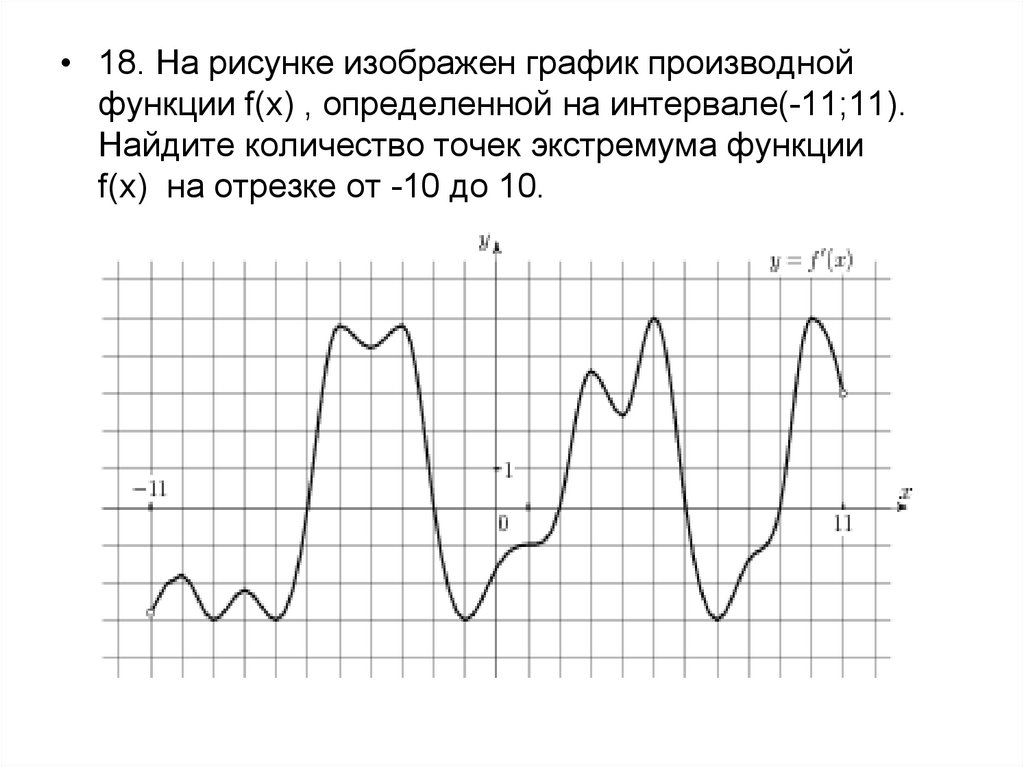

 Теперь общая ежемесячная плата представлена линейной функцией f(x) = 0,35x + 4,50, где x — количество фильмов, скачанных за месяц.
Теперь общая ежемесячная плата представлена линейной функцией f(x) = 0,35x + 4,50, где x — количество фильмов, скачанных за месяц.
 Это приводит к новой точке.
Это приводит к новой точке. 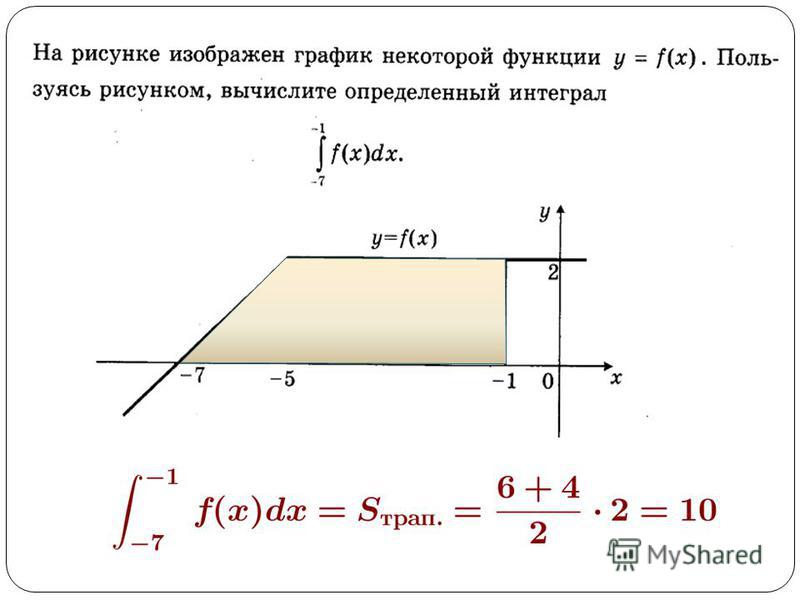
Leave A Comment