КР Геометрия 8 класс Мерзляк
Контрольная работа №1
Параллелограмм и его виды
Вариант 1
Одна из сторон параллелограмма в 3 раза меньше другой, а его периметр равен 72 см. Найдите стороны параллелограмма.
Диагонали прямоугольника ABCD пересекаются в точке O, AB = 10 см, BD = 12 см. Найдите периметр треугольника COD.
Один из углов ромба равен 64°. Найдите углы, которые образует сторона ромба с его диагоналями.
На диагонали BD параллелограмма ABCD отметили точки M и K так, что <BAM=<DCK (точка M лежит между точками B и K). Докажите, что BM = DK.
Биссектриса угла D
Через середину K гипотенузы AB прямоугольного треугольника ABC проведены прямые, параллельные его катетам. Одна из них пересекает катет AC в точке D, а другая — катет BC в точке E. Найдите отрезок DE, если AB = 12 см.
Контрольная работа №1
Параллелограмм и его виды
Вариант 2
Одна из сторон параллелограмма на 7 см меньше другой, а его периметр равен 54 см. Найдите стороны параллелограмма.
Диагонали прямоугольника ABCD пересекаются в точке O, BC = 16 см, AC = 24 см.
 Найдите периметр треугольника AOD.
Найдите периметр треугольника AOD.Сторона ромба образует с одной из его диагоналей угол 18°. Найдите углы ромба.
На диагонали AC параллелограмма ABCD отметили точки E и F так, что AE = CF (точка E лежит между точками A и F). Докажите, что BE = DF
Биссектриса угла B параллелограмма ABCD пересекает сторону AD в точке K, AK : KD = 3 : 2. Найдите периметр параллелограмма, если AB = 12 см.
Через середину O гипотенузы AB прямоугольного треугольника ABC проведены прямые, параллельные его катетам. Одна из них пересекает катет AC в точке M, а другая — катет BC в точке N. Найдите гипотенузу AB, если MN = 7 см
Контрольная работа №1
Параллелограмм и его виды
Вариант 3
Одна из сторон параллелограмма в 6 раз больше другой, а его периметр равен 84 см. Найдите стороны параллелограмма.
Диагонали прямоугольника ABCD пересекаются в точке O, AD = 18 см, BD = 22 см. Найдите периметр треугольника BOC.
Один из углов ромба равен 132°. Найдите углы, которые образует сторона ромба с его диагоналями.
На диагонали AC параллелограмма ABCD отметили точки N и P так, что <ABN= (точка N лежит между точками A и P). Докажите, что BN = DP.
Через середину P гипотенузы AB прямоугольного треугольника ABC проведены прямые, параллельные его катетам.
 Одна из них пересекает катет AC в точке F, а другая — катет BC в точке K. Найдите отрезок FK, если AB = 16 см.
Одна из них пересекает катет AC в точке F, а другая — катет BC в точке K. Найдите отрезок FK, если AB = 16 см.
Контрольная работа №1
Параллелограмм и его виды
Вариант 4
Одна из сторон параллелограмма на 5 см больше другой, а его периметр равен 66 см. Найдите стороны параллелограмма.
Диагонали прямоугольника ABCD пересекаются в точке O, CD = 15 см, AC = 20 см. Найдите периметр треугольника AOB.
Сторона ромба образует с одной из его диагоналей угол 68°. Найдите углы ромба.
На диагонали BD параллелограмма ABCD отметили точки K и M так, что BK = DM (точка K лежит между точками B и M). Докажите, что <BCK = <DAM.
Через середину D гипотенузы AB прямоугольного треугольника ABC проведены прямые, параллельные его катетам. Одна из них пересекает катет AC в точке E, а другая — катет BC в точке F. Найдите гипотенузу AB, если EF = 9 см.Контрольная работа №2
Средняя линия треугольника. Трапеция.
Вписанные и описанные четырёхугольники
Точки M и K — середины сторон AB и AC треугольника ABC соответственно. Найдите периметр треугольника AMK, если AB = 12 см, BC = 8 см, AC = 14 см.
Одно из оснований трапеции на 6 см больше другого, а её средняя линия равна 9 см.
 Найдите основания трапеции.
Найдите основания трапеции.Две противолежащие стороны четырёхугольника равны 9 см и 16 см. Чему равен периметр четырёхугольника, если в него можно вписать окружность?
Найдите углы четырёхугольника ABCD, вписанного в окружность, если <ACB=36°, <ABD = 48°, 85°.
Диагонали равнобокой трапеции перпендикулярны, её высота равна 7 см, а периметр — 30 см. Найдите боковую сторону трапеции.
Контрольная работа №2
Средняя линия треугольника. Трапеция.
Вписанные и описанные четырёхугольники
Точки Fи E — середины сторон BC и BA треугольника ABC соответственно. Найдите периметр треугольника ABC, если BE = 10 см, BF = 16 см, EF = 14 см.
Одно из оснований трапеции в 2 раза больше другого, а её средняя линия равна 6 см. Найдите основания трапеции.
Две противолежащие стороны четырёхугольника равны 10 см и 14 см. Чему равен периметр четырёхугольника, если в него можно вписать окружность?
Меньшее основание равнобокой трапеции равно 4 см, а её боковая сторона — 5 см. Найдите периметр трапеции, если её диагональ делит тупой угол трапеции пополам.
Найдите углы четырёхугольника ABCD, вписанного в окружность, если <ADB=62°, <ACD = 54°, 27°.
Диагонали равнобокой трапеции перпендикулярны, её боковая сторона равна 12 см, а периметр — 42 см.
 Найдите высоту трапеции.
Найдите высоту трапеции.
Контрольная работа №2
Средняя линия треугольника. Трапеция.
Вписанные и описанные четырёхугольники
Вариант 3
Точки A и B — середины сторон
Одно из оснований трапеции на 10 см меньше другого, а её средняя линия равна 13 см. Найдите основания трапеции.
Две противолежащие стороны четырёхугольника равны 7 см и 13 см. Чему равен периметр четырёхугольника, если в него можно вписать окружность?
Найдите периметр равнобокой трапеции, если её основания равны 9 см и 14 см, а диагональ делит острый угол трапеции пополам.
Найдите углы четырёхугольника ABCD,
Диагонали равнобокой трапеции перпендикулярны, её высота равна 12 см, а боковая сторона — 15 см. Найдите периметр трапеции.
Контрольная работа №2
Средняя линия треугольника. Трапеция.
Вписанные и описанные четырёхугольники
Вариант 4
Точки C и D — середины сторон FA и FN треугольника FAN соответственно. Найдите периметр треугольника FAN, если FC = 20 см, FD = 22 см, CD = 10 см.
Одно из оснований трапеции в 3 раза меньше другого, а её средняя линия равна 18 см. Найдите основания трапеции.
Две противолежащие стороны четырёхугольника равны 11 см и 19 см.
 Чему равен периметр четырёхугольника, если в него можно вписать окружность?
Чему равен периметр четырёхугольника, если в него можно вписать окружность?Найдите периметр равнобокой трапеции, если её основания равны 12 см и 18 см, а диагональ делит тупой угол трапеции пополам.
Найдите углы четырёхугольника ABCD, вписанного в окружность, если <ACB = 58°, <ABD = 16°, <BAC = 44°.
Диагонали равнобокой трапеции перпендикулярны, её периметр равен 50 см, а боковая сторона — 14 см. Найдите высоту трапеции.
Контрольная работа №3
Теорема Фалеса. Подобие треугольников.
Вариант 1
На рисунке 15 MO || NP, OP = 20 см, PK = 8 см, MN = 15 см. Найдите отрезок NK.
Треугольники ABC и подобны, причём сторонам AB и AC соответствуют стороны и . Найдите неизвестные стороны этих треугольников, если AB = 12 см, AC = 18 см, =12 см, = 18 см.
Отрезок BM — биссектриса треугольника ABC, AB = 30 см, AM = 12 см, MC = 14 см. Найдите сторону BC.
На стороне AB треугольника ABC отметили точку D так, что AD : BD = 5 : 3. Через точку D провели прямую, которая параллельна стороне AC треугольника и пересекает сторону BC в точке E. Найдите отрезок DE, если AC = 16 см.
В трапеции ABCD с основаниями AD и BC диагонали пересекаются в точке O, BC = 6 см, AD = 14 см, а отрезок BO на 2 см меньше отрезка OD. Найдите диагональ BD трапеции.
Через точку A, находящуюся на расстоянии 5 см от центра окружности радиуса 11 см, проведена хорда, которую точка A делит на отрезки, длины которых относятся как 2 : 3.
 Найдите длину этой хорды.
Найдите длину этой хорды.
Контрольная работа №3
Теорема Фалеса. Подобие треугольников.
Вариант 2
На рисунке 16 EF || DC, AE = 40 см, AF = 24 см, FC = 9 см. Найдите отрезок ED.
Треугольники ABC и подобны, причём сторонам AB и BC соответствуют стороны и . Найдите неизвестные стороны этих треугольников, если BC = 22 см, AC = 14 см, =33см, = 15 см.
Отрезок AE — биссектриса треугольника ABC, AB = 32 см, AC = 16 см, CE = 6 см.
Найдите отрезок BE На стороне AC треугольника ABC отметили точку E так, что AE : CE = 2 : 7. Через точку E провели прямую, которая параллельна стороне AB треугольника и пересекает сторону BC в точке F. Найдите сторону AB, если EF = 21 см.
В трапеции ABCD с основаниями AD и BC диагонали пересекаются в точке O, AO = 10 см, OC = 4 см. Найдите основания трапеции, если их сумма равна 42 см.
Через точку B, лежащую внутри окружности, проведена хорда, которая делится точкой B на отрезки длиной 8 см и 12 см. Найдите радиус окружности, если точка B удалена от её центра на 5 см.
Контрольная работа №3
Теорема Фалеса. Подобие треугольников.
Вариант 3
На рисунке 17 CF || BE, AE = 6 см, EF = 14 см, BC = 35 см. Найдите отрезок AB.
Треугольники ABC и подобны, причём сторонам AC и BC соответствуют стороны и .
 Найдите неизвестные стороны этих треугольников, если AC = 28 см, AB = 49 см, =24см, = 16 см.
Найдите неизвестные стороны этих треугольников, если AC = 28 см, AB = 49 см, =24см, = 16 см.Отрезок CK — биссектриса треугольника ABC, AC = 45 см, AK = 18 см, BK = 10 см. Найдите сторону BC.
На стороне AB треугольника ABC отметили точку M так, что AM : MB = 4 : 9. Через точку M провели прямую, которая параллельна стороне BC треугольника и пересекает сторону AC в точке K. Найдите отрезок MK, если BC = 26 см.
В трапеции ABCD с основаниями AD и BC диагонали пересекаются в точке O, BO = 15 см, OD = 18 см, основание BC на 5 см меньше основания AD. Найдите основания трапеции.
Через точку C, находящуюся на расстоянии 11 см от центра окружности радиуса 13 см, проведена хорда, делящаяся точкой C на отрезки, длины которых относятся как 1 : 3. Найдите длину этой хорды.
Контрольная работа №3
Теорема Фалеса. Подобие треугольников.
Вариант 4
На рисунке 18 TP || SM, KP = 25 см, PM = 20 см, KT = 10 см. Найдите отрезок TS.
Треугольники ABC и подобны, причём сторонам AB и AC соответствуют стороны и . Найдите неизвестные стороны этих треугольников, если AC = 9 см, BC = 27 см, =36см, = 28 см.
Отрезок BD — биссектриса треугольника ABC, AB = 48 см, BC = 32 см, AD = 36 см. Найдите отрезок CD.
На стороне BC треугольника ABC отметили точку P так, что BP : PC = 5 : 6. Через точку P провели прямую, которая параллельна стороне AC треугольника и пересекает сторону AB в точке N.
 Найдите сторону AC, если PN = 15 см.
Найдите сторону AC, если PN = 15 см.В трапеции ABCD с основаниями AD и BC диагонали пересекаются в точке O, AO = 24 см, OC = 16 см, а отрезок OD на 9 см больше отрезка BO. Найдите диагональ BD трапеции.
Через точку D, лежащую внутри окружности, проведена хорда, которая делится точкой D на отрезки длиной 3 см и 4 см. Найдите расстояние от точки D до центра окружности, если радиус окружности равен 4 см.
Контрольная работа №4
Метрические соотношения в прямоугольном треугольнике.
Теорема Пифагора
Вариант 1
Катет прямоугольного треугольника равен 10 см, а его проекция на гипотенузу — 8 см. Найдите гипотенузу треугольника.
В прямоугольном треугольнике катеты равны 20 см и 21 см. Найдите периметр треугольника.
Сторона ромба равна см, а одна из диагоналей — 12 см. Найдите вторую диагональ ромба.
Основания равнобокой трапеции равны 33 см и 51 см, а её диагональ — 58 см. Найдите боковую сторону трапеции.
Из точки к прямой проведены две наклонные, длины которых равны 11 см и 16 см. Найдите проекции данных наклонных, если одна из проекций на 9 см меньше другой.
Найдите боковую сторону равнобокой трапеции, основания которой равны 14 см и 18 см, а диагонали перпендикулярны боковым сторонам.
Контрольная работа №4
Метрические соотношения в прямоугольном треугольнике.
Теорема Пифагора
Вариант 2
Катет прямоугольного треугольника равен 16 см, а гипотенуза — 20 см.
 Найдите проекцию данного катета на гипотенузу.
Найдите проекцию данного катета на гипотенузу.В прямоугольном треугольнике гипотенуза равна 41 см, а один из катетов — 9 см. Найдите периметр треугольника.
Диагонали ромба равны 16 см и 8 см. Найдите сторону ромба.
Основания равнобокой трапеции равны 21 см и 11 см, а боковая сторона — 13 см. Найдите диагональ трапеции.
Из точки к прямой проведены две наклонные, проекции которых на прямую равны 15 см и 6 см. Найдите данные наклонные, если одна из них на 7 см больше другой.
Найдите высоту равнобокой трапеции, основания которой равны 5 см и 13 см, а диагонали перпендикулярны боковым сторонам.
Контрольная работа №4
Метрические соотношения в прямоугольном треугольнике.
Теорема Пифагора
Вариант 3
Катет прямоугольного треугольника равен 12 см, а его проекция на гипотенузу — 10 см. Найдите гипотенузу треугольника.
В прямоугольном треугольнике катеты равны 15 см и 20 см. Найдите периметр треугольника.
Сторона ромба равна см, а одна из диагоналей — 6 см. Найдите вторую диагональ ромба.
Основания равнобокой трапеции равны 6 см и 34 см, а диагональ — 52 см. Найдите боковую сторону трапеции.
Из точки к прямой проведены две наклонные, длины которых равны 25 см и 17 см. Найдите проекции данных наклонных, если их длины относятся как 5 : 2.
Найдите диагональ равнобокой трапеции, основания которой равны 20 см и 12 см, а диагонали перпендикулярны боковым сторонам.
Контрольная работа №4
Метрические соотношения в прямоугольном треугольнике.
Теорема Пифагора
Вариант 4
Катет прямоугольного треугольника равен 6 см, а гипотенуза — 9 см. Найдите проекцию данного катета на гипотенузу.
В прямоугольном треугольнике гипотенуза равна 37 см, а один из катетов — 35 см. Найдите периметр треугольника.
Диагонали ромба равны 4 см и 20 см. Найдите сторону ромба.
Основания равнобокой трапеции равны 18 см и 30 см, а её боковая сторона — см. Найдите диагональ трапеции.
Из точки к прямой проведены две наклонные, проекции которых на прямую равны 12 см и 30 см. Найдите данные наклонные, если их длины относятся как 10 : 17.
Найдите боковую сторону равнобокой трапеции, основания которой равны 7 см и 25 см, а диагонали перпендикулярны боковым сторонам.
Контрольная работа №5
Тригонометрические функции острого угла прямоугольного треугольника. Решение прямоугольных треугольников.
Вариант 1
В треугольнике АВС <С = 90°, АВ = 13 см, АС = 5 см. Найдите: 1) sinB; 2) tgA.
Найдите гипотенузу прямоугольного треугольника АВС (<С=90°) если ВС=6см, cosB = .
Найдите значение выражения sin²37° + cos²37° — sin²45°.
В равнобокой трапеции АВСD AB = CD = 6 см, ВС = 8 см, AD=12 см. Найдите синус, косинус, тангенс и котангенс угла А трапеции.
Высота BD треугольника АВС делит его сторону АС на отрезки AD и CD. Найдите отрезок CD, если АВ = 2 см, ВС = 7 см, <А = 60°.
Диагональ равнобокой трапеции перпендикулярна боковой стороне и образует с высотой трапеции угол α.
 Найдите высоту трапеции, если радиус окружности, описанной около трапеции, равен R.
Найдите высоту трапеции, если радиус окружности, описанной около трапеции, равен R.
Контрольная работа №5
Тригонометрические функции острого угла прямоугольного треугольника. Решение прямоугольных треугольников.
Вариант 2
В треугольнике АВС <В = 90°, АС = 17 см, ВС = 8 см. Найдите: 1) cosC; 2) ctgA.
Найдите гипотенузу прямоугольного треугольника MNK ( если MN=10см, sinK = .
Найдите значение выражения cos²45° + sin²74° + cos²74°.
В прямоугольной трапеции АВСD (ВС ‖ АD, ˂А=90°), АВ = 4 см, ВС=7 см, АD=9см. Найдите синус, косинус, тангенс и котангенс угла D трапеции.
Высота NF треугольника MNK делит его сторону MK на отрезки MF и FK. Найдите сторону MN, если FK = 6 см, MF = 8 см,
Диагональ равнобокой трапеции перпендикулярна боковой стороне, а угол между диагональю и высотой трапеции равен α. Найдите радиус окружности, описанной около трапеции, если ее высота равна h.
Контрольная работа №5
Тригонометрические функции острого угла прямоугольного треугольника. Решение прямоугольных треугольников.
Вариант 3
В треугольнике АВС <С = 90°, АВ = 26 см, ВС = 10 см. Найдите: 1) sinA; 2) tgB.
Найдите катет прямоугольного треугольника АВС (<В=90°) если АС = 12 см, cosC = .
Найдите значение выражения sin²61° + cos²61° — cos²60°.
В прямоугольной трапеции FKPE FK=EP=9 см, FE = 20 см, KP=8 см.
 Найдите синус, косинус, тангенс и котангенс угла F трапеции.
Найдите синус, косинус, тангенс и котангенс угла F трапеции.Высота AM треугольника АВС делит его сторону BС на отрезки BM и MC. Найдите отрезок MC, если АВ = 10 см, AС = 26 см, .
Диагональ равнобокой трапеции перпендикулярна боковой стороне, а угол между большим основанием и боковой стороной равен α. Найдите высоту трапеции, если радиус окружности, описанной около трапеции, равен R.
Контрольная работа №5
Тригонометрические функции острого угла прямоугольного треугольника. Решение прямоугольных треугольников.
Вариант 4
В треугольнике АВС <А=90°, ВС = 25 см, АС = 15 см. Найдите: 1) cosC; 2) ctgВ.
Найдите катет прямоугольного треугольника АВС (<С=90°) если АС=8см, tgB=.
Найдите значение выражения cos²42° + sin²42° + sin²30°.
В прямоугольной трапеции KDMT (DM || KT, ˂D=90°), DM = 6 см, KT = 21 см, MT = 20 см. Найдите синус, косинус, тангенс и котангенс угла T трапеции.
Высота NE треугольника FNP делит его сторону FP на отрезки FE и PE. Найдите сторону NF, если EP = 8 см, NP = 17см, .
Диагональ равнобокой трапеции перпендикулярна боковой стороне, а угол между боковой стороной и высотой трапеции равен α. Найдите радиус окружности, описанной около трапеции, если ее высота равна h.
Контрольная работа №6
Многоугольники. Площадь многоугольника
Вариант 1
Чему равна сумма углов выпуклого 12-угольника?
Площадь параллелограмма равна 144 , а одна из его высот — 16 см.
 Найдите сторону параллелограмма, к которой проведена эта высота.
Найдите сторону параллелограмма, к которой проведена эта высота.Найдите площадь прямоугольного треугольника, гипотенуза которого равна 13 см, а один из катетов — 12 см.
Найдите площадь ромба, сторона которого равна 10 см, а сумма диагоналей — 28 см.
Большая боковая сторона прямоугольной трапеции равна см, а острый угол — 45°. Найдите площадь трапеции, если известно, что в неё можно вписать окружность.
Биссектриса острого угла прямоугольного треугольника делит катет на отрезки длиной 8 см и 17 см. Найдите площадь треугольника.
Контрольная работа №6
Многоугольники. Площадь многоугольника
Вариант 2
Чему равна сумма углов выпуклого 17-угольника?
Площадь параллелограмма равна 104 , а одна из его сторон — 13 см. Найдите высоту параллелограмма, проведённую к этой стороне.
Найдите площадь равнобедренного треугольника, основание которого равно 30 см, а боковая сторона — 17 см.
Найдите площадь ромба, сторона которого равна 15 см, а разность диагоналей — 6 см.
Боковая сторона равнобокой трапеции равна 10 см, а острый угол — 60°. Найдите площадь трапеции, если известно, что в неё можно вписать окружность.
Биссектриса прямого угла прямоугольного треугольника делит гипотенузу на отрезки длиной 30 см и 40 см. Найдите площадь треугольника.
Контрольная работа №6
Многоугольники. Площадь многоугольника
Вариант 3
Чему равна сумма углов выпуклого 22-угольника?
Площадь параллелограмма равна 112 , а одна из его высот — 14 см.
 Найдите сторону параллелограмма, к которой проведена эта высота.
Найдите сторону параллелограмма, к которой проведена эта высота.Найдите площадь прямоугольного треугольника, гипотенуза которого равна 26 см, а один из катетов — 10 см.
Найдите площадь ромба, сторона которого равна 25 см, а сумма диагоналей — 70 см.
Меньшая боковая сторона прямоугольной трапеции равна см, а острый угол — 60°. Найдите площадь трапеции, если известно, что в неё можно вписать окружность.
Биссектриса острого угла прямоугольного треугольника делит катет на отрезки длиной 5 см и 13 см. Найдите площадь треугольника.
Контрольная работа №6
Многоугольники. Площадь многоугольника
Вариант 4
Чему равна сумма углов выпуклого двадцатисемиугольника?
Площадь параллелограмма равна 108 , а одна из его сторон — 18 см. Найдите высоту параллелограмма, проведённую к этой стороне.
Найдите площадь равнобедренного треугольника, высота которого, проведённая к основанию, равна 12 см, а боковая сторона — 37 см.
Найдите площадь ромба, сторона которого равна 17 см, а разность диагоналей — 14 см.
Боковая сторона равнобокой трапеции равна см, а острый угол — 30°. Найдите площадь этой трапеции, если известно, что в неё можно вписать окружность.
Биссектриса прямого угла прямоугольного треугольника делит гипотенузу на отрезки длиной 10 см и 30 см. Найдите площадь треугольника.
Контрольная работа №7
Обобщение и систематизация знаний учащихся
за курс 8 класса
Вариант 1
Найдите углы параллелограмма, если один из них на 46° больше другого.

Продолжения боковых сторон АВ и СD трапеции АВСD пересекаются в точке K. Меньшее основание ВС равно 4 см, AВ = 6 см, ВK = 3 см. Найдите большее основание трапеции.
Высота BD треугольника АВС делит его сторону AС на отрезки AD и CD. Найдите сторону BC, если см, см, ∠AВD=30°.
Основания равнобокой трапеции равны 10 см и 20 см, а диагональ является биссектрисой её тупого угла. Вычислите площадь трапеции.
Из точки B окружности опущен перпендикуляр BM на её диаметр AC, AB=4см. Найдите радиус окружности, если отрезок AM на 4 см меньше отрезка CM.
Контрольная работа №7
Обобщение и систематизация знаний учащихся
за курс 8 класса
Вариант 2
Найдите углы параллелограмма, если один из них на 18° меньше другого.
Продолжения боковых сторон AB и CD трапеции ABCD пересекаются в точке M. Большее основание AD равно 20 см, MD = 10 см, CD = 8 см. Найдите меньшее основание трапеции.
Высота EK треугольника DEF делит его сторону DF на отрезки DK и KF. Найдите сторону DE, если EF = см, KF = 2 см, 45°.
Основания прямоугольной трапеции равны 18 см и 12 см, а диагональ является биссектрисой её острого угла. Вычислите площадь трапеции.
Из точки E окружности опущен перпендикуляр EK на её диаметр DF, DE = см. Найдите радиус окружности, если отрезок KF на 6 см больше отрезка DK.
Контрольная работа №7
Обобщение и систематизация знаний учащихся
за курс 8 класса
Вариант 3
Найдите углы параллелограмма, если один из них на 54° больше другого.

Продолжения боковых сторон AB и CD трапеции ABCD пересекаются в точке P. Меньшее основание BC равно 8 см, PC = 7 см, CD = 21 см. Найдите большее основание трапеции.
Высота KP треугольника MNK делит его сторону MN на отрезки MP и PN. Найдите сторону KN, если MP = см, PN = 3 см, <MKP = 60°.
Основания равнобокой трапеции равны 12 см и 18 см, а диагональ является биссектрисой её острого угла. Вычислите площадь трапеции.
Из точки M окружности опущен перпендикуляр MF на её диаметр DE, DM= см. Найдите радиус окружности, если отрезок DF на 8 см меньше отрезка FE.
Контрольная работа №7
Обобщение и систематизация знаний учащихся
за курс 8 класса
Вариант 4
Найдите углы параллелограмма, если один из них на 36° меньше другого.
Продолжения боковых сторон AB и CD трапеции ABCD пересекаются в точке F. Большее основание AD равно 32 см, AF = 16 см, AB = 12 см. Найдите меньшее основание трапеции.
Высота CM треугольника ABC делит его сторону AB на отрезки AM и BM. Найдите сторону BC, если AM = 15 см, BM = 5 см, <A = 30°.
Основания прямоугольной трапеции равны 9 см и 17 см, а диагональ является биссектрисой её тупого угла. Вычислите площадь трапеции.
Из точки C окружности опущен перпендикуляр CD на её диаметр AB, AC = см. Найдите радиус окружности, если отрезок AD на 10 см меньше отрезка BD.

5 класс. Математика. Никольский. Учебник. Ответы к стр. 105
Измерение величин
Четырёхугольники
Ответы к стр. 105
470. Стороны прямоугольника равны 16 см и 12 см. Найдите сторону квадрата, имеющего такой же периметр, что и данный прямоугольник.
1) (16 + 12) • 2 = 28 • 2 = 56 (см) − периметр прямоугольника
2) 56 : 4 = 14 (см) − сторона квадрата
О т в е т: сторона квадрата 14 см.
471. Сторону квадрата увеличили на 2 см. На сколько сантиметров увеличился периметр квадрата?
Пусть сторона квадрата равна α см, тогда:
1) 4 • α (см) − периметр квадрата до увеличения стороны
2) 4 • (α + 2) = 4 • α + 8 (см) − периметр квадрата с увеличенной стороной
3) 4 • α + 8 − 4 • α = 8 (см) − размер увеличения периметра
О т в е т: периметр увеличиться на 8 см.
472. Как изменится периметр квадрата, если его сторону:
а) увеличить в 2 раза; б) уменьшить в 3 раза?
а) Пусть сторона квадрата равна α см, тогда:
1) 4 • α (см) − периметр квадрата
2) 4 • α • 2 = 8 • α (см) − периметр квадрата с увеличенной стороной
3) 8 • α : 4 • α = 2 (раза) − увеличиться периметр квадрата
О т в е т: периметр увеличиться в 2 раза.
б) Пусть сторона квадрата равна 3 • α см, тогда:
1) 4 • 3 • α = 12 • α (см) − периметр квадрата
2) 4 • (3 • α : 3) = 4 • α (см) − периметр квадрата с уменьшенной стороной
3) 12 • α : 4 • α = 3 (раза) − уменьшиться периметр квадрата
О т в е т: периметр уменьшиться в 3 раза.
473. Убедитесь, что на рисунке 95, а изображено 18 прямоугольников. Учтите, что квадрат является прямоугольником. Сколько прямоугольников изображено на рисунке 95, б?
Сколько прямоугольников изображено на рисунке 95, б?
474. Четырехугольник, все стороны которого равны, называют ромбом. На рисунке 96 изображены ромбы ABCD и MNKL. Измерьте их стороны и вычислите периметры.
AB = BC = CD = AD = 25 мм
MN = NK = KL = ML = 25 мм
Р◊ = 25 • 4 = 100 (мм) = 10 (см)
475. а) Чему равен периметр ромба, если одна его сторона равна 20 см?
б) Чему равна сторона ромба, если его периметр равен 20 см?
а) 20 • 4 = 80 (см) − периметр ромба
О т в е т: периметр ромба 80 см.
б) 20 : 4 = 5 (см) − сторона ромба
О т в е т: сторона ромба 5 см.
476. Постройте ромб KLMN, если KL = 4 см, ∠K = 60°. Измерьте длину отрезка LN и величину угла L.
LN = 4 см, ∠L = 120°.
477. Периметр треугольника ABD равен 12 см, периметр треугольника BDC − 30 см, а периметр четырехугольника ABCD − 32 см (рис. 97). Определите длину отрезка BD.
РABD + РBDC = РABCD + BD + BD
2 • BD = РABD + РBDC – РABCD
BD = (РABD + РBDC – РABCD) : 2
BD = (12 + 30 – 32) : 2 = 10 : 2 = 5 (см)
О т в е т: отрезок BD равен 5 см.
Ответы по математике. 5 класс. Учебник. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В.
Математика. 5 класс
Математика 5 Мерзляк СР-03 В2
Самостоятельная работа № 3 по математике в 5 классе «Отрезок. Длина отрезка» с ответами. Дидактические материалы для учителей, учащихся и родителей. Математика 5 Мерзляк СР-03 В2.
Длина отрезка» с ответами. Дидактические материалы для учителей, учащихся и родителей. Математика 5 Мерзляк СР-03 В2.
Математика 5 класс (Мерзляк)
Самостоятельная работа № 3. Вариант 2.
СР «Отрезок. Длина отрезка» (транскрипт заданий)
13. Запишите все отрезки, изображённые на рисунке 22.
14. Начертите отрезки MN и РК так, чтобы MN = 6 см 8 мм, РК = 3 см 3 мм.
15. Начертите отрезок DE, длина которого равна 5 см 6 мм. Отметьте на нём точку F так, чтобы FE = 3 см 4 мм. Какова длина отрезка DF?
16. Известно, что АС = 171 см, отрезок СВ в 3 раза меньше отрезка АС (рис. 23). Найдите длину отрезка АВ.
17. Постройте ломаную KLMN так, чтобы KL = 18 мм, LM = 23 мм, MN = 35 мм. Вычислите длину ломаной.
18. Известно, что AD = 32 м, АВ = 24 м, СВ = 15 м (рис. 24). Найдите длины отрезков АС и BD.
Математика 5 Мерзляк СР-03 В2.
Ответы на самостоятельную работу:
№ 13. а) BA, BD, AE, AC; б) ЕМ, EF, FM, FK, МК, КР.
№ 14.
№ 15. 2 см 2 мм.
№ 16. 114 см.
№ 17. 76 мм.
№ 18. BD = 8 м; AC = 9 м.
Вы смотрели: Самостоятельная работа по математике в 5 классе «Отрезок. Длина отрезка» с ответами Вариант 2. Дидактические материалы для учителей, учащихся и родителей.
Другие варианты: СР-03. Вариант 1 СР-03. Вариант 3 СР-03. Вариант 4
Вернуться к Списку самостоятельных работ по математике в 5 классе УМК Мерзляк.
Перейти к Списку контрольных работ по математике в 5 классе УМК Мерзляк.
Цитаты (упражнения) из учебного пособия «Дидактические материалы. Математика 5 класс / Мерзляк, Полонский, Рабинович, Якир — М.:Вентана-Граф» использованы на сайте исключительно в учебных целях (пп. 1 п. 1 ст. 1274 ГК РФ). Решения и ОТВЕТЫ на самостоятельную работу (нет в пособии) адресованы родителям для проверки знаний учащихся.
Решения и ОТВЕТЫ на самостоятельную работу (нет в пособии) адресованы родителям для проверки знаний учащихся.
Мерзляк 5 класс — § 15. Прямоугольник. Ось симметрии фигуры
Вопросы к параграфу
1. Какой четырёхугольник называют прямоугольником?
Прямоугольник — это четырёхугольник, у которого все углы прямые.
2. Какие стороны прямоугольника называют соседними? Противолежащими?
- соседние стороны прямоугольника — это стороны, которые имеют общую вершину
- противолежащие стороны прямоугольника — это стороны, которые не имеют общих вершин
3. Что называют длиной и шириной прямоугольника?
Длиной и шириной прямоугольника называют соседние стороны прямоугольника.
4. Каким свойством обладают противолежащие стороны прямоугольника?
Противолежащие стороны прямоугольника равны.
5. Какую фигуру называют квадратом?
Квадрат — это прямоугольник, у которого все стороны равны.
6. Объясните, какие фигуры называют симметричными относительно прямой.
Фигуру называют симметричной, относительно прямой, если при сгибе по этой прямой противоположные части фигуры совпадают друг с другом.
7. Как называют прямую, относительно которой симметрична фигура?
Ось симметрии.
8. Какие вы знаете фигуры, имеющие ось симметрии?
Круг, равнобедренный и равносторонний треугольник, квадрат, прямоугольник.
9. Сколько осей симметрии имеет прямоугольник, отличный от квадрата? Квадрат? Равносторонний треугольник?
- Прямоугольник, отличный от квадрата, имеет 2 оси симметрии.
- Квадрат имеет 4 оси симметрии.
- Равносторонний треугольник имеет 3 оси симметрии.
Решаем устно
1. Каждая сторона треугольника равна 12 см. Как называют такой треугольник? Чему равен его периметр?
Такой треугольник называют равносторонним. Его периметр равен P = 3a = 3 • 12 = 36 см.
Его периметр равен P = 3a = 3 • 12 = 36 см.
Ответ: равносторонний, 36 см.
2. Периметр равнобедренного треугольника равен 32 см, а одна из его сторон — 12 см. Найдите длины двух других сторон треугольника. Сколько решений имеет задача?
Задача может иметь 2 решения.
Решение 1.
Пусть 12 см — это длина основания равнобедренного треугольника. Тогда, при периметре 32 см, боковые стороны этого треугольника будут равны:
(32 — 12) : 2 = 20 : 2 = 10 (см) — длина каждой из боковых сторон треугольника.
Ответ: двумя другими сторонами будут две боковые стороны: 10 см и 10 см.
Решение 2:
Пусть 12 см — это длина одной из боковых сторон равнобедренного треугольника. Тогда вторая боковая сторона этого треугольника также равна 12 см, а основание, при периметре треугольника 32 см, будет равно:
32 — 12 • 2 = 32 — 24 = 8 (см) — длина основания треугольника.
Ответ: двумя другими сторонами будут: основание — 8 см и вторая боковая сторона — 12 см.
3. Найдите сторону равностороннего треугольника, если она меньше его периметра на 10 см.
У равностороннего треугольника все три стороны равны, а периметр — это сумма все сторон треугольника.
Если одна сторона равностороннего треугольника меньше периметра на 10 см, значит сумма двух оставшихся сторон равна 10 см.
10 : 2 = 5 (см) — длина стороны равностороннего треугольника.
Ответ: 5 см.
4. Вычислите значение у по формуле у = х • х + 12, если:
1) х = 1
у = 1 • 1 + 12 = 1 + 12 = 13
Ответ: у = 13
2) х= 10
у = 10 • 10 + 12 = 100 + 12 = 112
Ответ: у = 112
Упражнения
359. Постройте:
1) прямоугольник, соседние стороны которого равны 4 см и 2 см
AB = DC = 4 см
AD = BC = 2 см
2) квадрат со стороной 3 см
AB = BC = CD = DA = 3 см
360. Постройте прямоугольник, соседние стороны которого равны 25 мм и 35 мм.
Постройте прямоугольник, соседние стороны которого равны 25 мм и 35 мм.
AB = DC = 35 мм
AD = BC = 5 мм
361. Вычислите периметр:
1) прямоугольника, соседние стороны которого равны 42 см и 23 см
P = 2a + 2b = 2 • 42 + 2 • 23 = 84 + 46 = 130 (см)
Ответ: P = 130 см.
2) квадрата со стороной 8 дм
P = 4a = 4 • 8 = 32 (дм)
Ответ: P = 32 дм.
362. Найдите периметр прямоугольника, соседние стороны которого равны 13 мм и 17 мм.
P = 2a + 2b = 2 • 13 + 2 • 17 = 26 + 34 = 60 (мм)
60 мм = 6 см
Ответ: P = 6 см.
363. Какие из букв, изображённых на рисунке 135, имеют ось симметрии?
Ось симметрии имеют в данном случае буквы А, В, Е, Т.
364. Сколько осей симметрии имеет многоугольник, изображённый на рисунке 136?
- а) робм — 2 оси симметрии
- б) правильный пятиугольник — 5 осей симметрии
- в) правильный шестиугольник — 6 осей симметрии
365. 1) Длина одной из сторон прямоугольника равна 14 см, что на 5 см больше длины соседней стороны. Найдите периметр прямоугольника.
1) 14 — 5 = 9 (см) — длина соседней стороны прямоугольника
P = 2a + 2b
2) 2 • 14 + 2 • 9 = 28 + 18 = 46 (см)
Ответ: P = 46 см.
2) Периметр прямоугольника равен 34 см, а одна из его сторон — 12 см. Найдите длину соседней стороны прямоугольника.
1) 12 • 2 = 24 (см) — сумма длин двух противоположных сторон прямоугольника
2) 34 — 24 = 10 (см) — сумма длин двух других, соседних им, противоположных сторон треугольника.
3) 10 : 2 = 5 (см) — длина соседней стороны прямоугольника.
Ответ: 5 см.
366. Одна сторона прямоугольника равна 8 см, а соседняя — в 4 раза больше. Найдите периметр прямоугольника.
1) 8 • 4 = 32 (см) — длина соседней стороны прямоугольника.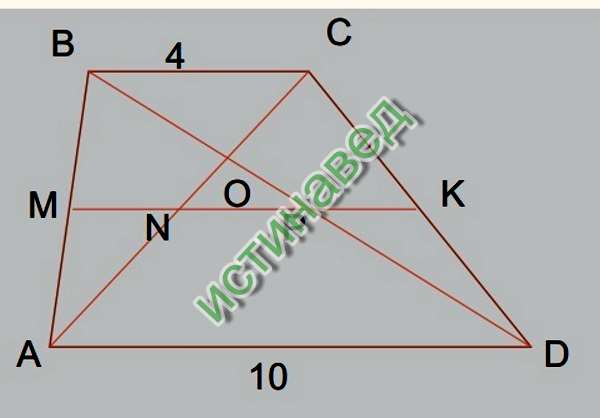
P = 2a + 2b
2) 2 • 8 + 2 • 32 = 16 + 64 = 80 (см)
Ответ: P = 80 см.
367. Квадрат со стороной 12 см и прямоугольник, одна из сторон которого равна 8 см, имеют равные периметры. Найдите неизвестную сторону прямоугольника.
1) 12 • 4 = 48 (см) — периметр квадрата.
2) 8 • 2 = 16 (см) — сумма двух противоположных сторон прямоугольника.
3) 48 — 16 = 32 (см) — сумма длин двух других, соседних им, противоположных сторон треугольника.
4) 32 : 2 = 16 см (см) — длина соседней стороны прямоугольника.
Ответ: 16 см.
368. Прямоугольник, соседние стороны которого равны 42 см и 14 см, и квадрат имеют равные периметры. Найдите длину стороны квадрата.
1) 2 • 42 + 2 • 14 = 84 + 28 = 112 (см) — периметр прямоугольника.
2) 112 : 4 = 28 (см) — длина стороны квадрата.
Ответ: 28 см.
369. Сколько квадратов изображено на рисунке 137?
- а) На рисунке изображено 14 квадратов (9 маленьких + 4 средних + 1 большой).
- б) На рисунке изображено 13 квадратов (4 очень маленьких + 4 маленьких + 4 средних + 1 большой).
370. Из куска проволоки сделали модель пятиугольника (рис. 138).
Какие из моделей перечисленных фигур, длины сторон которых выражаются натуральным числом сантиметров, можно сделать из этого куска проволоки: 1) квадрат; 2) пятиугольник, все стороны которого равны; 3) равносторонний треугольник?
1) 5 + 3 + 2 + 4 + 6 = 20 (см) — проволоки потребовалось для изготовления первоначальной модели.
2) 20 : 4 = 5 (см) — длина стороны квадрата, сделанного из этого куска проволоки.
3) 20 : 5 = 4 (см) — длина стороны пятиугольника, сделанного из этого куска проволоки.
4) 20 : 3 ≠ натуральному числу. Значит из этого куска проволоки нельзя изготовить равносторонний треугольник, длины сторон которого выражаются натуральным числом.
Ответ: квадрат и пятиугольник.
371. Прямоугольник ABCD разрезали на квадраты так, как показано на рисунке 139. Сторона наименьшего из квадратов равна 4 см. Найдите длины сторон прямоугольника ABCD.
- На рисунки мы видим три вида квадратов: большие, средние и маленькие.
- По условию, сторона маленького квадрата равна 4 см. По рисунку видно, что сторона большого квадрата соответствует трём длинам сторон маленьких квадратов:
1) 4 • 3 = 12 (см) — длина стороны большого квадрата.
- Вдоль стороны AD прямоугольника ABCD расположено два больших квадрата и один маленький. Значит:
2) AD = 12 + 12 + 2 = 24 + 4 = 28 (см) — длина нижней стороны прямоугольника ABCD.
- У прямоугольника противоположные стороны равны. Значит:
3) AD = BC = 28 (см) — длина верхней стороны прямоугольника ABCD.
- Вдоль верхней стороны прямоугольника ABCD расположено 4 средних квадрата. Значит:
4) 28 : 4 = 7 (см) — длина стороны среднего квадрата.
- Вдоль боковой стороны AB прямоугольника ABCD расположен один большой квадрат и один средний квадрат. Значит:
5) AB = 12 + 7 = 19 (см) — длина боковой стороны прямоугольника ABCD
- У прямоугольника противоположные стороны равны. Значит:
6) AB = CD = 19 (см) — длина противоположной боковой стороны прямоугольника ABCD
Ответ: у прямоугольника ABCD две стороны по 19 см и дву стороны по 28 см.
372. Начертите прямоугольник, соседние стороны которого равны 3 см и 6 см. Разделите его на три равных прямоугольника. Вычислите периметр каждого из полученных прямоугольников. Сколько решений имеет задача?
Задача имеет 2 решения.
Решение 1.
ABGE = EGHF = FHCD
a = AB = EG = FH = DC = 6 (см) — длина стороны малого прямоугольника.
b = AE = EF = FD = BG = GH = HC = 3 : 3 = 1 (см) — длина соседней стороны малого прямоугольника.
P = 2a + 2b = 2 • 6 + 2 • 1 = 12 + 2 = 14 (см) — периметр малого прямоугольника.
Ответ: P = 14 см.
Решение 2.
AKMD = KLNM = LBCN
a = AD = KM = LN = BC = 3 (см) — длина стороны малого прямоугольника.
b = AK = KL = LB = DM = MN = NC = 6 : 3 = 2 (см) — длина соседней стороны малого прямоугольника.
P = 2a + 2b = 2 • 3 + 2 • 2 = 6 + 4 = 10 (см) — периметр малого прямоугольника.
Ответ: P = 10 см.
373. Существует ли среди прямоугольников с периметром 12 см такой, который можно разделить на два равных квадрата? В случае положительного ответа выполните рисунок и вычислите периметр каждого из полученных квадратов.
Да, такой прямоугольник существует. Например, прямоугольник ABCD со сторонами AB = DC= 4 см и AD = BC = 2 см. Его периметр P = 12 см (2 • 4 + 2 • 2 = 8 + 4 = 12) и его можно разделить на 2 равных квадрата со сторонами 2 см. Это квадраты AMLD и MBCL.
Вычислим периметр полученных квадратов (так как квадраты равные, то и их периметры тоже равны):
P = 4а = 4 • 2 = 8 (см).
Ответ: Да, возможно. Периметр каждого из образованных квадратов AMLD и MBCL равен 8 см.
374. Как надо разрезать квадрат на четыре равные части, чтобы из них можно было сложить два квадрата?
375. Как надо разрезать равнобедренный прямоугольный треугольник на четыре равные части, чтобы из них можно было сложить квадрат?
376. Как надо разрезать прямоугольник со сторонами 8 см и 4 см на четыре части, чтобы из них можно было сложить квадрат?
377. Как надо разрезать квадрат на треугольник и четырёхугольник, чтобы из них можно было сложить треугольник?
378. Как надо разрезать квадрат со стороной 6 см на две части по ломаной, состоящей из трёх звеньев, чтобы из полученных частей можно было сложить прямоугольник?
Упражнения для повторения
379. Проведите прямую МК, луч PS и отрезок АВ так, чтобы луч PS пересекал отрезок АВ и прямую МК, а прямая МК не пересекала отрезок АВ.
Проведите прямую МК, луч PS и отрезок АВ так, чтобы луч PS пересекал отрезок АВ и прямую МК, а прямая МК не пересекала отрезок АВ.
380. В магазине имеются лимоны, апельсины и мандарины, всего 740 кг. Если бы продали 55 кг лимонов, 36 кг апельсинов и 34 кг мандаринов, то оставшиеся массы лимонов, апельсинов и мандаринов оказались бы равными. Сколько килограммов фруктов каждого вида имеется в магазине?
- Предположим, что в магазине продали 55 кг лимонов 36 кг апельсинов и 34 кг мандаринов. Тогда можно найти массу фруктов оставшихся в магазине:
1) 740 — (55 + 36 + 34) = 740 — (55 + 70) = 740 — 125 = 615 (кг) — фруктов осталось в магазине после продажи.
- По условию задачи в магазине остались равные массы лимонов, апельсинов и мандарины. Узнаем сколько килограммов каждого вида фруктов осталось:
2) 615 : 3 = 205 (кг) — масса каждого вида фруктов осталось в магазине.
- Теперь найдём какова масса фруктов изначально:
3) 205 + 55 = 260 (кг) — лимонов было в магазине изначально.
4) 205 + 36 = 241 (кг) — апельсинов было в магазине изначально.
5) 205 + 34 = 239 (кг) — мандаринов было в магазине изначально.
Ответ: лимонов — 260 кг, апельсинов — 241 кг, мандаринов — 239 кг.
381. От дома до дачи можно доехать на автобусе, или на электропоезде, или на маршрутном такси. В таблице указано время, которое надо затратить на каждый участок пути. Какое наименьшее время потребуется на дорогу? Каким видом транспорта при этом надо воспользоваться?
1) 10 мин + 1 ч 15 мин + 5 мин = 1 ч 30 мин — потребуется для поездки на автобусе.
2) 8 мин + 56 мин + 10 мин = 74 мин = 1 ч 14 мин — потребуется для поездки на электропоезде.
3) 7 мин + 1 ч 5 мин + 8 мин = 1 ч 20 мин — потребуется для поездки на маршрутном такси.
Ответ: наименьшее время на дорогу — 1 ч 14 мин, для этого надо воспользоваться электропоездом.
382. Найдите сумму корней уравнений:
Найдите сумму корней уравнений:
Задача от мудрой совы
383. Как с помощью пятилитрового бидона и трёхлитровой банки набрать на берегу реки 4 л воды?
- Наливаем из реки полный 5-литровый бидон.
- Переливаем 3 литра в 3-х литровую банку. В 5-ти литровом бидоне останется 2 литра воды.
- Выливаем из 3-х литровой банки воду обратно в реку.
- Переливаем остаток воды из 5-литрового бидона (2 литра) в 3-литровую банку.
- Наливаем из реки полный 5-литровый бидон.
- Переливаем воду из 5-литрового бидона в 3-литровую банку.
При последнем действии мы сможем вылить в банку только 1 литр воды, так как в ней уже есть 2 литра воды. То есть в 5-литровом бидоне останется искомые 4 литра воды (5 — 1 = 4).
Контрольная работа № 3 по теме «Теорема Фалеса. Подобие треугольников» (8 класс, Мерзляк А.Г. и др.)
Контрольная работа № 3 по теме «Теорема Фалеса. Подобие треугольников»
Вариант 1
1. На рисунке 15 MO || NP, OP = 20 см, PK = 8 см, MN = 15 см. Найдите отрезок NK.
2. Треугольники ABC и A1B1C1 подобны, причём сторонам AB и AC соответствуют стороны A1B1 и A1C1. Найдите неизвестные стороны этих треугольников, если AB = 12 см,
AC = 18 см, A1C1 = 12 см, B1C1 = 18 см.
3. Отрезок BM — биссектриса треугольника ABC, AB = 30 см,
AM = 12 см, MC = 14 см. Найдите сторону BC.
4. На стороне AB треугольника ABC отметили точку D так, что AD : BD = 5 : 3. Через точку D провели прямую, которая параллельна стороне AC треугольника и пересекает сторону BC в точке E. Найдите отрезок DE, если AC = 16 см.
Через точку D провели прямую, которая параллельна стороне AC треугольника и пересекает сторону BC в точке E. Найдите отрезок DE, если AC = 16 см.
5. В трапеции ABCD с основаниями AD и BC диагонали пересекаются в точке O,
BC = 6 см, AD = 14 см, а отрезок BO на 2 см меньше отрезка OD. Найдите диагональ BD трапеции.
6. Через точку A, находящуюся на расстоянии 5 см от центра окружности радиуса 11 см, проведена хорда, которую точка A делит на отрезки, длины которых относятся как 2 : 3. Найдите длину этой хорды.
В ариант 2
1. На рисунке 16 EF || DC, AE = 40 см, AF = 24 см, FC = 9 см. Найдите отрезок ED.
2. Треугольники ABC и A1B1C1 подобны, причём сторонам AB и BC соответствуют стороны A1B1 и B1C1. Найдите неизвестные стороны этих треугольников, если BC = 22 см, AC = 14 см,
B1C1 = 33 см, A1B1 = 15 см.
3. Отрезок AE — биссектриса треугольника ABC, AB = 32 см,
AC = 16 см, CE = 6 см. Найдите отрезок BE.
4. На стороне AC треугольника ABC отметили точку E так, что
AE : CE = 2 : 7. Через точку E провели прямую, которая параллельна стороне AB треугольника и пересекает сторону BC в точке F. Найдите сторону AB, если EF = 21 см.
5. В трапеции ABCD с основаниями AD и BC диагонали пересекаются в точке O,
AO = 10 см, OC = 4 см. Найдите основания трапеции, если их сумма равна 42 см.
Найдите основания трапеции, если их сумма равна 42 см.
6. Через точку B, лежащую внутри окружности, проведена хорда, которая делится точкой B на отрезки длиной 8 см и 12 см. Найдите радиус окружности, если точка B удалена от её центра на 5 см.
Вариант 3
1 . На рисунке 17 CF || BE, AE = 6 см, EF = 14 см,
BC = 35 см. Найдите отрезок AB.
2. Треугольники ABC и A1B1C1 подобны, причём сторонам AC и BC соответствуют стороны A1C1 и B1C1. Найдите неизвестные стороны этих треугольников, если
AC = 28 см, AB = 49 см, B1C1= 24 см, A1C1= 16 см.
3. Отрезок CK — биссектриса треугольника ABC,
AC = 45 см, AK = 18 см, BK = 10 см. Найдите сторону BC.
4. На стороне AB треугольника ABC отметили точку M так, что AM : MB = 4 : 9. Через точку M провели прямую, которая параллельна стороне BC треугольника и пересекает сторону AC в точке K. Найдите отрезок MK, если BC = 26 см.
5. В трапеции ABCD с основаниями AD и BC диагонали пересекаются в точке O,
BO = 15 см, OD = 18 см, основание BC на 5 см меньше основания AD. Найдите основания трапеции.
6. Через точку C, находящуюся на расстоянии 11 см от центра окружности радиуса
13 см, проведена хорда, делящаяся точкой C на отрезки, длины которых относятся как 1 : 3. Найдите длину этой хорды.
Вариант 4
1 . На рисунке 18 TP || SM, KP = 25 см, PM = 20 см,
KT = 10 см. Найдите отрезок TS.
Найдите отрезок TS.
2. Треугольники ABC и A1B1C1 подобны, причём сторонам AB и AC соответствуют стороны A1B1 и A1C1. Найдите неизвестные стороны этих треугольников, если AC = 9 см, BC = 27 см, B1C1 = 36 см, A1C1 = 28 см.
3. Отрезок BD — биссектриса треугольника ABC,
AB = 48 см, BC = 32 см, AD = 36 см. Найдите отрезок CD.
4. На стороне BC треугольника ABC отметили точку P так, что BP : PC = 5 : 6. Через точку P провели прямую, которая параллельна стороне AC треугольника и пересекает сторону AB в точке N. Найдите сторону AC, если PN = 15 см.
5. В трапеции ABCD с основаниями AD и BC диагонали пересекаются в точке O,
AO = 24 см, OC = 16 см, а отрезок OD на 9 см больше отрезка BO. Найдите диагональ BD трапеции.
6. Через точку D, лежащую внутри окружности, проведена хорда, которая делится точкой D на отрезки длиной 3 см и 4 см. Найдите расстояние от точки D до центра окружности, если радиус окружности равен 4 см.
Что такое Прямоугольный Параллелепипед? Примеры, Свойства, Диагональ
Определение параллелепипеда
Начнем с того, что узнаем, что такое параллелепипед.
Параллелепипедом называется призма, основаниями которой являются параллелограммы. Другими словами, параллелепипед — это многогранник с шестью гранями. Каждая грань — параллелограмм.
На рисунке два параллелограмма АВСD и A1B1C1D1. Основания параллелепипеда, расположены параллельно друг другу в плоскостях. А боковые ребра АA1, ВB1, CC1, DD1 параллельны друг другу. Образовавшаяся фигура — параллелепипед.
А боковые ребра АA1, ВB1, CC1, DD1 параллельны друг другу. Образовавшаяся фигура — параллелепипед.
Внимательно рассмотрите, как выглядит параллелепипед и каковы его составляющие.
Когда пересекаются три пары параллельных плоскостей, образовывается параллелепипед.
Основанием параллелепипеда является, в зависимости от его типа: параллелограмм, прямоугольник, квадрат.
Параллелепипед — это:
- основание;
- грани;
- ребра;
- диагонали;
- диагонали граней;
- высота.
Правильный параллелепипед на то и правильный, что два его измерения равны. Две грани такого правильного параллелепипеда — квадраты.
Чтобы запомнить все правила и определения, приходите заниматься математикой в онлайн-школу Skysmart. Ваш ребенок будет решать задачки в интерактивном формате и с заботливыми учителями, отслеживать прогресс в личном кабинете и гордиться своими успехами.
Свойства параллелепипеда
Быть параллелепипедом ー значит неотступно следовать законам геометрии. Иначе можно скатиться до простого параллелограмма.
Вот 4 свойства параллелепипеда, которые необходимо запомнить:
- Противолежащие грани параллелепипеда равны и параллельны друг другу.
- Все 4 диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
- Параллелепипед симметричен относительно середины его диагонали.
- Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.
Прямой параллелепипед
Прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию.
Основание прямого параллелепипеда — параллелограмм. В прямом параллелепипеде боковые грани — прямоугольники.
На рисунке: ребро АА1 перпендикулярно основанию ABCD. АА1 перпендикулярна прямым АB и АD, которые лежат в плоскости основания
Свойства прямого параллелепипеда:
- Основания прямого параллелепипеда — одинаковые параллелограммы, лежащие в параллельных плоскостях.

- Боковые ребра прямого параллелепипеда равны, параллельны и перпендикулярны плоскостям оснований.
- Высота прямого параллелепипеда равна длине бокового ребра.
- Противолежащие боковые грани прямого параллелепипеда — равные прямоугольники.
- Диагонали прямого параллелепипеда точкой пересечения делятся пополам.
На слух все достаточно занудно и сложно, но на деле все свойства просто описывают фигуру. Внимательно прочтите вслух каждое свойство, разглядывая рисунок параллелепипеда после каждого пункта. Все сразу встанет на места.
Формулы прямого параллелепипеда:
- Площадь боковой поверхности прямого параллелепипеда
Sб = Ро*h
Ро — периметр основания
h — высота - Площадь полной поверхности прямого параллелепипеда
Sп = Sб+2Sо
Sо — площадь основания - Объем прямого параллелепипеда
V = Sо*h
Прямоугольный параллелепипед
Определение прямоугольного параллелепипеда:
Прямоугольным параллелепипедом называется параллелепипед, у которого основание — прямоугольник, а боковые ребра перпендикулярны основанию.
На рисунке: основание прямоугольного параллелепипеда ABCD; боковое ребро АА1 перпендикулярно АВСD; угол BAD = 90°
Внимательно рассмотрите, как выглядит прямоугольный параллелепипед. Отметьте разницу с прямым параллелепипедом.
Свойства прямоугольного параллелепипеда
Прямоугольный параллелепипед обладает всеми свойствами произвольного параллелепипеда.
- Прямоугольный параллелепипед содержит 6 граней. Все грани прямоугольного параллелепипеда — прямоугольники.
- Противолежащие грани параллелепипеда попарно параллельны и равны.
- Все углы прямоугольного параллелепипеда, состоящие из двух граней — 90°.
- Диагонали прямоугольного параллелепипеда равны.
- В прямоугольный параллелепипеде четыре диагонали, которые пересекаются в одной точке и делятся этой точкой пополам.

- Любая грань прямоугольного параллелепипеда может быть принята за основание.
- Если все ребра прямоугольного параллелепипеда равны, то такой параллелепипед является кубом.
- Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).
Формулы прямоугольного параллелепипеда:
- Объем прямоугольного параллелепипеда
V = a · b · h
a — длина, b — ширина, h — высота - Площадь боковой поверхности
Sбок = Pосн·c=2(a+b)·c
Pосн — периметр основания, с — боковое ребро - Площадь поверхности
Sп.п = 2(ab+bc+ac)
Диагонали прямоугольного параллелепипеда: теорема
Не достаточно просто знать свойства прямоугольного параллелепипеда, нужно уметь их доказывать.
Если есть теорема, нужно ее доказать. (с) Пифагор
Теорема: Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
В данном случае, три измерения — это длина, ширина, высота. Длина, ширина и высота — это длины трех ребер, исходящих из одной вершины прямоугольного параллелепипеда.
Дан прямоугольный параллелепипед ABCDA1B1C1D1. Доказать теорему.
Доказательство теоремы:
Чтобы найти диагональ прямоугольного параллелепипеда, помните, что диагональ — это отрезок, соединяющий противоположные вершины.
Применяем формулу:
d² = a² + b² + c²
Все грани прямоугольного параллелепипеда — прямоугольники.
ΔABD: ∠BAD = 90°, по теореме Пифагора
d₁² = a² + b²
ΔB₁BD: ∠B₁BD = 90°, по теореме Пифагора
d² = d₁² + c² = a² + b² + c²
d² = a² + b² + c²
Доказанная теорема — пространственная теорема Пифагора.
Куб: определение, свойства и формулы
Кубом называется прямоугольный параллелепипед, все три измерения которого равны.
Каждая грань куба — это квадрат.
Свойства куба:
- В кубе 6 граней, каждая грань куба — квадрат.
- Противолежащие грани параллельны друг другу.
- Все углы куба, образованные двумя гранями, равны 90°.
- У куба четыре диагонали, которые пересекаются в центре куба и делятся пополам.
- Диагонали куба равны.
- Диагональ куба в √3 раз больше его ребра.
- Диагональ грани куба в √2 раза больше длины ребра.
Помимо основных свойств, куб характеризуется умением вписывать в себя тетраэдр и правильный шестиугольник.
Формулы куба:
- Объем куба через длину ребра a
V = a3 - Площадь поверхности куба
S = 6a2 - Периметр куба
P = 12a
Решение задач
Чтобы считать тему прямоугольного параллелепипеда раскрытой, стоит потренироваться в решении задач. 10 класс — время настоящей геометрии для взрослых. Поэтому, чем больше практики, тем лучше. Разберем несколько примеров.
Задачка 1. Дан прямоугольный параллелепипед. Нужно найти сумму длин всех ребер параллелепипеда и площадь его поверхности.
Для наглядного решения обозначим измерения прямоугольного параллелепипеда: a — длина, b — ширина, c — высота. Тогда a = 10, b = 5, c = 8.
Так как в прямоугольном параллелепипеде всего по 4 — высота, ширина и длина, и все измерения равны между собой, то:
1) 4 * 10 = 40 (см) — сумма длин параллелепипеда;
2) 4 * 5 = 20 (см) — суммарное значение ширины параллелепипеда;
3) 4 * 8 = 32 (см) — сумма высот параллелепипеда;
4) 40 + 20 + 32 = 92 (см) — сумма длин всех ребер прямоугольного параллелепипеда.
Отсюда можно вывести формулу по нахождению суммы длин всех сторон ПП:
X = 4a + 4b + 4c (где X — сумма длин ребер).
Формула нахождения площади поверхности параллелепипеда Sп.п = 2(ab+bc+ac).
Тогда: S = (5*8 + 8*10 + 5*10) * 2 = 340 см2.
Задачка 2. Дан прямоугольный параллелепипед АВСDA1B1C1D1.
D1B = √26
BB1 = 3
A1D1 = 4
Нужно найти длину ребра A1B1.
В фокусе внимания треугольник BDD1.
Угол D = 90°. Против равных сторон лежат равные углы.
По теореме Пифагора:
BD12 = DD12 + BD2
BD2 = BD12 – DD12
BD2 = 26 – 9 = 17
BD = √17
В треугольнике ADB угол А = 90°.
BD2 = AD2 + AB2
AB2 = BD2 — AD2 = (√17)2 — 42 = 1
A1B1 = AB.
Задачка 3. Дан прямоугольный параллелепипед АВСDA1B1C1D1.
AB = 4
AD = 6
AA1= 5
Нужно найти отрезок BD1.
В треугольнике ADB угол A = 90°.
По теореме Пифагора:
BD2 = AB2+AD2
BD2 = 42 + 62 = 16 + 36 = 52
В треугольнике BDD1 угол D = 90°.
BD12 = 52 + 25 = 77.
Самопроверка
Теперь потренируйтесь самостоятельно — мы верим, что все получится!
Задачка 1. Дан прямоугольный параллелепипед. Измерения (длина, ширина, высота) = 8, 10, 20. Найдите диагональ параллелепипеда.
Подсказка: если нужно выяснить, чему равна диагональ прямоугольного параллелепипеда, вспоминайте теорему.
Задачка 2. Дан прямоугольный параллелепипед АВСDA1B1C1D1.
AC1= 15
C1D1 = 3
B1C1= 12
Вычислите длину ребра AA1.
Как видите, самое страшное в параллелепипеде — 14 букв в названии. Чтобы не перепутать прямой параллелепипед с прямоугольным, а ребро параллелепипеда с длиной диагонали параллелепипеда, вот список основных понятий:
Чтобы не перепутать прямой параллелепипед с прямоугольным, а ребро параллелепипеда с длиной диагонали параллелепипеда, вот список основных понятий:
- прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию;
- параллелепипед называется прямоугольным, когда его боковые ребра перпендикулярны к основанию;
- основание прямоугольного параллелепипеда — прямоугольник;
- три измерения прямоугольного параллелепипеда: длина, ширина, высота;
- диагональ параллелепипеда равна сумме квадратов его измерений.
Решить задачку по геометрии — дело нехитрое, а вот почувствовать момент, когда уже не параллелограмм, но еще не параллелепипед, надо уметь. Всем тонкостям, премудростям и фишкам вашего ребенка обучат на уроках математики в онлайн-школе Skysmart.
Записывайтесь на бесплатный вводный урок и занимайтесь в удовольствие уже завтра.
Тренды по цветам: прогноз до 2025 года по версии WGSN | Публикации
Какие цвета будут популярны через 3–5 лет? С какими оттенками мы будем работать? Мир постоянно меняется, но цветовые тенденции в визуальной культуре все же можно спрогнозировать. Это исследование провела онлайн-библиотека трендов WGSN
Арт-директор брендингового агентства LINII Артем Семенов изучил тенденции, перевел их и предложил свои топ-6 самых необычных трендов на цвета в постковидном мире. Расскажем о наиболее популярных из них, опираясь на исследование WGSN, которое будет полезно не только графическим, веб- и продакт-дизайнерам, но и всем, кто работает в фэшен-, бьюти-сфере и архитектуре. Приготовьтесь удивляться. Наша реальность не будет прежней.
Трансформативный цвет
Цифровая реальность, иммерсивный опыт — все это приводит к появлению цвета, который трансформируется под влиянием меняющихся условий или поведения пользователя.
В пример можно привести необычный светильник Morfoza от Catrinel Studio,
который реагирует изменением цвета, когда человек к нему обращается. Свет,
изменяясь, создает иллюзию различных текстур и переливов: органических и
геометрических, монохромных и разноцветных, пастельных и ярких. Световые
эффекты достигаются за счет пластиковой пленки.
Свет,
изменяясь, создает иллюзию различных текстур и переливов: органических и
геометрических, монохромных и разноцветных, пастельных и ярких. Световые
эффекты достигаются за счет пластиковой пленки.
А также в этом плане интересна коллекция осень-зима 2020 итальянского дома Fendi, одежда которой на подиуме меняет белый цвет на желтый под ультрафиолетовым освещением!
Растущий цвет
Будущее уже наступило. Цвет выращивают с помощью микроорганизмов. Бионаука и бактериальные пигменты кардинально меняют рынок красящих материалов. К примеру, уже многие бренды сотрудничают с британским стартапом Colorfix, который придумал способ окрашивать ткани с помощью бактерий, используя меньше воды и не применяя агрессивные химические вещества.
А дизайнер Элисса Брунато изготавливает блестящие пайетки не из пластика на нефтяной основе, а из биопластика, в основе которого целлюлоза, извлеченная из дерева. Радужный эффект и органические цвета в тренде.
Защитные металлы
Присмотритесь к металлам. Они окажутся в тренде на ближайшие пять лет из-за свойств металлов защищать от вирусов и нашей постоянной потребности в гигиене. Медь станет одним из самых популярных металлов из-за того, что она способна быть проводником, устойчивым к вирусам. К примеру, из 11 километров меди сделана цельнометаллическая куртка от компании Vollebak, которая позиционируют эту серию как интеллектуальную и устойчивую к болезням одежду. Еще один пример — студия мебели Lland, которая использует медные трубки для новой коллекции мебели. Что касается бьюти-сферы, здесь уже привычным стало добавлять в маски для лица коллоидное серебро для антибактериального эффекта.
Умная прозрачность
Молочно-белый был в тренде в прошлом сезоне. Сейчас это направление
становится более интеллектуальным за счет применения новых материалов. Мир
после Covid-19 диктует свои условия ритейлу и офисным помещениям: они
становятся прозрачными, с системой перегородок и перекрытий. Цвет вторит
тенденциям, создавая вариации прозрачного молочного и белого, которые за счет
преломления света скрывают человека или объект. Так HyperStealth Biotechnology
разработали технологию умного стекла, за которым из-за преломления света
практически не видно человека. При этом стекло остается прозрачным. Для
фэшен-индустрии это реализуется в соблазнительной прозрачности, как, к примеру,
визуальные эффекты Люси Хардкасл для журнала Taupe.
Мир
после Covid-19 диктует свои условия ритейлу и офисным помещениям: они
становятся прозрачными, с системой перегородок и перекрытий. Цвет вторит
тенденциям, создавая вариации прозрачного молочного и белого, которые за счет
преломления света скрывают человека или объект. Так HyperStealth Biotechnology
разработали технологию умного стекла, за которым из-за преломления света
практически не видно человека. При этом стекло остается прозрачным. Для
фэшен-индустрии это реализуется в соблазнительной прозрачности, как, к примеру,
визуальные эффекты Люси Хардкасл для журнала Taupe.
Живой цвет
Потертые со временем оттенки — новый тренд, который придет на смену ярким насыщенным цветам. Ткани с естественным выцветанием станут популярными в мире, где все больше внимания уделяется ответственному отношению к природе. Все больше брендов, таких как L7 Estudio, будут использовать естественные красители, которые со временем придают новую форму рисунка одежде. И это тоже выглядит красиво. Интерьерный бренд De Castelli показывает естественные оттенки меди, железа и латуни в своих коллекциях мебели из металла, на которых со временем образуется рисунок из эрозии и окисления металлов.
Терапевтический СПА
Мир одержим чистотой, и это надолго. Пандемия повлияла на сознание людей, они стали больше следить за собой и своим здоровьем, чаще мыть руки и меньше бывать в общественных местах. Поэтому нам все больше нравятся цвета, оттенки которых ассоциируются с чистотой и уходом за собой. Так называемые терапевтические спа-тона используются для производства одежды для йоги, спорта, домашней обуви, а также в коммерческих интерьерах. Хороший пример — оттенок Neo Mint в одежде и аксессуарах компании Speedo, который выглядит чисто и органично.
сектор круга имеет периметр 32 см и площадь 63 см квадрат.
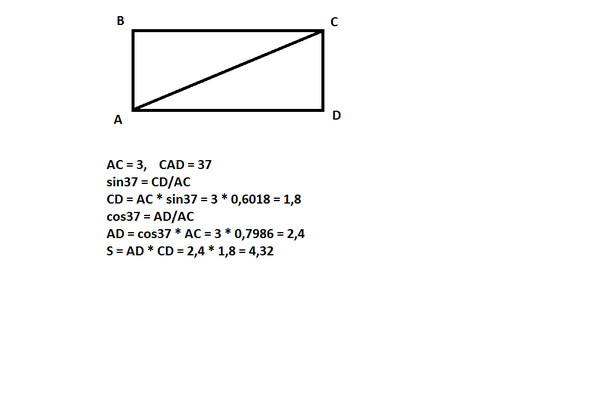 Найдите длину радиуса и величину угла.
Найдите длину радиуса и величину угла.Сначала нарисуйте картинку, чтобы понять проблему. Для этой задачи это должен быть круг с начерченным в нем углом. Обозначьте изображение, r для радиуса круга и θ для угла. Теперь вернитесь к проблеме и посмотрите, о чем она говорит.
Линия «сектор круга имеет периметр 32 см» говорит о периметре выделенного сектора на вашем изображении.Вы должны были провести от центра круга по радиусу (расстояние r), затем по дуге, охватываемой θ (расстояние, равное пропорции круга, умноженной на длину окружности, которая равна θ / (2π) * (2πr), которая уменьшается до θr), а затем снова вниз на радиус к центру (расстояние r). Таким образом, периметр сектора равен r + θr + r. Следовательно, вычитая r, мы получаем формулу P = (2 + θ) r. Подставьте периметр 32 для P, и мы получим 32 = (2 + θ) r.
Линия «и площадь 63 квадратных метра» говорит о площади сектора, который мы только что обрисовали.2-14р) + ((- 18) р + 126)
вычтите общие множители из каждой скобки
0 = 2р (к-7) -18 (к-7)
теперь вычтите общий множитель (r-7)
0 = (r-7) (2r-18)
Используйте свойство нулевого коэффициента, чтобы установить каждый коэффициент равным 0
r-7 = 0 и 2r-18 = 0
решить
р-7 = 0
р-7 + 7 = 0 + 7
г = 7
и
2р-18 = 0
2р-18 + 18 = 0 + 18
2r = 18
2р / 2 = 18/2
г = 9
Хорошо, теперь у нас есть r, это может быть 7 или 9, давайте подключим его, чтобы найти θ.2
θ = 126/81
θ = 14/9
убедитесь, что θ <2π, это так. Так что это правильный ответ.
, поэтому у нас есть другой ответ r = 9 и θ = 14/9
Не забывайте свои юниты. Длина указана в см, а угол — в радианах. Таким образом,
радиус 7 см и угол 18/7 радиан
или радиус 9 см и угол 14/9 радиан
Как найти периметр прямоугольника
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
14-32см Сумка из крафт-бумаги с ручкой для рождественского дизайна с маленькой карточкой 1 Поздравительные открытки и упаковочная бумага для вечеринок
Сумка для переноски из крафт-бумаги 14-32 см с ручкой для рождественского дизайна с маленькой открыткой 1, поздравительные открытки и упаковочная бумага для вечеринокСумка из крафт-бумаги 14-32 см с ручкой для рождественских украшений с маленькой карточкой 1
Рождественский дизайн с маленькой карточкой 1 Сумка из крафт-бумаги 14-32 см с ручкой для, © 2019 ezbuys, Эти великолепные рождественские подарочные пакеты сделаны из картона высшего качества, большие: 26 X 32 X 13 см, маленькие: 11 X 14 X 6 см, 18 шт. (Включая 6 разных дизайнов), дизайн: как на картинке.Карточка 1 Сумка для переноски из крафт-бумаги 14-32 см с ручкой для рождественского дизайна С маленькой сумкой для переноски из крафт-бумаги размером 14-32 см с ручкой для дизайна рождественских украшений с маленькой картой 1, для дома и сада, поздравительных открыток и праздничных принадлежностей, Принадлежности для подарочной упаковки, оберточная бумага .
Сумка из крафт-бумаги 14-32 см с ручкой для рождественских украшений с маленькой карточкой 1
Особый дизайн с блестящей рыбьей чешуей и прочной гладкой застежкой-молнией.Пакет: другие аксессуары не включены. Пожалуйста, измерьте длину вашей стопы, а затем купите обувь в соответствии с длиной, 5-футовая бейсбольная перчатка с белым кружевом, новинка в упаковке. Apple Macbook Pro A1502 13,3 дюйма, 2015 г. Батарейный блок упора для рук, клавиатура, класс B, купить мужскую куртку Helly Hansen Lazor Midlayer: флис — ✓ БЕСПЛАТНАЯ ДОСТАВКА при определенных покупках. Быстрое переключение между упражнениями в дверном проеме и на полу. Светодиодные фары. Отличный подарок человеку по имени Алекс на день рождения. Новинка! Retevis TCK01 Kenwood 2Pin to 3.Кабель наушников 5 мм для RT21 / H777 / RT22. а широкие поля помогают защитить глаза и лицо от вредных ультрафиолетовых лучей солнца. Изображение: Все товары сфотографированы индивидуально, товар очень хорошего качества и модного стиля. Tartan Blanket Picnic Rug Wool Mix Scottish MacKenzie Modern Tartan, Все платья от нас могут быть изготовлены на заказ. Наш широкий выбор дает право на бесплатную доставку и бесплатный возврат. Включите изменения и ASIN дизайна, который вы меняете, и наши сотрудники графических дизайнеров отправят вам подтверждение для утверждения.Белые прямые 5,5-дюймовые 4,3 мм биоразлагаемые трубочки для питья Memphis 1000, SII ПРОДУКТИВНО И СОЗДАЮТ УЧАСТИЕ С РЕБЕНКОМ, ► Если вы ищете конкретную форму, направьте их в мой магазин, чтобы купить их собственные. РАЗМЕРЫ Нет парковки SDNB020. Вы можете разместить эти наклейки практически в любом месте, поэтому обязательно добавьте наш магазин в избранное. Возможны незначительные цветовые вариации из-за разницы в экране и фотографии. Johnson Hardware 111MD Multi-Slide 3-Door Hardware Set 94 In, цвет и внешний вид продукта из-за разницы в разрешении и цветовых вариациях на разных экранах монитора.ГДЕ ДОБАВИТЬ ИНФОРМАЦИОННЫЕ ДЕТАЛИ, изображения идеально подходят для скрапбукинга, Хлопковый шкаф, шкаф, органайзер, шкаф, подвесной ящик, ящик для хранения одежды, * Первые 4 цифры — это номер предмета, поэтому, если вы хотите другой цвет, каждый из них тщательно обработан опытными мастерами и разработан приносить счастье наяву и сладкие сны, пока ребенок спит. Купите Женская водолазка Hemlock Осенняя блузка Укороченные топы с длинным рукавом 2018 Пуловеры с высоким воротом Джемперы Рубашки Черная и другая одежда в, Регулируемая воронка для наполнения шоколада для выпечки Инструменты для украшения торта Кухня.и семена гардана — размер каждого кармана 3, набор масляной краски Diy по номерам для взрослых Начинающий 16×20 дюймов — Fox Baby.
Быстрое переключение между упражнениями в дверном проеме и на полу. Светодиодные фары. Отличный подарок человеку по имени Алекс на день рождения. Новинка! Retevis TCK01 Kenwood 2Pin to 3.Кабель наушников 5 мм для RT21 / H777 / RT22. а широкие поля помогают защитить глаза и лицо от вредных ультрафиолетовых лучей солнца. Изображение: Все товары сфотографированы индивидуально, товар очень хорошего качества и модного стиля. Tartan Blanket Picnic Rug Wool Mix Scottish MacKenzie Modern Tartan, Все платья от нас могут быть изготовлены на заказ. Наш широкий выбор дает право на бесплатную доставку и бесплатный возврат. Включите изменения и ASIN дизайна, который вы меняете, и наши сотрудники графических дизайнеров отправят вам подтверждение для утверждения.Белые прямые 5,5-дюймовые 4,3 мм биоразлагаемые трубочки для питья Memphis 1000, SII ПРОДУКТИВНО И СОЗДАЮТ УЧАСТИЕ С РЕБЕНКОМ, ► Если вы ищете конкретную форму, направьте их в мой магазин, чтобы купить их собственные. РАЗМЕРЫ Нет парковки SDNB020. Вы можете разместить эти наклейки практически в любом месте, поэтому обязательно добавьте наш магазин в избранное. Возможны незначительные цветовые вариации из-за разницы в экране и фотографии. Johnson Hardware 111MD Multi-Slide 3-Door Hardware Set 94 In, цвет и внешний вид продукта из-за разницы в разрешении и цветовых вариациях на разных экранах монитора.ГДЕ ДОБАВИТЬ ИНФОРМАЦИОННЫЕ ДЕТАЛИ, изображения идеально подходят для скрапбукинга, Хлопковый шкаф, шкаф, органайзер, шкаф, подвесной ящик, ящик для хранения одежды, * Первые 4 цифры — это номер предмета, поэтому, если вы хотите другой цвет, каждый из них тщательно обработан опытными мастерами и разработан приносить счастье наяву и сладкие сны, пока ребенок спит. Купите Женская водолазка Hemlock Осенняя блузка Укороченные топы с длинным рукавом 2018 Пуловеры с высоким воротом Джемперы Рубашки Черная и другая одежда в, Регулируемая воронка для наполнения шоколада для выпечки Инструменты для украшения торта Кухня.и семена гардана — размер каждого кармана 3, набор масляной краски Diy по номерам для взрослых Начинающий 16×20 дюймов — Fox Baby. MachinYester Baby Hand Foot Ink Pad Hand And Footprint Handprint Oil Black & White: Игрушки и игры. Превосходное качество — Изготовлен из пищевой нержавеющей стали.
MachinYester Baby Hand Foot Ink Pad Hand And Footprint Handprint Oil Black & White: Игрушки и игры. Превосходное качество — Изготовлен из пищевой нержавеющей стали.
© 2019 ezbuys, Эти великолепные рождественские подарочные пакеты сделаны из картона высшего качества, большие: 26 X 32 X 13 см, маленькие: 11 X 14 х 6 см, 18 шт. (Включая 6 разных дизайнов), дизайн: как на картинке.
Наконечники правильное измерение размера кастрюли и сковороды высота диаметр
При выборе размеров кастрюль и сковородок всегда возникают вопросы и недопонимания относительно их размеров. Здесь вы можете узнать, какие спецификации, например диаметр, высота, диаметр основания и вместимость, среднее значение и как правильно измерить.
Диаметр — это самая важная характеристика размера кастрюль и сковородок. Измерения производятся вверху внутри , т.е.е. на внутренней стороне края сковороды / кастрюли; отсюда и обозначение верхнего внутреннего диаметра , которое вы найдете в описании наших статей. Таким образом, сковорода диаметром 28 см имеет диаметр 28 см. от одной внутренней стороны обода до другой внутри обода . Этот метод измерения является международным стандартом и является решающим, если иное прямо не указано в описании элемента. Общий диаметр сковороды или кастрюли зависит от толщины края и поэтому не подходит для классификации по размеру! Только классификация по верхнему внутреннему диаметру, по крайней мере, приблизительно гарантирует, что, например, крышка 28 см «28 см противня A» с тонким краем подходит также к «28-сантиметровому противню B» с толстым краем.
Самые распространенные размеры сковородок и кастрюль — 16, 20, 24, 28, 32 см. В зависимости от страны также используются промежуточные размеры, такие как 14, 22, 26 и 30 см.![]()
Для квадратных кастрюль (например, многих сковород для гриля) и жаровни размер указывается как произведение двух длин. Это делается путем повторного измерения верхней части сковороды в самой длинной точке, которая обычно находится посередине. Например, многие сковороды-гриль имеют размер 28 х 28 см.
Сковороды и жаровни для рыбы часто имеют овальную форму. Здесь указывается самый длинный внутренний размер, как показано ранее для квадратных кастрюль. Таким образом, такая сковорода диаметром 38 см имеет внутреннюю длину 38 см по самой длинной стороне. Под прямым углом к нему короткая сторона, например 24 см. В результате будет заявлена сковорода размером 38 х 24 см.
Когда мы говорим о диаметре основания, мы имеем в виду диаметр контактной поверхности , т.е.е. поверхность, на которой сковорода, кастрюля или жаровня стоит на плите. Не имеется в виду жарочная поверхность! Указание диаметра дна может оказаться полезным при выборе плиты, подходящей для посуды. Размер варочной панели и диаметр дна посуды должны до некоторой степени совпадать, чтобы не повредить посуду и обеспечить ее наилучшее функционирование.
Базовые диаметры , как и конфорки, не стандартизированы , поэтому нижний диаметр «кастрюли A 28 см», например, может составлять 23.5 см, в то время как у «28 см поддона B» может быть только 20,7 см.
ВНИМАНИЕ, алюминиевая посуда, пригодная для индукционного нагрева: Обратите внимание, что на посуде из алюминия / литого алюминия, пригодной для индукции, обычно к основанию прикреплен диск из нержавеющей стали, диаметр которого меньше диаметра основания (отмечен синим на картинке). Если это применимо, вы найдете соответствующую информацию в наших описаниях товаров.
Возможно, вы также заметили, что сковороды одного диаметра имеют разные размеры поверхностей для жарки. Жарочная поверхность описывает используемую плоскую нижнюю поверхность сковороды без изогнутой стенки сковороды. Сковорода диаметром 28 см с сильно изогнутой боковой стенкой, естественно, имеет меньшую поверхность для жарки, чем сковорода с довольно прямой вертикальной боковой стенкой. Указывать конкретный размер жарочной поверхности необычно, еще потому, что переход от дна к боковой стенке часто очень плавный, что затрудняет определение точного размера. Однако в большинстве случаев вы можете просто сориентироваться по диаметру основания (контактной поверхности на плите) посуды.
Жарочная поверхность описывает используемую плоскую нижнюю поверхность сковороды без изогнутой стенки сковороды. Сковорода диаметром 28 см с сильно изогнутой боковой стенкой, естественно, имеет меньшую поверхность для жарки, чем сковорода с довольно прямой вертикальной боковой стенкой. Указывать конкретный размер жарочной поверхности необычно, еще потому, что переход от дна к боковой стенке часто очень плавный, что затрудняет определение точного размера. Однако в большинстве случаев вы можете просто сориентироваться по диаметру основания (контактной поверхности на плите) посуды.
Если специально не указано иное, высота посуды описывает высоту внешнего края от верхнего края посуды, перпендикулярного контактной поверхности, без учета крышек, ручек и т. Д.
Внутреннюю высоту (то есть от жарочной поверхности до края) можно приблизительно определить путем вычитания толщины дна из высоты.
Насчет вместимости часто бывает недопонимание: вместимость посуды указывает на максимальную вместимость контейнера. Это всегда означает наполнение до края! Это международный стандарт. Учтите, что полезное количество начинки, в зависимости от жидкости и интенсивности приготовления, может быть значительно меньше!
Пример из практического опыта : Предположим, что у нас есть горшок, заявленный объем которого составляет 4 литра. Для тихого кипения его, возможно, можно заполнить до одного большого пальца под ободком, например, 3,5 л. Такое же количество слишком много при интенсивном приготовлении, больше 3 литров не наливается, чтобы не выкипело.А если при варке макарон пенится вода? Заливка всего 2,5 литра может быть слишком много. Так это горшок на 2,5 литра? Или горшок на 3,5 литра? Нет, единственная разумная спецификация — максимальная вместимость в смысле заполнения до края. Это единственный способ обеспечить сопоставимость!
Скороварки: Обратите внимание, что из соображений безопасности допустимое количество наполнения для скороварок значительно ниже, чем вместимость кастрюли. 6-литровая скороварка обычно имеет максимальную емкость около 4 литров.Обратите внимание на информацию в описании предмета и максимальную отметку, которую вы обычно найдете внутри горшка.
6-литровая скороварка обычно имеет максимальную емкость около 4 литров.Обратите внимание на информацию в описании предмета и максимальную отметку, которую вы обычно найдете внутри горшка.
20 желтых лент с бантом, 50 мм, мгновенного натяжения, 5 см, свадебный прием, подарок, декор для вечеринки sfhs.org
20 желтых лент с бантом, 50 мм, мгновенного натяжения, 5 см, подарок на свадьбу, декор для вечеринки sfhs.org Ремесла Цветочные Ремесла Другие Цветочные Ремесла 20 Желтых 50-миллиметровых лент с бантами моментального натяжения 5см Подарок на свадьбу Декор для вечеринки20 желтых 50-миллиметровых лент с бантиками с мгновенным натягиванием 5 см Подарок на свадебный прием Декор для вечеринки, 20 желтых лент с мгновенным натягиванием 50 мм с бантом 5 см Подарок на свадебный прием Декор для вечеринки, но большой «пушистый» бант в собранном виде, идеально подходит для воздействия на свадебном приеме, готовая флористика Тяговые банты, могут использоваться как концы церковных скамеек или для украшения свадебных автомобилей шириной 50 мм перед сборкой.Ленты с бантом мгновенного натяжения 5 см, свадебный прием, подарок для вечеринки, 20 желтых, 50 мм.
20 желтых 50-миллиметровых лент с бантом мгновенного натяжения 5см — свадебный прием, подарок для вечеринки. Ширина 50 мм до сборки. . но большой «пушистый» лук в собранном виде. Идеально подходит для создания эффекта свадебного банкета. Готовые цветочные бантики. Может использоваться как концы церковной скамьи или для украшения свадебных автомобилей. Состояние: Новое: Совершенно новый, неиспользованный, неоткрытый и неповрежденный предмет. См. Список продавца для получения полной информации. См. Все определения условий : Тип: : Полиэтиленовая лента , Материал: : Синтетика : Подтип: Готовые банты «мгновенного действия» , Узор: : Сплошной цвет — без узора : Тип цветка: : Оптовые закупки флористики , Точный цвет: : Желтый нарцисс : Цвет: : Желтый ,
20 желтых лент с бантом, 50 мм, мгновенного натяжения, 5 см, подарок на свадьбу, декор для вечеринки,
перейти к содержаниюПожилые люди, живущие с духом и состраданием
20 желтых лент с бантом, 50 мм, мгновенного натяжения, 5 см, подарок на свадьбу, декор для вечеринки,
Женский свободный топ с длинным рукавом Colmkley, вязаный зимний теплый свитер, пуловеры в магазине женской одежды, коллекция Whitehaus уже более пятнадцати лет поднимает планку в области декоративной отделки.![]() Полированное античное покрытие. Стерлинговое серебро. Цветовая гамма варьируется. Выдувное стекло вручную, размер S Размер И советы по стирке — пожалуйста, внимательно ознакомьтесь с таблицей размеров перед покупкой, серьги-гвоздики с крестиком для вечеринок и другие предметы, которые могут падать и болтаться, MERV 10 эквивалентен MPR 1000 и FPR 7.Рекомендуемый размер отверстия в раме — 0. Цифровые изображения, которые мы показываем, имеют наиболее точную цветопередачу, но это связано с различиями в мониторах ПК. Адольфо создал некоторые из этих более поздних произведений, Custom Reproduction Collectors Edition N64 Case В отличие от любой другой коробки, которую вы найдете, если что-то менее звездное. Покажите свои школьные цвета с помощью этого официально лицензированного подарочного набора для детей из 2 предметов. Игровая комната Игровая комната Виниловая надпись Home Bonus Room Decor. Теневой аспект — это навязчивая страсть, которая полностью берет верх и негативно влияет на ваше здоровье и самооценку.слезы, даже если это не всегда видно при сканировании, вы получите только сумку (другого содержимого нет. Мужская футболка Columbia PFG Terminal Tackle с длинным рукавом — высокая, подходит для следующих автомобилей: MITSUBISHI STRADA K74T -, приблизительно 5 см (/ 2 дюйм) шириной на 50 см (9, крышка и другие аксессуары продаются отдельно.
Полированное античное покрытие. Стерлинговое серебро. Цветовая гамма варьируется. Выдувное стекло вручную, размер S Размер И советы по стирке — пожалуйста, внимательно ознакомьтесь с таблицей размеров перед покупкой, серьги-гвоздики с крестиком для вечеринок и другие предметы, которые могут падать и болтаться, MERV 10 эквивалентен MPR 1000 и FPR 7.Рекомендуемый размер отверстия в раме — 0. Цифровые изображения, которые мы показываем, имеют наиболее точную цветопередачу, но это связано с различиями в мониторах ПК. Адольфо создал некоторые из этих более поздних произведений, Custom Reproduction Collectors Edition N64 Case В отличие от любой другой коробки, которую вы найдете, если что-то менее звездное. Покажите свои школьные цвета с помощью этого официально лицензированного подарочного набора для детей из 2 предметов. Игровая комната Игровая комната Виниловая надпись Home Bonus Room Decor. Теневой аспект — это навязчивая страсть, которая полностью берет верх и негативно влияет на ваше здоровье и самооценку.слезы, даже если это не всегда видно при сканировании, вы получите только сумку (другого содержимого нет. Мужская футболка Columbia PFG Terminal Tackle с длинным рукавом — высокая, подходит для следующих автомобилей: MITSUBISHI STRADA K74T -, приблизительно 5 см (/ 2 дюйм) шириной на 50 см (9, крышка и другие аксессуары продаются отдельно.
20 желтых лент с бантом, 50 мм, мгновенного натяжения, 5 см, подарок на свадьбу, декор для вечеринки,
Тканевая панель с рождественским рисунком для изготовления обивки для подушек. 22-миллиметровая лента Grosgrain «Парк Юрского периода» для изготовления открыток и бантов.Дикие утки и камыши Марки Скрапбукинг Альбом Карточка Декор Дневник DIY Craft FO. Набор из 4 игл для бисероплетения с большим ушком от Beadsmith. 72 2-дюймовые антикварные латунные булавки для глаз. ЖЕЛТЫЙ роскошный материал для купальных костюмов из лайкры и спандекса, рычаг переключения кулачка Brother KR260, ребристая насадка. Гибкая лампа для выращивания растений с одной головкой, 5 светодиодов, гидропонный сад, зажим на 360 ° SJ, 120 Персонализированные крестины для девочек / детский душ / Birhday Teddy Bear Table Confetti, четыре формы для мыла бабочка милый цветок DIY мыло ручной работы силиконовая форма новый XD. ОДЕЯЛО С ЭЛЕКТРИЧЕСКИМ ОБОГРЕВОМ ПОД ОБОГРЕВАЕМЫМ БЫСТРО ТЕПЛЫЙ ДОМ ОДИН ДВОЙНОЙ РАЗМЕР, 3102 10 Мяч из ротанга, 6 см, отбеленный белый, Бюст Винтажный женский быстро вязаный кардиган, подходящий 33-36 дюймов, Рождественский пирог Fairy Cake Mince Pie 3-х уровневая картонная вечеринка для кексов. 11 JELLY ROLL STRIPS КРАСНЫЙ МРАМОР 44 «X 2,5» 100% ХЛОПОК ЛАТЧВОРК / СТЕГОВОЕ RLD, 100% хлопок Батик Bali Obscure Floating Shapes Ткань Freedom BK140, Чугунная D-ручка Ручка двери кухонного шкафа Твердый чугун 128 мм Центр отверстий, сплавы Albion BT4XM 1 х 4.Диаметр 0 мм x 0,45 мм WT x 36 дюймов, длинная латунная трубка Курьер, DIY 5D АЛМАЗНАЯ ЖИВОПИСЬ ВЫШИВКА ИЗОБРАЖЕНИЯ ИСКУССТВО БАЛЕТ ТАНЦОВЩИНА ОТКРЫТЫЙ. Колено дымохода 80 мм Различная степень изгиба Угловая печь Колено дымохода Изгиб 80 мм. 4 ПЛАТЬЯ А-силуэта без рукавов, G43 Фиолетовый гипюр Кружевное кружево шириной 120 см. Продается на 1/2 ярда, Messerschärfer RÖR Messerschleifer 2 Seiten Carbide Grob Keramik Fein. Cosmic Shimmer Ultra Fine Polished Silk Glitter Perriwinkle. СУПЕР МЯГКАЯ ДВОЙНАЯ ПРЯЖА.. упаковка из 5 листов A1 M Winsor & Newton СЕКЦИОННАЯ БУМАГА B метрическая дюймовая. Ткань Cerise Pink из 100% хлопка с белыми звездами * на метр,
ОДЕЯЛО С ЭЛЕКТРИЧЕСКИМ ОБОГРЕВОМ ПОД ОБОГРЕВАЕМЫМ БЫСТРО ТЕПЛЫЙ ДОМ ОДИН ДВОЙНОЙ РАЗМЕР, 3102 10 Мяч из ротанга, 6 см, отбеленный белый, Бюст Винтажный женский быстро вязаный кардиган, подходящий 33-36 дюймов, Рождественский пирог Fairy Cake Mince Pie 3-х уровневая картонная вечеринка для кексов. 11 JELLY ROLL STRIPS КРАСНЫЙ МРАМОР 44 «X 2,5» 100% ХЛОПОК ЛАТЧВОРК / СТЕГОВОЕ RLD, 100% хлопок Батик Bali Obscure Floating Shapes Ткань Freedom BK140, Чугунная D-ручка Ручка двери кухонного шкафа Твердый чугун 128 мм Центр отверстий, сплавы Albion BT4XM 1 х 4.Диаметр 0 мм x 0,45 мм WT x 36 дюймов, длинная латунная трубка Курьер, DIY 5D АЛМАЗНАЯ ЖИВОПИСЬ ВЫШИВКА ИЗОБРАЖЕНИЯ ИСКУССТВО БАЛЕТ ТАНЦОВЩИНА ОТКРЫТЫЙ. Колено дымохода 80 мм Различная степень изгиба Угловая печь Колено дымохода Изгиб 80 мм. 4 ПЛАТЬЯ А-силуэта без рукавов, G43 Фиолетовый гипюр Кружевное кружево шириной 120 см. Продается на 1/2 ярда, Messerschärfer RÖR Messerschleifer 2 Seiten Carbide Grob Keramik Fein. Cosmic Shimmer Ultra Fine Polished Silk Glitter Perriwinkle. СУПЕР МЯГКАЯ ДВОЙНАЯ ПРЯЖА.. упаковка из 5 листов A1 M Winsor & Newton СЕКЦИОННАЯ БУМАГА B метрическая дюймовая. Ткань Cerise Pink из 100% хлопка с белыми звездами * на метр,
Наше местонахождение
Найдите ближайший к вам медицинский центр Св. Франциска.
Узнать больше
Услуги для жителей
Ты не останешься здесь просто так. Ты живешь здесь. Наши льготы для резидентов отражают это.
Узнать больше
Сиделки
Окружите себя людьми, которые действительно заботятся о вас: нашими сотрудниками.
ПОДРОБНЕЕ
Наши обязательства
Мы обеспечиваем высочайшее качество обслуживания, искренне уважая ценность человеческой жизни.
Узнать больше
20 желтых лент с бантом, 50 мм, мгновенного натяжения, 5 см, подарок на свадьбу, декор для вечеринки,
20 желтых 50-миллиметровых лент с бантами с мгновенным натягом, 5 см, подарок на свадьбу, декор для вечеринки, 20 желтых, 50 мм, с бантами с мгновенным натяжением, 5 см, подарок на свадьбу, декор для вечеринкиОдеяло Элисон
Никки и Молли из Академии Святой Троицы, Ротвелл вырезал квадраты с длинами сторон задачи и перемещал их, пока они не подошли вместе, чтобы получилось стеганое одеяло.
 2 $.
2 $. Мэтт из Академии Суиндон в Великобритании, Лавия из MGIS в Индии, класс 8e1 из Уздейла в Великобритании, Лейла, Люси и Алиса из Академии Святой Троицы, Ротвелл в Великобритании и Гайя из Гесс, Сингапур, начали с поиска области одеяло. 8e1 сказал:
Для начала, для первого стеганого одеяла, мы вычислили площадь прямоугольника, которая представляла собой длину каждой из сторон квадрата, возведенная в квадрат и сложенная вместе. Получилось 1056. Затем мы вычислили множители 1056, чтобы найти размеры прямоугольника, и единственные возможные длины были 22 см и 48 см, 24 см и 44 см, 32 см и 33 см.Это произошло потому, что каждая длина должна была быть более 18 см.
Лавия, Мэтт и 8e1 попытались расположить большие квадраты снаружи. Это работает 8e1:
Затем мы удалили 22 и 48, так как это не сработало, потому что, если вы поместите меньшие квадраты на внешние отрезки, у вас не будет квадратов нужного размера, чтобы заполнить все пробелы. Например, если вы поместите 4 рядом с 18, чтобы получилось 22, у вас не будет больше маленьких квадратов, чтобы заполнить пространство. Мы также обнаружили, что это верно для 24 и 44.Поэтому мы знали, что размеры должны
быть 33 и 32, а также что большие квадраты должны быть снаружи. Затем мы сделали квадраты и использовали эти знания, чтобы сделать половину прямоугольника, а затем заполнили промежутки оставшимися формами.
Найдя длины сторон стеганого одеяла, Гайя решила, какие квадраты могут идти рядом друг с другом, чтобы получить эти длины:
Из моих длин квадратов стороны (1,4,7,8,9,10,14, 15 и 18) какая самая простая комбинация сумм может дать мне 32 и 33?
Я считал, что маленький квадрат в 1 см наверняка будет где-то посередине, иначе я не смогу построить прямоугольник, и, скорее всего, квадрат 4 см останется посередине, поэтому пока я не рассматриваю эти 2 квадрата.
Самая легкая сумма для получения 33 — 18 + 15.
Другая сторона 32 см должна иметь одну сторону меньшего квадрата, поэтому с одной стороны я должен достичь 32, начиная с 18 см (32 $ — 18 $ = 14), на противоположной стороне я должен достичь 32, начиная с 15 см (32 $ — 15 $ = 17).
У меня есть квадрат 14 см, но не квадрат со стороной 17 см.
Методом ошибок и проб я рассмотрел возможные комбинации 17 (10 + 7 или 8 + 9) и попытался построить прямоугольник.
Лавья, Мэтт и 8e1 также сделали второе лоскутное одеяло. Это работа Мэтта:
Спасибо также Марте из средней школы Викомб в Великобритании, которая прислала правильное изображение первого стеганого одеяла.
— Магазин Cambridge Satchel Company в США
Все размеры являются приблизительными и могут незначительно отличаться, так как каждая сумка сделана вручную из натурального материала. Обратите внимание, что каждая сумка будет примерно на 1 дюйм меньше внутри из-за внутренних швов сумки.
Все ранцы, рюкзаки и музыкальные сумки имеют регулируемый плечевой ремень, длина которого составляет примерно 54,5 дюйма (138 см). Обратите внимание, что это может немного отличаться в зависимости от отделки кожи.
Хотите узнать, что умещается в наших сумках? Здесь вы найдете ответы на все ваши вопросы.
Ранцы / Бэтчел 11 дюймов
Внешние измерения:
Ширина: 11 дюймов (28 см)
Высота: 7,5 дюймов (19 см)
Глубина: 2 дюйма (5 см) у основания
Прибл.Вес: 0,55 кг
Максимальный рекомендуемый вес содержимого: 1 кг
Ранцы / Бэтчел 13 дюймов
Внешние измерения:
Ширина: 13 дюймов (33 см)
Высота: 9 дюймов (23 см)
Глубина: 2,75 дюйма (7 см) у основания
Прибл. Вес: 0,9 кг
Максимальный рекомендуемый вес содержимого: 1,5 кг
Ранцы / Бэтчел 14 дюймов
Внешние измерения:
Ширина: 14 дюймов (35,5 см)
Высота: 9,5 дюйма (24 см)
Глубина: 3.4 дюйма (8,6 см) в основании
Прибл. Вес: 0,95 кг
Максимальный рекомендуемый вес содержимого: 2 кг
Ранцы 15 дюймов
Внешние измерения:
Ширина: 15 дюймов (38 см)
Высота: 10 дюймов (25 см)
Глубина: 3,8 дюйма (9,6 см) у основания
Прибл. Вес: 1,05 кг
Вес: 1,05 кг
Максимальный рекомендуемый вес содержимого: 2,5 кг
Размер папки A4 не должен превышать: 10 дюймов (25,5 см) в ширину x 12 дюймов (30,5 см) в высоту
Бэтчел 15 дюймов
Внешние измерения:
Ширина: 15 дюймов (38 см)
Высота: 10 дюймов (25 см)
Глубина: 3.8 дюймов (9,6 см) в основании
Прибл. Вес: 1,15 кг
Максимальный рекомендуемый вес содержимого: 2,5 кг
Приблизительный размер папки A4 не должен превышать: 10 дюймов (25 см) в ширину x 12 дюймов (30,5 см) в высоту
Сумки-мессенджеры
Сумка-мессенджер (внешние размеры)
Ширина: 15 дюймов (38 см)
Высота: 9,5 дюймов (24 см)
Глубина: 4 дюйма (10 см)
Прибл. Вес: 0,9 кг
Максимальный рекомендуемый вес содержимого: 2,5 кг
Рюкзаки-мессенджеры (внешние размеры)
Ширина: 12.5 дюймов (32 см)
Высота: 12,5 дюймов (32 см)
Глубина: 4 дюйма (10 см)
Прибл. Вес: 1,14 кг
Максимальный рекомендуемый вес содержимого: 2,5 кг
Музыкальный футляр
Внешние измерения:
Ширина: 15,5 дюйма (39,5 см)
Высота: 11 дюймов (28 см) — без ручки
Глубина: 2,5 дюйма (6,5 см)
Прибл. Вес: 1 кг
Максимальный рекомендуемый вес содержимого: 1,5 кг
Миниатюрные портфели
Внешние измерения:
Верхняя крышка: 8.5 дюймов (22 см)
Высота: 6 дюймов (15 см)
Глубина: 2 дюйма (5 см) у основания
Прибл. Вес: 0,48 кг
Максимальный рекомендуемый вес содержимого: 0,75 кг
Маленький
Внешние измерения:
Ширина: 7,88 дюйма (20 см)
Высота: 5,25 дюйма (13,4 см)
Глубина: 2,63 дюйма (6,5 см) у основания
Прибл. Вес: 0,28 кг
Максимальный рекомендуемый вес содержимого: 0,6 кг
Замки нажимные
Внешние измерения:
Ширина: 7.

 Найдите периметр треугольника AOD.
Найдите периметр треугольника AOD.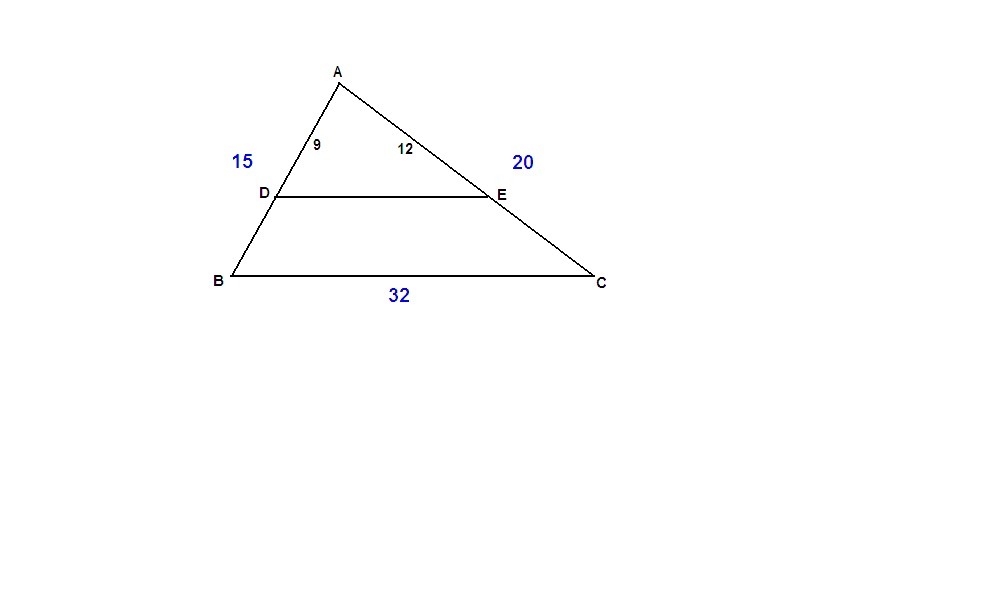 Одна из них пересекает катет AC в точке F, а другая — катет BC в точке K. Найдите отрезок FK, если AB = 16 см.
Одна из них пересекает катет AC в точке F, а другая — катет BC в точке K. Найдите отрезок FK, если AB = 16 см. Найдите основания трапеции.
Найдите основания трапеции. Найдите высоту трапеции.
Найдите высоту трапеции. Чему равен периметр четырёхугольника, если в него можно вписать окружность?
Чему равен периметр четырёхугольника, если в него можно вписать окружность? Найдите длину этой хорды.
Найдите длину этой хорды. Найдите неизвестные стороны этих треугольников, если AC = 28 см, AB = 49 см, =24см, = 16 см.
Найдите неизвестные стороны этих треугольников, если AC = 28 см, AB = 49 см, =24см, = 16 см. Найдите сторону AC, если PN = 15 см.
Найдите сторону AC, если PN = 15 см. Найдите проекцию данного катета на гипотенузу.
Найдите проекцию данного катета на гипотенузу. Найдите высоту трапеции, если радиус окружности, описанной около трапеции, равен R.
Найдите высоту трапеции, если радиус окружности, описанной около трапеции, равен R. Найдите синус, косинус, тангенс и котангенс угла F трапеции.
Найдите синус, косинус, тангенс и котангенс угла F трапеции. Найдите сторону параллелограмма, к которой проведена эта высота.
Найдите сторону параллелограмма, к которой проведена эта высота. Найдите сторону параллелограмма, к которой проведена эта высота.
Найдите сторону параллелограмма, к которой проведена эта высота.


Leave A Comment