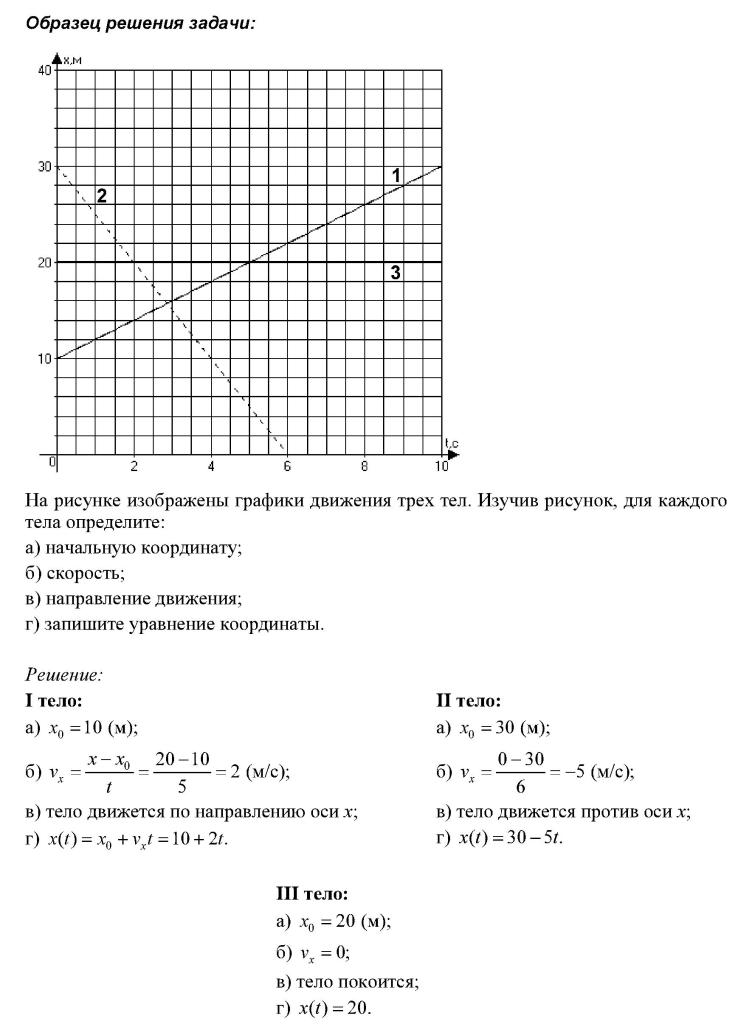
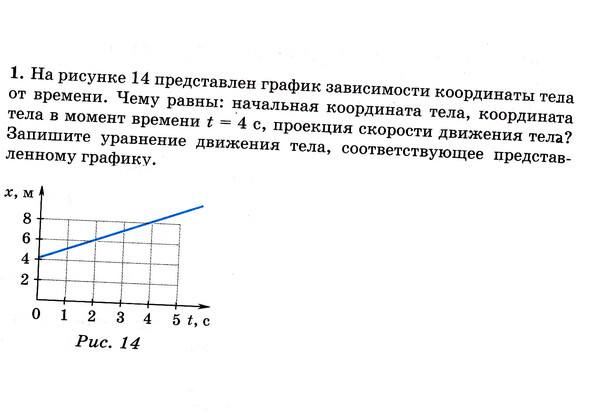
ПОМОГИТЕ , ПОЖАЛУЙСТА ! ОЧЕНЬ ПРОШУ! ПОЖАЛУЙСТА 2. На рисунке изображен график зависимости
znatok965 znatok965
- Физика
- 5 — 9 классы
ответ дан
3. Дано уравнение движения: х = -2 + 4t. Определите:
— вид движения тела;
— начальную координату;
— проекцию скорости тела;
— на координатной оси покажите откуда и куда движется тело.
4. Зависимость скорости движения тела от времени задана уравнением: υх = 6 + 1,5t. Определите :
— вид движения тела;
— начальную скорость;
— проекцию ускорения;
— на координатной оси покажите направления скорости и ускорения тела.
5. По графику зависимости проекции скорости от времени определите:
— характер движения тела на участках АВ и ВС;
— ускорение тела на этих участках;
— путь, пройденный телом за все время движения;
 2)/2a=(0-400)2*(-10)=-400/(-20)=20 м
2)/2a=(0-400)2*(-10)=-400/(-20)=20 мS= 20 м
Теперь сложим:
АВ+ВС=20+100=120м
Ответ: 120 м
Новые вопросы в Физика
Площа стопи слона рівна 700 см², а його маса рівна 4500 кг. Знайдіть тиск,який чинить слон на Землю
Очень срочно. Даю сотню!!!! Частина енергії двигуна автомобіля під час руху витрачається на взаємодію з повітрям. У яку енергію вона перетворюється. С … обьяснием, пожалуйста!
СРОЧНО! встановіть вІДПОВІДність між винаходом, дослідом Ta прізвищем ученого 1) ртутний барометр 2) магдебурзькі півкулі 3) залежність тиску від Еван … джеліста a) Паскаль Блез б) Отто фон Геріке стовпа рідини в) Торрічеллі г) Ньютон Ісаак висоти
Тиск рідини вимірюється… а) термометром; б) Динамометром в) манометром; г) спідометром
Тиск рідини вимірюється… а) термометром; б) Динамометром в) манометром; г) спідометром
Предыдущий
Следующий
§6. Примеры движения тела.
 Методы решения задач. — ЗФТШ, МФТИ
Методы решения задач. — ЗФТШ, МФТИРассмотрим некоторые характерные примеры движения тела, знание которых будет полезно при дальнейшем изучении физики.
1.Равномерное прямолинейное движение тела.
При равномерном прямолинейном движении тело совершает равные перемещения `Delta vecr` за одинаковые промежутки времени
При этом зависимость `vec r(t)` имеет вид:
где `vec r_0` — радиус-вектор тела в начальный момент времени $$ t=0$$ . В этой связи вспомним замечание о начальных условиях, сделанное в §4. Вектор $$ {\overrightarrow{r}}_{0}$$ здесь является тем начальным условием, которое позволяет однозначно определить радиус-вектор $$ \overrightarrow{r}$$ тела в любой момент времени в процессе движения.
Векторное уравнение (7) равносильно системе двух скалярных уравнений, выражающих зависимость от времени $$ t $$ координат $$ x$$ и $$ y$$ движущегося тела:
где $$ {x}_{0}$$ и $$ {y}_{0}$$ — начальные координаты тела в момент времени $$ t=0$$, а $$ {v}_{x}$$ и $$ {v}_{y}$$ -проекции вектора скорости `vecv` на координатные оси $$ Ox$$ и $$ Oy$$ соответственно.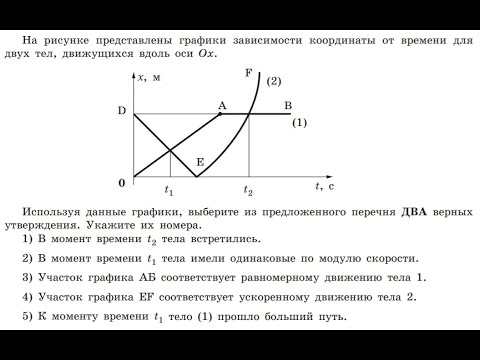
Траектория равномерного прямолинейного движения тела графически представляет собой отрезок прямой линии (рис. 9), тангенс угла наклона которой к оси абсцисс равен отношению проекций скорости на оси координат: $$ \mathrm{tg}\alpha ={v}_{y}/{v}_{x}$$. Аналитическое уравнение траектории, т. е. зависимость $$ y\left(x\right)$$, легко получить, исключив параметр $$ t$$ из системы уравнений (8):
2. Неравномерное движение тела.
Для неравномерного движения характерно то, что с течением времени изменяется скорость движущегося тела, а в общем случае и его ускорение. В качестве примера может служить движение, при котором тело проходит различные участки своего пути с разной скоростью. Такое движение принято характеризовать, прежде всего, средней путевой скоростью. Причём прилагательное «путевая» в условиях задач часто опускается.
Другим характерным примером неравномерного движения служит так называемое равнопеременное движение, которое целесообразно рассмотреть подробно, не выходя при этом за рамки школьной программы.
3. Равнопеременное движение.
Равнопеременным называется такое неравномерное движение, при котором скорость `vec v` за любые равные промежутки времени `Delta t` изменяется на одинаковую величину `Deltavecv`. В этом случае ускорение `veca` тела не зависит от времени и остаётся постоянным в процессе движения:
(при этом `vec v != «const»`, и траектория движения не обязательно прямолинейная).
При равнопеременном движении скорость $$ \overrightarrow{v}$$ тела изменяется с течением времени по закону
где `vecv_0` — скорость тела в начальный момент времени `t=0`.
В свою очередь, зависимость `vecr(t)` имеет вид:
где `vecr_0` — начальный радиус-вектор тела при `t=0`. Вновь заметим, что величины `vecv_0` и `vecr_0` представляют собой начальные условия, позволяющие в любой момент времени однозначно определить векторы `vecv` и `vecr`.
При координатном способе описания равнопеременного движения векторным уравнениям (11) и (12), равносильны следующие системы уравнений для проекций скорости и радиус-вектора тела на оси выбранной системы отсчёта. 2)/(2a_x)`.
2)/(2a_x)`.
Удобство этой формулы заключается в том, что она не содержит времени $$ t$$ в явном виде. Вместе с тем надо помнить, что формула получена в предположении о неизменности направления движения тела.
Одним из наиболее наглядных примеров равнопеременного движения является движение тела в поле тяжести Земли, которое мы имеем возможность наблюдать повседневно. Для решения задач в этом случае надо заменить в приведённых выше формулах вектор $$ \overrightarrow{a}$$ на ускорение свободного падения $$ \overrightarrow{g}$$, сообщаемое силой гравитационного притяжения всякому телу, движущемуся в поле тяжести Земли. Рассмотрим три конкретных случая такого движения.
Движение тела, брошенного вертикально.
Тело бросили с поверхности земли, сообщив ему начальную скорость $$ {\overrightarrow{v}}_{0}$$ направленную вертикально вверх. Пренебрегая сопротивлением воздуха, определите время $$ \tau $$ полёта тела до момента падения на землю; скорость тела в момент падения; максимальную высоту $$ H$$ подъёма тела над землёй; время $$ {\tau }_{1}$$ подъёма тела на максимальную высоту; путь `S`, пройденный телом за время полёта и перемещение тела.
 {2}+\mathrm{tg}\alpha x$$.
{2}+\mathrm{tg}\alpha x$$. График траектории тела представляетсобой участок параболы, ветви которой направлены вниз.
3.5 Графический анализ одномерного движения – биомеханика движений человека
График, как и картинка, стоит тысячи слов. Графики содержат не только числовую информацию; они также выявляют отношения между физическими величинами. В этом разделе используются графики зависимости смещения, скорости и ускорения от времени для иллюстрации одномерной кинематики.
Во-первых, обратите внимание, что графики в этом тексте имеют перпендикулярные оси, одну горизонтальную, а другую вертикальную. Когда две физические величины нанесены друг против друга на таком графике, горизонтальная ось обычно считается независимая переменная и вертикальная ось зависимая переменная . Если мы назовем горизонтальную ось осью x
у = mx + b
Здесь м — это уклон , определяется как подъем, деленный на прогон (как показано на рисунке) прямой линии. Буква b используется для y — точки пересечения , которая является точкой, в которой линия пересекает вертикальную ось.
Буква b используется для y — точки пересечения , которая является точкой, в которой линия пересекает вертикальную ось.
Время обычно является независимой переменной, от которой зависят другие величины, такие как смещение. Таким образом, график зависимости смещения от времени будет иметь p x (отображается как x на графике ниже) по вертикальной оси и t по горизонтальной оси. Рисунок 2, показанный ниже, является именно таким прямолинейным графиком. На нем показан график зависимости перемещения автомобиля с реактивным двигателем от времени на очень ровном дне высохшего озера в Неваде .
Рис. 2. График зависимости перемещения автомобиля с реактивным двигателем от времени на соляных равнинах Бонневилля.
Используя взаимосвязь между зависимыми и независимыми переменными, мы видим, что наклон на приведенном выше графике представляет собой среднюю скорость или [латекс]\boldsymbol{\bar{v}}[/латекс], а точка пересечения представляет собой смещение в нулевое время— то есть p x 0 . Подстановка этих символов в y = mx + b дает
стр. x = (средняя скорость) + p x o
Таким образом, график зависимости перемещения от времени дает общее соотношение между перемещением, скоростью и временем, а также дает подробную числовую информацию о конкретной ситуации.
НАКЛОН X VS. T
Наклон графика смещения p x от времени t есть скорость v .
наклон = подъем / подъем = Δp x /Δt = v x среднее значение или v x бар (по определению)
алгебраически получено из другого уравнения движения в предыдущем разделе.
Из рисунка видно, что автомобиль имеет перемещение 25 м за 0,50 с и 2000 м за 6,40 с. Его смещение в другое время можно прочитать на графике; кроме того, информацию о его скорости и ускорении также можно получить из графика.
Пример 1. Определение средней скорости по графику зависимости перемещения от времени: реактивный автомобиль
Найдите среднюю скорость автомобиля, положение которого показано на рисунке 2 выше. x по сравнению с t — средняя скорость, поскольку уклон равен подъему над пробегом. В этом случае подъем = изменение смещения и пробег = изменение во времени, так что
уклон = подъем / пробег = Δp x /Δt = v x среднее значение
Поскольку наклон здесь постоянный, любые две точки на графике можно использовать для определения наклона. (Вообще говоря, наиболее точно использовать две далеко отстоящие точки на прямой линии. Это связано с тем, что любая ошибка при считывании данных с графика пропорционально меньше, если интервал больше.)
(Вообще говоря, наиболее точно использовать две далеко отстоящие точки на прямой линии. Это связано с тем, что любая ошибка при считывании данных с графика пропорционально меньше, если интервал больше.)
Решение
1. Выберите две точки на прямой. В этом случае выбираем точки, отмеченные на графике: (6,4 с, 2000 м) и (0,50 с, 525 м). (Обратите внимание, однако, что вы можете выбрать любые две точки.)
2. Подставьте значения p x и t выбранных точек в уравнение. Помните, что при расчете изменения ( Δ ) мы всегда используем конечное значение минус начальное значение.
уклон = подъем / подъем = Δp x /Δt = v x среднее значение = (2000 м/с – 525 м/с) / (6,4 с усреднение – 0,50 с)
3
x = 250 м/сОбсуждение
Это впечатляюще высокая наземная скорость (900 км/ч или около 560 миль/ч): намного больше, чем типичный предел скорости на шоссе в 60 миль/ч (27 м/с или 96 км/ч), но значительно меньше рекорда 343 м / с (1234 км / ч или 766 миль / ч), установленного в 1997 году.
Графики на рисунке 3 ниже представляют движение автомобиля с реактивным двигателем, когда он разгоняется до максимальной скорости, но только в то время, когда его ускорение постоянно. Время для этого движения начинается с нуля (как если бы его измеряли секундомером), а перемещение и скорость изначально равны 200 м и 15 м/с соответственно.
Рис. 3. Графики движения автомобиля с реактивным двигателем в течение промежутка времени, когда его ускорение постоянно. (a) Наклон графика p x против t представляет собой скорость. Это показано в двух точках, а полученные мгновенные скорости нанесены на следующий график. Мгновенная скорость в любой точке равна наклону касательной в этой точке. (b) Наклон против x против t график является постоянным для этой части движения, что указывает на постоянное ускорение. (c) Ускорение имеет постоянное значение 5,0 м/с 2 на протяжении временного интервала, нанесенного на график.
График зависимости смещения от времени на рисунке 3 (а), показанном выше , представляет собой кривую, а не прямую линию. Наклон кривой становится круче с течением времени, показывая, что скорость увеличивается с течением времени. Наклон в любой точке графика зависимости перемещения от времени представляет собой мгновенную скорость в этой точке. Его находят, проводя прямую линию, касающуюся кривой в интересующей точке, и измеряя наклон этой прямой. Касательные линии показаны выше для двух точек на рисунке 3 (а). Если это сделать в каждой точке кривой и нанести значения в зависимости от времени, то получится график зависимости скорости от времени, показанный на рисунке 3 (b). Кроме того, наклон графика зависимости скорости от времени представляет собой ускорение, что показано на рис. 3(с).
Пример 2. Определение мгновенной скорости по наклону в точке: реактивный автомобиль
Рассчитайте скорость реактивного автомобиля за 25 с, найдя наклон p x против t график на графике ниже.
Стратегия
Наклон кривой в точке равен наклону прямой, касательной к кривой в этой точке. Этот принцип проиллюстрирован на рисунке выше, где Q — точка t = 25 с .
Решение
1. Найдите касательную к кривой в точке t = 25 с .
2. Определите конечные точки касательной. Они соответствуют положению 1300 м в момент времени 19с и положением 3120 м в момент времени 32 с.
3. Подставьте эти конечные точки в уравнение для определения наклона v . (3120 м2) с – 19 с )
Таким образом v x Q = ( 1820 м ) / ( 13 с) = 140 м/с
Обсуждение
0010 v x at t = 25 с .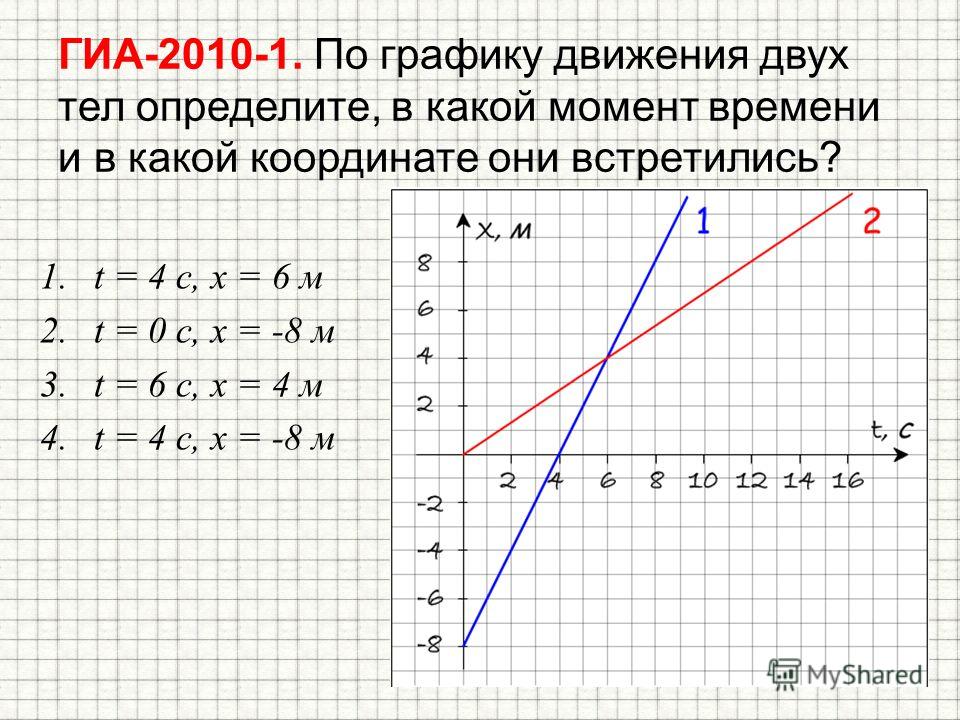 Значение 140 м/с для v x Q показано на рисунке 5(b). Таким образом можно получить весь график v x vs. t .
Значение 140 м/с для v x Q показано на рисунке 5(b). Таким образом можно получить весь график v x vs. t .
Делая еще один шаг вперед, мы отмечаем, что наклон графика зависимости скорости от времени представляет собой ускорение. Склон — это подъем, разделенный на пробег; на против против t график, подъем = изменение скорости Δ v и пробег = изменение во времени Δ t .
НАКЛОН V VS. T
Наклон графика зависимости скорости v от времени t равен ускорению a .
наклон = среднее ускорение = Δv / Δt
Поскольку график зависимости скорости от времени на рисунке 3 (b) представляет собой прямую линию, ее наклон везде одинаков, что означает, что ускорение постоянно. График зависимости ускорения от времени представлен на рис. 3(c) 9.0003
График зависимости ускорения от времени представлен на рис. 3(c) 9.0003
Дополнительную общую информацию можно получить из рисунка 6 и выражения для прямой линии y = mx + b .
В этом случае вертикальная ось y равна V , точка пересечения b равна v 0 10 10 900 0 м это а , а горизонтальная ось p x равна т . Замена этих символов дает
v = a t + v o или часто пишется v = v o + at
Общее соотношение скорости, ускорения и времени снова получено из графика. Обратите внимание, что это уравнение также было получено алгебраическим путем из других уравнений движения в предыдущих разделах.
Не случайно графическим анализом получаются те же самые уравнения, что и алгебраическими методами. На самом деле, важный способ обнаружить физических взаимосвязей — это измерить различные физические величины, а затем построить графики зависимости одной величины от другой, чтобы увидеть, связаны ли они каким-либо образом. Корреляции подразумевают физические отношения и могут быть показаны с помощью гладких графиков, таких как приведенные выше. По таким графикам иногда можно постулировать математические зависимости. Затем проводятся дальнейшие эксперименты для определения достоверности предполагаемых взаимосвязей.
На самом деле, важный способ обнаружить физических взаимосвязей — это измерить различные физические величины, а затем построить графики зависимости одной величины от другой, чтобы увидеть, связаны ли они каким-либо образом. Корреляции подразумевают физические отношения и могут быть показаны с помощью гладких графиков, таких как приведенные выше. По таким графикам иногда можно постулировать математические зависимости. Затем проводятся дальнейшие эксперименты для определения достоверности предполагаемых взаимосвязей.
Теперь рассмотрим движение реактивного автомобиля при изменении его скорости от 165 м/с до максимальной скорости 250 м/с, как показано на рис. 6 ниже. Время снова начинается с нуля, а начальное перемещение и скорость равны 2900 м и 165 м/с соответственно. (Это были конечное перемещение и скорость автомобиля в движении, показанном на рисунке 3. Ускорение постепенно уменьшается с 5,0 м/с 2 до нуля, когда автомобиль достигает скорости 250 м/с. Наклон кривой x против t график увеличивается до t = 55 с , после чего наклон становится постоянным Аналогично скорость увеличивается до 55 с, а затем становится постоянной, так как ускорение уменьшается до нуля на 55 с и остается нулевым
Наклон кривой x против t график увеличивается до t = 55 с , после чего наклон становится постоянным Аналогично скорость увеличивается до 55 с, а затем становится постоянной, так как ускорение уменьшается до нуля на 55 с и остается нулевым
Пример 3. Расчет ускорения по графику зависимости скорости от времени
Рассчитайте ускорение реактивного автомобиля за время 25 с, найдя наклон графика v и t на рисунке 6(b).
Стратегия
Наклон кривой в точке t = 25 с равен наклону касательной в этой точке, как показано на рис. 6(b)
Решение
6 900 конечные точки касательной на рисунке, а затем подставьте их в уравнение для определения наклона, и .наклон = Δv / Δ t = ( 260 м/с – 210 м/с) / ( 51 – 1,0 с) = 1,0 м/с 2
соответствует значению, изображенному на рисунке 6 (c) при t = 25 с .
График зависимости перемещения от времени можно использовать для построения графика зависимости скорости от времени, а график зависимости скорости от времени можно использовать для построения графика зависимости ускорения от времени. Мы делаем это, находя наклон графиков в каждой точке. Если график линейный (то есть линия с постоянным наклоном), легко найти наклон в любой точке, и у вас есть наклон для каждой точки. Графический анализ движения может быть использован для описания как частных, так и общих характеристик кинематики. Графики также могут быть использованы для других тем в физике. Важным аспектом изучения физических взаимосвязей является их графическое отображение и поиск лежащих в их основе взаимосвязей.
Графики также могут быть использованы для других тем в физике. Важным аспектом изучения физических взаимосвязей является их графическое отображение и поиск лежащих в их основе взаимосвязей.
- Графики движения можно использовать для анализа движения.
- Графические решения дают решения, идентичные математическим методам вывода уравнений движения.
- Наклон графика водоизмещения p x от времени t есть скорость v x .
- Наклон графика скорости v x от времени t график ускорения a x .
- Средняя скорость, мгновенная скорость и ускорение могут быть получены путем анализа графиков.
- независимая переменная
- переменная, относительно которой измеряется зависимая переменная; обычно наносится вдоль оси x
- зависимая переменная
- измеряемая переменная; обычно наносятся вдоль у -ось
- склон
- разность y -значение (подъем) деленное на разность x -значение (пробег) двух точек на прямой
- Y-точка пересечения
- y -значение, когда x = 0 , или когда график пересекает y -ось
графиков скорость-время — определение, примеры
Основные понятия
1. График зависимости скорости от времени
График зависимости скорости от времени
2. Наклон графика v-t = ускорение
3. Типы графиков зависимости скорости от времени
4. Смещение от графиков v-t
Скорость тела
9 при равноускоренном движении увеличивается на равные величины через равные промежутки времени. Это также указывает на то, что он движется с постоянным ускорением. При построении его скорости в разные моменты времени в зависимости от соответствующих значений времени график оказывается прямой линией, проходящей через начало координат (если считать, что движение тела начинается из состояния покоя) и наклоненной к оси х. ось (ось времени). Такой график, построенный для движущегося тела, может предоставить много информации о движении тела, такой как тип движения, скорость, ускорение и перемещение.Объяснение:
Ускорение на графике v-t: Наклон — это мера крутизны графика. Рассмотрим две точки A и B на диаграмме положение-время тела при равномерном движении и пусть их координаты равны (t 1 , v 1 ) и (t 2 , v 2 ) соответственно: как показано на рисунке ниже.
Наклон этого графика определяется выражением
Наклон, м = BC/AC
Или м = (v 2 – в 1 )/ (т 2 – 6 1 )
Фактически, наклон v-t график в конкретный момент времени дает ускорение тела в этот момент.
Это потому, что наклон представляет собой отношение изменения скорости к изменению времени, которое равно скорости тела.
Или, v = m = (v 2 – v 1 )/ (t 2 – 6 t
6 005
1 )
График скорость-время может выглядеть очень по-разному для разных видов движения. Вот некоторые из них:
Вот некоторые из них:
- График скорости тела при равномерном движении:0005 равномерная скорость преодолевает равные расстояния за равные промежутки времени. Это связано с тем, что его скорость остается постоянной на протяжении всего движения. Такое движение называется равномерным движением . Его график v-t представляет собой прямую линию , параллельную оси x, , как показано на графике ниже. Наклон графика скорости тела при равномерном движении равен нулю . Это указывает на то, что ускорение тела при таком движении равно ноль .
- График зависимости скорости равномерно и положительно ускоряющегося тела:
Объект, движущийся равномерно и положительно ускоренно, увеличивает свою скорость на равные величины через равные промежутки времени. Это потому, что его ускорение остается постоянным на протяжении всего движения.
 График v-t такого движения при построении оказывается прямой линией , проходящей через начало координат (если тело выходит из состояния покоя) с положительный наклон . Положительный и постоянный наклон указывает на положительное и постоянное ускорение тела.
График v-t такого движения при построении оказывается прямой линией , проходящей через начало координат (если тело выходит из состояния покоя) с положительный наклон . Положительный и постоянный наклон указывает на положительное и постоянное ускорение тела.- График зависимости скорости равномерно и отрицательно ускоряющегося тела:
Объект, движущийся равномерно и отрицательно ускоренно, уменьшает свою скорость на равные величины через равные промежутки времени. Это потому, что его ускорение остается постоянным , но отрицательным на протяжении всего движения. График v-t такого движения при построении оказывается прямая с отрицательным наклоном . Отрицательный и постоянный наклон указывает на отрицательное и постоянное ускорение тела.
Сравнение ускорений:Ускорения различных тел можно сравнить , посмотрев на крутизну (наклон) их графиков v-t.
 Например, на графике ниже показан график v-t двух тел, находящихся в равномерном движении с разными ускорениями. Из графика легко понять, что ускорение первого тела больше, чем второго.
Например, на графике ниже показан график v-t двух тел, находящихся в равномерном движении с разными ускорениями. Из графика легко понять, что ускорение первого тела больше, чем второго.- График скорости тела в состоянии покоя:
Скорость тела в состоянии покоя равна нулю , пока оно не начнет двигаться. Следовательно, график v-t тела в состоянии покоя представляет собой прямую линию , совпадающую с осью x (ось времени), как показано на рисунке ниже.
- График зависимости скорости тела от времени с возрастающим ускорением:
При этом типе движения величина ускорения тела продолжает увеличиваться со временем. График скорости и времени для такого движения равен изогнут так, как показано на рисунке ниже. График будет начинаться с начала координат , если тело изначально находилось в состоянии покоя .
 В противном случае он может начинаться с точки на оси x или y- или любой другой точки на декартовой плоскости. Наклон графика v-t тела, движущегося с увеличивающимся ускорением , продолжает увеличиваться , поскольку крутизна графика продолжает увеличиваться.
В противном случае он может начинаться с точки на оси x или y- или любой другой точки на декартовой плоскости. Наклон графика v-t тела, движущегося с увеличивающимся ускорением , продолжает увеличиваться , поскольку крутизна графика продолжает увеличиваться.- График скорости тела с уменьшающимся ускорением:
При этом типе движения величина ускорения тела со временем продолжает уменьшаться. График скорости и времени для такого движения изогнут так, как показано на рисунке ниже. График будет начинаться с начала координат , если тело изначально находилось в состоянии покоя . В противном случае он может начинаться с точки на оси x или y или любой другой точки на декартовой плоскости. Наклон v-t графика тела, движущегося с уменьшающимся ускорением продолжает уменьшаться , поскольку крутизна графика продолжает уменьшаться.
Перемещение на графике скорость-время:
Перемещение , покрываемое телом, равно площади под его графиком скорость-время . Пусть на приведенном ниже графике скорость-время координаты A и B равны (t, v) и (t, 0) соответственно.
Полное перемещение, покрываемое телом = площадь под графиком v-t (OA)
= площадь треугольника OAB.
Следовательно,
Полное перемещение = площадь (треугольник OAB)
1/2)vt
В других случаях график v-t может выглядеть иначе. Или нам может понадобиться найти перемещение тела на участке графика. Даже в этих случаях площадь под графиком дает смещение тела. Вот еще один пример.
Смещение = площадь под графиком v-t = площадь (трапеция OABD)
Или, s = площадь (ABC) + площадь (OACD)
Или, s = (1/2) x AC x BC + AC x CD
Или, s = (1/2) t 2 (v 2 – v 1 ) + t 2 v 1 ,
3 или
т 2 [(1/2) (v 2 – v 1 ) + v 1 ]Если требуется смещение части движения, то следует рассчитать площадь под соответствующей частью v-t графика .
Задачи
- Определите тип ускорения (положительное, отрицательное, нулевое и неравномерное), которому подвергается тело, анализируя каждый участок графика зависимости скорости от времени, показанного ниже.
- Неравномерно ускоренное движение
- Равноускоренное движение
- Равномерное движение
- Равномерно замедленное движение Равномерно ускоренное 4
- Движение с неравномерным замедлением
- Определите тип движения (равномерное, неравномерное, равномерное и неравномерно ускоренное/замедленное движение), которому подвергается тело, путем анализа каждого участка графика зависимости скорости от времени, показанного ниже.
- Неравноускоренное движение
- Равноускоренное движение
- Равномерное движение
- равноускоренное движение
- неравномерно замедленное движение
- График v-t движения тела показан на рисунке ниже.
 Вычислите его полное водоизмещение.
Вычислите его полное водоизмещение.
Полное водоизмещение = площадь (OABD) + площадь (BDC)
= 3 x 6 + (1/2) x 6 x ( 7 – 3)
= 18 + (1/2) x 6 x 4
= 18 + 12 900 = 30 м
- График v-t движения тела показан на рисунке ниже. Вычислите ускорение тела на каждом участке графика. В каком сечении тело имеет наибольшее ускорение?
Рассмотрим конечные точки на графике v-t с координатами (0,0) и (25, 50).
Ускорение = наклон = (50 – 0)/ (25 – 0)
s 2
РАЗРЕЗ – B Рассмотрим конечные точки на v-t график с координатами (25, 50) и (60, 50).

 График v-t такого движения при построении оказывается прямой линией , проходящей через начало координат (если тело выходит из состояния покоя) с положительный наклон . Положительный и постоянный наклон указывает на положительное и постоянное ускорение тела.
График v-t такого движения при построении оказывается прямой линией , проходящей через начало координат (если тело выходит из состояния покоя) с положительный наклон . Положительный и постоянный наклон указывает на положительное и постоянное ускорение тела. Например, на графике ниже показан график v-t двух тел, находящихся в равномерном движении с разными ускорениями. Из графика легко понять, что ускорение первого тела больше, чем второго.
Например, на графике ниже показан график v-t двух тел, находящихся в равномерном движении с разными ускорениями. Из графика легко понять, что ускорение первого тела больше, чем второго. В противном случае он может начинаться с точки на оси x или y- или любой другой точки на декартовой плоскости. Наклон графика v-t тела, движущегося с увеличивающимся ускорением , продолжает увеличиваться , поскольку крутизна графика продолжает увеличиваться.
В противном случае он может начинаться с точки на оси x или y- или любой другой точки на декартовой плоскости. Наклон графика v-t тела, движущегося с увеличивающимся ускорением , продолжает увеличиваться , поскольку крутизна графика продолжает увеличиваться.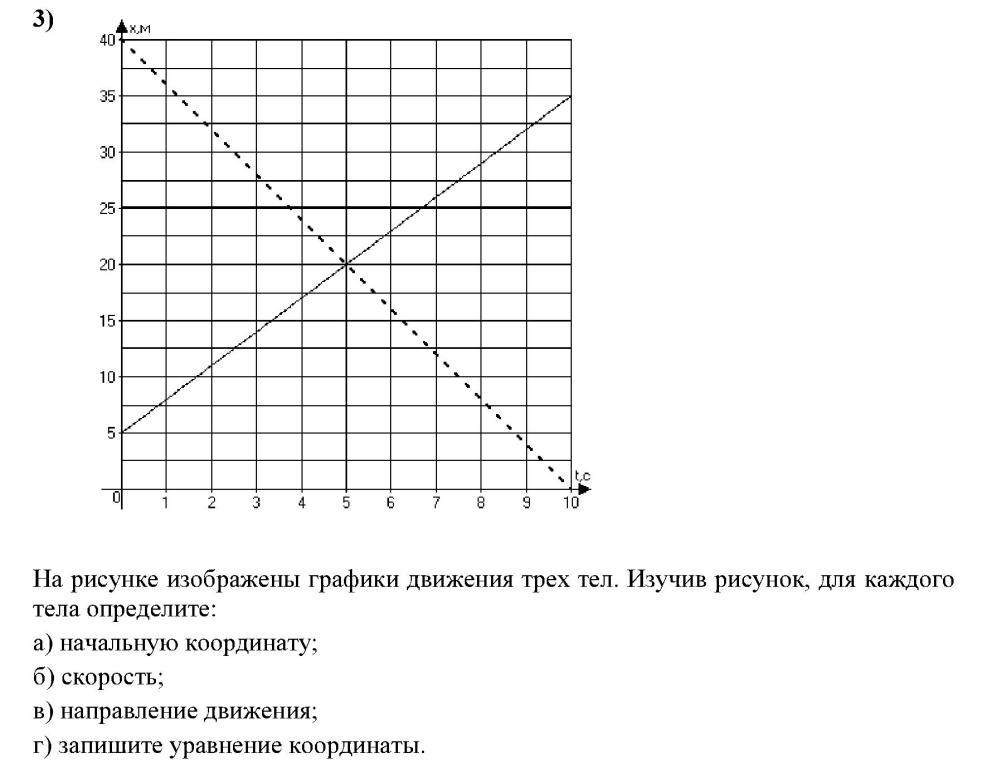
 Вычислите его полное водоизмещение.
Вычислите его полное водоизмещение.
Leave A Comment