На клетчатой бумаге с размером клетки корень из 5 на корень из 5 изображен треугольник: Решение №1723 На клетчатой бумаге с размером клетки корень √5х√5 изображен треугольник АВС.

Геометрия. Задачи на клетчатой бумаге и площади фигур

Чтобы уверенно решать задачи по геометрии — даже такие простые — необходимо выучить основные понятия и формулы.

Это формулы площадей фигур — треугольника (5 формул), параллелограмма, ромба, прямоугольника, произвольного четырехугольника, а также круга. Формулы для длины окружности, длины дуги и площади сектора. Для средней линии треугольника и средней линии трапеции.

Надо знать, что такое центральный и вписанный угол. Знать основные тригонометрические соотношения. В общем, учите основы планиметрии.

Больше полезных формул — в нашем ЕГЭ-Справочнике.

Смотри также материал: Как быстро выучить формулы

В этой статье — основные типы заданий №1 Базового ЕГЭ по математике. Задачи взяты из Банка заданий ФИПИ.

Вычисление длин отрезков, величин углов и площадей фигур по формулам 

1. На клетчатой бумаге с размером клетки  изображена трапеция. Найдите длину средней линии этой трапеции.

Средняя линия трапеции равна полусумме её оснований: 

Ответ: 3.

2. Найдите величину угла ABC. Ответ дайте в градусах.

Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Соединим точки А и С с центром окружности и проведем диаметры через точки А и С. Видим, что величина центрального угла АОС равна Тогда

Ответ: 45.

3. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на

Решение:

Проведем из точки В перпендикуляр к прямой ОА. Из прямоугольного треугольника ОВС по теореме Пифагора:

Осталось умножить найденное значение синуса на

Ответ: 1.

4. Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки  Ответ дайте в квадратных сантиметрах.

 

Самый простой способ — воспользоваться формулой площади ромба, выраженной через его диагонали:

 , где и — диагонали.

Получим: 

Ответ: 12.

5. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки  Ответ дайте в квадратных сантиметрах.

Площадь трапеции равна произведению полусуммы оснований на высоту:

Основания нашей трапеции равны 4 и 8, а высота равна боковой стороне (поскольку трапеция прямоугольная), то есть 3 см. Площадь трапеции

Ответ: 18.

Нахождение площадей многоугольников сложной формы

А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ и на авторских задачах.

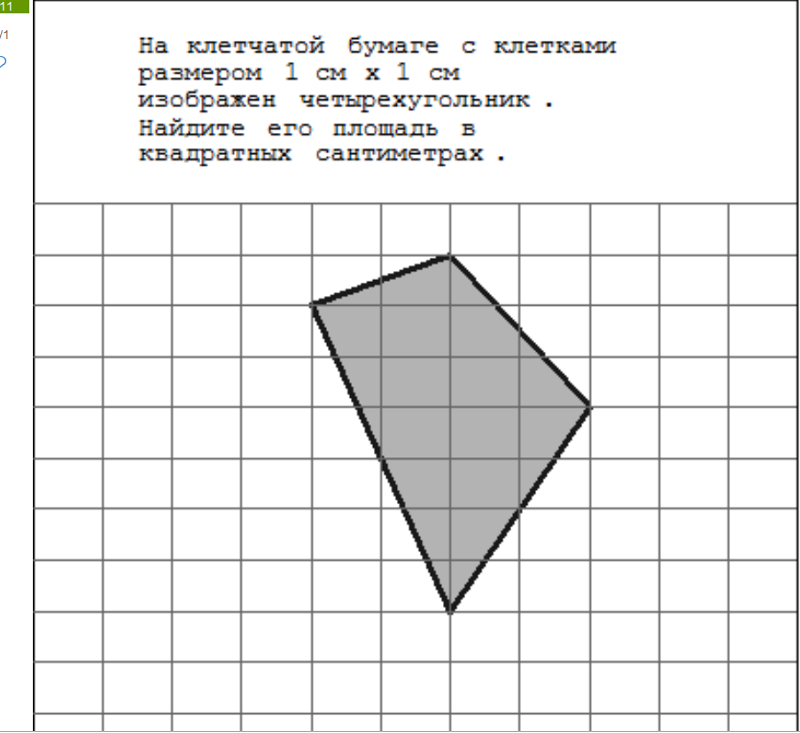
6. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.

Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным .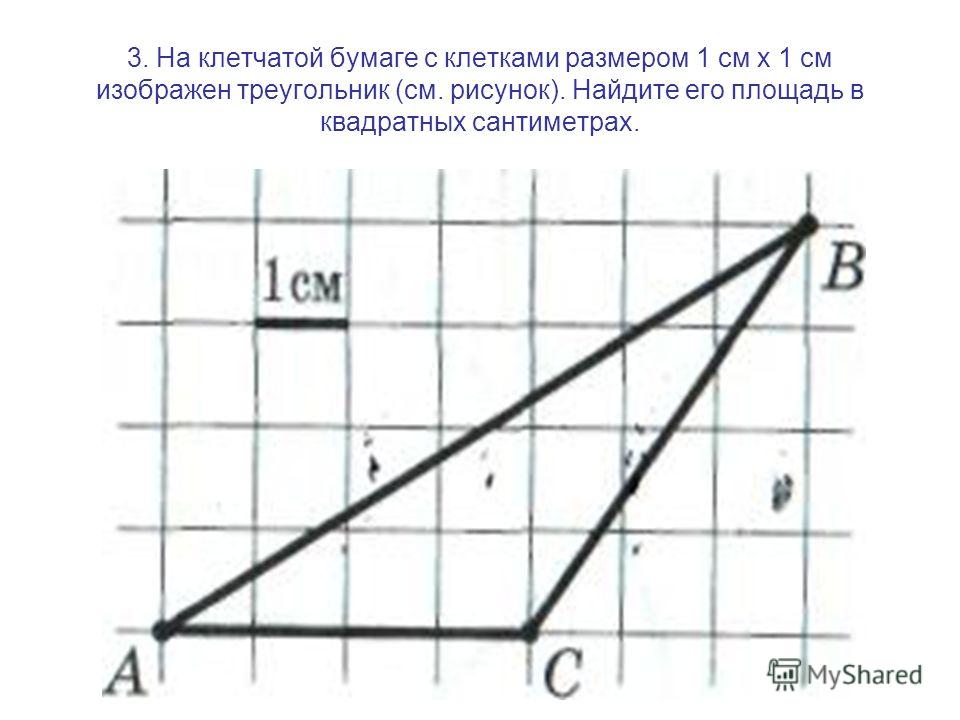

Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .

Ответ: .

7. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .

Ответ: .

Многие репетиторы рекомендуют в таких задачах пользоваться формулой Пика. В ней нет необходимости, однако эта формула довольно интересна.

Согласно формуле Пика, площадь многоугольника равна В+Г/2-1

где В — количество узлов внутри многоугольника, а Г — количество узлов на границе многоугольника.

Узлами здесь названы точки, в которых пересекаются линии нашей клетчатой бумаги.

Посмотрим, как решается задача 7 с помощью формулы Пика:

Синим на рисунке отмечены узлы внутри треугольника.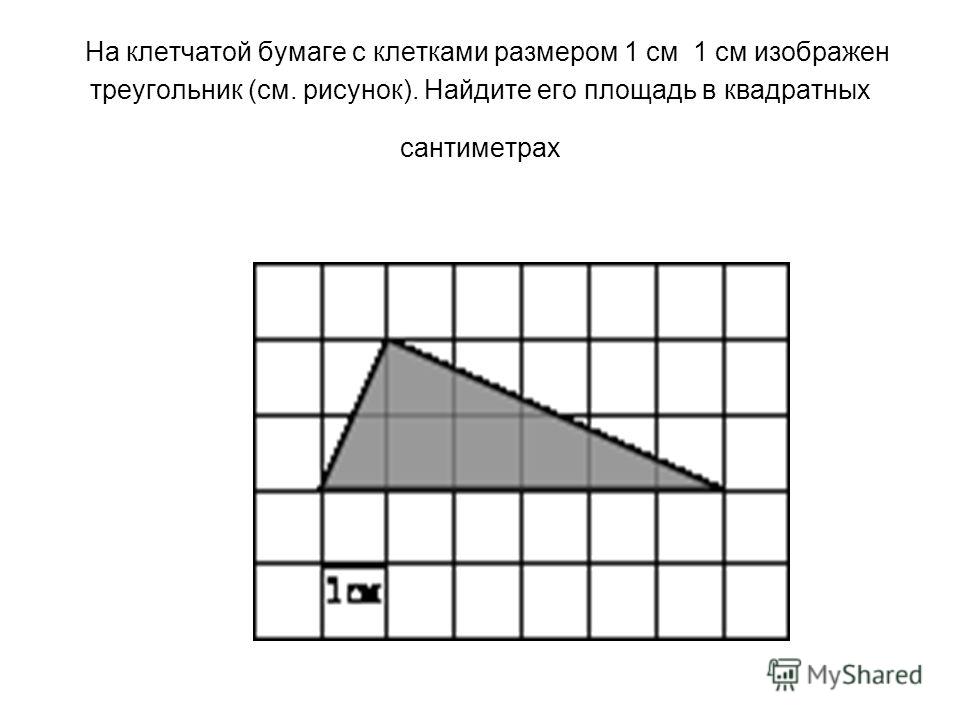 Зеленым — узлы на границе.

Аккуратно посчитав те и другие, получим, что В = 9, Г = 5, и площадь фигуры равна S = 9 + 5/2 — 1 = 10,5.

Выбирайте — какой способ вам больше нравится.

8. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки  

Такой четырехугольник получится, если от квадрата размером отрезать 2 прямоугольника и 4 треугольника. Найдите их на рисунке.

Площадь каждого из больших треугольников равна

Площадь каждого из маленьких треугольников равна

Тогда площадь четырехугольника

9. Авторская задача.  Найдите площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки 

Решение:

На рисунке изображен ромб с вырезанным из него квадратом.

Площадь ромба равна половине произведения его диагоналей.

Площадь вырезанного квадрата равна 4.

Площадь фигуры равна 36 — 4 = 32.

Ответ: 32.

Площадь круга, длина окружности, площадь части круга 

Длина дуги во столько раз меньше длины окружности, во сколько раз ее градусная мера меньше, чем полный круг, то есть 360 градусов.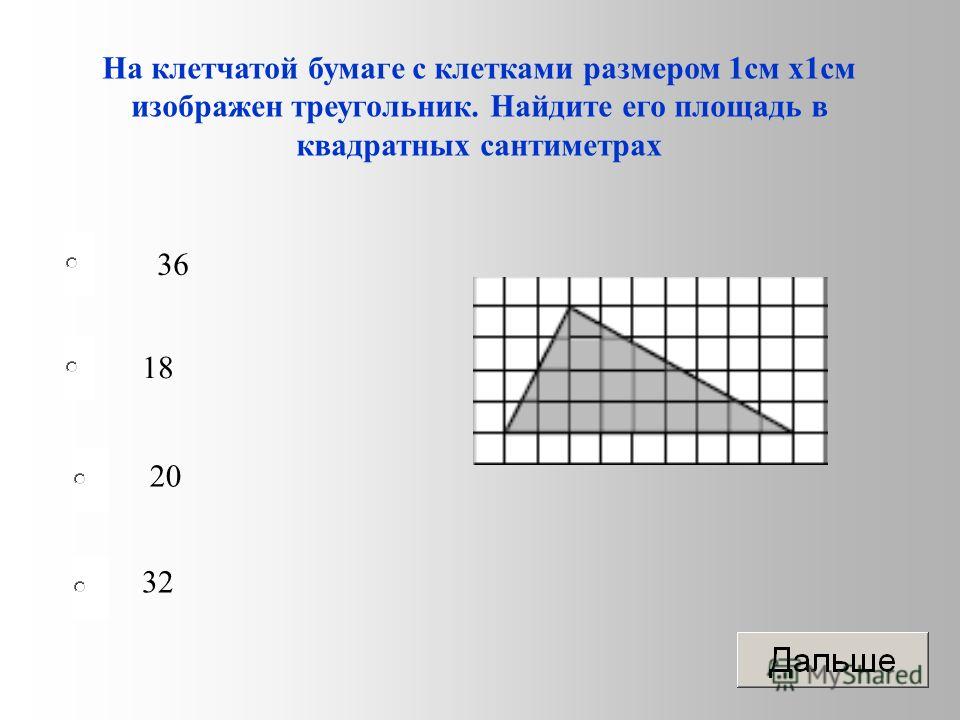

Площадь сектора во столько раз меньше площади всего круга, во сколько раз его градусная мера меньше, чем полный круг, то есть 360 градусов.

10. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .

На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в  раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в  раз меньше, чем площадь всего круга.

Ответ: .

 

11. На клетчатой бумаге нарисован круг площадью 2,8. Найдите площадь закрашенного сектора.

На рисунке изображен сектор, то есть часть круга.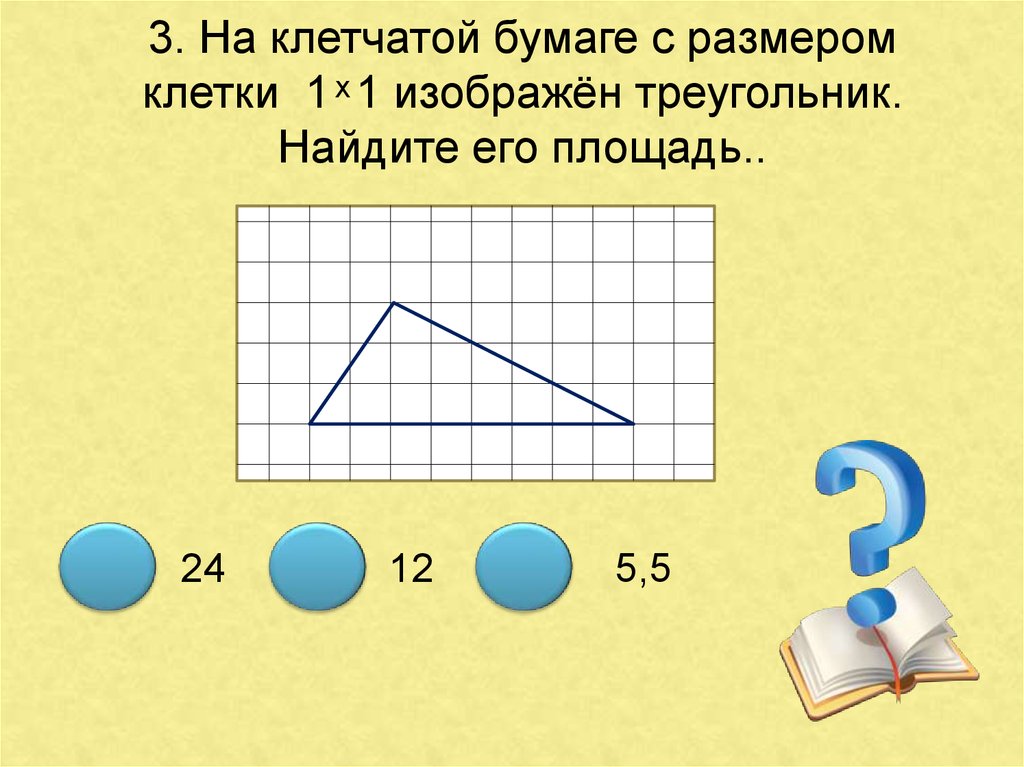

Но какая же это часть? Это четверть круга и еще круга, то есть круга.

Значит, нам надо умножить площадь круга на . Получим:

Ответ: 1,05.

12. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 9. Найдите площадь закрашенной фигуры.

Площадь фигуры равна разности площадей двух кругов, один из которых расположен внутри другого. По условию, площадь внутреннего круга равна 9. Радиус внешнего круга относится к радиусу внутреннего как 4 к 3. Площадь круга равна , то есть пропорциональна квадрату радиуса. Значит, площадь внешнего круга в раза больше площади внутреннего и равна 16. Тогда площадь фигуры равна 16 — 9 = 7.

Ответ: 7.

Задачи на координатной плоскости 

13. Найдите площадь четырехугольника, вершины которого имеют координаты (4;2), (8;4), (6;8), (2;6).

Заметим, что этот четырехугольник — квадрат. Сторона квадрата a является гипотенузой прямоугольного треугольника с катетами, равными 2 и 4. Тогда

Ответ: 20

14. Найдите площадь четырехугольника, вершины которого имеют координаты

На рисунке изображен параллелограмм (четырехугольник, имеющий две пары параллельных сторон). Площадь параллелограмма равна произведению основания на высоту. Основание равно 2, высота 8, площадь равна 16.

Ответ: 16.

 

Благодарим за то, что пользуйтесь нашими статьями. Информация на странице «Геометрия. Применение формул. Задача 1 Базового ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена: 08.04.2023

Вариант 18 » Незнайка — варианты ЕГЭ, ОГЭ, ВПР 2023

Математика Профильный уровень

Часть 1

Ответом на задания 1—12 должно быть целое число или десятичная дробь.

1

1

Система навигации самолёта информирует пассажира о том, что полёт проходит на высоте 35 000 футов. Выразите высоту полёта в метрах. Считайте, что 1 фут равен 30,5 см.

2

2

При работе фонарика батарейка постепенно разряжается и напряжение в электрической цепи фонарика падает. На графике показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по рисунку, за сколько часов напряжение упадёт с 1,4 вольта до 1 вольта.

3

3

На клетчатой бумаге с размером клетки 1х1 изображён треугольник ABC . Найдите длину его высоты, опущенной на сторону AB .

4

4

Вероятность того, что новый сканер прослужит больше года, равна 0,94. Вероятность того, что он прослужит больше двух лет, равна 0,87. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.

5

5

Найдите корень уравнения log₈ (5x + 47) = 3.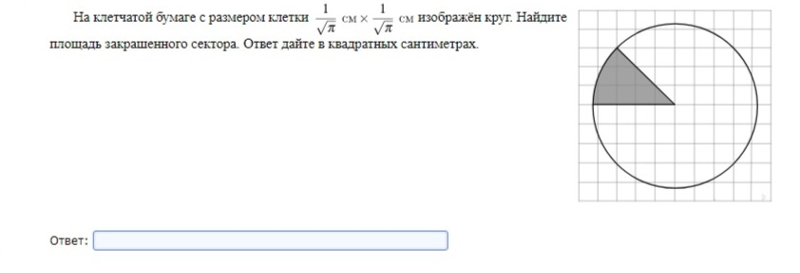 \sqrt2\right]\;[/math]

Ответ: а) 2,4 б) 2

14

В правильной четырёхугольной пирамиде SABCD с вершиной S расстояние между прямыми BD и AS равно 2.

а) Постройте сечение пирамиды плоскостью, проходящей через точки А и S перпендикулярно прямой BD.

б) Найдите объём данной пирамиды, если её боковое ребро равно 5.

Показать ответ

Решение:

а) Диагонали квадрата перпендикулярны, поэтому [math]\mathrm{AC}\perp\mathrm{BD}[/math] (см. рисунок) С другой стороны, так как пирамида правильная вершина [math]\mathrm S[/math] проецируется в центр основания, поэтому основание высоты и точка пересечения диагоналей квадрата [math]\mathrm{ABCD}[/math] совпадают. Обозначим эту точку [math]\mathrm O[/math], плоскость [math](\mathrm{SAO})\perp\mathrm{BD}[/math], так как содержит 2 пересекающиеся прямые, перпендикулярные BD. Сечение плоскостью [math]\mathrm{AOS}[/math] образует [math]\bigtriangleup SAC[/math], так как точки [math]A,O,C[/math] лежат на одной прямой. 2x-5\log_3x+2)<0[/math]

[math](x-1)(\log_3x-2)(2\log_3x-1)<0[/math]

На ОДЗ выражение [math]\log_3x-2=\log_3x-\log_39[/math] совпадает по знаку с выражением [math]x-9[/math], а выражение [math]2\log_3x-1=2(\log_3x-\log_3\sqrt3)[/math] — с выражением [math]x-\sqrt3[/math]. Получим, что исходное неравенство на ОДЗ равносильно неравенству [math](x-1)(x-9)(x-\sqrt3)<0[/math]. Решив его методом интервалов получим [math]x\in(-\infty;1)\cup(\sqrt3;9)[/math]. Учитывая ОДЗ [math]x\in(0;1)\cup(\sqrt3;9)[/math]

Ответ: [math]\left(0;\;1\right)\cup\left(\sqrt3;\;9\right)[/math]

16

Внутри прямого угла АОВ проведён луч ОС. В угол ВОС вписана окружность, касающаяся лучей ОВ и ОС в точках B и C соответственно, в угол АОС вписана окружность, касающаяся лучей ОА и ОС в точках А и С соответственно. Радиус одной из этих окружностей в 4 раза больше радиуса другой.

а) Докажите, что ОА = ОВ.

б) Найдите косинус меньшего из углов АОС и ВОС.

Показать ответ

Решение:

а) Не нарушая общности, можем считать, что большая окружность вписана в угол [math]AOC[/math]. 2\angle COQ-1=2\times\frac{33+5\sqrt{41}}{35+5\sqrt{41}}-1=\frac{3+\sqrt{41}}{10}[/math]

Ответ: [math]\frac{3+\sqrt{41}}{10}[/math].

17

Молокозавод ежедневно отправляет в магазины 12000 литровых пакетов молока (равное количество в каждый магазин). Подсчитано, что в понедельник выгоднее в четыре магазина молоко не отправлять, а предназначенное для них молоко распределять (в равной мере) среди остальных магазинов. При этом каждый магазин увеличивает количество разливного молока на 800 пакетов (это их предельная продажа). Сколько пакетов молока составляет предельная продажа?

Показать ответ

Решение:

Обозначим через [math]x[/math] количество магазинов, в которые молокозавод отправляет молоко. Тогда [math]\frac{12000}x[/math] пакетов молока реализуют магазины во все дни недели, кроме понедельника, а [math]\frac{12000}x+800[/math] в понедельник. По условию задачи в понедельник в четыре магазина молоко не отправляется , значит [math]\frac{12000}{x-4}[/math] пакетов отправляется в другие магазины по понедельникам. 2+10x+25=0[/math], то есть [math]x=-5\in\left[-6;2\right][/math]

Ответ: {-27/4}⋃(-13/2; 11/2]

19

Ежедневно в зоопарке каждой лисе полагается 2 кг мяса, тигру — 14 кг, льву — 21 кг. Известно, что у каждого льва бывает ежедневно 230 посетителей, у каждой лисы — 20, у каждого тигра — 160 и все эти звери есть в зоопарке.

а) Какое число посещений будет у этих животных, если ежедневно в зоопарке распределяют 70 кг мяса?

б) Может ли ежедневно распределяться 420 кг мяса, если известно, что посещений за 1 день было меньше 4000?

в) Каким может быть наибольшее ежедневное число посещений у этих зверей, если зоопарк ежедневно распределяет между ними 111 кг мяса?

Показать ответ

Решение:

Обозначим число лис в зоопарке буквой c, львов — l, тигров — t. Тогда им ежедневно дают [math]2c+14t+21l[/math] кг мяса, а посетителей бывает [math]20c+160t+230l=P[/math]

а) По условию [math]2c+14t+21l=70[/math], где [math]\{c,t,l\}\subset\mathbb{Z}[/math].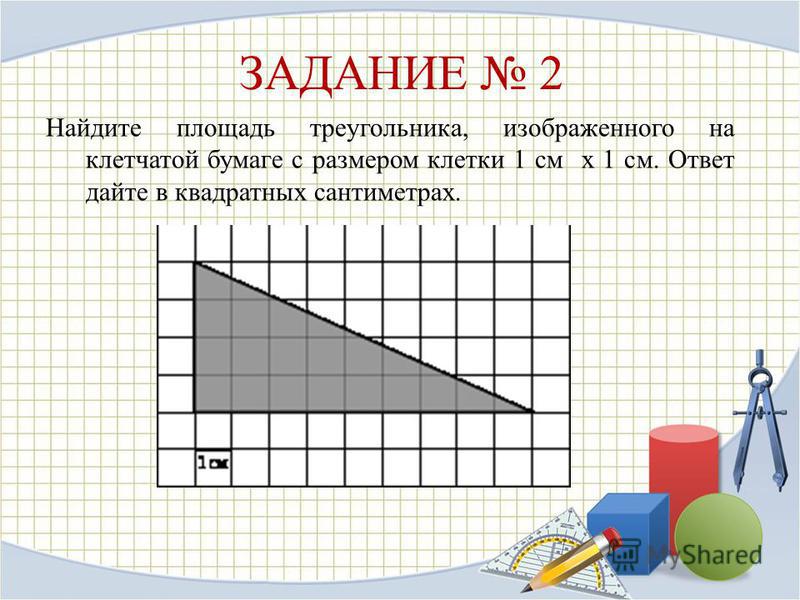 70 делится на 7 и [math]14t+21l[/math] делится на 7, значит 2с, а следовательно, и с делится на 7. Если [math]с=7[/math], то [math]14+7(2t+3l)=70[/math], [math]2t+3l=8[/math]. При [math]t\in\mathbb{N}\;l<\frac83[/math] и делится на 2, значит [math]l=2,t=1[/math] и число посетителей равно [math]20\times7+160\times1+230\times2=760[/math]

б) По условию, [math]2c+14t+21l=420[/math]. Может ли [math]20c+160]t+230l[/math] быть меньше 4000?

[math]20c+160t+230l=10(2c+16t+23l)>10(2c+14t+21l)=10\times420=4200[/math]. Получилось, что [math]20c+160t+230l>4200[/math], значит, при таких условиях не может ежедневно распределяться 420кг мяса

в) Нам дано, что [math]2c+14t+21l=111[/math]. Так как количество животных натуральные числа, [math]l[/math] нечетно и [math]21l\leq111-(2+14),\;[/math][math]21l\leq95,\;[/math][math]l\leq4,\;[/math] то есть [math]l=3[/math] или [math]l=1[/math]

1) [math]l=1[/math], тогда [math]2с+14t+21=111;[/math][math]2с+14t=90;[/math][math]с+7t=45;[/math][math]с=45-7t;[/math][math]t\leqslant6\frac27[/math]. Число посетителей:

[math]P=20c+160t+230l=20(45-7t)+160t+230=1130+20t[/math] наибольшее при наибольшем [math]t[/math], т.е.при [math]t=6[/math], [math]P=1130+20\times6=1250[/math].

2) [math]l=3[/math], тогда [math]2с+14t+21\times3=111;[/math][math]2с+14t=48;[/math][math]c=24-7t\geqslant1;[/math][math]t\leqslant3\frac27[/math]

[math]P=20c+160t+230\times3=20t+1170[/math] наибольшее при наибольшем [math]t[/math], т.е. при [math]t=3[/math]. [math]P=20\times3+1170=1230[/math]

Наибольшее число посетителей 1250.

Ответ: а) 760 б) не может в) 1250

6.2 Клеточный цикл – Концепции биологии – 1-е канадское издание

Перейти к содержанию

Глава 6: Введение в репродукцию на клеточном уровне

Цели обучения

К концу этого раздела вы сможете:

• Описывать три стадии интерфазы
• Обсудите поведение хромосом во время митоза и то, как содержимое цитоплазмы делится во время цитокинеза
• Определить состояние покоя G ₀ фаза
• Объясните, как возникают три контрольные точки внутреннего контроля в конце G ₁ , в переходе G ₂ –M и во время метафазы
.

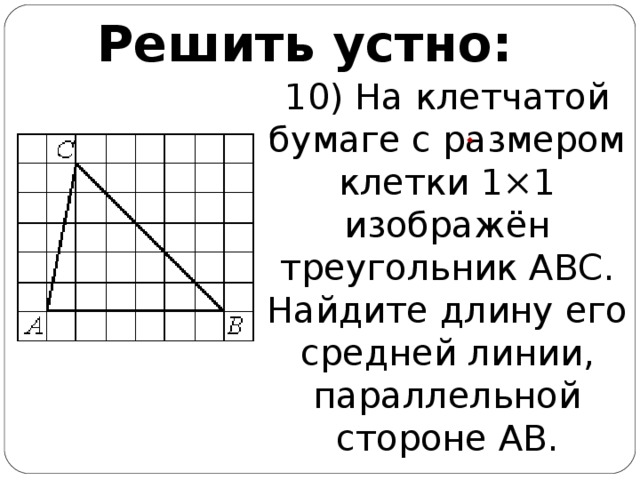
Клеточный цикл представляет собой упорядоченную серию событий, включающих рост и деление клеток, в результате которых образуются две новые дочерние клетки. Клетки на пути к клеточному делению проходят ряд точно рассчитанных по времени и тщательно регулируемых стадий роста, репликации ДНК и деления, в результате которых образуются две генетически идентичные клетки. Клеточный цикл состоит из двух основных фаз: интерфазы и митотической фазы (рис. 6.3). Во время интерфазы клетка растет, и ДНК реплицируется. Во время митотической фазы реплицированная ДНК и содержимое цитоплазмы разделяются, и клетка делится.

Посмотрите это видео о клеточном цикле: https://www.youtube.com/watch?v=Wy3N5NCZBHQ

Рис. 6.3. Клетка проходит через ряд фаз упорядоченным образом. Во время интерфазы G1 включает рост клеток и синтез белка, S-фаза включает репликацию ДНК и репликацию центросомы, а G2 включает дальнейший рост и синтез белка. Митотическая фаза следует за интерфазой. Митоз — это деление ядра, во время которого удвоенные хромосомы разделяются и распределяются в дочерние ядра.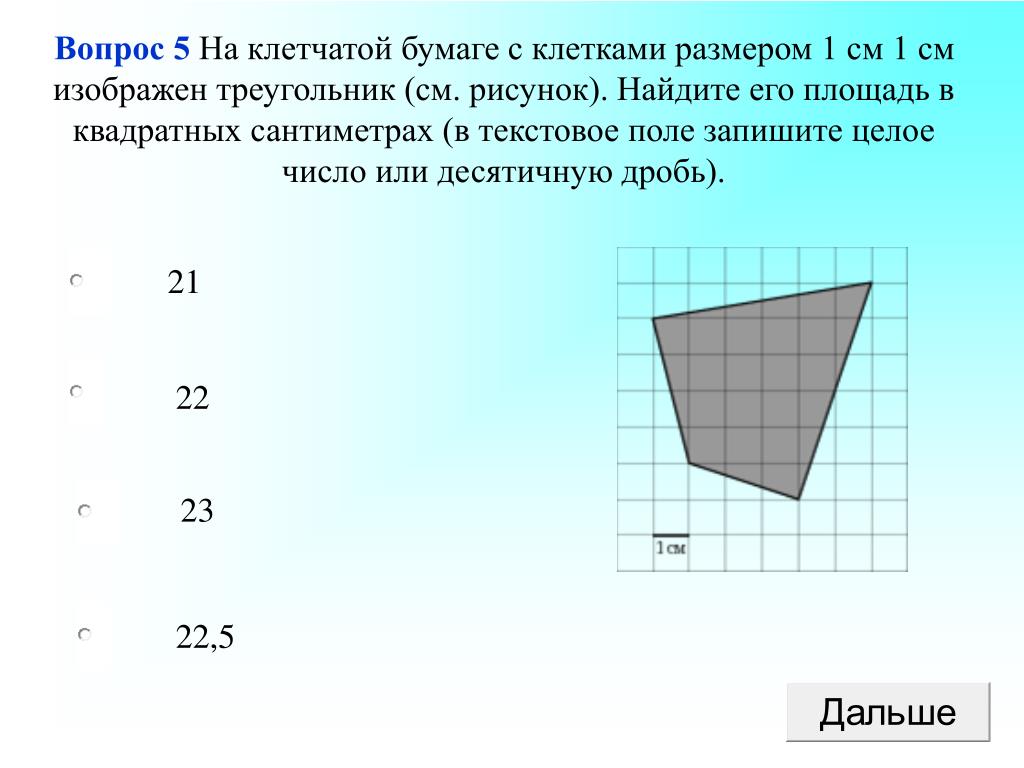 Обычно клетка делится после митоза в процессе, называемом цитокинезом, при котором цитоплазма делится и образуются две дочерние клетки.

Во время интерфазы в клетке происходят нормальные процессы, а также подготовка к клеточному делению. Для перехода клетки из интерфазы в митотическую фазу необходимо выполнение многих внутренних и внешних условий. Три стадии интерфазы называются G ₁ , S и G ₂ .

G

₁ Фаза

Первая стадия интерфазы называется фазой G ₁ , или первым промежутком, потому что видны небольшие изменения. Однако на стадии G ₁ клетка достаточно активна на биохимическом уровне. Клетка накапливает строительные блоки хромосомной ДНК и связанных с ней белков, а также накапливает достаточно запасов энергии для выполнения задачи репликации каждой хромосомы в ядре.

S Фаза

На протяжении всей интерфазы ядерная ДНК остается в полуконденсированной конфигурации хроматина. В фазе S (фаза синтеза) репликация ДНК приводит к образованию двух идентичных копий каждой хромосомы — сестринских хроматид, — которые прочно прикреплены в районе центромеры.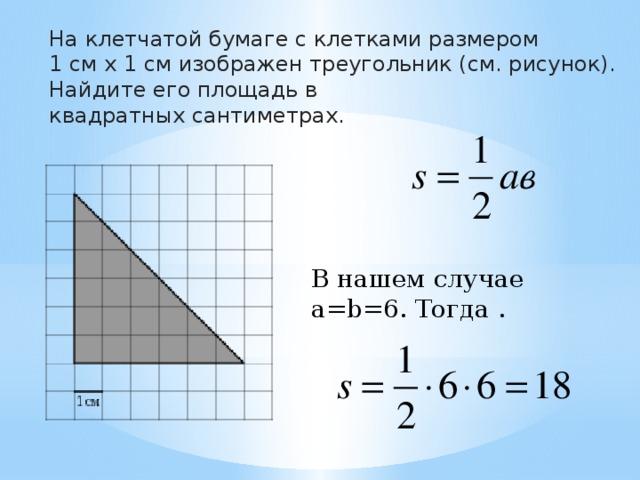 На этой стадии каждая хромосома состоит из двух сестринских хроматид и представляет собой удвоенную хромосому. Центросома удваивается во время S-фазы. Две центросомы дадут начало митотическому веретену, аппарату, который управляет движением хромосом во время митоза. Центросома состоит из пары палочковидных центриолей, расположенных под прямым углом друг к другу. Центриоли помогают организовать клеточное деление. Центриоли отсутствуют в центросомах многих эукариотических видов, таких как растения и большинство грибов.

G

₂ Фаза

В фазе G ₂ , или втором промежутке, клетка пополняет запасы энергии и синтезирует белки, необходимые для манипулирования хромосомами. Некоторые клеточные органеллы дублируются, а цитоскелет демонтируется, чтобы обеспечить ресурсы для митотического веретена. Во время G ₂ может наблюдаться дополнительный рост клеток. Окончательные приготовления к митотической фазе должны быть завершены до того, как клетка сможет вступить в первую стадию митоза.

Для образования двух дочерних клеток необходимо разделить содержимое ядра и цитоплазмы. Митотическая фаза представляет собой многоэтапный процесс, в ходе которого дуплицированные хромосомы выравниваются, разделяются и перемещаются к противоположным полюсам клетки, а затем клетка делится на две новые идентичные дочерние клетки . Первая часть митотической фазы, митоз, состоит из пяти стадий, на которых завершается деление ядра. Вторая часть митотической фазы, называемая цитокинезом, представляет собой физическое разделение компонентов цитоплазмы на две дочерние клетки.

Митоз

Митоз делится на серию фаз — профазу, прометафазу, метафазу, анафазу и телофазу, — которые приводят к делению клеточного ядра (рис. 6.4).

Рис. 6.4. Митоз клеток животных делится на пять стадий — профаза, прометафаза, метафаза, анафаза и телофаза, которые визуализируются здесь с помощью световой микроскопии с флуоресценцией. Митоз обычно сопровождается цитокинезом, показанным здесь с помощью просвечивающего электронного микроскопа.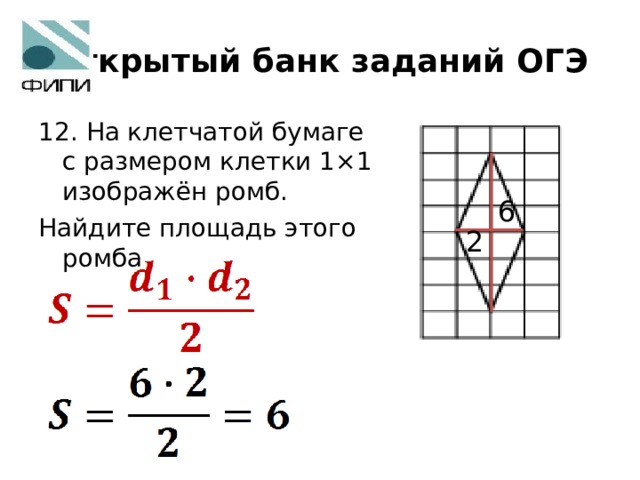 (кредит «диаграммы»: модификация работы Марианы Руис Вильярреал; кредит «микрофотографии митоза»: модификация работы Роя ван Хисбина; кредит «микрофотография цитокинеза»: модификация работы Центра Уодсворта, Департамент здравоохранения штата Нью-Йорк; пожертвовано Фонд Викимедиа; данные масштабной линейки от Мэтта Рассела)

Что из следующего является правильным порядком событий в митозе?

1. Сестринские хроматиды выстраиваются в ряд на метафазной пластинке. Кинетохора прикрепляется к митотическому веретену. Ядро восстанавливается, и клетка делится. Сестринские хроматиды расходятся.
2. Кинетохора прикрепляется к митотическому веретену. Сестринские хроматиды расходятся. Сестринские хроматиды выстраиваются на метафазной пластинке. Ядро восстанавливается, и клетка делится.
3. Кинетохора прикрепляется к метафазной пластинке. Сестринские хроматиды выстраиваются на метафазной пластинке. Кинетохора разрушается, и сестринские хроматиды расходятся. Ядро восстанавливается, и клетка делится.
4. Кинетохора прикрепляется к митотическому веретену. Сестринские хроматиды выстраиваются на метафазной пластинке. Кинетохора распадается, и сестринские хроматиды расходятся. Ядро восстанавливается, и клетка делится.

Во время профазы, «первой фазы», ​​должны произойти несколько событий, чтобы обеспечить доступ к хромосомам в ядре. Ядерная оболочка начинает распадаться на мелкие везикулы, а аппарат Гольджи и эндоплазматический ретикулум фрагментируются и расходятся к периферии клетки. Ядрышко исчезает. Центросомы начинают двигаться к противоположным полюсам клетки. Микротрубочки, образующие основу митотического веретена, простираются между центросомами, отталкивая их дальше друг от друга по мере удлинения волокон микротрубочек. Сестринские хроматиды начинают более плотно скручиваться и становятся видимыми под световым микроскопом.

Во время прометафазы многие процессы, начавшиеся в профазе, продолжают развиваться и завершаются образованием связи между хромосомами и цитоскелетом.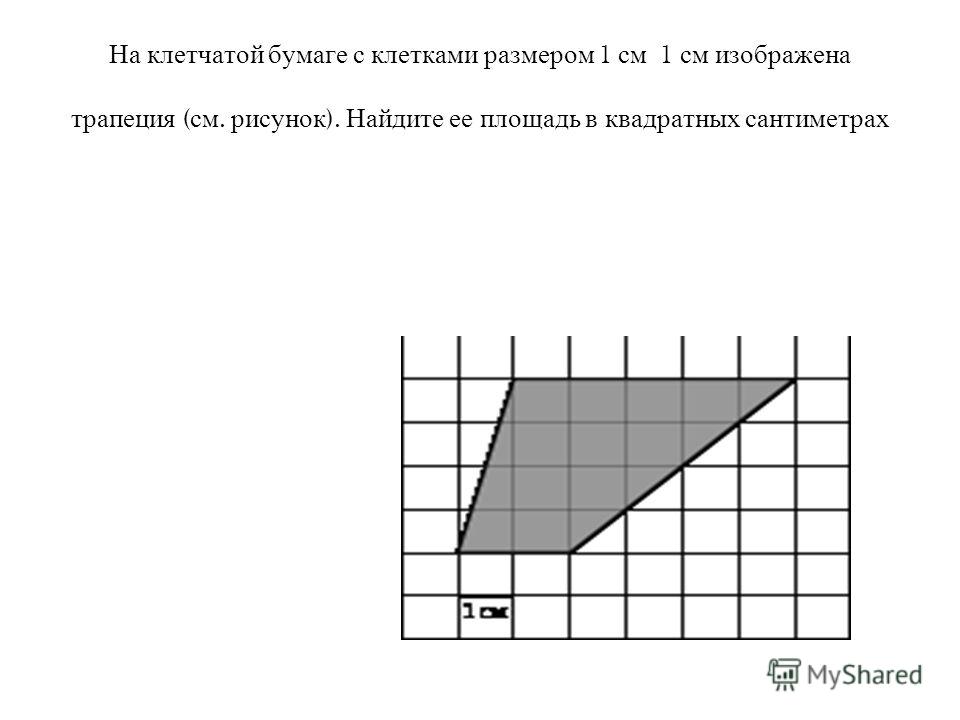 Остатки ядерной оболочки исчезают. Митотическое веретено продолжает развиваться по мере того, как все больше микротрубочек собирается и растягивается по длине бывшей ядерной области. Хромосомы становятся более конденсированными и визуально дискретными. Каждая сестринская хроматида прикрепляется к микротрубочкам веретена на центромере через белковый комплекс, называемый кинетохорой.

Во время метафазы все хромосомы выстраиваются в плоскости, называемой метафазной пластинкой, или экваториальной плоскости, на полпути между двумя полюсами клетки. Сестринские хроматиды по-прежнему тесно связаны друг с другом. В это время хромосомы максимально конденсированы.

Во время анафазы сестринские хроматиды в экваториальной плоскости расходятся в центромере. Каждая хроматида, называемая сейчас хромосомой, быстро притягивается к центросоме, к которой была прикреплена ее микротрубочка. Клетка становится заметно удлиненной по мере того, как микротрубочки, не являющиеся кинетохорами, скользят друг относительно друга на метафазной пластинке, где они перекрываются.

Во время телофазы все события, которые настраивают дуплицированные хромосомы для митоза в течение первых трех фаз, обращаются вспять. Хромосомы достигают противоположных полюсов и начинают деконденсироваться (распутываться). Митотические веретена расщепляются на мономеры, которые будут использоваться для сборки компонентов цитоскелета каждой дочерней клетки. Ядерные оболочки формируются вокруг хромосом.

Концепция в действии

На этой странице фильмов показаны различные аспекты митоза. Посмотрите фильм «ДИК-микроскопия деления клеток в клетке легкого тритона» и определите фазы митоза.

Цитокинез

Цитокинез является второй частью митотической фазы, во время которой клеточное деление завершается физическим разделением цитоплазматических компонентов на две дочерние клетки. Хотя стадии митоза сходны у большинства эукариот, процесс цитокинеза у эукариот, имеющих клеточные стенки, таких как растительные клетки, сильно отличается.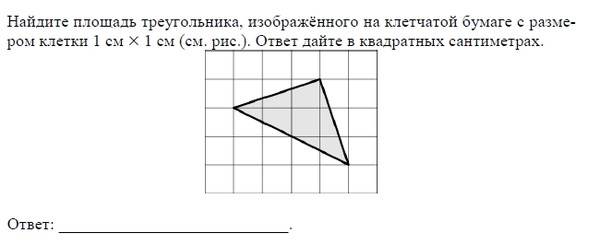

В клетках, таких как клетки животных, у которых отсутствуют клеточные стенки, цитокинез начинается после наступления анафазы. Сократительное кольцо, состоящее из актиновых филаментов, формируется непосредственно внутри плазматической мембраны на бывшей метафазной пластинке. Актиновые филаменты тянут экватор клетки внутрь, образуя щель. Эта трещина, или «трещина», называется бороздой расщепления. Борозда углубляется по мере сокращения актинового кольца, и в конце концов мембрана и клетка расщепляются надвое (рис. 6.5).

В растительных клетках борозда дробления невозможна из-за жестких клеточных стенок, окружающих плазматическую мембрану. Между дочерними клетками должна образоваться новая клеточная стенка. Во время интерфазы в аппарате Гольджи накапливаются ферменты, структурные белки и молекулы глюкозы, после чего они распадаются на везикулы и распределяются по делящейся клетке. Во время телофазы эти везикулы Гольджи перемещаются по микротрубочкам, собираясь на метафазной пластинке. Там везикулы сливаются от центра к клеточным стенкам; эта структура называется клеточной пластинкой. По мере слияния большего количества везикул клеточная пластинка увеличивается до тех пор, пока не сливается с клеточной стенкой на периферии клетки. Ферменты используют глюкозу, накопившуюся между слоями мембраны, для построения новой клеточной стенки из целлюлозы. Мембраны Гольджи становятся плазматической мембраной по обе стороны от новой клеточной стенки (рис. 6.5).

Рис. 6.5. В части (а) борозда деления образуется на бывшей метафазной пластинке в животной клетке. Плазматическая мембрана втягивается кольцом актиновых волокон, сокращающихся непосредственно внутри мембраны. Борозда деления углубляется до тех пор, пока клетки не будут пережаты надвое. В части (b) везикулы Гольджи сливаются на бывшей метафазной пластинке в растительной клетке. Везикулы сливаются и образуют клеточную пластинку. Клеточная пластинка растет от центра к клеточным стенкам. Новые клеточные стенки формируются из содержимого пузырьков.

Не все клетки придерживаются классического паттерна клеточного цикла, при котором вновь образованная дочерняя клетка сразу же входит в интерфазу, за которой следует митотическая фаза. Клетки в фазе G ₀ не готовятся активно к делению . Клетка находится в покоящейся (неактивной) стадии, выйдя из клеточного цикла. Некоторые клетки временно входят в G ₀ , пока внешний сигнал не вызовет начало G ₁ . Другие клетки, которые никогда не делятся или редко делятся, такие как зрелые клетки сердечной мышцы и нервные клетки, остаются в G9.0020 0 постоянно (рис. 6.6).

Рис. 6.6. Клетки, которые активно не готовятся к делению, вступают в альтернативную фазу, называемую G0. В некоторых случаях это временное состояние до тех пор, пока оно не будет активировано для входа в G1. В других случаях ячейка навсегда останется в G0.

Контроль клеточного цикла

Продолжительность клеточного цикла сильно варьирует даже внутри клеток отдельного организма. У людей частота оборота клеток колеблется от нескольких часов в раннем эмбриональном развитии до в среднем от двух до пяти дней для эпителиальных клеток или до всей жизни человека, проведенной в G9.0020 0 специализированными клетками, такими как нейроны коры или клетки сердечной мышцы. Также различается время, которое клетка проводит в каждой фазе клеточного цикла. При выращивании быстроделящихся клеток млекопитающих в культуре (вне организма при оптимальных условиях выращивания) продолжительность цикла составляет приблизительно 24 часа. В быстро делящихся клетках человека с 24-часовым клеточным циклом фаза G ₁ длится приблизительно 11 часов. Время событий в клеточном цикле контролируется механизмами, которые являются как внутренними, так и внешними по отношению к клетке.

Очень важно, чтобы дочерние клетки были точными копиями родительской клетки. Ошибки в удвоении или распределении хромосом приводят к мутациям, которые могут передаваться каждой новой клетке, полученной из аномальной клетки.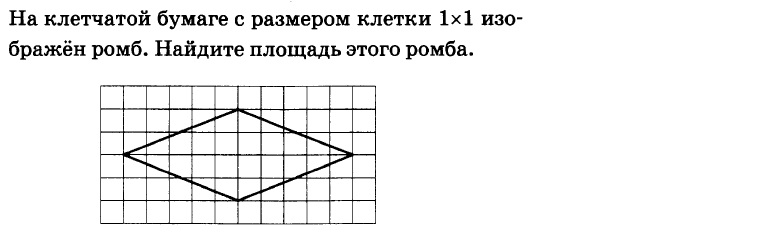 Чтобы предотвратить дальнейшее деление скомпрометированной клетки, существуют механизмы внутреннего контроля, которые работают в трех основных контрольных точках клеточного цикла, в которых клеточный цикл может быть остановлен до тех пор, пока условия не станут благоприятными. Эти контрольные точки происходят ближе к концу G ₁ , на переходе G ₂ –М и ​​во время метафазы (рис. 6.7).

Рис. 6.7. Клеточный цикл контролируется тремя контрольными точками. Целостность ДНК оценивается на контрольной точке G1. Правильная дупликация хромосом оценивается в контрольной точке G2. Прикрепление каждой кинетохоры к волокну веретена оценивают в контрольной точке М.

G

₁ КПП

Контрольная точка G ₁ определяет, все ли условия благоприятны для продолжения деления клеток. G ₁ Контрольная точка, также называемая точкой рестрикции, представляет собой точку, в которой клетка необратимо вступает в процесс клеточного деления. В дополнение к адекватным запасам и размеру клеток, есть проверка на повреждение геномной ДНК в контрольной точке G ₁ . Ячейка, которая не соответствует всем требованиям, не будет выпущена в фазу S.

G

₂ КПП

Контрольная точка G ₂ блокирует вход в митотическую фазу, если не выполняются определенные условия. Как в Г ₁ Контрольная точка, размер клеток и запасы белка оцениваются. Однако самая важная роль контрольной точки G ₂ заключается в том, чтобы гарантировать, что все хромосомы были реплицированы и что реплицированная ДНК не повреждена.

Контрольно-пропускной пункт М

Контрольная точка М возникает ближе к концу метафазной стадии митоза. Контрольная точка М также известна как контрольная точка веретена, потому что она определяет, правильно ли все сестринские хроматиды прикреплены к микротрубочкам веретена. Поскольку разделение сестринских хроматид во время анафазы является необратимым этапом, цикл не будет продолжаться до тех пор, пока кинетохоры каждой пары сестринских хроматид не будут прочно прикреплены к волокнам веретена деления, отходящим от противоположных полюсов клетки.

Концепция в действии

Посмотрите, что происходит в контрольных точках G ₁ , G ₂ и M, посетив эту анимацию клеточного цикла.

Клеточный цикл представляет собой упорядоченную последовательность событий. Клетки на пути к клеточному делению проходят серию точно рассчитанных по времени и тщательно регулируемых стадий. У эукариот клеточный цикл состоит из длительного подготовительного периода, называемого интерфазой. Интерфаза делится на G ₁ , S и G ₂ фазы. Митоз состоит из пяти стадий: профазы, прометафазы, метафазы, анафазы и телофазы. Митоз обычно сопровождается цитокинезом, в ходе которого цитоплазматические компоненты дочерних клеток разделяются либо актиновым кольцом (животные клетки), либо образованием клеточной пластинки (растительные клетки).

Каждый этап клеточного цикла контролируется внутренними средствами контроля, называемыми контрольными точками. В клеточном цикле есть три основных контрольных точки: одна в конце G ₁ , вторая в G ₂ –М переход, а третья во время метафазы.

Глоссарий

анафаза : стадия митоза, во время которой сестринские хроматиды отделяются друг от друга

клеточный цикл следующий

контрольных точек клеточного цикла: механизма, которые контролируют готовность эукариотической клетки к прохождению через различные стадии клеточного цикла

клеточная пластинка: структура, образующаяся во время цитокинеза растительной клетки путем слияния пузырьков Гольджи на метафазной пластинке; в конечном итоге приведет к образованию клеточной стенки для разделения двух дочерних клеток

центриоль: парная палочковидная структура, построенная из микротрубочек в центре каждой животной клетки центросома

борозда деления: перетяжка, образованная актиновое кольцо во время цитокинеза животных клеток, что приводит к цитоплазматическому делению

цитокинез : деление цитоплазмы после митоза с образованием двух дочерних клеток

G ₀ фаза : фаза клеточного цикла, отличная от фазы G ₁ интерфазы; клетка в G ₀ не готовится к делению

G ₁ фаза : (также первый разрыв) фаза клеточного цикла; первая фаза интерфазы сосредоточена на росте клеток во время митоза

G ₂ фаза: (также второй пробел) фаза клеточного цикла; третья фаза интерфазы, когда клетка проходит окончательную подготовку к митозу

интерфаза: период клеточного цикла, предшествующий митозу; включает фазы G ₁ , S и G ₂ ; промежуток между двумя последовательными клеточными делениями

кинетохора : белковая структура в центромере каждой сестринской хроматиды, которая привлекает и связывает микротрубочки веретена во время прометафазы

метафазная пластинка: экваториальная плоскость на полпути между двумя полюсами клетки, где хромосомы выстраиваются во время метафазы

метафаза период клеточного цикла, при котором дуплицированные хромосомы разделяются на идентичные ядра; включает профазу, прометафазу, метафазу, анафазу и телофазу

митотическая фаза: период клеточного цикла, когда удвоенные хромосомы распределяются по двум ядрам и содержимое цитоплазмы делится; включает митоз и цитокинез

митотическое веретено: аппарат микротрубочек, который управляет движением хромосом во время митоза 0054 : сцена митоза, во время которого хромосомы конденсируются и начинает формироваться митотическое веретено

покоящаяся: описывает клетку, которая выполняет нормальные клеточные функции и не инициировала подготовку к клеточному делению

S-фаза: вторая, или фаза синтеза, интерфазы, во время которой происходит репликация ДНК

телофаза: стадия митоза, во время которой хромосомы достигают противоположных полюсов, деконденсируются и окружаются новыми ядерными оболочками

License

Concepts of Biology — 1st Canadian Edition Чарльза Молнара и Джейн Гейр распространяется по лицензии Creative Commons Attribution 4. 0 International License, если не указано иное.

Поделиться этой книгой

Поделиться в Твиттере

Глава 5: Геодезия и GPS

Бринкер, Р. К. и Вольф, П. Р. (1984). Элементарная геодезия (7-е изд.). Нью-Йорк: Харпер и Роу.

Дана, П. Х. (1998). Обзор системы глобального позиционирования. Поделка географа проект . Получено 2 августа 1999 г. с сайта http://www.colorado.edu/geography/gcraft/notes/gps/gps_f.html

Doyle, D. R. (1994). Развитие Национальной пространственной системы отсчета. Получено 10 февраля 2008 г. с http://www.ngs.noaa.gov/PUBS_LIB/develop_NSRS.html 9.0003

Федеральный комитет геодезического надзора (1988). Стандарты геометрической геодезической точности и спецификации для использования методов относительного позиционирования GPS. Получено 10 февраля 2008 г. с http://www.ngs.noaa.gov/FGCS/tech_pub/GeomGeod.pdf Получено 14 сентября 2013 г. с http://docs.lib.noaa.gov/noaa_documents/NOS/NGS. /Geom_Geod_Accu_Standards. pdf

Hall, GW (1996). Дифференциальная служба GPS-навигации USCG . Получено 9 ноября 2005 г. с http://www.navcen.uscg.gov/pdf/dgps/dgpsdoc.pdf 9.0003

Hodgson, C.V. Измерительная база с инваровой лентой. Лента идет. Базовая линия и астропати , ок. 1916. Коллекция исторических фотографий NOAA (2004). Получено 20 апреля 2006 г. с http://www.photolib.noaa.gov/.

Херн, Дж. (1989). GPS: Путеводитель по следующей утилите . Саннивейл, Калифорния: Trimble Navigation Ltd.

Hurn, J. (1993). Дифференциальный GPS Объяснение . Саннивейл, Калифорния: Trimble Navigation Ltd.

Monmonier, M. (1995). Пограничный спор и карта как доказательство. В Проведение линии: рассказы о картах и ​​картоспоры . Нью-Йорк: Генри Холт.

Национальная геодезическая служба (без даты). Получено 4 ноября 2009 г. с http://www.ngs.noaa.gov

National Geodetic Survey (nd). Национальная геодезическая служба — CORS, постоянно действующая опорная станция . Получено 15 августа 2012 г. с http://www.ngs.noaa.gov/CORS/

Офис совместной программы NAVSTAR GPS. Получено 21 октября 2000 г. с http://gps.losangeles.af.mil/ (на пенсии)

Norse, ET (2004). Отслеживание новых сигналов из космоса — модернизация GPS и технология Trimble R-Track . Получено 9 ноября 2005 г. с http://www.trimble.com/survey_wp_gpssys.asp?Nav=Collection-27596 Получено 17 июня 2014 г. с http://www.aimil.com/Resources/ResourceFile/107_r-track_wp_022543 -078_0304_lr.pdf

Раис, Э. (1948). Серия McGraw-Hill по географии: Общая картография (2-е изд.). Йорк, Пенсильвания: The Maple Press Company.

Робинсон, А. и др. (1995). Элементы картографии (5-е изд.). Нью-Йорк: Джон Уайли и сыновья.

Смитсоновский национальный музей авиации и космонавтики (1998 г.). GPS: новое созвездие . Получено 2 августа 1999 г. с http://www.nasm.si.edu/gps/

Snay, R. (2005, 13 сентября). Форум пользователей CORS — к позиционированию в реальном времени . Презентация в Power Point, представленная на Форуме пользователей CORS 2005, Лонг-Бич, Калифорния. Презентация получена 26 октября 2005 г. с http://www.ngs.noaa.gov/CORS/Presentations/CORSForum2005/Richard_Snay_Forum2005.pdf 9.0003

Томпсон, М. М. (1988). Карты Америки, картографические продукты Геологической службы США и др. (3-е изд.). Рестон, Вирджиния: Геологическая служба США.

Навигационный центр береговой охраны США (без даты). Общая информация DGPS . Получено 10 февраля 2008 г. с http://www.navcen.uscg.gov/?pageName=dgpsMainwww.navcen.uscg.gov/

Федерального авиационного управления США (2007a). Часто задаваемые вопросы . Получено 10 февраля 2008 г. с http://www.faa.gov/about/office_org/headquarters_offices/ato/service_units/techops/navservices/gnss/faq/gps/9.0003

Федеральное авиационное управление США (2007b). Глобальная система позиционирования: как это работает. Получено 10 февраля 2008 г. с http://www.faa.gov/about/office_org/headquarters_offices/ato/service_units/techops/navservices/gnss/gps/howitworks/

Федерального авиационного управления США.