На клетчатой бумаге с размером клетки 1х1 изображен: На клетчатой бумаге с размером клетки 1х1 изображен треугольник. Найдите его площадь.

. Что означает свертка 1×1 в нейронной сети?

спросил 7 лет, 1 месяц назад

Изменено 1 год, 4 месяца назад

Просмотрено 181к раз

$\begingroup$

В настоящее время я изучаю Учебник по глубокому обучению Udacity. В Уроке 3 речь идет о свертке 1×1. Эта свертка 1×1 используется в начальном модуле Google. У меня проблемы с пониманием того, что такое свертка 1×1.

Я также видел этот пост Янна Лекуна.

Не мог бы кто-нибудь объяснить мне это?

• нейронные сети
• глубокое обучение
• свертка
• свертка нейронная сеть

$\endgroup$

5

$\begingroup$

Предположим, что у меня есть конверсионный слой, который выводит тензор в форме $(N, F, H, W)$, где:

• $N$ — размер партии
• $F$ — количество сверточных фильтров
• $H, W$ — пространственные размеры

Предположим, что входные данные подаются в конверсионный слой с фильтрами $F_1$ 1×1, нулевым отступом и шагом 1.

Таким образом, фильтры преобразования 1×1 можно использовать для изменения размерности в пространстве фильтров. Если $F_1 > F$, то мы увеличиваем размерность, если $F_1 < F$, мы уменьшаем размерность в размерности фильтра.

Действительно, в статье Google Inception Going Deeper with Convolutions говорится (жирным шрифтом выделено мной, а не первоначальными авторами):

Одна большая проблема с вышеупомянутыми модулями, по крайней мере, в этой наивной форме, заключается в том, что даже скромное количество сверток 5×5 может быть непомерно дорогим поверх сверточных слоев с большим количеством фильтров.

Это приводит ко второй идее предлагаемой архитектуры: разумно применять уменьшение размерности и проекции везде, где в противном случае вычислительные требования слишком сильно возросли бы. Это основано на успехе вложений: даже вложения с низкой размерностью могут содержать много информации об относительно большом фрагменте изображения. .. 1×1 свертки используются для вычисления сокращений перед дорогостоящими свертками 3×3 и 5×5. Помимо использования в качестве редукторов, они также включают использование выпрямленной линейной активации, что делает их двойного назначения.

Итак, в архитектуре Inception мы используем сверточные фильтры 1×1 для уменьшения размерности в измерении фильтра. Как я объяснял выше, эти конверсионные слои 1×1 можно использовать в целом для изменения размерности пространства фильтра (либо увеличения, либо уменьшения), и в начальной архитектуре мы видим, насколько эффективными могут быть эти фильтры 1×1 для уменьшения размерности, явно в пространстве измерения фильтра. , а не пространственное измерение пространства.

Возможно, существуют и другие интерпретации фильтров преобразования 1×1, но я предпочитаю это объяснение, особенно в контексте архитектуры Google Inception.

$\endgroup$

4

$\begingroup$

Свертка 1×1 просто отображает входной пиксель со всеми его каналами в выходной пиксель, не глядя ни на что вокруг себя. Он часто используется для уменьшения количества каналов глубины, так как умножение объемов с очень большой глубиной часто происходит очень медленно.

 ввод (глубина 256) -> свертка 1x1 (глубина 64) -> свертка 4x4 (глубина 256)
ввод (глубина 256) -> свертка 4x4 (глубина 256)
 

Нижний примерно в 3,7 раза медленнее.

Теоретически нейронная сеть может «выбрать», какие входные «цвета» смотреть, используя это, вместо грубой силы, умножающей все.

$\endgroup$

4

$\begingroup$

Основная причина, по которой я не понимал сверток 1×1, заключается в том, что я не понимал, как на самом деле работают свертки $any$ — ключевым фактором является то, как работает вычисление свертки нескольких каналов/фильтров. Чтобы понять это, я также нашел этот ответ полезным:

https://datascience.stackexchange.com/questions/9175/how-do-subsequent-convolution-layers-work

В частности, тип 2.

Еще один полезный ответ:

https://ai.stackexchange.com/questions/5769/in-a-cnn-does-each-new-filter-have-different-weights-for-each-input-channel-or

Этот ответ объясняет как у вас есть отдельный фильтр для каждой комбинации входных/выходных каналов . После вычисления каждого из них результаты суммируются по входным каналам осей, оставляя выходных каналов значений.

Вот видео, которое помогло мне понять, как работает свертка 1×1.

https://www.coursera.org/lecture/convolutional-neural-networks/networks-in-networks-and-1×1-convolutions-ZTb8x

Вот главное, что я из этого вынес:

• вводом для свертки 1×1 обычно являются предыдущие свертки размером $m$ x $n$. Но если в последнем слое сверток были фильтры $f_1$, вы получаете матрицу в форме $(m, n, f_1)$. Свертка 1×1 на самом деле представляет собой вектор размером $f_1$, который свертывается по всему изображению, создавая один выходной фильтр размером $m$ x $n$. Если у вас есть $f_2$ сверток 1×1, то результат всех сверток 1×1 равен размеру $(m, n, f_2)$.
• Таким образом, свертка 1×1, предполагающая $f_2 < f_1$, может рассматриваться как повторное представление фильтров $f_1$ через фильтры $f_2$. Это позволяет сети обучаться тому, как наиболее эффективно уменьшать измерение.

$\endgroup$

1

$\begingroup$

Постараюсь объяснить более понятно и кратко с иллюстрациями!

A 1*1 конв. (он же Сеть в сети )?

допустим, вы ввели ($n_H$,$n_W$, $n_{c_{prev}}$). Вы можете представить из (1*1*$n_{c_{prev}}$) как один нейрон (полностью связанная сеть — т.е. почему

Таким образом, вы можете использовать слой пула для уменьшения пространственных размеров ($n_H$,$n_W$) и можете использовать 1*1 conv для уменьшения $n_{c_{prev}}$(т.е. количества каналов), что сохраняет много вычислений. Например

Следовательно, уберите

• Вы можете использовать сверточный слой 1×1 для уменьшения $n_C$, но не $n_H$, $n_W$.

• Вы можете использовать объединяющий слой для сокращения $n_H$, $n_W$ и $n_C$.

Другими словами,

• что вы делаете с помощью фильтра 1*1 CONV? вы в основном берете веса размера «1 * 1 * num_input_channel_of_featureMap» и сворачиваете (поэлементно *, за которым следует +) этот объем по изображению/featureMap размера «W H num_input_channel_of_featureMap», и вы получите вывод размером «W*H».

• Теперь вы можете использовать номер «#filters» типа «1*1*num_input_channel_of_featureMap» и получить объем «W H #filter» в качестве окончательного вывода!

• Точнее, вы умножаете «1*1» таких 32 различных весов (1*1 объем) на один срез в одном и том же месте на карте входных объектов, за которым следует ReLu, и получаете одно сгенерированное соответствующее число, которое отображается зеленым цветом. цветной пиксель!

• 1*1 CONV помогает сократить количество каналов и сэкономить на вычислениях в некоторых сетях (НАЧАЛО).!

• Но, конечно, если вы хотите, чтобы количество каналов было таким же, как и на входной карте объектов, это тоже хорошо, единственное, что делает 1 * 1 CONV, — это просто применяет к нему нелинейность ReLU, что позволяет ему учиться сложные функции в NN

  .

$\endgroup$

1

$\begingroup$

В терминологии машинного обучения данные часто имеют больше измерений, чем обычно описывается, например. Данные 2D-изображения обычно представляют собой 3D-изображения с размерами:

• $w$ ширина изображения
• $h$ высота изображения
• $k$ (размером $3$) RGB-каналы изображения

(в изображении в оттенках серого $|k|=1$).

При описании $1\times1$ сверточных слоев это обычно неявно означает $1\times1\times k$, где $k$ — количество каналов, т.е. фильтр уменьшает размерность по каналам (например, усреднение значения по трем отдельным каналам RGB).

$\endgroup$

$\begingroup$

Еще одна идея по уменьшению размерности в контексте фильтров 1×1:

Возьмем для примера слой 4096x8x8 fc7 из FCN. Что произойдет, если следующий слой (назовем его fc8) имеет размер 2048x8x8 с размером фильтра 1? fc7 находится очень глубоко внутри сети, каждая из его 4096 функций семантически богата, но каждый нейрон (например, входное изображение 250x250x3) имеет большое рецептивное поле. Другими словами, если нейрон очень активен, мы знаем, что где-то в его семантическом поле присутствует соответствующий признак.

Возьмем, к примеру, самый левый верхний нейрон в fc8 с фильтром 1×1. Он соединяется со всеми 4096 нейронами/признаками только в одном и том же рецептивном поле (верхний левый угол изображения), каждый из которых активируется одним признаком. Некоторые (допустим, те же 500) из них очень активны. Если полученный нейрон также очень активен, это означает, что он, вероятно, научился идентифицировать 1 или несколько признаков в этом рецептивном поле. После того, как вы проделаете это 2048 раз для самых левых верхних нейронов в fc8, многие из них (например, 250) будут очень активными, то есть они «соберут» признаки из одного и того же рецептивного поля через fc7, а многие, скорее всего, даже больше, чем один.

Если вы продолжите уменьшать размерность, уменьшающееся число нейронов будет изучать все большее количество признаков одного и того же рецептивного поля. А поскольку пространственные параметры 8×8 остаются прежними, мы не меняем «вид» каждого нейрона, а значит, не уменьшаем пространственную грубость.

Вы можете взглянуть на «Полностью сверточные сети» Лонга, Шелхамера и Даррела.

$\endgroup$

4

$\begingroup$

Математическая операция свертки означает вычисление произведения двух (непрерывных или дискретных) функций по всем возможным позициям сдвига.

В двумерном (оттенки серого) изображении свертка выполняется с помощью операции скользящего окна, где окно (ядро двумерной свертки) представляет собой матрицу $v \times v$.

Применение нейронных сетей для обработки изображений — включая сверточные нейронные сети — были рассмотрены в: [M. Эгмонт-Петерсен, Д. де Риддер, Х. Гендельс. Обработка изображений с помощью нейронных сетей — обзор , Распознавание образов , Vol. 35, № 10, стр. 2279-2301, 2002].

$\endgroup$

$\begingroup$

3×3 против 1×1 Convolution

 импортный резак
импортировать torch.nn как nn
изображение = факел.randn(1, 3, 1280, 1920)
# свертка 3x3 + заполнение, сохраняющее постоянные пространственные размеры
модель = nn.Conv2d (in_channels = 3, out_channels = 2, kernel_size = 3, padding = 1)
вывод = модель (изображение)
print(output.shape) # torch.Size([1, 2, 1280, 1920])
num_elements = sum(p. numel() для p в model.parameters(), если p.requires_grad)
print(num_elements) # 56 == вес + смещение
# веса = входные_каналы * исходящие_каналы * размер_ядра * размер_ядра
# => 3 * 2 * 3 * 3 = 54
# смещение = out_channels => 2
###
# свертка 1x1
модель = nn.Conv2d (in_channels = 3, out_channels = 2, kernel_size = 1, padding = 0)
вывод = модель (изображение)
print(output.shape) # torch.Size([1, 2, 1280, 1920])
num_elements = sum(p.numel() для p в model.parameters(), если p.requires_grad)
print(num_elements) # 8 == веса + смещение
# веса = входные_каналы * исходящие_каналы * размер_ядра * размер_ядра
# => 3 * 2 * 1 * 1 = 6
# смещение = out_channels => 2
№ 8 << 56 :)
 

$\endgroup$

Диффузия клеток в агаре: биология и химия Научная деятельность

Биологические клетки могут выжить только в том случае, если материалы могут входить и выходить из них. В этой закуске вы использовали кубики агара, чтобы визуализировать, как меняется диффузия в зависимости от размера объекта, поглощающего материал.

Диффузия происходит, когда молекулы из области с более высокой концентрацией перемещаются в область с более низкой концентрацией. По мере того, как ионы водорода из уксуса перемещаются в кубик агара, цвет кубика меняется, позволяя вам увидеть, насколько далеко они распространились. В то время как случайное молекулярное движение заставит отдельные молекулы и ионы продолжать двигаться вперед и назад между кубиком и раствором уксуса, общие концентрации останутся в равновесии с одинаковыми концентрациями внутри и снаружи кубика агара.

Как вы нашли процент куба, который был пронизан ионами водорода в различные промежутки времени? Один из способов сделать это — начать с объема куба, в который было пройдено , а не , — другими словами, той части в центре, которая еще не изменила цвет. Чтобы определить объем этого внутреннего куба, измерьте длину этого внутреннего куба и умножьте ее на ширину и высоту. Вычтите это из первоначального объема куба, и вы получите объем куба, в который проникли.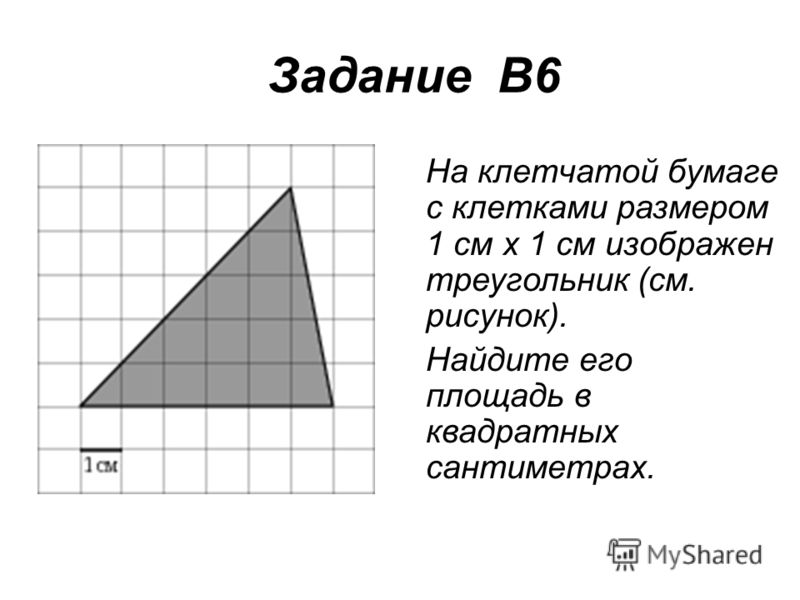 Разделив это число на первоначальный объем и умножив на 100%, можно определить процент проникновения для каждого куба.

Вы, возможно, заметили, что чем больше становится пропитанный уксусом куб, тем больше времени требуется для диффузии дополнительного количества уксуса в куб, но не линейным образом. Другими словами, если размеры куба удвоить, то время, необходимое для полной диффузии ионов водорода, увеличится более чем в два раза. Когда вы утроите размер, время рассеивания НАМНОГО больше, чем в три раза. Почему это произошло?

По мере увеличения размера объекта объем также увеличивается, но больше, чем вы думаете. Например, когда куб удваивается с длины 1 см до длины 2 см, площадь поверхности увеличивается в четыре раза, начиная с 6 см ² (1 см x 1 см x 6 сторон) до 24 см ² (2 см x 2 см x 6 сторон). Однако объем увеличивается в восемь раз, увеличивается с 1 см ^{3 (1 см x 1 см x 1 см) до 8 см 3 (2 см x 2 см x 2 см).}

Поскольку объем увеличивается в большей степени, чем площадь поверхности, отношение площади поверхности к объему уменьшается. По мере увеличения размера куба отношение площади поверхности к объему уменьшается (щелкните, чтобы увеличить таблицу ниже). Уксус может проникать в куб только через его поверхность, поэтому при уменьшении этого соотношения время, необходимое для диффузии по всему объему, значительно увеличивается.

Все, что входит в клетку (например, кислород и пища) или выходит из нее (например, отходы), должно проходить через клеточную мембрану. По мере того, как клетки становятся больше, отношение площади поверхности к объему резко уменьшается, как и в ваших кубиках агара. Более крупные клетки должны по-прежнему транспортировать вещества через свои мембраны, но иметь больший объем для снабжения и пропорционально меньшую площадь поверхности для этого.

Бактериальные клетки довольно малы и имеют сравнительно большее отношение площади поверхности к объему.