Задания по теме «Квадратная решётка, координатная плоскость»
Тематические задания по подготовке к ЕГЭ по математике Квадратная решётка, координатная плоскость
Единый государственный экзамен по математике является обязательным испытанием для всех выпускников российских школ. Абсолютно все 11-классники должны сдавать ЕГЭ по математике базового уровня, а если выпускник планирует после окончания школы поступать в вузы на специальности, где требуются результаты экзамена по математике, ему необходимо сдать ЕГЭ профильного уровня. С каждым годом экзамены меняются, усложняются и совершенствуются задания. Поэтому в ходе подготовки к испытаниям необходимо учитывать все нюансы и подводные камни предстоящего ЕГЭ.
Все задачи с кратким ответом на самом экзамене (профильный уровень) безошибочно решает лишь небольшая часть сдающих, а именно около 25 процентов.
Найдите синус угла В ответе укажите значение синуса, умноженное на
Решение.
Проведем высоту из точки на продолжение стороны Тогда:
Ответ: 1.
2. На клетчатой бумаге с размером клетки 1 1 изображён угол. Найдите тангенс этого угла.
Решение.
Достроим угол до треугольника OBA, OB = BA. BK делит основание OAпополам, значит, BK — высота. Из рисунка находим
Примечание.
Можно заметить и доказать, что равнобедренный треугольник ABO является прямоугольным. Тогда углы AOB и OАB равны 45°, а их тангенсы равны 1.
Ответ: 1.
3. Найдите тангенс угла AOB. Сторона одной клетки равна 1.
Решение.
Достроим угол до треугольника Из рисунка находим: , , Воспользуемся теоремой косинусов:
Тогда:
Поэтому угол равен 135°, а его тангенс равен −1.
Ответ: −1.
4. На клетчатой бумаге с размером клетки изображён четырёхугольник ABCD . Найдите его периметр.
Решение.
По теореме Пифагора для прямоугольных треугольников, гипотенузы которых являются сторонами заданного четырехугольника, имеем:
тогда периметр равен
Ответ: 30.
5.
На клетчатой бумаге с размером клетки изображён квадрат. Найдите радиус окружности, вписанной в этот квадрат.
Решение.
радиус окружности, вписанной в квадрат, равен половине его стороны.
Ответ: 2.
6. На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC.
Найдите длину его высоты, опущенной на продолжение стороны AB.
Решение.
Формулировка задания некорректна: на сторону АВ высоту опустить нельзя. Из точки С можно опустить перпендикуляр к прямой, содержащей сторону АВ. Этот перпендикуляр будет являться высотой треугольника АВС, его длина равна 3.
Ответ: 3.
7. Найдите радиус окружности, вписанной в изображенный на рисунке треугольник ABC, считая стороны квадратных клеток равными 1.
Решение.
Радиус окружности, вписанной в прямоугольный треугольник равен полуразности суммы катетов и гипотенузы. Заметим, что в треугольнике с катетами 3 и 4 гипотенуза равна 5, откуда
Ответ: 1.
8. На клетчатой бумаге с размером клетки изображён треугольник. Найдите радиус его описанной окружности.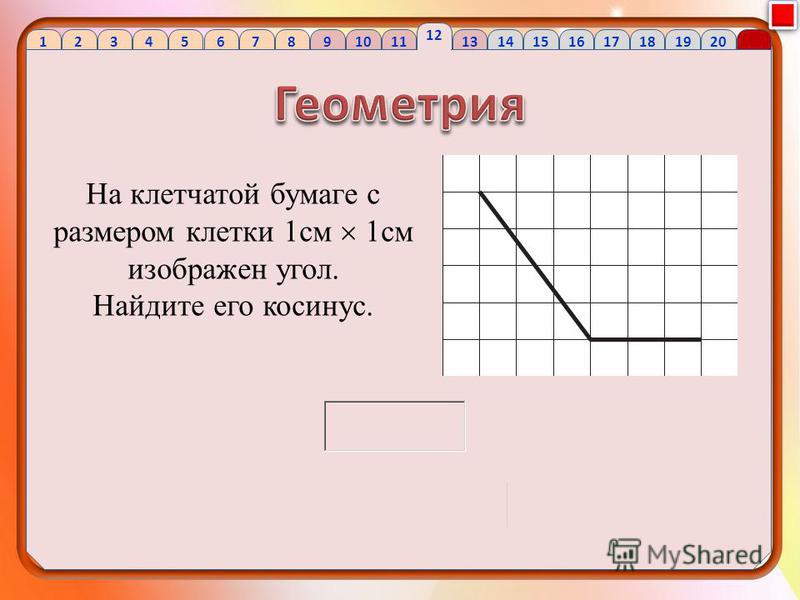
Решение.
Найдём радиус окружности, описанной вокруг этого треугольника, по теореме Пифагора:
Ответ: 5.
9. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Решение.
Площадь четырехугольника равна разности площади большого прямоугольника и двух одинаковых треугольников, площади которых равны половине произведения основания на высоту, проведенную к этому основанию. Поэтому
10.
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Решение.
Площадь четырехугольника (в том числе невыпуклого) равна половине произведения диагоналей на синус угла между ними.
Диагонали изображенного на рисунке четырехугольника являются взаимно перпендикулярными диагоналями квадратов со стороной 1. Поэтому длины диагоналей равны , а синус угла между ними равен 1. Тем самым, площадь четырехугольника равна 1.
Ответ: 1.
11. На клетчатой бумаге с размером клетки изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.
Решение.
Отрежем от закрашенной фигуры сектор, отмеченный синим цветом, и добавим к ней сектор, выделенный красным цветом. Указанные секторы равны, поэтому площадь фигуры не изменилась. Следовательно, она равна трём четвертям площади круга, радиус которого см. Поэтому
см2.
Ответ: 12.
12.
На клетчатой бумаге с размером клетки 1 1 изображён прямоугольный треугольник. Найдите радиус окружности, описанной около этого треугольника.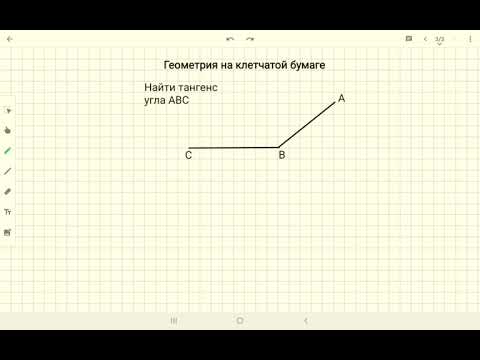
Решение.
Треугольник прямоугольный, значит, радиус описанной вокруг него окружности равен половине гипотенузы.
Ответ: 2,5.
13. На клетчатой бумаге с размером клетки 1 см 1 см изображено кольцо. Найдите его площадь. В ответ запишите площадь, делённую на . Ответ дайте в квадратных сантиметрах.
Решение.
Площадь кольца равна разности площади большого и малого кругов. Радиус большого круга равен 2, а малого — 1, откуда
Поэтому
Ответ: 3.
14. На клетчатой бумаге с размером клетки изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.
Решение.
Выполним дополнительное построение и из прямоугольного треугольника с катетами 2 и 4 найдем квадрат радиуса круга: см2 (см.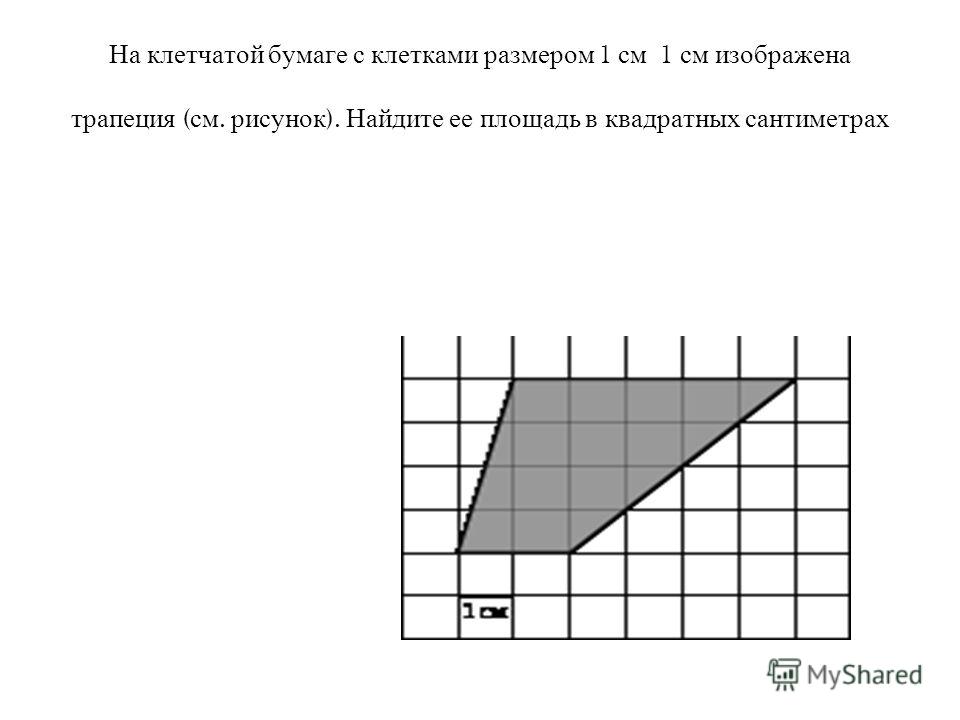
рис. 1). Площадь фигуры равна трем восьмым площади этого круга (см. рис. 2). Поэтому
см2.
Ответ: 7,5.
15. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 1. Найдите площадь заштрихованной фигуры.
Решение.
Площади кругов относятся как квадраты их радиусов. Радиус внешнего круга равен 6, радиус внутреннего равен 3. Поскольку радиус большего круга вдвое больше радиуса наименьшего круга, площадь большего круга вчетверо больше площади меньшего. Следовательно, она равна 4. Площадь заштрихованной фигуры равна разности площадей кругов: 4 − 1 = 3.
Ответ: 3.
16.
На клетчатой бумаге изображён круг. Какова площадь круга, если площадь заштрихованного сектора равна 32?
Решение.
Заметим, что Тогда поэтому Поэтому площадь сектора равна от площади круга. Следовательно, площадь круга равна 3 · 32 = 96.
Ответ:96.
17. Найдите площадь закрашенной фигуры на координатной плоскости.
Решение.
Площадь закрашенной фигуры равна разности площади большого и маленького ромбов. Площадь ромба равна половине произведения его диагоналей. Поэтому
Ответ: 24.
18.
Найдите площадь ромба, вершины которого имеют координаты (6;3), (9;4), (10;7), (7;6).
Решение.
Площадь четырехугольника равна разности площади квадрата 4х4, четырех равных прямоугольных треугольников с катетами 1 и 3 и двух равных квадратов 1х1. Поэтому
см2.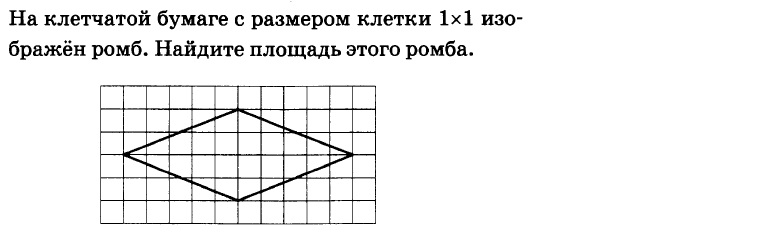
Ответ: 8.
Что такое синус и косинус? Что такое тангенс и котангенс?
Откуда появилась тригонометрия?
Знакомство наше начнём с глубокой древности. С древнего Египта, Вавилона и Китая. Не переживайте, все 20 веков тригонометрии мы с вами освоим всего за 20 минут. Можете засекать время.)
Итак, откуда же и как появилась тригонометрия?
Первоначально, на заре своего становления, тригонометрия не являлась самостоятельным разделом математики. Она, скорее, была частью астрономии. Дело всё в том, что древним астрономам, которые интересовались нашими главными небесными телами (Луной и Солнцем) и вовсю изучали их поведение, постоянно приходилось просчитывать и расстояния до них. С достаточной точностью для того далёкого времени, между прочим.) Скажем, чтобы предсказывать затмения. Или приливы/отливы. Просчитывать эти самые расстояния древним людям приходилось с помощью обыкновенного… треугольника.
Чуть позже, по мере развития цивилизации, большинство учёных стало осознавать чрезвычайную важность тригонометрии не только в астрономии, но и в других областях жизни. Это, в первую очередь, артиллерия, оптика, навигация в дальних морских походах, геодезия и картография… Слово «триангуляция» (разбиение местности на 
Эти пирамидки — и есть тригонометрические знаки. Или геодезические пункты. Они служили верой и правдой геодезистам и картографам тех далёких времён для составления карт местности.) Этих знаков сохранилось по России очень много.)
Короче, в любых областях, где приходилось сталкиваться с обычным
А дальше — теория колебаний, электричество, акустика, радиосвязь… И в основе всего этого богатства — тоже тригонометрия, да…)
И не было бы у нас сегодня ни мобильников, ни телевизоров, ни микроволновок, ни спутниковых навигаторов, ни многих других современных атрибутов комфортной жизни, кажущихся нам обыденностью…
Итак, в основе всей тригонометрии лежит обыкновенный треугольник! Да-да! Именно так.
Почему именно треугольник и откуда собственно взялось это красивое слово «тригонометрия» — об этом далее.
)
Синус, косинус, тангенс и котангенс… Что за звери?
Для начала нарисуем в тетрадке самый обычный прямоугольный треугольник. Стороны его обозначим как a, b и c, а один из острых углов обозначим буквой α. Это греческая буква «альфа», при написании очень похожая на «двойку без головы». Самая распространённая буква в тригонометрии для обозначения углов. Привыкаем.)
Вот такая картинка у нас получится:
На всякий случай, напомню, что стороны, образующие прямой угол, называются катетами (a и b — катеты), а третья сторона, лежащая напротив прямого угла, называется гипотенузой (c — гипотенуза).
Казалось бы, треугольник и треугольник, эка невидаль! Что с ним делать-то? Спокойствие. Сейчас всё узнаете.)
Сейчас, как и древние люди, мы будем наш треугольник измерять. Да-да! Кстати, страшное слово «тригонометрия» с древнегреческого языка на русский так и переводится — измерение треугольников.
Вот и измеряем. На рисунке специально клеточки нарисованы, как и в заданиях ЕГЭ или ОГЭ бывает. Чему равен катет a? Трём клеточкам (a = 3). А катет b? Не вопрос! Четырём клеточкам он равен (b = 4). А гипотенуза? Гипотенузу, конечно, по клеточкам не посчитаешь, но, воспользовавшись великой и могучей теоремой Пифагора, легко можно получить, что гипотенуза равна пяти (c = 5).
Кстати сказать, прямоугольный треугольник со сторонами 3, 4, 5 — весьма интересная фигура! Он известен ещё с античных времён и называется египетским треугольником. Ибо активно применялся для построения прямых углов египетскими землемерами и архитекторами. В том числе и при построении пирамид, между прочим.)
А вообще, целые числа a, b, c, которые могут быть длинами сторон прямоугольного треугольника, т.е. для которых выполняется теорема Пифагора
a2 + b2 = c2,
в математике так и называются — пифагоровыми тройками.
Тройка (3; 4; 5) — самая известная. Ещё распространена тройка чисел (5; 12; 13). Или (8; 15; 17). Таких троек известно очень и очень много. Кому интересно, прогуляйтесь по ссылке и почитайте. Для самообразования.)
А мы продолжим. Теперь сделаем следующее. Поделим длину катета a на длину катета b. Или, как принято говорить в математике, возьмём отношение a к b.
Получим:
a/b = 3/4
Можно наоборот, поделить b на a. Получим 4/3. Или, скажем, поделить a на c. Получим 3/5. Иными словами, можно брать любые стороны прямоугольного треугольника, делить их длины друг на друга и получать какие-то числа. Безразмерные.
И что из этого? Согласен, пока ничего особенного. Бессмысленное занятие, одним словом.)
А теперь я поступлю следующим образом. Увеличу треугольник, продлив стороны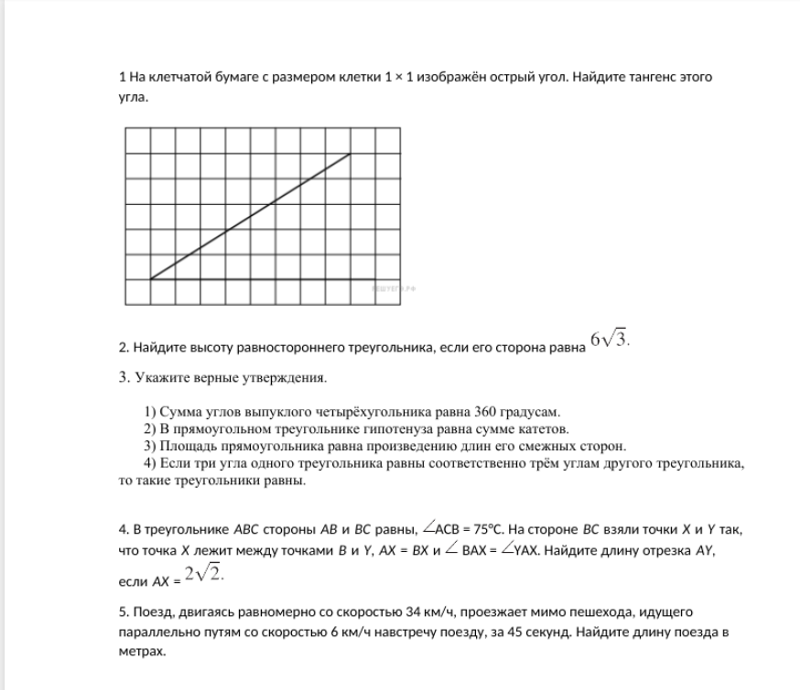 
Это важно. На картинке я для удобства увеличил все стороны треугольника в два раза.
Вот так:
Угол α, как видно, остался прежним. Старые стороны a, b и с превратились в новые стороны x, y, z. Их длины, естественно, изменились, увеличившись вдвое:
x = 6
y = 8
z = 10
А вот отношения
Смотрите сами.
Было: a/b = 3/4.
Стало: x/y = 6/8 = 3/4.
И для других соответствующих сторон их отношения также не изменятся. Можно что угодно делать с треугольником — увеличивать, уменьшать, сохраняя при этом угол α, а отношения соответствующих сторон всё равно останутся прежними. Кому интересно, можете попробовать и проверить. Это полезно.)
А вот это уже крайне важно! Соотношения сторон в прямоугольном треугольнике никак не зависят от длин этих самых сторон при одном и том же угле α.
Синус угла α — это отношение противолежащего катета к гипотенузе:
sin α = a/c
Косинус угла α — это отношение прилежащего катета к гипотенузе:
cos α
Тангенс угла α — это отношение противолежащего катета к прилежащему:
tg α = a/b
Котангенс угла α — это отношение прилежащего катета к противолежащему:
ctg α = b/a
Вот такая вот весёлая семейка.
sec α = c/b
cosec α = c/a
Но эти соотношения никакого практического смысла не имеют и в школе не рассматриваются. И мы тоже не будем.)
Вся эта великолепная четвёрка (синус, косинус, тангенс и котангенс) называется тригонометрическими функциями.
Зачем я всё это так занудно повторяю и некоторые слова выделяю жирным шрифтом? Да затем, что это надо запомнить! Причём запомнить железно. Улавливаете?
Процесс запоминания можно существенно облегчить, если для начала запомнить, что в тангенсе и котангенсе сидят только катеты, а в синусе и косинусе гипотенуза появляется.
Кроме того, ещё могут нахлынуть сомнения, какой из катетов, противолежащий или прилежащий, сидит соответственно у синуса/косинуса. Да и у тангенса/котангенса тоже. Здесь работает принцип под условным названием «дальше/ближе».
Например: синус угла — это отношения дальнего от угла (т.е. противолежащего) катета к гипотенузе, а косинус — отношение ближнего (т.е. прилежащего) катета к гипотенузе.
Тангенс — отношение дальнего от угла катета к ближнему. А котангенс — наоборот.
Подведём предварительный итог. Как вы видите, всё просто. Синус, косинус, тангенс и котангенс — это просто какие-то числа. Безразмерные. Ни больше ни меньше. Для каждого конкретного угла — свои персональные.
А теперь давайте поразмышляем вот над чем. Как вы думаете, почему мы всегда говорим синус, косинус, тангенс и котангенс угла? Вроде бы мы отношения сторон считаем.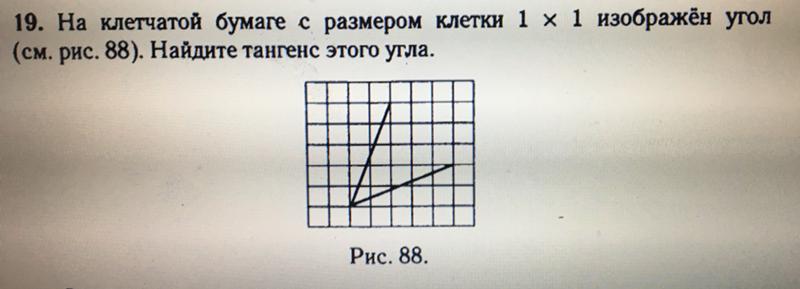
Угол-то тут при чём? Догадались? Если нет, то тогда смотрим на следующую картинку:
Что здесь нового? Я изменил (увеличил) угол с α до β («бета»). При этом все отношения сторон стали другими!
Скажем, было a/b = 3/4, а стало m/b = 5/4. И все остальные отношения сторон также поменялись. Какой вывод можно сделать? Да! При одном и том же угле α отношения длин сторон никак не зависят от их длин. Но при этом колоссально зависят от этого самого угла! И только от него. Именно поэтому тригонометрические функции (синус, косинус, тангенс и котангенс) относятся к углу. И говорить, скажем, о тангенсе, без конкретного угла — бессмысленно. Угол — ключевая действующая фигура в тригонометрии.
Отсюда можно сделать важный вывод: если нам известен некий угол, то мы автоматически знаем и все его тригонометрические функции. Это неразрывная связь, которую надо уяснить железно.
Стало быть, если нам дан угол, то считается, что все его тригонометрические функции нам тоже известны. Полностью весь комплект, от синуса до котангенса. И наоборот, если нам дана какая-то из тригонометрических функций угла (скажем, косинус), то автоматически нам известен и сам угол.
Запоминаем: если нам известен угол, то нам автоматически известны и ВСЕ его тригонометрические функции. И наоборот — известна какая-то из тригонометрических функций (хотя бы одна), то известен и сам угол.
У каждого угла есть свои персональные синус и косинус. И почти у каждого — свои тангенс и котангенс.
Слово «почти» для тангенса и котангенса стоит не случайно. Об этом узнаете дальше.)
Сейчас, в век калькуляторов и компьютеров, найти тригонометрическую функцию какого-либо угла — не проблема. И наоборот, по функции найти угол. Нажал нужную кнопочку и — ответ готов.) А вот раньше, во времена отсутствия вычислительной техники, для тригонометрических функций углов существовали свои специальные таблицы.
Таблицы Брадиса назывались. Они, конечно же, существуют и поныне, но, благодаря техническому прогрессу, давно отошли на задний план и пылятся на полках. Но знать об их существовании и уметь ими пользоваться — очень и очень полезно.
Конечно же, запомнить все-все значения тригонометрических функций всех-всех углов нереально. И не нужно.) Но среди всего многообразия углов есть некоторые углы, про которые вы обязаны знать всё. Об этом в следующих уроках будет. Но общий принцип «знаю угол — знаю его тригонометрические функции» срабатывает всегда! Безотказно.)
А зачем нам вообще нужны все эти синусы, косинусы, тангенсы и котангенсы — спросите вы? Вопрос резонный.
Пожалуйста! Вот вам типичная задачка из ЕГЭ:
Всё. Никаких данных, кроме тех, что на картинке, больше нет. Нужно найти длину катета AB.
Что делать будем? Клеточки не спасают: треугольник как-то неправильно ориентирован. Специально, похоже.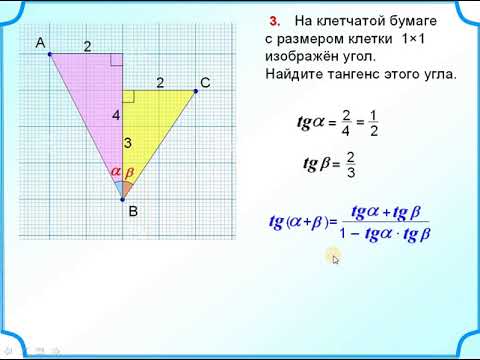
) Известна длина гипотенузы (6 клеток). Зачем-то дан ещё и угол…
Вот тут самое время вспомнить про тригонометрию. Раз нам дан угол, то вспоминаем заклинание: «знаю угол — знаю и его тригонометрические функции!» И какую же из функций в дело пускать? А что нам дано в задачке? Нам дана гипотенуза AB, дан угол А, а найти просят прилежащий к этому углу катет.
Понятное дело, что надо косинус в дело пускать. Вот и действуем. Прямо по определению косинуса (отношение прилежащего катета к гипотенузе) пишем:
cos A = AB/AC
Гипотенуза AC равна 6 клеток, угол А у нас 60 градусов. Про этот угол известно, что его косинус равен 1/2. Это одно из тех значений, которое ученик знать обязан. Безо всяких таблиц и безо всяких калькуляторов!
Подставляем наши данные и получаем:
1/2 = АВ/6
Простенькое линейное уравнение с величиной АВ в качестве неизвестного.
Решаем и получаем:
АВ = 3
Что и является верным ответом.
В этой задачке нам, конечно, пришлось вспомнить, чему равен косинус угла в 60 градусов. Для знающих учеников никаких проблем. А вот у новичков, ещё не знакомых с тригонометрическими функциями популярных углов, пока остаются вопросы… Откуда и почему именно 1/2? А не 1? Или, может быть, 2/3…
Ответы на эти вопросы будут позже. В соответствующем уроке.)
Ещё из той же оперы, ближе к нашей теме. Уже чисто на определение и понимание смысла тригонометрических функций. Никаких конкретных табличных значений знать не требуется.
На клетчатой бумаге с размером клетки 1х1 изображён угол. Найдите тангенс этого угла.
Внушает? Вспоминаем определение тангенса — отношение противолежащего катета к прилежащему. Но… где здесь катеты? Дан просто угол, а для тангенса нам позарез нужен прямоугольный треугольник.
Где его взять?!
Не беда! Раз надо, значит… сделаем!) Привяжем наш угол к некоторому прямоугольному треугольнику, про который мы точно знаем всё что нам нужно. А именно — катеты. Первое что напрашивается — опустить перпендикуляр из точки А на сторону ОВ.
Вот так:
Ну и как? Осеняет? Вот вам и прямоугольный треугольник и катеты! Противолежащий катет AH = 2, а прилежащий OH = 4.
Прямо по определению тангенса записываем и считаем:
И все дела.) Это правильный ответ.
А теперь задачка для самостоятельного решения.
На клетчатой бумаге с размером клетки 1х1 изображён угол. Найдите все тригонометрические функции этого угла.
Что, круто, да? Да-да, надо найти полный набор функций — от синуса до котангенса включительно. Тренироваться так тренироваться.)
Но где здесь прямоугольный треугольник? Нету его! Да и угол как-то совсем уж скверно расположен.
Ни одну из сторон напрямую по клеточкам не посчитать, да…
Что ж, подскажу немного, что именно надо дополнительно построить, чтобы не надорваться. Снова, как и в предыдущей задаче, опускаем перпендикуляр из точки А на сторону OB. Получим прямоугольный треугольник AHO.
Смотрим картинку:
А теперь внимание! Клеточки, конечно, дело хорошее, удобное и красивое. Но… Кто гарантировал, что основание перпендикуляра (точка Н) уляжется ровно на середину отрезка OB (т.е. строго в один из узлов сетки)? Интуиция? Интуиция в математике — штука опасная. Особенно при рисовании картинок, да…
Поэтому, прежде чем что-то решать, что-то считать, делаем задание по элементарной геометрии. На доказательство. А именно — докажите, что отрезок AH, проведённый так, как показано на картинке, действительно будет перпендикулярен отрезку OB. Или, что то же самое, треугольник AHO — действительно прямоугольный.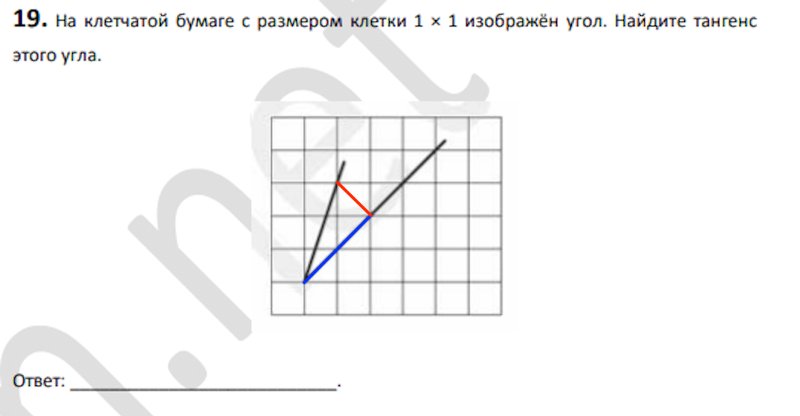
И да помогут вам вспомогательные синие пунктирные линии и теорема Пифагора (это подсказка)! Ну и клеточки спасут, само собой.:)
Без доказательства этого важного факта и без прямоугольного треугольника говорить о каких-либо тригонометрических функциях бессмысленно. Пока что… Придёт время — и мы с вами научимся считать любые тригонометрические функции любых углов без прямоугольного треугольника. Вообще. Как? Совсем скоро узнаете. Всему своё время.)
А пока — доказываем перпендикулярность отрезков, а затем считаем синус, косинус, тангенс и котангенс угла. После доказательства все необходимые данные для расчёта тригонометрических функций у вас уже будут. Обязательно.)
Ответы (в беспорядке):
А где какая функция — это уж вы сами как-нибудь.)
Итак, вот мы с вами и освоили синус, косинус, тангенс и котангенс на самом примитивном уровне. С помощью обычного прямоугольного треугольника.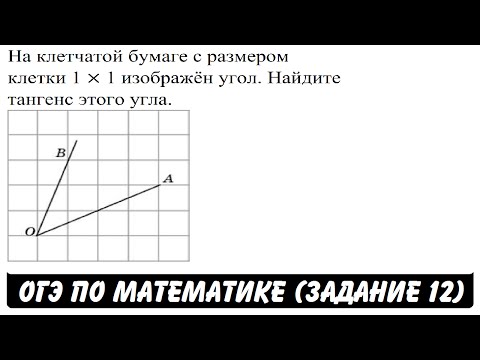
Leave A Comment