На каком рисунке изображен график функции: Работа № 1. Вариант 1. Часть 1. № 15. ГДЗ Алгебра 9 класс ОГЭ Кузнецова. На каком рисунке изображен график? – Рамблер/класс

2+bx+c

, где числа

a

,

b

и

c

— целые. Найдите

f(-5)

.
  

[Ответ: -29]

Смотреть видеоразбор похожего >>

8. На рисунке изображён график функции

f(x)=\frac{k}{x}+a

. Найдите

f(0.1)

.
  

[Ответ: -17]

Смотреть видеоразбор похожего >>

9. На рисунке изображён график функции

f(x)=\frac{k}{x}+a

. Найдите, при каком значении

x

значение функции равно

-4.4

.
  

[Ответ: -12.5]

Смотреть видеоразбор похожего >>

10. На рисунке изображён график функции

f(x)=\frac{k}{x+a}

. Найдите

f(-3.5)

.
  

[Ответ: 6]

Смотреть видеоразбор похожего >>

11. На рисунке изображён график функции

f(x)=\frac{k}{x+a}

. Найдите значение

x

, при котором

f(x) = 10

.
  

[Ответ: 0.6]

Смотреть видеоразбор похожего >>

12. На рисунке изображён график функции

f(x)=\frac{kx+a}{x+b}

. Найдите

k

.
  

[Ответ: 1]

Смотреть видеоразбор похожего >>

13. На рисунке изображён график функции

f(x)=\frac{kx+a}{x+b}

. Найдите

a

.
  

[Ответ: 2]

Смотреть видеоразбор похожего >>

14. На рисунке изображён график функции

f(x)=b+log_ax

. Найдите

f(\frac{1}{9})

.
  

[Ответ: 3]

Смотреть видеоразбор похожего >>

15. На рисунке изображён график функции

f(x)=b+log_ax

. Найдите значение

x

, при котором

f(x)=-11

.
  

[Ответ: 64]

Смотреть видеоразбор похожего >>

16. На рисунке изображён график функции

f(x)=log_a(x+b)

. Найдите

f(26)

.
  

[Ответ: -2]

Смотреть видеоразбор похожего >>

17. {x+b}

. Найдите значение

x

, при котором

f(x) = 64

.
  

[Ответ: 8]

Смотреть видеоразбор похожего >>

22. На рисунке изображён график функции

f(x) = k\sqrt{x}

. Найдите

f(8.41)

.
  

[Ответ: 8.7]

Смотреть видеоразбор похожего >>

23. На рисунке изображён график функции

f(x) = k\sqrt{x}

. Найдите значение

x

, при котором

f(x)=-6.75

.
  

[Ответ: 7.29]

Смотреть видеоразбор похожего >>

24. На рисунке изображены графики функций

f(x)=-4x+22

и

g(x)=ax^2+bx+c

, которые пересекаются в точках A и B.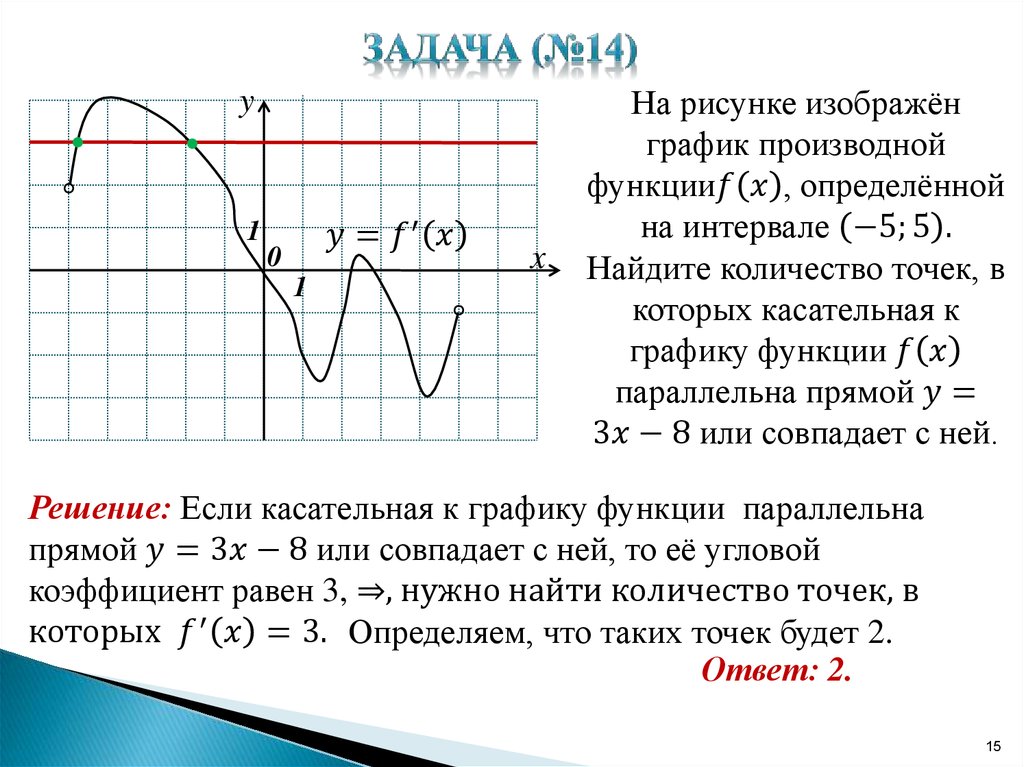 2+bx+c

, которые пересекаются в точках A и B. Найдите ординату точки B.
  

[Ответ: 38]

Смотреть видеоразбор похожего >>

26. На рисунке изображены графики функций

f(x)=\frac{k}{x}

и

g(x)=ax+b

, которые пересекаются в точках A и B. Найдите абсциссу точки B.
  

[Ответ: 0.2]

Смотреть видеоразбор похожего >>

27. На рисунке изображены графики функций

f(x)=\frac{k}{x}

и

g(x)=ax+b

, которые пересекаются в точках A и B. Найдите ординату точки B.
  

[Ответ: 20]

Смотреть видеоразбор похожего >>

28. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.
  

[Ответ: -2.08]

Смотреть видеоразбор похожего >>

29. На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков.
  

[Ответ: -2.4]

Смотреть видеоразбор похожего >>

30. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.
  

[Ответ: -11.3]

Смотреть видеоразбор похожего >>

31. На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков.
  

[Ответ: 6.8]

Смотреть видеоразбор похожего >>

32. На рисунке изображены графики функций

f(x) = 2x^2+16x+30

и

g(x) = ax^2+bx+c

, которые пересекаются в точках A и B. 2+bx+c

, которые пересекаются в точках A и B. Найдите ординату точки B.
  

[Ответ: -13]

Смотреть видеоразбор похожего >>

34. На рисунке изображены графики функций

f(x)=a\sqrt{x}

и

g(x)=kx+b

, которые пересекаются в точке A. Найдите абсциссу точки A.
  

[Ответ: 3.24]

Смотреть видеоразбор похожего >>

35. На рисунке изображены графики функций

f(x)=a\sqrt{x}

и

g(x)=kx+b

, которые пересекаются в точке A. Найдите ординату точки A.
  

[Ответ: 9]

Смотреть видеоразбор похожего >>

36. На рисунке изображён график функции

f(x) = a\sin{x}+b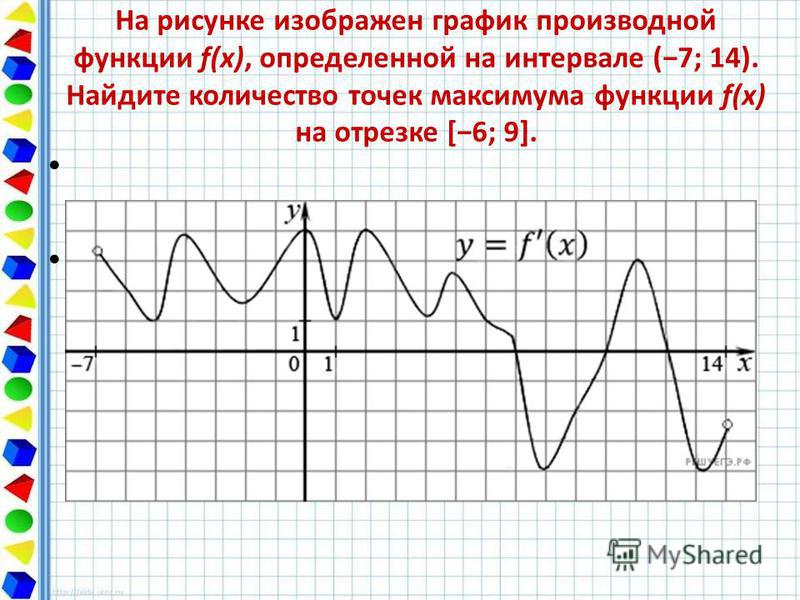

. Найдите

a

.
  

[Ответ: 2]

Смотреть видеоразбор похожего >>

37. На рисунке изображён график функции

f(x) = a\sin{x}+b

. Найдите

b

.
  

[Ответ: 1,5]

Смотреть видеоразбор похожего >>

38. На рисунке изображён график функции

f(x) = a\cos{x}+b

. Найдите

a

.
  

[Ответ: 1,5]

Смотреть видеоразбор похожего >>

39. На рисунке изображён график функции

f(x) = a\cos{x}+b

. Найдите

b

.
  

[Ответ: −1]

Смотреть видеоразбор похожего >>

40.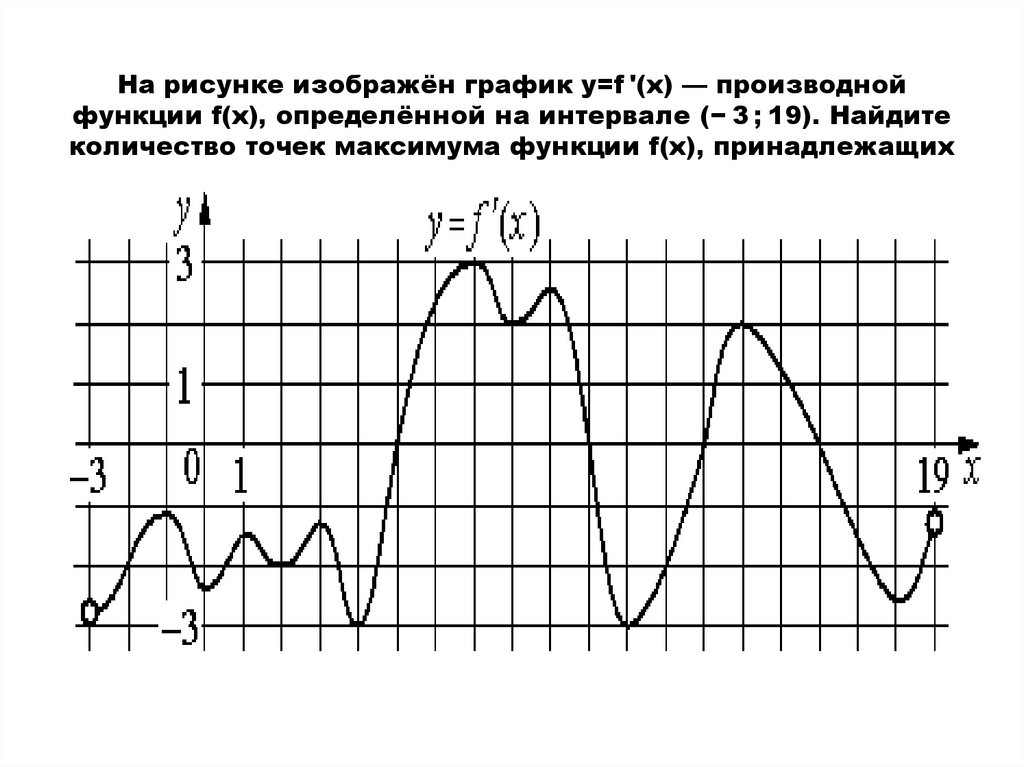 На рисунке изображён график функции

f(x) = a\;tg{x}+b

. Найдите

a

.
  

[Ответ: 2]

Смотреть видеоразбор похожего >>

41. На рисунке изображён график функции

f(x) = a\;tg{x}+b

. Найдите

b

.
  

[Ответ: −1,5]

Смотреть видеоразбор похожего >>

На рисунке изображен график функции вида

564198. На рисунке изображен график функции вида

Найдите f(13).

График функции имеет горизонтальную асимптоту y=2, значит с=2. Вертикальная асимптота x=3, то есть b= -3. По графику дана точка f(2)=1, можем записать:Таким образомОтвет: 2,1

Еще вариант решения: Вспомним, что гипербола y=a/x по сути идентична гиперболеНо! Что тут делают коэффициенты и как они «участвуют»? Как влияют на график?

Коэффициент  а – влияет на «приближение-отдаление» ветвей гиперболы относительно осей. Попробуйте построить графики с разными коэффициентами, например 0,25;  0,5;  2; 4 и увидите, как это выглядит.

Коэффициент  b – влияет на сдвиг графика вдоль оси ох (правее-левее). Если непосредственно перед коэффициентом стоит знак ПЛЮС формула, то гипербола смещена в отрицательном направлении оси; если МИНУС, то в положительном направлении.

Коэффициент  с – влияет на сдвиг графика вдоль оси оу (вверх-вниз). Если перед коэффициентом стоит ПЛЮС, то график смещен в положительном направлении; если МИНУС, то в отрицательном.

*Например:График сдвинут вдоль оси оу на три единицы в положительном направлении, и вдоль оси ох на пять единиц в положительном направлении.График сдвинут вдоль оси оу на четыре единицы в отрицательном направлении, и вдоль оси ох на десять единиц в отрицательном направлении.

Если вы имеете практику в работе графиком и пониманием того как он располагается в зависимости от коэффициентов, то вы легко эти коэффициенты определите.

В данной задаче видим, что центр симметрии гиперболы имеет координату (3;2), то есть он смещен по оси оу на две единицы в положительном направлении, значит  с=2.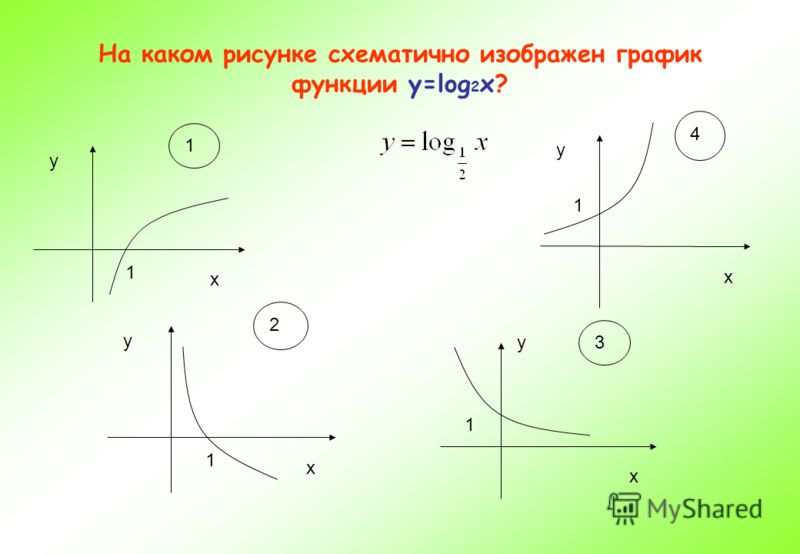 По оси ох смещен в положительном направлении на три единицы, значит b=–3.

Коэффициент a=1. Это для опытных. Видно, что это каноническая гипербола у=1/х. Просто она смещена.

Записываем:Ответ: 2,1

*Конечно же, можно записать  формулу в следующем виде (преобразовываем знаменатель):

Просто тогда будет так  =>  с=2  и  b=3. Суть не меняется.

На рисунке изображен график функции

Найдите при каком значении х значение функции равно 0,8.

Отметим, что гипербола сдвинута вдоль оси оу на единицу вверх (в положительном направлении). Центром симметрии графика является точка (0;1).

На графике обозначена точка (3;2), так как нам известен центр симметрии, то еще одну точку через которую проходит график установить не трудно (-3;0). Подставляем значения в функцию и находим коэффициенты:Вычисляем a (подставим в первое уравнение полученное значение k):Коэффициенты найдены. Вычисляем х при котором значение функции равно 0,8:Ответ: -15

508971. На рисунке изображен график функции
Найдите f(19)

Отметим, что гипербола сдвинута вдоль оси ох на единицу влево (в отрицательном направлении).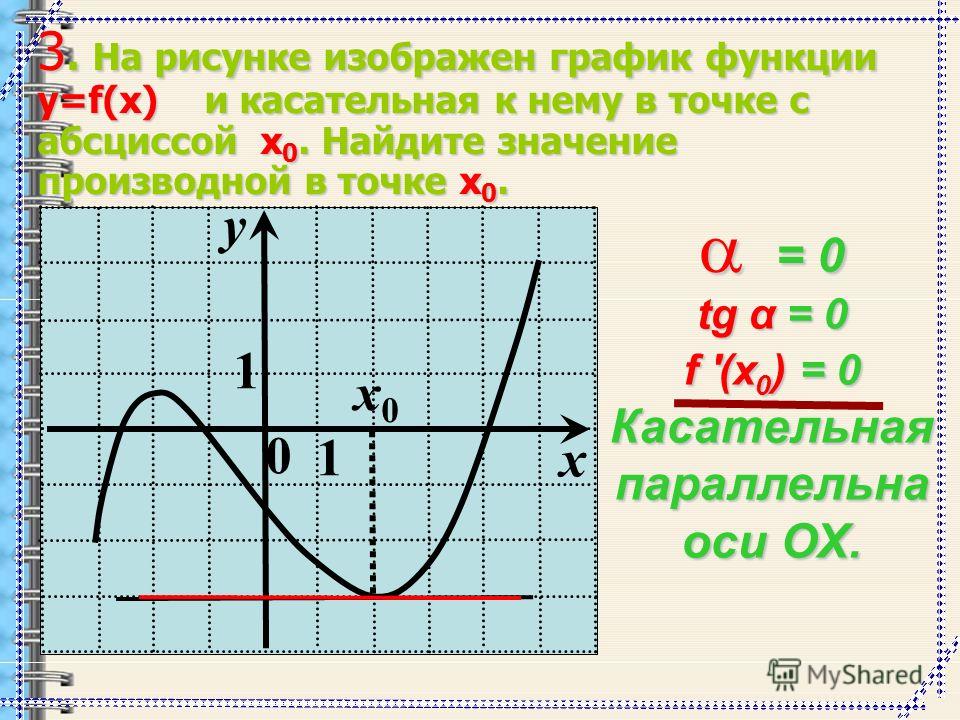 Центром симметрии графика является точка (-1;0).

На графике обозначена точка (2;1), используя центр симметрии установим еще одну (-4;-1). Подставляем значения в функцию и находим коэффициенты:СледовательноОтвет: 0,15

На прилагаемом рисунке показан график неопределенной функции f(x, y) и частных производных fx(x, y) и fy(x, y). Определите, что есть что, и объясните. х, у), II — fy(x, y)c)I -f(x,y), II — fx(x, y), III — fy(x, y)d)I -f(x,y) ), III — fx(x, y), II — fy(x, y) Правильный ответ — вариант «А». Можете ли вы объяснить этот ответ?

Описание вопроса
На прилагаемом рисунке показан график неопределенной функции f(x, y) и частных производных fx(x, y) и fy(x, y). Определите, что есть что, и объясните. х, у), II — fy(x, y)c)I -f(x,y), II — fx(x, y), III — fy(x, y)d)I -f(x,y) ), III — fx(x, y), II — fy(x, y) Правильный ответ — вариант «А». Можете ли вы объяснить этот ответ? по физике 2023 является частью подготовки по физике. Вопрос и ответы подготовлены в соответствии с программа ЕГЭ по физике. Информация о Прилагаемом рисунке показан график неопределенной функции f(x, y) и частных производных fx(x, y) и fy(x, y). Определите, что есть что, и объясните. х, у), II — fy(x, y)c)I -f(x,y), II — fx(x, y), III — fy(x, y)d)I -f(x,y) ), III — fx(x, y), II — fy(x, y) Правильный ответ — вариант «А». Можете ли вы объяснить этот ответ? охватывает все темы и решения для экзамена по физике 2023 года. Найдите важные определения, вопросы, значения, примеры, упражнения и тесты ниже для На прилагаемом рисунке показан график неопределенной функции f(x, y) и частных производных fx(x, y) и fy(x, y). Определите, что есть что, и объясните. х, у), II — fy(x, y)c)I -f(x,y), II — fx(x, y), III — fy(x, y)d)I -f(x,y) ), III — fx(x, y), II — fy(x, y) Правильный ответ — вариант «А». Можете ли вы объяснить этот ответ?

Решения для На прилагаемом рисунке показан график неопределенной функции f(x, y) и частных производных fx(x, y) и fy(x, y).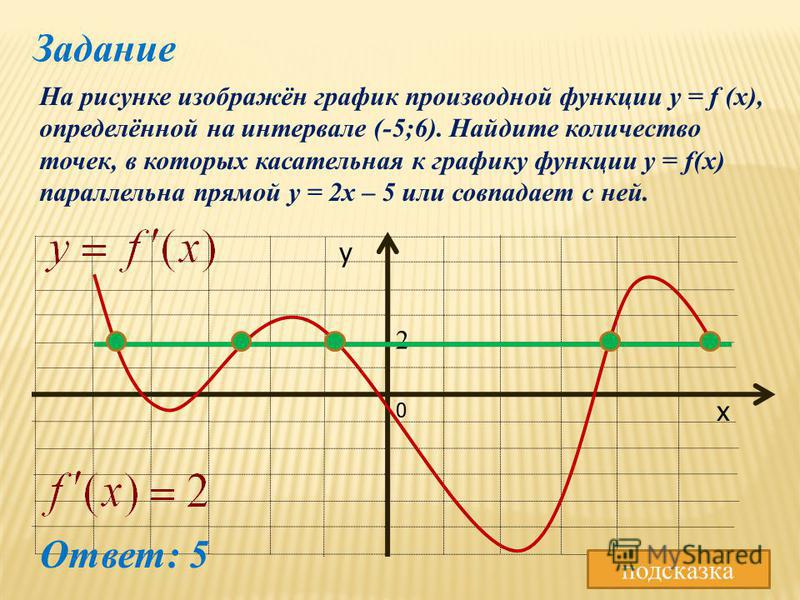 Определите, что есть что, и объясните. х, у), II — fy(x, y)c)I -f(x,y), II — fx(x, y), III — fy(x, y)d)I -f(x,y) ), III — fx(x, y), II — fy(x, y) Правильный ответ — вариант «А». Можете ли вы объяснить этот ответ? на английском и хинди доступны как часть наших курсов по физике. Загрузите более важные темы, заметки, лекции и пробные тесты для экзамена по физике, зарегистрировавшись бесплатно.

Здесь вы можете найти значение На прилагаемом рисунке показан график неопределенной функции f(x, y) и частных производных fx(x, y) и fy(x, y). Определите, что есть что, и объясните. х, у), II — fy(x, y)c)I -f(x,y), II — fx(x, y), III — fy(x, y)d)I -f(x,y) ), III — fx(x, y), II — fy(x, y) Правильный ответ — вариант «А». Можете ли вы объяснить этот ответ? определено и объяснено самым простым способом. Помимо объяснения причин На прилагаемом рисунке показан график неопределенной функции f(x, y) и частных производных fx(x, y) и fy(x, y).

Определите, что есть что, и объясните. х, у), II — fy(x, y)c)I -f(x,y), II — fx(x, y), III — fy(x, y)d)I -f(x,y) ), III — fx(x, y), II — fy(x, y) Правильный ответ — вариант «А». Можете ли вы объяснить этот ответ? Подробное решение для На прилагаемом рисунке показан график неопределенной функции f (x, y) и частных производных fx (x, y) и fy (x, y). Определите, что есть что, и объясните. х, у), II — fy(x, y)c)I -f(x,y), II — fx(x, y), III — fy(x, y)d)I -f(x,y) ), III — fx(x, y), II — fy(x, y) Правильный ответ — вариант «А». Можете ли вы объяснить этот ответ? был предоставлен вместе с типами. На прилагаемом рисунке показан график неопределенной функции f (x, y) и частных производных fx (x, y) и fy (x, y). Определите, что есть что, и объясните. х, у), II — fy(x, y)c)I -f(x,y), II — fx(x, y), III — fy(x, y)d)I -f(x,y) ), III — fx(x, y), II — fy(x, y) Правильный ответ — вариант «А». Можете ли вы объяснить этот ответ? теории, EduRev дает вам большое количество вопросов для практики На прилагаемом рисунке показан график неопределенной функции f(x, y) и частных производных fx(x, y) и fy(x, y).

Определите, что есть что, и объясните. х, у), II — fy(x, y)c)I -f(x,y), II — fx(x, y), III — fy(x, y)d)I -f(x,y) ), III — fx(x, y), II — fy(x, y) Правильный ответ — вариант «А». Можете ли вы объяснить этот ответ? тесты, примеры, а также практиковать тесты по физике.

Как строить графики родительских функций

В математике вы снова и снова видите определенные графики. По этой причине эти исходные общие функции называются родительскими графами , , и они включают в себя графики квадратичных функций, квадратных корней, абсолютных значений, кубических чисел и кубических корней .

График квадратичных функций

Квадратичные функции — это функции, в которых 2-я степень, или квадрат, является наибольшей, до которой возводится неизвестная величина или переменная. Функция

y =x ² или f ( x ) = x ² является квадратичной функцией для всех других квадратичных функций и является родительским квадратичным графиком.

Быстрый способ построения графика функции f ( x ) = x ² состоит в том, чтобы начать с точки (0, 0) (начало координат ) и отметить точку, называемую вершиной . Обратите внимание, что точка (0, 0) является вершиной только родительской функции. В исчислении эта точка называется

критическая точка, и некоторые преподаватели предварительного исчисления также используют эту терминологию. Не вдаваясь в определение исчисления, это означает, что точка особенная.

График любой квадратичной функции называется параболой . Все параболы имеют одинаковую базовую форму. Чтобы получить другие точки, вы наносите точки (1,1 ² )=(1,1), (2,2 ² )=(2,4), (3,3 ² )=( 3,9) и т. д. Этот график появляется и на другой стороне вершины и продолжается, но обычно всего пара точек по обе стороны от вершины дает вам хорошее представление о том, как выглядит график.

На этом рисунке показан пример квадратичной функции в виде графика.

Графики функций квадратного корня

Граф квадратного корня связан с квадратичным графом. Квадратичный граф равен f ( x ) = x ² , тогда как граф квадратного корня равен g ( x ) = x ^{1/2 90. График функции квадратного корня выглядит как левая половина параболы, повернутой на 90 градусов по часовой стрелке. Вы также можете записать функцию извлечения квадратного корня как}

Однако существует только половина параболы по двум причинам. Во-первых, его родительский граф существует только тогда, когда x равно нулю или положительно (потому что вы не можете найти квадратный корень из отрицательных чисел [и в любом случае сохранить их реальными]). Во-вторых, парабола существует только тогда, когда

г ( x ) положительно, потому что когда вас просят найти

вас просят найти только главный или положительный корень из x ..

Этот график начинается с начала координат (0, 0), а затем переходит к (1, sqrt(1))=(1,1), (2, sqrt(2)) , (3, sqrt(3)) и т.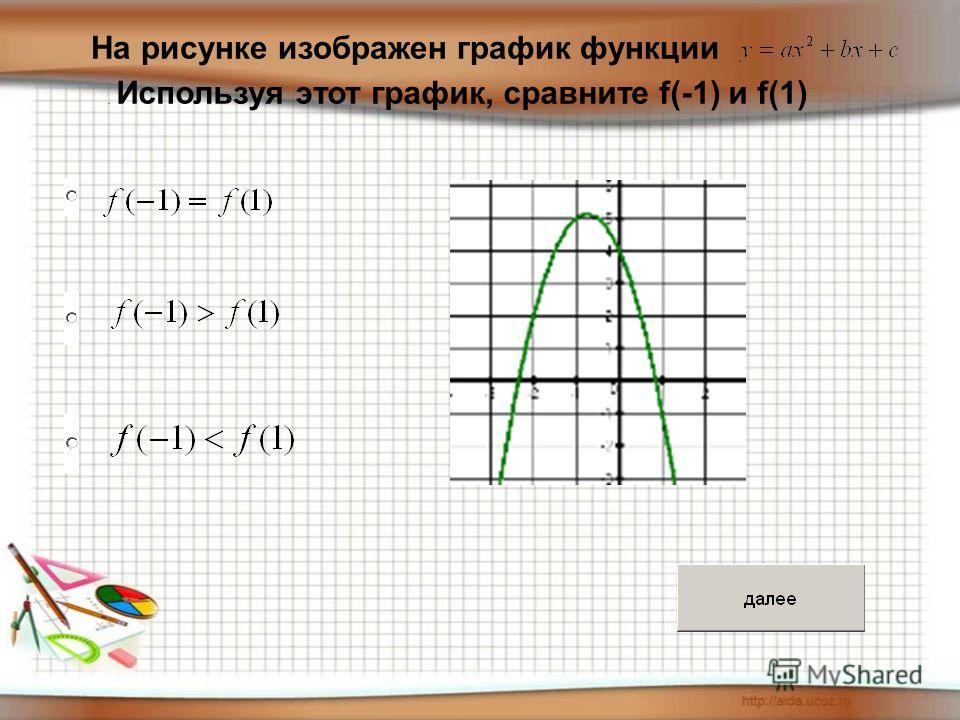  д.

Эта цифра,

показывает график для родительской функции квадратного корня

Обратите внимание, что значения, которые вы получаете, нанося последовательные точки, не дают вам самых хороших чисел. Вместо этого попробуйте выбрать значения, для которых вы можете легко найти квадратный корень. Вот как это работает: начните с (0,sqrt(0))=(0,0), затем перейдите к (1,sqrt(1))=(1,1), затем к (4,sqrt(4)) =(4,2), затем в (9,sqrt(9))=(9,3) и т.д.

Графики функций абсолютного значения

Родительский график абсолютного значения функции г = | х | превращает все входы в неотрицательные (0 или положительные). Чтобы построить график функций абсолютного значения, вы начинаете с начала координат, а затем каждое положительное число сопоставляется само с собой, а каждое отрицательное число сопоставляется со своим положительным аналогом.

На этом рисунке показан график функции абсолютного значения.

Графики кубических функций

В кубической функции высшая степень любой переменной равна трем.