Корни этого ур-ния $$x_{1} = 0$$ $$x_{2} = 3.28103090528$$ $$x_{3} = -0.373548376565$$ Зн. экстремумы в точках:
(0, -1)
(3.28103090528, 1.01984828342285)
(-0.373548376565, -0.977554081645009)
Интервалы возрастания и убывания функции:
Найдём интервалы, где функция возрастает и убывает, а также минимумы и максимумы функции, для этого смотрим как ведёт себя функция в экстремумах при малейшем отклонении от экстремума:
Минимумы функции в точках: $$x_{3} = 0$$ Максимумы функции в точках: $$x_{3} = 3.28103090528$$ $$x_{3} = -0.373548376565$$ Убывает на промежутках
(-oo, -0.373548376565] U [0, oo)
Возрастает на промежутках
(-oo, 0] U [3.28103090528, oo)
Также можно найти производную этой функции онлайн https://www.kontrolnaya-rabota.ru/s/proizvodnaya-funktsii/one/ — приравниваем ее к нулю и находим корни уравнения. Эти корни и будут экстремумами этой функции.
Вообще — зачем нужен экстремум?
В некоторых задачах физики и экономики требуется знать при каких условиях данная величина (функция) имеет максимум или минимум — в помощь и приходит теория экстремума функции
Определение экстремума функции
Экстремумом функции называется такая точка x, при которой производная этой функции равна нулю
исследование на экстремум функции онлайн
Вы искали исследование на экстремум функции онлайн? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и исследование функции на экстремум онлайн, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как исследование на экстремум функции онлайн,исследование функции на экстремум онлайн,исследование функции онлайн на экстремум,исследовать на экстремум функцию калькулятор онлайн,исследовать на экстремум функцию онлайн,исследовать на экстремум функцию онлайн калькулятор,исследовать на экстремум функцию онлайн с подробным решением,исследовать функцию двух переменных на экстремум онлайн калькулятор,исследовать функцию на экстремум онлайн,исследовать функцию на экстремум онлайн калькулятор,исследовать функцию на экстремум онлайн с подробным решением,исследуйте на экстремум функцию онлайн,калькулятор онлайн экстремумы функции,критические точки функции онлайн,максимум и минимум функции онлайн,максимум функции онлайн,минимум и максимум функции онлайн,минимум функции онлайн,найдите экстремумы функции,найти критические точки функции онлайн,найти максимум и минимум функции калькулятор онлайн,найти максимум и минимум функции онлайн,найти максимум и минимум функции онлайн калькулятор,найти максимум функции онлайн,найти максимум функции онлайн калькулятор,найти минимум и максимум функции калькулятор онлайн,найти минимум и максимум функции онлайн,найти минимум и максимум функции онлайн калькулятор,найти минимум функции онлайн,найти наибольшее значение функции на отрезке онлайн калькулятор,найти наибольшее значение функции онлайн,найти наименьшее значение функции онлайн,найти стационарную точку функции онлайн,найти стационарные точки функции онлайн,найти точки максимума и минимума функции онлайн,найти точки минимума и максимума функции онлайн,найти точки экстремума,найти точки экстремума функции онлайн,найти точки экстремума функции онлайн калькулятор с решением,найти точку максимума функции онлайн,найти точку максимума функции онлайн с решением,найти точку минимума функции онлайн,найти условный экстремум функции онлайн,найти экстремум,найти экстремум функции онлайн,найти экстремум функции онлайн калькулятор с решением,найти экстремумы,найти экстремумы функции,найти экстремумы функции онлайн,найти экстремумы функции онлайн с решением,нахождение максимума и минимума функции онлайн,нахождение минимума и максимума функции онлайн,нахождение точки минимума функции онлайн,онлайн калькулятор исследовать на экстремум функцию,онлайн калькулятор исследовать функцию на экстремум,онлайн минимум функции,онлайн нахождение минимума функции,стационарные точки функции онлайн,стационарными точками функции онлайн,точка максимума функции онлайн калькулятор,точки максимума и минимума функции онлайн,точки минимума и максимума функции онлайн,точки экстремума онлайн,точки экстремума функции онлайн,экстремум онлайн,экстремум функции онлайн,экстремум функции трех переменных онлайн,экстремумы онлайн,экстремумы функции двух переменных онлайн,экстремумы функции онлайн,экстремумы функции онлайн калькулятор.
Где можно решить любую задачу по математике, а так же исследование на экстремум функции онлайн Онлайн?
Решить задачу исследование на экстремум функции онлайн вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Экстремумы функции
На этой странице вы сможете посмотреть несколько примеров для нахождения экстремумов функции, в каждом из них есть своя уникальность, поэтому рекомендую посмотреть все.
Здесь часто используется нахождение производной, что бы лучше понимать, как её надо находить, то сначала посмотрите мои таблицу производных.
- Имеем функцию:
Найдём её производную:
Прировняем производную к нулю и найдём значение переменной.
Наносим x=0 на координатную прямую и смотрим, где производная будет отрицательной, а где положительной. То есть до нашей точки (для этого берём любое значение до ноля ну, например, -1 и подставляем его в формулу с производной, видим что выйдем -2, то есть знак минус) и после неё (всё точно также берём любое число по праву сторону от ноля, например, 1 результат будет 2 – значит знак плюс).
Видим, что при прохождении через точку
- Всё аналогично делаем и в следующем примере.
Наносим точку x=0 на координатную прямую, и вычисляем соответствующие значения.
Видим, что здесь знак производной не меняется, то есть данная точка не будет экстремумом. - Приступим к следующему примеру:
Как всегда найдём производную и прировняем её к нулю. Поскольку в нас дробь, то к нолю надо приравнивать, только числитель.
Ещё надо учитывать
Наносим все эти данные на координатную прямую и находим знак производной на каждом из промежутков.
Видим, что при прохождении через точки -1 и 1 производная не меняет знака, эти точки не будут экстремумами, а при прохождении через 0 меняет с плюса на минус, поэтому точка x=0 будет максимумом. - Ну и рассмотрим ещё один небольшой пример:
Опять находим производную и приравниваем её к нолю:
Полученные значения переменных наносим на координатную прямую и высчитываем знак производной на каждом из промежутков. Ну например, для первого возьмём
Видим, что при прохождении через точку -1 производная меняет знак с минуса на плюс, то есть это будет минимум, а при прохождении через 1 – меняет знак и плюса на минус, соответственно это будет максимум.
Материалы по теме:
Поделиться с друзьями:
Загрузка…Экстремумы функции (Лекция №9)

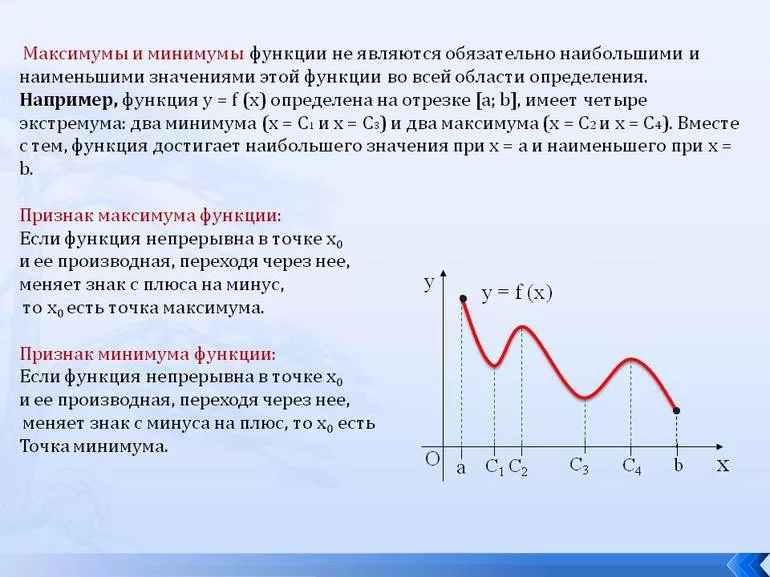
Значение функции в точке x1 будет больше значений функции во всех соседних точках как слева, так и справа от x1. В этом случае говорят, что функция имеет в точке x1 максимум. В точке x3 функция, очевидно, также имеет максимум. Если рассмотреть точку x2, то в ней значение функции меньше всех соседних значений. В этом случае говорят, что функция имеет в точке x2 минимум. Аналогично для точки x4.
Функция y=f(x) в точке x0 имеет максимум, если значение функции в этой точке больше, чем ее значения во всех точках некоторого интервала, содержащего точку x0, т.е. если существует такая окрестность точки x0, что для всех x≠x0, принадлежащих этой окрестности, имеет место неравенство f(x)<f(x0).
Функция y=f(x) имеет минимум в точке x0, если существует такая окрестность точки x0, что для всех x≠x0, принадлежащих этой окрестности, имеет место неравенство f(x)>f(x0.
Точки, в которых функция достигает максимума и минимума, называются точками экстремума, а значения функции в этих точках экстремумами функции.
Обратим внимание на то, что функция, определенная на отрезке, может достигать максимума и минимума только в точках, заключенных внутри рассматриваемого отрезка.
Отмети, что если функция
имеет в точке максимум, то это не означает, что в этой точке функция имеет
наибольшее значение во всей области определения. На рисунке, рассмотренном выше,
функция в точке x1 имеет максимум, хотя
есть точки, в которых значения функции больше, чем в точке x1. В частности, f(x1) < f(x4)
т.е. минимум функции больше максимума. Из определения максимума следует только,
что это самое большое значение функции в точках, достаточно близкихк точке максимума.
В частности, f(x1) < f(x4)
т.е. минимум функции больше максимума. Из определения максимума следует только,
что это самое большое значение функции в точках, достаточно близкихк точке максимума.
Теорема 1. (Необходимое условие существования экстремума.) Если дифференцируемая функция y=f(x) имеет в точке x= x0 экстремум, то ее производная в этой точке обращается в нуль.
Доказательство. Пусть для определенности в точке x0 функция имеет максимум. Тогда при достаточно малых приращениях Δx имеем f(x0+ Δx)<f(x0), т.е. Но тогда
Переходя в этих неравенствах к пределу при Δx→ 0 и учитывая, что производная f ‘(x0) существует, а следовательно предел, стоящий слева, не зависит от того как Δx → 0, получаем: при Δx → 0 – 0 f’(x0) ≥ 0 а при Δx → 0 + 0 f’(x0) ≤ 0. Так как f ‘(x0) определяет число, то эти два неравенства совместны только в том случае, когда f ‘(x0) = 0.
Доказанная теорема утверждает, что точки максимума и минимума могут находиться только среди тех значений аргумента, при которых производная обращается в нуль.
Мы рассмотрели случай, когда функция во всех точках некоторого отрезка имеет производную. Как же обстоит дело в тех случаях, когда производная не существует? Рассмотрим примеры.
Примеры.
- y=|x|.
Функция не имеет производной в точке x=0 (в этой точке график функции не имеет определенной касательной), но в этой точке функция имеет минимум, так как y(0)=0, а при всех x≠ 0y > 0.
-
Функция не имеет производной при x=0, так как обращается в бесконечность приx=0.
 Но в этой точке функция имеет максимум.
Но в этой точке функция имеет максимум. -
Функция не имеет производной при x=0, так как при x→0. В этой точке функция не имеет ни максимума, ни минимума. Действительно, f(x)=0 и при x<0f(x)<0, а при x>0f(x)>0.
Таким образом, из приведенных примеров и сформулированной теоремы видно, что функция может иметь экстремум лишь в двух случаях: 1) в точках, где производная существует и равна нулю; 2) в точке, где производная не существует.
Однако, если в некоторой точке x0 мы знаем, что f ‘(x0)=0, то отсюда нельзя делать вывод, что в точке x0 функция имеет экстремум.
Например. .
Но точка x=0 не является точкой экстремума, поскольку слева от этой точки значения функции расположены ниже оси Ox, а справа выше.
Значения аргумента из области определения функции, при которых производная функции обращается в нуль или не существует, называются критическими точками.
Из всего вышесказанного следует, что точки экстремума функции находятся среди критических точек, и, однако, не всякая критическая точка является точкой экстремума. Поэтому, чтобы найти экстремум функции, нужно найти все критические точки функции, а затем каждую из этих точек исследовать отдельно на максимум и минимум. Для этого служит следующая теорема.
Теорема 2. (Достаточное условие существования экстремума.) Пусть функция непрерывна на некотором интервале, содержащем критическую точку x0, и дифференцируема во всех точках этого интервала (кроме, быть может, самой точки x0). Если при переходе слева направо через эту точку производная меняет знак с плюса на минус, то в точке x = x0 функция имеет максимум.
 Если же при переходе через x0
слева направо производная меняет знак с минуса на плюс, то функция имеет в этой
точке минимум.
Если же при переходе через x0
слева направо производная меняет знак с минуса на плюс, то функция имеет в этой
точке минимум.Таким образом, если
- f ‘(x)>0 при x<x0 и f ‘(x)<0 при x> x0, то x0 – точка максимума;
- при x<x0 и f ‘(x)>0 при x> x0, то x0 – точка минимума.
Доказательство. Предположим сначала, что при переходе через x0 производная меняет знак с плюса на минус, т.е. при всех x, близких к точке x0f ‘(x)>0 для x< x0, f ‘(x)<0 для x> x0. Применим теорему Лагранжа к разности f(x) — f(x0) = f ‘(c)(x- x0), где c лежит между x и x0.
- Пусть x < x0. Тогда c< x0 и f ‘(c)>0. Поэтомуf ‘(c)(x- x0)<0и, следовательно,
f(x) — f(x0)<0,т.е. f(x)< f(x0).
- Пусть x > x0. Тогда c> x0 и f ‘(c)<0. Значитf ‘(c)(x- x0)<0. Поэтому f(x) — f(x0)<0,т.е.f(x) < f(x0).
Таким образом, для всех значений x достаточно близких к x0f(x) < f(x0). А это значит, что в точке x0 функция имеет максимум.
Аналогично доказывается вторая часть теоремы о минимуме.
Проиллюстрируем смысл этой теоремы на рисунке. Пусть f ‘(x1)=0 и для любых x, достаточно близких к x1, выполняются неравенства
f ‘(x)<0 при x< x1, f ‘(x)>0 при x> x1.

Тогда слева от точки x1 функция возрастает, а справа убывает, следовательно, при x = x1 функция переходит от возрастания к убыванию, то есть имеет максимум.
Аналогично можно рассматривать точки x2 и x3.
Схематически все вышесказанное можно изобразить на картинке:Правило исследования функции y=f(x) на экстремум
- Найти область определения функции f(x).
- Найти первую производную функции f ‘(x).
- Определить критические
точки, для этого:
- найти действительные корни уравнения f ‘(x)=0;
- найти все значения x при которых производная f ‘(x) не существует.
- Определить знак производной слева и справа от критической точки. Так как знак производной остается постоянным между двумя критическими точками, то достаточно определить знак производной в какой-либо одной точке слева и в одной точке справа от критической точки.
- Вычислить значение функции в точках экстремума.
Примеры. Исследовать функции на минимум и максимум.
- . Область определения функции D(y)=R.
Найдем производную заданной функции
Определим критические точки . Производная не существует при х2= 0. Следовательно, критические точки: 0 и 2/5. Нанесем их на числовую ось и определим знак производной на каждом из полученных промежутков.
-
Критическая точка функции x =3. Точка x= –1 не входит в область определения функции.
НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ ФУНКЦИИ НА ОТРЕЗКЕ
Наибольшим значением функции на отрезке называется самое большое из всех ее значений на этом отрезке, а наименьшим – самое маленькое из всех ее значений.

Рассмотрим функцию y=f(x) непрерывную на отрезке [a, b]. Как известно, такая функция достигает своего наибольшего и наименьшего значений, либо на границе отрезка, либо внутри него. Если наибольшее или наименьшее значение функции достигается во внутренней точке отрезка, то это значение является максимумом или минимумом функции, то есть достигается в критических точках.
Таким образом, получаем следующее правило нахождения наибольшего и наименьшего значений функции на отрезке[a, b]:
- Найти все критические точки функции в интервале (a, b) и вычислить значения функции в этих точках.
- Вычислить значения функции на концах отрезка при x = a, x = b.
- Из всех полученных значений выбрать наибольшее и наименьшее.
Примеры.
- Найти наибольшее и наименьшее значения функции на отрезке [–2; –0,5].
Найдем критические точки функции.
Вычислим значения функции в найденной точке и на концах заданного отрезка.
Итак,
- Найти наибольшее и наименьшее значения функцииy=x-2·ln x на [1; e].
- Чему равна наименьшая площадь боковой поверхности
прямого кругового конуса объема 3π?
По теореме Пифагора
.
Следовательно, .
.
Найдем критические точки функции S: S‘ = 0, т.е.
Покажем, что при найденном значении h функция Sбок достигает минимума.
.
Найти радиус основания и высоту цилиндра наибольшего объема, который можно вписать в шар радиусом R.
Пусть r – радиус основания цилиндра, h – высота.
 2
2
Поиск корней и экстремумов функции. Построение графика
Поиск корней и экстремумов функции. Построение графика
Задание: отделить корни уравнения f(x)=0, предварительно проанализировав область определения аргумента х. Используя процедуру Поиск решения найти: А) все корни данного уравнения Б) все имеющиеся экстремумы данной функции. Построить график функции на конечном отрезке.
х3+х2+3=0
Решение:
Область определения функции (-∞;+∞)
Составим таблицу знаков функции f(x), полагая x равным:
a) критическим значениям функции (корням производной) или близким к ним;
b) граничным значениям (исходя из области допустимых значений неизвестного).
Имеем: 3х2+2х
Производная имеет 2 корня: x1=0; x2=-2/3x
— ∞
-2/3
0
+ ∞
знак f(x)
—
+
+
+
Из таблицы видно, что функция 1 раз меняет знак, значит уравнение имеет 1 корень.
Уменьшим промежуток, в котором находится корень:x
— 2
-2/3
знак f(x)
—
+
Следовательно, x1 принадлежит промежутку ( -2; -2/3 ) .
 2+3. Эту формулу вставим в ячейку В1
2+3. Эту формулу вставим в ячейку В1
Выберем Сервис→Поиск решения. Установим параметры:Получим корень уравнения x1=-1.864 y=0
б) все экстремумы данной функции.
Найдем экстремумы функции с помощью команды Данные→Поиск решения. Установим параметры для поиска максимума:Получим максимум в точке х=-0.667, y=3.148:
Найдем минимум функции с помощью процедуры Поиск решения. Введем параметры:
Получим минимум в точке х=0, y=3.Введем таблицу значений функции на промежутке [-2;1] с шагом 0,2. На основании данных таблицы построим график функции f(x). Для этого выберем команду главного меню Вставка→Диаграмма.
Получим график функцииЭкстремальные значения функции. Экстремумы функции: признаки существования, примеры решений
Функцияy = f(x) называется возрастающей (убывающей ) в некотором интервале, если при x 1 f(x 2)).
Если дифференцируемая функцияy = f(x) на отрезке возрастает (убывает), то ее производная на этом отрезке f » (x) > 0 , (f » (x)
Точкаx о называется точкой локального максимума (минимума ) функции f(x), если существует окрестность точки x о , для всех точек которой верно неравенство f(x) ≤ f(x о), (f(x) ≥f(x о)).
Точки максимума и минимума называются точками экстремума , а значения функции в этих точках — ее экстремумами.
Точки экстремума
Необходимые условия экстремума . Если точка x о является точкой экстремума функции f(x), то либо f » (x о) = 0, либо f (x о) не существует. Такие точки называют критическими, причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек.

Первое достаточное условие. Пусть x о — критическая точка. Если f » (x) при переходе через точку x о меняет знак плюс на минус, то в точке x о функция имеет максимум, в противном случае — минимум. Если при переходе через критическую точку производная не меняет знак, то в точке x о экстремума нет.
Второе достаточное условие. Пусть функция f(x) имеет f » (x) в окрестности точки x о и вторую производную f «» (x 0) в самой точке x о . Если f » (x о) = 0, f «» (x 0)>0, (f «» (x 0) x о является точкой локального минимума (максимума) функции f(x). Если же f «» (x 0)=0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие .
На отрезке функция y =f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка .
Пример 3.22. Найти экстремумы функции f(x) = 2x 3 — 15x 2 + 36x — 14.
Решение. Так как f » (x) = 6x 2 — 30x +36 = 6(x -2)(x — 3), то критические точки функции x 1 = 2 и x 2 = 3. Экстремумы могут быть только в этих точках. Так как при переходе через точку x 1 = 2 производная меняет знак плюс на минус, то в этой точке функция имеет максимум. При переходе через точку x 2 = 3 производная меняет знак минус на плюс, поэтому в точке x 2 = 3 у функции минимум. Вычислив значения функции в точках x 1 = 2 и x 2 = 3, найдем экстремумы функции: максимум f(2) = 14 и минимум f(3) = 13.
Задачи на нахождения экстремума функции
Пример 3.23. a
Решение. x и y . Площадь площадки равна S =xy. Пусть y — это длина стороны, примыкающей к стене. Тогда по условию должно выполняться равенство 2x +y =a. Поэтому y = a — 2x и S =x(a — 2x), где 0 ≤x ≤a/2 (длина и ширина площадки не могут быть отрицательными). S » = a — 4x, a — 4x = 0 при x = a/4, откуда y = a — 2×a/4 = a/2. Поскольку x = a/4 — единственная критическая точка, проверим, меняется ли знак производной при переходе через эту точку.
 При x 0, а при x > a/4, S »
При x 0, а при x > a/4, S »Пример 3.24.
Решение.
R = 2, Н = 16/4 = 4.Пример 3.22. Найти экстремумы функцииf(x) = 2x 3 — 15x 2 + 36x — 14.
Решение. Так как f » (x) = 6x 2 — 30x +36 = 6(x -2)(x — 3), то критические точки функции x 1 = 2 и x 2 = 3. Экстремумы могут быть только в этих точках. Так как при переходе через точку x 1 = 2 производная меняет знак плюс на минус, то в этой точке функция имеет максимум. При переходе через точку x 2 = 3 производная меняет знак минус на плюс, поэтому в точке x 2 = 3 у функции минимум. Вычислив значения функции в точках x 1 = 2 и x 2 = 3, найдем экстремумы функции: максимумf(2) = 14 и минимумf(3) = 13.
Пример 3.23. Нужно построить прямоугольную площадку возле каменной стены так, чтобы с трех сторон она была отгорожена проволочной сеткой, а четвертой стороной примыкала к стене. Для этого имеетсяa погонных метров сетки. При каком соотношении сторон площадка будет иметь наибольшую площадь?
Решение. Обозначим стороны площадки черезx иy . Площадь площадки равна S = xy. Пусть y — это длина стороны, примыкающей к стене. Тогда по условию должно выполняться равенство 2x +y =a. Поэтому y = a — 2x и S = x(a — 2x), где
0 ≤x ≤a/2 (длина и ширина площадки не могут быть отрицательными). S » = a — 4x, a — 4x = 0 при x = a/4, откуда
y = a — 2a/4 = a/2. Поскольку x = a/4 — единственная критическая точка, проверим, меняется ли знак производной при переходе через эту точку. Приx 0, а при x >a/4 S »Пример 3.24. Требуется изготовить закрытый цилиндрический бак вместимостью V=16p ≈ 50 м 3 . Каковы должны быть размеры бака (радиус R и высота Н), чтобы на его изготовление пошло наименьшее количество материала?
Решение. Площадь полной поверхности цилиндра равна S = 2pR(R+Н). Мы знаем объем цилиндра V = pR 2 Н Þ Н = V/pR 2 =16p/ pR 2 = 16/ R 2 . Значит, S(R) = 2p(R 2 +16/R). Находим производную этой функции:
S » (R) = 2p(2R- 16/R 2) = 4p (R- 8/R 2). S » (R) = 0 при R 3 = 8, следовательно,
S » (R) = 0 при R 3 = 8, следовательно,
R = 2, Н = 16/4 = 4.Прежде, чем научиться находить экстремумы функции, необходимо понять, что же такое экстремум. Самое общее определение экстремума гласит, что это употребляемое в математике наименьшее или наибольшее значение функции на определенном множестве числовой линии или графике. В том месте, где находится минимум, появляется экстремум минимума, а там, где максимум – экстремум максимума. Также в такой дисциплине, как математический анализ, выделяют локальные экстремумы функции. Теперь давайте рассмотрим, как найти экстремумы.
Экстремумы в математике относятся к важнейшим характеристикам функции, они показывают её самое большое и самое маленькое значение. Находятся экстремумы преимущественно в критических точках находимых функций. Стоит отметить, что именно в точке экстремума функция кардинально меняет своё направление. Если просчитать производную от точки экстремума, то она, согласно определению, должна быть равна нулю или же вовсе будет отсутствовать. Таким образом, чтобы узнать, как найти экстремум функции, необходимо выполнить две последовательные задачи:
- найти производную для той функции, которую необходимо определить заданием;
- найти корни уравнения.
Последовательность нахождения экстремума
- Оформите в письменном виде функцию f(x), которая задана. Найдите её производную первого порядка f «(x). То выражение, которое получится, приравняйте к нулю.
- Теперь вам предстоит решить то уравнение, которое получилось. Результирующие решения и будут корнями уравнения, а также критическими точками определяемой функции.
- Теперь определяем, какими именно критическими точками (максимума или минимума) являются найденные корни. Следующим этапом, после того, как мы узнали, как находить точки экстремума функции, является нахождение второй производной от искомой функции f » (x). Необходимо будет подставить в конкретное неравенство значения найденных критических точек и затем посчитать, что получится.
 Если произойдет так, что вторая производная окажется больше нуля в критической точке, то ею и будет являться точка минимума, а в противном случае – это будет точка максимума.
Если произойдет так, что вторая производная окажется больше нуля в критической точке, то ею и будет являться точка минимума, а в противном случае – это будет точка максимума. - Остаётся посчитать значение начальной функции в необходимых точках максимума и минимума функции. Чтобы это сделать, подставляем полученные значения в функцию и рассчитываем. Однако стоит отметить, что, если критическая точка оказалась максимумом, то и экстремум будет максимальным, а если минимумом, то минимальным по аналогии.
Алгоритм нахождения экстремума
Чтобы обобщить полученные знания, составим краткий алгоритм того, как находить точки экстремума.
- Находим область определения заданной функции и её интервалы, которые точно определяют, на каких промежутках функция непрерывна.
- Находим производную от функции f «(x).
- Вычисляем критические точки уравнения y = f (x).
- Анализируем изменения направления функции f (x), а также знак производной f «(x) там, где критические точки разделяют область определения данной функции.
- Теперь определяем, является ли каждая точка на графике максимумом или минимумом.
- Находим значения функции в тех точках, которые являются экстремумами.
- Фиксируем результат данного исследования – экстремумы и промежутки монотонности. Вот и все. Теперь мы рассмотрели, как можно найти экстремум на любом промежутке. Если вам необходимо найти экстремум на определенном промежутке функции, то делается это аналогичным образом, только обязательно учитываются границы производимого исследования.
Итак, мы рассмотрели, как найти точки экстремума функции. При помощи несложных вычислений, а также знаний о нахождении производных, можно найти любой экстремум и вычислить его, а также графически его обозначить. Нахождение экстремумов является одним из важнейших разделов математики, как в школе, так и в Высшем учебном заведении, поэтому, если вы научитесь правильно их определять, то учиться станет намного проще и интереснее.

Это довольно-таки занятный раздел математики, с которым сталкиваются абсолютно все ученики выпускных классов и студенты. Тем не менее далеко не каждому нравится матан. Некоторые не могут понять даже элементарных вещей наподобие, казалось бы, стандартного исследования функции. Данная статья призвана исправить подобную оплошность. Хотите поподробнее узнать об анализе функции? Желаете узнать, что такое точки экстремума и как их найти? Тогда данная статья для вас.
Исследование графика функции
Для начала стоит понять, зачем вообще необходимо анализировать график. Существуют простые функции, начертить которые не составит труда. Ярким примером подобной функции может служить парабола. Начертить ее график не составит труда. Все что необходимо, так это с помощью простого преобразования найти числа, при которых функция принимает значение 0. И в принципе это все что знать для того, чтобы начертить график параболы.
Но что делать, если функция, график которой нам нужно начертить, намного сложнее? Поскольку свойства сложных функций довольно-таки неочевидны, необходимо проводить целый анализ. Только после этого можно изобразить функцию графически. Как же это сделать? Ответ на этот вопрос вы сможете найти в данной статье.
План анализа функции
Первое, что необходимо сделать, так это провести поверхностное исследование функции, в ходе которого мы найдем область определения. Итак, начнем по порядку. Область определения — это совокупность тех значений, которыми функция задается. Проще говоря, это те числа, которые можно использовать в функции вместо х. Для того чтобы определить область определения, необходимо просто взглянуть на запись. К примеру, очевидно, что у функции у (х) = х 3 + х 2 — х + 43 область определения — множество действительных чисел. Ну а с функцией наподобие (х 2 — 2х)/х все немного иначе. Поскольку число в знаменателе не должно равняться 0, то областью определения данной функции будут все действительные числа, помимо нуля.
Далее необходимо найти так называемые нули функции.
 Это те значения аргумента, при которых вся функция принимает значения ноль. Для этого необходимо приравнять функцию к нулю, подробно ее рассмотреть и совершить некоторые преобразования. Возьмём уже знакомую нам функцию у(х) = (х 2 — 2х)/х. Из школьного курса мы знаем, что дробь равна 0 тогда, когда числитель равен нулю. Поэтому знаменатель мы отбрасываем и начинаем работать с числителем, приравнивая его к нулю. Получаем х 2 — 2х = 0 и выносим х за скобочки. Отсюда х (х — 2) = 0. В итоге получаем, что наша функция равна нулю тогда, когда х равняется 0 или же 2.
Это те значения аргумента, при которых вся функция принимает значения ноль. Для этого необходимо приравнять функцию к нулю, подробно ее рассмотреть и совершить некоторые преобразования. Возьмём уже знакомую нам функцию у(х) = (х 2 — 2х)/х. Из школьного курса мы знаем, что дробь равна 0 тогда, когда числитель равен нулю. Поэтому знаменатель мы отбрасываем и начинаем работать с числителем, приравнивая его к нулю. Получаем х 2 — 2х = 0 и выносим х за скобочки. Отсюда х (х — 2) = 0. В итоге получаем, что наша функция равна нулю тогда, когда х равняется 0 или же 2.Во время исследования графика функции многие сталкиваются с проблемой в виде точек экстремума. И это странно. Ведь экстремумы — это довольно-таки простая тема. Не верите? Убедитесь сами, прочитав данную часть статьи, в которой мы поговорим о точках минимума и максимума.
Для начала стоит разобраться в том, что собой представляет экстремум. Экстремум — это предельное значений, которое достигает функция на графике. Отсюда получается, что существует два крайних значения — максимум и минимум. Для наглядности можно посмотреть на картинку, что расположена выше. На исследованной области точка -1 является максимумом функции у (х) = х 5 — 5х, а точка 1, соответственно, минимумом.
Также не стоит путать между собой понятия. Точки экстремума функции — это те аргументы, при которых заданная функция приобретает крайние значения. В свою очередь, экстремумом называют значение минимумов и максимумов функции. К примеру, вновь рассмотрим рисунок выше. -1 и 1 — это точки экстремума функции, а 4 и -4 — это сами экстремумы.
Нахождение точек экстремума
Но как все-таки найти точки экстремума функции? Все довольно-таки просто. Первое, что необходимо сделать — найти производную уравнения. Допустим, мы получили задание: «Найдите точки экстремума функции y (x), x — аргумент. Для наглядности возьмем функцию у (х) = х 3 + 2х 2 + х + 54. Проведем дифференцирование и получим следующее уравнение: 3х 2 + 4х + 1.
 В итоге мы получили стандартное квадратное уравнение. Все, что необходимо сделать дальше — приравнять его к нулю и найти корни. Поскольку дискриминант больше нуля (D = 16 — 12 = 4), данное уравнение определяется двумя корнями. Находим их и получаем два значения: 1/3 и -1. Это и будут точки экстремума функции. Однако как все-таки определить, кто есть кто? Какая точка является максимумом, а какая минимумом? Для этого нужно взять соседнюю точку и узнать ее значение. К примеру, возьмем число -2, которое находится слева по координатной прямой от -1. Подставляем это значение в наше уравнение у(-2) = 12 — 8 + 1 = 5. В итоге мы получили положительное число. Это значит, что на промежутке от 1/3 до -1 функция возрастает. Это, в свою очередь, обозначает, что на промежутках от минус бесконечности до 1/3 и от -1 до плюс бесконечности функция убывает. Таким образом, можно сделать вывод, что число 1/3 — точка минимума функции на исследованном промежутке, а -1 — точка максимума.
В итоге мы получили стандартное квадратное уравнение. Все, что необходимо сделать дальше — приравнять его к нулю и найти корни. Поскольку дискриминант больше нуля (D = 16 — 12 = 4), данное уравнение определяется двумя корнями. Находим их и получаем два значения: 1/3 и -1. Это и будут точки экстремума функции. Однако как все-таки определить, кто есть кто? Какая точка является максимумом, а какая минимумом? Для этого нужно взять соседнюю точку и узнать ее значение. К примеру, возьмем число -2, которое находится слева по координатной прямой от -1. Подставляем это значение в наше уравнение у(-2) = 12 — 8 + 1 = 5. В итоге мы получили положительное число. Это значит, что на промежутке от 1/3 до -1 функция возрастает. Это, в свою очередь, обозначает, что на промежутках от минус бесконечности до 1/3 и от -1 до плюс бесконечности функция убывает. Таким образом, можно сделать вывод, что число 1/3 — точка минимума функции на исследованном промежутке, а -1 — точка максимума.Также стоит отметить, что на ЕГЭ требуют не просто найти точки экстремума, Но и провести с ними какую-то операцию (прибавить, умножить и т.д.). Именно по этой причине стоит обратить особое внимание на условия задачи. Ведь из-за невнимательности можно потерять баллы.
С помощью данного сервиса можно найти наибольшее и наименьшее значение функции одной переменной f(x) с оформлением решения в Word . Если же задана функция f(x,y) , следовательно, необходимо найти экстремум функции двух переменных . Также можно найти интервалы возрастания и убывания функции .
Правила ввода функций :
Необходимое условие экстремума функции одной переменной
Уравнение f» 0 (x *) = 0 — это необходимое условие экстремума функции одной переменной, т.е. в точке x * первая производная функции должна обращаться в нуль. Оно выделяет стационарные точки x с, в которых функция не возрастает и не убывает.Достаточное условие экстремума функции одной переменной
Пусть f 0 (x) дважды дифференцируемая по x , принадлежащему множеству D . Если в точке x * выполняется условие:
Если в точке x * выполняется условие:F» 0 (x *) = 0
f»» 0 (x *) > 0То точка x * является точкой локального (глобального) минимума функции.
Если в точке x * выполняется условие:
F» 0 (x *) = 0
f»» 0 (x *)То точка x * — локальный (глобальный) максимум.
Пример №1 . Найти наибольшее и наименьшее значения функции: на отрезке .
Решение.
Критическая точка одна x 1 = 2 (f’(x)=0). Эта точка принадлежит отрезку . (Точка x=0 не является критической, так как 0∉).
Вычисляем значения функции на концах отрезка и в критической точке.
f(1)=9, f(2)= 5 / 2 , f(3)=3 8 / 81
Ответ: f min = 5 / 2 при x=2; f max =9 при x=1Пример №2 . С помощью производных высших порядков найти экстремум функции y=x-2sin(x) .
Решение.
Находим производную функции: y’=1-2cos(x) . Найдем критические точки: 1-cos(x)=2, cos(x)=½, x=± π / 3 +2πk, k∈Z. Находим y’’=2sin(x), вычисляем , значит x= π / 3 +2πk, k∈Z – точки минимума функции; , значит x=- π / 3 +2πk, k∈Z – точки максимума функции.Пример №3 . Исследовать на экстремум фцнкцию в окрестностях точки x=0.
Решение. Здесь необходимо найти экстремумы функции. Если экстремум x=0 , то выяснить его тип (минимум или максимум). Если среди найденных точек нет x = 0, то вычислить значение функции f(x=0).
Следует обратить внимание, что когда производная с каждой стороны от данной точки не меняет своего знака, не исчерпываются возможные ситуации даже для дифференцируемых функций: может случиться, что для сколь угодно малой окрестности по одну из сторон от точки x 0 или по обе стороны производная меняет знак. В этих точках приходится применять другие методы для исследования функций на экстремум.Пример №4 . Разбить число 49 на два слагаемых, произведение которых будет наибольшим.
Решение. Обозначим x — первое слагаемое. Тогда (49-x) — второе слагаемое.
Произведение будет максимальным: x·(49-x) → max
или
49x — x 2Наибольший объем цилиндра
Найти размеры цилиндра наибольшего объема, изготовленного из заготовки в форме шара радиуса R .
Решение:
Объем цилиндра равен: V = πr 2 H
где H = 2h,
Подставим эти значения в целевую функцию.V → max
Найдем экстремум функции. Поскольку функция объема V(h) зависит только от одной переменной, то найдем производную с помощью сервисаИз данной статьи читатель узнает о том, что такое экстремум функционального значения, а также об особенностях его использования в практической деятельности. Изучение такого концепта крайне важно для понимания основ высшей математики. Эта тема является основополагающей для более глубокого изучения курса.
Вконтакте
Что такое экстремум?
В школьном курсе дается множество определений понятия «экстремум». Данная статья призвана дать самое глубокое и четкое представление о термине для несведущих в вопросе лиц. Итак, под термином понимают, насколько функциональный промежуток приобретает минимальное либо максимальное значение на том или ином множестве.
Экстремум – это и минимальное значение функции, и максимальное одновременно. Различают точку минимума и точку максимума, то есть крайние значения аргумента на графике. Основные науки, в которых используют данный концепт:
- статистика;
- машинное управление;
- эконометрика.
Точки экстремума играют важную роль в определении последовательности заданной функции. Система координат на графике в лучшем виде показывает изменение экстремального положения в зависимости от изменения функциональности.
Экстремумы производной функции
Имеет также место такое явление, как «производная». Она необходима для определения точки экстремума. Важно не путать точки минимума либо максимума с наибольшим и наименьшим значением. Это разные понятия, хотя могут показаться похожими.
Значение функции является основным фактором для определения того, как найти точку максимума. Производная не образуется от значений, а исключительно от крайнего ее положения в том или ином его порядке.
Сама же по себе производная определяется на основе данных точек экстремума, а не наибольшего или наименьшего значения.
 В российских школах недостаточно четко проводят грань между этими двумя концептами, что влияет на понимание данной темы вообще.
В российских школах недостаточно четко проводят грань между этими двумя концептами, что влияет на понимание данной темы вообще.Давайте теперь рассмотрим такое понятие как «острый экстремум». На сегодняшний день выделяют острый минимум значения и острый максимум значения. Определение дано в соответствии с российской классификацией критических точек функции. Концепт точки экстремума лежит в основе нахождения критических точек на графике.
Для определения такого понятия прибегают к использованию теоремы Ферма. Она является важнейшей в ходе изучения крайних точек и дает четкое представление об их существовании в том или ином их виде. Для обеспечения экстремальности важно создать определенные условия для убывания либо возрастания на графике.
Для точного ответить на вопрос «как найти точку максимума», необходимо следовать таким положениям:
- Нахождение точной области определения на графике.
- Поиск производной функции и точки экстремума.
- Решать стандартные неравенства на область нахождения аргумента.
- Уметь доказывать, в каких функциях точка на графике определена и непрерывна.
Внимание! Поиск критической точки функции возможен только в случае существования производной не менее второго порядка, что обеспечивается высокой долей наличия точки экстремума.
Необходимое условие экстремума функции
Для того чтобы существовал экстремум, важно, чтобы были как точки минимума, так и точки максимума. В случае если это правило соблюдено лишь частично, то условие существование экстремума нарушается.
Каждая функция в любом положении должна быть продифференцирована с целью выявления ее новых значений. Важно понимать, что случай обращения точки в ноль не является основным принципом нахождения дифференцируемой точки.
Острый экстремум, также как и минимум функции – это крайне важный аспект решения математической задачи с использованием экстремальных значений. Для того чтобы лучше понимать данную составляющую, важно обратиться к табличным значениям по заданию функционала.

Полное исследование значения Построение графика значения 1. Определение точек возрастания и убывания значений. 2. Нахождение точек разрыва, экстремума и пересечение с координатными осями.
3. Процесс определения изменений положения на графике.
4. Определение показателя и направления выпуклости и выгнутости с учетом наличия асимптот.
5. Создание сводной таблицы исследования с точки зрения определения ее координат.
6. Нахождение промежутков возрастания и убывания крайних и острых точек.
7. Определение выпуклости и вогнутости кривой.
8. Построение графика с учетом исследования позволяет найти минимум либо максимум.
Основным элементом при необходимости работы с экстремумами является точное построение его графика. Школьные учителя не часто уделяют столь важному аспекту максимум внимания, что является грубейшим нарушением учебного процесса.
Построение графика происходит только по итогам исследования функциональных данных, определения острых экстремумов, а также точек на графике.
Острые экстремумы производной функции отображаются на графике точных значений, с использованием стандартной процедуры определения асимптот.
Точки максимума и минимума функции сопровождаются более сложными построениями графика. Это обусловлено более глубокой необходимостью прорабатывать проблему острого экстремума.
Необходимо также находить производную сложной и простой функции, так как это одно из самых главных понятий проблематики экстремума.
Экстремум функционала
Для того чтобы отыскать вышеозначенное значение, необходимо придерживаться следующих правил:
- определить необходимое условие экстремального отношения;
- учитывать достаточное условие крайних точек на графике;
- осуществлять расчет острого экстремума.
Используются также такие понятия, как слабый минимум и сильный минимум.
 Это необходимо учитывать при определении экстремума и точного его расчета. При этом острый функционал – это поиск и создание всех необходимых условий для работы с графиком функции.
Это необходимо учитывать при определении экстремума и точного его расчета. При этом острый функционал – это поиск и создание всех необходимых условий для работы с графиком функции.минимум функции калькулятора
Поиск инструмента
Минимум функции
Инструмент для определения минимального значения функции: минимального значения, которое может принимать функция. Это глобальный минимум, а не локальный минимум.
Результаты
Минимум функции — dCode
Тег (и): Функции
Поделиться
dCode и другие
dCode является бесплатным, а его инструменты являются ценным подспорьем в играх, математике, геокешинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !Калькулятор минимумов
Калькулятор максимума
Инструмент для определения минимального значения функции: минимального значения, которое может принимать функция.Это глобальный минимум, а не локальный минимум.
Ответы на вопросы (FAQ)
Каково определение минимума функции?
Для любой функции $ f $, определенной на интервале $ I $ и $ m $ действительное число, принадлежащее $ I $, если $ f (x) минимальное значение функции, достигнутое при $ x = m $.
Минимум функции всегда определяется с интервалом (который может быть областью определения функции).
Как найти минимум функции?
Нахождение минимума функции $ f $ эквивалентно вычислению $ f (m) $.2 $ определен над $ \ mathbb {R} $, его производная равна $ f ‘(x) = 2x $, которая равна нулю в $ x = 0 $, потому что $ f’ (x) = 0 \ iff 2x = 0 \ iff x = 0 $. Производная изменяется от отрицательной к положительной в $ x = 0 $, поэтому функция имеет минимум в $ x = 0 $, $ f (x = 0) = 0 $ и $ f (x)> = 0 $ над $ \ mathbb {R} $.
 2 + 4 a c) / (4 a) $, когда $ x = — \ frac {b} {2a} $
2 + 4 a c) / (4 a) $, когда $ x = — \ frac {b} {2a} $— Если $
Задайте новый вопросИсходный код
dCode сохраняет за собой право собственности на исходный код онлайн-инструмента «Минимум функции».За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / free), любой алгоритм, апплет или фрагмент (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любая функция (преобразование, решение, дешифрование / encrypt, decipher / cipher, decode / encode, translate), написанные на любом информатическом языке (PHP, Java, C #, Python, Javascript, Matlab и т. д.), доступ к данным, скриптам, копированию и API не будет бесплатным. , то же самое для минимальной загрузки функции для автономного использования на ПК, планшете, iPhone или Android!
Нужна помощь?
Пожалуйста, заходите в наше сообщество Discord, чтобы получить помощь! Также для зашифрованных сообщений проверьте наш автоматический идентификатор шифра!
Вопросы / комментарии
Сводка
Инструменты аналогичные
Поддержка
Форум / Справка
Ключевые слова
минимум, функция, производная, вычислитель, максимум, экстремум
Ссылки
Источник: https: // www.dcode.fr/minimum-function
© 2021 dCode — Идеальный «инструментарий» для решения любых игр / загадок / геокэшинга / CTF.минимум функции калькулятора
Поиск инструмента
Минимум функции
Инструмент для определения минимального значения функции: минимального значения, которое может принимать функция. Это глобальный минимум, а не локальный минимум.
Результаты
Минимум функции — dCode
Тег (и): Функции
Поделиться
dCode и другие
dCode является бесплатным, а его инструменты являются ценным подспорьем в играх, математике, геокешинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !Калькулятор минимумов
Калькулятор максимума
Инструмент для определения минимального значения функции: минимального значения, которое может принимать функция.
 Это глобальный минимум, а не локальный минимум.
Это глобальный минимум, а не локальный минимум.Ответы на вопросы (FAQ)
Каково определение минимума функции?
Для любой функции $ f $, определенной на интервале $ I $ и $ m $ действительное число, принадлежащее $ I $, если $ f (x) минимальное значение функции, достигнутое при $ x = m $.
Минимум функции всегда определяется с интервалом (который может быть областью определения функции).
Как найти минимум функции?
Нахождение минимума функции $ f $ эквивалентно вычислению $ f (m) $.2 $ определен над $ \ mathbb {R} $, его производная равна $ f ‘(x) = 2x $, которая равна нулю в $ x = 0 $, потому что $ f’ (x) = 0 \ iff 2x = 0 \ iff x = 0 $. Производная изменяется от отрицательной к положительной в $ x = 0 $, поэтому функция имеет минимум в $ x = 0 $, $ f (x = 0) = 0 $ и $ f (x)> = 0 $ над $ \ mathbb {R} $.
Как рассчитать локальный минимум на интервале?
Добавьте одно или несколько условий, указывающих ограничения интервала для каждой переменной.
Пример: Найдите минимум $ \ sin {x} $ для $ 0
Укажите несколько уравнений с помощью оператора логического И &&, чтобы разделить уравнения
Что такое минорант функции?
Минорант — это любое значение, меньшее или равное минимальному значению, достигаемому функцией.
Каков минимум постоянной функции?
Постоянная функция $ f (x) = c $ — это линия, которая всегда равна $ c $, поэтому ее минимум равен $ c $, достигается при любом значении $ x $.
Каков минимум аффинной функции?
Линейная / аффинная функция $ f (x) = ax + b $ всегда имеет минимум $ — \ infty $
— Если $ a
— Если $ a> 0 $, минимум $ f $ равен $ — \ infty $, когда $ x $ стремится к $ — \ infty $
Каков минимум полиномиальной функции 2-й степени?
Квадратичная полиномиальная функция вида $ f (x) = ax ^ 2 + bx + c $, тогда
— Если $ a> 0 $, минимум $ f $ равен $ (-b ^ 2 + 4 a c) / (4 a) $, когда $ x = — \ frac {b} {2a} $
— Если $
Задайте новый вопросИсходный код
dCode сохраняет за собой право собственности на исходный код онлайн-инструмента «Минимум функции».
 За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / free), любой алгоритм, апплет или фрагмент (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любая функция (преобразование, решение, дешифрование / encrypt, decipher / cipher, decode / encode, translate), написанные на любом информатическом языке (PHP, Java, C #, Python, Javascript, Matlab и т. д.), доступ к данным, скриптам, копированию и API не будет бесплатным. , то же самое для минимальной загрузки функции для автономного использования на ПК, планшете, iPhone или Android!
За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / free), любой алгоритм, апплет или фрагмент (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любая функция (преобразование, решение, дешифрование / encrypt, decipher / cipher, decode / encode, translate), написанные на любом информатическом языке (PHP, Java, C #, Python, Javascript, Matlab и т. д.), доступ к данным, скриптам, копированию и API не будет бесплатным. , то же самое для минимальной загрузки функции для автономного использования на ПК, планшете, iPhone или Android!Нужна помощь?
Пожалуйста, заходите в наше сообщество Discord, чтобы получить помощь! Также для зашифрованных сообщений проверьте наш автоматический идентификатор шифра!
Вопросы / комментарии
Сводка
Инструменты аналогичные
Поддержка
Форум / Справка
Ключевые слова
минимум, функция, производная, вычислитель, максимум, экстремум
Ссылки
Источник: https: // www.dcode.fr/minimum-function
© 2021 dCode — Идеальный «инструментарий» для решения любых игр / загадок / геокэшинга / CTF.Калькулятор минимумов и максимумов
Пример: использование калькулятора минимумов и максимумов
Скажите, что вы недавно начали кататься на велосипеде и решили использовать приложение, чтобы узнать расстояния, которые вам удалось преодолеть. С каждой поездкой вы чувствуете, что деятельность становится все менее и менее утомительной, а сожженные калории укрепляют мышцы бедер.
Но, помимо визуальных эффектов, вы решаете взглянуть на числа . В частности, вы хотели бы увидеть, насколько хорошо вы справились в свой худший и лучший день, то есть , когда вы прошли самое короткое и самое длинное расстояние соответственно.
 Что ж, поправьте нас, если мы ошибаемся, но это выглядит как задача для нашего калькулятора минимумов и максимумов ! (Спойлер: нас не нужно поправлять; мы оказались правы.)
Что ж, поправьте нас, если мы ошибаемся, но это выглядит как задача для нашего калькулятора минимумов и максимумов ! (Спойлер: нас не нужно поправлять; мы оказались правы.)Вы просматриваете данные, собранные приложением, и видите последних двадцати пройденных вами расстояний .Их:
4,5 миль,5,2 миль,3,9 миль,6,1 миль,7,5 миль,4,2 миль,6,3 миль,6,3 миль,5,9 миль,8,9 миль,9,2 миль,11,2 миль,6,4 миль,7 миль,7,2 миль,5,9 миль,11,4 миль,4,8 миль,9,8 миль,10,5 миль.(Для наших друзей по метрике мы рекомендуем конвертер длины, чтобы иметь значения в выбранных вами единицах измерения.)
В калькуляторе минимума и максимума мы видим полей пронумерованных переменных , куда мы вводим наши данные. По очереди вводим полученные значения. Обратите внимание, как первоначально инструмент показывает только восемь таких полей, но новых появляются в тот момент, когда вы, кажется, достигли конца (фактически, вы можете ввести от до пятидесяти чисел ). Также обратите внимание, что калькулятор минимума и максимума показывает результат уже для двух чисел и корректирует его при каждой новой записи. Как только мы введем последний, мы можем просто считать ответ .
Однако для времена крайней необходимости, когда нет Wi-Fi около , давайте посмотрим, как найти минимум и максимум без помощи калькулятора Omni max и min.
Прежде всего, как упоминалось в предыдущем разделе, нам нужно упорядочить наш набор данных от наименьшего к наибольшему. Обратите внимание, как при использовании калькулятора максимума и минимума инструмент уже делает это за нас и даже показывает нам наименьшее количество упорядоченных элементов внизу.

В нашем случае сортировка чисел изменит необработанную последовательность:
4.5 миль,5,2 миль,3,9 миль,6,1 миль,7,5 миль,4,2 миль,6,3 миль,6,3 миль,5,9 миль,8,9 миль,9,2 миль,11,2 миль,6,4 миль,7 миль,7,2 миль,5,9 миль,11,4 миль,4,8 миль,9,8 миль,10,5 миль,в:
3.9 миль,4.2 миль,4.5 миль,4,8 миль,5,2 миль,5,9 миль,5,9 миль,6,1 миль,6,3 миль,6,3 миль,6,4 миль,7 миль,7,2 миль,7,5 миль,8,9 миль,9,2 миль,9,8 миль,10,5 миль,11,2 миль,11,4 миль.Так какой же минимум? Это , первое число выше. А какой максимум? Это , последний .Другими словами,
минимум = 3,9 миль,максимум = 11,4 миль.Значительная разница , не так ли? Или мы должны назвать это прогресс ? В любом случае, это звучит обнадеживающе, особенно если учесть, что регулярные упражнения могут продлить вашу жизнь!
И если вы хотите проанализировать свои данные дальше , обязательно ознакомьтесь с другими инструментами Omni, которые могут вам помочь!
Онлайн-справка — Быстрая справка
найти-мин-макс
Последнее обновление: 13.07.2018
Из строки состояния
Когда вы выделяете столбец, несколько столбцов или диапазон данных на листе, основная статистика выбора отображается в строке состояния, расположенной в нижней части рабочего пространства Origin.

По умолчанию Мин. И Макс. Не отображаются. Вы можете щелкнуть правой кнопкой мыши на строке состояния и проверить Мин, Макс и т. Д. Вы также можете щелкнуть правой кнопкой мыши на строке состояния и Копировать статистику.
Для получения дополнительной информации см. Строку состояния.
Инструмент «Статистика по столбцам» / «Статистика по строкам»
Если набор данных находится в столбце или строке, вы можете сообщить статистику и получить минимальное или максимальное значение. Чтобы вызвать эти инструменты, выберите Статистика: Описательная статистика: Статистика по столбцам / Статистика по строкам .В любом диалоговом окне вы найдете флажки для Минимум и Максимум в ветви Количества для вычисления >> Количества .
См .:
- * Диалоговое окно «Статистика по столбцам».
- * Диалоговое окно «Статистика по строкам».
Использование функций LabTalk
Следующие функции LabTalk (max () и min ()) предназначены для поиска максимума и минимума, функция list () находит номер индекса, а функция xvalue () находит соответствующее значение xvalue по заданному номеру индекса.Вы можете запустить приведенный ниже сценарий LabTalk в окне сценария (выделите один из предоставленных сценариев ниже и нажмите , введите ):
Чтобы найти максимум и минимум в столбце B: bMax = max (столбец (B)); bMin = min (столбец (B)); Чтобы найти соответствующий порядковый номер: maxIndex = список (макс (столбец (B)), столбец (B)); minIndex = список (min (col (B)), col (B)); Чтобы найти соответствующее значение x: 1) Найдите соответствующее значение в столбце x: xvalue (список (макс (столбец (B)), столбец (B)), столбец (B)) xvalue (список (min (col (B)), col (B)), col (B)) 2) Найдите соответствующее значение в другом столбце C: v1 = col (C) [список (max (col (B)), col (B))]; v2 = col (C) [список (min (col (B)), col (B))]; v3 = Таблица (столбец (B), столбец (C), Макс (столбец (B))) v4 = Таблица (столбец (B), столбец (C), Min (столбец (B)))Использование формулы столбца
Вы можете использовать функции LabTalk в диалоговом окне F (x) = cell или Set Values), чтобы найти максимальное значение и минимальное значение , номер индекса , соответствующее значение xvalue или соответствующее значение в любом столбце.

Начиная с Origin 2017, Origin поддерживает нотацию ячеек электронной таблицы в формуле столбца, поэтому вы можете напрямую использовать B , а также col (B) .
Например, добавить новый столбец на лист. Введите следующее в ячейку F (x) или ее диалоговое окно «Установить значения» :
- Чтобы найти максимум и минимум в столбце B:
макс (B) мин (B)
- Чтобы найти соответствующий номер индекса строки максимального или минимального значения в столбце B: Если есть повторяющиеся максимальные / минимальные значения в столбце B, он возвращает номер индекса строки первого появления максимального / минимального значения.Список
(макс. (B), B) список (min (B), B)
- Чтобы найти соответствующее значение x максимального или минимального значения в столбце B, предположим, что B — столбец Y.
xvalue (список (макс (B), B), B) xvalue (список (min (B), B), B) - Чтобы найти соответствующее значение в столбце C в той же строке, где найдено максимальное или минимальное значение столбца B:
C [список (макс. (B), B)] C [список (min (B), B)] Таблица (B, C, Макс (B)) Таблица (B, C, Min (B))
Примечание. Вам нужно будет ввести col (B), а не B для Origin 2016 и старше.
Ключевые слова: описательная статистика, строка состояния, статистика по столбцам, статистика по строкам, значение индекса, соответствующее значение
Аппроксимация функции с регрессионным анализом
Проблема аппроксимации функции состоит в том, как выбрать функцию из четко определенного класса, которая близко соответствует («приближает») целевой неизвестной функции.
Этот калькулятор использует предоставленные данные таблицы целевой функции в виде точек {x, f (x)} для построения нескольких регрессионных моделей, а именно: линейная регрессия, квадратичная регрессия, кубическая регрессия, степенная регрессия, логарифмическая регрессия, гиперболическая регрессия, ab- экспоненциальная регрессия и экспоненциальная регрессия.
 Результаты можно сравнить с помощью коэффициента корреляции, коэффициента детерминации, средней относительной ошибки (стандартной ошибки регрессии) и визуально на графике. Теория и формулы, как обычно, приведены под калькулятором.
Результаты можно сравнить с помощью коэффициента корреляции, коэффициента детерминации, средней относительной ошибки (стандартной ошибки регрессии) и визуально на графике. Теория и формулы, как обычно, приведены под калькулятором. Аппроксимация функций с регрессионным анализом
83 71 64 69 69 64 68 59 81 91 57 65 58 62Значения X, разделенные пробелом
183 168 171 178 176 172 165 158 183 182 163 175 164 175Значения Y, разделенные пробелом
ab-Экспоненциальная регрессия Точность вычисленияЦифры после десятичной точки: 4
Коэффициент линейной корреляции
Коэффициент детерминации
Средняя относительная погрешность,%
Коэффициент корреляции
Определение коэффициента
Средняя относительная погрешность,%
Коэффициент корреляции
Коэффициент детерминации
Средняя относительная погрешность,%
Коэффициент корреляции
Коэффициент относительнойКоэффициент
%
ab-Экспоненциальная регрессия
Коэффициент корреляции
Коэффициент детерминации
Средняя относительная погрешность,%
Коэффициент корреляции
Коэффициент относительной погрешности
%
Коэффициент корреляции
Коэффициент детерминации
Средняя относительная ошибка,%
Коэффициент корреляции
Коэффициент детерминации
Результаты
файл очень большой.Во время загрузки и создания может произойти замедление работы браузера.
Скачать закрыть
content_copy Ссылка сохранить Сохранить расширение Виджет
Линейная регрессия
Уравнение:
коэффициент
b коэффициент
Коэффициент линейной корреляции
Коэффициент детерминации
Стандартная ошибка регрессии
Квадратичная регрессия
Уравнение:
Система уравнений для поиска a, b и c
Коэффициент корреляции
,
гдеКоэффициент детерминации
Стандартная ошибка регрессии
Кубическая регрессия
Уравнение:
Система уравнений для поиска a, b, c и d
Коэффициент корреляции, коэффициент детерминации, стандартная ошибка регрессии — те же формулы, что и в случае квадратичной регрессии.

Регрессия мощности
Уравнение:
b коэффициент
коэффициент
Коэффициент корреляции, коэффициент детерминации, стандартная ошибка регрессии — те же формулы, что и выше.
ab-Экспоненциальная регрессия
Уравнение:
b коэффициент
коэффициент
Коэффициент корреляции, коэффициент детерминации, стандартная ошибка регрессии — то же.
Гиперболическая регрессия
Уравнение:
b коэффициент
коэффициент
Коэффициент корреляции, коэффициент детерминации, стандартная ошибка регрессии — то же, что и выше.
Логарифмическая регрессия
Уравнение:
b коэффициент
коэффициент
Коэффициент корреляции, коэффициент детерминации, стандартная ошибка регрессии — то же, что и выше.
Экспоненциальная регрессия
Уравнение:
b коэффициент
коэффициент
Коэффициент корреляции, коэффициент детерминации, стандартная ошибка регрессии — то же, что и выше.
Вывод формул
Начнем с задачи:
У нас есть неизвестная функция y = f (x), заданная в виде табличных данных (например, таких как полученные из экспериментов).
Нам нужно найти функцию известного типа (линейная, квадратичная и т. Д.).) y = F (x), эти значения должны быть как можно ближе к табличным значениям в тех же точках. На практике тип функции определяется путем визуального сравнения точек таблицы с графиками известных функций.В результате мы должны получить формулу y = F (x), названную эмпирической формулой (уравнение регрессии, аппроксимация функции), которая позволяет нам вычислить y для x, отсутствующих в таблице. Таким образом, эмпирическая формула «сглаживает» значения y.
Мы используем метод наименьших квадратов , чтобы получить параметры F для наилучшего соответствия.
 Наилучшее соответствие в смысле наименьших квадратов минимизирует сумму квадратов остатков, при этом остаток представляет собой разницу между наблюдаемым значением и подобранным значением, предоставленным моделью.
Наилучшее соответствие в смысле наименьших квадратов минимизирует сумму квадратов остатков, при этом остаток представляет собой разницу между наблюдаемым значением и подобранным значением, предоставленным моделью.Таким образом, когда нам нужно найти функцию F, такую как сумму квадратов остатков, S будет минимальным
Опишем решение этой проблемы на примере линейной регрессии F = ax + b.
Нам нужно найти наилучшее соответствие для коэффициентов a и b, таким образом, S является функцией от a и b. Чтобы найти минимум, мы найдем точки экстремума, в которых частные производные равны нулю.Используя формулу производной комплексной функции, мы получим следующие уравнения:
Для функций частные производные:
,Раскладывая первые формулы частными производными, мы получим следующие уравнения:
После снятия скобок получим:
Из этих уравнений мы можем получить формулы для a и b, которые будут такими же, как формулы, перечисленные выше.
Используя ту же технику, мы можем получить формулы для всех оставшихся регрессий.
7. Прикладные задачи о максимуме и минимуме
М. Борна
Процесс поиска максимальных или минимальных значений называется оптимизацией . Мы пытаемся сделать такие вещи, как максимизация прибыли в компании, или минимизация затрат, или найти наименьшее количество материала для изготовления конкретного объекта.
Они очень важны в мире промышленности.
Пример 1
Дневная прибыль, P , нефтеперерабатывающего завода дается
P = 8 x — 0.2) = -0,04 <0` для всех x, так что у нас есть максимум.
Когда x = 200, P = 800 долларов.
Итак, если компания перерабатывает 200 баррелей в день, достигается максимальная прибыль в 800 долларов.
Максимальная точка `(200, 800)` обозначена на графике пурпурной точкой.
 2) = — 4 <0 \" для всех "\ x`
2) = — 4 <0 \" для всех "\ x`Так что это максимум.
Таким образом, максимальная площадь достигается, когда x = 200, `y = 400`, а эта область равна:
A = 200 × 400 = 80000 м 2 = 8 га
Пример 3
[Эта проблема была представлены для обсуждения ранее во введении к дифференциации.]
Коробка с квадратным основанием не имеет верха. Если используется 64 см 2 материала, каков максимально возможный объем для коробка?
Ответ
Сеть для этого ящика будет:
Объем коробки V = x 2 y
Нам сказали, что площадь ящика составляет 64 см 2 .2) = — (3x) / 2`
, и это отрицательно, когда x положительно. Так что это МАКС.
Итак, размеры коробки составляют:
Основание 4,62 см × 4,62 см и стороны 2,31 см.
Максимально возможный объем составляет
V = 4,62 × 4,62 × 2,31 ≈ 49,3 см 3
Проверка : Область материала:
x 2 + 4 xy = 21,3 + 4 × 4,62 × 2.31 = 64
Проверяет ОК.
Встроенные функции— документация Python 3.9.2
Откройте файл и верните соответствующий файловый объект. Если файл не может быть открыт, возникает ошибка OSError
файл — это объект, похожий на путь, дающий имя пути (абсолютное или относительно текущего рабочего каталога) открываемого файла или целочисленный файловый дескриптор файла, который нужно обернуть.(Если дескриптор файла задано, он закрывается, когда возвращенный объект ввода-вывода закрывается, если только closefd установлено значение
Ложь.)режим — дополнительная строка, указывающая режим, в котором файл открыт.
 По умолчанию это
По умолчанию это 'r', что означает открытие для чтения в текстовом режиме. Другие общие значения:'w'для записи (усечение файла, если он уже существует),'x'для исключительного создания и'a'для добавления (что на некоторых системах Unix означает, что все записи добавляются в конец файл независимо от текущей позиции поиска).В текстовом режиме, если Кодировка не указана, используемая кодировка зависит от платформы:locale.getpreferredencoding (False) Вызываетсядля получения текущей локали кодирование. (Для чтения и записи сырых байтов используйте двоичный режим и оставьте кодировка не указана.) Доступные режимы:Знак
Значение
'r'открыто для чтения (по умолчанию)
ширинаоткрыт для записи, сначала обрезка файла
'x'открыто для монопольного создания, ошибка, если файл уже существует
'а'открыто для записи, добавляется в конец файла, если он существует
'b'двоичный режим
'т'текстовый режим (по умолчанию)
'+'открыт для обновления (чтение и запись)
Режим по умолчанию —
'r'(открыт для чтения текста, синоним'rt').Режимы'w +'и'w + b'открывают и обрезают файл. Режимы'r +'и'r + b'открывают файл без усечения.Как упоминалось в обзоре, Python различает двоичные и текстовый ввод / вывод.
 Файлы, открытые в двоичном режиме (включая
Файлы, открытые в двоичном режиме (включая 'b'в режиме аргумент) возвращает содержимое какбайтовобъектов без какого-либо декодирования. В текстовый режим (по умолчанию или когда't'включен в аргумент mode ), содержимое файла возвращается какstr, байты были сначала декодируется с использованием платформенно-зависимого кодирования или с использованием указанного кодирование , если указано.Разрешен дополнительный символ режима,
'U', который больше не имеет какой-либо эффект и считается устаревшим. Ранее он был включен универсальные символы новой строки в текстовом режиме, которые стали поведением по умолчанию в Python 3.0. См. Документацию параметр новой строки для получения дополнительных сведений.Примечание
Python не зависит от представления текста операционной системой. файлы; вся обработка выполняется самим Python и, следовательно, независимая платформа.
буферизация — необязательное целое число, используемое для установки политики буферизации. Пройдено 0 для выключения буферизации (разрешено только в двоичном режиме), 1 для выбора строки буферизация (может использоваться только в текстовом режиме) и целое число> 1, чтобы указать размер в байтах буфера фрагментов фиксированного размера. Если нет буферизации аргумента Учитывая, что политика буферизации по умолчанию работает следующим образом:
Двоичные файлы буферизуются фрагментами фиксированного размера; размер буфера выбранный с помощью эвристики, пытающейся определить «блокировку» основного устройства размер »и возвращается к
io.РАЗМЕР_БУФЕРА_ДЕФА. Во многих системах размер буфера обычно составляет 4096 или 8192 байта.«Интерактивные» текстовые файлы (файлы, для которых
isatty ()возвращаетИстина) использовать буферизацию строки. Другие текстовые файлы используют политику описано выше для двоичных файлов.
кодировка — это имя кодировки, используемой для декодирования или кодирования файла. Это следует использовать только в текстовом режиме. Кодировка по умолчанию — платформа. зависимый (независимо от
locale.getpreferredencoding ()возвращает), но любой кодировка текста, поддерживаемая Python может быть использован. См. Модуль кодековошибок — необязательная строка, определяющая способ кодирования и декодирования. ошибки должны обрабатываться — это не может использоваться в двоичном режиме. Доступны различные стандартные обработчики ошибок. (перечислены в разделе «Обработчики ошибок»), хотя любые имя обработки ошибок, которое было зарегистрировано с
codecs.register_error ()также допустим.Стандартные имена включают:'strict', чтобы вызвать исключениеValueError, если есть ошибка кодировки. Значение по умолчаниюНетимеет то же самое эффект.'ignore'игнорирует ошибки. Обратите внимание, что игнорирование ошибок кодирования может привести к потере данных.'replace'вызывает вставку замещающего маркера (например,'?') где есть искаженные данные.'surrogateescape'будет представлять любые неправильные байты как код точек в области частного использования Unicode в диапазоне от U + DC80 до U + DCFF.Эти частные кодовые точки будут затем снова превращены в те же байты при использовании обработчика ошибокsurrogateescapeпри записи данных. Это полезно для обработки файлов в неизвестная кодировка.'xmlcharrefreplace'поддерживается только при записи в файл. Символы, не поддерживаемые кодировкой, заменяются символами ссылка на соответствующий символ XML& # nnn;.'backslashreplace'заменяет искаженные данные на обратную косую черту Python escape-последовательности.
'namereplace'(также поддерживается только при записи) заменяет неподдерживаемые символы управляющими последовательностями\ N {...}.
новая строка управляет тем, как работает универсальный режим новой строки (только относится к текстовому режиму). Это может быть
Нет,'','\ n','\ r'и'\ r \ n'. Он работает следующим образом:При чтении ввода из потока, если перевод строки равен
Нет, универсальный Режим новой строки включен.Строки на входе могут заканчиваться на'\ n','\ r'или'\ r \ n', и они переводятся в'\ n'перед возвращаются вызывающему. Если это'', универсальный режим новой строки включен, но окончания строк возвращаются вызывающему абоненту без перевода. Если оно имеет любое из других допустимых значений, строки ввода заканчиваются только заданная строка, и конец строки возвращается вызывающему абоненту без перевода.При записи вывода в поток, если перевод строки равен
Нет, любой'\ n'написанные символы переводятся в системный разделитель строк по умолчанию,ос.linesep. Если новая строка — это''или'\ n', перевода нет происходит. Если новая строка — любое другое допустимое значение, любое'\ n'написанные символы переводятся в заданную строку.
Если closefd —
Ложьи был указан дескриптор файла, а не имя файла. задано, базовый дескриптор файла будет оставаться открытым, когда файл закрыто. Если указано имя файла closefd должно бытьTrue(по умолчанию) в противном случае возникнет ошибка.Можно использовать настраиваемый открыватель, передав вызываемый объект как открыватель .
 Лежащий в основе
файловый дескриптор для файлового объекта затем получается путем вызова открывателя с
( файл , флаги ). открыватель должен возвращать дескриптор открытого файла (передавая
Лежащий в основе
файловый дескриптор для файлового объекта затем получается путем вызова открывателя с
( файл , флаги ). открыватель должен возвращать дескриптор открытого файла (передавая os.openas открыватель приводит к функциональности, аналогичной передачеНет).Вновь созданный файл не наследуется.
В следующем примере используется параметр dir_fd
ос.open (), чтобы открыть файл, относящийся к заданному каталогу:>>> импорт ОС >>> dir_fd = os.open ('somedir', os.O_RDONLY) >>> def opener (путь, флаги): ... вернуть os.open (путь, флаги, dir_fd = dir_fd) ... >>> с open ('spamspam.txt', 'w', opener = opener) как f: ... print ('Это будет записано в somedir / spamspam.txt', file = f) ... >>> os.close (dir_fd) # не допускать утечки файлового дескриптораТип файлового объекта, возвращаемого функцией
open (). зависит от режима.Когдаopen ()используется для открытия файла в тексте mode ('w','r','wt','rt'и т. д.), он возвращает подклассio.TextIOBase(в частности,io.TextIOWrapper). При использовании чтобы открыть файл в двоичном режиме с буферизацией, возвращаемый класс — подклассio.BufferedIOBase. Точный класс варьируется: в прочтении двоичный режим, он возвращаетio.BufferedReader; в записи двоичного кода и добавить двоичные режимы, он возвращаетio.BufferedWriter, а в режим чтения / записи, он возвращаетio.BufferedRandom. Когда буферизация отключен, необработанный поток, подклассio.RawIOBase,io.FileIO, возвращается.См. Также модули обработки файлов, например,
fileinput,io(где объявленopen ()),os,os.path,tempfile, ишутил.

 Но в этой точке функция имеет максимум.
Но в этой точке функция имеет максимум. Если же при переходе через x0
слева направо производная меняет знак с минуса на плюс, то функция имеет в этой
точке минимум.
Если же при переходе через x0
слева направо производная меняет знак с минуса на плюс, то функция имеет в этой
точке минимум.

 2
2
 2+3. Эту формулу вставим в ячейку В1
2+3. Эту формулу вставим в ячейку В1
 При x 0, а при x > a/4, S »
При x 0, а при x > a/4, S »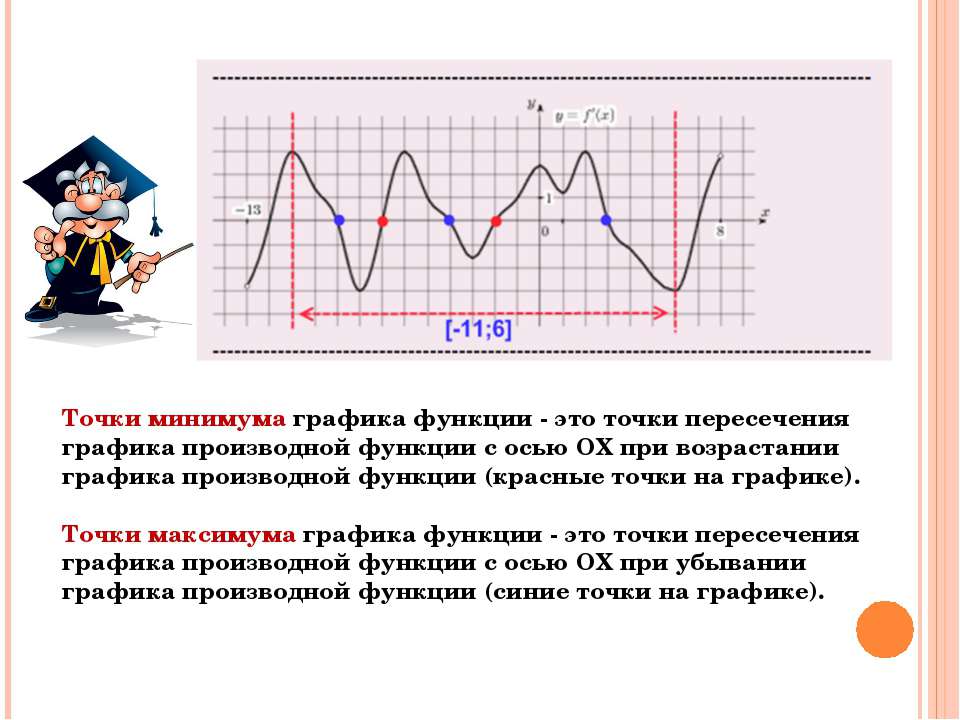 S » (R) = 0 при R 3 = 8, следовательно,
S » (R) = 0 при R 3 = 8, следовательно,  Если произойдет так, что вторая производная окажется больше нуля в критической точке, то ею и будет являться точка минимума, а в противном случае – это будет точка максимума.
Если произойдет так, что вторая производная окажется больше нуля в критической точке, то ею и будет являться точка минимума, а в противном случае – это будет точка максимума.
 Это те значения аргумента, при которых вся функция принимает значения ноль. Для этого необходимо приравнять функцию к нулю, подробно ее рассмотреть и совершить некоторые преобразования. Возьмём уже знакомую нам функцию у(х) = (х 2 — 2х)/х. Из школьного курса мы знаем, что дробь равна 0 тогда, когда числитель равен нулю. Поэтому знаменатель мы отбрасываем и начинаем работать с числителем, приравнивая его к нулю. Получаем х 2 — 2х = 0 и выносим х за скобочки. Отсюда х (х — 2) = 0. В итоге получаем, что наша функция равна нулю тогда, когда х равняется 0 или же 2.
Это те значения аргумента, при которых вся функция принимает значения ноль. Для этого необходимо приравнять функцию к нулю, подробно ее рассмотреть и совершить некоторые преобразования. Возьмём уже знакомую нам функцию у(х) = (х 2 — 2х)/х. Из школьного курса мы знаем, что дробь равна 0 тогда, когда числитель равен нулю. Поэтому знаменатель мы отбрасываем и начинаем работать с числителем, приравнивая его к нулю. Получаем х 2 — 2х = 0 и выносим х за скобочки. Отсюда х (х — 2) = 0. В итоге получаем, что наша функция равна нулю тогда, когда х равняется 0 или же 2. В итоге мы получили стандартное квадратное уравнение. Все, что необходимо сделать дальше — приравнять его к нулю и найти корни. Поскольку дискриминант больше нуля (D = 16 — 12 = 4), данное уравнение определяется двумя корнями. Находим их и получаем два значения: 1/3 и -1. Это и будут точки экстремума функции. Однако как все-таки определить, кто есть кто? Какая точка является максимумом, а какая минимумом? Для этого нужно взять соседнюю точку и узнать ее значение. К примеру, возьмем число -2, которое находится слева по координатной прямой от -1. Подставляем это значение в наше уравнение у(-2) = 12 — 8 + 1 = 5. В итоге мы получили положительное число. Это значит, что на промежутке от 1/3 до -1 функция возрастает. Это, в свою очередь, обозначает, что на промежутках от минус бесконечности до 1/3 и от -1 до плюс бесконечности функция убывает. Таким образом, можно сделать вывод, что число 1/3 — точка минимума функции на исследованном промежутке, а -1 — точка максимума.
В итоге мы получили стандартное квадратное уравнение. Все, что необходимо сделать дальше — приравнять его к нулю и найти корни. Поскольку дискриминант больше нуля (D = 16 — 12 = 4), данное уравнение определяется двумя корнями. Находим их и получаем два значения: 1/3 и -1. Это и будут точки экстремума функции. Однако как все-таки определить, кто есть кто? Какая точка является максимумом, а какая минимумом? Для этого нужно взять соседнюю точку и узнать ее значение. К примеру, возьмем число -2, которое находится слева по координатной прямой от -1. Подставляем это значение в наше уравнение у(-2) = 12 — 8 + 1 = 5. В итоге мы получили положительное число. Это значит, что на промежутке от 1/3 до -1 функция возрастает. Это, в свою очередь, обозначает, что на промежутках от минус бесконечности до 1/3 и от -1 до плюс бесконечности функция убывает. Таким образом, можно сделать вывод, что число 1/3 — точка минимума функции на исследованном промежутке, а -1 — точка максимума. Если в точке x * выполняется условие:
Если в точке x * выполняется условие:
 В российских школах недостаточно четко проводят грань между этими двумя концептами, что влияет на понимание данной темы вообще.
В российских школах недостаточно четко проводят грань между этими двумя концептами, что влияет на понимание данной темы вообще.
 Это необходимо учитывать при определении экстремума и точного его расчета. При этом острый функционал – это поиск и создание всех необходимых условий для работы с графиком функции.
Это необходимо учитывать при определении экстремума и точного его расчета. При этом острый функционал – это поиск и создание всех необходимых условий для работы с графиком функции. 2 + 4 a c) / (4 a) $, когда $ x = — \ frac {b} {2a} $
2 + 4 a c) / (4 a) $, когда $ x = — \ frac {b} {2a} $ Это глобальный минимум, а не локальный минимум.
Это глобальный минимум, а не локальный минимум. За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / free), любой алгоритм, апплет или фрагмент (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любая функция (преобразование, решение, дешифрование / encrypt, decipher / cipher, decode / encode, translate), написанные на любом информатическом языке (PHP, Java, C #, Python, Javascript, Matlab и т. д.), доступ к данным, скриптам, копированию и API не будет бесплатным. , то же самое для минимальной загрузки функции для автономного использования на ПК, планшете, iPhone или Android!
За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / free), любой алгоритм, апплет или фрагмент (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любая функция (преобразование, решение, дешифрование / encrypt, decipher / cipher, decode / encode, translate), написанные на любом информатическом языке (PHP, Java, C #, Python, Javascript, Matlab и т. д.), доступ к данным, скриптам, копированию и API не будет бесплатным. , то же самое для минимальной загрузки функции для автономного использования на ПК, планшете, iPhone или Android! Что ж, поправьте нас, если мы ошибаемся, но это выглядит как задача для нашего калькулятора минимумов и максимумов ! (Спойлер: нас не нужно поправлять; мы оказались правы.)
Что ж, поправьте нас, если мы ошибаемся, но это выглядит как задача для нашего калькулятора минимумов и максимумов ! (Спойлер: нас не нужно поправлять; мы оказались правы.)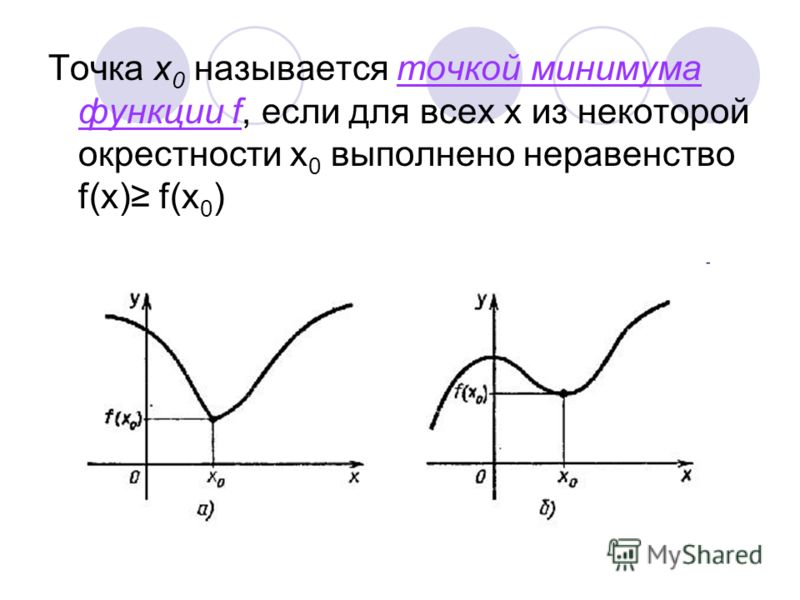
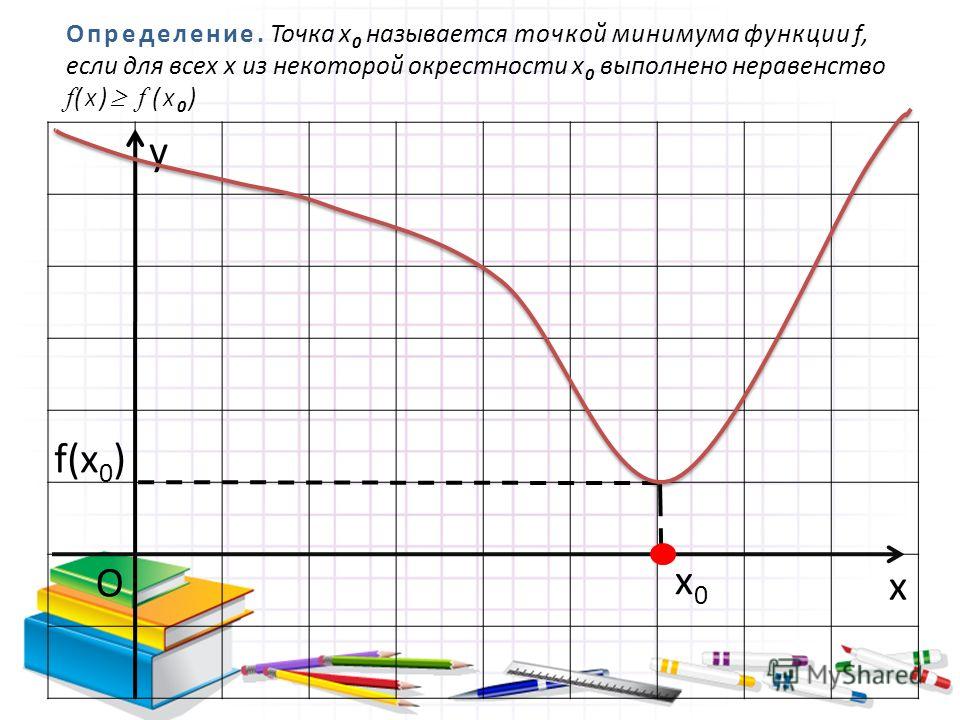

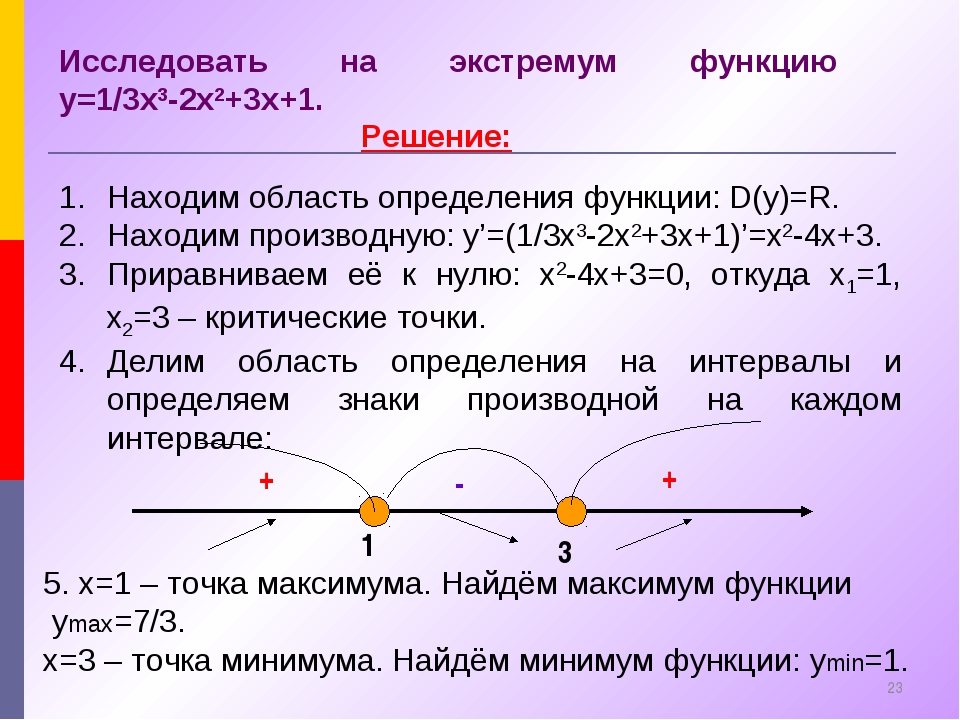 Результаты можно сравнить с помощью коэффициента корреляции, коэффициента детерминации, средней относительной ошибки (стандартной ошибки регрессии) и визуально на графике. Теория и формулы, как обычно, приведены под калькулятором.
Результаты можно сравнить с помощью коэффициента корреляции, коэффициента детерминации, средней относительной ошибки (стандартной ошибки регрессии) и визуально на графике. Теория и формулы, как обычно, приведены под калькулятором. 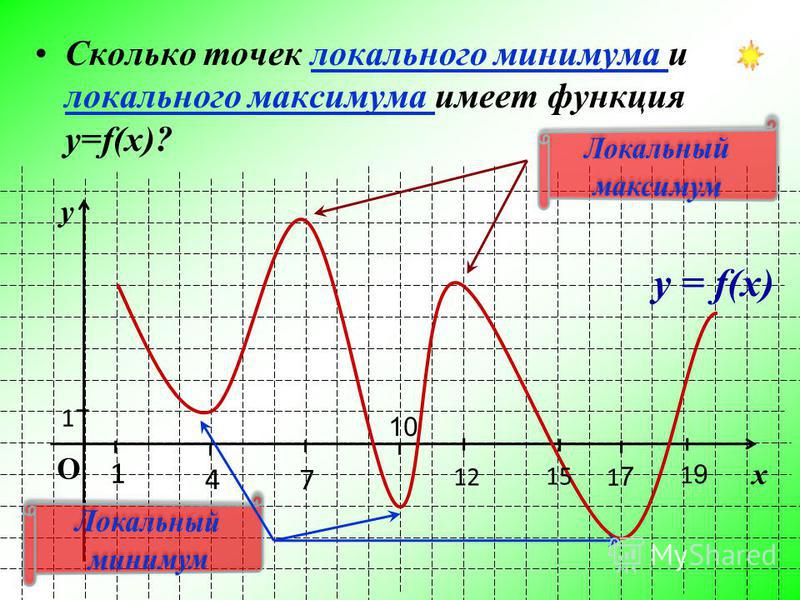
 Наилучшее соответствие в смысле наименьших квадратов минимизирует сумму квадратов остатков, при этом остаток представляет собой разницу между наблюдаемым значением и подобранным значением, предоставленным моделью.
Наилучшее соответствие в смысле наименьших квадратов минимизирует сумму квадратов остатков, при этом остаток представляет собой разницу между наблюдаемым значением и подобранным значением, предоставленным моделью.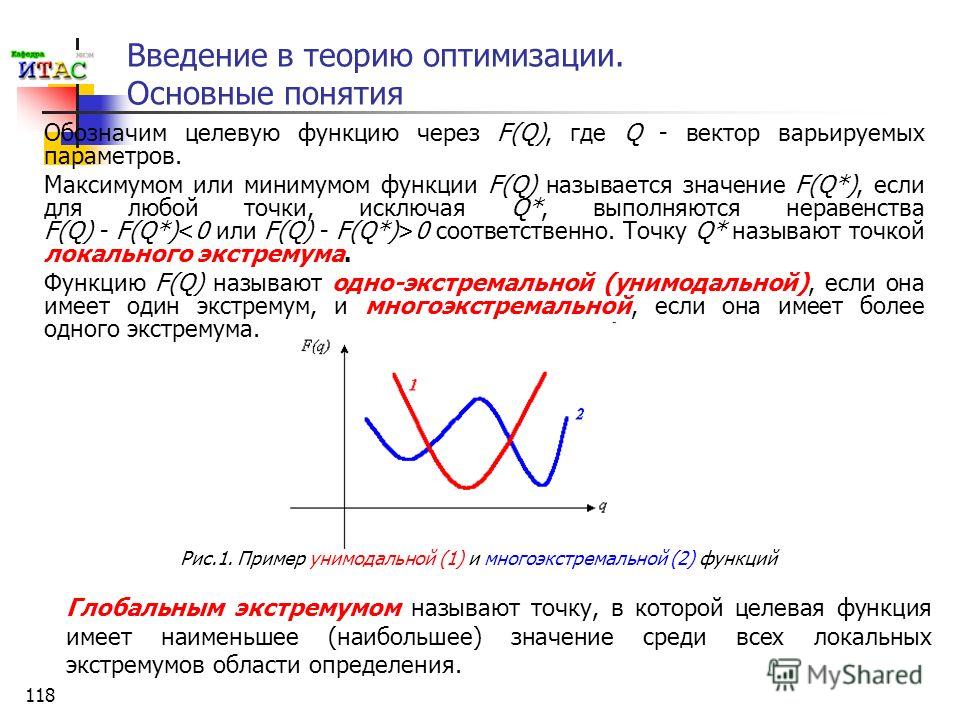 2) = — 4 <0 \" для всех "\ x`
2) = — 4 <0 \" для всех "\ x`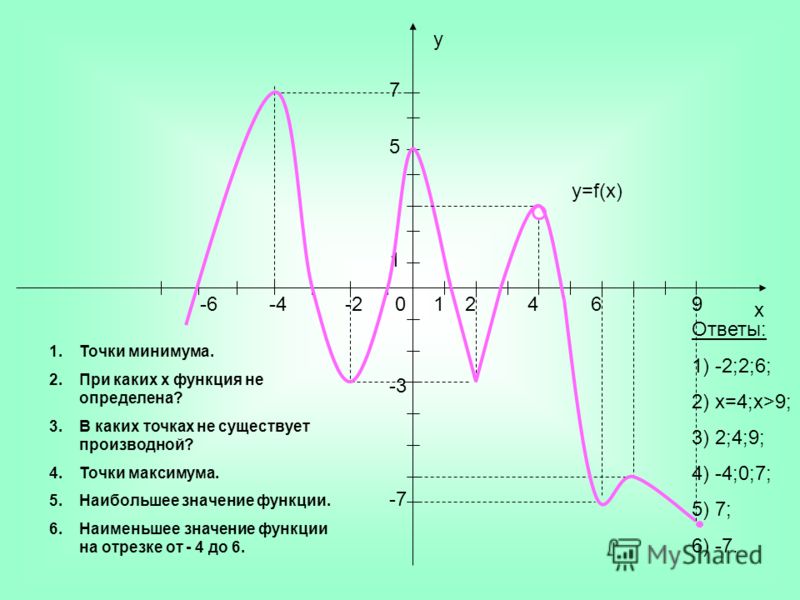 По умолчанию это
По умолчанию это  Файлы, открытые в двоичном режиме (включая
Файлы, открытые в двоичном режиме (включая 
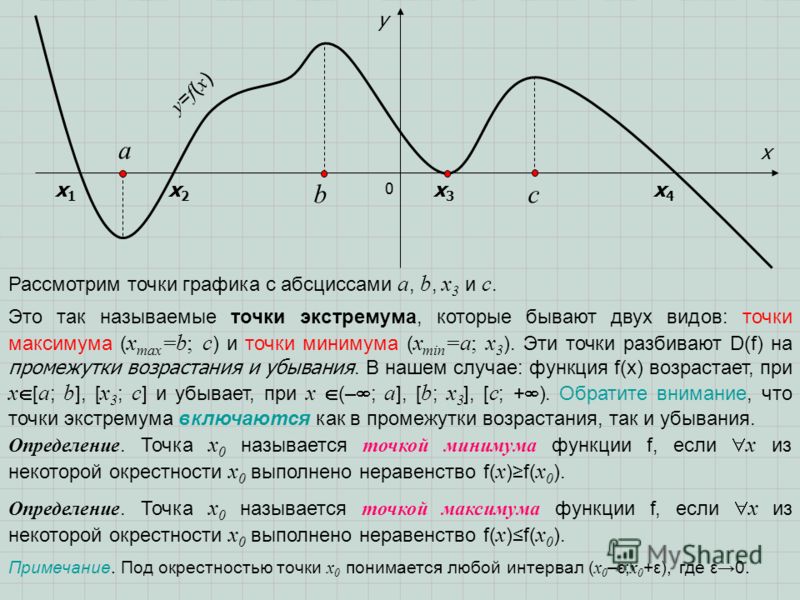
 Лежащий в основе
файловый дескриптор для файлового объекта затем получается путем вызова открывателя с
( файл , флаги ). открыватель должен возвращать дескриптор открытого файла (передавая
Лежащий в основе
файловый дескриптор для файлового объекта затем получается путем вызова открывателя с
( файл , флаги ). открыватель должен возвращать дескриптор открытого файла (передавая 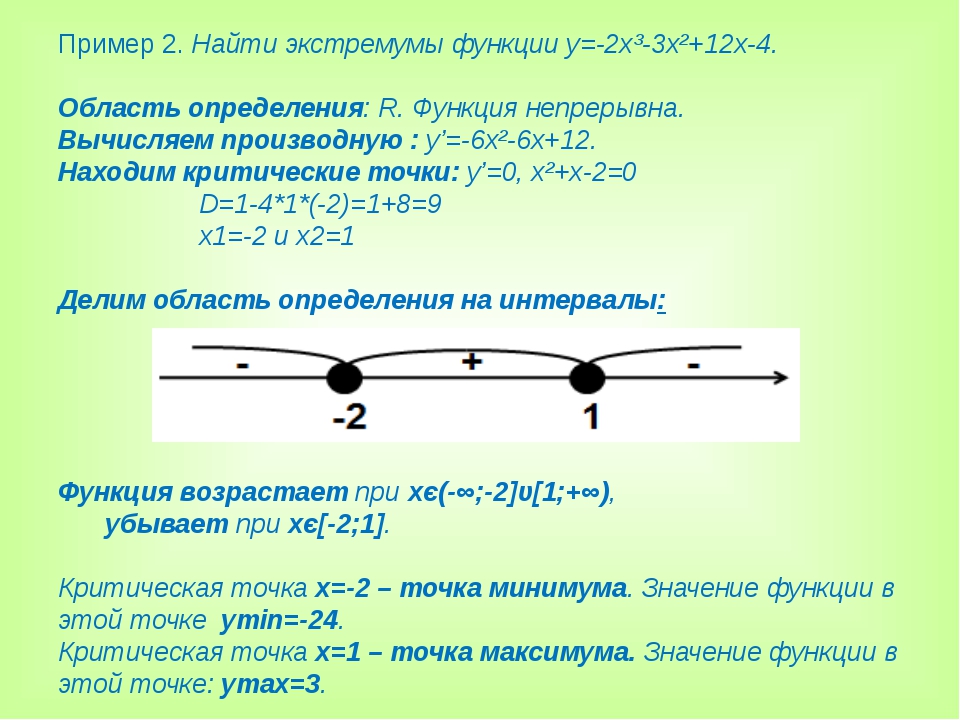
Leave A Comment