Медиана равнобедренного треугольника проведенная из вершины угла: . Какие из следующих утверждений верны? 1. Медиана равнобедренного треугольника, проведённая из вершины, противолежащей…

проведенной к основанию, боковым сторонам

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Определение и свойства медианы в равнобедренном треугольнике

В данной статье мы рассмотрим определение и свойства медиан, проведенных к основанию и боковым сторонам равнобедренного треугольника, а также разберем пример решения задачи для закрепления теоретического материала.

• Определение медианы
• Свойства медианы в равнобедренном треугольнике
  • Свойство 1
  • Свойство 2
  • Свойство 3
  • Свойство 4
  • Свойство 5
  • Свойство 6
• Пример задачи

Определение медианы

Медианой называется отрезок в треугольнике, который соединяет вершину и середину противоположной стороны.

• BD – медиана △ABC;
• AD = DC.

Треугольник является равнобедренным, если две его стороны равны (боковые), а третья сторона – это основание фигуры.

• AB = BC – боковые стороны;
• AC – основание.

Свойства медианы в равнобедренном треугольнике

Свойство 1

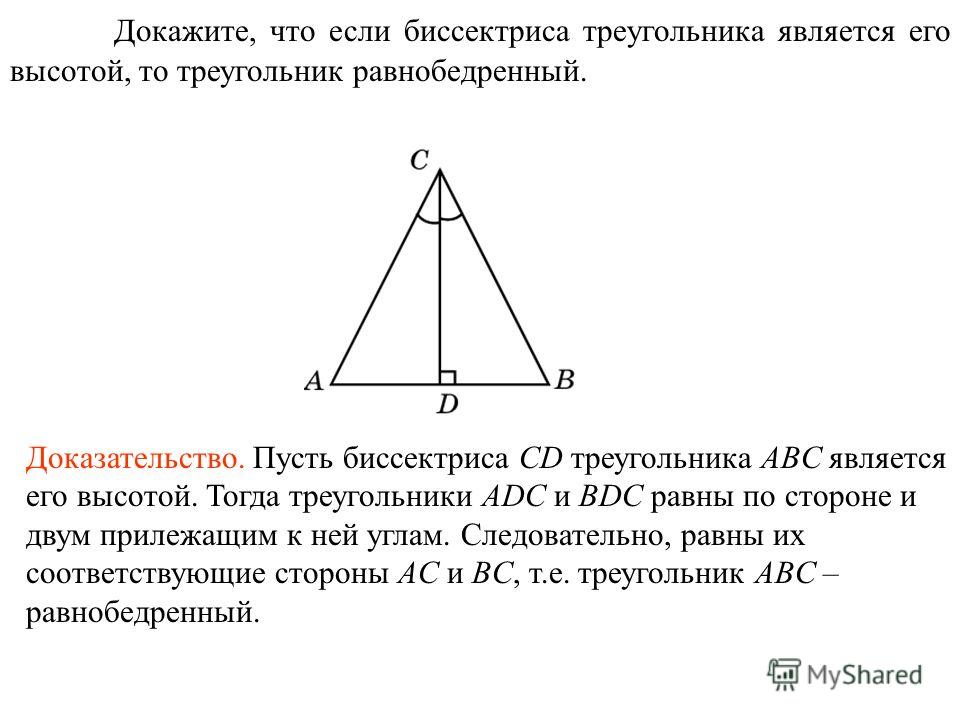
Медиана в равнобедренном треугольнике, проведенная к основанию, одновременно является высотой, опущенной на основание, и биссектрисой угла, из которого она проведена.

• BD – медиана и высота, опущенная на основание
  AC, а также биссектриса угла ABC.
• ∠ABD = ∠CBD

Свойство 2

В равнобедренном треугольнике медианы пресекаются в одной точке (центр тяжести) и делятся в этой точке в отношении 2:1.

• O – центр тяжести или центроид треугольника;
• AO = 2OF;
• BO = 2OD;
• CO = 2OE.

Свойство 3

Медиана делит равнобедренный треугольник на 2 равных по площади (равновеликих) треугольника. Следовательно, S₁ = S₂.

Свойство 4

Если провести три медианы в равнобедренном треугольнике, образуются 6 равновеликих треугольников (S₁ = S₂ = S₃ = S₄ = S₅ = S₆).

Свойство 5

Длину медианы в равнобедренном треугольнике, проведенную к основанию, можно найти по следующей формуле:

• a – основание;
• b – боковая сторона.

Свойство 6

Данной свойство, в отличие от перечисленных выше, не относится к медиане, опущенной на основание фигуры. Оно гласит:

Медианы, проведенные к боковым сторонам равнобедренного треугольника, равны между собой.

AF = CE, следовательно, AE = EB = BF = FC.

Пример задачи

Основание равнобедренного треугольника равняется 7 см, а боковая сторона – 12 см. Найдите длину медианы, проведенной к основанию фигуры.

Решение
Воспользуемся формулой, представленной в Свойстве 5, подставив в нее известные нам по условиям задачи значения:

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Медиана треугольника.

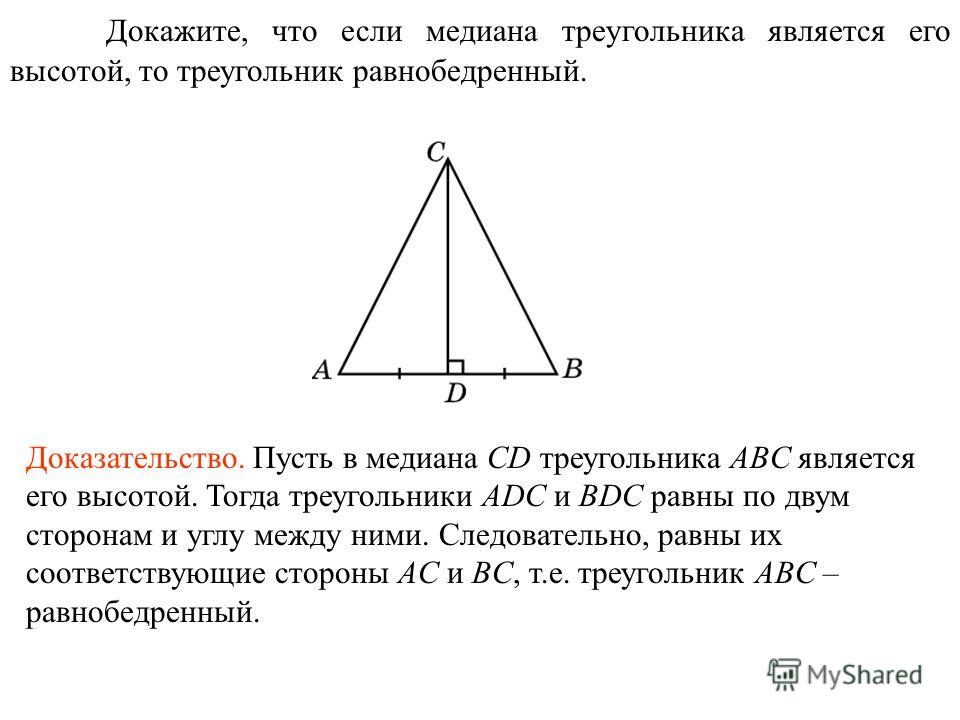Теорема равнобедренного треугольника.

• Альфашкола
• Статьи
• Медиана треугольника

Что такое медиана треугольника?

 

Медиана треугольника — это отрезок, соединяющий вершину треугольника c серединой противоположной стороны. Прямая тоже может быть медианой. Треугольник имеет три стороны, поэтому у него всегда ровно три медианы, каждая из которых выходит из вершины к середине противоположной стороны треугольника.

Что такое

 

Давайте введем определение высоты:

Для построения медианы необходимо:

1. найти середину стороны и обозначить ее точкой;
2. соединить найденную точку с  противолежащей вершиной треугольника.

Медиана в равнобедренном треугольнике

Напомним про свойства равнобедренного треугольника из теоремы:

 

Если мы проведем медиану к основанию в равнобедренном треугольнике, то увидим что она также является и высотой:

Напомним, что такое биссектриса:

 

Все медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2 к 1.

Свойства медианы

Медиана — это значение, которое делит упорядоченный набор данных на две равные части, то есть 50% значений находятся выше медианы, а 50% — ниже. Вот некоторые свойства медианы:

1. Медиана не зависит от выбросов в данных. Это означает, что если в наборе данных есть несколько значений, которые являются выбросами (то есть существенно отличаются от остальных значений), то медиана останется той же самой.

2. Медиана может быть использована для измерения центральной тенденции. В отличие от среднего значения, медиана более устойчива к выбросам и не будет искажена ими.

3. Если набор данных имеет четное количество значений, то медианой будет среднее значение двух средних элементов. Если же набор данных имеет нечетное количество значений, то медианой будет средний элемент.

4. Медиана может быть использована для определения дисперсии. Дисперсия — это мера распределения данных вокруг центральной тенденции. Медиана может быть использована для определения интерквартильного размаха, который является мерой разброса данных вокруг медианы.

5. Медиана может быть использована для определения выбросов. Если значение в наборе данных существенно отличается от медианы, то оно может быть классифицировано как выброс.

6. Медиана может быть использована для проверки симметричности распределения. Если медиана равна среднему значению, то распределение является симметричным. Если же медиана смещена вправо или влево от среднего значения, то распределение считается асимметричным.

Задача 1:

В равнобедренном треугольнике медиана, исходящая из вершины, которая не является вершиной угла с наименьшей мерой, равна 12 см. Найдите боковую сторону треугольника.

Ответ: 

Ответ: 12 см. В равнобедренном треугольнике медиана, исходящая из вершины, которая не является вершиной угла с наименьшей мерой, равна половине основания треугольника, т.е. равна боковой стороне треугольника.

Задача 2

В треугольнике ABC медиана, проведенная из вершины А, равна 8 см, а медиана, проведенная из вершины B, равна 6 см. Найдите длину медианы, проведенной из вершины C.

Ответ: 10 см. В треугольнике ABC медиана, проведенная из вершины А, делит сторону BC пополам, а медиана, проведенная из вершины B, делит сторону AC пополам. По свойству медиан треугольника, точка их пересечения делит каждую медиану в отношении 2:1. Значит, медиана, проведенная из вершины C, делит сторону AB в отношении 2:1, т.е. длина медианы из вершины C равна 10 см.

Задача 3

В треугольнике ABC медиана, проведенная из вершины А, равна 6 см, а медиана, проведенная из вершины B, равна 8 см. Известно, что периметр треугольника равен 30 см. Найдите длину стороны AB.

Ответ: 8 см. Рассмотрим треугольник ABC. По свойству медиан треугольника, медиана, проведенная из вершины А, делит сторону BC пополам, а медиана, проведенная из вершины B, делит сторону AC пополам. Значит, длины сторон BC и AC равны соответственно 2 * 6 = 12 см и 2 * 8 = 16 см. Так как периметр треугольника равен 30 см, то длина стороны AB равна 30 — 12 — 16 = 2 см. Таким образом, сторона AB равна 2 см, а медиана, проведенная из вершины C, делит эту сторону пополам, значит, ее длина равна 8 см.

 

Часто задаваемые вопросы

✅ Что такое медиана?

↪ Медиана треугольника — это линия, которая соединяет вершину треугольника с серединой противолежащей стороны.

✅ Какие свойства медианы треугольника?

↪ Мы используем разнообразные материалы, такие как учебники, аудио и видео материалы, игры иМедиана треугольника соединяет вершину треугольника с серединой противолежащей стороны. В треугольнике каждая сторона имеет свою медиану. Медианы треугольника пересекаются в точке, называемой центром тяжести, которая делит каждую медиану в отношении 2:1. Медиана является высотой того треугольника, в котором она проходит через вершину. Длина медианы, исходящей из вершины, равна половине основания треугольника в равнобедренном треугольнике. Медиана является наибольшей из линий, проведенных из вершины треугольника, и ограниченных точками пересечения медиан с противолежащими сторонами. тесты. Все материалы выбираются исходя из возраста и уровня владения языком ученика.

✅ Что такое высота треугольника?

org/Answer»>↪ Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на противолежащую сторону или ее продолжение.

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Людмила Иннокентьевна Пьянкова

Репетитор по математике

Стаж (лет)

Образование:

Пермский государственный университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Анастасия Сергеевна Черная

Репетитор по математике

Стаж (лет)

Образование:

Кубанский Государственный Университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Раиса Степановна Веренич

Репетитор по математике

Стаж (лет)

Образование:

Одесский Национальный университет имени Мечникова

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Предметы

• Математика
• Репетитор по физике
• Репетитор по химии
• Репетитор по русскому языку
• Репетитор по английскому языку
• Репетитор по обществознанию
• Репетитор по истории России
• Репетитор по биологии
• Репетитор по географии
• Репетитор по информатике

Специализации

• Подготовка к ЕГЭ по математике (профильный уровень)
• Репетитор по химии для подготовки к ЕГЭ
• Подготовка к олимпиадам по английскому языку
• Английский язык для начинающих
• ВПР по математике
• Репетитор для подготовки к ЕГЭ по обществознанию
• Репетитор по биологии для подготовки к ЕГЭ
• Репетитор по географии для подготовки к ЕГЭ
• Репетитор по географии для подготовки к ОГЭ
• Подготовка к ОГЭ по литературе

Похожие статьи

• Признаки делимости (Часть 2)
• Рациональные неравенства
• ОГЭ по математике. Числа и вычисления
• ЕГЭ по математике, базовый уровень. Преобразование алгебраических выражений
• ЕГЭ по математике, базовый уровень. Задачи с прикладным содержанием (вариант 3)
• Безопасное лето: 9 способов защитить ребенка от паразитов
• Ребенок левша: особенности обучения письму
• Что из математики реально пригодится в жизни?

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Текст с ошибкой:

Расскажите, что не так

Объяснение урока: Следствия теорем о равнобедренном треугольнике

В этом объяснении мы научимся использовать следствия теорем о равнобедренном треугольнике Теоремы треугольника для нахождения недостающих длин и углов в равнобедренных треугольниках.

Начнем с точного определения равнобедренного треугольника. Отзывать что конгруэнтность означает наличие одной и той же меры; например, равные стороны имеют одинаковая длина и равные углы имеют одинаковую меру.

Определение: равнобедренный треугольник

Равнобедренный треугольник — это треугольник, у которого две стороны равны.

Конгруэнтные стороны называются катетами треугольника, а третья сторона называется основанием .

Поскольку у равнобедренных треугольников две конгруэнтные стороны, это приводит нас к важное свойство углов равнобедренных треугольников.

Теорема: Теорема о равнобедренном треугольнике

Если две стороны треугольника равны, то углы, противолежащие этим сторонам конгруэнтны.

Конгруэнтные углы называются углами при основании . Третий угол называется углом при вершине .

В △𝐴𝐵𝐶, 𝐵𝐴=𝐵𝐶, поэтому 𝑚∠𝐴=𝑚∠𝐶.

Мы знаем, что равнобедренные треугольники по определению имеют две конгруэнтные стороны, и по предыдущей теореме у них два равных угла.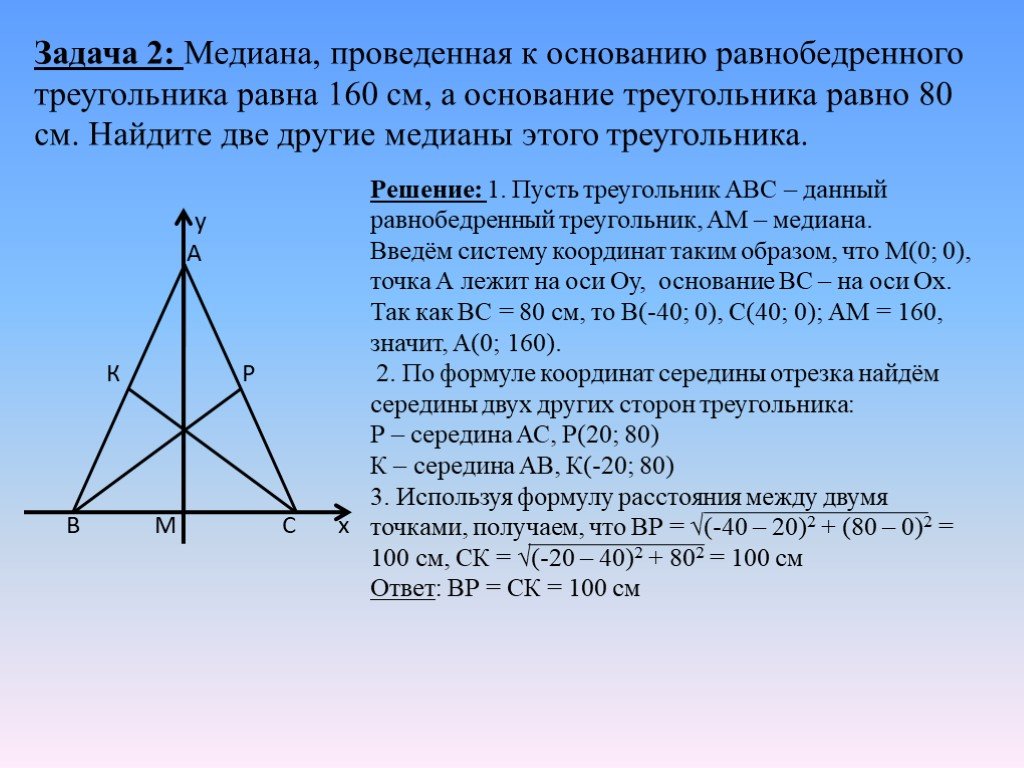 Обратное это верно; то есть, если треугольник имеет два угла, которые равны, то это равнобедренный треугольник. Это определено в следующей теореме.

Теорема: обратная теорема о равнобедренном треугольнике

Если два угла треугольника равны, стороны, противоположные этим углам также конгруэнтны.

В этом объяснителе мы рассмотрим ряд следствий из этих теорем. Эти следствия позволяют выявить дополнительные геометрические свойства о равнобедренные треугольники. Давайте посмотрим на первое из этих следствий.

Следствие теорем о равнобедренном треугольнике: медиана Равнобедренный треугольник

Медиана равнобедренного треугольника, проведенная из угла при вершине, делит его пополам и равна перпендикулярно основанию.

Мы можем доказать это следствие следующим образом.

Медиана треугольника — это отрезок, соединяющий вершину с серединой противоположной стороны и, таким образом, делит эту сторону пополам. В равнобедренном треугольнике 𝐴𝐵𝐶 ниже медиана угла при вершине 𝐴 представляет собой отрезок, соединяющий 𝐴 с серединой (𝐷) основания, 𝐵𝐶.

Поскольку 𝐷 является серединой 𝐵𝐶, мы знаем, что 𝐶𝐷=𝐵𝐷.

Мы также можем написать, что 𝐴𝐶=𝐴𝐵, (поскольку треугольник равнобедренный) и 𝐴𝐷=𝐴𝐷.(общая сторона)

Так как есть три конгруэнтных стороны, то △𝐴𝐷𝐶 конгруэнтно △𝐴𝐷𝐵 по критерию конгруэнтности SSS.

Следовательно, мы можем написать, что 𝑚∠𝐴𝐷𝐶=𝑚∠𝐴𝐷𝐵, а так как 𝐵𝐶 — прямая, эти углы оба должны быть 90∘. Мы можем также обратите внимание, что 𝑚∠𝐶𝐴𝐷=𝑚∠𝐵𝐴𝐷, поэтому медиана из вершины равнобедренный треугольник также делит вершину пополам.

Учитывая, что 𝐴𝐷 является медианой, мы можем говорят, что медиана угла при вершине делит основание пополам, но здесь мы имеем также продемонстрировал, что он делает это под углом 90∘.

Следовательно, медиана равнобедренного треугольника, проведенная из угла при вершине, равна серединный перпендикуляр треугольника.

Из этого следствия мы можем заметить, что полезное свойство медианы равнобедренного треугольника состоит в том, что он также образует ось симметрии равнобедренный треугольник и разбивает равнобедренный треугольник на две равные части прямоугольные треугольники.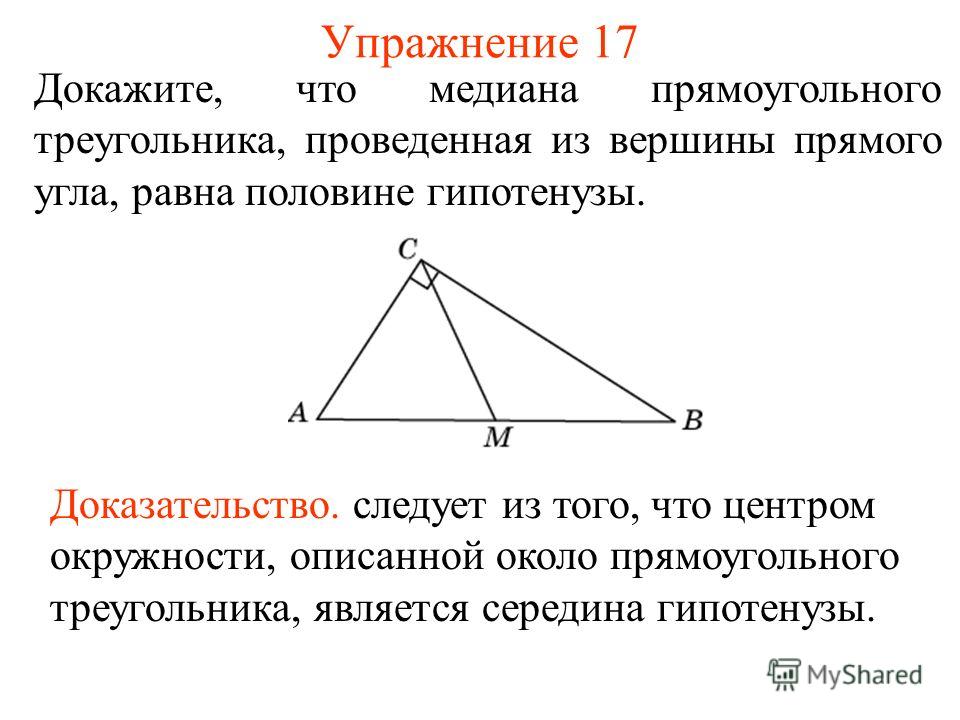

Теперь мы увидим, как мы можем применить это следствие в следующем примере.

Пример 1: Нахождение значений в треугольнике по заданной биссектрисе

Для каких значений 𝑥 и 𝑦 𝐴𝐷 серединный перпендикуляр к 𝐵𝐶?

Ответ

На рисунке видно, что △𝐴𝐵𝐶 представляется равнобедренным треугольником. Хотя мы не можем этого доказать, мы можем использовать некоторые свойства равнобедренных треугольников, чтобы помочь. равнобедренный треугольник — это треугольник, у которого две равные стороны. Напомним, что медиана равнобедренного треугольника из угла при вершине является перпендикуляром биссектриса основания.

Следовательно, 𝐴𝐷 — всего лишь перпендикуляр биссектриса 𝐵𝐶 в случае равнобедренный треугольник. Поэтому нам необходимо определить значения 𝑥 и 𝑦 такие, что 𝐴𝐵=𝐴𝐶 (две конгруэнтные ноги) и 𝐵𝐷=𝐶𝐷 (основание разделено пополам).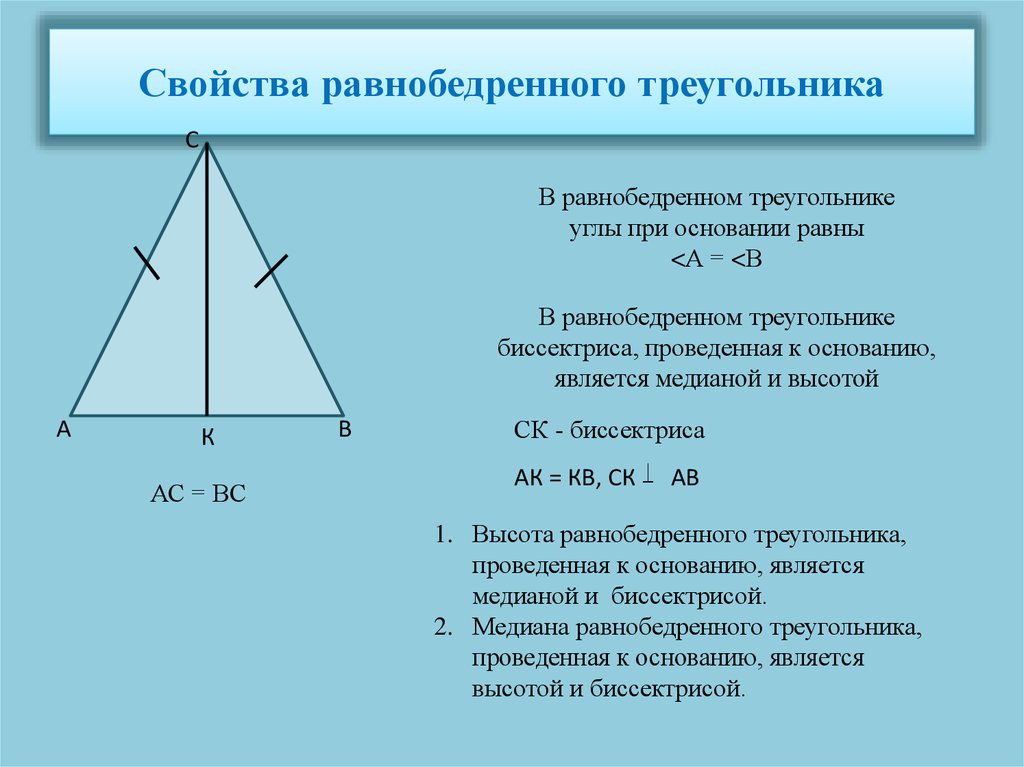

Мы можем начать с подстановки в данных выражениях вместо 𝐴𝐵 и 𝐴𝐶. Это дает 𝐴𝐵=𝐴𝐶3𝑥+2=5𝑦+33𝑥−1=5𝑦.

Таким же образом для 𝐵𝐷 и 𝐶𝐷, мы можем составить второе уравнение как следует: 𝐵𝐷=𝐶𝐷5𝑦−1=10−3𝑥5𝑦=11−3𝑥.

Чтобы найти значения 𝑥 и 𝑦, решаем эти два уравнения одновременно, либо подстановкой, либо исключением. Они есть:

3𝑥−1=5𝑦,11−3𝑥=5𝑦.

(1)(2)

Поскольку оба уравнения имеют член 5𝑦 в правой части каждого уравнения можно положить левую часть каждого уравнения равной единице другой и решить для 𝑥. Это дает нам 3𝑥−1=11−3𝑥6𝑥−1=116𝑥=12𝑥=2.

Далее подставляем 𝑥=2 в любое уравнение (1) или (2). Подстановка в уравнение (1) дает 3(2)−1=5𝑦6−1=5𝑦5=5𝑦𝑦=1.

Таким образом, мы можем ответить, что 𝐴𝐷 — это серединный перпендикуляр к 𝐵𝐶, когда 𝑥=2 и 𝑦=1.

Рассмотрим еще одно следствие.

Следствие теорем о равнобедренном треугольнике: биссектриса Vertex Angle

Биссектриса угла при вершине равнобедренного треугольника является перпендикуляром биссектриса основания.

Мы можем доказать это следующим образом. Рассмотрим равнобедренный треугольник 𝐸𝐹𝐺. Биссектриса угла при вершине, 𝐸, был нарисован.

Мы можем обозначить точку пересечения биссектрисы 𝐺𝐹 как 𝐻. Поскольку 𝐸𝐻 — биссектриса угла, мы знаем, что 𝑚∠𝐺𝐸𝐻=𝑚∠𝐹𝐸𝐻.

Теперь есть 2 пары конгруэнтных сторон: 𝐸𝐺=𝐸𝐹△𝐸𝐹𝐺𝐸𝐻.(так как равнобедренный)andisacommonside

Имея конгруэнтную пару вложенных углов, мы можем сказать, что △𝐸𝐺𝐻 соответствует △𝐸𝐹𝐻 по условию SAS (две равные стороны и прилежащий угол). Вы можете быть знакомы с этим критерием, хотя мы не будем прямо докажите это в этом объяснителе.

Это означает, что соответствующие углы равны и 𝑚∠𝐸𝐻𝐺=𝑚∠𝐸𝐻𝐹. С эти два угла лежат на прямой 𝐺𝐹, тогда они оба должны быть равны 90∘.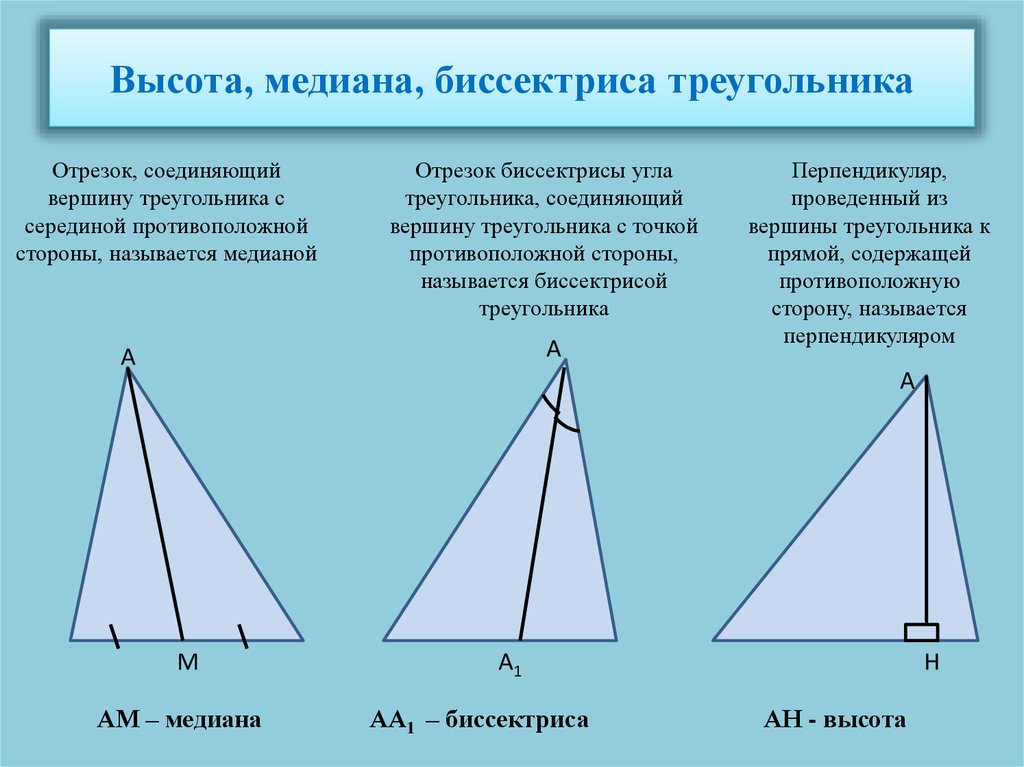 Кроме того, стороны 𝐺𝐻 и 𝐹𝐻 соответствуют, а значит, и конгруэнтный.

Итак, мы доказали следствие того, что биссектриса при вершине угла 𝐸 также является серединным перпендикуляром равнобедренного треугольника 𝐸𝐹𝐺.

Давайте посмотрим, как это можно применить на следующем примере.

Пример 2. Нахождение недостающей длины в равнобедренном треугольнике с помощью биссектриса вершинного угла

1. Заполните пропуск: На этом рисунке, если 𝐴𝐵=𝐴𝐶, 𝐴𝐷∩𝐵𝐶={𝐷}, где 𝐷𝐶=8см, и 𝑚∠𝐶𝐴𝐷=𝑚∠𝐵𝐴𝐷=35∘, длина 𝐵𝐷 равна см.
2. Найдите 𝑚∠𝐴𝐶𝐵.

Ответ

Для рисунка нам дана информация, что △𝐴𝐵𝐶 имеет две конгруэнтные стороны (𝐴𝐵=𝐴𝐶). Это значит, что △𝐴𝐵𝐶 — равнобедренный треугольник. Мы тоже учитывая, что точка пересечения 𝐴𝐷 и 𝐵𝐶 это точка 𝐷.

Часть 1

Начнем с добавления угловых измерений, 𝑚∠𝐶𝐴𝐷=𝑚∠𝐵𝐴𝐷=35∘, к рисунку вместе с отметкой конгруэнтных сторон.

Заметим, что, поскольку эти два угла равны по размеру, это означает, что угол при вершине 𝐴 равнобедренного треугольника равен разделенный пополам. Напомним, что одно из следствий Теорема о равнобедренном треугольнике говорит нам, что биссектриса угла при вершине равнобедренного треугольника является серединным перпендикуляром к основанию. Этот позволяет вычислить длину 𝐵𝐷. Обратите внимание, что если бы у нас не было этого сведения об углах, мы не смогли бы доказать, что 𝐴𝐷 — биссектриса.

Поскольку 𝐵𝐶 было разделено пополам, тогда мы знаем, что 𝐵𝐷=𝐷𝐶.

Судя по диаграмме, 𝐷𝐶=8см. Следовательно, 𝐵𝐷=8.cm

Таким образом, мы можем заполнить пробел: длина 𝐵𝐷 это 8 см.

Часть 2

Чтобы найти 𝑚∠𝐴𝐶𝐵, мы можем использовать тот факт, что 𝐴𝐷 — серединный перпендикуляр к △𝐴𝐵𝐶. Это значит, что 𝑚∠𝐴𝐷𝐶=90∘.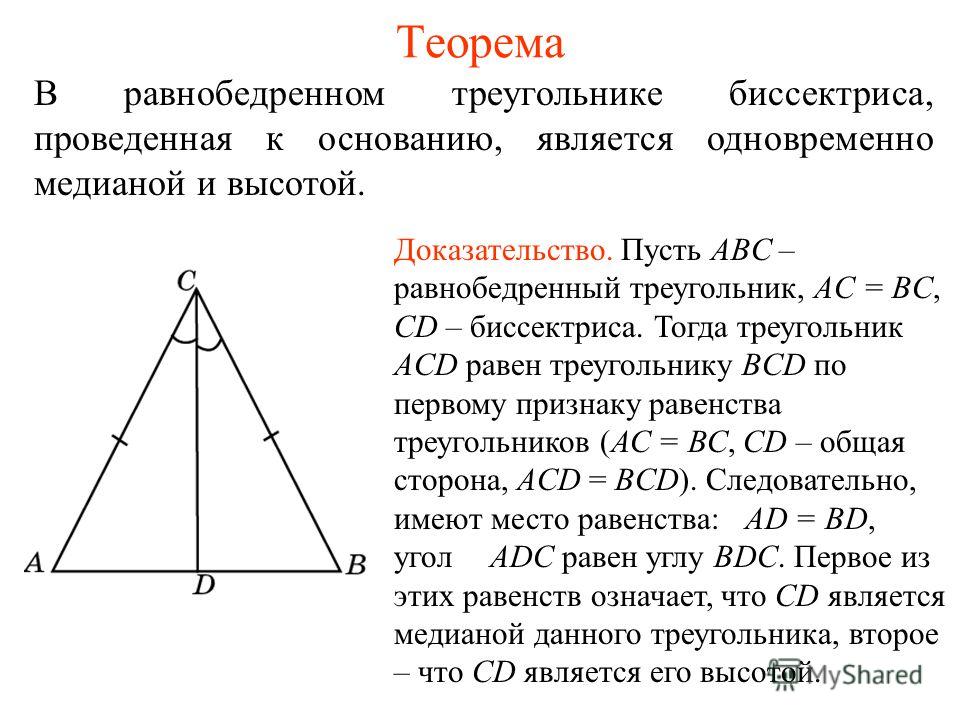

Использование △𝐴𝐶𝐷 и тот факт, что интерьер сумма углов в треугольнике равна 180∘, мы имеем 𝑚∠𝐴𝐶𝐷+𝑚∠𝐶𝐴𝐷+𝑚∠𝐴𝐷𝐶=180𝑚∠𝐴𝐶𝐷+35+90=180𝑚∠𝐴𝐶𝐷+125=180𝑚∠𝐴𝐶𝐷=180−125=55.∘∘∘∘∘∘∘∘∘

∠𝐴𝐶𝐵, мы можем дать ответ, что 𝑚∠𝐴𝐶𝐵 это 55∘.

Теперь мы рассмотрим еще одно следствие теоремы о равнобедренном треугольнике.

Следствие теоремы о равнобедренном треугольнике: перпендикуляр к основанию

Прямая, проходящая через угол при вершине равнобедренного треугольника и перпендикулярна основанию, делит пополам основание и угол при вершине.

Мы можем доказать это, рассмотрев пример прямой линии, проходящей через угол при вершине равнобедренного треугольника, △𝑃𝑄𝑅 снизу, в точке 90° к основанию. Мы можно определить точку, в которой линия пересекается 𝑅𝑄 как 𝑇.

На данный момент нам нужно установить, как эта линия влияет на угол вершины 𝑃 и база 𝑅𝑄.

Учитывая, что линия перпендикулярна основанию, мы признаем, что 𝑚∠𝑃𝑇𝑅=𝑚∠𝑃𝑇𝑄=90. ∘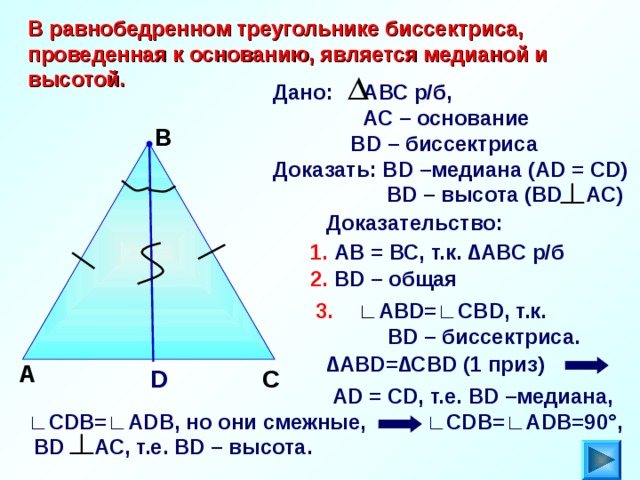

Поскольку треугольник равнобедренный, мы знаем, что 𝑅𝑃=𝑄𝑃.

Мы можем заметить, что 𝑅𝑃 и 𝑄𝑃 — гипотенузы соответствующих прямоугольные треугольники, △𝑃𝑅𝑇 и △𝑃𝑄𝑇.

Кроме того, поскольку 𝑃𝑇 является общей стороной как △𝑃𝑅𝑇, так и △𝑃𝑄𝑇, мы знаем, что это конгруэнтная сторона в эти треугольники. Поэтому, применяя РГО (прямой угол-гипотенуза-сторона) критерий конгруэнтности, мы можем доказать, что △𝑃𝑅𝑇≅△𝑃𝑄𝑇.

Следствие можно проверить: основание 𝑅𝑄 делится пополам, и так как 𝑅𝑇 и 𝑄𝑇 — соответствующие стороны у двух равных треугольников равны и сами стороны. Это значит, что основание 𝑅𝑄 разделено пополам. Угол при вершине 𝑃 также был разделен пополам, поскольку мы знаем, что его два составляющих угла, ∠𝑅𝑃𝑇 и ∠𝑄𝑃𝑇 — соответствующие углы два равных треугольника и, следовательно, имеют равные меры.

Теперь мы увидим, как мы можем применить это следствие в следующем примере.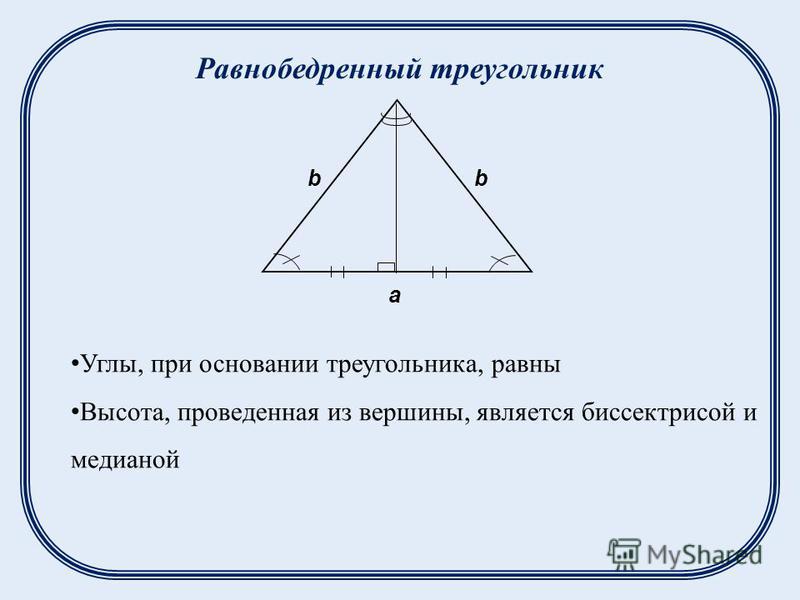

Пример 3. Нахождение меры угла в равнобедренном треугольнике Используя его свойства

Найдите 𝑚∠𝐷𝐴𝐵.

Ответ

На рисунке видно, что самый большой треугольник, △𝐴𝐵𝐶, имеет две конгруэнтные стороны, отмеченные, чтобы показать нам, что 𝐴𝐶=𝐴𝐵. Следовательно, △𝐴𝐵𝐶 должен быть равнобедренный треугольник.

Нам дано, что 𝑚∠𝐴𝐷𝐵=90∘. Этот означает, что отрезок 𝐴𝐷, от угла при вершине равнобедренного треугольника перпендикулярен основанию. Напомним, что одно из следствий теорем о равнобедренном треугольнике утверждает, что прямая, проходящая через угол при вершине равнобедренный треугольник и перпендикуляр к основанию делит основание пополам и угол при вершине. Это полезно, поскольку позволяет нам определить 𝑚∠𝐷𝐴𝐵.

Так как ∠𝐶𝐴𝐵 было разделено пополам, то 𝑚∠𝐷𝐴𝐵=𝑚∠𝐶𝐴𝐷.

Из диаграммы имеем 𝑚∠𝐶𝐴𝐷=25∘; следовательно, мы можем определить, что ответ 𝑚∠𝐷𝐴𝐵=25. ∘

Теперь мы увидим два примера, где нам нужно применить некоторые из этих следствия теорем о равнобедренном треугольнике для нахождения мер неизвестных углы и стороны.

Пример 4. Доказательство геометрического утверждения с использованием следствий Теоремы о равнобедренном треугольнике

На следующем рисунке, если 𝐿𝑋=𝑌𝑋, 𝐿𝑍=𝑌𝑍, 𝑚∠𝐿𝑌𝑋=30∘, 𝑚∠𝑍𝐿𝑌=55∘, а 𝑀 — середина 𝐿𝑌, найдите 𝑚∠𝑀𝑍𝐿 и 𝑚∠𝐿𝑀𝑋.

Ответ

Нам дали информацию, что 𝐿𝑋=𝑌𝑋 и 𝐿𝑍=𝑌𝑍. Это означает, что в каждом из △𝐿𝑍𝑌 и △𝐿𝑋𝑌, есть пара равных сторон. Треугольник с двумя равными сторонами есть, по определению равнобедренный треугольник. Поэтому, △𝐿𝑍𝑌 и △𝐿𝑋𝑌 оба равнобедренные. Знание свойств равнобедренных треугольников, заданных в следствиях теоремы о равнобедренном треугольнике будут полезны при вычислении искомых углов.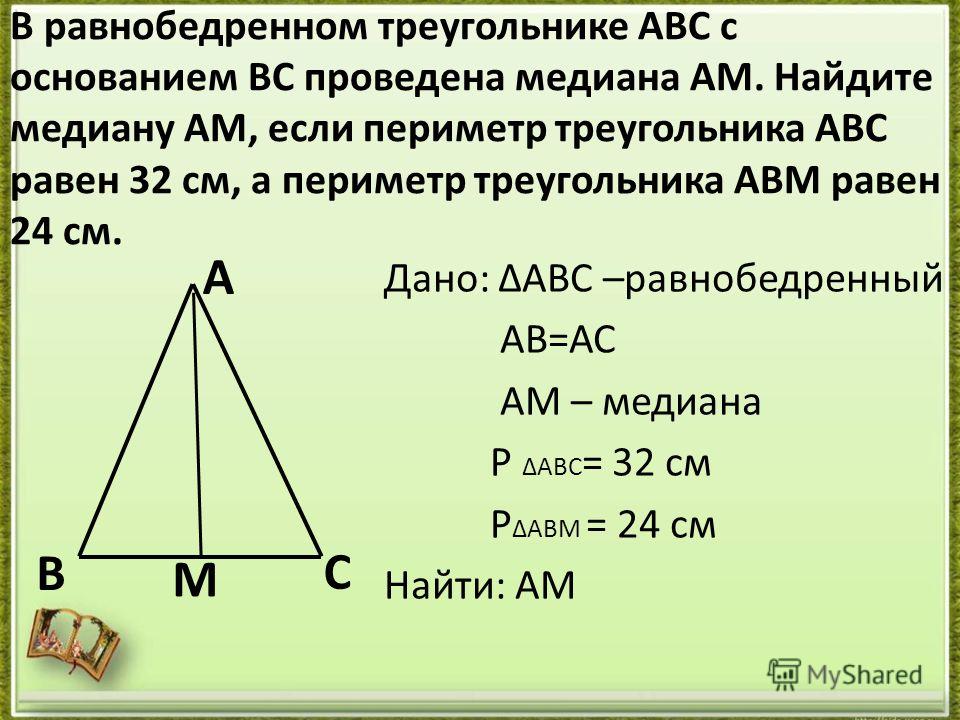

Начнем с построения сегмента 𝑍𝑀, которая создает первый требуемый угол, ∠𝑀𝑍𝐿.

Так как 𝑀 является серединой 𝐿𝑌, мы это знаем 𝑍𝑀 должна быть медианой равнобедренного треугольника 𝐿𝑍𝑌. Напомним, что медиана равнобедренного треугольника из угол при вершине является серединным перпендикуляром к основанию. Как 𝑍𝑀 — серединный перпендикуляр к 𝐿𝑌, тогда 𝑚∠𝐿𝑀𝑍=90.∘

Внутри △𝐿𝑀𝑍 мы можем использовать свойство, которое внутренний угол в треугольнике равен сумме 180∘, чтобы помочь нам найти 𝑚∠𝑀𝑍𝐿. При условии 𝑚∠𝑍𝐿𝑀=55∘ и 𝑚∠𝐿𝑀𝑍=90∘, мы имеем 𝑚 Хорошо 𝑍𝐿𝑀+𝑚 Вs𝐿𝑀𝑍+𝑚omTr𝑀𝑍𝐿 = 18055+90+𝑚omTr𝑀𝑍𝐿 = 180145+𝑚omt должен определить 𝑚∠𝐿𝑀𝑋. Построим отрезок 𝑀𝑋 для создания этого угла.

В том же процессе, что и раньше, мы знаем, что △𝐿𝑋𝑌 равнобедренный. С 𝑀 является серединой 𝐿𝑌, тогда медиана угла при вершине 𝑋 есть серединный перпендикуляр к основанию. Это значит, что 𝑚∠𝐿𝑀𝑋=90.∘

Мы можем дать ответы для 𝑚∠𝑀𝑍𝐿 и 𝑚∠𝐿𝑀𝑋 как 3590.∘∘и

Теперь мы рассмотрим последний пример.

Пример 5. Доказательство геометрического утверждения с использованием следствий Теоремы о равнобедренном треугольнике

На рисунке ниже 𝐴𝐶∩𝐵𝐷=𝑀, 𝑀𝐷=𝑀𝐶, 𝐴𝐵⫽𝐶𝐷 и 𝑚∠𝑀𝐶𝐷=40∘. Рисовать 𝑀𝐸⊥𝐶𝐷 и вырезать 𝐶𝐷 в 𝐸, затем нарисуйте 𝑀𝐹⊥𝐴𝐵 и вырезать 𝐴𝐵 в 𝐹. Находить 𝑚∠𝐶𝑀𝐸 и 𝑚∠𝐵𝑀𝐹.

Ответ

Мы можем начать с построения двух сегментов 𝑀𝐸 и 𝑀𝐹, которые перпендикулярны 𝐶𝐷 и 𝐴𝐵 соответственно. Мы также можем заполнить данные информация об углах, которая 𝑚∠𝑀𝐶𝐷=40∘, и отметьте на схеме, что 𝑀𝐷=𝑀𝐶.

В нижнем треугольнике △𝐶𝑀𝐷 есть два конгруэнтные отрезки. Это значит, что △𝐶𝑀𝐷 должен быть равнобедренным треугольником. Там есть несколько способов, которыми мы можем найти 𝑚∠𝐶𝑀𝐸. Один из методов заключается в использовании △𝐶𝑀𝐸 и напомним, что внутренний угол меры в сумме треугольника к 180∘. При условии 𝑚∠𝑀𝐶𝐸=40∘ и 𝑚∠𝐶𝐸𝑀=90∘, имеем 𝑚 Хорошо 𝑀𝐶𝐸+𝑚 Вs𝐶𝐸𝑀+𝑚 В Ниборог = 18040+90+𝑚 𝑚 Хорошо = 180130+𝑚 Ворта0003

Далее нам нужно рассчитать требуемый угол, 𝑚∠𝐵𝑀𝐹. При условии △𝐶𝑀𝐷 — равнобедренный треугольник, мы можем использовать тот факт, что прямая, проходящая через угол при вершине равнобедренный треугольник и перпендикулярен основанию, делит основание пополам и угол вершины. Это значит, что 𝑚∠𝐷𝑀𝐸=𝑚∠𝐶𝑀𝐸=50.∘

Учитывая, что 𝐴𝐵⫽𝐶𝐷, 𝑀𝐸⊥𝐶𝐷 и 𝑀𝐹⊥𝐴𝐵 с 𝑀𝐸 и 𝑀𝐹 встреча в точке 𝑀, тогда 𝐸𝐹 — прямая. Мы можем тогда обратите внимание, что ∠𝐷𝑀𝐸 и ∠𝐵𝑀𝐹 вертикально противоположны и, следовательно, конгруэнтны.

Следовательно, мы можем дать ответ, что неизвестные меры угла равны 𝑚∠𝐶𝑀𝐸=50𝑚∠𝐵𝑀𝐹=50.∘∘и

Подведем итоги.

Ключевые моменты

• Равнобедренный треугольник — это треугольник, две стороны которого равны.
• Если две стороны треугольника равны, то углы, противоположные эти стороны равны.
• Если два угла треугольника равны, то стороны, противолежащие этим углы тоже равны.
• Медиана равнобедренного треугольника, проведенная из угла при вершине, равна серединный перпендикуляр к основанию и делит пополам угол при вершине.
• Биссектриса угла при вершине равнобедренного треугольника серединный перпендикуляр к основанию.
• Прямая, проходящая через угол при вершине равнобедренного треугольника и перпендикулярен основанию, делит пополам основание и угол при вершине.
• Ось симметрии равнобедренного треугольника — это медиана, делящая его пополам. база.

Углы и аргументы

Ни одна концептуальная группа по вопросам геометрии GMAT не является более важной, чем треугольники, и никакое обсуждение треугольников на GMAT не будет полностью исчерпывающим, если не охватывать медианы, высоты и биссектрисы углов. Итак, в сегодняшней статье давайте вместе обсудим эти интересные концепции треугольников и покажем, как их можно применить к сложным вопросам геометрии GMAT. Для начала мы предполагаем, что вы знаете термины медиана, биссектриса угла и высота, но тем не менее, просто чтобы быть уверенными, мы начнем сегодняшнее обсуждение с их определения:

 

Медиана – отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

 

Биссектриса угла – Отрезок, соединяющий вершину треугольника с противоположной стороной так, что угол при вершине делится на две равные части.

 

Высота – Отрезок, соединяющий вершину треугольника с противоположной стороной, так что этот отрезок перпендикулярен противоположной стороне.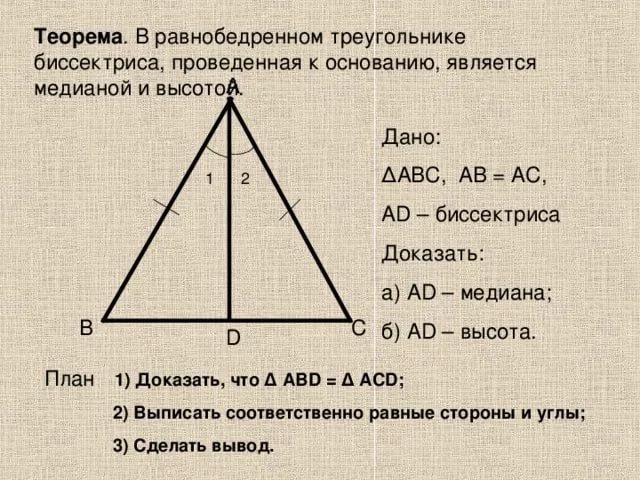

 

Обычно медианы, биссектрисы и высоты, проведенные из одной и той же вершины треугольника, являются разными отрезками. Но, что немаловажно, в особых треугольниках, таких как равнобедренные и равнобедренные треугольники, они могут перекрываться. И, как всегда, каждый раз, когда вы можете идентифицировать треугольник как особый треугольник, у вас есть еще больше правил, которые вы можете применить, чтобы лучше понять его. Сейчас мы дадим вам некоторые из этих свойств, которые могут быть очень полезными.

 

I.

В равнобедренном треугольнике (основание – сторона, не равная ни одной другой стороне):

– высота, проведенная к основанию, – медиана и биссектриса угла;

– медиана, проведенная к основанию, есть высота и биссектриса угла;

– биссектриса угла, противоположного основанию, является высотой и медианой.

 

II.

Верно и обратное тому, что мы только что узнали. Рассмотрим треугольник ABC:

– Если биссектриса угла вершины A также является медианой, треугольник является равнобедренным, так что AB = AC и BC является основанием.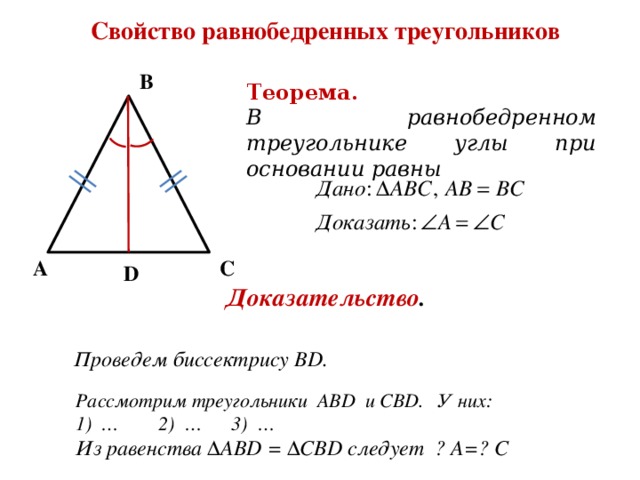 Следовательно, эта биссектриса угла также является высотой.

– Если высота, проведенная из вершины A, также является медианой, то треугольник равнобедренный, так что AB = AC и BC является основанием. Следовательно, эта высота также является биссектрисой угла.

– Если медиана, проведенная из вершины A, также является биссектрисой угла, треугольник равнобедренный, так что AB = AC и BC является основанием. Следовательно, эта медиана также является высотой.

и так далее…

 

III.

В  равностороннем треугольнике каждая высота, медиана и биссектриса угла, проведенные из одной и той же вершины, перекрываются.

Попробуйте доказать все эти свойства самостоятельно. Так вы их не забудете.

 

Из этого следует несколько вещей:

— Должна ли биссектриса угла в треугольнике, который также является медианой, быть перпендикулярной противоположной стороне? Да.

— Можем ли мы иметь биссектрису угла, которая также является медианой, которая не перпендикулярна? Нет.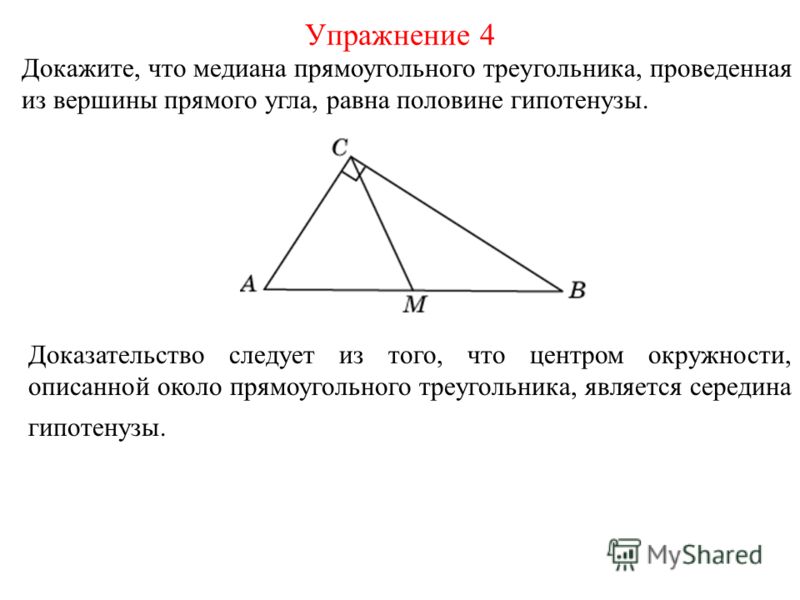 Биссектриса угла, которая также является медианой, подразумевает равнобедренный треугольник, который подразумевает, что это также высота.

-Можем ли мы иметь медиану из вершины A, которая перпендикулярна BC, но не делит пополам угол A? Нет. Медиана, являющаяся высотой, означает, что треугольник равнобедренный, что означает, что он также является биссектрисой угла.

и так далее…

 

Давайте рассмотрим пример вопроса достаточности данных, чтобы продемонстрировать применимость этих концепций:

 

Вопрос : Какова мера угла A в треугольнике ABC?

Утверждение 1. Биссектриса угла A является медианой треугольника ABC.
Утверждение 2: высота от B до AC является медианой в треугольнике ABC.

 

(A) Утверждения (1) ОДНОГО достаточно, но одного утверждения (2) недостаточно для ответа на заданный вопрос.

(B) Утверждения (2) ОДНОГО достаточно, но одного утверждения (1) недостаточно для ответа на поставленный вопрос.

(C) ОБА утверждения (1) и (2) ВМЕСТЕ достаточны для ответа на заданный вопрос, но НИ ОДНОГО утверждения недостаточно для ответа на заданный вопрос.

(D) КАЖДОГО ОТДЕЛЬНОГО утверждения достаточно, чтобы ответить на заданный вопрос.

(E) Утверждения (1) и (2) ВМЕСТЕ НЕ достаточны для ответа на заданный вопрос, и необходимы дополнительные данные, относящиеся к проблеме.

 

Решение . Нам дан треугольник ABC, но мы не знаем, что это за треугольник.

Итак, давайте перейдем непосредственно к операторам.

 

Утверждение 1. Биссектриса угла A является медианой треугольника ABC.

Биссектриса угла также является медианой. Это означает, что треугольник ABC должен быть равнобедренным, так что AB = AC. Но мы понятия не имеем о мере угла А. Одного этого утверждения недостаточно.

 

Утверждение 2. Высота угла B к AC является медианой в треугольнике ABC.

Высота также является медианой. Это означает, что треугольник ABC должен быть равнобедренным треугольником таким, что AB = BC (обратите внимание, что высота здесь взята из вершины B). Но мы понятия не имеем о мере угла А. Одного этого утверждения недостаточно.

 

Используя оба утверждения вместе, мы видим, что AB = AC = BC. Значит треугольник равносторонний! Значит угол А должен быть 60 градусов. Достаточный! Поэтому правильный ответ (С).

 

И очень важный вывод из этой проблемы: здесь мы смогли использовать наши знания о том, как появляются медианы, высоты и биссектрисы в особых типах треугольников, чтобы доказать, что мы имеем дело с особым равносторонним треугольником. Это важный урок как для концепций медиан и высот, так и для геометрии GMAT в целом, особенно в достаточности данных. Вы должны активно искать специальные треугольники, потому что специальные треугольники позволяют вам определить довольно много фактов из ограниченного набора информации. Они идеально подходят для обеспечения достаточности данных, когда весь тип вопроса зависит от «умело скрытой» информации, которую можно разблокировать путем распознавания ключевых понятий.