Преобразования по методу Box-Cox, по методу арксинуса и логарифмические—Справка
Доступно с лицензией Geostatistical Analyst.
Некоторые методы ArcGIS Geostatistical Analyst Extension требуют нормального распределения данных. Если данные сдвинуты (распределение несимметрично), то может понадобиться преобразовать данные к нормальному распределению. Гистограмма позволяет изучать эффекты различных преобразований на распределение набора данных. Если модель интерполяции, которую вы строите, использует один из методов кригинга, и одним из шагов выбрано преобразование данных, проинтерполированные значения будут преобразованы к исходному масштабу проинтерполированной поверхности.
ArcGIS Geostatistical Analyst Extension позволяет применять несколько преобразований, включая преобразование по методу Box-Cox (степенное преобразование), преобразование по методу арксинуса и логарифмическое преобразование. Предположим, вы наблюдаете за данными Z(s) и применяете некоторое преобразование
Более подробно о преобразованиях и трендах
Более подробно о преобразованиях по методу Box-Cox, по методу арксинуса и логарифмических преобразованиях
Преобразование по методу Box-Cox
Преобразование по методу Box-Cox:
Y(ю) = (Z(ю)λ - 1)/λ,при λ≠ 0.
Например, предположим, что ваши данные состоят из подсчетов некоторого явления. Для каждого из этих типов данных дисперсия часто связана со средним значением. Если у вас малые подсчеты в одной части изучаемой территории, дисперсия в этом регионе будет меньше, чем в другом регионе, где подсчеты выше. В этом случае преобразование по методу квадратного корня может сделать дисперсию более постоянной на изучаемой территории, а также часто приводит данные к нормальному распределению. Преобразование по методу квадратного корня ― это частный случай преобразования Box-Cox с λ = ½.
Логарифмическое преобразование
Логарифмическое преобразование ― это частный случай преобразования по методу Box-Cox с λ = 0. Оно имеет вид:
Y(ю) = ln(Z(ю)),где Z(ю) > 0, а ln – натуральный логарифм.
Логарифмическое преобразование часто используется, когда данные смещены в положительном направлении (см. ниже) и присутствует мало очень больших значений. Если эти большие значения расположены в области наблюдения, логарифмическое преобразование поможет сделать дисперсию более постоянной и привести данные к нормальному распределению. О терминологии: когда логарифмическое преобразование применяется с кригингом, метод интерполяции определяется как логарифмически нормальный кригинг, тогда как при остальных значениях λ связанный метод кригинга определяется как трансгауссов кригинг.
Преобразование по методу арксинуса
Преобразование по методу арксинуса показано ниже:
Y(ю) = sin-1(Z(ю)),для Z(s) от 0 до 1.
Преобразование по методу арксинуса может быть использовано для данных, которые представляют относительное содержание или проценты. Часто, когда данные представляют относительное содержание, дисперсия ниже в окрестности 0 и 1 и выше в окрестности 0,5. Преобразование по методу арксинуса поможет сделать дисперсию более постоянной на изучаемой территории, а также часто приводит данные к нормальному распределению.
desktop.arcgis.com
Тождественные преобразования показательных и логарифмических выражений
3.
Тождественные преобразования показательных и логарифмических выражений
Комментарий. Для выполнения заданий этой группы требуется хорошо знать свойства логарифмов и уметь их применять. Эта работа очень полезна для подготовки к решению логарифмических и показательных уравнений и неравенств. Рассмотрим далее задания, связанные с упрощением показательных и логарифмических выражений.
Формулы для справок
Вспомним основные свойства логарифмов.
-
.
Комментарий. Логарифм единицы по любому основанию равен нулю. Для того, чтобы убедиться в истинности данной формулы, достаточно вспомнить, что любое число (кроме нуля) в нулевой степени равно единице.
-
.
Комментарий. Логарифм равен единице в случае равенства чисел (выражений) — основания логарифма и выражения, стоящего под логарифмом.
-
.
Комментарий. Представленная формула является одним из вариантов записи определения логарифма.
-
.
-
.
-
.
-
.
-
.
Комментарий.
Данная формула называемая формулой перехода к новому основанию, имеет два важных следствия. Приравняем в формуле , тогда . Рассмотрим числитель полученной дроби. Поставим вопрос: в какую степень следует возвести число b, чтобы получить число b. Ответ — в первую степень, т.е. числитель рассматриваемой дроби равен единице. Таким образом, . В ряде задач полезно бывает полученную формулу записать в преобразованном виде: .
-
.
Комментарий. Предполагается, что во всех представленных формулах параметры принимают допустимые значения.
Пример 3.1
Вычислить
Решение
Представим в виде степени числа 5, тогда
Далее воспользуемся правилом умножения степеней одинаковым основанием (при умножении степеней с одинаковым основанием показатели складываются):
.
Преобразуем полученную в процессе решения разность логарифмов (по одному основанию) и применим определение логарифма (зададим вопрос: В какую степень следует возвести основание логарифма 3, чтобы получить число, стоящее под логарифмом — 9?):
Ответ: 25.
Пример 3.2.
Упростить выражение
Решение
Упростим показатель степени подкоренного выражения:
Тогда
Ответ: 27.
Пример 3.3.
Упростить выражение:
Решение
Вначале упростим логарифмируемое выражение. Если Вы уже занимались упрощением алгебраических выражений, то вид первого множителя в знаменателе вызовет предположение, что перед нами полный квадрат. Действительно, Тогда:
Следовательно,
Ответ: 1/2.
Пример 3.4.
Найти значение выражения
Решение
Разделим на знаменатель каждое слагаемое числителя по отдельности:
Переходя далее в каждом слагаемом к новому основанию 18, получаем, что:
Преобразуем далее сумму логарифмов с одинаковым основанием в логарифм произведения и используем определение логарифма:
Ответ: 1.
Пример 3.5.
Вычислить
Решение
Для преобразования данного выражения перейдем во всех логарифмах к основанию 4:
.
Тогда выражение принимает вид:
Далее разложим на множители логарифмируемые выражения, выделяя в каждом из них множитель вида 4n:
28 = 4 ∙
7, 112 = 16 ∙
7 = 4
Продолжим преобразование выражения, используя свойства логарифмов:
Ответ: 2.
Пример 3.6.
Вычислить
Решение
Представим числа 2 и 1 в виде: Тогда
Ответ: 2.
Пример 3.7.
Найти если
Решение
Обратим внимание на то, что в каждом логарифме (либо в основании, либо в аргументе) присутствует множитель 7. Поэтому перейдем к основанию 7 во всех логарифмах:
Обратим внимание, что , тогда:
Следовательно, для вычисления этого логарифма нужно знать значения и Воспользуемся формулами перехода к новому основанию:
Подставим далее найденные значения в преобразованное исходное выражение:
Ответ:
Пример 3.8.
Известно, что лежит между числами 8 и 13, а принимает целые значения. Найти количество этих значений.
Решение
Перейдем в обоих логарифмах к основанию b.
Для этого воспользуемся сначала формулой «логарифм частного»: . Обратим далее внимание, что .
Получаем, что
Решим методом интервалов неравенство: .
Для этого перейдем к систем нестрогих неравенств: .
Рассматривая каждое из записанных неравенств отдельно и впоследствии находя решение как пересечение множеств (решений первого и второго неравенств), получаем:
Выполним преобразования полученного двойного неравенства.
Прибавим 1 ко всем частям неравенства: Поскольку его значения задаются неравенством:
или
Следовательно, может принимать 6 целых значений – от 11 до 16.
Ответ: 6.
www.e-biblio.ru
Преобразование логарифмических выражений
ВИДЕОУРОКИЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
Предлагаю вам видеорешение такого задания:
Вычислить значение выражения , если
Такого рода преобразования часто встречаются при решении логарифмических уравнений, и они не должны вызывать затруднений.
Порядок действий такой:
1. Приводим логарифм к выражению, содержащему . Для этого используем формулу перехода к новому основанию, а затем «растаскиваем» выражение .
2. Делаем замену , решаем уравнение относительно и находим значение .
3. «Растаскиваем» выражение , так, чтобы оно представляло комбинацию .
4. Подставляем значение в полученное выражение и находим значение выражения.
ege-ok.ru
Задача B7 — преобразование логарифмических и показательных выражений
В задаче B7 дается некоторое выражение, которое нужно упростить. В результате должно получиться обычное число, которое можно записать в бланке ответов. Все выражения условно делятся на три типа:
- Логарифмические,
- Показательные,
- Комбинированные.
Показательные и логарифмические выражения в чистом виде практически не встречаются. Однако знать, как они вычисляются, совершенно необходимо.
В целом, задача B7 решается достаточно просто и вполне под силу среднему выпускнику. Отсутствие четких алгоритмов компенсируется в ней стандартностью и однообразностью. Научиться решать такие задачи можно просто за счет большого количества тренировок.
Логарифмические выражения
Подавляющее большинство задач B7 содержат логарифмы в том или ином виде. Эта тема традиционно считается сложной, поскольку ее изучение приходится, как правило, на 11 класс — эпоху массовой подготовки к выпускным экзаменам. В результате многие выпускники имеют весьма смутное представление о логарифмах.
Но в этой задаче никто и не требует глубоких теоретических познаний. Нам будут встречаться лишь самые простые выражения, которые требуют незамысловатых рассуждений и вполне могут быть освоены самостоятельно. Ниже приведены основные формулы, которые надо знать, чтобы справиться с логарифмами:
- logax + logay = loga (x · y)
- logax − logay = loga (x : y)
- logaxn = n · logax
Кроме того, надо уметь заменять корни и дроби на степени с рациональным показателем, иначе в некоторых выражениях выносить из под знака логарифма будет просто нечего. Формулы замены:
Задача. Найти значения выражений:
log6 270 − log6 7,5
log5 775 − log5 6,2
Первые два выражения преобразуются как разность логарифмов:
log6 270 − log6 7,5 = log6 (270 : 7,5) = log6 36 = 2;
log5 775 − log5 6,2 = log5 (775 : 6,2) = log5 125 = 3.
Для вычисления третьего выражения придется выделять степени — как в основании, так и в аргументе. Для начала найдем внутренний логарифм:
Затем — внешний:
Конструкции вида loga logbx многим кажутся сложными и непонятыми. А между тем, это всего лишь логарифм от логарифма, т.е. loga (logbx). Сначала вычисляется внутренний логарифм (положим logbx = c), а затем внешний: logac.
Показательные выражения
Будем называть показательным выражением любую конструкцию вида ak, где числа a и k — произвольные постоянные, причем a > 0. Методы работы с такими выражениями достаточно просты и рассматриваются на уроках алгебры 8-го класса.
Ниже приведены основные формулы, которые обязательно надо знать. Применение этих формул на практике, как правило, не вызывает проблем.
- an · am = an + m;
- an / am = an − m;
- (an)m = an · m;
- (a · b)n = an · bn;
- (a : b)n = an : bn.
Если встретилось сложное выражение со степенями, и не понятно, как к нему подступиться, используют универсальный прием — разложение на простые множители. В результате большие числа в основаниях степеней заменяются простыми и понятными элементами. Затем останется лишь применить указанные выше формулы — и задача будет решена.
Задача. Найти значения выражений: 79 · 311 : 218, 247 : 36 : 165, 306 : 65 : 252.
Решение. Разложим все основания степеней на простые множители:
79 · 311 : 218 = 79 · 311 : (7 · 3)8 = 79 · 311 : (78 · 38) = 79 · 311 : 78 : 38 = 7 · 33 = 189.
247 : 36 : 165 = (3 · 23)7 : 36 : (24)5 = 37 · 221 : 36 : 220 = 3 · 2 = 6.
306 : 65 : 252 = (5 · 3 · 2)6 : (3 · 2)5 : (52)2 = 56 · 36 · 26 : 35 : 25 : 54 = 52 · 3 · 2 = 150.
Комбинированные задачи
Если знать формулы, то все показательные и логарифмические выражения решаются буквально в одну строчку. Однако в задаче B7 степени и логарифмы могут объединяться, образуя довольно неслабые комбинации.
Из определения логарифма вытекают две формулы, которые постоянно встречаются в реальных задачах. Эти формулы позволяют заменить знак логарифма нормальными числами:
- logaan = n
В чистом виде они, как правило, не встречаются, поэтому общая схема решения комбинированных задач выглядит так:
- Записать там, где это возможно, числа в виде степеней. Например, 25 = 52, 16 = 24, 27 = 33… дальше сами. Корни и дроби тоже надо заменить степенями по уже известным формулам:
- Избавиться от степеней в основаниях логарифмов, если они там есть. Затем все множители, стоящие перед знаком логарифма, нужно внести в аргумент. Например, 5 · log7 2 = log7 25 = log7 32.
- Воспользоваться формулами замены логарифмов, которые приведены выше. Как правило, этого будет достаточно.
На первый взгляд эта схема кажется громоздкой и далеко не оптимальной. Но стоит немного потренироваться — и комбинированные задачи будут решаться за несколько секунд. Особо продвинутые решают их устно.
Задача. Найти значения выражений:
Будем действовать по схеме. Для первого выражения все очевидно:
Для второго выражения заметим, что
Поэтому имеем:
Аналогично поступим с третьим выражением:
В результате получим:
Смотрите также:
- Задача B3 — работа с графиками
- Системы линейных уравнений: основные понятия
- Сравнение дробей
- Пробный ЕГЭ 2012 от 7 декабря. Вариант 2 (без логарифмов)
- Как быстро извлекать квадратные корни
www.berdov.com
Материалы к уроку «Тождественные преобразования логарифмических выражений» (10-11 класс)
ЕГОРОВА ВИКТОРИЯ ВАЛЕРЬЕВНА
Учитель математики
высшей квалификационной категории
ТЕМА: «ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ
ЛОГАРИФМИЧЕСКИХ ВЫРАЖЕНИЙ»
Знания и навыки, которыми должны овладеть учащиеся после изучения данного урока:
знать определение логарифма числа, основное логарифмическое тождество, свойства логарифмов;
уметь выполнять преобразования выражений, содержащих логарифмы, вычислять логарифмы.
Литература:
1. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. и др. Алгебра и начала анализа: учебник для 10-11 классов общеобразовательных учреждений. – М.: Просвещение, 2001.
2. Кочагин В.В., Кочагина М.В., Интенсивный курс подготовки к ЕГЭ. – М.:Эксмо, 2009.
3. Мерзляк А.Г., Полонский В.Б., Якир М.С., Алгебраический тренажер: Пособие для школьников и абитуриентов. – М.:Илекса, 2005.
4. Гусев В.А., Мордкович А.Г. Математика: Справочные материалы: Книга для учащихся. – М.: Просвещение, 2001.
План урока:
Немного истории.
Определение логарифма и основное логарифмическое тождество. Решение примеров.
Натуральный и десятичный логарифмы. Решение примеров.
Формула логарифма произведения двух положительных чисел. Решение примеров.
Формула логарифма частного двух положительных чисел. Решение примеров.
Формула логарифма степени. Решение примеров.
Формула перехода к новому основанию. Решение примеров.
Формула
 . Решение примеров.
. Решение примеров.Решение более сложных примеров.
Подведение итогов.
Контрольное тестирование.
Ход урока:
1) Логарифм – это греческое слово, которое состоит из 2-х слов: “логос”- отношение, “аритмос”- число. Значит, логарифм есть число, измеряющее отношение. В публикации тысяча шестьсот четырнадцатого года сообщалось, что Непер изобрёл логарифмы. Позже им были составлены логарифмические таблицы, которые теперь известны нам как таблицы Брадиса. Менее чем за одно столетие таблицы распространились по всему миру и сделались незаменимым вычислительным средством. В дальнейшем они были, как бы встроены в удобное устройство, чрезвычайно ускоряющее процесс вычисления – логарифмическую линейку, которой пользовались до семидесятых годов двадцатого века.
Приложение 1.
2) Логарифмом положительного числа b по основанию a, причём а больше нуля и не равно единицы, называется показатель степени, в которую нужно возвести число a, чтобы получить число b.
Это равенство, выражающее определение логарифма, называется основным логарифмическим тождеством.
Ц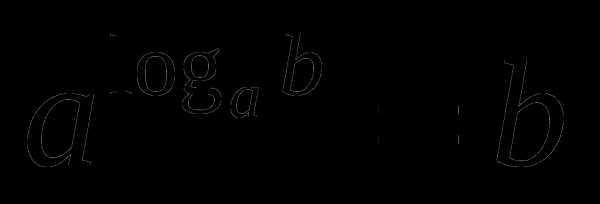
Обратите внимание на основание степени и основание логарифма – они одинаковы.
ОР 1П
Основание степени и основание логарифма семнадцать, значит по основному логарифмическому тождеству значение выражения равно трём.
оработаем устно:ЩЕЛЧОК
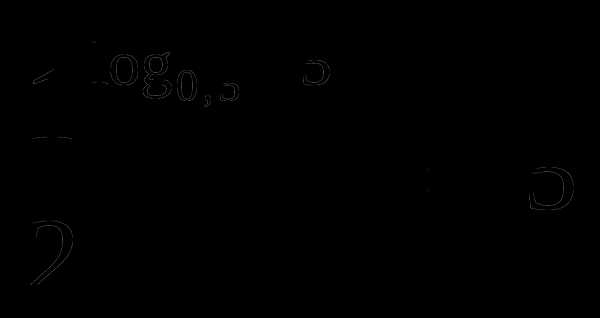
Одна вторая равна нуль целых пяти десятым, значит выражение равно арифметическому квадратному корню из пяти.
П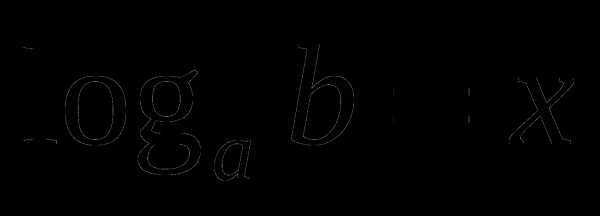
 риложение 2.
риложение 2.
Равенство означает, что
Из определения логарифма получаются следующие важные равенства:
Например:
Приложение 3.
Перейдем к заданиям ЕГЭ:
Приложение 4.
3) Для логарифма по основанию десять существует специальное обозначение и название десятичный логарифм.
Логарифм по основанию е называется натуральным логарифмом.
Например,
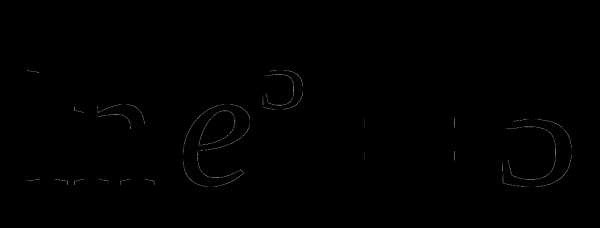

4) Из определения логарифма вытекают следующие его свойства. Все свойства формулируются и доказываются только для положительных значений переменных, содержащихся под знаками логарифмов.
Логарифм произведения двух положительных чисел по основанию а равен сумме логарифмов этих чисел с тем же основанием.
ЦОР 2
Например,
Задание 1.
Задание 2. Упростите выражение
Воспользуемся решением предыдущего примера. Заменим
Обратите внимание на то, что логарифм в квадрате, поэтому и сумму необходимо возвести в квадрат. Применяя формулу квадрата суммы, раскроем скобки. Приведём подобные слагаемые.
5) Логарифм частного равен разности логарифмов делимого и делителя.
Ц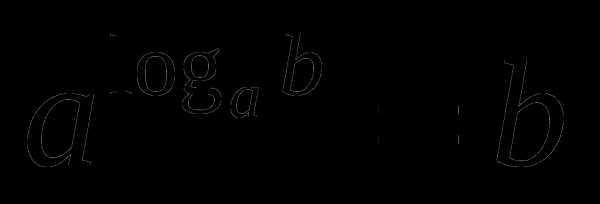
Обратите внимание на основание степени и основание логарифма – они одинаковы.
ОР 3 Р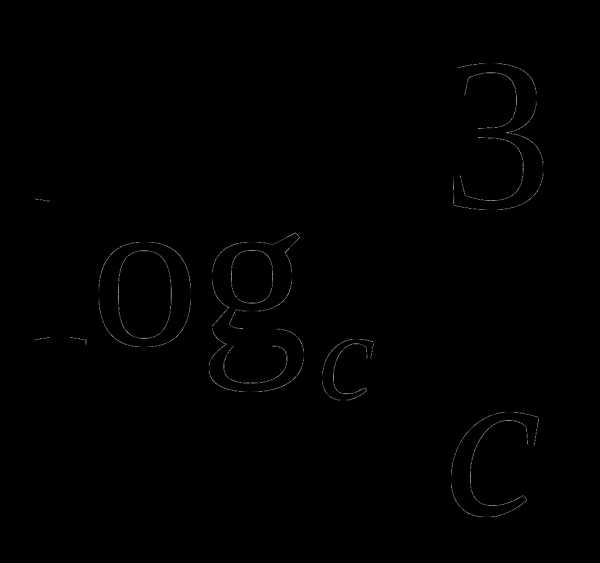
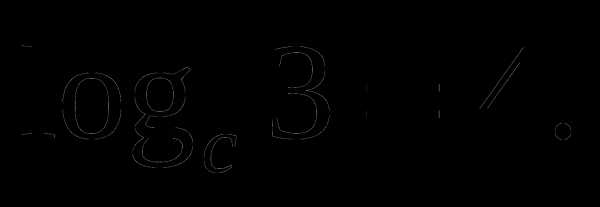 ассмотрим применение этой формулы на примере:
ассмотрим применение этой формулы на примере:
Задание 1. Найдите значение выражения , если
Задание 2. Найдите значение b по его логарифму
6) Логарифм степени по основанию а, равен произведению показателя степени на логарифм по тому же основанию.
ЦОР 4
Например,
З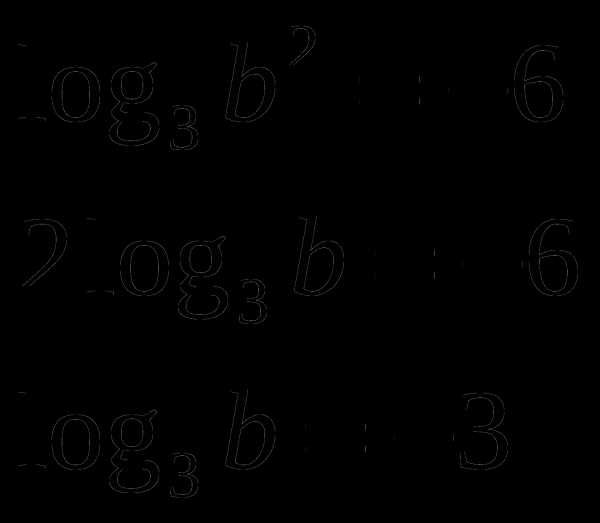 адание 1. Вычислите , если
адание 1. Вычислите , если
Упростим выражение
Формула
называется формулой перехода к новому основанию.
З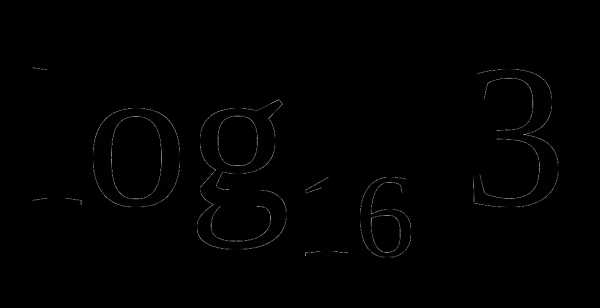 адание 1. Выразить через логарифм с основанием 2.
адание 1. Выразить через логарифм с основанием 2.
Задание 2. Вычислите
ЦОР 5
8)
ЦОР 6
Например,
Задание 1. Вычислите
Задание 2. Вычислите
9) К логарифмическим преобразованиям можно приступать, только в том случаи, если вы запомнили все свойства логарифмов. Повторив их, рассмотрим задания на преобразования логарифмических выражений с другой стороны.
Для преобразования суммы или разности логарифмических выражений иногда достаточно использовать определение логарифма, а чаще всего свойства логарифма произведения или частного.
Задание 1. Вычислите
Решим двумя способами.
1 способ, используя определение логарифма:
2 способ, опираясь на свойство логарифма частного:
Задание 2. Найдите значение выражения
Применим сначала формулу логарифма произведения, затем определение логарифма.
Основное логарифмическое тождество используется при преобразовании выражений, содержащих логарифм в показателе степени. Идея таких операций заключается в получении равных основания степени и основания логарифма.
Иногда необходимо преобразовывать выражение по свойствам логарифма и по свойствам степени, так же можно легко перейти от одного основания к другому, используя формулу перехода. В других случаях следует применять несколько свойств.
З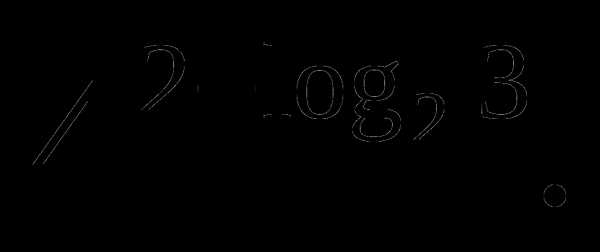 адание 3. Вычислите
адание 3. Вычислите
З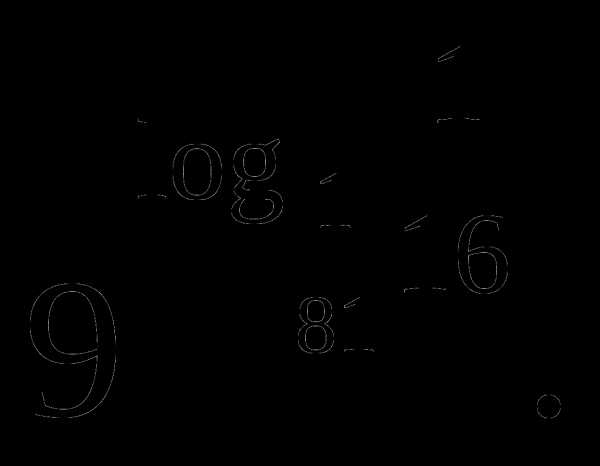 адание 4. Найдите значение выражения
адание 4. Найдите значение выражения
Задание 5. Найдите значение выражения
Задание 6. Представьте в виде разности логарифмов
Наибольшую трудность представляют преобразования логарифмических выражений, находящихся под радикалом. В процессе преобразований приходится рассматривать модули логарифмических выражений, для раскрытия которых требуется сравнить иррациональные числа или рациональное и иррациональное число. Будем действовать последовательно. Рассмотрим выражение, стоящее под внутренним радикалом.
Подставим в исходное выражение.
Раскроем модуль, учитывая, что знаменатель положителен, а числитель отрицателен.
Меняем знаки в числителе и упрощаем.
Получим исходное выражение, равное разности логарифмов.
Такие и подобные примеры вам могут встретиться при решении заданий Единого Государственного экзамена.. Следует отметить, что с преобразованием логарифмических выражений можно встретиться и при решении уравнений и неравенств или исследовании функций, поэтому в неявном виде они могут присутствовать и в заданиях групп В и С.
10) Подведение итогов. Вопросы:
Логарифм по основанию 10 называется
2) Какие значения может принимать x в выражении
3) Чему равен
4) Чему равен
5) Укажите соотношение, которое верно для всех x ≠ 0.
6) Укажите верное соотношение для формулы перехода к новому основанию.
7) Укажите верное равенство при
11) Контрольное тестирование.
infourok.ru
Логарифмические выражения
Логарифмические выражения, решение примеров. В этой статье мы рассмотрим задачи связанные с решением логарифмов. В заданиях ставится вопрос о нахождении значения выражения. Нужно отметить, что понятие логарифма используется во многих заданиях и понимать его смысл крайне важно. Что касается ЕГЭ, то логарифм используется при решении уравнений, в прикладных задачах, также в заданиях связанных с исследованием функций.
Приведём примеры для понимания самого смысла логарифма:
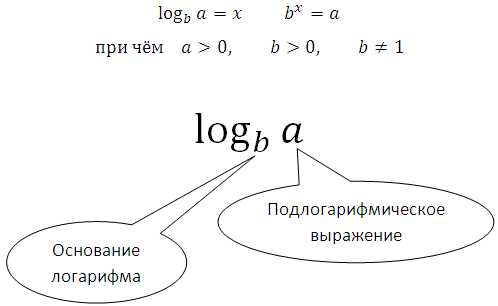
Основное логарифмическое тождество:
Свойства логарифмов, которые необходимо всегда помнить:
*Логарифм произведения равен сумме логарифмов сомножителей.
* * *
*Логарифм частного (дроби) равен разности логарифмов сомножителей.
* * *
*Логарифм степени равен произведению показателя степени на логарифм ее основания.
* * *
*Переход к новому основанию
* * *
Ещё свойства:
* * *
Вычисление логарифмов тесно связано с использованием свойств показателей степени.
Перечислим некоторые из них:
Суть данного свойства заключается в том, что при переносе числителя в знаменатель и наоборот, знак показателя степени меняется на противоположный. Например:
Следствие из данного свойства:
* * *
При возведении степени в степень основание остаётся прежним, а показатели перемножаются.
* * *
При возведении в степень произведения в эту же степень возводится каждый множитель.
Так же необходимо знать следующее свойство:
Рассмотрим примеры:
*Данный контент (более 20 подробно решённых примеров) доступен только для зарегистрированных пользователей! Вкладка регистрации (входа) находится в ГЛАВНОМ МЕНЮ сайта. После прохождения регистрации войдите на сайт и обновите данную страницу.
Как вы убедились само понятие логарифма несложное. Главное то, что необходима хорошая практика, которая даёт определённый навык. Разумеется знание формул обязательно. Если навык в преобразовании элементарных логарифмов не сформирован, то при решении простых заданий можно легко допустить ошибку.
Практикуйтесь, решайте сначала простейшие примеры из курса математики, затем переходите к более сложным. В будущем обязательно покажу, как решаются «страшненькие» логарифмы, таких на ЕГЭ не будет, но они представляют интерес, не пропустите!
На этом всё! Успеха Вам!
С уважением, Александр Крутицких
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
matematikalegko.ru
Логарифмическое преобразование — Большая Энциклопедия Нефти и Газа, статья, страница 4
Логарифмическое преобразование
Cтраница 4
В табл. 7.22 приведены результаты определения ванадия в четырех пробах золы, выполненные спектрографическим и спектрофотометрическим методами. Применение / — критерия здесь также указывает на неоднородность дисперсий, поэтому было применено логарифмическое преобразование. Результаты дисперсионного анализа представлены в табл. 7.23. Здесь также значимой оказалась дисперсия, обусловленная эффектом взаимодействия. [46]
Однако требуется показать другой процесс, поэтому мы пойде-м иным путем и к указанным выше ограничениям применим логарифмические преобразования. [47]
Зависимость квадратичной ошибки от концентрации определяемого компонента становится доминирующим фактором. С подобной ситуацией часто приходится встречаться в различных областях техники и обычно в этом случае от асимметричных распределений удается перейти к нормальному распределению путем логарифмического преобразования) случайной переменной. [48]
Нормальное распределение хорошо изучено, для него составлены многочисленные таблицы. Например, логарифмическое преобразование заменяет резко асимметричное распределение распределением, близким к нормальному. [49]
Требование простой интерпретации свертки является обязательным для любого преобразования, предназначенного для исследования динамических систем. Естественно поэтому искать преобразование, лишенное упомянутых недостатков, в классе преобразований, переводящих свертку оригиналов в сумму изображений. К этому классу относится, например, логарифмическое преобразование Лапласа. Благодаря тому что оно лишено третьего недостатка преобразования Лапласа, оно нашло сравнительно широкое распространение, особенно при приближенных расчетах. Однако это преобразование ни в коей мере не лишено двух других недостатков, что затрудняет его использование для неминимально-фазовых систем. Ниже сделана попытка получить преобразование, лишенное всех трех перечисленных недостатков. В дискретной форме это преобразование совпадает с формулами Ньютона [1] и модификацией приближенного метода Бернулли решения алгебраических уравнений Хильдебрандом. [50]
Во второй колонке приведены данные о динамическом диапазоне после соответствующего преобразования. В четвертой колонке приведены данные о прогнозирующей способности двух классификаторов образов, а в пятой — средние значения этой способности на рассматриваемом первом этапе. Наилучшие результаты по прогнозирующей способности на первом этапе обеспечивает логарифмическое преобразование. В шестой колонке представлены данные о наличии неясных положений пг / е, обнаруженных на этом первом этапе. Чем меньше ширина динамического диапазона, тем меньше неясных положений гп / е выявляет классификатор. [51]
Пусть даны среднее значение и среднее квадратичное отклонение логарифма. Алгоритм позволяет получить случайное число, распределенное по нормальному закону, и вычислить длительность интервала времени. Этот алгоритм отличается от датчика измерений, распределенных по нормальному закону, лишь наличием логарифмического преобразования. [53]
В соответствии со стадиями обработки информации алгоритм функционирования нечеткого контроллера по аналогии с классической теорией автоматического регулирования можно интерпретировать как модель регулятора в терминах вход — выход в некотором новом пространстве, переход в которое из пространства оригиналов ( физические переменные) осуществляется с помощью оператора fuzz. После проведения в новом пространстве ( аналог пространства изображений в преобразовании Лапласа) некоторых операций, осуществляется обратное преобразование с помощью оператора dfz в исходное пространство. Сопоставление преобразований Фурье и Лапласа, принятых в классической теории автоматического регулирования, с преобразованием переменных типа fuzz и dfz, используемых в теории нечеткого управления, показано на рис. 3.16. Подобная ситуация имеет место также в элементарной математике, когда такие относительно сложные операции, как умножение и деление, путем логарифмического преобразования могут быть заменены более простыми арифметическими операциями сложения и вычитания, и затем полученный результат с помощью обратного преобразования ( антилогарифмирование) преобразуется в искомый результат. [54]
Нормальное распределение хорошо изучено, для него составлены многочисленные таблицы. Поэтому, если выборочное распределение не согласуется с законом нормального распределения, пытаются подобрать какое-нибудь преобразование результатов измерения Хг, чтобы преобразованные величины Уг 1 ( Хг) подчинялись нормальному закону. Например, логарифмическое преобразование заменяет резко асимметричное распределение распределением, близким к нормальному. [55]
Выполнимость этого постулата проверяется с помощью критериев однородности дисперсий в разных точках факторного пространства. Нарушение этого постулата недопустимо. Если однородность дисперсий все же отсутствует, то необходимо такое преобразование у, которое делает дисперсии однородными. Довольно часто помогает логарифмическое преобразование, с которого обычно начинают поиски. [56]
В обучающую выборку включили 250 случайно выбранных спектров, а оставшиеся 200 спектров — в контрольную выборку. Затем отобранные в соответствии с изложенной выше процедурой перекрестные члены размещали по вакантным положениям и снова обучали классификатор, периодически проверяя прогнозирующую способность. Результаты данного исследования представлены в табл. 6.2. Испытания проводили в три цикла на разных обучающих выборках А, Б, В. Интенсивности всех пиков подвергали логарифмическому преобразованию. [57]
Он доказал, что при разумном агрегировании производственная функция должна быть сепарабельной. При этом объем продукции равен сумме двух составляющих, одна из которых связана с трудом, а другая с капиталом. Это условие накладывает сильные ограничения. Из трех уже рассмотренных производственных функций модель затраты-выпуск, очевидно, сепа-рабельна. Функция Кобба-Дугласа не отвечает этому условию, но после логарифмического преобразования становится сепарабельной; это объяснение клейновского использования средних геометрических. [58]
Страницы: 1 2 3 4
www.ngpedia.ru

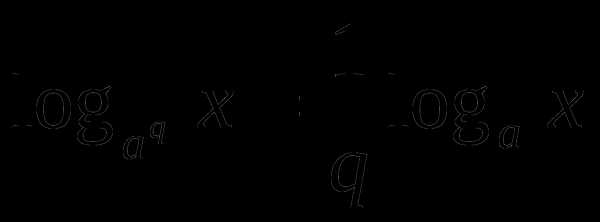 . Решение примеров.
. Решение примеров.
Leave A Comment