/ 2 \ /29 \ |/29\ 14*29 | log|-- - 2|*||--| - ----- + 49|1681*log(10) 1681*log(9) - ------------ + -----------
значит одно из решений нашего неравенства будет при:
$$x \leq 3$$_____ _____ \ / -------•-------•------- x1 x2
Другие решения неравенства будем получать переходом на следующий полюс
и т.д.
Ответ:
$$x \leq 3$$
$$x \geq 7$$
Логарифмические уравнения
Логарифмические уравнения. Продолжаем рассматривать задачи из части В ЕГЭ по математике. Мы с вами уже рассмотрели решения некоторых уравнений в статьях «Тригонометрические уравнения», «Решение рациональных уравнений». В этой статье рассмотрим логарифмические уравнения. Сразу скажу, что никаких сложных преобразований при решении таких уравнений на ЕГЭ не будет. Они просты.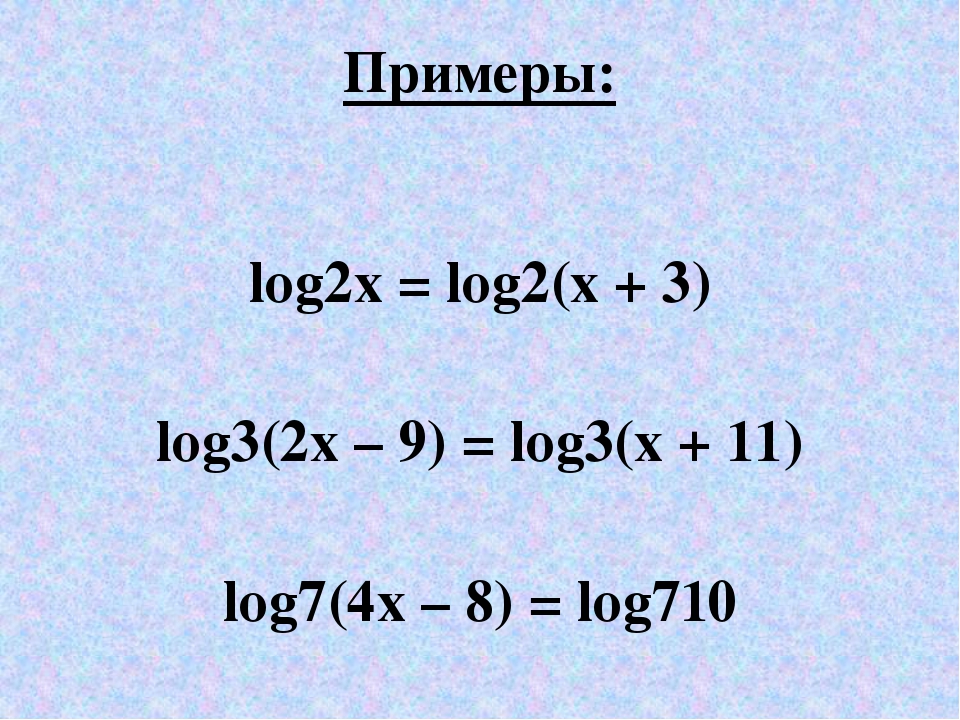
Достаточно знать и понимать основное логарифмическое тождество, знать свойства логарифма. Обратите внимание на то, то после решения ОБЯЗАТЕЛЬНО нужно сделать проверку — подставить полученное значение в исходное уравнение и вычислить, в итоге должно получиться верное равенство.
Определение:
Логарифмом числа a по основанию b называется показатель степени, в который нужно возвести b, чтобы получить a.
Основное логарифмическое тождество:
Например:
log39 = 2, так как 32 = 9
Свойства логарифмов:
Частные случаи логарифмов:
Решим задачи. В первом примере мы сделаем проверку. В последующих проверку сделайте самостоятельно.
Найдите корень уравнения: log3(4–x) = 4
Используем основное логарифмическое тождество.
Так как logba = x bx = a, то
34 = 4 – x
x = 4 – 81
x = – 77
Проверка:
log3(4–(–77)) = 4
log381 = 4
34 = 81 Верно.
Ответ: – 77
Решите самостоятельно:
Найдите корень уравнения: log2 (4 – x) = 7
Посмотреть решение
Найдите корень уравнения log5 (4 + x) = 2
Используем основное логарифмическое тождество.
Так как logab = x bx = a, то
52 = 4 + x
x =52 – 4
x = 21
Проверка:
log5(4 + 21) = 2
log525 = 2
52 = 25 Верно.
Ответ: 21
Найдите корень уравнения log3(14 – x) = log35.
Имеет место следующее свойство, смысл его таков: если в левой и правой частях уравнения имеем логарифмы с одинаковым основанием, то можем приравнять выражения, стоящие под знаками логарифмов.
Если logca = logcb, то a = b
14 – x = 5
x = 9
Сделайте проверку.
Ответ: 9
Решите самостоятельно:
Найдите корень уравнения log5(5 – x) = log53.
Посмотреть решение
Найдите корень уравнения: log4(x + 3) = log4(4x – 15).
Если logca = logcb, то a = b
x + 3 = 4x – 15
3x = 18
x = 6
Сделайте проверку.
Ответ: 6
Найдите корень уравнения log1/8(13 – x) = – 2.
(1/8)–2 = 13 – x
82 = 13 – x
x = 13 – 64
x = – 51
Сделайте проверку.
Небольшое дополнение – здесь используется свойство
степени (отрицательная степень дроби).
Ответ: – 51
Решите самостоятельно:
Найдите корень уравнения: log1/7(7 – x) = – 2
Посмотреть решение
Найдите корень уравнения log2 (4 – x) = 2 log2 5.
Преобразуем правую часть. воспользуемся свойством:
logabm = m∙logab
log2(4 – x) = log252
Если logca = logcb, то a = b
4 – x = 52
4 – x = 25
x = – 21
Сделайте проверку.
Ответ: – 21
Решите самостоятельно:
Найдите корень уравнения: log5(5 – x) = 2 log5 3
Посмотреть решение
Решите уравнение log5(x2 + 4x) = log5(x2 + 11)
Если logca = logcb, то a = b
x2 + 4x = x2 + 11
4x = 11
x = 2,75
Сделайте проверку.
Ответ: 2,75
Решите самостоятельно:
Найдите корень уравнения log5(x2 + x) = log5(x2 + 10).
Посмотреть решение
Решите уравнение log2(2 – x) = log2(2 – 3x) +1.
Необходимо с правой стороны уравнения получить выражение вида:
log2 (……)
Представляем 1 как логарифм с основанием 2:
1 = log2 2
Далее применяем свойство:
logс(ab) = logсa + logсb
log2(2 – x) = log2(2 – 3x) + log22
Получаем:
log2(2 – x) = log2 2 (2 – 3x)
Если logca = logcb, то a = b, значит
2 – x = 4 – 6x
5x = 2
x = 0,4
Сделайте проверку.
Ответ: 0,4
Решите самостоятельно:
Найдите корень уравнения log5(7 – x) = log5(3 – x) +1
Посмотреть решение
Решите уравнение logх–125 = 2. Если уравнение имеет более одного корня, в ответе укажите меньший из них.
Воспользуемся основным логарифмическим тождеством:
(x – 1)2= 25
Далее необходимо решить квадратное уравнение. Кстати, квадратное уравнение, как вы поняли, это очень важная «буковка» в математической азбуке. К нему сводятся очень многие решения совершенно различных задач. Помнить формулы дискриминанта и корней нужно обязательно, и уметь решать такое уравнение вы должны очень быстро, периодически практикуйтесь.
Конечно же, опытный глаз сразу увидит, что в нашем примере выражение, стоящее под знаком квадрата равно 5 или – 5, так как только эти два числа при возведении в квадрат дают 25, устно можно посчитать:
корни равны 6 и – 4.
Корень «–4» не является решением, так как основание логарифма должно быть больше нуля, а при «– 4» оно равно «–5». Решением является корень 6. Сделайте проверку.
Ответ: 6.
Решите самостоятельно:
Решите уравнение logx–5 49 = 2. Если уравнение имеет более одного корня, в ответе укажите меньший из них.
Посмотреть решение
Как вы убедились, никаких сложных преобразований с логарифмическими уравнениями нет. Достаточно знать свойства логарифма и уметь применять их. В задачах ЕГЭ, связанных с преобразованием логарифмических выражений, выполняются более серьёзные преобразования и требуются более глубокие навыки в решении. Такие примеры мы рассмотрим, не пропустите! Успехов вам!!!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Как найти область определения функции?
Для того, чтобы понять, что такое область определения функции, необходимо знать области определения основных элементарных функций. Для этого нужно углубить знания данной статьей. Будут рассмотрены различные сложнейшие комбинации функций вида y=x+x-2 или y=5·x2+1·x3, y=xx-5 или y=x-15-3. Рассмотрим теорию и решим несколько примеров с подобными заданиями.
Для этого нужно углубить знания данной статьей. Будут рассмотрены различные сложнейшие комбинации функций вида y=x+x-2 или y=5·x2+1·x3, y=xx-5 или y=x-15-3. Рассмотрим теорию и решим несколько примеров с подобными заданиями.
Что значит найти область определения
После того, как функция задается, указывается ее область определения. Иначе говоря, без области определения функция не рассматривается. При задании функции вида y=f(x) область определения не указывается, так как ее ОДЗ для переменной x будет любым. Таким образом, функция определена на всей области определения.
Ограничение области определения
Область определения рассматривается еще в школьной курсе. у действительных чисел она может быть (0, +∞) или такой [−3, 1)∪[5, 7). Еще по виду функции можно визуально определить ее ОДЗ. Рассмотрим, на что может указывать наличие области определения:
- при имеющемся знаменателе необходимо производить деление такого типа функции как y=x+2·xx4-1;
- при наличии переменной под знаком корня необходимо обращать внимание на корень четной степени типа y=x+1 или y=23·x+3x;
- при наличии переменной в основании степени с отрицательным или нецелым показателем такого типа, как y=5·(x+1)-3, y=-1+x113, y=(x3-x+1)2, которые определены не для всех чисел;
- при наличии переменной под знаком логарифма или в основании вида y=lnx2+x4 или y=1+logx-1(x+1) причем основание является числом положительным, как и число под знаком логарифма;
- при наличии переменной, находящейся под знаком тангенса и котангенса вида y=x3+tg2·x+5 или y=ctg(3·x3-1), так как они существуют не для любого числа;
- при наличии переменной, расположенной под знаком арксинуса или арккосинуса вида y=arcsin(x+2)+2·x2, y=arccosx-1+x, область определения которых определяется ни интервале от -1 до 1.

При отсутствии хотя бы одного признака, область определения приходится искать другим образом. Рассмотрим пример функции вида y=x4+2·x2-x+12+223·x. Видно, что никаких ограничений она не имеет, так как в знаменателе нет переменной.
Правила нахождения области определения
Для примера рассмотрим функцию типа y=2·x+1. Для вычисления ее значения можем определить x. Из выражения 2·x+1 видно, что функция определена на множестве всех действительных чисел. Рассмотрим еще один пример для подробного определения.
Если задана функция типа y=3x-1, а необходимо найти область определения, тогда понятно, что следует обратить внимание на знаменатель. Известно, что на ноль делить нельзя. Отсюда получаем, что 3x-1знаменатель равняется нулю при х=1, поэтому искомая область определения данной функции примет вид (−∞, 1)∪(1, +∞) и считается числовым множеством.
На рассмотрении примера y=x2-5·x+6 видно, что имеется подкоренное выражение, которое всегда больше или равно нулю.
При подготовке ЕГЭ и ОГЭ можно встретить множество комбинированных заданий для функций, где необходимо в первую очередь обращать внимание на ОДЗ. Только после его определения можно приступать к дальнейшему решению.
Область определения суммы, разности и произведения функций
Перед началом решения необходимо научиться правильно определять область определения суммы функций. Для этого нужно, чтобы имело место следующее утверждение:
Когда функция ff считается суммой n функций f1, f2, …, fn, иначе говоря, эта функция задается при помощи формулы y=f1(x)+f2(x)+…+fn(x)
D(f)=D(f1)D(f2)…D(fn)
Поэтому при решении рекомендуется использование фигурной скобки при записи условий, так как это является удобным способом для понимания перечисления числовых множеств.
Найти область определения функции вида y=x7+x+5+tgx.
Решение
Заданная функция представляется как сумма четырех: степенной с показателем 7,степенной с показателем 1, постоянной, функции тангенса.
По таблице определения видим, что D(f1)=(−∞, +∞), D(f2)=(−∞, +∞), D(f3)=(−∞, +∞), причем область определения тангенса включает в себя все действительные числа, кроме π2+π·k, k∈Z.
Областью определения заданной функции f является пересечение областей определения f1, f2, f3 и f4. То есть для функции существует такое количество действительных чисел, куда не входит π2+π·k, k∈Z.
Ответ: все действительные числа кроме π2+π·k, k∈Z.
Для нахождения области определения произведения функций необходимо применять правило:
Определение 2Когда функция f считается произведением n функций f1, f2, f3 и fn, тогда существует такая функция f, которую можно задать при помощи формулы y=f1(x)·f2(x)·…·fn(x)
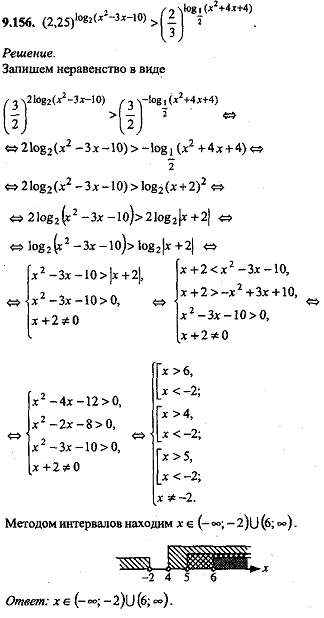
Запишется D(f)=D(f1)D(f2)…D(fn)
Пример 2Найти область определения функции y=3·arctg x·ln x.
Решение
Правая часть формулы рассматривается как f1(x)·f2(x)·f3(x), где за f1является постоянной функцией, f2является арктангенсом, f3– логарифмической функцией с основанием e. По условию имеем, что D(f1)=(−∞, +∞), D(f2)=(−∞, +∞) и D(f3)=(0, +∞). Мы получаем, что
D(f)=D(f1)D(f2)D(fn)=(-∞, +∞)(-∞, +∞)D(0, +∞)=(0, +∞)
Ответ: область определения y=3·arctg x·ln x – множество всех действительных чисел.
Необходимо остановиться на нахождении области определения y=C·f(x), где С является действительным числом. Отсюда видно, что ее областью определения и областью определения f совпадающими.
Функция y=C·f(x)– произведение постоянной функции и f. Область определения – это все действительные числа области определения D(f). Отсюда видим, что область определения функции y=C·f(x)является -∞, +∞D(f)=D(f).
Получили, что область определения y=f(x) и y=C·f(x), где C является некоторое действительное число, совпадают. Это видно на примере определения корня y=x считается [0, +∞), потому как область определения функции y=-5·x — [0, +∞).
Области определения y=f(x) и y=−f(x)совпадают , что говорит о том, что его область определения разности функции такая же, как и область определения их суммы.
Пример 3Найти область определения функции y=log3x−3·2x.
Решение
Необходимо рассмотреть как разность двух функций f1 и f2.
f1(x)=log3x и f2(x)=3·2x. Тогда получим, что D(f)=D(f1)D(f2).
Область определения записывается как D(f1)=(0, +∞)
Для нахождения области определения функции y=log3x−3·2x получим, что
D(f)=D(f1)D(f2)=(0, +∞)-∞, +∞
Ответ: (0, +∞).
Необходимо озвучить утверждение о том, что областью определения y=anxn+an-1xn-1+…+a1x+a0 является множество действительных чисел.
Рассмотрим y=anxn+an-1xn-1+…+a1x+a0, где в правой части имеется многочлен с одной переменной стандартного вида в виде степени n с действительными коэффициентами. Допускается рассматривать ее в качестве суммы (n+1)-ой функции. Область определения для каждой из таких функций включается множество действительных чисел, которое называется R.
Найти область определения f1(x)=x5+7×3-2×2+12.
Решение
Примем обозначение f за разность двух функций, тогда получим, что f1(x)=x5+7×3-2×2+12 и f2(x)=3·x-ln 5. Выше было показано, что D(f1)=R. Область определения для f2 является совпадающей со степенной при показателе –ln5, иначе говоря, что D(f2)=(0, +∞).
Получаем, что D(f)=D(f1)D(f2)=-∞, +∞(0, +∞)=(0, +∞).
Ответ: (0, +∞).
Область определения сложной функции
Для решения данного вопроса необходимо рассмотреть сложную функцию вида y=f1(f2(x))
 Известно, что D(f)является множеством всех x из определения функции f2, где область определения f2(x) принадлежит области определения f1.
Известно, что D(f)является множеством всех x из определения функции f2, где область определения f2(x) принадлежит области определения f1.Видно, что область определения сложной функции вида y=f1(f2(x)) находится на пересечении двух множеств таких, где x∈D(f2) и f2(x)∈D(f1). В стандартном обозначении это примет вид
x∈D(f2)f2(x)∈D(f1)
Рассмотрим решение нескольких примеров.
Пример 5Найти область определения y=ln x2.
Решение
Данную функцию представляем в виде y=f1(f2(x)), где имеем, что f1 является логарифмом с основанием e, а f2 – степенная функция с показателем 2.
Для решения необходимо использовать известные области определения D(f1)=(0, +∞) и D(f2)=(−∞, +∞).
Тогда получим систему неравенств вида
x∈D(f2)f2(x)∈D(f1)⇔x∈-∞, +∞x2∈(0, +∞)⇔⇔x∈(-∞, +∞)x2>0⇔x∈(-∞, +∞)x∈(-∞, 0)∪(0, +∞)⇔⇔x∈(-∞, 0)∪(0, +∞)
Искомая область определения найдена. Вся ось действительных чисел кроме нуля является областью определения.
Ответ: (−∞, 0)∪(0, +∞).
Пример 6Найти область определения функции y=(arcsin x)-12.
Решение
Так как дана сложная функция, необходимо рассматривать ее как y=f1(f2(x)), где f1 является степенной функцией с показателем -12, а f2 функция арксинуса, теперь необходимо искать ее область определения. Необходимо рассмотреть D(f1)=(0, +∞) и D(f2)=[−1, 1]. Теперь найдем все множества значений x, где x∈D(f2) и f2(x)∈D(f1). Получаем систему неравенств вида
x∈D(f2)f2(x)∈D(f1)⇔x∈-1, 1arcsin x∈(0, +∞)⇔⇔x∈-1, 1arcsin x>0
Для решения arcsin x>0 необходимо прибегнуть к свойствам функции арксинуса. Его возрастание происходит на области определения [−1, 1], причем обращается в ноль при х=0, значит, что arcsin x>0 из определения x принадлежит промежутку (0, 1].
Преобразуем систему вида
x∈-1, 1arcsin x>0⇔x∈-1, 1x∈(0, 1]⇔x∈(0, 1]
Область определения искомой функции имеет интервал равный (0, 1].
Ответ: (0, 1].
Постепенно подошли к тому, что будем работать со сложными функциями общего вида y=f1(f2(…fn(x)))). Область определения такой функции ищется из x∈D(fn)fn(x)∈D(fn-1)fn-1(fn(x))∈D(fn-2)…f2(f3(…(fn(x)))∈D(f1).
Пример 7Найти область определения y=sin(lg x4).
Решение
Заданная функция может быть расписана, как y=f1(f2(f3(x))), где имеем f1 – функция синуса, f2 – функция с корнем 4 степени, f3– логарифмическая функция.
Имеем, что по условию D(f1)=(−∞, +∞), D(f2)=[0, +∞), D(f3)=(0, +∞). Тогда областью определения функции – это пересечение множеств таких значений, где x∈D(f3), f3(x)∈D(f2), f2(f3(x))∈D(f1). Получаем, что
x∈D(f3)f3(x)∈D(f2)f2(f3(x))∈D(f1)⇔x∈(0, +∞)lg x∈[0, +∞)lg x4∈-∞, +∞
Условие lg x4∈-∞, +∞ аналогично условию lg x∈[0, +∞), значит
x∈(0, +∞)lg x∈[0, +∞)lg x4∈-∞, +∞⇔x∈(0, +∞)lg x∈[0, +∞)lg x∈[0, +∞)⇔⇔x∈(0, +∞)lg x∈[0, +∞)⇔x∈(0, +∞)lg x≥0⇔⇔x∈(0, +∞)lg x≥lg 1⇔x∈(0, +∞)x≥1⇔⇔x∈[1, +∞)
Ответ: [1, +∞).
При решении примеров были взяты функции, которые были составлены при помощи элементарных функций, чтобы детально рассмотреть область определения.
Область определения дроби
Рассмотрим функцию вида f1(x)f2(x). Стоит обратить внимание на то, что данная дробь определяется из множества обеих функций, причем f2(х) не должна обращаться в ноль. Тогда получаем, что область определения f для всех x записывается в виде x∈D(f1)x∈D(f2)f2(x)≠0.
Запишем функцию y=f1(x)f2(x) в виде y=f1(x)·(f2(x))-1. Тогда получим произведение функций вида y=f1(x) с y=(f2(x))-1. Областью определения функции y=f1(x) является множество D(f1), а для сложной y=(f2(x))-1 определим из системы вида x∈D(f2)f2(x)∈(-∞, 0)∪(0, +∞)⇔x∈D(f2)f2(x)≠0.
Значит, x∈D(f1)x∈D(f2)f2(x)∈(-∞, 0)∪(0, +∞)⇔x∈D(f1)x∈D(f2)f2(x)≠0.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание Пример 8Найти область определения y=tg(2·x+1)x2-x-6.
Решение
Заданная функция дробная, поэтому f1 – сложная функция, где y=tg(2·x+1) и f2 – целая рациональная функция, где y=x2−x−6, а область определения считается множеством всех чисел. Можно записать это в виде
x∈D(f1)x∈D(f2)f2(x)≠0
Представление сложной функции y=f3(f4(x)), где f3–это функция тангенс, где в область определения включены все числа, кроме π2+π·k, k∈Z, а f4– это целая рациональная функция y=2·x+1 с областью определения D(f4)=(−∞, +∞). После чего приступаем к нахождению области определения f1:
x∈D(f4)2·x+1∈D(f3)⇔x∈(-∞, +∞)2x+1≠π2+π·k, k∈Z⇔x≠π4-12+π2·k, k∈Z
Еще необходимо рассмотреть нижнюю область определения y=tg(2·x+1)x2-x-6. Тогда получаем, что
x∈D(f1)x∈D(f2)f2(x)≠0⇔x≠π4-12+π2·k, k∈Zx∈-∞, +∞x2-x-6≠0⇔⇔x≠π4-12+π2·k, k∈Zx≠-2x≠3
Ответ: множество действительных чисел, кроме -2, 3 и π4-12+π2·k, k∈Z.
Область определения логарифма с переменной в основании
Определение 3Определение логарифма существует для положительных оснований не равных 1. Отсюда видно, что функция y=logf2(x)f1(x) имеет область определения, которая выглядит так:
Отсюда видно, что функция y=logf2(x)f1(x) имеет область определения, которая выглядит так:
x∈D(f1)f1(x)>0x∈D(f2)f2(x)>0f2(x)≠1
А аналогичному заключению можно прийти, когда функцию можно изобразить в таком виде:
y=logaf1(x)logaf2(x), a>0, a≠1. После чего можно приступать к области определения дробной функции.
Область определения логарифмической функции – это множество действительных положительных чисел, тогда области определения сложных функций типа y=logaf1(x) и y=logaf2(x) можно определить из получившейся системы вида x∈D(f1)f1(x)>0 и x∈D(f2)f2(x)>0. Иначе эту область можно записать в виде y=logaf1(x)logaf2(x), a>0, a≠1, что означает нахождение y=logf2(x)f1(x) из самой системы вида
x∈D(f1)f1(x)>0x∈D(f2)f2(x)>0logaf2(x)≠0=x∈D(f1)f1(x)>0x∈D(f2)f2(x)>0f2(x)≠1
Пример 9Обозначить область определения функции y=log2·x(x2-6x+5).
Решение
Следует принять обозначения f1(x)=x2−6·x+5 и f2(x)=2·x, отсюда D(f1)=(−∞, +∞) и D(f2)=(−∞, +∞). Необходимо приступить к поиску множества x, где выполняется условие x∈D(f1), f1(x)>0, x∈D(f2), f2(x)>0, f2(x)≠1. Тогда получаем систему вида
Необходимо приступить к поиску множества x, где выполняется условие x∈D(f1), f1(x)>0, x∈D(f2), f2(x)>0, f2(x)≠1. Тогда получаем систему вида
x∈(-∞, +∞)x2-6x+5>0x∈(-∞, +∞)2·x>02·x≠1⇔x∈(-∞, +∞)x∈(-∞, 1)∪(5, +∞)x∈(-∞, +∞)x>0x≠12⇔⇔x∈0, 12∪12, 1∪(5, +∞)
Отсюда видим, что искомой областью функции y=log2·x(x2-6x+5) считается множнство, удовлетворяющее условию 0, 12∪12, 1∪(5, +∞).
Ответ: 0, 12∪12, 1∪(5, +∞).
Область определения показательно-степенной функции
Показательно-степенная функция задается формулой вида y=(f1(x))f2(x). Ее область определения включает в себя такие значения x, которые удовлетворяют системе x∈D(f1)x∈D(f2)f1(x)>0.
Эта область позволяет переходить от показательно-степенной к сложной вида y=aloga(f1(x))f2(x)=af2(x)·logaf1(x), где где a>0, a≠1.
Пример 10Найти область определения показательно-степенной функции y=(x2-1)x3-9·x.
Решение
Примем за обозначение f1(x)=x2−1 и f2(x)=x3-9·x.
Функция f1определена на множестве действительных чисел, тогда получаем область определения вида D(f1)=(−∞, +∞). Функция f2является сложной, поэтому ее представление примет вид y=f3(f4(x)), а f3 – квадратным корнем с областью определения D(f3)=[0, +∞), а функция f4 – целой рациональной,D(f4)=(−∞, +∞). Получаем систему вида
x∈D(f4)f4(x)∈D(f3)⇔x∈(-∞, +∞)x3-9·x≥0⇔⇔x∈(-∞, +∞)x∈-3, 0∪[3, +∞)⇔x∈-3, 0∪[3, +∞)
Значит, область определения для функции f2имеет вид D(f2)=[−3, 0]∪[3, +∞). После чего необходимо найти область определения показательно-степенной функции по условию x∈D(f1)x∈D(f2)f1(x)>0.
Получаем систему вида x∈-∞, +∞x∈-3, 0∪[3, +∞)x2-1>0⇔x∈-∞, +∞x∈-3, 0∪[3, +∞)x∈(-∞, -1)∪(1, +∞)⇔⇔x∈-3, -1∪[3, +∞)
Ответ: [−3, −1)∪[3, +∞)
В общем случае
Для решения обязательным образом необходимо искать область определения, которая может быть представлена в виде суммы или разности функций, их произведений. Области определения сложных и дробных функций нередко вызывают сложность. Благодаря выше указанным правилам можно правильно определять ОДЗ и быстро решать задание на области определения.
Области определения сложных и дробных функций нередко вызывают сложность. Благодаря выше указанным правилам можно правильно определять ОДЗ и быстро решать задание на области определения.
Таблицы основных результатов
Весь изученный материал поместим для удобства в таблицу для удобного расположения и быстрого запоминания.Ф
| Функция | Ее область определения |
Сумма, разность, произведение функций f1, f2,…, fn | Пересечение множеств D(f1), D(f2), …, D(fn) |
Сложная функция y=f1(f2(f3(…fn(x))))
В частности, y=f1(f2(x)) | Множество всех x, одновременно удовлетворяющих условиям x∈D(fn),fn(x)∈D(fn-1),fn-1(fn(x))∈D(fn-2),… ,f2(f3(…fn(x)))∈D(f1)
x∈D(f2),f2(x)∈D(f1) |
Расположим функции и их области определения.
| Функция | Ее область определения |
Прямая пропорциональность y=k·x | R |
| Линейная y=k·x+b | R |
Обратная пропорциональность y=kx | -∞, 0∪0, +∞ |
| Квадратичная y=a·x2+b·x+c | R |
| y=anxn+an-1xn-1+…+a1x+a0 | R |
| Целая рациональная | R |
| y=C·f(x), где C — число | D(f) |
Дробная y=f1(x)f2(x)
В частности, если f1(x), f2(x) — многочлены | Множество всех x, которые одновременно удовлетворяют условиям
f2(x)≠0 |
| y=f(x)n, где n — четное | x∈D(f1), f(x)≥0 |
y=logf2(x)f1(x)
В частности, y=logaf1(x)
В частности, y=logf2(x)a | x∈D(f1), f1(x)>0,x∈D(f2), f2(x)>0, f2(x)≠1
x∈D(f1), f1(x)>0
x∈D(f2), f2>0, f2(x)≠1 |
| Показательно-степенная y=(f1(x))f2(x) | x∈D(f1), x∈D(f2), f1(x)>0 |
Отметим, что преобразования можно выполнять, начиная с правой части выражения. Отсюда видно, что допускаются тождественные преобразования, которые на область определения не влияют. Например, y=x2-4x-2 и y=x+2 являются разными функциями, так как первая определяется на (−∞, 2)∪(2, +∞), а вторая из множества действительных чисел. Из преобразования y=x2-4x-2=x-2x+2x-2=x+2 видно, что функция имеет смысл при x≠2.
Отсюда видно, что допускаются тождественные преобразования, которые на область определения не влияют. Например, y=x2-4x-2 и y=x+2 являются разными функциями, так как первая определяется на (−∞, 2)∪(2, +∞), а вторая из множества действительных чисел. Из преобразования y=x2-4x-2=x-2x+2x-2=x+2 видно, что функция имеет смысл при x≠2.
Решение логарифмических уравнений с экспонентами
Purplemath
Второй тип логарифмического уравнения требует использования отношения:
—Взаимосвязь—
y = b x
……….. эквивалентно …………
(означает то же самое, что и)
журнал b ( y ) = x
В анимированной форме два уравнения связаны, как показано ниже:
MathHelp.
 com
comОбратите внимание, что основание как в экспоненциальной форме уравнения, так и в логарифмической форме уравнения — «b», но что x и y меняют сторону при переключении между двумя уравнениями.Если вы помните это — что бы ни было , было аргументом журнала, становится «равно», а все, что было «равно», становится экспонентой в экспоненте, и наоборот — тогда у вас не должно быть слишком много проблема с решением уравнений журнала.
Поскольку это уравнение имеет форму «журнал (чего-то) равен числу», а не «журнал (чего-то) равен журналу (чего-то еще)», я могу решить уравнение, используя Соотношение:
журнал 2 ( x ) = 4
2 4 = x
16 = x
Я могу решить эту проблему, преобразовав логарифмический оператор в его эквивалентную экспоненциальную форму, используя соотношение:
Но 8 = 2 3 , поэтому я могу приравнять степени двойки:
Обратите внимание, что это также можно было решить, работая непосредственно с определением логарифма.
Какая сила, когда поставлена на «2», даст вам 8? Конечно же, сила 3!
Если вы хотите много работать, вы также можете сделать это в своем калькуляторе, используя формулу замены базы:
Вставьте это в свой калькулятор, и вы получите «3» в качестве ответа. Хотя этот метод смены базы не особенно полезен в данном случае, вы можете видеть, что он действительно работает. (Попробуйте это на своем калькуляторе, если вы еще этого не сделали, чтобы быть уверенным, что вы знаете, какие клавиши нажимать и в каком порядке.Эта техника понадобится вам в последующих задачах.
Я не говорю, что вам обязательно понадобится, чтобы решал уравнения, используя формулу изменения базы, или всегда используя определение журналов, или любой другой конкретный метод. Но я предлагаю вам убедиться, что вы знакомы с различными методами, и что вы не должны паниковать, если вы и ваш друг использовали совершенно разных методов для решения одного и того же уравнения.
Журнал решения
2 ( x ) + лог 2 ( x — 2) = 3
Я пока ничего не могу сделать с этим уравнением, потому что у меня его еще нет в форме «журнал (чего-то) равно числу». Поэтому мне нужно использовать правила журнала, чтобы объединить два члена в левой части уравнения:
журнал 2 ( x ) + журнал 2 ( x — 2) = 3
журнал 2 [( x ) ( x — 2)] = 3
журнал 2 ( x 2 -2 x ) = 3
Теперь уравнение устроено в удобной форме.На этом этапе я могу использовать Отношение для преобразования логарифмической формы уравнения в соответствующую экспоненциальную форму, а затем могу решить результат:
журнал 2 ( x 2 -2 x ) = 3
2 3 = x 2 -2 x
8 = x 2 -2 x
0 = x 2 — 2 x — 8
0 = ( x -4) ( x + 2)
x = 4, –2
Но если x = –2, тогда аргумент «log 2 ( x )» из исходного логарифмического уравнения будет иметь отрицательное число (как и термин «log 2 ( x — 2) «). Поскольку журналы не могут иметь нулевых или отрицательных аргументов, решение исходного уравнения не может быть x = –2.
Поскольку журналы не могут иметь нулевых или отрицательных аргументов, решение исходного уравнения не может быть x = –2.
Тогда мое решение:
Имейте в виду, что вы всегда можете проверить свои ответы на любое упражнение «решение», вставив эти ответы обратно в исходное уравнение и проверив, что решение «работает». В этом случае я вставлю свое значение решения в любую сторону исходного уравнения и проверю, что каждая сторона оценивает одно и то же число:
левая сторона:
бревно 2 ( x ) + полено 2 ( x -2)
= журнал 2 (4) + журнал 2 (4-2) 3
= журнал 2 (4) + журнал 2 (2)
= журнал 2 (2 2 ) + журнал 2 (2 1 )
= 2 + 1 = 3
Правая часть исходного уравнения уже была упрощена до «3», поэтому это решение проверяется.
Это уравнение может показаться слишком сложным, но это всего лишь еще одно логарифмическое уравнение. Чтобы решить эту проблему, мне нужно дважды применить The Relationship. Я начинаю с исходного уравнения и работаю с «внешним» журналом:
Отношение преобразует вышеуказанное в:
Теперь я применю Отношение во второй раз:
Тогда решение:
Журнал решения
2 ( x 2 ) = (журнал 2 ( x )) 2
Сначала я раскрою квадрат справа, чтобы он был явным произведением двух журналов:
журнал 2 ( x 2 ) = [журнал 2 ( x )] 2
журнал 2 ( x 2 ) = [журнал 2 ( x )] [журнал 2 ( x )]
Затем я применяю правило журнала, чтобы переместить «квадрат» изнутри журнала в левой части уравнения, вынимая его перед этим журналом в качестве множителя:
2 · журнал 2 ( x ) = [журнал 2 ( x )] [журнал 2 ( x )]
Затем я перенесу этот член из левой части уравнения в правую:
0 = [журнал 2 ( x )] [журнал 2 ( x )] — 2 · журнал 2 ( x )
Это уравнение может выглядеть плохо, но внимательно присмотритесь. На данный момент это не более чем упражнение по факторингу. Итак, я фактор, а затем я решу факторы, используя The Relationship:
На данный момент это не более чем упражнение по факторингу. Итак, я фактор, а затем я решу факторы, используя The Relationship:
0 = [журнал 2 ( x )] [журнал 2 ( x ) — 2]
журнал 2 ( x ) = 0 или журнал 2 ( x ) — 2 = 0
2 0 = x или лог 2 ( x ) = 2
1 = x или 2 2 = x
1 = x или 4 = x
Тогда мое решение:
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в решении логарифмических уравнений (или пропустите виджет и продолжите урок).Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway.
Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway.
(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.)
URL: https://www.purplemath.com/modules/solvelog2.htm
Вопрос 311717: log (2x-3) + log (x-2) = 2logx Решите для x и покажите работу, спасибо Найдено 2 решения от ankor @ dixie-net.2 Они не равны Следовательно; x = 1, а не решение Таким образом, значение x в данном вопросе будет 6 (x = 6) Удачи! |
Mohamed G. Gouda CS 313K
Осень 2012, упражнение 13 1. Покажите прямым выводом, что функция f (x) = 10 есть Theta (g (x)), где
г (х) = 1. Sol:
Доказательство того, что f (x) есть O (g (x)):
| f (x) | = | 10 |
= 10
= 10 * 1
= C * | 1 | для C = 10
== C * | g (x) | для K любое значение и C = 10 2.2 | для C = (1/2)
= C * | g (x) | для K = 4 и C = (1/2) 4. Покажите прямым выводом, что f (x) = 5 * log (x) есть Theta (g (x)), где
г (х) = журнал (х). Sol:
Доказательство того, что f (x) есть O (g (x)):
| f (x) | = | 5 * журнал (x) |
= 5 * log (x) для x> 2
= C * log (x) для C = 5
= C * | журнал (x) |
= 2
> = (4) * журнал (x)
= C * log (x) для C = 4
= C * | журнал (x) |
= C * | g (x) | для K = 2 и C = 4 5. Покажите прямым выводом, что f (x) = потолок (x) есть Theta (g (x)), где
г (х) = х. Sol:
Доказательство того, что f (x) есть O (g (x)):
| f (x) | = | потолок (x) |
= потолок (x) для x> 1
= 1
> = х
= C * | x | для C = 1
= C * | g (x) | для K = 1 и C = 1 6.
Gouda CS 313K
Осень 2012, упражнение 13 1. Покажите прямым выводом, что функция f (x) = 10 есть Theta (g (x)), где
г (х) = 1. Sol:
Доказательство того, что f (x) есть O (g (x)):
| f (x) | = | 10 |
= 10
= 10 * 1
= C * | 1 | для C = 10
== C * | g (x) | для K любое значение и C = 10 2.2 | для C = (1/2)
= C * | g (x) | для K = 4 и C = (1/2) 4. Покажите прямым выводом, что f (x) = 5 * log (x) есть Theta (g (x)), где
г (х) = журнал (х). Sol:
Доказательство того, что f (x) есть O (g (x)):
| f (x) | = | 5 * журнал (x) |
= 5 * log (x) для x> 2
= C * log (x) для C = 5
= C * | журнал (x) |
= 2
> = (4) * журнал (x)
= C * log (x) для C = 4
= C * | журнал (x) |
= C * | g (x) | для K = 2 и C = 4 5. Покажите прямым выводом, что f (x) = потолок (x) есть Theta (g (x)), где
г (х) = х. Sol:
Доказательство того, что f (x) есть O (g (x)):
| f (x) | = | потолок (x) |
= потолок (x) для x> 1
= 1
> = х
= C * | x | для C = 1
= C * | g (x) | для K = 1 и C = 1 6. 2) / (2 * х)
= (1/2) * х
= C * | x | для C = (1/2)
= C * | g (x) | для K = 1 и C = (1/2) 7. Покажите прямым выводом, что
(f1 (x) равно O (g1 (x))) и (f2 (x) равно O (g2 (x)))
=> (f1 (x) * f2 (x) равно O (g1 (x) * g2 (x))) Sol:
(f1 (x) равно O (g1 (x))) и (f2 (x) равно O (g2 (x)))
=> {Определение «О»}
(Существуют K1, C1, K2, C2,
(Все x> K1, | f1 (x) | = K2, | f2 (x) | = {Пусть K будет max (K1, K2)}
(Существуют K, C1, C2,
(Все x> K, | f1 (x) | = K, | f2 (x) | = {Арифметика}
(Существуют K, C1, C2,
(Все x> K, | f1 (x) | = {Арифметика}
(Существуют K, C1, C2,
(Все x> K, | f1 (x) | * | f2 (x) | = {Арифметика}
(Существуют K, C1, C2,
(Все x> K, | f1 (x) * f2 (x) | = {Пусть C будет C1 * C2}
(Существуют K, C,
(Все x> K, | f1 (x) * f2 (x) | = {Определение «O»}
(f1 (x) * f2 (x)) равно O (g1 (x) * g2 (x)) 8.2 + 5 * log (x)) / (2x + 1) для x> 1
= 1
=
2) / (2 * х)
= (1/2) * х
= C * | x | для C = (1/2)
= C * | g (x) | для K = 1 и C = (1/2) 7. Покажите прямым выводом, что
(f1 (x) равно O (g1 (x))) и (f2 (x) равно O (g2 (x)))
=> (f1 (x) * f2 (x) равно O (g1 (x) * g2 (x))) Sol:
(f1 (x) равно O (g1 (x))) и (f2 (x) равно O (g2 (x)))
=> {Определение «О»}
(Существуют K1, C1, K2, C2,
(Все x> K1, | f1 (x) | = K2, | f2 (x) | = {Пусть K будет max (K1, K2)}
(Существуют K, C1, C2,
(Все x> K, | f1 (x) | = K, | f2 (x) | = {Арифметика}
(Существуют K, C1, C2,
(Все x> K, | f1 (x) | = {Арифметика}
(Существуют K, C1, C2,
(Все x> K, | f1 (x) | * | f2 (x) | = {Арифметика}
(Существуют K, C1, C2,
(Все x> K, | f1 (x) * f2 (x) | = {Пусть C будет C1 * C2}
(Существуют K, C,
(Все x> K, | f1 (x) * f2 (x) | = {Определение «O»}
(f1 (x) * f2 (x)) равно O (g1 (x) * g2 (x)) 8.2 + 5 * log (x)) / (2x + 1) для x> 1
= 1
=
Решение экспоненциальных уравнений с использованием логарифмов
На предыдущем уроке вы узнали, как решать экспоненциальные уравнения без логарифмов. На этот раз мы хотим решить экспоненциальное уравнение , требующее использования логарифмов . Почему? Причина в том, что мы не можем манипулировать экспоненциальным уравнением, чтобы иметь одинаковую или общую основу для обеих сторон уравнения. Если вы столкнулись с проблемой такого типа, выполните следующие действия:
На этот раз мы хотим решить экспоненциальное уравнение , требующее использования логарифмов . Почему? Причина в том, что мы не можем манипулировать экспоненциальным уравнением, чтобы иметь одинаковую или общую основу для обеих сторон уравнения. Если вы столкнулись с проблемой такого типа, выполните следующие действия:
Шаги для решения экспоненциальных уравнений с использованием логарифмов
1) Оставьте экспоненциальное выражение отдельно на одной стороне уравнения.
2) Найдите логарифмы обеих частей уравнения. Вы можете использовать любых баз для логов.
3) Найдите переменную. Ответьте точнее или используйте десятичные дроби. В дополнение к шагам, описанным выше, обязательно ознакомьтесь с основными правилами логарифмирования, потому что вы будете использовать их так или иначе.
Давайте рассмотрим несколько примеров!
Примеры решения экспоненциальных уравнений с использованием логарифмов
Пример 1: Решите экспоненциальное уравнение {5 ^ {2x}} = 21.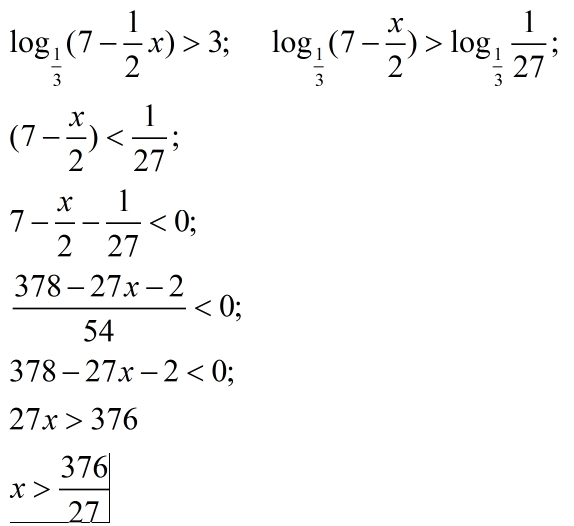
Преимущество этого уравнения в том, что экспоненциальное выражение уже выделено в левой части. Теперь мы можем логарифмировать обе части уравнения. Неважно, какое основание логарифма использовать. Окончательный ответ должен быть таким же. Наилучший выбор для базы логарифмической операции — 5, поскольку она является базой самого экспоненциального выражения. Тем не менее, мы также будем использовать в вычислениях общую основу 10 и естественную основу \ color {red} e (обозначенную \ color {blue} ln), чтобы показать, что в конечном итоге все они имеют одинаковые ответы. .{x — 5}}} \ right) = 12.
Как видите, экспоненциальное выражение слева не само по себе. Мы должны исключить число 2, умножающее экспоненциальное выражение. Для этого разделите обе части на 2. В результате мы получим только экспоненциальное выражение слева и 6 справа после упрощения.
Пора взять бревно с обеих сторон. Поскольку экспоненциальное выражение имеет основание 3, это удобное основание для работы с журналом. Кроме того, мы также решим эту проблему, используя естественное основание e, чтобы сравнить, согласуются ли наши окончательные результаты.{x — 2}}}}}}} \ right) — 7 = 13.
Кроме того, мы также решим эту проблему, используя естественное основание e, чтобы сравнить, согласуются ли наши окончательные результаты.{x — 2}}}}}}} \ right) — 7 = 13.
Сначала это похоже на беспорядок. Однако если вы знаете, с чего начать, решение этой проблемы становится простым. В первую очередь нам следует упростить выражение внутри скобок. Используйте правило деления экспоненты, скопировав общее основание числа е и вычтя верхнюю на нижнюю степень.
Теперь выделите экспоненциальное выражение, сложив обе части на 7, а затем разделив все уравнение на 2.
Возьмите логарифм обеих сторон.х} + 3 = 53.
Обратите внимание, что экспоненциальное выражение увеличивается до x. Упростите это, применив Силу к Правилу Силы. Сделайте это, скопировав основание 10 и умножив его показатель на внешний показатель. После этого он должен выглядеть так.
Теперь мы можем изолировать экспоненциальное выражение, вычтя обе части на 3, а затем умножив обе стороны на 2.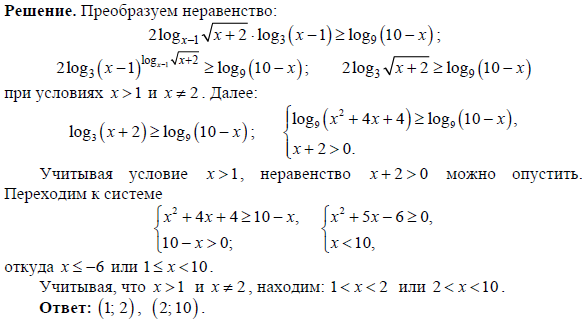
Возьмите логарифм обеих сторон с основанием 10. Если вы просто видите журнал \ color {red} без какой-либо конкретной базы , предполагается, что в его основе лежит 10.х снова.
Наконец, установите каждый коэффициент равным нулю и решите относительно x, как обычно, используя логарифмы.
Возможно, вас также заинтересует:
Решение экспоненциальных уравнений без логарифмов
| ’62 Центр театра и танца, ’62 Центр | ||
| Касса | 597-2425 | |
| Магазин костюмов | 597-3373 | |
| Менеджер мероприятий / Помощник менеджера | 597-4808 | 597-4815 факс |
| Производство | 597-4474 факс | |
| Магазин сцен | 597-2439 | |
| ’68 Центр карьерного роста, Мирс | 597-2311 | 597-4078 факс |
| Академические ресурсы, Парески | 597-4672 | 597-4959 факс |
| Служба поддержки инвалидов, Парески | 597-4672 | |
| Прием, Вестон Холл | 597-2211 | 597-4052 факс |
| Affirmative Action, Hopkins Hall | 597-4376 | |
| Africana Studies, Hollander | 597-2242 | 597-4222 факс |
| Американские исследования, Шапиро | 597-2074 | 597-4620 факс |
| Антропология и социология, Холландер | 597-2076 | 597-4305 факс |
| Архивы и специальные коллекции, Sawyer | 597-4200 | 597-2929 факс |
| Читальный зал | 597-4200 | |
| Искусство (история, студия), Spencer Studio Art / Lawrence | 597-3578 | 597-3693 факс |
| Архитектурная студия, Spencer Studio Art | 597-3134 | |
| Фотография Студия, Spencer Studio Art | 597-2030 | |
| Printmaking Studio, Spencer Studio Art | 597-2496 | |
| Студия скульптуры, Спенсер Студия искусства | 597-3101 | |
| Senior Studio, Spencer Studio Art | 597-3224 | |
| Видео / фотостудия, Spencer Studio Art | 597-3193 | |
| Азиатские исследования, Холландер | 597-2391 | 597-3028 факс |
| Астрономия / Астрофизика, Thompson Physics | 597-2482 | 597-3200 факс |
| Департамент легкой атлетики, физическое воспитание, отдых, Ласелл | 597-2366 | 597-4272 факс |
| Спортивный директор | 597-3511 | |
| Лодочный домик, Озеро Онота | 443-9851 | |
| Автобусы | 597-2366 | |
| Фитнес-центр | 597-3182 | |
| Hockey Rink Ice Line, Lansing Chapman | 597-2433 | |
| Intramurals, Атлетический центр Чандлера | 597-3321 | |
| Физическое воспитание | 597-2141 | |
| Pool Wet Line, Атлетический центр Чандлера | 597-2419 | |
| Sports Information, Hopkins Hall | 597-4982 | 597-4158 факс |
| Спортивная медицина | 597-2493 | 597-3052 факс |
| Площадки для сквоша | 597-2485 | |
| Поле для гольфа Taconic | 458-3997 | |
| Биохимия и молекулярная биология, Thompson Biology | 597-2126 | |
| Биоинформатика, геномика и протеомика, Bronfman | 597-2124 | |
| Биология, Thompson Biology | 597-2126 | 597-3495 факс |
| Охрана и безопасность кампуса, Хопкинс-холл | 597-4444 | 597-3512 факс |
| Карты доступа / системы сигнализации | 597-4970 / 4033 | |
| Служба сопровождения, Хопкинс Холл | 597-4400 | |
| Офицеры и диспетчеры | 597-4444 | |
| Секретарь, удостоверения личности | 597-4343 | |
| Коммутатор | 597-3131 | |
| Центр развития творческих сообществ, 66 Stetson Court | 884-0093 | |
| Центр экономики развития, 1065 Main St | 597-2148 | 597-4076 факс |
| Компьютерный зал | 597-2522 | |
| Вестибюль | 597-4383 | |
Центр экологических исследований, класс 1966 г. Экологический центр Экологический центр | 597-2346 | 597-3489 факс |
| Лаборатория экологических наук, Морли | 597-2380 | |
| Экологические исследования | 597-2346 | |
| Лаборатория ГИС | 597-3183 | |
| Центр иностранных языков, литератур и культур, Холландер | 597-2391 | 597-3028 факс |
| Арабские исследования, Холландер | 597-2391 | 597-3028 факс |
| Сравнительная литература, Холландер | 597-2391 | |
| Критические языки, Холландер | 597-2391 | 597-3028 факс |
| лингафонный кабинет | 597-3260 | |
| Россия, Холландер | 597-2391 | |
| Центр обучения в действии, Brooks House | 597-4588 | 597-3090 факс |
| Библиотека редких книг Чапина, Сойер | 597-2462 | 597-2929 факс |
| Читальный зал | 597-4200 | |
| Офис капелланов, Парески | 597-2483 | 597-3955 факс |
| Еврейский религиозный центр, Стетсон-Корт 24, | 597-2483 | |
| Мусульманская молитвенная комната, часовня Томпсона (нижний уровень) | 597-2483 | |
| Католическая часовня Ньюмана, часовня Томпсона (нижний уровень) | 597-2483 | |
| Химия, Thompson Chemistry | 597-2323 | 597-4150 факс |
| Классика (греческий и латинский), Hollander | 597-2242 | 597-4222 факс |
| Когнитивная наука, Бронфман | 597-4594 | |
| College Marshal, Thompson Physics | 597-2008 | |
| Отношения с колледжем | 597-4057 | |
| Программа 25-го воссоединения, Фогт | 597-4208 | 597-4039 факс |
| Программа 50-го воссоединения, Фогт | 597-4284 | 597-4039 факс |
| Advancement Operations, Мирс-Уэст | 597-4154 | 597-4333 факс |
| Мероприятия для выпускников, Vogt | 597-4146 | 597-4548 факс |
| Фонд выпускников | 597-4153 | 597-4036 факс |
| Связи с выпускниками, Мирс-Уэст | 597-4151 | 597-4178 факс |
| Почтовые службы для выпускников / разработчиков, Мирс-Вест | 597-4369 | |
| Развитие, Vogt | 597-4256 | |
| Отношения с донорами, Vogt | 597-3234 | 597-4039 факс |
| Офис по планированию подарков, Vogt | 597-3538 | 597-4039 факс |
| Grants Office, Mears West | 597-4025 | 597-4333 факс |
| Программа крупных подарков, Vogt | 597-4256 | 597-4548 факс |
| Parents Fund, Vogt | 597-4357 | 597-4036 факс |
| Prospect Management & Research, Мирс | 597-4119 | 597-4178 факс |
| Начало занятий и академические мероприятия, Jesup | 597-2347 | 597-4435 факс |
| Communications, Hopkins Hall | 597-4277 | 597-4158 факс |
| Sports Information, Hopkins Hall | 597-4982 | 597-4158 факс |
| Web Team, Southworth Schoolhouse | ||
| Williams Magazines (ранее Alumni Review), Hopkins Hall | 597-4278 | |
| Компьютерные науки, Thompson Chemistry | 597-3218 | 597-4250 факс |
| Conferences & Events, Paresky | 597-2591 | 597-4748 факс |
Запросы Elm Tree House, Mt. Ферма Надежды, Ферма Надежды, | 597-2591 | |
| Офис контролера, Хопкинс-холл | 597-4412 | 597-4404 факс |
| Счета к оплате и ввод данных, Хопкинс-холл | 597-4453 | |
| Bursar & Cash Receipts, Hopkins Hall | 597-4396 | |
| Financial Information Systems, Hopkins Hall | 597-4023 | |
| Purchasing Cards, Hopkins Hall | 597-4413 | |
| Студенческие ссуды, Хопкинс-холл | 597-4683 | |
| Dance, 62 Центр | 597-2410 | |
| Центр Дэвиса (ранее Мультикультурный центр), Дженнесс | 597-3340 | 597-3456 факс |
| Харди Хаус | 597-2129 | |
| Jenness House | 597-3344 | |
| Райс Хаус | 597-2453 | |
| Декан колледжа, Хопкинс-холл | 597-4171 | 597-3507 факс |
| Декан факультета Хопкинс Холл | 597-4351 | 597-3553 факс |
| Столовая, капельницы | 597-2121 | 597-4618 факс |
| ’82 Гриль, Парески | 597-4585 | |
| Кондитерская, Паресский | 597-4511 | |
| Общественное питание, факультет | 597-2452 | |
| Driscoll Dining Hall, Дрисколл | 597-2238 | |
| Eco Café, Science Center | 597-2383 | |
| Grab ‘n Go, Парески | 597-4398 | |
| Lee Snack Bar, Парески | 597-3487 | |
| Обеденный зал Mission Park, Mission Park | 597-2281 | |
| Whitmans ‘, Paresky | 597-2889 | |
| Экономика, Шапиро | 597-2476 | 597-4045 факс |
| Английский, Холландер | 597-2114 | 597-4032 факс |
| Сооружения, служебное здание | 597-2301 | |
| College Car Request | 597-2302 | |
| Скорая помощь вечером / в выходные дни | 597-4444 | |
| Запросы на работу производственных помещений | 597-4141 факс | |
| Особые мероприятия | 597-4020 | |
| Кладовая | 597-2143 | 597-4013 факс |
| Клуб преподавателей, Дом факультетов / Центр выпускников | 597-2451 | 597-4722 факс |
| Бронирование | 597-3089 | |
| Fellowships Office, Hopkins Hall | 597-3044 | 597-3507 факс |
| Financial Aid, Weston Hall | 597-4181 | 597-2999 факс |
| Geosciences, Clark Hall | 597-2221 | 597-4116 факс |
| Немецко-русский, Hollander | 597-2391 | 597-3028 факс |
| Глобальные исследования, Холландер | 597-2247 | |
| Программа магистратуры по истории искусств, Кларк | 458-2317 факс | |
| Службы здравоохранения и хорошего самочувствия, Thompson Ctr Health | 597-2206 | 597-2982 факс |
| Медицинское просвещение | 597-3013 | |
| Услуги интегративного благополучия (консультирование) | 597-2353 | |
| Чрезвычайные ситуации с опасностью для жизни | Позвоните 911 | |
| Медицинские услуги | 597-2206 | |
| История, Холландер | 597-2394 | 597-3673 факс |
| История науки, Бронфман | 597-4116 факс | |
| Лес Хопкинса | 597-4353 | |
| Розенбург Центр | 458-3080 | |
| Отдел кадров, B&L Building | 597-2681 | 597-3516 факс |
| Услуги няни, корпус B&L | 597-4587 | |
| Льготы | 597-4355 | |
| Программа помощи сотрудникам | 800-828-6025 | |
| Занятость | 597-2681 | |
| Заработная плата | 597-4162 | |
| Ресурсы для супруга / партнера | 597-4587 | |
| Занятость студентов | 597-4568 | |
| Погодная линия (ICEY) | 597-4239 | |
| Humanities, Schapiro | 597-2076 | |
| Информационные технологии, Jesup | 597-2094 | 597-4103 факс |
| Пакеты для чтения курса, Drop Box для офисных услуг | 597-4090 | |
| Центр ссуды на оборудование, приложение Додда | 597-4091 | |
| Служба поддержки преподавателей / сотрудников, [адрес электронной почты защищен] | 597-4090 | |
| Медиауслуги и справка в классе | 597-2112 | |
| Служба поддержки студентов, [электронная почта] | 597-3088 | |
| Телекоммуникации / Телефоны | 597-4090 | |
| Междисциплинарные исследования, Hollander | 597-2552 | |
| Международное образование и учеба, Хопкинс-холл | 597-4262 | 597-3507 факс |
| Инвестиционный офис, Хопкинс Холл | 597-4447 | |
| Бостонский офис | 617-502-2400 | 617-426-5784 факс |
| Еврейские исследования, Мазер | 597-3539 | |
| Правосудие и закон, Холландер | 597-2102 | |
| Latina / o Studies, Hollander | 597-2242 | 597-4222 факс |
| Исследования лидерства, Шапиро | 597-2074 | 597-4620 факс |
| Морские исследования, Бронфман | 597-2297 | |
| Математика и статистика, Bascom | 597-2438 | 597-4061 факс |
| Музыка, Бернхард | 597-2127 | 597-3100 факс |
| Concertline (записанная информация) | 597-3146 | |
| Неврология, Thompson Biology | 597-4107 | 597-2085 факс |
| Окли Центр, Окли | 597-2177 | 597-4126 факс |
| Управление институционального разнообразия и справедливости, Hopkins Hall | 597-4376 | 597-4015 факс |
| Управление счетов студентов, Хопкинс-холл | 597-4396 | 597-4404 факс |
| Performance Studies, ’62 Center | 597-4366 | |
| Философия, Шапиро | 597-2074 | 597-4620 факс |
| Физика, Thompson Physics | 597-2482 | 597-4116 факс |
| Планетарий / Обсерватория Хопкинса | 597-3030 | |
| Старый театр обсерватории Хопкинса | 597-4828 | |
| Бронирование | 597-2188 | |
| Политическая экономия, Шапиро | 597-2327 | |
| Политология, Шапиро | 597-2168 | 597-4194 факс |
| Офис президента, Хопкинс Холл | 597-4233 | 597-4015 факс |
| Дом Президента | 597-2388 | 597-4848 факс |
| Услуги печати / почты для преподавателей / сотрудников, ’37 House | 597-2022 | |
| Программа обучения, Бронфман | 597-4522 | 597-2085 факс |
| Офис Провоста, Хопкинс Холл | 597-4352 | 597-3553 факс |
| Психология, психологические кабинеты и лаборатории | 597-2441 | 597-2085 факс |
| Недвижимость, B&L Building | 597-2195 / 4238 | 597-5031 факс |
| Ипотека для преподавателей / сотрудников | 597-4238 | |
| Преподаватели / сотрудники Арендное жилье | 597-2195 | |
| Офис регистратора, Хопкинс Холл | 597-4286 | 597-4010 факс |
| Религия, Холландер | 597-2076 | 597-4222 факс |
| Romance Languages, Hollander | 597-2391 | 597-3028 факс |
| Планировщик помещений | 597-2555 | |
| Соответствие требованиям безопасности и охраны окружающей среды, класс ’37, дом | 597-3003 | |
| Библиотека Сойера, Сойер | 597-2501 | 597-4106 факс |
| Службы доступа | 597-2501 | |
| Приобретения / Серийные номера | 597-2506 | |
| Каталогизация / Службы метаданных | 597-2507 | |
| Межбиблиотечный абонемент | 597-2005 | 597-2478 факс |
| Исследовательские и справочные службы | 597-2515 | |
| Стеллаж | 597-4955 | 597-4948 факс |
| Системы | 597-2084 | |
| Научная библиотека Шоу, Научный центр | 597-4500 | 597-4600 факс |
| Исследования в области науки и технологий, Бронфман | 597-2239 | |
| Научный центр, Бронфман | 597-4116 факс | |
| Магазин электроники | 597-2205 | |
| Станочно-модельный цех | 597-2230 | |
| Безопасность | 597-4444 | |
| Специальные академические программы, Харди | 597-3747 | 597-4530 факс |
| Sports Information, Hopkins Hall | 597-4982 | 597-4158 факс |
| Студенческая жизнь, Парески | 597-4747 | |
| Планировщик помещений | 597-2555 | |
| Управление студенческими центрами | 597-4191 | |
| Организация студенческих мероприятий | 597-2546 | |
| Студенческий дом, Парески | 597-2555 | |
| Участие студентов | 597-4749 | |
| Программы проживания для старших классов | 597-4625 | |
| Студенческая почта, Парески, | 597-2150 | |
| Центр устойчивого развития / Зилха Центр, Харпер | 597-4462 | |
| Коммутатор, Хопкинс Холл | 597-3131 | |
| Книжный магазин Уильямса | 458-8071 | 458-0249 факс |
| Театр, 62 Центр | 597-2342 | 597-4170 факс |
| Trust & Estate Administration, Sears House | 597-4259 | |
| Учебники | 597-2580 | |
| Вице-президент по работе в кампусе, Хопкинс-холл, | 597-2044 | 597-3996 факс |
| Вице-президент по связям с колледжем, Мирс | 597-4057 | 597-4178 факс |
| Вице-президент по финансам и администрированию, Hopkins Hall | 597-4421 | 597-4192 факс |
| Центр визуальных ресурсов, Лоуренс | 597-2015 | 597-3498 факс |
| Детский центр Williams College, Детский центр Williams | 597-4008 | 597-4889 факс |
| Музей искусств колледжа Уильямс (WCMA), Лоуренс | 597-2429 | 597-5000 факс |
| Подготовка музея | 597-2426 | |
| Служба безопасности музея | 597-2376 | |
| Музейный магазин | 597-3233 | |
| Уильямс Интернэшнл | 597-2161 | |
| Williams Outing Club, Парески | 597-2317 | |
| Оборудование / стол для студентов | 597-4784 | |
| Проект Уильямса по экономике высшего образования, Мирс-Вест | 597-2192 | |
| Williams Record, Парески | 597-2400 | 597-2450 факс |
| Программа Уильямса-Эксетера в Оксфорде, Оксфордский университет | 011-44-1865-512345 | |
| Программа Williams-Mystic, Mystic Seaport Museum | 860-572-5359 | 860-572-5329 факс |
| Исследования женщин, гендера и сексуальности, Schapiro | 597-3143 | 597-4620 факс |
| Написание программ, Hopkins Hall | 597-4615 | |
| Центр экологических инициатив «Зилха», Харпер | 597-4462 |
5.
 Производная логарифмической функции
Производная логарифмической функцииМ. Борна
Во-первых, давайте посмотрим на график функции журнала с базой e , то есть:
f ( x ) = log e ( x ) (обычно пишется «ln x »).
Касательная при x = 2 включена в график.
Наклон тангенса угла y = ln x при x = 2 равен 1/2.(Мы можем наблюдать это на графике, посмотрев на соотношение подъем / ход).
Если y = ln x ,
| x | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| наклон графика | `1` | `1/2` | `1/3` | `1/4` | `1/5` |
| `1 / x` | `1` | `1/2` | `1/3` | `1/4` | `1/5` |
Мы видим, что наклон графика для каждого значения x равен «1 / x». Это работает для любого положительного значения x (конечно, у нас не может быть логарифма отрицательного числа).
Это работает для любого положительного значения x (конечно, у нас не может быть логарифма отрицательного числа).
Если бы мы сделали еще много примеров, мы могли бы сделать вывод, что производная логарифмической функции y = ln x равна
`dy / dx = 1 / x`
Примечание 1: Фактически, этот результат исходит из первых принципов.
Примечание 2: Мы используем логарифмы с основанием e . Если вам нужно напоминание о функциях журнала, ознакомьтесь с базой журнала и ранее.
Производная логарифма
y = ln xПроизводная логарифмической функции y = ln x определяется по формуле:
`d / (dx) (ln \ x) = 1 / x`
Вы также увидите, что это написано несколькими другими способами. Следующие эквиваленты:
`d / (dx) log_ex = 1 / x`
Если y = ln x , то `(dy) / (dx) = 1 / x`
Теперь мы покажем, откуда взялась формула для производной от log_e x, используя первые принципы. {1 «/» t} `приближается к значению` e ~~ 2.71828`.)
{1 «/» t} `приближается к значению` e ~~ 2.71828`.)
Я напишу `log (x)` для обозначения `log_e (x) = ln (x)`, чтобы облегчить чтение.
У нас есть `f (x) = log (x)`, поэтому производная будет равна:
`(df) / (dx) = lim_ {h-> 0} (log (x + h) -log (x)) / h`
Теперь верхняя часть нашей дроби —
`log (x + h) -log (x)` `= log ((x + h) / x)` `= log (1 + h / x)`.
Чтобы упростить алгебру, мы теперь подставляем `t = h / x`, и это дает нам` h = xt`.{1 «/» t}) `
`= 1 / x журнал (е)`
`= 1 / x`
Наконечник
Для некоторых задач мы можем использовать законы логарифмирования, чтобы упростить логарифмическое выражение перед его дифференцированием.
Пример 1
Найдите производную от
y = ln 2 x
Ответ
Используем лог-закон:
журнал ab = журнал a + журнал b
Мы можем написать наш вопрос как:
y = ln 2 x = ln 2 + ln x
Теперь производная константы равна 0, поэтому
`d / (dx) ln \ 2 = 0`
Итак, у нас осталось (из нашей формулы выше)
`d / (dx) (ln \ x) = 1 / x`
Окончательный ответ:
`(dy) / (dx) = 1 / x`
Из следующего графика видно, что наклон y = ln 2 x (кривая зеленого цвета, касательная пурпурный) такой же, как наклон y = ln x (кривая серого цвета, касательная пунктирно серым) в точке x = 2.
Пример 2
Найдите производную от
y = ln x 2
Ответ
Используем лог-закон:
журнал a n = n журнал a
Итак, мы можем написать вопрос как
y = ln x 2 = 2 ln x
Производная будет просто в 2 раза больше производной ln x .2) «на самом деле имеет 2« руки », одно на отрицательной стороне, а другое на положительной. На приведенном выше графике для простоты показано только положительное плечо.
Производная от
y = ln u (где u является функцией x )К сожалению, мы можем использовать только законы логарифма, чтобы помочь нам в ограниченном количестве типов вопросов логарифмической дифференциации.
Чаще всего нам нужно найти производную логарифма некоторой функции x . Например, нам может потребоваться найти производную от y = 2 ln (3 x 2 — 1).
Например, нам может потребоваться найти производную от y = 2 ln (3 x 2 — 1).
Для решения таких задач нам понадобится следующая формула.
Если
y = ln u
и u — некоторая функция от x , тогда:
`(dy) / (dx) = (u ‘) / u`
, где u ‘ — производная от u
Другой способ записать это —
`(dy) / (dx) = 1 / u (du) / (dx)`
Вы также можете увидеть следующую форму.Это означает то же самое.
Если
y = ln f ( x ),
, то производная y определяется по формуле:
`(dy) / (dx) = (f ‘(x)) / (f (x)`
Пример 3
Найдите производную из
y = 2 ln (3 x 2 — 1).
2 + 1)`
Дифференцирование логарифмических функций с основанием, отличным от
eЕсли
u = f ( x ) является функцией x ,
и
y = log b u — логарифм с основанием b ,
, то мы можем получить производную функции логарифма с основанием b , используя:
`(dy) / (dx) = (log_be) (u ‘) / u`
где
u является производной от u
log b e — константа.См. Изменение базового правила, чтобы узнать, как вычислить такие константы на вашем калькуляторе.)
Примечание 1: Эта формула основана на первых принципах.
Примечание 2: Если мы выберем e в качестве основы, тогда производная ln u , где u является функцией x , просто даст нам нашу формулу выше:
`(dy) / (dx) = (u ‘) / u`
[Напомним, что журнал e e = 1.
]
[См. Главу, посвященную экспоненциальным и логарифмическим функциям, основание и , если вам нужно освежить в памяти все это.]
Пример 6
Найдите производную из y = бревно 2 6 x .
Ответ
Начнем с использования следующего правила журнала, чтобы упростить наш вопрос:
журнал ab = журнал a + журнал b
Мы можем написать наш вопрос как:
y = бревно 2 6 x = бревно 2 6 + лог 2 x
Первый член, log 2 6, является константой, поэтому его производная равна 0.
Производная второго члена выглядит следующим образом по нашей формуле:
`(dy) / (dx) = (log_2e) (1 / x) = (log_2e) / x`
Член сверху, log 2 e , является константой. 3-x`
3-x`
`x ≠ ± sqrt (0.5) `,
`x ≠ 0`
ПРИМЕЧАНИЕ: Мы должны быть осторожны с областью этого решения, так как это верно только для определенных значений размером x .
График y = ln (2 x 3 — x ) 2 (который имеет степень 2 ) определен для всех x , кроме
`± sqrt (0,5), 0`
Его график выглядит следующим образом:
График y = 2 ln (2 x 3 — x ), однако (у него 2 x спереди) определен только для более ограниченного домен (поскольку у нас не может быть логарифма отрицательного номер.)
Таким образом, мы можем иметь только x в диапазоне `-sqrt 0.5 sqrt0.5.`
Итак, когда мы находим дифференцирование логарифма с помощью
ярлык, указанный выше, мы должны быть осторожны, чтобы домен
указаны функция и область определения производной. 2`
2`
3.x (x \ cot \ x + ln (sin x)) `
График функции в упражнении 5 довольно интересен:
График y = (sin x ) x .
Используйте однозначное свойство логарифмов для решения логарифмических уравнений
Как и в случае с экспоненциальными уравнениями, мы можем использовать однозначное свойство для решения логарифмических уравнений. Однозначное свойство логарифмических функций говорит нам, что для любых действительных чисел x > 0, S > 0, T > 0 и любого положительного действительного числа b , где [latex] b \ ne 1 [/ латекс],
[латекс] {\ mathrm {log}} _ {b} S = {\ mathrm {log}} _ {b} T \ text {тогда и только тогда, когда} S = T [/ latex].
Например,
[латекс] \ text {If} {\ mathrm {log}} _ {2} \ left (x — 1 \ right) = {\ mathrm {log}} _ {2} \ left (8 \ right), \ текст {then} x — 1 = 8 [/ latex].
Итак, если [latex] x — 1 = 8 [/ latex], то мы можем решить для x , и мы получим x = 9. Чтобы проверить, мы можем подставить x = 9 в исходное уравнение. : [латекс] {\ mathrm {log}} _ {2} \ left (9-1 \ right) = {\ mathrm {log}} _ {2} \ left (8 \ right) = 3 [/ latex]. Другими словами, когда логарифмическое уравнение имеет одинаковое основание с каждой стороны, аргументы должны быть равны.Это также применимо, когда аргументы являются алгебраическими выражениями. Следовательно, когда дано уравнение с журналами с одинаковым основанием на каждой стороне, мы можем использовать правила логарифмов, чтобы переписать каждую сторону как один логарифм. Затем мы используем тот факт, что логарифмические функции взаимно однозначны, чтобы установить аргументы, равные друг другу, и найти неизвестное.
Чтобы проверить, мы можем подставить x = 9 в исходное уравнение. : [латекс] {\ mathrm {log}} _ {2} \ left (9-1 \ right) = {\ mathrm {log}} _ {2} \ left (8 \ right) = 3 [/ latex]. Другими словами, когда логарифмическое уравнение имеет одинаковое основание с каждой стороны, аргументы должны быть равны.Это также применимо, когда аргументы являются алгебраическими выражениями. Следовательно, когда дано уравнение с журналами с одинаковым основанием на каждой стороне, мы можем использовать правила логарифмов, чтобы переписать каждую сторону как один логарифм. Затем мы используем тот факт, что логарифмические функции взаимно однозначны, чтобы установить аргументы, равные друг другу, и найти неизвестное.
Например, рассмотрим уравнение [латекс] \ mathrm {log} \ left (3x — 2 \ right) — \ mathrm {log} \ left (2 \ right) = \ mathrm {log} \ left (x + 4 \ справа) [/ латекс]. Чтобы решить это уравнение, мы можем использовать правила логарифмов, чтобы переписать левую часть как единичный логарифм, а затем применить свойство «один к одному», чтобы найти x :
[латекс] \ begin {case} \ mathrm {log} \ left (3x — 2 \ right) — \ mathrm {log} \ left (2 \ right) = \ mathrm {log} \ left (x + 4 \ right) ) \ hfill & \ hfill \\ \ text {} \ mathrm {log} \ left (\ frac {3x — 2} {2} \ right) = \ mathrm {log} \ left (x + 4 \ right) \ hfill & \ text {Применить правило частного логарифмов}. \ hfill \\ \ text {} \ frac {3x — 2} {2} = x + 4 \ hfill & \ text {Применить свойство логарифма один к одному}. \ hfill \\ \ text {} 3x — 2 = 2x + 8 \ hfill & \ text {Умножьте обе части уравнения на} 2. \ hfill \\ \ text {} x = 10 \ hfill & \ text {Вычтите 2} x \ text {и добавьте 2}. \ hfill \ end {case} [/ latex]
\ hfill \\ \ text {} \ frac {3x — 2} {2} = x + 4 \ hfill & \ text {Применить свойство логарифма один к одному}. \ hfill \\ \ text {} 3x — 2 = 2x + 8 \ hfill & \ text {Умножьте обе части уравнения на} 2. \ hfill \\ \ text {} x = 10 \ hfill & \ text {Вычтите 2} x \ text {и добавьте 2}. \ hfill \ end {case} [/ latex]
Чтобы проверить результат, подставьте x = 10 в [latex] \ mathrm {log} \ left (3x — 2 \ right) — \ mathrm {log} \ left (2 \ right) = \ mathrm {log} \ left (x + 4 \ right) [/ латекс].
[латекс] \ begin {case} \ mathrm {log} \ left (3 \ left (10 \ right) -2 \ right) — \ mathrm {log} \ left (2 \ right) = \ mathrm {log} \ left (\ left (10 \ right) +4 \ right) \ hfill & \ hfill \\ \ text {} \ mathrm {log} \ left (28 \ right) — \ mathrm {log} \ left (2 \ right) = \ mathrm {log} \ left (14 \ right) \ hfill & \ hfill \\ \ text {} \ mathrm {log} \ left (\ frac {28} {2} \ right) = \ mathrm {log} \ left (14 \ right) \ hfill & \ text {Решение проверяет}.\ hfill \ end {case} [/ latex]
Общее примечание: использование однозначного свойства логарифмов для решения логарифмических уравнений
Для любых алгебраических выражений S и T и любого положительного действительного числа b , где [latex] b \ ne 1 [/ latex],
[латекс] {\ mathrm {log}} _ {b} S = {\ mathrm {log}} _ {b} T \ text {тогда и только тогда, когда} S = T [/ latex]
Обратите внимание: при решении уравнения, включающего логарифмы, всегда проверяйте, верен ли ответ или нет ли это постороннее решение.

 2 + 1)`
2 + 1)`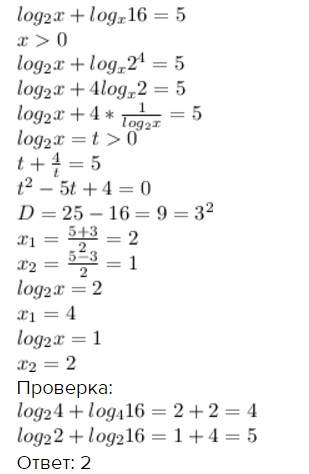 ]
]
Leave A Comment