тригонометрические формулы синус косинус суммы углов разности углов синус косинус двойного тройного углов синус косинус тангенс через тангенс половинного угла



Справочник по математикеТригонометрия

Содержание

Связи между тригонометрическими функциями одного угла
Тригонометрические функции суммы и разности двух углов
Тригонометрические функции двойного угла
Формулы понижения степени для квадратов тригонометрических функций
Формулы понижения степени для кубов синуса и косинуса
Выражение тангенса угла через синус и косинус двойного угла
Преобразование суммы тригонометрических функций в произведение
Преобразование произведения тригонометрических функций в сумму
Выражение тригонометрических функций через тангенс половинного угла
Тригонометрические функции тройного угла

Связи между тригонометрическими функциями одного угла

sin2α + cos2α = 1

Тригонометрические функции суммы и разности двух углов

ФормулаНазвание формулы
sin (α + β) = sin α cos β + cos α sin βСинус суммы
sin (α – β) = sin α cos β – cos α sin βСинус разности
cos (α + β) = cos α cos β – sin α sin βКосинус суммы
cos (α – β) = cos α cos β + sin α sin βКосинус разности
Тангенс суммы
Тангенс разности
Синус суммы
sin (α + β) = sin α cos β +
+ cos α sin β
Синус разности
sin (α – β) = sin α cos β –
– cos α sin β
Косинус суммы
cos (α + β) = cos α cos β –
– sin α sin β
Косинус разности
cos (α – β) = cos α cos β +
+ sin α sin β
Тангенс суммы
Тангенс разности

Тригонометрические функции двойного угла

ФормулаНазвание формулы
sin 2α = 2 sin α cos αСинус двойного угла

cos 2α = cos 2α – sin2α

cos 2α = 2cos 2α – 1

cos 2α = 1 – 2sin 2α

Косинус двойного угла
Тангенс двойного угла
Синус двойного угла
sin 2α = 2 sin α cos α
Косинус двойного угла

cos 2α = cos 2α – sin2α

cos 2α = 2cos 2α – 1

cos 2α = 1 – 2sin 2α

Тангенс двойного угла

Формулы понижения степени для квадратов тригонометрических функций

ФормулаНазвание формулы

Выражение квадрата синуса через косинус двойного угла

Выражение квадрата косинуса через косинус двойного угла

Выражение квадрата тангенса через косинус двойного угла

Выражение квадрата синуса через косинус двойного угла
Выражение квадрата косинуса через косинус двойного угла
Выражение квадрата тангенса через косинус двойного угла

Формулы понижения степени для кубов синуса и косинуса

ФормулаНазвание формулы

Выражение куба синуса через синус угла и синус тройного угла

Выражение куба косинуса через косинус угла и косинус тройного угла

Выражение куба синуса через синус угла и синус тройного угла

Выражение куба косинуса через косинус угла и косинус тройного угла

Выражение тангенса через синус и косинус двойного угла

Преобразование суммы тригонометрических функций в произведение

ФормулаНазвание формулы
Сумма синусов
Разность синусов
Сумма косинусов
Разность косинусов
Сумма тангенсов
Разность тангенсов
Сумма синусов
Разность синусов
Сумма косинусов
Разность косинусов
Сумма тангенсов
Разность тангенсов

Преобразование произведения тригонометрических функций в сумму

ФормулаНазвание формулы
Произведение синусов
Произведение косинусов
Произведение синуса и косинуса
Произведение синусов
Произведение косинусов
Произведение синуса и косинуса

Выражение тригонометрических функций через тангенс половинного угла

ФормулаНазвание формулы

Выражение синуса угла через тангенс половинного угла

Выражение косинуса угла через тангенс половинного угла

Выражение тангенса угла через тангенс половинного угла

Выражение синуса угла через тангенс половинного угла
Выражение косинуса угла через тангенс половинного угла
Выражение тангенса угла через тангенс половинного угла

Тригонометрические функции тройного угла

ФормулаНазвание формулы
sin 3α = 3sin α – 4sin3αСинус тройного угла
cos 3α = 4cos3α –3cos αКосинус тройного угла
Тангенс тройного угла
Синус тройного угла
sin 3α = 3sin α – 4sin3α
Косинус тройного угла
cos 3α = 4cos3α –3cos α
Тангенс тройного угла

Наверх

Демонстрационные варианты ЕГЭ и ОГЭ

С демонстрационными вариантами ЕГЭ и ОГЭ по всем предметам, опубликованными на официальном информационном портале Единого Государственного Экзамена, можно ознакомиться на специальной страничке нашего сайта.

Наши учебные пособия для школьников

При подготовке к ЕГЭ и к ОГЭ по математике Вам могут также пригодиться наши учебные пособия.

  • Решение рациональных неравенств

  • Задачи на проценты

  • Решение показательных неравенств

  • Квадратный трехчлен

  • Метод координат на плоскости

  • Решение иррациональных неравенств

  • Фигуры на координатной плоскости

  • Решение алгебраических уравнений

  • Уравнения и неравенства с модулями

  • Решение показательных уравнений

  • Арифметическая и геометрическая прогрессии

  • Решение логарифмических уравнений

  • Решение логарифмических неравенств

  • Системы уравнений

  • Решение тригонометрических уравнений

  • Тригонометрия в ЕГЭ по математике

  • Степень с рациональным показателем

Тангенс — что это такое (отношение чего к чему) и как его найти (по формулам и по клеточкам)

Обновлено 21 февраля 2023 Просмотров: 144 752 Автор: Дмитрий Петров

Живущим людям на Земле
всегда хотелось знать,
как путь найти в пустыне, море,
и можно к звёздам ли попасть.

Хотелось труд свой облегчить,
создать машины, чтоб летать.
И чтоб вопросы разрешить,
пришлось про тангенс всем узнать.

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Впервые встречаясь с тригонометрией в восьмом классе на геометрии, школьники оглядываются на свою жизнь, задавая вопрос, насколько пригодится им эта область науки в дальнейшем.

Редко кто задумывается, что раздел математики, позволяющий рассказать о заданном треугольнике всё (найти все его стороны и углы, выделить особенности), позволил в своё время сделать великие открытия.

Тригонометрия, дав возможность строить корабли и самолёты, отправлять человека в космос, создавать приборы для ориентирования на море, в лесу, в пустыне, определять расстояния, не измеряя их непосредственно линейкой, шагами или чем-то иным, помогла упростить жизнь человечества, раскрыть новые горизонты знаний.

Тангенс угла

Первые встречи с тангенсом происходят при изучении прямоугольных треугольников.

В них соотношения сторон, образующих прямой угол (катетов), и стороны, лежащей напротив угла в 90º (гипотенузы), задают важные параметры для изучения углов.

Для понимания связи между объектами рассматриваются отношения различных отрезков. Задавая связь между ними, вводят понятия синуса, косинуса (это что?), тангенса, котангенса.

Важно, что это отвлечённые понятия, не связанные с какими-либо единицами измерения.

Введя функции угла, определяют их свойства. Некоторые полученные формулы могут иметь довольно громоздкий вид. Чтобы избежать затруднённого чтения, вводятся другие объекты.

Так произошло и с тангенсом. Ему посчастливилось получить два определения. Каждое характеризует заданное отношение по-своему. С одной стороны, рассматривается связь между катетами и острыми углами прямоугольного треугольника, с другой – даётся возможность упростить формулы, содержащие синусы и косинусы.

Мало кто задумывается, изучая тангенс в школе, что первоначально он был необходим, чтобы найти касательные линии к заданной кривой. Само понятие возникло от латинского слова tangens, которое означает «трогающий», «касающийся» и является причастием настоящего времени от tangere («трогать», «касаться»).

Тангенс — это отношение…

Итак, есть два определения:

  1. Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

    Это определение удобно использовать при изучении геометрических фигур. Оно даёт возможность, минуя вычисления гипотенузы, находить углы или катеты. Выделяя прямоугольные треугольники в произвольных фигурах, задача по изучению свойств исследуемых объектов становится проще.

  2. Тангенс – это отношение синуса к косинусу.

    Благодаря этому определению, многие тригонометрические формулы принимают более удобный вид, становятся легче воспринимаемыми.

Приняты обозначения:

Вместо «тангенс угла альфа» пишут: tgα.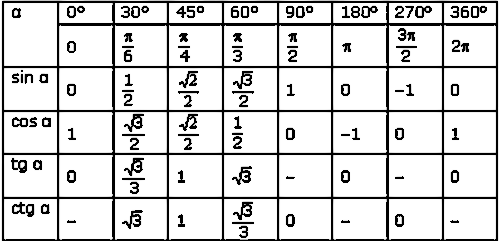 На калькуляторах, в различных программах ЭВМ и ПК закрепилось другое обозначение: tan⁡(α).

Как найти тангенс угла (формулы)

Первое свойство тангенса вытекает из его определения как отношения катетов.

Сумма двух непрямых углов прямоугольного треугольника равна 90º. Поэтому

Так как тангенс – это отношение катетов, то

Получается, что

Учитывая особенности некоторых треугольников (равностороннего, прямоугольного, равнобедренного), а также записанное свойство, была составлена таблица значений тангенса для углов 30º, 45º, 60º.

В частности,

Задача нахождения других углов по значению тангенса была решена с помощью составления более обширных таблиц. За счёт появления современных вычислительных средств необходимость применения табулированных значений уменьшилась.

Как найти тангенс по клеточкам

Учитывая первое определение, можно определить, как найти его по клеточкам. Рисунок дополняется перпендикулярными линиями (строится высота), затем считается количество клеточек в полученном прямоугольном треугольнике на катетах, противолежащем и прилежащем искомому углу, а затем берётся их отношение.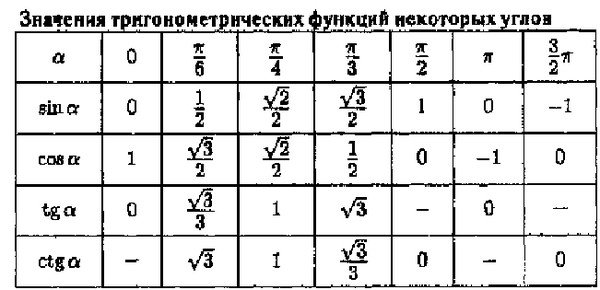

Благодаря второму определению, задачу, как найти тангенс угла, можно решить, минуя таблицы и построение прямоугольных треугольников. Достаточно знать синус и косинус, связанные между собой основным тригонометрическим тождеством:

Из формулы тангенсов, записывающей кратко второе определение

и основного тригонометрического тождества можно понять, как найти тангенс, зная только косинус или синус угла.

Достаточно поделить основное тригонометрическое тождество на квадрат косинуса, подставить формулу тангенса. В результате получится его зависимость от косинуса:

Если выразить в последнем случае косинус, то запишется связь между тангенсом и синусом:

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

  • Математика

6.

20: Теорема о касательной секущей — K12 LibreTexts
  1. Последнее обновление
  2. Сохранить как PDF
  • Идентификатор страницы
    5045

    • Произведение внешнего отрезка и всей секущей равно квадрату касательной к той же точке. 92=b(b+c)\).

    Рисунок \(\PageIndex{1}\)

    Что если вам дан круг с касательной и секущей, которые пересекаются вне круга? Как можно использовать длину некоторых отрезков, образованных их пересечением, для определения длин неизвестных отрезков?

    Пример \(\PageIndex{1}\)

    Найти \(x\). Упростите любые радикалы.

    Рисунок \(\PageIndex{2}\)

    Решение

    Используйте теорему о касательном секущем отрезке. 2&=10(10+x) \\ 324&=100+10x \\ 224&=10x \\ x&=22,4\end{выровнено}\) 92 \\ \dfrac{2\sqrt{15}}{3}&=y \color{red} \leftarrow \text{y \underline{не} правильно}\end{выровнено}\)

    Решите для неизвестная переменная.

    1. Рисунок \(\PageIndex{12}\)
    2. Рисунок \(\PageIndex{13}\)
    3. Рисунок \(\PageIndex{14}\)
    4. Рисунок \(\PageIndex{15}\)
    5. Рисунок \(\PageIndex{16}\)
    6. Рисунок \(\PageIndex{17}\)
    7. Рисунок \(\PageIndex{18}\)
    8. Рисунок \(\PageIndex{19}\)
    9. Рисунок \(\PageIndex{20}\)
    10. Рисунок \(\PageIndex{21}\)

    Обзор (ответы)

    Чтобы просмотреть ответы на обзор, откройте этот PDF-файл и найдите раздел 9.11.

    Словарь

    92 = Ь(Ь+с)\).
    Срок Определение
    центральный угол Угол, образованный двумя радиусами, вершина которого находится в центре окружности.
    хорда Отрезок, концы которого лежат на окружности.
    круг Набор всех точек, находящихся на одинаковом расстоянии от определенной точки, называемой центром .
    диаметр Хорда, проходящая через центр окружности. Длина диаметра в два раза больше длины радиуса.
    угол вписанный Угол с вершиной на окружности и сторонами которого являются хорды.
    перехваченная дуга Дуга внутри вписанного угла, концы которой лежат на этом угле.
    точка касания Точка, в которой касательная касается окружности.
    радиус Расстояние от центра до внешнего края круга.
    Секущая Секанс угла прямоугольного треугольника — это значение, которое находится путем деления длины гипотенузы на длину стороны, примыкающей к данному углу. Отношение секущей обратно пропорционально отношению косинуса.
    Касательные секущие отрезки Теорема

    Дополнительные ресурсы

    Интерактивный элемент

    Упражнения: Сегменты секущих и касательных Вопросы для обсуждения

    Учебные пособия: Окружности: Сегменты и длины Учебное пособие

    Практика: Секан касательных t Теорема

    Эта страница под названием 6. 20: Теорема касательной секущей распространяется под лицензией CK-12 и была создана, изменена и/или курирована Фондом CK-12 с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

    ПОД ЛИЦЕНЗИЕЙ

    1. Наверх
      • Была ли эта статья полезной?
      1. Тип изделия
        Раздел или Страница
        Автор
        СК12
        Лицензия
        СК-12
        Программа OER или Publisher
        СК-12
        Показать оглавление
        нет
      2. Теги
        1. источник@https://www. ck12.org/c/geometry

      Функция тангенса-квадрата — исчисление

      Эта статья о конкретной функции от подмножества действительных чисел до действительных чисел. В статье представлена ​​информация о функции, включая ее домен, диапазон и ключевые данные, относящиеся к построению графиков, дифференцированию и интегрированию.
      См. полный список конкретных функций на этой вики.
      Для функций, включающих углы (тригонометрические функции, обратные тригонометрические функции и т. д.), мы следуем соглашению, согласно которому все углы измеряются в радианах. Так, например, угол измеряется как .

      Содержание

      • 1 Определение
      • 2 Ключевые данные
      • 3 Дифференциация
        • 3.1 Первая производная
      • 4 Интеграция
        • 4.1 Первая первообразная
        • 4.2 Вторая первообразная
        • 4.3 Высшие производные
        • 4. 4 Интегрирование произведений с полиномами

      Определение

      Эта функция определяется как композиция функции квадрата и функции тангенса. В явном виде это функция:

      записывается как стенография.

      Ключевые данные

      Товар Значение
      Домен по умолчанию все действительные числа кроме нечетные целые числа кратные .
      диапазон , т. е. . Все неотрицательные действительные числа.
      нет абсолютного максимального значения; абсолютное минимальное значение 0
      период , т. е. .
      локальные максимальные значения и точки достижения Нет локальных максимальных значений
      локальные минимальные значения и точки достижения 0 во всех целых кратных .
      точек перегиба (обе координаты) Нет
      вертикальные асимптоты во всех нечетных кратных , с функцией, идущей в обоих направлениях в каждом случае.
      производная
      первообразная . Обратите внимание, что значение должно быть постоянным в пределах каждого интервала между последовательными нечетными числами, кратными , но может отличаться в разных интервалах. Домен вообще не подключен.
      Описание интервала на основе увеличения/уменьшения и вогнутости вверх/вниз Для каждого целого числа:
      по убыванию и вогнутости от до
      по возрастанию и вогнутости от до .

      Дифференцирование

      Первая производная

      Первую производную можно вычислить, комбинируя цепное правило дифференцирования и знание производных функции квадрата и функции тангенса:

      Интеграция

      Первая первообразная

      Используем тождество:

      Используя это, мы перепишем:

      где мы используем, что функция тангенса является первообразной для функции квадрата секанса

      Вторая первообразная

      Можно еще раз антидифференцировать функцию:

      Старшие первообразные

      Невозможно вычислить высшие первообразные в терминах элементарных функций, но мы можем вычислить их с помощью полилогарифма.