Фотоэффект
Задачи на фотоэффект: определение красной границы, работы выхода, массы фотона.
Задача 1. Красная граница фотоэффекта для натрия нм. Найти работу выхода электрона из натрия.
Работа выхода (Дж) определяется формулой:
Выражая в эВ, получим
Ответ: Дж, или 2,27 эВ.
Задача 2. Какова наименьшая частота света, при которой еще наблюдается фотоэффект, если работа выхода электрона из металла Дж?
Из формулы предыдущей задачи имеем:
Ответ: длина волны 600 нм, частота Гц.
Задача 3. Вычислить длину волны красной границы фотоэффекта для серебра. 19.62.
Работа выхода для серебра равна Дж. Тогда длина волны равна
Ответ: м, или 300 нм.
Задача 4. Красная граница фотоэффекта для некоторого металла . Чему равно минимальное значение энергии фотона, вызывающего фотоэффект?
Минимальная энергия фотона – такая, что вызывает выход электрона из металла, но на сообщение электрону кинетической энергии ее уже не хватает. Поэтому
В электронвольтах это
Ответ: Дж, или 4,5 эВ.
Задача 5. Будет ли наблюдаться фотоэффект, если работа выхода электрона из металла Дж, а свет имеет длину волны м?
Сравним работу выхода и минимальную энергию фотона. Если окажется, что работа выхода больше энергии фотона, то фотоэффект не будет происходить.
Так как , то фотоэффект будет наблюдаться.
Задача 6. Красная граница фотоэффекта для некоторого металла . Какова масса фотона, вызывающего фотоэффект?
Ответ: кг.
Задача 7. Для некоторого металла красная граница фотоэффекта Гц. Определить работу выхода электрона из этого металла.
В электронвольтах это
Ответ: Дж, или 1,78 эВ.
Лабораторная работа № 13 Определение красной границы фотоэффекта и работы выхода электрона из металла
88
Цель работы: изучение явления внешнего фотоэффекта, нахождение его красной границы и работы выхода электрона из металла.
1. Введение
Внешним фотоэффектом называется испускание электронов веществом под действием света. Энергетический баланс при фотоэффекте выражается уравнением Эйнштейна
, (1)
где hν – энергия светового кванта, переданная электрону; A – работа выхода электрона за пределы вещества; – максимальная кинетическая энергия освободившегося электрона. Уравнение (1) получено в предположении, что электромагнитное излучение представляет собой поток частиц, называемых фотонами. Фотон несет энергию, при этом он неделим и при взаимодействии отдает свою энергию полностью. Фотон обладает также импульсом. Фотоэффект можно рассматривать как процесс соударения фотона с электроном.
Уравнение (1) дает теоретическое обоснование законов фотоэффекта, экспериментально установленных Столетовым:
1) фототок насыщения пропорционален световому потоку;
2) максимальная скорость фотоэлектронов определяется частотой света и не зависит от его интенсивности;
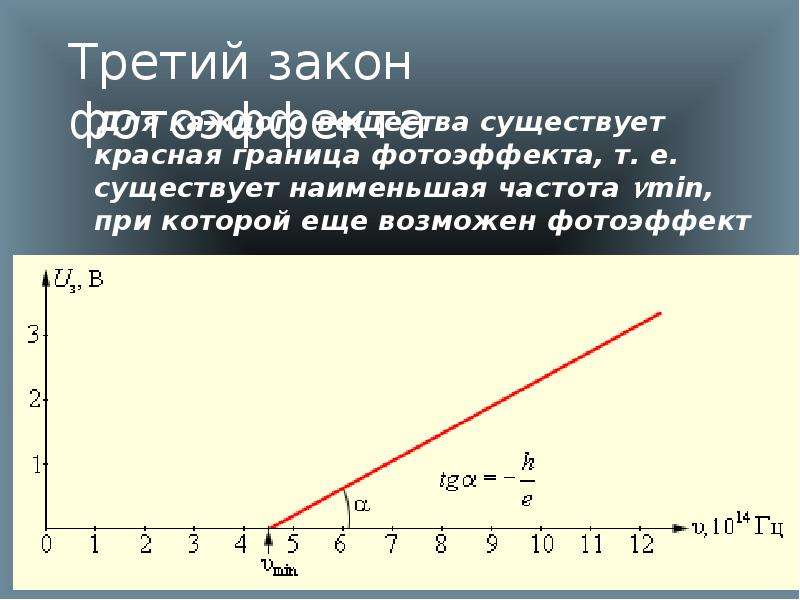
3) для каждой поверхности существует минимальная частота ν0 (красная граница фотоэффекта), ниже которой фотоэффект не возможен:
. (2)
Определив ν0 экспериментально, из формулы (2) можно найти работу выхода электронов A для данного вещества.
Простейшим
прибором для наблюдения фотоэффекта
является вакуумный фотоэлемент (рис.1).
Это откачанный стеклянный баллон, одна
половина которого покрыта изнутри
металлом, играющим роль фотокатода К. Анод А обычно выполняется в форме кольца или
шарика. Между катодом и анодом с помощью
батареи Б создается ускоряющая разность потенциалов.
При освещении катода он испускает
электроны, которые подхватываются полем
и попадают на анод. Цепь замыкается, и
в ней течет ток. В данной установке
использован фотоэлемент с катодом,
красная граница которого лежит в видимой
области спектра. Это позволяет использовать
в качестве источника света лампу
накаливания.
Анод А обычно выполняется в форме кольца или
шарика. Между катодом и анодом с помощью
батареи Б создается ускоряющая разность потенциалов.
При освещении катода он испускает
электроны, которые подхватываются полем
и попадают на анод. Цепь замыкается, и
в ней течет ток. В данной установке
использован фотоэлемент с катодом,
красная граница которого лежит в видимой
области спектра. Это позволяет использовать
в качестве источника света лампу
накаливания.
Один из способов определения работы выхода и красной границы фотоэффекта состоит в следующем. Поменяв полярность батареи Б (рис. 1), можно создать тормозящее поле, препятствующее попаданию электронов на анод А. При некоторой | Рис. 1 |
разности потенциалов Uзадер. ни одному из электронов, даже обладающему при вылете из катода К наибольшим значением скорости , не удастся достигнуть анодаА. Фототок прекращается. Это условие можно записать:
, (3)
Измерив задерживающее напряжение Uзадер и, зная частоту излучения , из формулы (1) можно найти работу выхода А, затем по формуле (2) определить красную границу фотоэффекта 0.
В данной работе для определения красной границы при неизменной ускоряющей разности потенциалов будем изменять частоту падающего излучения . При некоторой частоте 0 фототок должен прекратится. Однако этот метод требует более тщательного, хотя бы качественного анализа причин, определяющих величину фототока. Очевидно, что фототок при данной частоте излучения определяется числом фотонов
. (4)
(4)
Число фотонов в световом потоке Nфот() определяется излучательной способностью источника света R,T. Если предположить, что лампа накаливания излучает как чёрное тело (см. введение к работе 14), то её излучательная способность может быть представлена графиком, приведенным на рис. 2.
Рис. 2 | Рис. 3 |
Количество энергии, излучаемой лампой в области частот от до +, определяется площадью, заштрихованной на графике рис. 2: W= R,T·. Тогда число фотонов, излучаемых в интервале частот будет равно: .
В области низких частот справедлив закон Релея-Джинса, согласно которому R,T ~ 2. Следовательно, в этой области отношение , равное, будет пропорционально (рис. 3). В области ожидаемого значения красной границы,
Величина
второго сомножителя
в формуле (4) определяется многими
причинами. Одним из решающих факторов
является число электронов, взаимодействие
с которыми может привести к появлению
фототока. Электроны проводимости в
металле не могут самопроизвольно
покинуть вещество, так как металл
представляет для них потенциальную
яму.
тоном, энергия которого больше , электрон, находящийся вблизи уровня Ферми, покидает металл, обладая кинетической энергией. Однако такой фотон может выбить и электроны, лежащие ниже уровня Ферми (заштрихованная область на рис. 4). Число таких электронов пропорционально раз- | Рис. 4 |
ности , которая равна. Следовательно, вероятность выбивания электрона из металла.
В итоге, в формуле (4) число фотонов, испускаемых лампой накаливания в единицу времени в области частот, лежащих вблизи красной границы, остается величиной постоянной на разных частотах, а вероятность взаимодействия фотона с электроном пропорциональна разности частот . Следовательно, в области красной границы фототок пропорционален разности. При больших частотах фототок должен уменьшаться с ростом за счет уменьшения числа фотонов, излучаемых источником света в этой спек тральной области. Таким образом, ожидаемая зависимость фототока от частоты должна
иметь
вид представленный на рис. 5. Так как
при температуре T > 0 К распределение электронов вблизи
уровня Ферми размывается (электроны
переходят на уровни, лежащие выше
уровня Ферми), то и зависимость iф от
вблизи красной границы 0 будет размыта (пунктирная линия на
рис. Важно отметить, что, поскольку работа выхода $A_{вых}$ и масса электрона $m_e$ имеют некоторое положительное значение, а скорость электрона $v$ не может быть отрицательной, то и частота $nu$ будет иметь некоторое значение больше нуля. Минимальное значение будет достигаться, если $v=0$: $$nu_{min}={A_{вых}over h}$$ Частота $nu_{min}$ называется «красной границей фотоэффекта», а приведенное соотношение — это формула красной границы фотоэффекта. Если фотон имеет частоту ниже, то его энергии недостаточно для разрыва связей электрона с ядром, фотоэффект с таким фотоном невозможен. Термин «красная граница» был введен А. Столетовым, который провел наиболее глубокие исследования фотоэффекта в конце XIX в. Третий закон Столетова гласит, что для каждого вещества есть некоторая минимальная частота фотонов, ниже которой фотоэффект исчезает. Рис. 2. Законы фотоэффекта Столетова.
Рис. 3. Красный фонарь для фотопечати. Что мы узнали?Красная граница фотоэффекта — это минимальная частота, при которой наблюдается фотоэффект. Если частота излучения меньше, то энергии фотонов не хватает для совершения работы выхода, и фотоэффект исчезает. ПредыдущаяФизикаВнутренний фотоэффект – применение, формула и определение кратко Красная граница фотоэффекта — это… Что такое Красная граница фотоэффекта?
Wikimedia Foundation.
Смотреть что такое «Красная граница фотоэффекта» в других словарях:
Фотоэффект – онлайн-тренажер для подготовки к ЕНТ, итоговой аттестации и ВОУДФотоэффе́кт, Фотоэлектрический эффект – испускание электронов веществом под действием света (или любого другого электромагнитного излучения). В конденсированных (твердых и жидких) веществах выделяют внешний и внутренний фотоэффект. Законы Столетова для фотоэффекта Формулировка 1-го закона фотоэффекта: Сила фототока прямо пропорциональна плотности светового потока. Согласно 2-му закону фотоэффекта, максимальная кинетическая энергия вырываемых светом электронов линейно возрастает с частотой света и не зависит от его интенсивности. 3-й закон фотоэффекта: для каждого вещества существует красная граница фотоэффекта, то есть минимальная частота света \(v_0\) (или максимальная длина волны \(\lambda_0\)), при которой еще возможен фотоэффект, и если \(\nu<\nu_{красной \ границы}\) то фотоэффект уже не происходит. Теоретическое объяснение этих законов было дано в 1905 году Эйнштейном. Согласно ему, электромагнитное излучение представляет собой поток отдельных квантов (фотонов) с энергией \(hv\) каждый, где \(h\) – постоянная Планка. При фотоэффекте часть падающего электромагнитного излучения от поверхности металла отражается, а часть проникает внутрь поверхностного слоя металла и там поглощается. Исследования фотоэффекта были одними из самых первых квантовомеханических исследований. Фотоэффект — Всё для чайниковФотоэффект
Документальные учебные фильмы. Серия «Физика».
Фотоэлектрическим эффектом или фотоэффектом называется испускание электронов веществом под действием света. Это явление было открыто Г. Герцем в 1887 г. Он заметил, что проскакивание искры между шариками разрядника значительно облегчается, если один из шариков осветить ультрафиолетовыми лучами. В 1888—1889 гг. А. Г. Столетов подверг фотоэффект систематическому исследованию с помощью установки, схема которой показана на рис. 9.1. Конденсатор, образованный проволочной сеткой и сплошной пластиной, был включен последовательно с гальванометром G в цепь батареи. Свет, проходя через сетку, падал на сплошную пластину. В результате в цепи возникал ток, регистрировавшийся гальванометром. На основании своих опытов Столетов пришел к следующим выводам: 1) наибольшее действие оказывают ультрафиолетовые лучи; 2) сила тока возрастает с увеличением освещенности пластины; 3) испускаемые под действием света заряды имеют отрицательный знак, Спустя 10 лет (в 1898 г.) Ленард и Томсон, измерив удельный заряд испускаемых под действием света частиц, установили, что эти частицы являются электронами. Ленард и другие исследователи усовершенствовали прибор Столетова, поместив электроды в эвакуированный баллон [(рис. 9.2). Свет, проникающий через кварцевое1) окошко освещает катод К, изготовленный из исследуемого материала. Электроны, испущенные вследствие фотоэффекта, перемещаются под действием электрического поля к аноду А. В результате в цепи прибора течет фототок, измеряемый гальванометром G. Напряжение между анодом и катодом можно изменять с помощью потенциометра Я. Полученная на таком приборе вольт-амперная характеристика (т. е. кривая зависимости фототока I от напряжения между электродами U) приведена на рис. 9.3. Естественно, что характеристика снимается при неизменном потоке света Ф. Из этой кривой видно, что при некотором не очень большом напряжении фототок достигает насыщения — все электроны, испущенные катодом, попадают на анод. Следовательно, сила тока насыщения Iн определяется количеством электронов, испускаемых катодом в единицу времени под действием света. Пологий ход кривой указывает на то, что электроны вылетают из катода с различными по величине скоростями. Доля электронов, отвечающая силе тока при U = 0, обладает скоростями, достаточными для того, чтобы долететь до анода «самостоятельно», без помощи ускоряющего поля. Для обращения силы тока в нуль нужно приложить задерживающее напряжение Uз.При таком напряжении ни одному из электронов, даже обладающему при вылете из катода наибольшим значением скорости Um,не удается преодолеть задерживающее поле и достигнуть анода. Поэтому можно написать, что где т — масса электрона. Таким образом, измерив задерживающее напряжение Us, можно определить максимальное значение скорости фотоэлектронов. К 1905 г. было выяснено, что максимальная скорость фотоэлектронов не зависит от интенсивности света, а зависит только от его частоты — увеличение частоты приводит к возрастанию скорости. Установленные экспериментально зависимости не укладываются в рамки классических представлений. В 1905 г. А, Эйнштейн показал, что все закономерности фотоэффекта легко объясняются, если предположить, что свет поглощается такими же порциями hω (квантами), какими он, по предположению Планка, испускается. По мысли Эйнштейна, энергия, полученная электроном, доставляется ему в виде кванта hω, который усваивается им целиком. Часть этой энергии, равная работе выхода А1), затрачивается на то, чтобы электрон мог покинуть тело. Если электрон освобождается светом не у самой поверхности, а на некоторой глубине, то часть энергии, равная Е’, может быть потеряна вследствие случайных столкновений в веществе. Остаток энергии образует кинетическую энергию Ек электрона, покинувшего вещество. Энергия Ек будет максимальна, если E’ = 0. В этом случае должно выполняться соотношение которое называется формулой Эйнштейна. Фотоэффект и работа выхода в сильной степени зависят от состояния поверхности металла (в частности, от находящихся на ней окислов и адсорбированных веществ). Поэтому долгое время не удавалось проверить формулу Эйнштейна с достаточной точностью. В 1916 г. Милликен создал приборов котором исследуемые поверхности подвергались очистке в вакууме, после чего измерялась работа выхода и исследовалась зависимость максимальной кинетической энергии фотоэлектронов от частоты света (эта энергия определялась путем измерения задерживающего потенциала Us), Результаты оказались в полном согласии с формулой (9.2).
Подставив в формулу (9.2) измеренные значения А и (при данной ω), Милликен определил значение постоянной Планка h, которое оказалось совпадающим со значениями, найденными из спектрального распределения равновесного теплового излучения и из коротковолновой границы тормозного рентгеновского спектра. Дальнейшее усовершенствование методики исследования фотоэффекта было осуществлено в 1928 г. Из формулы (6.2) вытекает, что в случае, когда работа выхода А превышает энергию кванта hω, электроны не могут покинуть металл. Следовательно, для возникновения фотоэффекта необходимо выполнение условия , или Соответственно для длины волны получается условие Частота ω0 или длина волны λ0 называется красной границей фотоэффекта. Число высвобождаемых вследствие фотоэффекта электронов должно быть пропорционально числу падающих на поверхность квантов света. Вместе с тем световой поток Ф определяется количеством квантов света, падаюших на поверхность в единицу времени. В соответствии с этим ток насыщения Iн должен быть пропорционален падающему световому потоку: Эта зависимость также подтверждается экспериментально. Заметим, что лишь малая часть квантов передает свою энергию фотоэлектронам. Энергия остальных квантов затрачивается на нагревание вещества, поглощающего свет. В рассмотренном выше явлении фотоэффекта электрон получает энергию от одного лишь фотона. Такие процессы называются однофотонными. С изобретением лазеров были получены недостижимые до тех пор мощности световых пучков. Это дало возможность осуществить многофотонные процессы. В частности, был наблюден многофотонный фотоэффект, в ходе которого электрон, вылетающий из металла, получает энергию не от одного, а от N фотонов (N = 2, 3,4, 5). Формула Эйнштейна в случае многофотонного фотоэффекта выглядит следующим образом: Соответственно красная граница фотоэффекта смещается в сторону более длинных волн (λ0 увеличивается в N раз).
Уравнение фотоэффекта в физикеОпределение и уравнение фотоэффектаФотоэффект является одним из примеров проявления корпускулярных свойств света. Вылет электронов из освещенных тел, называется внешним фотоэффектом. Сущность внутреннего фотоэффекта состоит в том, что при освещении полупроводников и диэлектриков от некоторых атомов отрываются электроны, которые, однако, в отличие от внешнего фотоэффекта, не выходят через поверхность тела, а остаются внутри него. В результате внутреннего фотоэффекта возникают электроны в зоне проводимости и сопротивление полупроводников и диэлектриков уменьшается. При освещении границы раздела между полупроводниками с различным типом проводимости возникает электродвижущая сила. Это явление называется вентильным фотоэффектом. Уравнение Эйнштейна для внешнего фотоэффектаОсновным уравнением, описывающим внешний фотоэффект, является уравнение Эйнштейна для внешнего фотоэффекта:
где – энергия фотона монохроматической волны света, — масса электрона, — работа выхода электрона из фотокатода. Уравнение фотоэффекта (1) является следствием закона сохранения энергии. В соответствии с законами сохранения энергии и импульса, поглощение фотона свободными электронами невозможно, и фотоэффект возможен только на электронах, связанных в атомах, молекулах и ионах, а также на электронах твердых и жидких тел. Из уравнения фотоэффекта существует ряд важных выводов, которые характеризуют это явление:
Примеры решения задач
Фотоэлектрический эффект | Физика IIЦели обученияК концу этого раздела вы сможете:
Когда свет падает на материалы, он может выбрасывать из них электроны.Это называется фотоэлектрическим эффектом , что означает, что свет (фото , фото ) производит электричество. Одно из распространенных применений фотоэлектрического эффекта — это люксметры, например, те, которые регулируют автоматическую диафрагму на различных типах камер. Аналогичным образом, другое применение — солнечные элементы, которые вы, вероятно, использовали в своем калькуляторе или видели на крыше или на дорожных знаках. Они используют фотоэлектрический эффект для преобразования света в электричество для работы различных устройств. Рисунок 1.Фотоэлектрический эффект можно наблюдать, позволяя свету падать на металлическую пластину в этой откачанной трубке. Электроны, испускаемые светом, собираются на коллекторном проводе и измеряются как ток. Этот эффект известен уже более века и может быть изучен с помощью такого устройства, как показано на рисунке 1.На этом рисунке показана вакуумная трубка с металлической пластиной и коллекторным проводом, которые соединены источником переменного напряжения, причем коллектор более отрицательный, чем пластина. Когда свет (или другое электромагнитное излучение) попадает на пластину в откачанной трубке, она может выбрасывать электроны. Если энергия электронов в электрон-вольтах (эВ) превышает разность потенциалов между пластиной и проводом в вольтах, некоторое количество электронов будет собираться на проводе. Поскольку энергия электронов в эВ составляет эВ, , где q — заряд электрона, а В, — разность потенциалов, энергию электронов можно измерить, регулируя тормозящее напряжение между проводом и пластиной.Напряжение, при котором электроны не достигают провода, равно энергии в эВ. Например, если –3,00 В едва останавливает электроны, их энергия составляет 3,00 эВ. Количество выброшенных электронов можно определить, измерив ток между проводом и пластиной. Чем больше света, тем больше электронов; небольшая схема позволяет использовать это устройство в качестве экспонометра. Что действительно важно в фотоэффекте, так это то, что из него вывел Альберт Эйнштейн. Эйнштейн понял, что существует несколько характеристик фотоэлектрического эффекта, которые можно объяснить, только если ЭМ-излучение само квантовать : очевидно, непрерывный поток энергии в ЭМ-волне на самом деле состоит из квантов энергии, называемых фотонами.В своем объяснении фотоэлектрического эффекта Эйнштейн определил квантованную единицу или квант электромагнитной энергии, которую мы теперь называем фотоном , с энергией, пропорциональной частоте электромагнитного излучения. Рис. 2. Электромагнитная волна с частотой f состоит из фотонов или отдельных квантов электромагнитного излучения. Энергия каждого фотона составляет E = hf , где h — постоянная Планка, а f — частота электромагнитного излучения.Более высокая интенсивность означает больше фотонов на единицу площади. Фонарь излучает большое количество фотонов с множеством разных частот, следовательно, другие имеют энергию E ′ = hf ′ и так далее. Фотоэлектрический эффект имеет свойства, описанные ниже. Все эти свойства согласуются с идеей о том, что отдельные фотоны электромагнитного излучения поглощаются отдельными электронами в материале, при этом электрон получает энергию фотона. Некоторые из этих свойств несовместимы с представлением о том, что электромагнитное излучение представляет собой простую волну.
Рисунок 3.Фотоэлектрический эффект. График кинетической энергии выброшенного электрона, KE e , в зависимости от частоты электромагнитного излучения, падающего на определенный материал. Существует пороговая частота, ниже которой электроны не выбрасываются, потому что отдельный фотон, взаимодействующий с отдельным электроном, имеет недостаточную энергию, чтобы оторвать его. Выше пороговой энергии KE e линейно увеличивается с f , что соответствует KE e = hf — BE. Идея Эйнштейна о квантовании электромагнитного излучения сыграла решающую роль в зарождении квантовой механики. Это гораздо более общая концепция, чем может предполагать ее объяснение фотоэлектрического эффекта. Все ЭМ-излучение также можно моделировать в виде фотонов, и характеристики ЭМ-излучения полностью соответствуют этому факту.(Как мы увидим в следующем разделе, многие аспекты электромагнитного излучения, такие как опасность ультрафиолетового (УФ) излучения, можно объяснить только свойствами фотонов.) Более известный своей современной теорией относительности Эйнштейн заложил важное семя для квантовая механика в 1905 году, в том же году он опубликовал свою первую статью по специальной теории относительности. Его объяснение фотоэлектрического эффекта легло в основу Нобелевской премии, присужденной ему в 1921 году. Хотя в этой награде были отмечены и другие его вклады в теоретическую физику, специальная и общая теория относительности не были полностью признаны, несмотря на то, что были частично подтверждены экспериментом. к 1921 г.Хотя этот великий человек почитался как герой, он так и не получил Нобелевского признания за свою самую известную работу — относительность. Пример 1. Расчет энергии фотона и фотоэлектрического эффекта: фиолетовый свет1. Какова энергия в джоулях и электрон-вольтах у фотона фиолетового света с длиной волны 420 нм? 2. Какова максимальная кинетическая энергия электронов, выбрасываемых из кальция фиолетовым светом с длиной волны 420 нм, при условии, что энергия связи (или работа выхода) электронов для металлического кальция равна 2.71 эВ? Стратегия Чтобы решить часть 1, обратите внимание, что энергия фотона определяется как E = hf . Решение для Части 1Энергия фотона определяется как E = hf . Поскольку нам дается длина волны, а не частота, мы решаем знакомую зависимость c = fλ для частоты, получая [латекс] f = \ frac {c} {\ lambda} \\ [/ latex ].{-19} \ text {J}} = 2,96 \ text {eV} \\ [/ latex] Решение для Части 2Теперь определение кинетической энергии выброшенного электрона представляет собой простое приложение уравнения KE e = hf — BE. Подстановка энергии фотона и энергии связи дает KE e = hf — BE = 2,96 эВ — 2,71 эВ = 0,246 эВ. Обсуждение Энергия этого 420-нм фотона фиолетового света составляет крошечную долю джоуля, поэтому неудивительно, что нам было бы трудно ощутить непосредственно один фотон — люди больше настроены на энергии порядка джоуля. .Но глядя на энергию в электрон-вольтах, мы видим, что у этого фотона достаточно энергии, чтобы воздействовать на атомы и молекулы. Молекула ДНК может быть разрушена с помощью энергии около 1 эВ, а типичные атомные и молекулярные энергии имеют порядок эВ, так что УФ-фотон в этом примере может иметь биологические эффекты. Выброшенный электрон (так называемый фотоэлектрон ) имеет довольно низкую энергию, и он не улетит далеко, кроме как в вакууме. Электрон будет остановлен тормозящим потенциалом, равным нулю.26 эВ. Фактически, если бы длина волны фотона была больше, а его энергия была бы меньше 2,71 эВ, то формула дала бы отрицательную кинетическую энергию, что невозможно. Это просто означает, что фотоны с длиной волны 420 нм с их энергией 2,96 эВ ненамного превышают порог частоты. Вы можете сами убедиться, что пороговая длина волны составляет 459 нм (синий свет). Исследования PhET: фотоэлектрический эффектПосмотрите, как свет сбивает электроны с металлической мишени, и воссоздайте эксперимент, положивший начало квантовой механике. Щелкните, чтобы загрузить симуляцию. Запускать на Java. Сводка раздела
Концептуальные вопросы
Задачи и упражнения
Глоссарийфотоэлектрический эффект: явление, при котором некоторые материалы выбрасывают электроны, когда на них попадает свет фотон: квант или частица электромагнитного излучения энергия фотона: количество энергии фотона; E = hf энергия связи: также называется работой выхода; количество энергии, необходимое для выброса электрона из материала Избранные решения проблем и упражнения 1. 3. 3.69 эВ 5. 0,483 эВ 7. 2,25 эВ 9. (а) 264 нм; (б) Ультрафиолет 11. 1,95 × 10 6 м / с 13. (а) 4.02 × 10 15 с; (б) 0,256 мВт 15. (a) −1.90 эВ; (б) отрицательная кинетическая энергия; (c) Электроны будут выбиты. Фотоэлектрический эффектФотоэлектрический эффектПожалуйста, посмотрите анимацию 8.1: Фотоэлектрический эффект
Фотоэлектрический эффект — это наблюдение, что при определенных условиях свет, падающий на металлическую поверхность, может вызвать выброс электронов. В анимации энергия света увеличивается по мере перехода от красного к от оранжевого до желтого, до зеленого, а затем до синего. Уведомление как только зеленый и синий с более высокой энергией могут вызвать выброс электронов. Определение фотонов Эйнштейном происходит от этого фотоэлектрического эффекта и следующий эксперимент. Достаточно высокий разница напряжений создается между двумя металлическими частями. Наблюдения заключаются в следующем: Первоначально, когда пластины находятся в темноте, электроны не проходят. между пластинами и ток не течет. Когда мы светим светом на пластины, переходя от низкоэнергетического красного к высокоэнергетическому синий, внезапно начинает течь ток. Как? Эйнштейн объяснил результат описанием световых волн как пакетов энергия. Он назвал пакеты энергия фотонов. У каждого фотона есть удельная энергия, чем короче длина волны, тем выше энергия. Когда фотон высокой энергии попадает в пластину (например, зеленый или синий), фотон имеет достаточно энергии, чтобы выбить электрон, а затем и электрон, будучи отрицательный, полетит в положительную сторону.В в этот момент течет ток. Фотоны с более низкой энергией не могут узнать электроны и не имеют энергии может течь. Интересно отметить, что энергия рассматривается как частица или
пакет, это согласуется с фактом, что энергии не аддитивны. Что делать, если энергия фотона превышает пороговую, необходимую для вылета? электрон? Дополнительная энергия просто переходит в кинетическую энергию электрона. Это соотношение можно описать следующим уравнением. hf = ш + KE , где hf — энергия фотона. Вт — энергия, необходимая для удара электрона. KE — кинетическая энергия электрона. Если энергия фотона меньше w, электрон не испускается. Теория и расчет атомного фотоэффектаОсновные моменты
Abstract Так называемая элементарная теория атомного фотоэффекта представлена в форме, удобной для практического численного расчета сечений подоболочки и угловых распределений эмитируемых фотоэлектронов.Состояния атомов описываются в приближении независимых электронов со связанными и свободными одноэлектронными орбиталями, которые являются решениями уравнения Дирака с самосогласованным потенциалом Дирака – Хартри – Фока – Слейтера конфигурации основного состояния. Дан подробный вывод сечений подоболочки как для возбуждения на дискретные связанные уровни, так и для ионизации. В случае ионизации дифференциал поперечного сечения в направлении фотоэлектрона получается для частично поляризованных фотонов, причем поляризация задается с помощью параметров Стокса.Теоретические формулы были реализованы в компьютерной программе под названием photacs, которая рассчитывает таблицы сечений возбуждения и ионизации для любого элемента и подоболочки. Ключевые словаФотоэффект Сечения подоболочки Угловое распределение фотоэлектронов Поляризация фотонов Приближение независимых электронов Самосогласованный потенциал Дирака-Хартри-Фока-Слейтера (Рекомендуемые статьи) АннотацияCopyright © 2015 Авторы.Опубликовано Elsevier B.V. Рекомендуемые статьиЦитирующие статьиФормулы физики фотоэффектов. Фотоэффект. ФотоныФотоэлектрический эффект — это явление отрыва электронов от металла (внешний) Фотоэлектрический эффект — это испускание электронов веществом под действием света (или любого другого электромагнитного излучения). В конденсированных веществах (твердых и жидких) различают внешние и внутренние фотоэлектрические эффекты. Внешний фотоэлектрический эффект (фотоэлектронная эмиссия) — это испускание электронов веществом под действием электромагнитного излучения. Электроны, испускаемые веществом во время внешнего фотоэлектрического эффекта, называются фотоэлектронами, а электричество, образованное ими при упорядоченном движении во внешнем электрическом поле, называется фототоком. Внутренний фотоэффект — это перераспределение электронов по энергетическим состояниям в твердых и жидких полупроводниках и диэлектриках, происходящее под действием излучения.Он проявляется в изменении концентрации носителей заряда в среде и приводит к появлению фотопроводимости или безвентиляторного фотоэффекта. Фотопроводимость — это увеличение электропроводности вещества под действием излучения. Фотоэлектрический эффект затвора — это тип внутреннего фотоэлектрического эффекта, который представляет собой возникновение ЭДС (фото-ЭДС) при освещении контакта двух разных полупроводников или полупроводника и металла (при отсутствии внешнего электрического поля). фотоэлектрический эффект открывает путь прямого преобразования солнечной энергии в электрическую. Многофотонный фотоэлектрический эффект возможен при очень большой интенсивности света (например, при использовании лазерных лучей). В этом случае испускаемый металлом электрон может одновременно получать энергию не от одного, а от нескольких фотонов. Законы Столетова Первый закон Фототок насыщения пропорционален световому потоку, падающему на металл. T.k. сила тока определяется величиной заряда, а световой поток определяется энергией светового луча, то можно сказать: число электронов, выбитых из вещества за 1 с, пропорционально интенсивности света, падающего на это вещество. Второй закон Путем изменения условий освещения на той же установке А.Г. Столетов открыл второй закон фотоэффекта: кинетическая энергия фотоэлектронов не зависит от интенсивности падающего света, а зависит от его частоты. Из опыта следует, что если увеличить частоту света, то при постоянном световом потоке увеличивается блокирующее напряжение, а, следовательно, увеличивается и кинетическая энергия фотоэлектронов. Таким образом, кинетическая энергия фотоэлектронов линейно увеличивается с частотой света. Третий закон Заменив в устройстве материал фотокатода, Столетов установил третий закон фотоэффекта: для каждого вещества существует красная граница фотоэффекта, т.е.е. существует наименьшая частота nmin, при которой фотоэлектрический эффект все еще возможен. Закон сохранения энергии, записанный Эйнштейном для фотоэлектрического эффекта, состоит в утверждении, что энергия фотона, приобретенная электроном, позволяет ему покинуть поверхность проводника, совершив работу выхода. Остальная энергия реализуется в виде кинетической энергии теперь свободного электрона Энергия падающего фотона расходуется на электрон, выполняющий работу вывода A из металла, и на передачу кинетической энергии mv2max / 2 испускаемому фотоэлектрону.Согласно закону сохранения энергии, (203,1) Уравнение (203.1) называется уравнением Эйнштейна для внешнего фотоэлектрического эффекта. Эффект Комптона Изменение длины волны света при рассеянии на связанных электронах ОПЫТ РЕЗЕРФОРДА. МОДЕЛЬ ПЛАНЕТАРНОГО АТОМА Эксперименты Резерфорда. Масса электронов в несколько тысяч раз меньше массы атомов. Поскольку атом в целом нейтрален, следовательно, основная масса атома приходится на его положительно заряженную часть. Для экспериментального изучения распределения положительного заряда и, следовательно, массы внутри атома Эрнест Резерфорд в 1906 году предложил использовать зондирование атома с помощью β-частиц. Эти частицы возникают при распаде радия и некоторых других элементов. Их масса примерно в 8000 раз больше массы электрона, а положительный заряд по модулю равен удвоенному заряду электрона. Это не что иное, как полностью ионизированные атомы гелия. Скорость частиц очень высока: это 1/15 скорости света. Резерфорд бомбардировал атомы тяжелых элементов этими частицами. Из-за своей малой массы электроны не могут заметно изменить траекторию частицы, так же как камешек весом в несколько десятков граммов при столкновении с автомобилем не может существенно изменить его скорость. Модель планетарного атома. На основе своих экспериментов Резерфорд создал планетарную модель атома. В центре атома находится положительно заряженное ядро, в котором сосредоточена почти вся масса атома.В общем, атом нейтрален. Следовательно, количество внутриатомных электронов, как и заряд ядра, равно порядковому номеру элемента в периодической системе. Понятно, что электроны внутри атома не могут отдыхать, так как они упадут на ядро. Они движутся вокруг ядра, как планеты вращаются вокруг Солнца. Такой характер движения электронов определяется действием сил кулоновского притяжения со стороны ядра. Фотоэлектрический эффект Он был открыт в 1887 году немецким физиком Г.Герца и в 1888-1890 гг. Экспериментально исследовал А. Г. Столетов. Наиболее полное исследование фотоэффекта было проведено Ф. Ленардом в 1900 г. К тому времени уже был открыт электрон (1897 г., Дж. Томсон), и стало ясно, что фотоэлектрический эффект (а точнее, внешний фотоэлектрический эффект) заключается в удалении электронов из вещества под действием падающего на него света. Схема экспериментальной установки для исследования фотоэффекта представлена на рис.5.2.1. В экспериментах использовался стеклянный вакуумный цилиндр с двумя металлическими электродами, поверхность которого тщательно очищалась. Некоторое напряжение подавалось на электроды U , полярность которых могла быть изменена с помощью двойного ключа. Один из электродов (катод К) освещался через кварцевое окно монохроматическим светом некоторой длины волны λ. При постоянном световом потоке зависимость силы фототока I снималась от приложенного напряжения. На рис.5.2.2 приведены типичные кривые такой зависимости, полученные для двух значений интенсивности падающего на катод светового потока. Кривые показывают, что при достаточно высоких положительных напряжениях на аноде A фототок достигает насыщения, так как все электроны, оторванные светом от катода, достигают анода. Тщательные измерения показали, что ток насыщения I n прямо пропорционален интенсивности падающего света. Когда напряжение на аноде отрицательное, электрическое поле между катодом и анодом замедляет движение электронов.До анодов могут добраться только те электроны, кинетическая энергия которых превышает | eU |. Если напряжение на аноде меньше — U ч, фототок прекращается. Измерив U h, можно определить максимальную кинетическую энергию фотоэлектронов: К удивлению ученых величина U h оказалась независимой от интенсивности падающего светового потока. Тщательные измерения показали, что блокирующий потенциал линейно возрастает с увеличением частоты света ν (рис.5.2.3). Многочисленные экспериментаторы установили следующие основные законы фотоэлектрического эффекта: 1. Максимальная кинетическая энергия фотоэлектронов линейно возрастает с увеличением частоты света ν и не зависит от его интенсивности. 2. Для каждого вещества существует так называемый фотоэффект с красной рамкой , т. Е. Наименьшая частота ν min, при которой еще возможен внешний фотоэффект. 3. Количество фотоэлектронов, вытягиваемых светом из катода за 1 с, прямо пропорционально интенсивности света. 4. Фотоэффект практически безынерционен, фототок появляется сразу после засветки катода при условии, что частота света ν> ν min. Все эти законы фотоэффекта в корне противоречили представлениям классической физики о взаимодействии света с веществом. Согласно волновым представлениям, при взаимодействии с электромагнитной световой волной электрон должен постепенно накапливать энергию, и в зависимости от интенсивности света электрону потребуется значительное время, чтобы накопить достаточно энергии, чтобы вылететь из катода.Как показывают расчеты, это время следовало исчислять в минутах или часах. Однако опыт показывает, что фотоэлектроны появляются сразу после того, как катод начинает светиться. В этой модели также было невозможно понять существование красной границы фотоэффекта. Волновая теория света не могла объяснить независимость энергии фотоэлектронов от интенсивности светового потока и пропорциональность максимальной кинетической энергии частоте света. Таким образом, электромагнитная теория Светы не смогла объяснить эти закономерности. Выход был найден А. Эйнштейном в 1905 году. Теоретическое объяснение наблюдаемых закономерностей фотоэлектрического эффекта было дано Эйнштейном на основе гипотезы М. Планка о том, что свет излучается и поглощается определенными порциями, а энергия каждая такая часть определяется по формуле E = h ν, где h — постоянная Планка. Эйнштейн сделал следующий шаг в развитии квантовых представлений.Он пришел к выводу, что свет имеет прерывистую (дискретную) структуру . Электромагнитная волна состоит из отдельных частей — квантов , впоследствии названных фотонами . При взаимодействии с веществом фотон передает всю свою энергию целиком h ν одному электрону. Электрон может рассеять часть этой энергии при столкновении с атомами вещества. Кроме того, часть энергии электронов расходуется на преодоление потенциального барьера на границе металл-вакуум.Для этого электрон должен совершить работу на выходе A в зависимости от свойств материала катода. Наибольшая кинетическая энергия, которую может иметь фотоэлектрон, испускаемый катодом, определяется законом сохранения энергии: Эта формула называется уравнением Эйнштейна для фотоэлектрического эффекта . Используя уравнение Эйнштейна, можно объяснить все законы внешнего фотоэлектрического эффекта.Из уравнения Эйнштейна следует линейная зависимость максимальной кинетической энергии от частоты и независимость от интенсивности света, наличие красной границы и инерция фотоэлектрического эффекта. Общее количество фотоэлектронов, покидающих поверхность катода за 1 с, должно быть пропорционально количеству фотонов, падающих на поверхность за то же время. Из этого следует, что ток насыщения должен быть прямо пропорционален интенсивности светового потока. Как следует из уравнения Эйнштейна, наклон прямой, выражающей зависимость запирающего потенциала U h от частоты ν (рис.5.2.3), равно отношению постоянной Планка h к заряду электрона e : Это позволяет экспериментально определить значение постоянной Планка. Такие измерения были выполнены в 1914 г. Р. Милликеном и хорошо согласуются с величиной, найденной Планком. Эти измерения также позволили нам определить работу выхода A : , где c — скорость света, λ kr — длина волны, соответствующая красной границе фотоэлектрического эффекта.У большинства металлов работа выхода A составляет несколько электрон-вольт (1 эВ = 1,602 · 10 -19 Дж). В квантовой физике электрон-вольт часто используется как единица измерения энергии. Значение постоянной Планка, выраженное в электрон-вольтах в секунду, составляет .Среди металлов щелочные элементы имеют наименьшую работу выхода. Например, в натрии A = 1,9 эВ, что соответствует красной границе фотоэффекта λ кр ≈ 680 нм. Поэтому соединения щелочных металлов используются для создания катодов в фотоэлементах предназначен для регистрации видимого света. Итак, законы фотоэлектрического эффекта показывают, что свет при испускании и поглощении ведет себя как поток частиц, называемых фотонами или кванты света . Энергия фотона равна следует, что фотон имеет импульс Таким образом, учение о свете, совершив двухвековую революцию, снова вернулось к концепции световых частиц — корпускул. Но это не было механическим возвратом к корпускулярной теории Ньютона.В начале 20 века стало ясно, что свет имеет двойственную природу. При распространении света у него проявляются волновые свойства (интерференция, дифракция, поляризация), а при взаимодействии с веществом — корпускулярные (фотоэлектрический эффект). Эта двойственная природа света называется дуальностью волна-частица , о котором говорил Ломоносов. Двойственная природа была позже открыта электронами и другими. элементарные частицы. Классическая физика не может дать наглядную модель сочетания волновых и корпускулярных свойств в микрообъектах.Движение микрообъектов контролируется не законами классической механики Ньютона, а законами квантовой механики. Теория излучения черного тела, разработанная М. Планком, и квантовая теория фотоэлектрического эффекта Эйнштейна лежат в основе этой современной науки. Одним из явлений, подтверждающих гипотезу фотонов , является фотоэлектрический эффект . Основное влияние на характер протекания фотоэффекта оказывают свойства облучаемого материала (проводник, полупроводник, диэлектрик), а также энергия фотона, так как для каждого материала существует минимальное значение фотона энергия, при которой фотоэлектрический эффект прекращается.
Рис. 2.4. Генрих Рудольф Герц (1857–1894) Явление фотоэлектрического эффекта было впервые замечено Г. Герцем в 1887 году. Суть явления состоит в том, что при освещении ультрафиолетовыми лучами металлическое тело теряет электроны. Фотоэлектрический эффект можно наблюдать, например, когда свет освещает электрическую дугу цинковой пластины, подключенной к электрометру (см. Рис. 2.5). Фиг.2.5. Зажигание заряженной цинковой пластины светом электрической дуги: Если цинковая пластина заряжена отрицательно, то при облучении электрометр быстро разряжается. Если пластина заряжена положительно, то при облучении ее заряд не меняется.
Рис. 2.6. Александр Григорьевич Столетов (1839–1896)
Фиг.2.7. Филип Эдвард Антон фон Ленард (1862–1947) Первые количественные исследования фотоэффекта принадлежат русскому физику А.Г. Столетову, установившему основные законы фотоэффекта. Рис. 2.8. Описание опыта Столетов А.Г. «Два металлических диска (« арматура »,« электроды ») диаметром 22 см были установлены вертикально и параллельно друг другу перед электрической лампой Дубоска, из которой были вынуты все очки.В фонаре была лампа с дугой А. Один из дисков, примыкающих к фонарю, был сделан из тонкой металлической сетки, латуни или железа, иногда покрытой другим металлом, натянутым в круглое кольцо; другой твердый диск (металлическая пластина) »[Столетов А.Г. Избранные сочинения / Под ред. А.К. Тимирязев.- М .; Л .: Гос. изд. тех.-теор. лит., 1950. — 660 с.]. Измерения проводились зеркальным гальванометром G, источником тока служили гальванические батареи разного количества элементов. Позже установка Столетова была усовершенствована F.E.A. Ленард (Нобелевская премия 1905 г. за исследование катодных лучей) и другие исследователи (рис. 2.2).
Рис. 2.9. Схема экспериментов по исследованию внешнего фотоэффекта Свет, проникая через кварцевое окно К в (кварц пропускает ультрафиолетовые лучи), освещает катод ТО , сделанный из исследуемого материала.Электроны, испускаемые за счет фотоэлектрического эффекта, перемещаются под действием электрического поля к аноду НО . В цепи возникает фототок, измеряемый миллиамперметром. С помощью потенциометра P можно изменять напряжение между катодом и анодом, которое показывает вольтметр В . Исследования привели к установлению следующих основных законов фотоэлектрического эффекта:
Проанализируем вольт-амперную характеристику (т.е. зависимость фототока I от напряжения между электродами U) , полученную в результате фотоэлектрического эффекта. Из кривой на рис. Рисунок 2.10 показывает, что при некотором напряжении фототок достигает насыщения — все электроны, испускаемые катодом, попадают на анод.
Рис. 2.10. Вольт-амперная характеристика фотоэффекта Следовательно, сила тока насыщения определяется количеством электронов, испускаемых катодом в единицу времени под действием света. Следовательно, сила фототока насыщения прямо пропорциональна световому потоку где k — коэффициент пропорциональности , характеризующий «чувствительность» данного вещества к свету.
Рис. 2.11. Зависимость силы фототока насыщения от светового потока Анализ кривой показывает, что электроны вылетают из катода с разной скоростью. Часть электронов имеет достаточные скорости, чтобы при U = 0 лететь к аноду «самостоятельно» и создавать фототок без помощи ускоряющего поля. Чтобы обнулить фототок, необходимо приложить некоторое напряжение задержки .По величине разности тормозных потенциалов , при котором фототок исчезает, мы можем определить скорость самых быстрых фотоэлектронов: где масса, величина заряда ( e> 0 ) и максимальная скорость этих электронов. Экспериментально установлено, что максимальная скорость фотоэлектронов не зависит от интенсивности света, а зависит только от частоты облучения.Растущая линейная зависимость на рис. 2.4 указывает на то, что увеличение частоты приводит к увеличению максимальной скорости фотоэлектронов.
Фиг.2 .4 . Зависимость напряжения задержки от частоты Это подопытное зависимость не укладывается в рамки классической электродинамики, поскольку скорость фотоэлектронов согласно классическим представлениям должна зависеть от интенсивности электромагнитной волны, а не от ее частоты. В 1905 году А. Эйнштейн показал, что все законы фотоэлектрического эффекта легко объяснимы, если предположить, что свет распространяется и поглощается одними и теми же порциями (квантами) , поскольку он, согласно Планку, испускается. Взаимодействуя с электроном вещества, фотон может обмениваться с ним энергией и импульсом. Фотоэлектрический эффект возникает при неупругом столкновении фотона с электроном. При таком столкновении фотон поглощается, а его энергия передается электрону.Таким образом, электрон приобретает кинетическую энергию не постепенно, а сразу — в результате однократного столкновения. Этим объясняется инерция фотоэффекта. Рис. 2.13. Схема возникновения фотоэффекта в металле под действием падающих фотонов Энергия, полученная электроном, передается ему в виде кванта. Электрон тратит часть этой энергии, чтобы «ускользнуть» из металла. Каждый материал имеет свой собственный результат работы A ВЫХОД Остальная энергия фотона преобразуется в кинетическую энергию TO электрон.Кинетическая энергия максимальна, если электрон образуется у поверхности вещества и не расходует энергию при случайных столкновениях в веществе. В этом случае будет выполняться коэффициент Эйнштейна для фотоэффекта (2.7). Нобелевская премия по физике 1921 года была присуждена Эйнштейну за его «важные физико-математические исследования и — особенно за открытие законов фотоэлектрического эффекта ».(Знаменитая теория относительности даже не упоминается в приведенной выше формулировке). Уравнение Эйнштейна объясняет законы фотоэлектрического эффекта. Действительно, из соотношения Эйнштейна прямо следует, что максимальная кинетическая энергия фотоэлектрона линейно возрастает с увеличением частоты падающего излучения и не зависит от его интенсивности. Поскольку кинетическая энергия фотоэлектронов уменьшается с уменьшением частоты падающего света (для данного катодного вещества A OUT постоянная), то при достижении определенной критической частоты кинетическая энергия фотоэлектронов становится равной нулю и фотоэлектрический эффект прекращается. По Эйнштейну частота представляет фотоэффект с красной рамкой для данного вещества. Он зависит только от работы выхода электрона, то есть от химической природы вещества и состояния его поверхности. Используя выражение (2.8) для красной границы и соотношение (2.6), перепишем уравнение Эйнштейна в виде , что объясняет экспериментальную линейную зависимость (см.рис.2.4) запаздывающего потенциала от частоты падающего электромагнитного излучения. Таким образом, согласно Эйнштейну, свет с частотой w не только излучается, как предполагал Планк, но также распространяется в пространстве и поглощается материей отдельными порциями (квантами), энергия которых В 1914 году были проведены модифицированные эксперименты по фотоэлектрическому эффекту: лучи направлялись на металлическую пыль, помещенную в конденсатор. Фотоэффект происходит практически мгновенно: при столкновении пылинки с фотонами из нее выбиваются электроны, пылинка приобретает заряд и начинает двигаться в поле конденсатора.Движение пылевых частиц наблюдалось сразу после включения источника радиация. Если , если бы излучение было классической электромагнитной волной, тогда волна заняла бы довольно заметное время в эксперименте, чтобы раскачать электроны, сообщить им энергию, равную работу выхода и, таким образом, вырвать их из пыли. Отсутствие такой задержки наглядно продемонстрировало корпускулярную природу фотоэффекта. Эффект от устройств называется фотоэлементами .На рис. 2.14 показано устройство вакуумного фотоэлемента.
Рис. 2.14. Вакуумный фотоэлемент На внутреннюю поверхность металлического цилиндра нанесен фоточувствительный слой, служащий катодом. Он подключен к отрицательному полюсу источника тока. В центре цилиндра помещено проволочное кольцо, служащее анодом. Анод подключается к положительному полюсу источника тока. Свет проникает через прозрачное окно в передней стенке контейнера и, проходя через проволочное кольцо, сбивает фотоэлектроны с катода.Под действием электрического поля фотоэлектроны движутся к аноду, цепь замыкается и через нее начинает течь ток. I f . Если на пути световых лучей появится непрозрачный барьер, то свет перестанет попадать на катод, прекратится излучение фотоэлектронов и прервется ток в цепи. В этом случае сработает то или иное реле, подключенное к записывающему устройству. Рис. 2.15. Солнечные батареи на международной космической станции.При освещении области контакта различных полупроводников появляется фото-ЭДС, позволяющая преобразовывать световую энергию в электрическую. Фотоэлементыявляются основной частью различных фотоэлементов , которые широко используются в промышленности. С помощью фотореле можно управлять различными приборами и установками, включая и выключая их автоматически при включении света фотоэлемента или, наоборот, при его выключении. Пример 1 На поверхность лития падает монохроматический свет с длиной волны.Чтобы остановить эмиссию электронов, необходимо применить задерживающую разность потенциалов не менее c — скорости света в вакууме. Тогда уравнение Эйнштейна принимает вид Решив ее, находим скорость электронов , что действительно близко к скорости света в вакууме . Называется совокупность методов измерения температуры тел, основанных на законах теплового излучения. Используемые для этого устройства называются пирометрами. Эти методы очень удобны для измерения температуры различных объектов, где сложно или невозможно использовать традиционные контактные датчики. В первую очередь это относится к измерению высоких температур. В оптической пирометрии различают следующие температуры тела: излучение (когда измерение проводится в широком диапазоне длин волн), цвет (когда в узком интервале — интервал видимого света), яркость (на одной длине волны). . 1. Температура излучения T r — это температура черного тела, при которой его энергия светимости R равна энергии светимости R m данного тела в широком диапазоне длин волн. Если мы измеряем мощность, излучаемую некоторым телом с единичной поверхности в достаточно широком диапазоне волн и сравнивая ее значение с энергетической светимостью полностью черного тела, то по формуле (11) мы можем вычислить температуру этого тело как Определенная таким образом температура T p будет достаточно точной, чтобы соответствовать истинной температуре T , только если исследуемый объект полностью черный. Для серого тела закон Стефана-Больцмана можно записать как R m (T) = α T σT 4; Где α T Подставляя это выражение в формулу (1), получаем Для серого тела занижено значение радиационной температуры ( T p T), т.е. истинная температура серого тела всегда выше радиационной. 2. Цветовая температура T c — это температура черного тела, при которой относительные распределения спектральной плотности энергетической светимости этого тела и рассматриваемого тела максимально близки в видимой области спектра. Обычно для определения цветовой температуры выбираются длины волн λ 1 = 655 нм (красный), λ 2 = 470 нм (зелено-синий). Спектральная плотность энергетической светимости серых тел (или тел близких к ним по свойствам) с точностью до постоянного отношения (коэффициента монохроматического поглощения) пропорциональна спектральной плотности энергетической светимости полностью черного тела. Следовательно, распределение энергии в спектре серого тела такое же, как в спектре полностью черного тела при той же температуре. Для определения температуры серого тела достаточно измерить мощность I (λ, T) , излучаемую единичной поверхностью тела в достаточно узком спектральном диапазоне (пропорционально r (λ, T) ) , для двух разных волн. Отношение I (λ, T) для двух длин волн равно отношению зависимостей f (λ, T) для этих волн, вид которого задается формулой (2) предыдущего абзаца: ( 2) Из этого равенства математически можно получить температуру T .Полученная таким образом температура называется цветом. Цветовая температура тела, определяемая по формуле (2), будет соответствовать истинной. Цветовая температура серого тела, совпадающая с истинной, также может быть найдена из закона смещения Вина. 3. Яркостная температура (T i) температура черного тела, при которой его спектральная плотность светимости энергии f (λ, T) для любой конкретной длины волны равна спектральной плотности светимости энергии r (λ, T) данного тела для той же самой длина волны. Так как для не-черного тела спектральная плотность энергии светимости при определенной температуре всегда будет ниже, чем у полностью черного тела, истинная температура тела всегда будет выше, чем яркость. В качестве пирометра яркости используется пирометр затухания . Принцип определения температуры основан на визуальном сравнении яркости накаливания лампы накаливания пирометра с яркостью изображения исследуемого объекта.Равенство яркости наблюдается через монохроматический фильтр (обычно измерения проводятся на длине волны λ = 660 нм), определяется по исчезновению изображения резьбы пирометрической лампы на фоне изображения горячего объекта. Нить накаливания лампы пирометра регулируется реостатом, а температура нити накала определяется калибровочной кривой или таблицей. Предположим, что в результате измерений получено равенство яркостей нити пирометра и исследуемого объекта и определена температура нити пирометра по графику T 1 .Тогда на основании формулы (3) можно записать: f (λ, T 1) α 1 (λ, T 1) = f (λ, T 2) α 2 (λ, T 2) , , где α 1 (λ, T 1) и α 2 (λ, T 2) — коэффициенты монохроматического поглощения материала нити пирометра и исследуемого объекта соответственно. T 1 и T 2 — температура резьбы пирометра и объекта. Как видно из этой формулы, равенство температур объекта и нитей пирометра будет наблюдаться только при равенстве их коэффициентов монохроматического поглощения в наблюдаемой области спектра α 1 (λ, T 1) = α 2 (λ, T 2) .Если α 1 (λ, T 1) > α 2 (λ, T 2) , получаем заниженное значение температуры объекта, с обратным соотношением — завышенное значение температуры. Внешний фотоэффект Называется явление эмиссии электронов веществом под действием электромагнитного излучения. Внутренний фотоэффект Явление, называемое появлением свободных электронов в веществе (полупроводниках) под действием электромагнитного излучения.Связанные (или валентные) электроны становятся свободными (внутри вещества). В результате сопротивление вещества снижается. Законы внешнего фотоэффекта : 1. При постоянном спектральном составе излучения сила тока насыщения (или количество фотоэлектронов, испускаемых катодом в единицу времени) прямо пропорциональна потоку излучения (интенсивности излучения), падающему на фотокатод. 2. Для данного фотокатода максимальная начальная скорость фотоэлектронов и, следовательно, их максимальная кинетическая энергия определяется частотой излучения и не зависит от его интенсивности. 3. Для каждого вещества существует красная граница фотоэффекта, т.е. минимальная частота излучения ν 0, , в котором еще возможен внешний фотоэлектрический эффект. Отметим, что значение ν 0 зависит от материала фотокатода и состояния его поверхности. Объяснение внешнего фотоэффекта с точки зрения теории волн света противоречило экспериментальным данным. Согласно волновой теории, под действием поля электромагнитной волны в металле возникают вынужденные колебания электронов в атоме с амплитудой тем больше, чем больше амплитуда вектора электрического поля волны E o (и, следовательно, интенсивность света I ~ E o 2). В результате этого электроны могут покидать металл и покидать его, т.е. может наблюдаться внешний фотоэффект. Чем выше должна быть скорость испускаемых электронов, т.е. кинетическая энергия фотоэлектронов должна зависеть от интенсивности излучения, что противоречит экспериментальным данным. Согласно этой теории, излучение любой частоты, но достаточно высокой интенсивности должно вытягивать электроны из металла, т.е. не должно быть красной границы для фотоэффекта. А. Эйнштейн в 1905 г. показал, что явление фотоэлектрического эффекта и его законы можно объяснить на основе квантовой теории М. Планка. Согласно Эйнштейну, свет (излучение) с частотой ν не только испускается, как предполагал М. Планк, но также распространяется в пространстве и поглощается веществом отдельными порциями (квантами), энергия которых Е о = hν , (1) где h = 6,626176 * 10-34 Дж × с — постоянная Планка, Позже кванты излучения были названы фотонами .Согласно Эйнштейну, каждый квант поглощается только одним электроном. Если энергия кванта больше работы выхода электрона из металла, т.е. hν> = A o , то электрон может покинуть поверхность металла. Остальная часть энергии кванта используется для создания кинетической энергии электрона, покинувшего вещество. Если электрон высвобождается излучением не на самой поверхности, а на определенной глубине, то часть полученной энергии может быть потеряна из-за случайных столкновений электрона в веществе, и его кинетическая энергия будет меньше.Следовательно, энергия кванта излучения, падающего на вещество, расходуется на электрон для выполнения работы вывода и передачи кинетической энергии испускаемого фотоэлектрона. Закон сохранения энергии для такого процесса будет выражаться равенством (2) Это уравнение называется уравнением Эйнштейна для внешнего фотоэлектрического эффекта . Непосредственно из уравнения Эйнштейна следует, что максимальная кинетическая энергия или скорость фотоэлектрона зависит от частоты излучения.С уменьшением частоты излучения кинетическая энергия уменьшается и на определенной частоте может стать равной нулю. Уравнение Эйнштейна в этом случае будет иметь вид ч ν 0 = А вых. Частота ν 0, соответствующая этому отношению, будет иметь минимальное значение и является красной границей фотоэффекта. Из последнего видно, что красная граница фотоэффекта определяется работой выхода электрона и зависит от химической природы вещества и состояния его поверхности.Длину волны, соответствующую красной границе фотоэффекта, можно рассчитать по формуле . При hνF. С изобретением лазеров были получены большие мощности излучения, в этом случае один электрон может поглотить два и более (N) фотонов (N = 2 … 7). Это явление называется многофотонным (нелинейным) фотоэлектрическим эффектом. Уравнение Эйнштейна для многофотонного фотоэффекта имеет вид В этом случае красная граница фотоэффекта может смещаться в сторону более длинных волн. Характер зависимости фототока I от разности потенциалов между анодом и катодом U (вольт-амперная характеристика или ВАХ) при постоянном потоке излучения на фотокатод монохроматического излучения показан на рис.1. Наличие фототока при напряжении U = 0 из-за того, что эмитируемые катодом фотоэлектроны имеют определенную начальную скорость и, соответственно, кинетическую энергию, а значит, могут достигать анода без внешнего электрического поля.По мере увеличения значения U (в случае положительного потенциала на аноде) фототок постепенно увеличивается, т.е. все большее количество фотоэлектронов достигает анода. Плоский характер этого участка вольт-амперной характеристики указывает на то, что электроны вылетают из катода с разной скоростью. Максимальное значение фототока, называемое током насыщения I us , достигается при этом значении U , при котором все электроны, испускаемые катодом, попадают на анод.Стоимость I мс. определяется количеством фотоэлектронов, испускаемых катодом на 1 с , и зависит от величины потока излучения, падающего на фотокатод. Если анод имеет отрицательный потенциал, генерируемое электрическое поле препятствует движению фотоэлектронов. Это приводит к уменьшению количества электронов, достигающих анода, и, как следствие, к уменьшению фототока. Минимальное значение напряжения отрицательной полярности, при котором ни один из электронов, даже имея максимальную скорость, когда он покидает катод, не может достичь анода, т.е.е. фототок становится равным нулю, что называется напряжением удержания U o. Значение удерживающего напряжения связано с начальной максимальной кинетической энергией электронов соотношением С учетом этого, уравнение Эйнштейна также можно записать в виде hν = A o + eU 0 . Если изменить величину потока излучения, падающего на катод с тем же спектральным составом, то вольт-амперные характеристики будут иметь вид, показанный на рис.2. Если при постоянном значении потока излучения изменить его спектральный состав, т.е. частоту излучения, то вольт-амперные характеристики изменятся, как показано на рис. 3. U 0 0 U U 03 U 02 U 01 0 U F 3> F 2> F 1 n = const n 3> n 2> n 1 F = const Воздействие излучения на электрические процессы называется фотоэлектрическим эффектом или фотоэффектом. Различают внешний и внутренний фотоэффект. Внешний фотоэлектрический эффект называется испусканием электронов из вещества под действием излучения. Большие достижения в изучении фотоэффекта принадлежат русскому ученому Столетову. В опытах Столетова свет через сетчатый электрод попадал на непрерывный, вытягивал из него электроны, которые попадали на сетчатый электрод, и в цепи возникал ток. С увеличением напряжения ток в цепи увеличивается и достигает насыщения.Если увеличить световой поток, то ток насыщения будет больше. Эти эксперименты позволили установить 1-й закон внешнего фотоэффекта : Фототок насыщения пропорционален световому потоку, падающему на электрод. График показывает, что даже при нулевом напряжении ток не равен нулю. Это означает, что излучение, вытягивающее электроны, дает им кинетическую энергию. Меняем полярность включения и обратное напряжение будем увеличивать.При некоторых своих значениях ток прекратится, это напряжение называется , блокирующим . Это означает, что даже самые быстрые электроны не могут преодолеть тормозящее действие поля. В данном случае соотношение: Зная заряд электрона и измерив напряжение блокировки, можно определить максимальную кинетическую энергию электронов, выделяемую излучением. Эти эксперименты позволили установить 2-й закон фотоэлектрического эффекта : максимальная кинетическая энергия выбитых излучением электронов не зависит от интенсивности излучения, а определяется длиной волны или частотой и материалом электрода.Направляя на электрод излучение разных цветов, мы заметили, что с увеличением длины волны на определенной длине волны, определенной для данного материала, фототок прекращается. Самая большая длина волны, на которой все еще можно наблюдать фотоэлектрический эффект, называется , красная граница фотоэлектрического эффекта для этого материала . Эксперименты с различными материалами позволили установить 3-й закон фотоэлектрического эффекта : Красная граница фотоэлектрического эффекта определяется только материалом электрода и не зависит от интенсивности излучения. Объяснение законов внешнего фотоэффекта на основе квантовой теории. Эйнштейн объяснил законы фотоэлектрического эффекта в 1905 году. Согласно его объяснению, при поглощении одного кванта вырывается ровно один электрон, следовательно, чем больше интенсивность излучения, тем больше квантов попадает на электрод, тем больше может быть их количество. поглощается, что означает, что электроны выбиваются, чем выше ток насыщения. Следовательно, фототок насыщения пропорционален световому потоку, падающему на электрод.Это объяснение 1-го закона. Энергия поглощенного кванта частично расходуется на выполнение работы выхода, а остальная часть — кинетическая энергия электронов. Причем наибольшей энергией будут обладать электроны, которые поглотили кванты у поверхности металла и не успели ее потерять при столкновении с другими частицами. Математически это выражается формулой Эйнштейна для фотоэффекта : Это показывает, что максимальная кинетическая энергия электронов, выбитых излучением, зависит только от энергии кванта и, следовательно, от частоты или длины волны излучения, а также от работы выхода и, следовательно, от материала электрода.Это объяснение 2-го закона. Если энергия кванта меньше работы выхода, то фотоэлектрический эффект не будет наблюдаться ни при какой интенсивности излучения. Если энергия кванта равна работе выхода, фотоэлектрический эффект все еще может наблюдаться: Из этого видно, что красная граница зависит от работы выхода, а значит, не зависит от материала электрода от интенсивности излучения. Это объяснение 3-го закона. Внутренний фотоэффект. В 1873 году английские электрики Мэй и Смит использовали селен в качестве изолятора для прокладки подводного кабеля и заметили, что изоляционные свойства селена на свету резко ухудшаются, поскольку селен является полупроводником, в световых парах образуются: электрон- дырка, т.е. носители заряда. Генерация свободных носителей заряда в полупроводнике под действием излучения называется внутренним фотоэффектом.Дополнительная проводимость полупроводника из-за облучения называется фотопроводимостью. Внутренний фотоэффект отличается от внешнего тем, что при этом внутренние заряды остаются внутри вещества, а при внешнем вылетают. Следовательно, внутренний фотоэлектрический эффект может быть вызван излучением с большей длиной волны. Внутренний фотоэффект используется в устройстве фото сопротивлений и фотоэлементов. Применение фотоэлектрического эффекта. а) Фоторезистент выполнен следующим образом: тонкий слой полупроводника наносится на изолятор с помощью электродов в виде полос и покрывается пленкой прозрачного лака. В качестве полупроводника используют: кремний, селен, сульфид таллия, сульфид кадмия и др. Преимущество фоторезистора : простота изготовления, длительный срок службы, малые габариты, высокая светочувствительность, возможность выбора фоторезистора для нужного диапазона длин волн, в том числе для инфракрасной области. Недостатки : отсутствие пропорциональности между силой тока и силой света, влияние инерции окружающей среды. б) Фотоэлементы с внутренним фотоэффектом выполнены следующим образом: на полупроводник n типа наносят тонкий слой полупроводника r типа порядка 1 мкм с контактами для вывода во внешнюю цепь. Под действием излучения в полупроводнике типа r образуются электронно-дырочные пары, которые, не успев рекомбинировать, попадают в pn — переход, где происходит разделение зарядов.Дырки выбрасываются в область r , а электроны — в область n . Есть ЭДС, а при замыкании цепи — ток. Фотоэлемент может дать до 25 миллиампер на квадратный сантиметр освещенной поверхности. Коэффициент полезного действия 12-16%, в лабораторных условиях 18%. В ближайшее время реально создать фотоэлемент с КПД 35-40%. Кремниевые фотоэлементы чувствительны к солнечному излучению и называются солнечными панелями . Солнечные элементы используются для питания автономных систем и космического электрооборудования на солнечных электростанциях, что является экологически чистым и экономичным. дюйма) Фотоэлементы с внешним фотоэлектрическим эффектом марка: стеклянный вакуумный распылитель с 2 электродами. Выводы — металлические колпачки. Один электрод выполнен в виде сетки или диска внутри банки, а второй электрод представляет собой светочувствительный слой, нанесенный внутри банки, для этого слоя используются щелочные металлы. Dignity : безынерционный и пропорциональный фототоку интенсивности излучения. Недостаток : малый ток, недостаточная чувствительность к длинноволновому излучению, хрупкость и сравнительная сложность изготовления. Используются в автоматизации и для воспроизведения оптических звукозаписей. Обозначение на схемах: Явления люминесценции. Люминесценция — холодное свечение. Есть три типа люминесценции: электролюминесценция, фотолюминесценция и катодолюминесценция. 1) электролюминесценция — свечение разреженного газа при прохождении тока. Прямой ток через pn Переход сопровождается интенсивной рекомбинацией электронов и дырок с выделением квантового излучения. 2) фотолюминесценция — переизлучение. Различают два типа фотолюминесценции: флуоресценция (время после свечения короткое) и фосфоресценция (время после свечения большое). Кристаллические вещества, сильно и долго фосфоресцирующие, называются кристаллофосфором . Люминесцентные композиции, в которых фосфоресценция обусловлена наличием небольшого количества примесей активаторов, называются люминофорами . Правила Стокса : спектр фотолюминесценции смещен в сторону длинных волн по сравнению со спектром поглощенного излучения: hn = hn 0 — A Энергия испускаемых квантов меньше энергии поглощенных, а значит, длина волны больше, так как часть энергии теряется.Спектр излучения зависит от вещества, он используется в люминесцентном анализе. Чувствительность метода достаточно высока: достаточно 10 -7 — 10 -9 г вещества на 1 см3. 3) катодолюминесценция — свечение экранов при воздействии заряженных частиц. Люминесценция широко используется в источниках света, рекламных трубках при изготовлении телевизионных экранов, люминесцентных красок. Люминофоры используются для обнаружения рентгеновского и ультрафиолетового излучения, а также инфракрасных лучей.Под воздействием инфракрасных лучей светящиеся экраны быстро темнеют. Для простых кинескопов используются кристаллофоры, содержащие смесь сульфида цинка и сульфида кадмия, активируемую серебром, дающую голубоватое свечение. В кинескопах цветного телевидения зерна трех кристаллических люминофоров расположены на экране по порядку и светятся красным, зеленым и синим светом. Они возбуждаются тремя отдельными электронными лучами. Интенсивность этих лучей контролируется видеосигналами от трех передающих трубок с красным, зеленым и синим фильтрами соответственно. Word 2016: форматирование изображенийУрок 19: Форматирование изображений/ ru / word2016 / images-and-text-wrapping / content / ВведениеЕсть много способов отформатировать картинку в Word. Например, вы можете изменить размер или форму изображения в соответствии с вашим документом. Вы также можете улучшить его внешний вид с помощью инструментов настройки изображения Word. Необязательно: загрузите наш практический документ. Посмотрите видео ниже, чтобы узнать больше о форматировании изображений.
Для кадрирования изображения:При кадрировании изображения часть изображения удаляется . Обрезка может быть полезна, если вы работаете со слишком большим изображением и хотите сосредоточиться только на части его.
Угловые ручки используются для одновременной обрезки изображения по горизонтали и по вертикали . Чтобы обрезать изображение до формы:
Чтобы добавить рамку к изображению:
Корректировка изображенияС помощью инструментов настройки изображения Word вы можете легко настроить такие свойства, как цвет, контраст, насыщенность и тон. Word также предлагает встроенные стили изображений , которые можно использовать для добавления рамки, тени и других предопределенных эффектов. Когда вы будете готовы настроить изображение, просто выберите его. Затем используйте параметры ниже, которые можно найти на вкладке Формат . ИсправленияОтсюда вы можете повысить резкость или смягчить изображение, чтобы настроить его четкость или размытость. Вы также можете настроить яркость и контраст , которые влияют на яркость и общую интенсивность изображения. ЦветС помощью этой команды вы можете настроить насыщенность изображения, (насколько яркие цвета появляются), тон, (цветовую температуру изображения, от холодного до теплого) и цветовой тон, (общий оттенок изображения) . Художественные эффектыЗдесь вы можете применить к изображению специальных эффектов , таких как пастель, акварель или светящиеся края. Поскольку результаты такие смелые, вы можете использовать эти эффекты экономно (особенно в профессиональных документах). Группа стилей изображенияЭта группа содержит множество различных предопределенных стилей , которые еще больше упрощают форматирование изображений. Стили изображения предназначены для рамки вашего изображения без изменения его основных настроек или эффектов. Сжатие изображенийЕсли вы планируете отправить документ, содержащий изображения, по электронной почте, вам необходимо следить за его размером файла . Большие изображения с высоким разрешением могут привести к тому, что ваш документ станет очень большим, что может затруднить прикрепление к электронному письму. Кроме того, обрезанных областей изображений сохраняются в документе по умолчанию, что может увеличить размер файла. К счастью, вы можете уменьшить размер файла документа на , сжав изображение.Это снизит их разрешение и удалит обрезанные области . Сжатие изображения может заметно повлиять на его качество (например, изображение может стать размытым или пиксельным). Поэтому мы рекомендуем сохранить дополнительную копию документа перед сжатием изображений. В качестве альтернативы, будьте готовы использовать команду Отменить , если вы недовольны результатами. Для сжатия изображения:
Вызов!
/ ru / word2016 / shape / content / Классных фотоэффектов | Добавьте фотоэффекты и фотофильтры к вашему изображению онлайнКлассные фотоэффекты | Добавьте фотоэффекты и фотофильтры к вашему изображению онлайн | Фоторедактор FotorСтильные шаблоны крутых фотоэффектовКрутая и особенная эстетика поможет вам легко выделиться на платформах социальных сетей, особенно сейчас, когда мы живем в мире, ориентированном на образы.Онлайн-редактор фотографий Fotor предлагает вам набор классных шаблонов фотоэффектов, такие как фотоэффект «Холодный синий», фотоэффект «Красная охра», фотофильтр «Вирджиния»… есть на любой случай. НачатьЛегко создавайте потрясающие изображения с помощью крутых фотоэффектовУпростите задачу, используя потрясающие, хорошо продуманные шаблоны крутых фотоэффектов в онлайн-редакторе фотографий Fotor, чтобы украсьте свои фотографии и удивите своих друзей и аудиторию.Все, что вам нужно сделать, это подготовить свой образ, нажмите на понравившийся шаблон крутого фотоэффекта и отрегулируйте интенсивность. Затем он будет автоматически применен к вашему изображению. Сделайте красивое изображение с крутыми фотоэффектами в один клик. НачатьСделайте свои изображения профессиональными с помощью крутых фотоэффектовВ фоторедакторе Fotor вам доступна огромная библиотека классных фотоэффектов.Классный фотофильтр позволяет скрыть мелкие недочеты и недочеты, плюс улучшайте ваши изображения, как профессиональный фотограф. Ознакомьтесь с хорошо составленным списком классных шаблонов фотоэффектов и продолжайте свое путешествие по редактированию фотографий. НачатьПотрясающие результаты с классными графическими эффектами Fotor!В комплекте с классными фотоэффектами и фотофильтрами, Потрясающие крутые графические эффекты Fotor — лучшие в Интернете! Используя передовые технологии обработки изображений, вы найдете все лучшие онлайн-фотоэффекты на сайте Фотор, позволяя вам превратить обыденное в необычное! Начать Достигните творческого совершенства с помощью крутых графических эффектов FotorКак добавить к фотографии крутые фотоэффекты?
Часто задаваемые вопросы о крутых фотоэффектахКак мне сделать мои фотографии крутыми?Как добавить к моим фотографиям спецэффекты?Fotor — это не просто лучшие крутые фотоэффектыЛучшие бесплатные онлайн-эффекты для фотоС бесплатными классными фотоэффектами Fotor вы можете сделать свои фотографии более профессиональными. в несколько кликов.Fotor также предлагает вам различные фотофильтры с разными стилями на выбор. от и максимизировать ваши эффекты изображения! Коробочная модельКоробочная модельСодержание
Модель блока CSS описывает прямоугольные блоки, которые сгенерирован для элементов в документе дерево и разложено согласно визуальному форматированию модель. В каждой коробке есть область содержимого (например, текст, изображение и т. д.) и необязательное окружение набивка , граница , и маржа области; размер каждой области определяется свойствами, определенными ниже. Следующее диаграмма показывает, как эти области связаны, и терминология, используемая для обозначения на части поля, границы и заполнения: Поля, граница и отступы могут быть разбиты на верхнюю, правую и нижний и левый сегменты (напр.г., на схеме «LM» для левого поля, «RP» для правого отступа, «TB» для верхней границы и т. Д.). Периметр каждой из четырех областей (контент, отступ, граница, и поле) называется «краем», поэтому каждый блок имеет четыре края:
Каждый край может быть разбит на верхний, правый, нижний и левый край. Размеры области содержимого блока — ширина содержимого и высота содержимого — зависят от нескольких факторов: генерирует ли элемент коробка имеет ширину или свойство ‘высота’ установить, содержит ли поле текст или другие поля, независимо от того, ящик стол и т. д.Ширина и высота коробки обсуждаются. в главе о визуальном форматировании детали модели. Стиль фона содержимого, отступов и границ области поле определяется свойством ‘background’ генерирующий элемент. Фон полей всегда прозрачен. В этом примере показано, как поля, отступы и границы взаимодействовать. Пример HTML-документа:
<ГОЛОВА>
| ||||||||||||||||

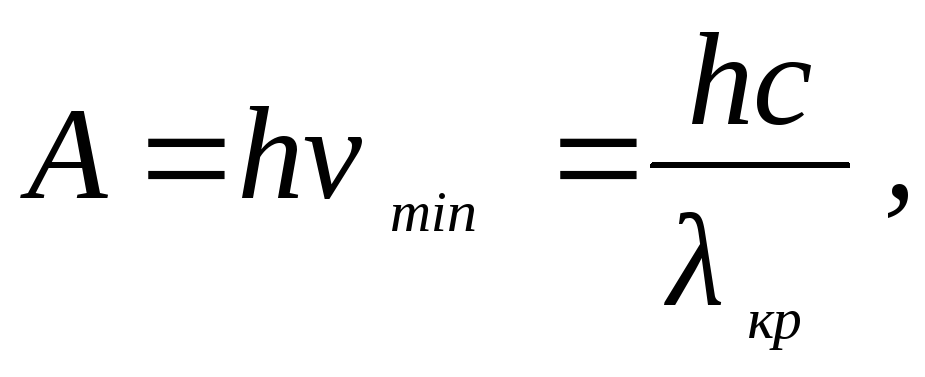 2over 2})$$
2over 2})$$ 2010.
2010.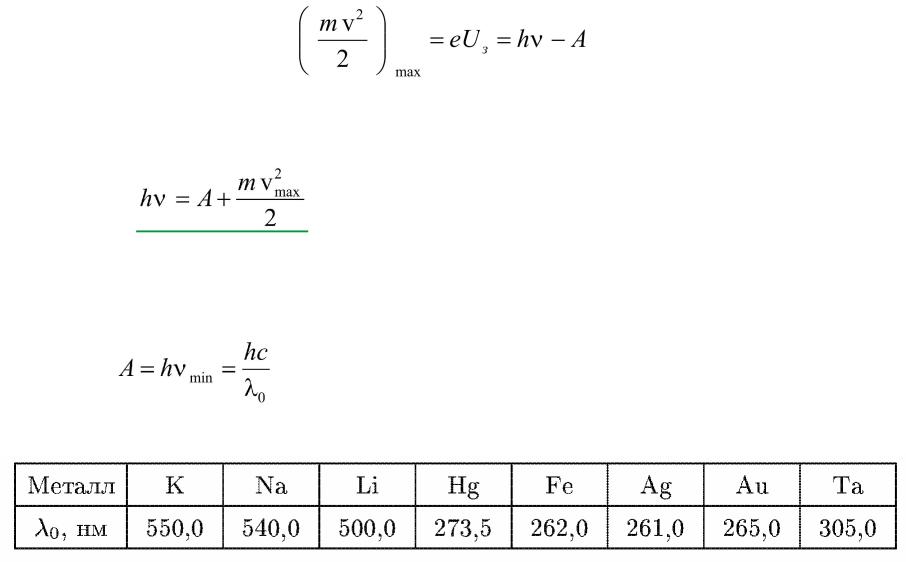 .. Математическая формулировка … Основа … Википедия
.. Математическая формулировка … Основа … Википедия 2}2\) – максимальная кинетическая энергия вылетающего электрона, \(v\) – частота падающего фотона с энергией \(hv, \ h\) – постоянная Планка. Из этой формулы следует существование красной границы фотоэффекта, то есть существование наименьшей частоты \((hv_{\min}=\varphi)\), ниже которой энергии фотона уже недостаточно для того, чтобы «выбить» электрон из металла. Суть формулы заключается в том, что энергия фотона расходуется на ионизацию атома вещества и на работу, необходимую для «вырывания» электрона, а остаток переходит в кинетическую энергию электрона.
2}2\) – максимальная кинетическая энергия вылетающего электрона, \(v\) – частота падающего фотона с энергией \(hv, \ h\) – постоянная Планка. Из этой формулы следует существование красной границы фотоэффекта, то есть существование наименьшей частоты \((hv_{\min}=\varphi)\), ниже которой энергии фотона уже недостаточно для того, чтобы «выбить» электрон из металла. Суть формулы заключается в том, что энергия фотона расходуется на ионизацию атома вещества и на работу, необходимую для «вырывания» электрона, а остаток переходит в кинетическую энергию электрона.
 Например, скорость фотоэлектронов по классическим понятиям должна возрастать с амплитудой, а, следовательно, и с интенсивностью электромагнитной волны.
Например, скорость фотоэлектронов по классическим понятиям должна возрастать с амплитудой, а, следовательно, и с интенсивностью электромагнитной волны. П. И. Лукирским и С. С. Прилежаевым, которые создали прибор в виде сферического конденсатора. Анодом в их приборе служили посеребренные стенки стеклянного сферического баллона. В центре баллона помещался катод в виде шарика. При такой форме электродов вольт-амперная характеристика идет круче, что позволяет повысить точность определения задерживающего потенциала.
П. И. Лукирским и С. С. Прилежаевым, которые создали прибор в виде сферического конденсатора. Анодом в их приборе служили посеребренные стенки стеклянного сферического баллона. В центре баллона помещался катод в виде шарика. При такой форме электродов вольт-амперная характеристика идет круче, что позволяет повысить точность определения задерживающего потенциала. Формула (9.5) в случае N-фотонного эффекта имеет вид
Формула (9.5) в случае N-фотонного эффекта имеет вид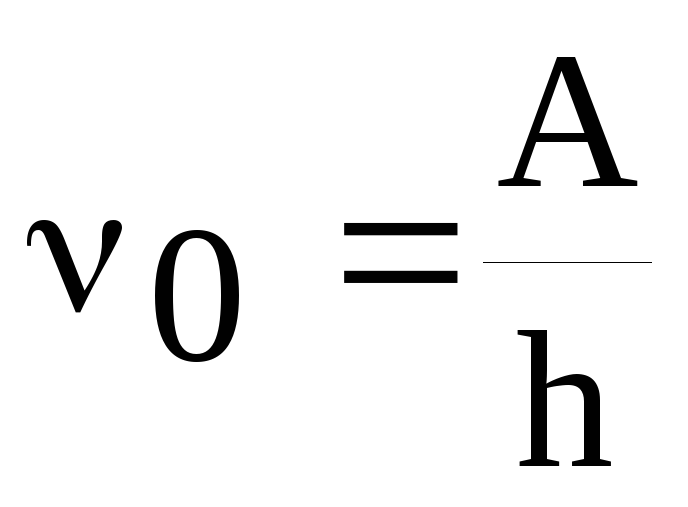
 Затем можно отрегулировать замедляющее напряжение между коллекторным проводом и пластиной, чтобы определить энергию выброшенных электронов. Например, если он достаточно отрицательный, никакие электроны не достигнут провода. (кредит: П. П. Урон)
Затем можно отрегулировать замедляющее напряжение между коллекторным проводом и пластиной, чтобы определить энергию выброшенных электронов. Например, если он достаточно отрицательный, никакие электроны не достигнут провода. (кредит: П. П. Урон) В форме уравнения энергия фотона равна E = hf , где E — энергия фотона с частотой f и h — постоянная Планка. Эта революционная идея похожа на квантование Планком энергетических состояний в генераторах черного тела, но это совсем другое.Это квантование самого электромагнитного излучения. Электромагнитные волны состоят из фотонов и не являются непрерывными гладкими волнами, как описано в предыдущих главах, посвященных оптике. Их энергия поглощается и испускается кусками, а не непрерывно. Это в точности согласуется с квантованием уровней энергии в генераторах черного тела Планком, поскольку эти генераторы увеличивают и уменьшают свою энергию с шагом hf , поглощая и испуская фотоны с E = hf . Мы не наблюдаем это своими глазами, потому что в обычных источниках света так много фотонов, что отдельные фотоны остаются незамеченными.(См. Рис. 2.) Следующий раздел текста (Энергии фотонов и электромагнитный спектр) посвящен обсуждению фотонов и некоторых их характеристик и значений. А пока мы будем использовать концепцию фотона для объяснения фотоэлектрического эффекта, как это делал Эйнштейн.
В форме уравнения энергия фотона равна E = hf , где E — энергия фотона с частотой f и h — постоянная Планка. Эта революционная идея похожа на квантование Планком энергетических состояний в генераторах черного тела, но это совсем другое.Это квантование самого электромагнитного излучения. Электромагнитные волны состоят из фотонов и не являются непрерывными гладкими волнами, как описано в предыдущих главах, посвященных оптике. Их энергия поглощается и испускается кусками, а не непрерывно. Это в точности согласуется с квантованием уровней энергии в генераторах черного тела Планком, поскольку эти генераторы увеличивают и уменьшают свою энергию с шагом hf , поглощая и испуская фотоны с E = hf . Мы не наблюдаем это своими глазами, потому что в обычных источниках света так много фотонов, что отдельные фотоны остаются незамеченными.(См. Рис. 2.) Следующий раздел текста (Энергии фотонов и электромагнитный спектр) посвящен обсуждению фотонов и некоторых их характеристик и значений. А пока мы будем использовать концепцию фотона для объяснения фотоэлектрического эффекта, как это делал Эйнштейн. Для простоты рассмотрим, что происходит с монохроматическим электромагнитным излучением, в котором все фотоны имеют одинаковую энергию hf .
Для простоты рассмотрим, что происходит с монохроматическим электромагнитным излучением, в котором все фотоны имеют одинаковую энергию hf . Если бы электромагнитное излучение было простой волной, более высокая интенсивность могла бы дать больше энергии, и электроны с более высокой энергией были бы выброшены.
Если бы электромагнитное излучение было простой волной, более высокая интенсивность могла бы дать больше энергии, и электроны с более высокой энергией были бы выброшены. Наклон этой линии составляет h — данные могут быть использованы для экспериментального определения постоянной Планка. Эйнштейн дал первое успешное объяснение таким данным, предложив идею фотонов — квантов электромагнитного излучения.
Наклон этой линии составляет h — данные могут быть использованы для экспериментального определения постоянной Планка. Эйнштейн дал первое успешное объяснение таким данным, предложив идею фотонов — квантов электромагнитного излучения. Для Части 2, как только энергия фотона вычислена, это прямое применение KE e = hf — BE для определения максимальной кинетической энергии выброшенного электрона, поскольку BE дано.
Для Части 2, как только энергия фотона вычислена, это прямое применение KE e = hf — BE для определения максимальной кинетической энергии выброшенного электрона, поскольку BE дано. Это означает, что если в люксметре используется металлический кальций, он будет нечувствителен к длинам волн более длинных, чем у синего света. Такой люксметр, например, будет совершенно нечувствителен к красному свету.
Это означает, что если в люксметре используется металлический кальций, он будет нечувствителен к длинам волн более длинных, чем у синего света. Такой люксметр, например, будет совершенно нечувствителен к красному свету.
 Эти фотоны видны?
Эти фотоны видны? 263 нм
263 нм Если мы сможем поразить электроны светом на частоте 600 терагерц, мы не сможем просто
используйте 300 терагерц в два раза больше времени и все еще ожидайте, что электроны будут ударить.
Если мы сможем поразить электроны светом на частоте 600 терагерц, мы не сможем просто
используйте 300 терагерц в два раза больше времени и все еще ожидайте, что электроны будут ударить.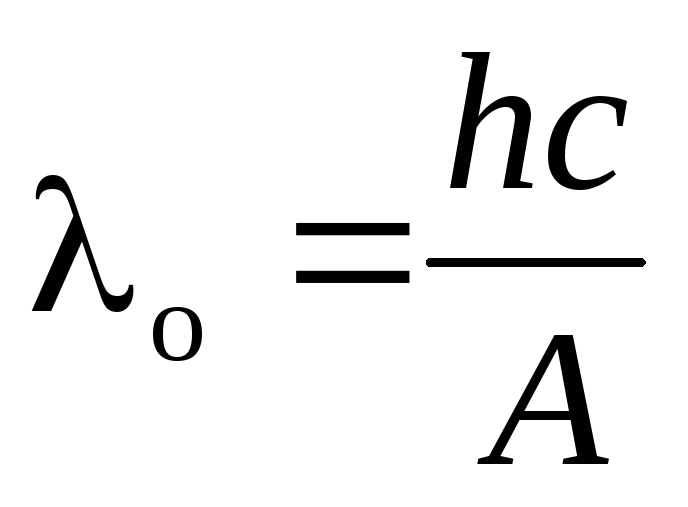 Численные расчеты применимы для возбуждений в конечные состояния с главным квантовым числом примерно до 20 и для ионизации фотонами с энергией примерно до 2 МэВ. Описаны сложные схемы экстраполяции для определения сечения подоболочки для возбуждения на связанные уровни с большими главными квантовыми числами и для ионизации фотонами с более высокими энергиями.Влияние конечной ширины атомных энергетических уровней учитывается путем свертки рассчитанного поперечного сечения подоболочки с лоренцевым профилем.
Численные расчеты применимы для возбуждений в конечные состояния с главным квантовым числом примерно до 20 и для ионизации фотонами с энергией примерно до 2 МэВ. Описаны сложные схемы экстраполяции для определения сечения подоболочки для возбуждения на связанные уровни с большими главными квантовыми числами и для ионизации фотонами с более высокими энергиями.Влияние конечной ширины атомных энергетических уровней учитывается путем свертки рассчитанного поперечного сечения подоболочки с лоренцевым профилем.