Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Осевое сечение цилиндра –квадрат, диагональ которого равна 4 см. 3 -152
3 -152
Пользуйтесь нашим приложением
Основное Тригонометрическое Тождество — Доказательство
Поможем понять и полюбить математику
Начать учиться
109.8K
Там, где заканчиваются границы привычной и давно знакомой алгебры, начинаются владения тригонометрии. Давайте вооружимся всеми необходимыми формулами, чтобы в полном обмундировании преодолеть любые тригонометрические испытания.
Связь между sin и cos одного угла
Вы уже наверняка знаете, что тождественный — это равный.
Основные тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Это значит, что любую из этих функций можно найти, если известна другая функция.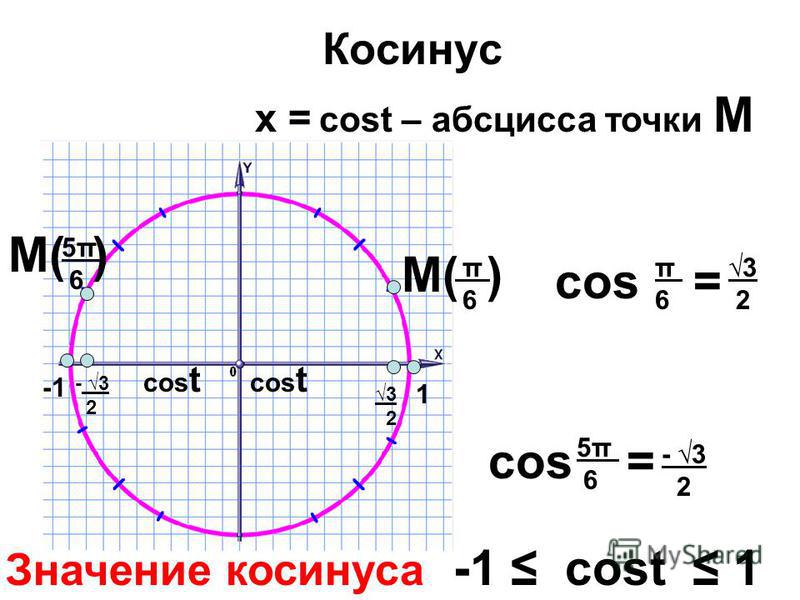
Ключ к сердцу тригонометрии — основное тригонометрическое тождество. Запомните и полюбите его, чтобы отношения с тригонометрией сложились самым наилучшим образом:
sin2α + cos2α = 1 |
Из основного тождества вытекают равенства тангенса и котангенса, поэтому оно — ключевое.
Равенство tg2α + 1 = 1/cos2α и равенство 1 + сtg2α + 1 = 1/sin2α выводят из основного тождества, разделив обе части на sin2α и cos2α.
В результате деления получаем:
Поэтому основному тригонометрическому тождеству уделяется максимум внимания. Но какая же «метрия» может обойтись без доказательств. Видите тождество — доказывайте, не раздумывая.
sin2α + cos2α = 1
Сумма квадратов синуса и косинуса одного угла тождественно равна единице.
Чтобы доказать тождество, обратимся к теме единичной окружности.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат. Радиус единичной окружности равен единице.
Докажем тождество sin2α + cos2α = 1
- Итак, нам известны координаты точки A (1; 0).
Произвольный угол α, тогда cos α = x0 = ОB.
- По определениям:
- Синус угла (sin α) — это отношение противолежащего катета к гипотенузе.
- Косинус угла (cos α) — это отношение прилежащего катета к гипотенузе.
- Опускаем перпендикулярную прямую A1B на x0 из точки A1.

Образовался прямоугольный треугольник OA1B.
|A1
|OB| = |x|.
- Гипотенуза OA1 имеет значение, равное радиусу единичной окружности.
|OA1| = 1.
- Применяя полученное выражение, записываем равенство по теореме Пифагора, поскольку получившийся угол — прямой:
|A1B|2 + |OB|2 = |OA1|2.
- Записываем в виде: |y|2 + |x|2 = 12.
Это значит, что y2 + x2 = 1.
sin угла α = y
cos угла α = x - Вставляем данные угла вместо координат точек:
OB = cos α
A1B = sin α
A1O = 1 - Получаем основное тригонометрическое тождество: sin2α + cos2α = 1.
Что и требовалось доказать.
Основное тригонометрическое тождество связывает синус угла и косинус угла. Зная одно, вы легко можете найти другое. Нужно лишь извлечь квадратный корень по формулам:
Зная одно, вы легко можете найти другое. Нужно лишь извлечь квадратный корень по формулам:
- sin α = ±
- cos α = ±
Как видите, перед корнем может стоять и минус, и плюс. Основное тригонометрическое тождество не дает понять, положительным или отрицательным был исходный синус/косинус угла.
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Тангенс и котангенс через синус и косинус
Немного вводных:
- Синус угла — это ордината y.
- Косинус угла — это абсцисса x.
- Тангенс угла — это отношение ординаты к абсциссе.

- Котангенс угла — это отношение абсциссы к ординате.
Из всего этого множества красивых, но не сильно понятных слов, можно сделать вывод о зависимости одного от другого. Такая связь помогает отдельно преобразовывать нужные величины.
- tg α =
- ctg α =
Исходя из определений:
- tg α = =
- ctg α = =
Это позволяет сделать вывод, что тригонометрические тождества
задаются sin и cos углов.
Отсюда следует, что тангенс угла — это отношение синуса угла к косинусу. А котангенс угла — это отношение косинуса к синусу.
Отдельно стоит обратить внимание на то, что тригонометрические тождества
верны для всех углов α, значения которых вписываются в диапазон.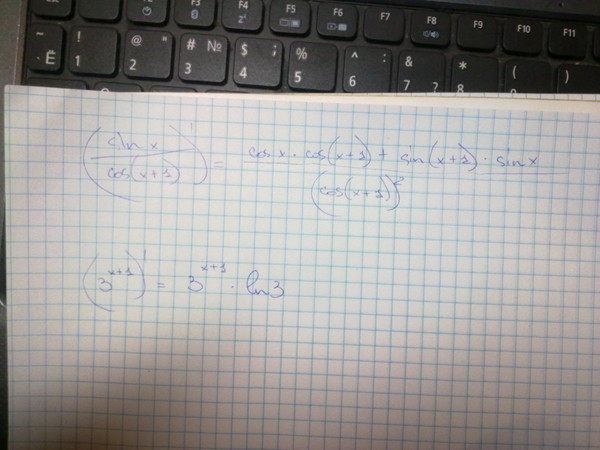
- Например, выражение применимо для любого угла α, не равного + π + z, где z — это любое целое число. В противном случае, в знаменателе будет стоять 0.
Выражение
применимо для любого угла α, не равного π * z, где z — это любое целое число.
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Связь между тангенсом и котангенсом
Уж насколько очевидной кажется связь между ранее рассмотренными тождествами, настолько еще более наглядна связь между тангенсом и котангенсом одного угла.
- Тождество записывается в следующем виде:
tg α * ctg α = 1.
Такое тождество применимо и справедливо при любых углах α, значение которых не равняются π/2 * z, где z — это любое целое число. В противном случае, функции не будут определены.
Как и любое другое, данное тригонометрическое тождество подлежит доказательству. Доказывать его очень просто.
tg α * ctg α = 1.
- По определению:
tg α = y/x
ctg α = x/y
- Отсюда следует, что tg α * ctg α = y/x * x/y = 1
- Преобразовываем выражение, подставляем и ,
получаем:
Получается, что тангенс и котангенс одного угла, при котором они имеют смысл — это взаимно обратные числа.
Если числа a и b взаимно обратные — это значит, что число a — это число, обратное числу b, а число b — это число, обратное числу a. Кроме того, это значит, что числу a обратно число b, а числу b обратно число a. Короче, и так, и эдак.
Короче, и так, и эдак.
Какие, какие числа?🤯
Взаимно обратные числа — это два числа, произведение которых равно 1.
Тангенс и косинус, котангенс и синус
Все тождества выше позволяют сделать вывод, что тангенс угла связан с косинусом угла, а котангенс угла — с синусом.
Эта связь становится очевидна, если взглянуть на тождества:
- tg2α + 1 =
Сумма квадрата тангенса угла и единицы равна числу, обратному квадрату косинуса этого угла.
- 1 + ctg2α =
Сумма единицы и квадрата котангенса угла равна числу, обратному квадрату синуса этого угла.
Вывести оба этих тождества можно из основного тригонометрического тождества:
sin2α + cos2α = 1.
- Для этого нужно поделить обе части тождества на cos2α, где косинус не равен нулю.

- В результате деления получаем формулу tg2α + 1 =
- Если обе части основного тригонометрического тождества sin2α + cos2α = 1 разделить на sin2α, где синус не равен нулю, то получим тождество:
1 + ctg2α = . - Отсюда можно сделать вывод, что тригонометрическое тождество tg2α + 1 = применимо для любого угла α, не равного + π + z, где z — это любое целое число.
- А тригонометрическое тождество 1 + ctg2α = применимо для любого угла, не равного π * z, где z — это любое целое число.
Хорошо бы выучить все формулы и запомнить формулировки тождеств наизусть. Чтобы это сделать, сохраняйте себе табличку с основными формулами.
Основные тригонометрические тождества
1 | sin2α + cos2α = 1 |
2 | |
3 | |
4 | tgα * ctgα = 1 |
5 | tg2α + 1 = |
6 | 1 + ctg2α = |
Чтобы тратить еще меньше времени на решение задач, сохраняйте таблицу значений тригонометрических функции углов, которые чаще всего встречаются в задачах.
Примеры решения задач
Разберем пару задачек, для решения которых нужно знать основные тождества. Рассмотрите внимательно предложенные решения и потренируйтесь самостоятельно.
Задачка 1. Найдите cos α, tg α, ctg α при условии, что sin α = 12/13.
Как решаем:
- Чтобы решить задачу, необходимы следующие тригонометрические тождества:
- Выражаем cos α из тригонометрической единицы:
- Далее подставляем значения sin α:
- Вычисляем:
- Нам известны значения sin α и cos α, поэтому можно легко найти тангенс, используя формулу:
- Таким же образом, используя формулу, вычисляем значение котангенса:
Ответ:
Задачка 2. Найдите значение cos α,
Найдите значение cos α,
если:
Как решаем:
- Чтобы решить задачу, необходимы следующие тригонометрические тождества:
- Выражаем cos α из тригонометрической единицы:
- Далее подставляем значения sin α:
- Вычисляем:
- То же самое проделываем со вторым значение sin α
Подставляем значения sin α:
- Вычисляем:
Ответ:
Как видите, задачи решаются достаточно просто, нужно лишь верно применять формулы основных тождеств.
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Анастасия Белова
К предыдущей статье
Числовые и буквенные выражения
К следующей статье
204. 4K
4K
Сравнение дробей: как правильно
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
| На последних страницах вы видели довольно много тригонометрических тождеств. Удобно иметь их сводку для справки. Эти тождества в основном относятся к одному углу, обозначенному θ , но есть и такие, которые включают два угла, и для них два угла обозначаются α и β . | |
Более важные тождества.Вам не нужно знать все личности наизусть. Но это вы должны. | |
Определяющие отношения для тангенса, котангенса, секанса и косеканса через синус и косинус. | |
| Формула Пифагора для синусов и косинусов. Это, вероятно, самая важная триггерная идентичность. | |
| Тождества, выражающие триггерные функции через их дополнения. В этом нет ничего особенного. Каждая из шести триггерных функций равна своей кофункции, оцениваемой под дополнительным углом. | |
| Периодичность триггерных функций. Синус, косинус, секанс и косеканс имеют период 2 π , а тангенс и котангенс имеют период π . | |
| Тождества для отрицательных углов. Синус, тангенс, котангенс и косеканс — нечетные функции, а косинус и секанс — четные функции. | |
| Тождества Птолемея, формулы суммы и разности для синуса и косинуса. | |
Формулы двойного угла для синуса и косинуса. Обратите внимание, что существует три формы формулы двойного угла для косинуса. Вам нужно знать только одно, но уметь вывести два других из формулы Пифагора. Вам нужно знать только одно, но уметь вывести два других из формулы Пифагора. | |
Менее важные тождества.Вы должны знать, что эти личности есть, но они не так важны, как упомянутые выше. Все они могут быть получены из приведенных выше, но иногда для этого требуется некоторая работа. | |
| Формула Пифагора для тангенсов и секансов. Есть также один для котангенсов и косекансов, но, поскольку котангенсы и косекансы нужны редко, он не нужен. | |
| Тождества, выражающие триггерные функции через их дополнения. | |
| Формулы суммы, разности и двойного угла для тангенса. | |
Формулы половинного угла. Синус и косинус принимают положительный или отрицательный квадратный корень в зависимости от квадранта угла θ /2. Например, если θ /2 — острый угол, то будет использоваться положительный корень.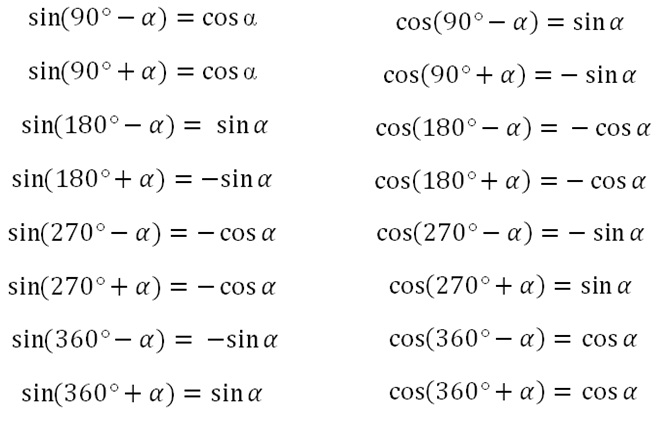 | |
Совершенно неясные личности.Они просто здесь для извращенности. Нет, не совсем. У них есть несколько приложений, но обычно это узкие приложения, и о них можно просто забыть, пока они не понадобятся. | |
| Тождества произведения-суммы. Эта группа тождеств позволяет преобразовать сумму или разность синусов или косинусов в произведение синусов и косинусов. | |
Идентификаторы продуктов. В стороне: как ни странно, эти тождества произведений использовались до того, как были изобретены логарифмы для выполнения умножения. Вот как можно использовать второй. Если вы хотите умножить x x y, используйте таблицу, чтобы найти угол α , косинус которого равен x , и угол β , косинус которого равен y . Найдите косинусы суммы α + β . а разница α – β . Усредните эти два косинуса. Вы получаете товар xy ! Три поиска в таблице и вычисление суммы, разности и среднего, а не одного умножения. Тихо Браге (1546–1601), среди прочих, использовал этот алгоритм, известный как простафаэрез. Усредните эти два косинуса. Вы получаете товар xy ! Три поиска в таблице и вычисление суммы, разности и среднего, а не одного умножения. Тихо Браге (1546–1601), среди прочих, использовал этот алгоритм, известный как простафаэрез. | |
| Формулы тройного угла. Вы можете легко восстановить их по формулам сложения и двойного угла. | |
| Больше формул половинного угла. Они описывают основные триггерные функции в терминах тангенса половины угла. Они используются в исчислении для особого вида замены в интегралах, иногда называемых Вейерштрассом t -замена. | |

 06.18
06.18


 Более поздние части
это эссе не часто зависит от предыдущих частей, поэтому, пожалуйста, не стесняйтесь просматривать
пропустите непонятный текст, пока не найдете то, что вам удобно.
Более поздние части
это эссе не часто зависит от предыдущих частей, поэтому, пожалуйста, не стесняйтесь просматривать
пропустите непонятный текст, пока не найдете то, что вам удобно. Вышеприведенное тождество может быть тогда
интерпретируется как говорящая о том, что точка (cos(t), sin(t)) находится на
единичный круг. Кроме того, этот подход приводит к определению cos(t) и sin(t) для всех реальных t .
Вышеприведенное тождество может быть тогда
интерпретируется как говорящая о том, что точка (cos(t), sin(t)) находится на
единичный круг. Кроме того, этот подход приводит к определению cos(t) и sin(t) для всех реальных t . глядя на графики y = cos 2 (x) и г =
грех 2 (х) .
глядя на графики y = cos 2 (x) и г =
грех 2 (х) .
 Определитель
квадратная матрица имеет простую геометрическую интерпретацию. это площадь
коэффициент масштабирования. При вращении площадь не меняется, поэтому определитель
должно быть 1 . Итак, личность cos 2 (t)+sin 2 (t)=1 можно интерпретировать
как выражение довольно очевидного факта, что вращение объекта в (x,y) плоскость не меняет своей площади.
Определитель
квадратная матрица имеет простую геометрическую интерпретацию. это площадь
коэффициент масштабирования. При вращении площадь не меняется, поэтому определитель
должно быть 1 . Итак, личность cos 2 (t)+sin 2 (t)=1 можно интерпретировать
как выражение довольно очевидного факта, что вращение объекта в (x,y) плоскость не меняет своей площади. Это означает, что приведенные выше три уравнения будут
верно, когда e 1 равно (cos(t), sin(t)) и е 2 есть (-sin(t), cos(t)) . Два уравнения е 1 .е 1 = 1 и e 2 .e 2 = 1 являются переформулировкой cos 2 (t) + sin 2 (t) =
1 , а e 1 .e 2 = 0 является заявлением об идентичности cos(t)(-sin(t))+sin(t)cos(t) = 0 .
Как ни странно, даже е 1 .е 2 заявление является
проявление личности, как показано ниже.
Это означает, что приведенные выше три уравнения будут
верно, когда e 1 равно (cos(t), sin(t)) и е 2 есть (-sin(t), cos(t)) . Два уравнения е 1 .е 1 = 1 и e 2 .e 2 = 1 являются переформулировкой cos 2 (t) + sin 2 (t) =
1 , а e 1 .e 2 = 0 является заявлением об идентичности cos(t)(-sin(t))+sin(t)cos(t) = 0 .
Как ни странно, даже е 1 .е 2 заявление является
проявление личности, как показано ниже. Этот результат может
доказываться непосредственно. Это легче всего увидеть, взглянув на Паскаля.
треугольник, и сложение терминов подряд в двух разных
способы. Кроме того, использование расширений степенных рядов для расширения
определение cos и sin в комплексные числа, мы
теперь известно, что тождество верно для комплекса т . Благодаря
Боб Ува за указание на это.
Этот результат может
доказываться непосредственно. Это легче всего увидеть, взглянув на Паскаля.
треугольник, и сложение терминов подряд в двух разных
способы. Кроме того, использование расширений степенных рядов для расширения
определение cos и sin в комплексные числа, мы
теперь известно, что тождество верно для комплекса т . Благодаря
Боб Ува за указание на это.
 Если вы еще этого не видели, то это
пересчет a 2 -b 2 = (a-b)(a+b) .
Используя комплексные числа, мы получаем, что -b 2 равно (ib) 2 , что приводит к а 2 +b 2 = а 2 -(-b 2 ) =
a 2 — (ib) 2 = (a-ib)(a+ib) . Кстати,
конечно также верно, что 2 +б 2 =
(b-ia)(b+ia) . В любом случае, применяя факторизацию к cos 2 (x)+sin 2 (x) , получаем (cos(x)+isin(x))(cos(x)-isin(x)) , то есть e ix e -ix . Использование w для представления e ix , тот факт, что cos 2 (x)+sin 2 (x)=1 просто
запутанный способ сказать w(1/w)=1 .
Если вы еще этого не видели, то это
пересчет a 2 -b 2 = (a-b)(a+b) .
Используя комплексные числа, мы получаем, что -b 2 равно (ib) 2 , что приводит к а 2 +b 2 = а 2 -(-b 2 ) =
a 2 — (ib) 2 = (a-ib)(a+ib) . Кстати,
конечно также верно, что 2 +б 2 =
(b-ia)(b+ia) . В любом случае, применяя факторизацию к cos 2 (x)+sin 2 (x) , получаем (cos(x)+isin(x))(cos(x)-isin(x)) , то есть e ix e -ix . Использование w для представления e ix , тот факт, что cos 2 (x)+sin 2 (x)=1 просто
запутанный способ сказать w(1/w)=1 .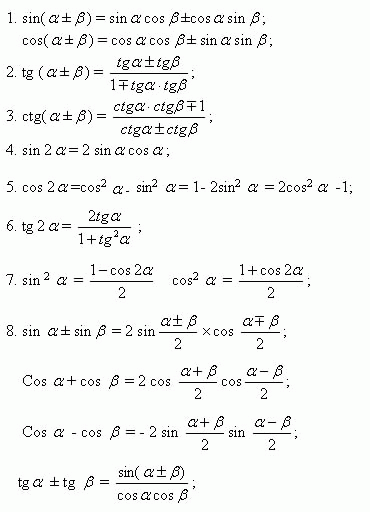 Дифференцируя, имеем c'(t) =
(-sin(t), cos(t)) . с'(т) . c'(t) равно (-sin(t))(-sin(t))
+ cos(t)cos(t) , что просто cos 2 (t)+sin 2 (t) . Тот факт, что это 1 говорит нам, что параметризованная кривая на самом деле
параметризуется длиной дуги. Таким образом, тригонометрическое тождество может быть
рассматривается как просто констатация того факта, что радианы пересекают единицу
круг с единичной скоростью. Наконец, снова дифференцируя, получаем c»(t) = (-cos(t), -sin(t)) . Очевидно, c»(t).c»(t) =
cos 2 (t) + sin 2 (t) , так что тождество
говорит нам о том, что равномерное движение по окружности приводит к
ускорение постоянной величины.
Дифференцируя, имеем c'(t) =
(-sin(t), cos(t)) . с'(т) . c'(t) равно (-sin(t))(-sin(t))
+ cos(t)cos(t) , что просто cos 2 (t)+sin 2 (t) . Тот факт, что это 1 говорит нам, что параметризованная кривая на самом деле
параметризуется длиной дуги. Таким образом, тригонометрическое тождество может быть
рассматривается как просто констатация того факта, что радианы пересекают единицу
круг с единичной скоростью. Наконец, снова дифференцируя, получаем c»(t) = (-cos(t), -sin(t)) . Очевидно, c»(t).c»(t) =
cos 2 (t) + sin 2 (t) , так что тождество
говорит нам о том, что равномерное движение по окружности приводит к
ускорение постоянной величины. е. для некоторого значения x , cos 2 (x)+sin 2 (x) равно 1 .
последнее свойство быстро устанавливается: беря x = 0 , cos(x)=1 и sin(x)= 0 . Четко 1 2 +0 2 =1 .
е. для некоторого значения x , cos 2 (x)+sin 2 (x) равно 1 .
последнее свойство быстро устанавливается: беря x = 0 , cos(x)=1 и sin(x)= 0 . Четко 1 2 +0 2 =1 .

Leave A Comment