Синус, косинус, тангенс и котангенс в тригонометрии: определения, формулы, примеры

Тригонометрия — раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой нужной науки внесли ученые Ближнего Востока и Индии, которые придумали наиболее важные понятия, объяснили многие свойства, предложили варианты измерения и др.

Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии без таблиц и графиков.

Синус, косинус, тангенс и котангенс. Определения

Зачем разделять понятия синуса, косинуса, тангенса и котангенса?

Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.

Определения тригонометрических функций

Что такое синус?

Синус угла (sin α) — это отношение противолежащего этому углу катета к гипотенузе.

Что такое косинус?

Косинус угла (cosα) — это отношение прилежащего катета к гипотенузе.

Что такое тангенс?

Тангенс угла (tg α) — это отношение противолежащего катета к прилежащему.

Котангенс угла (ctg α) — отношение прилежащего катета к противолежащему.

Данные определения даны для острого угла прямоугольного треугольника!

Синус и косинус можно представить через экспоненту (экспоненциальная функция).

Приведем иллюстрацию. 

В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.

Означения синуса, косинуса, тангенса и котангенса позволяют вычислять (находить) значения этих функций по известным длинам сторон треугольника.

Что и почему важно и принято помнить в ходе такого нахождения?

Важно помнить!

Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тг и ктг — вся числовая прямая, то есть эти функции могут принимать любые значения.

Как найти синус? Для начала нужно определиться, какой перед нами треугольник: прямоугольный или произвольный. В первом случае можно использовать обычный тригонометрический метод, а во втором — теорему косинусов.

Как найти косинус? Соответственно, нам нужно знать значения прилежающего катета и гипотенузы. 

Как найти тангенс? Если треугольник прямоугольный, то тангенс вычисляется при помощи значений противоположного катета и прилежащего (в уравнении нужно поделить одно на другое). Если речь идет о числах, тупых, развернутых углов и углов, превышающих 360 градусов, то тангенс определяется при помощи синуса и косинуса (посредством их отношения и деления).

Теорема синусов и косинусов используется для того чтобы искать элементы в произвольном треугольнике. Такой поиск используется часто.

Угол поворота

Определения, данные выше, относятся к острым углам.

В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от -∞ до +∞. 

В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность (круг) с центром в начале декартовой системы координат.

                                                                 

Начальная точка A с координатами (1, 0) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A1. Определение дается через координаты точки A1(x , y). 

Синус (sin или син) угла поворота

Синус угла поворота α — это ордината точки A1(x , y). sin α=y

Косинус (cos) угла поворота

Косинус угла поворота α — это абсцисса точки A1(x , y). cos α=икс

Тангенс (tg) угла поворота

Тангенс угла поворота α — это отношение ординаты точки A1(x , y) к ее абсциссе.  tg α=yx

Котангенс (ctg) угла поворота

Котанг угла поворота α — это отношение абсциссы точки A1(x , y) к ее ординате. ctg α=xy

Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой (0, 1) и (0, -1). В таких случаях выражение для тангенса tg α=yx просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогична ситуация с котангенсом. Отличие состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.

Важно помнить!

Простое правило: синус и косинус определены для любых углов α.

Тангенс определен для всех углов, кроме α=90°+180°·k, k∈Z (α=π2+π·k, k∈Z)

Котангенс определен для всех углов, кроме α=180°·k, k∈Z (α=π·k, k∈Z)

При решении практических примеров не говорят «синус угла поворота α».

Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь. 

Числа

Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?

Синус, косинус, тангенс, котангенс числа

Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.

Например, синус числа 10π равен синусу угла поворота величиной 10π рад.

Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.

Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.

Начальная точка на окружности — точка A c координатами (1, 0).

Положительному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t.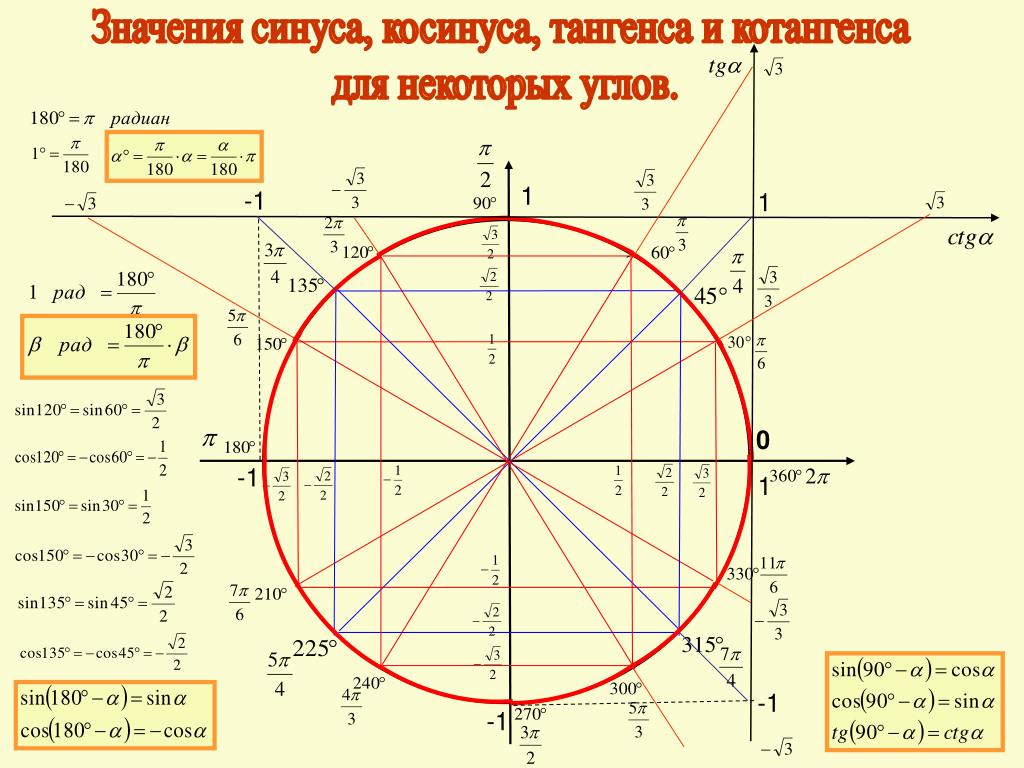

Отрицательному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t.

Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.

Синус (sin) числа t

Синус числа t — ордината точки единичной окружности, соответствующей числу t. sin t=y

Косинус (cos) числа t

Косинус числа t — абсцисса точки единичной окружности, соответствующей числу t. cos t=x

Тангенс (tg) числа t

Тангенс числа t — отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. tg t=yx=sin tcos t

Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.

Тригонометрические функции углового и числового аргумента

Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α, отличным от α = 90 ° + 180 ° · k ,   k ∈ Z   ( α = π 2 + π · k ,   k ∈ Z ) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α, кроме α = 180 ° · k ,   k ∈ Z   ( α = π · k ,   k ∈ Z ). 

Можно сказать, что sin α, cos α, tg α, ctg α — это функции угла альфа, или функции углового аргумента. 

Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t. Всем числам, отличным от π 2 + π · k ,   k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k ,   k ∈ Z.

Основные функции тригонометрии

Синус, косинус, тангенс и котангенс — основные тригонометрические функции.

Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело. 

Связь определений sin, cos, tg и ctg из геометрии и тригонометрии

Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью  соотношений сторон прямоугольного треугольника. Покажем это.

                                                                     

Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A(1,0) на угол величиной до 90 градусов и проведем из полученной точки A1(x,y) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A1OH равен углу поворота α, длина катета OH равна абсциссе точки A1(x,y). Длина катета, противолежащего углу, равна ординате точки A1(x,y), а длина гипотенузы равна единице, так как она является радиусом единичной окружности.  

В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе. 

sin α=A1HOA1=y1=y

Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α, при альфа лежащем в пределах от 0 до 90 градусов.

Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.

Синус, косинус, тангенс и котангенс: основные формулы

​​​​​​​

Тригонометрические формулы

(1) Основное тригонометрическое тождествоsin2(α) + cos2(α) = 1
(2) Основное тождество через тангенс и косинус 1 + tg2(α) = 1/cos2(α)
(3) Основное тождество через котангенс и синус 1 + ctg2(α) = 1/sin2(α)
(4)		 Соотношение между тангенсом и котангенсомtg(α)ctg(α) = 1
(5) Синус двойного углаsin(2α) = 2sin(α)cos(α)
(6) Косинус двойного углаcos(2α) = cos2(α) – sin2(α) = 2cos2(α) – 1 = 1 – 2sin2(α)
(7) Тангенс двойного угла
tg(2α) =   2tg(α)
1 – tg2(α)
(8) Котангенс двойного угла
ctg(2α) =ctg2(α) – 1
  2ctg(α)
(9) Синус тройного углаsin(3α) = 3sin(α)cos2(α) – sin3(α)
(10) Косинус тройного углаcos(3α) = cos3(α) – 3cos(α)sin2(α)
(11) Косинус суммы/разностиcos(α±β) = cos(α)cos(β) ∓ sin(α)sin(β)
(12) Синус суммы/разностиsin(α±β) = sin(α)cos(β) ± cos(α)sin(β)
(13) Тангенс суммы/разности tg(α±β) = (tg(α) ± tg(β))/(1 ∓ tg(α)tg(β))
(14) Котангенс суммы/разности ctg(α±β) = (-1 ± ctg(α)ctg(β))/(ctg(&alpha) ± ctg(β))
(15) Произведение синусовsin(α)sin(β) = ½(cos(α–β) – cos(α+β))
(16) Произведение косинусовcos(α)cos(β) = ½(cos(α+β) + cos(α–β))
(17) Произведение синуса на косинусsin(α)cos(β) = ½(sin(α+β) + sin(α–β))
(18) Сумма/разность синусовsin(α) ± sin(β) = 2sin(½(α±β))cos(½(α∓β))
(19) Сумма косинусовcos(α) + cos(β) = 2cos(½(α+β))cos(½(α–β))
(20) Разность косинусовcos(α) – cos(β) = –2sin(½(α+β))sin(½(α–β))
(21) Сумма/разность тангенсов tg(α) ± tg(β) = sin(α±β)/cos(α)cos(β)
(22) Формула понижения степени синусаsin2(α) = ½(1 – cos(2α))
(23) Формула понижения степени косинусаcos2(α) = ½(1 + cos(2α))
(24) Сумма/разность синуса и косинуса sin(α) ± cos(α) = &sqrt;2sin(α±π/4)
(25) Сумма/разность синуса и косинуса с коэффициентами Asin(α) ± Bcos(α) = Корень(A²+B²)(sin(α ± arccos(A/Корень(A²+B²)))
(26) Основное соотношение арксинуса и арккосинусаarcsin(x) + arccos(x) = π/2
(27) Основное соотношение арктангенса и арккотангенсаarctg(x) + arcctg(x) = π/2
(1) Формула понижения nй четной степени синуса
(2) Формула понижения nй четной степени косинуса
(3) Формула понижения nй нечетной степени синуса
(4) Формула понижения nй нечетной степени косинуса

4.

Формулы половинного угла

М. Борна

На этой странице…

Sin — тождество половины угла
Cos — тождество половины угла
Tan — тождество половины угла

Разработаем формулы для синуса, косинуса и тангенса половинного угла.

Формула половинного угла — синус

Начнем с формулы косинуса двойного угла, с которой мы познакомились в прошлом разделе.

cos 2 θ = 1− 2sin2 θ

92(α/2) = (1 − cos α)/2`

Решение дает нам следующий синус полуугла тождество:

`sin (альфа/2)=+-sqrt((1-cos альфа)/2`

Знак (положительный или отрицательный) `sin(alpha/2)` зависит от квадранта в котором лежит `α/2`.

Если `α/2` находится в первом или втором квадрантах , формула использует положительный регистр:

`sin (альфа/2)=sqrt(1-cos альфа)/2`

Если `α/2` находится в третий или четвертый квадранты , в формуле используется отрицательный регистр:

`sin (альфа/2)=-sqrt(1-cos альфа)/2`

Формула половинного угла — косинус

Используя аналогичный процесс, с той же заменой `theta=alpha/2` (таким образом, 2 θ = α ) мы подставляем в личность

cos 2 θ = 2cos 2 θ − 1 (см. 2(alpha/2)-1` 92(альфа/2)=(1+кос альфа)/2`

Решая `cos(α/2)`, получаем:

`cos (альфа/2)=+-sqrt((1+cos альфа)/2`

Как и прежде, нужный нам знак зависит от квадранта.

Если `α/2` находится в первом или четвертом квадрантах , формула использует положительный регистр:

`cos (альфа/2)=sqrt((1+cos альфа)/2`

Если `α/2` находится в втором или третьем квадрантах , формула использует отрицательный регистр:

`cos (альфа/2)=-sqrt((1+cos альфа)/2`

Формула половинного угла — касательная

Тангенс половинного угла определяется как:

`tan (альфа/2)=(1-cos альфа)/(sin альфа)`

Доказательство

Сначала вспомним `tan x = (sin x) / (cos x)`.

`tan a/2=(sin a/2)/(cos a/2)`

Затем мы используем синус и косинус половины угла, как указано выше:

`=sqrt((1-cos a)/2)/sqrt((1+cos a)/2)`

Следующая строка является результатом умножения верхнего и нижнего на `sqrt 2`.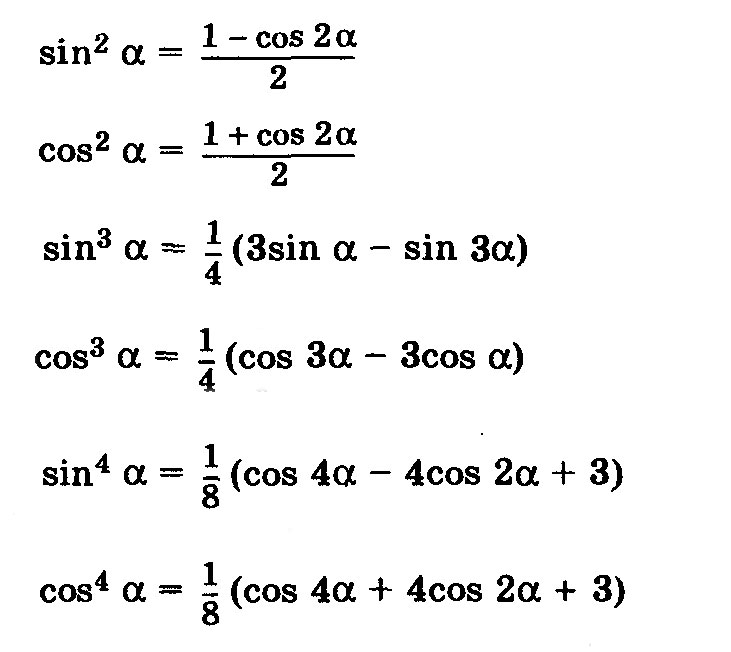 92a))`

Затем мы находим квадратный корень:

`=(1-cos a)/(sin a)`

Конечно, мы должны учитывать положительные и отрицательные знаки, в зависимости от квадранта обсуждаемый.

Мы также можем записать тангенс половинного угла следующим образом:

`tan (альфа/2)=(sin альфа)/(1+cos альфа)`

Доказательство

Мы умножаем числитель (вверху) и знаменатель (внизу) правой части нашего первого результата на `1+cos alpha` и получаем: 92alpha)/(sin alpha(1+cos alpha))`

Наконец, мы сокращаем sin α.

`=(sin alpha)/(1+cos alpha`

Резюме Tan половины угла

`tan (альфа/2)=(1-cos альфа)/(sin альфа)=(sin альфа)/(1+cos альфа`

Использование

т

Иногда полезно определить t как тангенс половины угла:

`t=тангенс (альфа/2)`

Это дает нам результаты:

`sin a=(2t)/(1+t^2)` 9(text(o)))/2)`

`=+-sqrt(((1+0,866))/2)`

`=0,9659`

Первый квадрант, так что положительный.

2. Найдите значение `sin(alpha/2)`, если `cos alpha=12/13`, где 0° < α < 90°.

Ответить

`sin (альфа/2)=+-sqrt((1-cos alpha)/2)`

`=sqrt((1-12/13)/2)`

`=sqrt((1/13) )/2)`

`=sqrt(1/26)`

`=0,1961`

Мы выбираем положительное, потому что находимся в первом квадранте. 92sec\ theta`

`=(1+cos theta)sec\ theta`

`=(1+cos theta)1/(cos theta)`

`=sec\ theta+1`

`=» RHS»`

Формулы сложения косинусов — Задача 3

Итак, вот более сложная задача, которая включает в себя формулы сложения косинусов. В нем говорится, что если синус альфа равен 12 или 13, а альфа находится между пи больше 2 и пи, а косинус бета равен -3 больше 5, а бета находится между пи и 3 пи больше 2, a; найди косинус альфа минус бета и у меня там написано и b; найти косинус альфа плюс бета. Мы сделаем это через секунду.

Прежде всего помните, что формулы сложения косинуса имеют как косинус альфа, так и косинус бета, синус альфа и синус бета, поэтому мне просто не нужны эти два значения. Итак, сначала позвольте мне нарисовать угол альфа на единичной окружности.

Теперь он говорит, что альфа находится между числом пи и 2, она будет где-то в этом квадранте, а синус альфы равен 12 на 13. Теперь синус даст мне вторую координату точки на единичной окружности, и 12 на 13 довольно близко к 1, поэтому я поставлю его здесь. Итак, это мой угол альфа, и это будет что-то вроде запятой 12 на 13, я назову это x.

Теперь мне нужно выяснить, что такое x, x — это косинус альфы, и он мне понадобится в моей формуле, поэтому давайте воспользуемся тем фактом, что x² плюс 12 на 13² равно чему? 1, верно? Это происходит из-за того, что x² плюс y² равняется 1 для единичного круга. Это единичный круг, и это уравнение, поэтому любая точка на единичном круге должна удовлетворять этому уравнению.

Итак, у нас есть x² плюс 144 на 169 равно, это 169 на 169, это то, что 1. Итак, я вычитаю, я получаю x² равно 169 минус 144 это 25 и это означает, что x плюс или минус 5 на 13 и мы знаем, что поскольку мы находимся во втором квадранте, координата x должна быть отрицательной, поэтому мы знаем, что должны выбрать -5 вместо 13, что дает нам косинус альфы, и нам это понадобится через секунду. Давайте сделаем то же самое для бета-версии.

В нем сказано, что косинус бета равен -3 больше 5, а бета находится в пределах от пи до 3 пи больше 2. Ну, это означает, что бета находится в третьем квадранте между пи и 3 пи больше 2, и если косинус равен -3 больше 5, это как -0,6, так что здесь у нас есть точка зрения. -3/5, некоторое значение y, это мой угол бета.

Мне нужно найти значение y, и я сделаю это так же, как здесь. Я собираюсь использовать тот факт, что x² плюс y² равно 1. Таким образом, x минус 3/5 в квадрате плюс y² равно, и когда я возведу это в квадрат, я получу 25 в знаменателе, поэтому у меня будет 25. старше 25. Это 9больше 25 плюс y² равно 25 больше 25, а затем я вычитаю. Y² 16 больше 25, а это означает, что y плюс-минус 4/5. Так что это?

Ну, я нахожусь в третьем квадранте, и синус, и косинус здесь будут отрицательными, поэтому y должно быть -4/5. Теперь это заняло так много времени, что я не помню, где я был в проблеме, мне нужно снова посмотреть. Итак, я пытаюсь найти косинус альфа минус бета. Помните, в разнице косинусов в формуле мне нужны косинус альфа и косинус бета, синус альфа и синус бета.

Итак, это будет косинус, косинус, синус, синус, и помните, что синус меняется с формулой сложения косинуса, поэтому минус становится плюсом. Теперь косинус альфы — это число, первая координата. Это альфа. Первая координата -5 на 13. Косинус бета, возвращающийся сюда, является первой координатой этой точки, это угол бета, а косинус будет -3/5 плюс синус альфа, нам дано, что 12 на 13 и тогда синус бета -4/5 вторая координата а остальное просто арифметика с дробями, но арифметика.

Итак, у нас будет знаменатель, на самом деле давайте отменим. Позвольте мне повременить с этим. Таким образом, у нас будет знаменатель 15 на 65 минус, потому что у меня здесь минус 48 на 65. 15 минус 48 равно -33 на 65. Теперь оказывается, что на самом деле это не уменьшает, так что это было хорошо. идея не сокращать эти дроби раньше времени. Это наш окончательный ответ для косинуса альфа минус бета.