[PDF] 2010 год. 301 вариант. С2 Шарик массой m = 200 г

  • Home
  • 2010 год. 301 вариант. С2 Шарик массой m = 200 г

May 5, 2018 | Author: Anonymous | Category: Математика

Share Embed

Report this link

Short Description

Download 2010 год. 301 вариант. С2 Шарик массой m = 200 г…

Description

2010 год. 301 вариант. С2 Шарик массой m = 200 г , подвешенный к потолку на легкой нерастяжимой нити длиной L = 1,5 м. Шарик привели в движение так, что он движется по окружности в горизонтальной плоскости, образуя конический маятник (см. рисунок). Модуль силы натяжения нити Т = 2,7 Н. Чему равен период обращения τ, за который маятник делает один оборот по окружности? (Решение) 2006 год. 61 вариант. С1 Мяч, брошенный под углом 45° к горизонту с расстояния L = 6,4 м от забора, перелетел через него, коснувшись его в самой верхней точке траектории. Какова высота забора над уровнем, с которого брошен мяч? (Решение) 2010 год. 00 вариант. С2 На озере два рыбака сидят в покоящейся лодке, масса которой М = 100 кг и длина L= 6 м: один — на носу, а второй — на корме. Их массы равны соответственно m1 = 60 кг и m2= 80 кг. Насколько сместится лодка относительно берега озера, если второй рыбак перейдёт к первому? (Трением пренебречь.) (Решение) 2009 год. 135 вариант. С2 На гладкой горизонтальной плоскости находится длинная доска массой М = 2 кг. По доске скользит шайба массой m. Коэффициент трения между шайбой и доской μ = 0,2. В начальный момент времени скорость шайбы v0 = 2 м/с, а доска покоится. В момент t = 0,8 с шайба перестает скользить по доске. Чему равна масса шайбы m? (Решение) 2009 год. 107 вариант. С2 Два шарика, массы которых отличаются в 3 раза, висят соприкасаясь, на вертикальных нитях (см.

рисунок). Лёгкий шарик отклоняют на угол 90° и отпускают без начальной скорости. Найти отношение импульса легкого шарика к импульсу тяжелого шарика сразу после абсолютно упругого центрального соударения. (Решение)

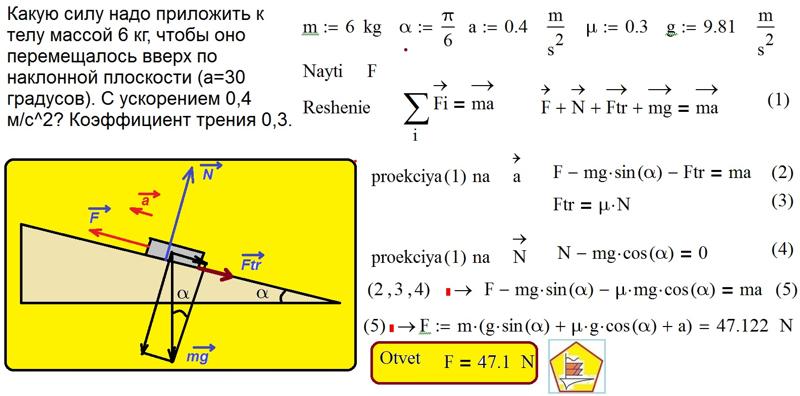
2008 год. 1 вариант. С1 Из пружинного пистолета выстрелили вертикально вниз в мишень, находящуюся на расстоянии 2 м от него. Совершив работу 0,12 Дж, пуля застряла в мишени. Какова масса пули, если пружина была сжата перед выстрелом на 2 см, а ее жесткость 100 Н/м? (Решение) 2008 год. 05205946 вариант. С1 Тело, свободно падающее с некоторой высоты, за время t = 1 с после начала движения, проходит путь в n = 5 раз меньший, чем за такой же промежуток времени в конце движения. Найдите высоту, с которой падало тело. (Решение) 2008 год. 5941 вариант. С1 Маленький шарик падает вертикально вниз на плоскость, имеющую угол наклона к горизонту 30° и упруго отражается от неё. Следующий удар шарика о плоскость происходит на расстоянии 20 см от места первого удара. Определите промежуток времени между первым и вторым ударами шарика о плоскость.
(Решение) 2007 год. 6 вариант. С1 Наклонная плоскость пересекается с горизонтальной плоскостью по прямой АВ. Угол между плоскостями α = 30°. Маленькая шайба начинает движение вверх по наклонной плоскости из точки А с начальной скоростью v под углом 60° к

прямой АВ. В ходе движения шайба съезжает на прямую АВ в точке В. Найдите v, если АВ = 1 м. Трением между шайбой и наклонной плоскостью пренебречь. (Решение)

2007 год. 30 вариант. С1 Пушка, закрепленная на высоте 5 м, стреляет в горизонтальном направлении снарядами массы 10 кг. Вследствие отдачи ее ствол, имеющий массу 1000 кг, сжимает на 1 м пружину жесткости 6•103 Н/м, производящую перезарядку пушки. Считая, что относительная доля μ = 1/6 энергии отдачи идет на сжатие пружины, найдите дальность полета снаряда.(Решение) 2007 год. 25 вариант. C1 Брусок массой m скользит по горизонтальной поверхности стола и нагоняет брусок массой 6 m, скользящий по столу в том же направлении. В результате неупругого соударения бруски слипаются.

Их скорости перед ударом были v0 = 7 м/с и v0/З. Коэффициент трения скольжения между брусками и столом μ = 0,5. На какое расстояние переместятся слипшиеся бруски к моменту, когда их скорость станет 2v0/7? (Решение) 2006 год. 33 вариант. С1 Шар массой 1 кг, подвешенный на нити длиной 90 см, отводят от положения равновесия на угол 60° и отпускают. В момент прохождения шаром положения равновесия в него попадает пуля массой 10 г, летящая навстречу шару, она пробивает его и продолжает двигаться горизонтально со скоростью 200 м/с. С какой скоростью летела пуля, если шар, продолжая движение в горизонтальном направлении, отклоняется на угол 39°? (Массу шара считать неизменной, диаметр шара — пренебрежимо малым по сравнению с длиной нити, cos 39° = 7/9). (Решение) 2005 год. 91 вариант. С1 Пуля, летящая горизонтально со скоростью v0 = 120 м/с, пробивает лежащую на горизонтальной поверхности стола коробку и продолжает движение в прежнем направлении, потеряв 80% скорости. Масса коробки в 16 раз больше массы пули.
Коэффициент трения скольжения между коробкой и столом μ = 0,5. На какое расстояние переместится коробка к моменту, когда её скорость уменьшится вдвое? (Решение) 2004 год. 99 вариант. С1 С некоторой высоты Н свободно падает стальной шарик. Через t = 1 с после начала падения он сталкивается с неподвижной плитой, плоскость которой наклонена под углом 45° к горизонту, и до момента падения на Землю пролетает по горизонтали расстояние S = 20 м. Каково значение Н? Сопротивление воздуха не учитывать. Удар шарика о плиту считать абсолютно упругим. (Решение) 2004 год. 119 вариант. C1 Брусок массой m1 = 500 г соскальзывает по наклонной плоскости высотой h = 0,8 м и сталкивается с неподвижным бруском массой m2 = 300 г, лежащим на горизонтальной поверхности. Считая столкновение упругим, определите кинетическую энергию первого бруска после столкновения. Трением при движении пренебречь. (Решение) 2004 год. 97 вариант. С5 Брусок массой m1 = 1 кг лежит на наклонной плоскости с углом при основании, равным α = 53°.
Коэффициент трения бруска с плоскостью равен μ = 0,5. К бруску привязана невесомая нить, другой конец которой перекинут через неподвижный идеальный блок. К этому концу нити подвешивается

груз массой m2 = 1 кг. Определите, придет ли в движение брусок при подвешивании груза. Если придет в движение, то в каком направлении? (sin 53° = 0,8; cos 53° = 0,6) (Решение) 2002 год. 265 вариант. С1 Нить маятника длиной l = 1 м, к которой подвешен груз массы m = 0,1 кг, отклонена на угол α от вертикального положения и отпущена. Сила натяжения нити T в момент прохождения маятником положения равновесия равна 2 Н. Чему равен угол α? (Решение) 2009 год. 02 вариант. С2 Радиус планеты Плюк в 2 раза меньше радиуса Земли, а период обращения спутника, движущегося вокруг Плюка по низкой круговой орбите, совпадает с периодом обращения аналогичного спутника Земли. Чему равно отношение средних плотностей Плюка и Земли? Объём шара пропорционален кубу радиуса (V ~ R3). (Решение)

View more. ..

Comments

Простая физика — EASY-PHYSIC

Будем искать силы натяжения стержней при скольжении, ускорения досок, вращать диски с грузиками на них…

Задача 1.

На гладкой горизонтальной поверхности стола лежит доска массой , по которой скользит брусок массой . Чему равно ускорение доски при её движении вдоль стола, если , а коэффициент трения бруска о доску равен ? Ответ выразить в м/, округлив до целых. Ускорение свободного падения принять равным м/.


К задаче 1

Решение.

Так как по условию скольжение бруска по доске есть, то сила трения вышла на максимум, и по третьему закону Ньютона доска разгоняется силой

Из второго закона Ньютона для доски получаем, что   откуда с учётом , найдём, что ускорение доски равно

Ответ: 5 м/.

 

Задача 2.

Брусок толкнули вверх по наклонной плоскости, составляющей с горизонтом. Через с брусок остановился, а еще через с вернулся в исходную точку.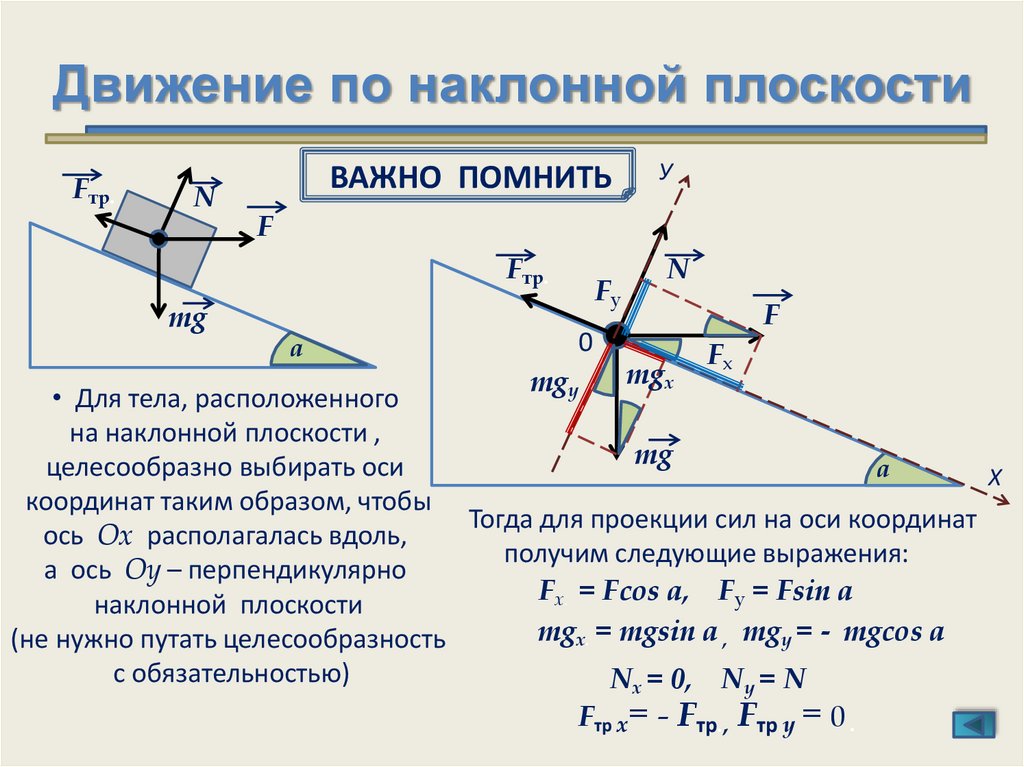 Чему равен коэффициент трения? Ответ округлить до сотых.


Задача 2. Движение вверх.


Задача 2. Движение вниз.

Решение.

Из второго закона Ньютона получаем, что

Запишем второй закон Ньютона в проекции на ось , направленную вверх вдоль плоскости при движении груза вверх. Получим, что

где

Откуда проекция ускорения равна

При движении вниз направим ось таким же образом. Проекция ускорения равна

Перемещение выражается по формуле , поэтому

Подставляя выражения для и и решая уравнение, получаем коэффициент трения, равный

Ответ: 0,35.

 

Задача 3.

Наибольшее значение силы трения покоя между вращающимся диском и расположенным на нём грузом массой кг равно Н. На некотором максимальном расстоянии от оси вращения груз будет удерживаться на диске, не скользя по нему, если диск станет вращаться с частотой об/с? Чему равна сила трения груза о диск в тот момент, когда груз находится от оси вращения на половине найденного расстояния? Ответ выразить в Н, округлив до сотых.

Решение.

На предельном расстоянии на тело действуют силы тяжести, реакции опоры и сила трения, сообщающие ему центростремительное ускорение. Из второго закона Ньютона в проекции на ось , направленную по радиусу к центру вращающегося диска, получаем, что

где , тогда

Таким образом, максимальное расстояние от оси вращения, на котором груз будет удерживаться на диске, выражается по формуле

Когда груз находится от оси вращения на половине найденного расстояния, центростремительное ускорение ему обеспечивает сила трения, равная

Ответ: 12,25 Н.

Задача 4.

Неподвижный клин с углом при основании имеет гладкую нижнюю и шероховатую верхнюю части своей наклонной плоскости. На верхней части клина удерживают тонкий однородный жёсткий стержень массой кг, расположенный в плоскости рисунка. Коэффициент трения между стержнем и верхней частью клина равен . После того как стержень отпускают, он начинает поступательно скользить по клину. Найдите максимальное значение силы натяжения стержня в процессе его движения. Влиянием воздуха пренебречь. Ответ выразить в Н, округлив до целых. Ускорение свободного падения принять равным м/


К задаче 4

Решение.

Введём ось которая параллельна стержню и направлена вниз по клину. В тот момент, когда на гладкой поверхности клина оказывается часть стержня массой , где , на неё вдоль оси действует составляющая силы тяжести и сила натяжения со стороны верхней части стержня, направленная противоположно оси , и равная . Запишем уравнение движения нижней части стержня вдоль оси . Получим, что

где — ускорение любой точки стержня вдоль оси , так как стержень твёрдый и движется поступательно.

В рассматриваемый момент на верхнюю часть стержня вдоль оси наряду с составляющей силы тяжести со стороны клина действует направленная противоположно оси сила сухого трения скольжения , а со стороны нижней части стержня действует направленная вдоль оси сила натяжения . Уравнение движения этой части стержня в проекции на ось имеет вид

Решая совместно составленные уравнения, получаем

Видно, что сила натяжения стержня в сечении, которое находится на границе между гладкой и шероховатой частями клина, зависит от значения коэффициента .Она будет максимальной при , т.е. когда одна половина стержня окажется на гладкой нижней части клина, а другая половина — на его шероховатой верхней части. В таком случае

Ответ: 1 Н.

Задача 5.

Тело равномерно скользит по наклонной плоскости с углом наклона . Определить коэффициент трения тела о плоскость. Ответ округлить до сотых.

Решение.

Так как тело скользит равномерно, векторная сумма сил, действующих на него, равна нулю. Можно действующие на тело силы , , , изобразить в виде векторного треугольника. Из которого

Ответ: 0,84.

 

Наклонные плоскости — Простые машины для детей — Изобретатели завтрашнего дня

На первом занятии по простым машинам мы рассмотрели наклонные плоскости и шкивы.

Ключевым моментом наклонных плоскостей является то, что подъем тяжелого груза с помощью наклонной плоскости (или пандуса) требует меньшего усилия, чем просто подъем его прямо вверх, но груз перемещается на большее расстояние. Вы можете дать детям тяжелый груз и попросить их поднять его прямо на стол, полку или платформу на горке. Затем дайте им короткую крутую рампу, чтобы подтолкнуть ее вверх. Тогда дайте им гораздо более длинный и не такой крутой пандус. Что легче всего/наименее работает?

Мы проиллюстрировали это с помощью стремянки, плюшевого слона и доски. «Может ли этот слон запрыгнуть на верхнюю платформу по лестнице? Нет! Сможете ли вы поднять слона на высокую платформу? Нет. Что, если мы поместим этот крутой пандус здесь? Теперь он может это сделать? Да, но это действительно крутой холм. Что, если мы поставим вот эту длинную, не очень крутую доску? Теперь это намного проще. Слону нужно пройти гораздо дальше, но это легкая прогулка».

Сколько работы?

Привяжите маленькие ведерки к игрушечным машинкам. Установите неглубокий пандус, подперев доску книгами или блоками. Накиньте ведро на конец пандуса. Бросьте пенни или шарики в ведро. Сколько копеек нужно, чтобы вес подтянул машину к вершине пандуса? Теперь установите более крутой пандус. Сколько копеек (т.е. сколько работы) нужно, чтобы вытащить машину наверх? Эта идея и фотография слева взяты из книги «Простые машины» Деборы Ходж. Второе фото наше из класса.

 

Примечание. В учебных ресурсах есть набор упражнений «Сила и движение», который позволяет детям экспериментировать с маятниками и наклонными плоскостями. Я его не видел, но по картинкам видно, что в наборе есть материалы, которые можно использовать для этого занятия. Я лично предпочитаю проводить эксперименты с материалами, которые есть у каждого дома, а не покупать специальное оборудование, потому что это делает его более удобным для воспроизведения дома, но вы можете предпочесть сборные.

Измерение

Это хорошо для детей в возрасте от 6 лет и старше: Имейте 5 книг или 5 кубиков (все одного размера), линейку с углублением в центре, карандаш, графические листы, мрамор, измерительную ленту.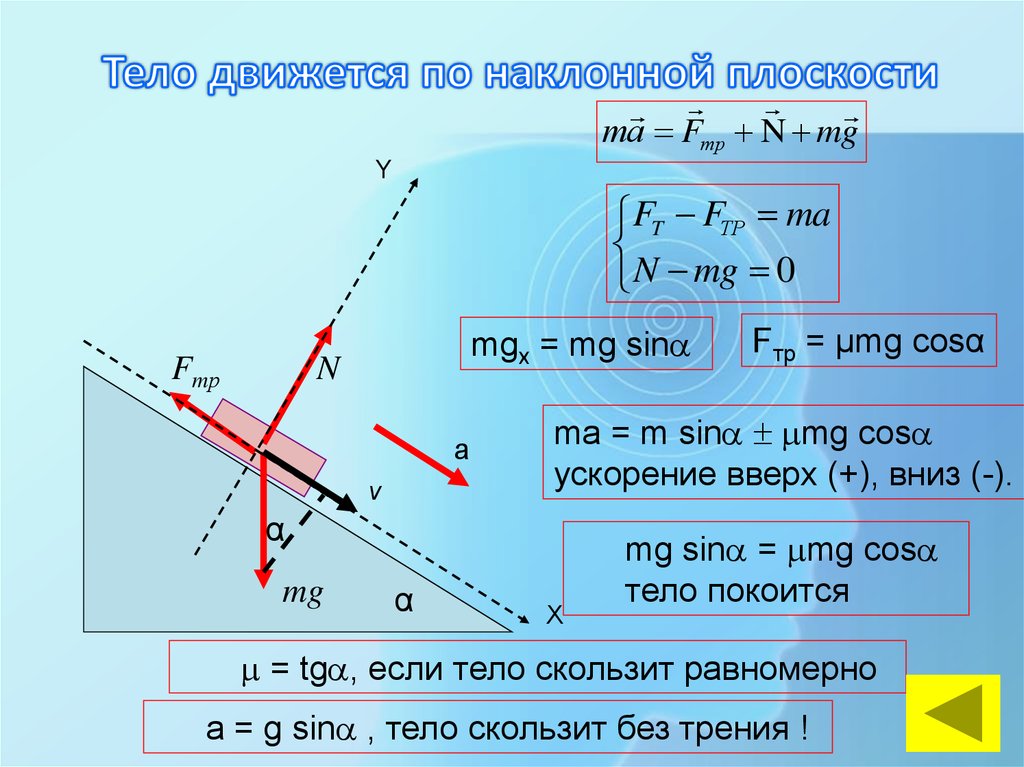 Они подпирают линейку одной книгой. Прокатите шарик по канавке, измерьте, как далеко он ушел. Запись на графике. Потом две книги, потом три…  (Идея из книги Energy Lab)

Искусство и опыт

Мы попросили детей украсить свои собственные наклонные плоскости (деревянными мешалками для краски или длинными деревянными прокладками). Вы можете использовать акриловые краски или маркеры и мазки для бинго. Мы использовали меловые маркеры, которые прекрасно работают с деревом (они предназначены для смывания с непористых поверхностей, таких как стекло, и предостерегают вас от использования на пористых поверхностях, потому что они не смываются — это было именно то, что мы хотели! )

Затем они могли перенести свои пандусы на испытательный стол, поставить их на стопки книг или блоков и скатить по ним блоки цилиндров. Это был отличный способ проверить идею о том, что чем круче пандус, тем быстрее они катятся. (Обратите внимание на рисунок ниже, на барьеры, которые мы установили, чтобы удерживать их на столе! Мы не сделали этого заранее, и наши дюбели продолжали ускользать, но, к счастью, вмешался папа, чтобы решить проблему их катания по полу. )

Яичный рулет

Пандусы чаще всего используются для перемещения тяжелых предметов. Еще один способ использования пандусов — сделать поездку вниз более плавной. Отличный способ проиллюстрировать это — бросить яйцо в кастрюлю высотой от 6 до 12 дюймов. Это сломается. Спросите: как я могу опустить это более мягко? Затем используйте некрутую рампу, чтобы аккуратно опустить его в кастрюлю. Мы не делали этого в классе, потому что не хотели кучу разбитых яиц! Но это забавная возможность сделать это на собственной кухне в следующий раз, когда вы готовите яичницу-болтунью. Или вы можете сделать то же, что и мы, когда тестируем задание «Капнуть яйцо»: сделать «пробное яйцо». Возьмите пластиковое пасхальное яйцо и поместите в него попрыгунчик. Если обращаться с ним достаточно бережно, оно не разобьется — как настоящее яйцо. Но при сильном ударе оно разобьется — как настоящее яйцо, но без липкой кашицы.

Сенсорная игра

У нас была игрушка с конвейерной лентой, и дети могли проворачивать колесо (еще один простой механизм), чтобы создать действие шкива для перемещения риса вверх по наклонной плоскости. Вы также можете просто предложить пандусы, чтобы высыпать рис: попробуйте использовать несколько кусков бамбука, вырезанных в форме желоба, или трубочки от бумажных полотенец, разрезанные пополам вдоль, или картон, сложенный в пандусы со стенками.

 

На уровне грунтовых вод мы сделали каскад из пакетов из-под молока, чтобы через него выливалась вода.

Мастерский проект

Мы подготовили для изучения мраморную дорожку своими руками. Или мне также нравится использовать Tumble Trax.

Гараж

В нашем игрушечном гараже есть наклонные плоскости (пандусы) для движения машинок вверх и вниз, а также лифт на шкиве (две простые машинки в одной игрушке).

Большой мотор

У нас есть небольшая горка (наклонная плоскость), которую мы устанавливаем в помещении. У нас также было два клиновидных коврика и один треугольный коврик. Дети устроили полосу препятствий и обнаружили, что подниматься по некрутому клину гораздо проще, чем по крутому треугольнику.

Outdoor Time

Дети играли на горке и катались на велосипедах вверх и вниз по холмам. Мы отметили, что ехать в гору было труднее, чем ехать по равнине, а также то, насколько быстрее они едут, спускаясь с холма.

Еще один отличный эксперимент (особенно если вы прочитали «Поднятие мешка с игрушками по кругу») — предложить детям поднять груз на вершину платформы для скольжения. Вы можете протестировать варианты как со шкивами, так и с наклонной плоскостью.

Мы читаем «Форт на Четвертой улице: рассказ о шести простых машинах» и «Поднятие мешка с игрушками: шкив против наклонной плоскости». Информацию о других книгах Simple Machines можно найти здесь.

Песня: Мы повторили нашу музыкальную тему Simple Machines.

Музыка / Видео : Sid the Science Kid имеет эпизод о наклонных плоскостях под названием My Slide. Он включает в себя песню «Push it Up the Inclined Plane», которую вы можете найти здесь . Мы играем и подпеваем.

Через неделю после занятий родители могут попросить ребенка заметить наклонные плоскости в их мире. Самый простой пример — движущийся фургон или грузовик для доставки: вместо того, чтобы стоять рядом с платформой грузовика и поднимать ящик высоко на платформу, рабочий поднимается по пандусу — это большее расстояние, но меньше работы. Они могут помочь своим детям заметить склоны и холмы: «Это крутой холм. Трудно подниматься вверх». «Будь осторожен, спускаясь с холма на велосипеде. Это заставит вас двигаться быстрее».

На этой неделе мой четырехлетний ребенок хотел переместить большую коробку вверх по лестнице — она была достаточно большой, чтобы скользить вверх, потому что занимала пару ступенек — и он много говорил о том, как наклонная плоскость помогла ему переместить большой тяжелый вещи.

Примечание . Все действия, описанные в моих постах , относятся к Лаборатории Семейных Изобретателей, кооперативному классу родителей и детей в Белвью, штат Вашингтон. Мы представляем собой игровой класс, ориентированный на STEM, для детей дошкольного и младшего школьного возраста (от 3 до 7 лет). Мы проводим множество веселых практических занятий, чтобы узнать о науке, инструментах, технике, природе и искусстве. Мы также поем песни и читаем сказки. Большинство наших мероприятий дешевы, просты и используют повседневные материалы, которые у большинства семей были бы дома (или в их мусорных баках!), Так что наши мероприятия подходят для классных учителей, родителей, которые обучаются на дому, или после школьных программ.

Примерно так:

Нравится Загрузка…

Коробка размером H xx B xx R держится на наклонной плоскости без трения, как показано на рисунке. Камень брошен из угла P со скоростью u параллельно потолку ящика так, что он упал на пол ящика. В тот же момент коробка отпускается и скользит по плоскости. Рассчитать время полета.

FIITJEE-KINEMATICS-SECTION(II): MCQ (SINGLE CORRECT)

20 видео

РЕКЛАМА

Ab Padhai karo bina ads ke

Khareedo DN Про и дехо сари видео бина киси ад ки рукаават ке!

Обновлено на: 27-06-2022

Текстовое решение

A

√2HGCOSθ

C

√hgcosθ

D

не может быть рассчитано

Ответ

. Ответ

Пошаговое решение от экспертов, которое поможет вам избавиться от сомнений и получить отличные оценки на экзаменах.

Похожие видео

Большой тяжелый ящик скользит без трения по гладкой плоскости с наклоном θ . Из точки P на дне ящика внутрь ящика падает частица. Начальная скорость частицы относительно ящика равна u, а направление проецирования составляет угол α с дном, как показано на рисунке.
(а) Найдите расстояние вдоль дна ящика между точкой проекции p и точкой Q, куда приземляется частица. (Предположим, что частица не ударяется ни о какую другую поверхность ящика. Сопротивлением воздуха пренебрегаем.)
(b) Если горизонтальное перемещение частицы, наблюдаемое наблюдателем с земли, равно нулю, найдите скорость ящика относительно земли в момент, когда частица была сброшена.

10058446

Ящик массой 4 кг лежит на наклонной плоскости Этот наклон постепенно увеличивается до тех пор, пока ящик не начнет скользить по плоскости. На данном этапе наклон плоскости равен 1 к 3. Найдите коэффициент трения между ящиком и плоскостью. Какая сила, приложенная к ящику параллельно плоскости, заставит ящик двигаться только вверх по плоскости?

11763929

Ящик лежит на наклонной плоскости Каков будет коэффициент трения покоя, если ящик начинает скользить при угле наклона 60∘

15716733

Прямоугольный ящик скользит по гладкой наклонной плоскости тета. При t=0 ящик начинает двигаться по наклонной плоскости. Болт начинает падать из точки А. Найдите время, через которое болт ударится о нижнюю поверхность коробки.

18253787

Очень тяжелый ящик держится на наклонной плоскости без трения, наклоненной под углом θ к горизонтали. Коробка имеет другую наклонную плоскость без трения, наклонную плоскость, как показано на рисунке. На этой наклонной плоскости внутри ящика держится брусок массы m. Ускорение блока относительно коробка

36825317

Коробку массой 20 кг аккуратно помещают на шероховатую наклонную плоскость с углом наклона 30° к горизонтали.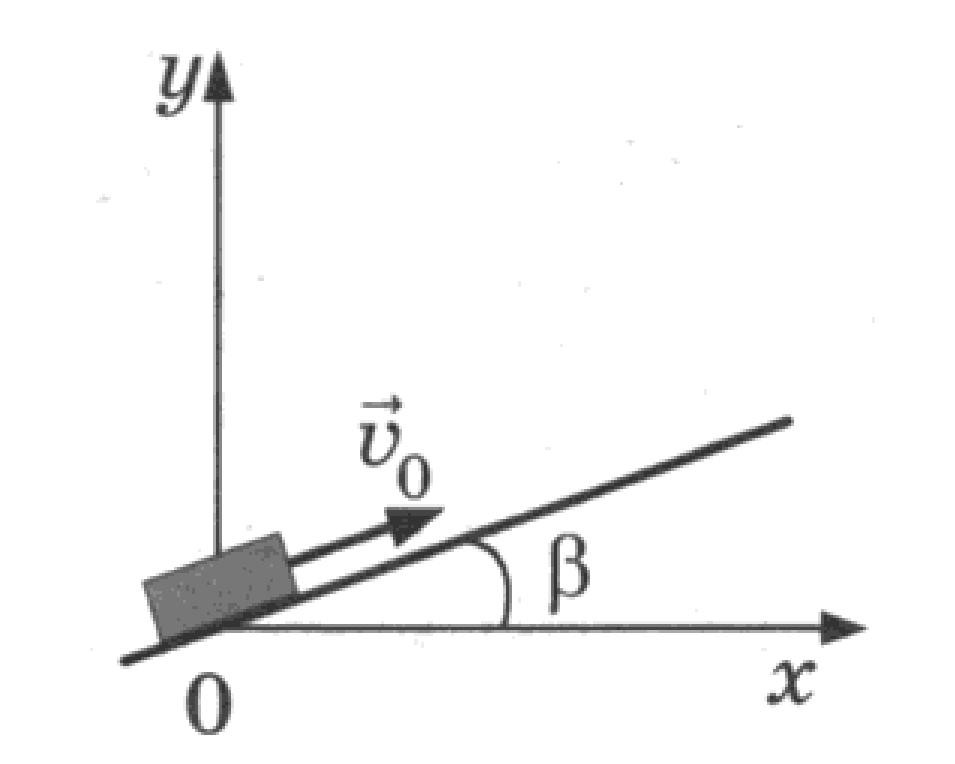 Коэффициент трения скольжения между коробкой и плоскостью равен 0,5. Найдите ускорение коробки вниз по склону.

212490548

Прямоугольный ящик лежит на шероховатой наклонной поверхности. Коэффициент трения между поверхностью и ящиком равен (μ). Пусть масса ящика равна m.
При каком угле наклона θ плоскости к горизонту коробка только начнет скользить по плоскости? 9(@) тогда коэффициент статического трения коробки и плоскости равен?

417979146

На наклонной плоскости лежит деревянный ящик. Чему равен коэффициент трения, если ящик начинает скользить при угле наклона 45°?

427216333

Прямоугольный ящик лежит на шероховатой наклонной поверхности. Коэффициент трения между поверхностью и коробкой равен µ. Пусть масса ящика m.
(а) При каком угле наклона θ плоскости к горизонту коробка только начнет скользить по плоскости?
(b) Какова сила, действующая на ящик вниз по плоскости, если угол наклона плоскости увеличить до α>θ?
(c) Какую силу необходимо приложить вверх по плоскости, чтобы ящик либо оставался неподвижным, либо просто двигался вверх с постоянной скоростью?
(d) Какую силу необходимо приложить вверх по плоскости, чтобы ящик двигался вверх по плоскости с ускорением a?

642507214

Большой тяжелый ящик скользит без трения по гладкой плоскости наклона θ . Из точки P на дне ящика внутрь ящика падает частица. Начальная скорость частицы относительно ящика равна u, а направление проецирования составляет угол α с дном, как показано на рисунке.
(a) Найдите расстояние по дну ящика между точкой проекции p и точкой Q, куда приземляется частица. (Предположим, что частица не ударяется ни о какую другую поверхность ящика. Сопротивлением воздуха пренебрегаем.)
(b) Если горизонтальное смещение частицы, наблюдаемое наблюдателем на земле, равно нулю, найдите скорость ящика относительно на землю в момент выброса частицы.

642752695

Ящик, поставленный на гладкую наклонную плоскость, может свободно двигаться. Найдите период колебаний простого маятника, прикрепленного к потолку ящика. 9@ с горизонталью так, чтобы легкое постукивание вызывало скольжение коробки. Рассчитайте коэффициент трения покоя для соприкасающихся поверхностей ящика и наклонной плоскости.

643049850

Прямоугольный ящик скользит по гладкой наклонной плоскости с наклоном α, как показано на рисунке. При t = 0 ящик начинает двигаться по наклонной плоскости. Болт начинает падать из точки А. Найдите время, через которое болт ударится о нижнюю поверхность ящика.

644362581

Большой тяжелый ящик скользит без трения по гладкой плоскости с наклоном θ . Из точки P на дне ящика внутрь ящика падает частица. Начальная скорость частицы относительно ящика равна u, а направление проецирования составляет угол α с дном, как показано на рисунке.
Найдите расстояние по дну ящика между точкой проекции p и точкой Q, куда приземляется частица. (Предположим, что частица не ударяется ни о какую другую поверхность ящика. Сопротивлением воздуха пренебрегаем.

644639849

Большой тяжелый ящик скользит без трения по гладкой наклонной плоскости θ . Из точки P на дне ящика внутрь ящика падает частица. Начальная скорость частицы относительно ящика равна u, а направление проецирования составляет угол α с дном, как показано на рисунке.