Определение координаты движущегося тела (9 класс)
Как определить координаты движущегося тела? Для этого необходимо знать такие понятия, как механическое движение, пройденный путь, скорость, перемещение.
Механическое движение
При механическом движении происходит изменение положения тела в пространстве относительно других тел за промежуток времени. Оно бывает равномерным и неравномерным.
Равномерное движение
При равномерном движении тело за равные промежутки времени проходит одинаковые расстояния (т.е. движется с постоянной скоростью).
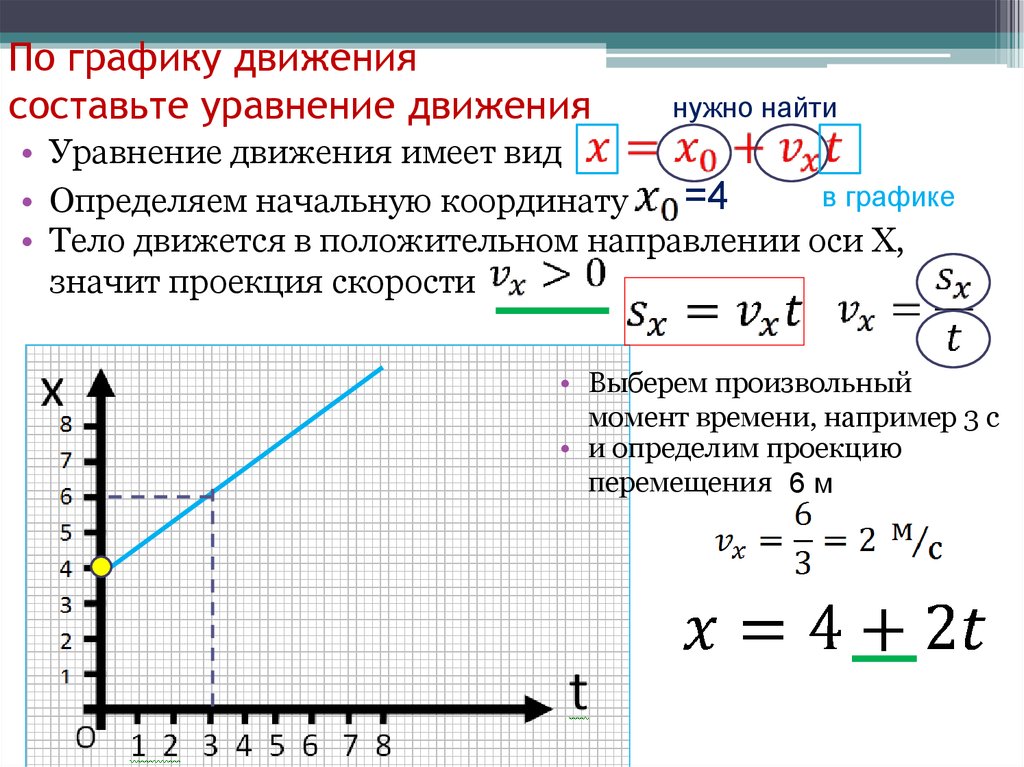
Путь, пройденный при равномерном движении равен: Sx=Vxt=x-xо
Следовательно, при равномерном движении координата тела изменяется по следующей зависимости:
Рис. 1. Формула координаты тела при прямолинейном равномерном движенииГде:
- Xо – начальная координата тела;
- X – координата в момент времени t;
- Vx – проекция скорости на ось X.
Неравномерное движение
Неравномерное движение – движение, при котором тело за равные промежутки времени проходит неодинаковые расстояния (движется с непостоянной скоростью), то есть движется с ускорением.
Если тело движется неравномерно, то скорость тела в разные моменты отличается не только по величине, но и (или) по направлению. Средняя скорость тела при неравномерном движении определяется по формуле: V (ср)= S (весь)/t (весь)
Ускорение – величина, показывающая, как изменяется скорость за 1 секунду.
Рис. 2. Формула ускоренияСледовательно, скорость в любой момент времени можно найти следующим образом:
V=Vо+at
Если скорость с течением времени увеличивается, то a больше 0, если скорость с течением времени уменьшается, то a меньше 0.
Как найти путь при равноускоренном движении?
Рис. 3. Прямолинейное равноускоренное движениеПройденный путь численно равен площади под графиком.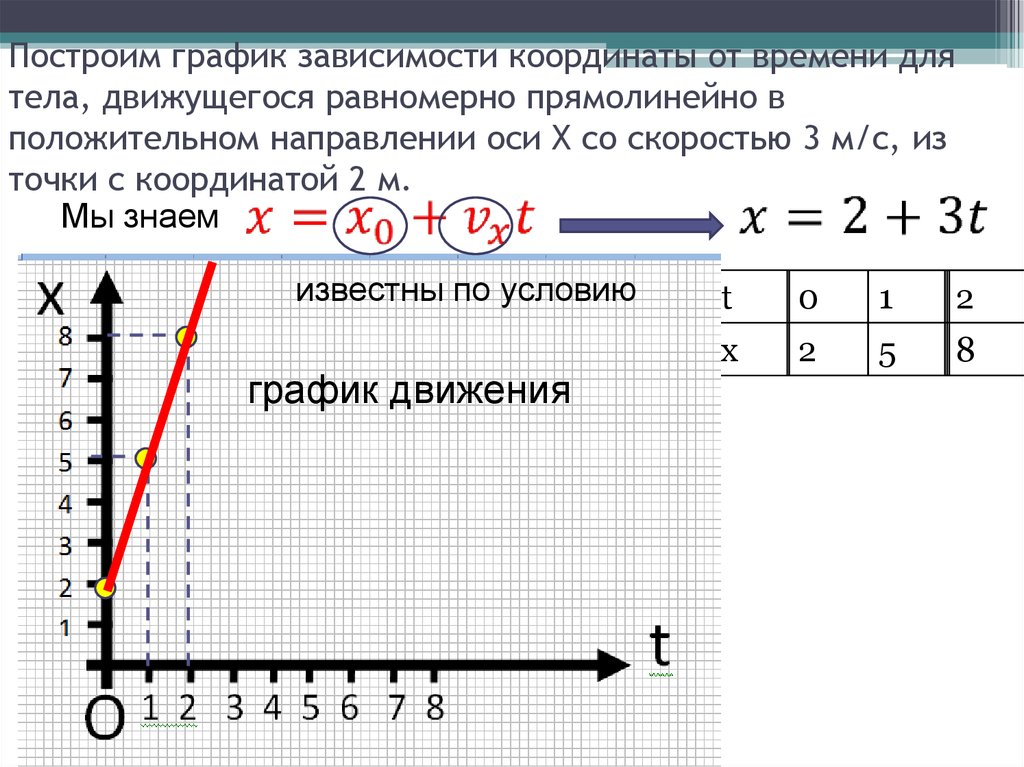
То есть Sx=(Vox+Vx)t/2
Скорость в любой момент времени равна Vx=Vox+axt, следовательно Sx=Voxt+axt2/2
Так как перемещение тела равно разности конечной и начальной координат (Sx=X-Xo), то координата в любой момент времени вычисляется по формуле X=Xo+Sx, или
X=Xo+Voxt+axt2/2
Движение тела по вертикали
Если тело движется по вертикали, а не по горизонтали, то такое движение всегда является равноускоренным. Когда тело падает вниз, то падает оно всегда с одинаковым ускорением – ускорением свободного падения.
При движении по вертикали формула скорости приобретает вид: Vy=Voy+gt,
где Vy и Voy – проекции начальной и конечной скоростей на ось OY.
Координату же можно рассчитать по формуле: Y=Yo+Voyt+gt2/2
Движение тела по окружности
При движении по окружности численное значение скорости может и не изменяться, но поскольку обязательно изменяется направление, то движение по окружности – это всегда равноускоренное движение.
Что мы узнали?
Тема «Определение координаты движущего тела», которую изучают в 9 классе, поможет ученикам систематизировать информацию о том, что движение может быть равномерным и неравномерным. Так же для того чтобы знать пройденный путь, нужно выбрать тело отсчета и использовать прибор для отсчета времени.
Оценка доклада
А какая ваша оценка?
Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
09.16
| ||||||||||||
09.16
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Физика
| Похожие вопросы |
Льдинка падает с высоты 4 м.
Определите время, за которое она пролетела последний метр, а так же среднюю скорость её движения
Решено
Измерьте среднюю скорость движения висящего на нити шарика. Рекомендации:используйте нить длиной 30-40 см,угол отклонения 20-30градусов(угол измеряется транспортиром).
Сплошной груз взвесили с помощью динамометра. Сначала его целиком погрузили в воду, а затем в керосин. В первом случае показания прибора составили P1=3,1 Н, а во втором – P2=3,5 Н.
Решено
Задачи на перемещение при равноускоренном прямолинейном движении
Помогите с задачами.
Пользуйтесь нашим приложением
Об аэрокосмических системах координат — MATLAB & Simulink
Об аэрокосмических системах координат
Основные концепции системы координат
Системы координат позволяют отслеживать положение самолета или космического корабля и
ориентация в пространстве.
Системы координат Aerospace Blockset™ основаны на этих основных концепциях из
геодезии, астрономии и физики.
Определения
В наборе блоков используется правосторонний (RH) Декартово системы координат. Правило правой руки устанавливает x — y — z последовательность координатные оси.
Инерциальная система отсчета представляет собой неускоряющуюся систему отсчета движения. В В инерциальной системе отсчета выполняется второй закон Ньютона: сила = масса x ускорение. свободно говоря, ускорение определяется по отношению к далекому космосу, а инерциальную систему отсчета часто называют неускоренной относительно фиксированной звезды. Поскольку Земля и звезды движутся так медленно относительно друг друга, это предположение является очень точным приближением.
Строго определенная, инерциальная система отсчета является членом множества всех неускоряющихся отсчетов
относительно друг друга. Неинерциальная система отсчета — это любая система отсчета, ускоряющаяся относительно
к инерциальной системе отсчета.
Его ускорение, вообще говоря, включает в себя как поступательное
и вращательные компоненты, в результате чего псевдосил ( псевдогравитация, а также Кориолисовы и центробежные
сил ).
Набор блоков моделирует форму Земли ( геоид ) в виде сплюснутого сфероида, особый тип эллипсоида с двумя равными длинными осями (определяющий экваториальная плоскость ) и третья, немного короче ( геополярный ) ось симметрии. Экватор – это пересечение экваториальной плоскости и земной поверхности. Географические полюса являются пересечением земной поверхности и геополярной оси. В целом, Геополярная ось и ось вращения Земли не идентичны.
Широты параллельны экватору. Долготы параллельны геополярной оси. ноль долгота или начальный меридиан проходит через Гринвич, Англия.
Приближения
Набор блоков делает три стандартных приближения при определении
системы координат относительно Земли.
Поверхность Земли или геоид представляет собой сплюснутый сфероид, определяемый более длинная экваториальная и более короткая геополярная оси. В действительности Земля является слегка деформирован по отношению к стандартному геоиду.
Ось вращения Земли и экваториальная плоскость перпендикулярны, поэтому что оси вращения и геополярные оси идентичны. В действительности эти оси немного смещены, а экваториальная плоскость качается, когда Земля вращается. В большинстве приложений этот эффект незначителен.
Единственный неинерционный эффект в земных координатах связан с Вращение Земли вокруг своей оси. Это вращающийся, геоцентрическая система . Блокчейн игнорирует Землю ускорение вокруг Солнца, ускорение Солнца в Галактике и Ускорение галактики через космос. В большинстве приложений только Вращение Земли имеет значение.
Это приближение должно быть изменено для космического корабля, отправленного в глубокое космос, например, за пределами системы Земля-Луна, и гелиоцентрическая система является предпочтительным.
Пассивные преобразования
Все кватернионы в Aerospace Blockset являются пассивными преобразованиями. При пассивном преобразовании вектор не меняется, а система координат, в которой он определен, поворачивается. Для большего информацию о преобразованиях см. в разделе Активные и пассивные преобразования.
Движение относительно других планет
Набор блоков использует стандартный геоид WGS-84 для моделирования Земли. Вы можете изменить длину экваториальной оси, сглаживание и скорость вращения.
Вы можете изобразить движение космического корабля относительно любой небесное тело, которое хорошо аппроксимируется сплюснутым сфероидом изменение размера сфероида, сглаживания и скорости вращения. Если небесное тело вращается на запад (ретроградно), сделайте вращение оценка отрицательная.
Системы координат для моделирования
Моделирование самолетов и космических аппаратов проще всего, если использовать систему координат, закрепленную в теле
сам.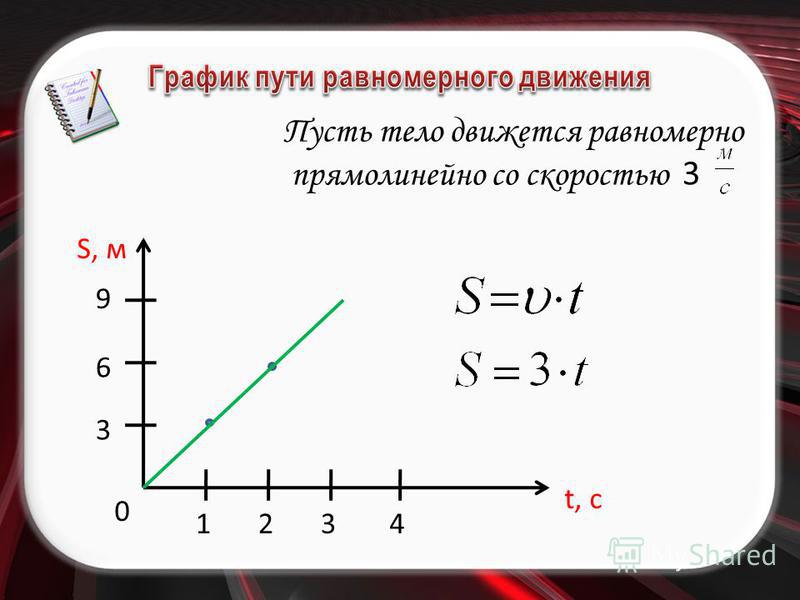
В случае самолета направление вперед изменяется наличием
ветра, и движение корабля по воздуху не совпадает с его движением относительно
на землю.
См. уравнения движения для получения дополнительной информации о том, как набор блоков реализует тело и ветер координаты.
Координаты тела
Неинерциальная система координат тела фиксируется как в начале координат, так и в ориентации движущееся судно. Судно считается жестким.
Ориентация осей координат тела зафиксирована в форме тела.
Ось x указывает через нос корабля.
Ось y указывает справа от x -ось (лицом в направлении взгляда пилота), перпендикулярно x — ось.
Ось z указывает вниз через дно корабля, перпендикулярно плоскости xy и удовлетворяющей RH правило.
Поступательные степени свободы
Поступательные движения определяются перемещением вдоль этих осей на расстояния x , y и z от
Происхождение.
Степени свободы вращения
Вращения определяются углами Эйлера Р , Q , R или Φ, Θ, Ψ. They are:
| P or Φ | Roll about the x -axis |
| Q or Θ | Pitch about the y -axis |
| R или Ψ | Рыскание относительно оси z |
Если не указано иное, по умолчанию программа использует порядок вращения ZYX для углов Эйлера.
Координаты ветра
Начало неинерциальной системы координат ветра зафиксировано в твердом самолете. Ориентация системы координат определяется относительно скорости корабля V .
Ориентация осей координат ветра фиксируется скоростью V .
Ось x указывает направление В .
Ось y указывает справа от x — ось (обращенная в направлении V ), перпендикулярная x — ось.
Ось z указывает перпендикулярно xy плоскость любым способом, необходимым для удовлетворения RH правило относительно x — и и -оси.
Поступательные степени свободы
Поступательные движения определяются перемещением вдоль этих осей на расстояния x , y и z от Происхождение.
График вращения Свободы
Определяют углы Эйлера φ, γ, χ:
| φ | БАНКАНСКИЙ УЛЛЕВОСТО ЗАЯВЛЕНИЕ 1147 —8 φ | . Траектория полета вокруг оси y |
| χ | Курсовой угол относительно оси z |
Если не указано иное, по умолчанию программа использует порядок ротации ZYX.
для углов Эйлера.
Системы координат для навигации
Моделирование аэрокосмических траекторий требует позиционирования и ориентации самолета или космического корабля относительно вращающейся Земли. Навигация координаты определяются относительно центра и поверхности Земля.
Геоцентрическая и геодезическая широта
геоцентрическая широта λ на поверхности Земли определяется углом стягивается радиус-вектором от центра Земли к точке поверхности с экваториальная плоскость.
геодезическая широта µ на поверхности Земли определяется углом опирается на вектор нормали к поверхности n и экваториальную плоскость.
Координаты NED
Система северо-восток-вниз (NED) представляет собой неинерциальную систему, начало которой зафиксировано на самолете. или центр тяжести космического корабля. Его оси ориентированы по геодезической направления, определяемые земной поверхностью.
Ось x указывает на север параллельно геоиду поверхности в полярном направлении.
Ось y указывает на восток параллельно геоиду поверхность, вдоль кривой широты.
Ось z направлена вниз, к Земле поверхность, антипараллельная внешней нормали к поверхности n .
Полет на постоянной высоте означает полет на постоянной z над поверхностью Земли.
Координаты ECI
Геоцентрическая инерциальная система (ECI) не вращается. Для большинства приложений предположим, что это система инерциальна, хотя плоскости равноденствия и экватора очень сильно смещаются. немного со временем. Система ЭКИ считается истинно инерционной для высокоточные расчеты орбиты, когда экватор и равноденствие определены в конкретная эпоха (например, J2000). Аэрокосмические функции и блоки, использующие конкретная реализация системы координат ECI обеспечивает эту информацию в их документация. Начало системы ECI зафиксировано в центре Земли. (см. рисунок).
Ось x указывает на точку весеннего равноденствия (первая Точка Овна ♈).
Ось y указывает на 90 градусов к востоку от x — ось в экваториальной плоскости.
Ось z указывает на север вдоль Земли ось вращения.
Система координат с центром на Земле
Координаты ECEF
Система координат с центром на Земле и с привязкой к Земле (ECEF) неинерциальна и вращается вместе с Землей. Его начало координат зафиксировано в центре Земли (см. предыдущий рисунок).
Ось x ′ указывает на пересечение Экваториальная плоскость Земли и Гринвичский меридиан.
Ось y ′ указывает на 90 градусов к востоку от x ’-ось в экваториальной плоскости.
Ось z ′ указывает на север вдоль Земли. ось вращения.
Системы координат для отображения
Несколько инструментов отображения доступны для использования с продуктом Aerospace Blockset.
У каждого есть определенная система координат для рендеринга движения.
Графические координаты MATLAB
См. Внешний вид осей для получения дополнительной информации о MATLAB ® Graphics координатные оси.
MATLAB Graphics использует эту ориентацию оси координат по умолчанию:
Ось x указывает за пределы экрана.
Ось y указывает вправо.
Ось z направлена вверх.
Координаты FlightGear
FlightGear — это сторонний симулятор полета с открытым исходным кодом. интерфейс, поддерживаемый набором блоков.
Работа с интерфейсом симулятора полета обсуждает интерфейс blockset для FlightGear.
Полную информацию см. в документации FlightGear по адресу
www.flightgear.org. об этом авиасимуляторе.
Координаты FlightGear образуют специальную фиксированную систему, повернута от стандартной системы координат тела относительно г -ось на -180 градусов:
Ось x положительна к задней части транспортное средство.
Ось y положительна вправо от транспортное средство.
Ось z направлена вверх, например, колеса обычно имеют самые низкие значения z .
Координаты AC3D
AC3D — недорогой, широко используемый редактор геометрии, доступный на https://www.inivis.com . Его фиксированные координаты тела
образована инвертированием трех стандартных осей координат тела:
Ось x положительна к задней части транспортное средство.
Ось y направлена вверх, например, колеса обычно имеют самые низкие значения y .
Ось z положительна слева от транспортное средство.
Каталожные номера
[1] Рекомендуется Практика координат атмосферных и космических летательных аппаратов Systems , R-004-1992, ANSI/AIAA, февраль 1992 г.
[2] Rogers, R. M., Прикладная математика в интегрированных навигационных системах, AIAA,
Рестон, Вирджиния, 2000.
[3] Собел, Д., Долгота , Walker & Company, Нью-Йорк, 1995.
[4] Стивенс Б.Л. и Ф.Л. Льюис, Управление и моделирование самолетов, 2-е изд., Управление самолетом и моделирование, Wiley-Interscience, новый York, 2003.
[5] Thomson, W. T., Введение в космическую динамику, John Wiley & Sons, New Йорк, 1961/Dover Publications, Минеола, Нью-Йорк, 1986.
Внешние веб-сайты
- Управление геоматики
Вы щелкнули ссылку, соответствующую этой команде MATLAB:
Запустите команду, введя ее в Окно команд MATLAB. Веб-браузеры не поддерживают команды MATLAB.
Выберите веб-сайт, чтобы получить переведенный контент, где он доступен, и ознакомиться с местными событиями и предложениями. В зависимости от вашего местоположения мы рекомендуем вам выбрать: .
Вы также можете выбрать веб-сайт из следующего списка:
Европа
Обратитесь в местный офис
ньютоновская механика — Другая система координат в отличие от другой системы отсчета
Это проблема, с которой я уже сталкивался раньше.
Проблема в том, что большинство учебников недостаточно ясно дают определения фиксированной и вращающейся систем отсчета. Я старался быть как можно более исчерпывающим в своем ответе, надеюсь, это поможет!
Для описания движения твердого тела в пространстве мы должны использовать две отдельные системы отсчета:
Во-первых, фиксированную (т.е. инерциальную) систему отсчета с набором ортонормированных базисных векторов $\mathbf{ е}_i$. Эти векторы постоянны во времени для всех инерциальных наблюдателей. Я буду называть инерциальную систему отсчета $K$, а этот набор векторов $S = \{\mathbf{e}_1, \mathbf{e}_2, \mathbf{e}_3\}$.
Во-вторых, каркас кузова — неинерциальная система отсчета, которая движется вместе с твердым телом. Второй набор ортонормированных базисных векторов $\mathbf{e}’_j$ перемещается вместе с этой системой отсчета. Я буду называть эту систему отсчета $K’$, а этот набор векторов $S’ = \{\mathbf{e}_1′, \mathbf{e}_2′, \mathbf{e}_3’\}$.
3$)
$$
\mathbf{A} = \sum_i A_i\mathbf{e}_i = \sum_j A’_j\mathbf{e}’_j.
$$В частности, если вектор $\mathbf{A}$ фиксирован на твердом теле, то проекция $\mathbf{A}$ на каждую из $\mathbf{e}_i$ меняется со временем и таким образом, компоненты $A_i$ являются функциями времени. Однако, поскольку проекция $\mathbf{A}$ на каждую из $\mathbf{e}’_j$ постоянна со временем, компоненты $A’_j$ также постоянны со временем. Этот аргумент верен, если вектор $\mathbf{A}$ зафиксирован в инерциальной системе отсчета , $K$, или если вектор $\mathbf{A}$ зафиксирован в рама кузова , $K’$.
Важно отметить, что наблюдатель из любой системы отсчета может использовать любой набор базисных векторов . Разница заключается в том, как они рассматривают поведение каждого набора векторов: с точки зрения $K$ базисные векторы $\mathbf{e}_i$ фиксированы, а базисные векторы $\mathbf{e}’_j$ являются функциями времени; однако для наблюдателя в $K’$, т. е. с точки зрения твердого тела, $\mathbf{e}’_j$ фиксированы, а векторы $\mathbf{e}_i$ представляют собой время зависимый.
Таким образом, при наблюдении из $K’$ $$ \left(\frac{\text{d}}{\text{d}t}\right)_{K’}\mathbf{e}’_j = \mathbf{0}. $$ Таким образом, скорость изменения вектора $\mathbf{A} = \sum_j A’_j\mathbf{e}’_j$ оказывается равной $$ \left(\frac{\text{d}\mathbf{A}}{\text{d}t}\right)_{K’} = \sum_j \dot{A’}_j\mathbf{e}’_j . $$ Однако при записи в терминах ортонормированного множества $S$ базисные векторы $\mathbf{e}’_j$ являются функциями времени. Ниже я покажу, что, как видно из $K$, $$ \left(\frac{\text{d}}{\text{d}t}\right)_{K}\mathbf{e}’_j = \boldsymbol{\omega}\times\mathbf{e}’_j \, \тег{1} $$ для некоторого зависящего от времени вектора $\boldsymbol{\omega}= \boldsymbol{\omega}(t)$. Так, \начать{выравнивать} \left(\frac{\text{d}\mathbf{A}}{\text{d}t}\right)_{K} «=» \left(\frac{\text{d}\sum_j {A’}_j\mathbf{e}’_j {\text{d}t}\right)_{K} &&\текст{по построению} \\ «=» \sum_j \dot{A’}_j\mathbf{e}’_j +A’_j\dot{\mathbf{e}}’_j &&\text{правило продукта} \\ & = \sum_j \dot{A’}_j\mathbf{e}’_j + A’_j \boldsymbol{\omega}\times\mathbf{e}’_j &&\текст{по уравнению~1} \\ & =\sum_j \dot{A’}_j\mathbf{e}’_j+ \boldsymbol{\omega}\times(A’_j \mathbf{e}’_j) &&\текст{однородность} \\ & = \sum_j \left(\dot{A’}_j\mathbf{e}’_j\right) +\boldsymbol{\omega}\times\mathbf{A}.
&&\текст{линейность}
\end{выравнивание}
Таким образом, мы пишем, что
$$
\left(\frac{\text{d}\mathbf{A}}{\text{d}t}\right)_{K’} = \left(\frac{\text{d}\mathbf{A} {\text{d}t}\right)_{K} — \boldsymbol{\omega}\times\mathbf{A}. \тег{2}
$$
В этом суть проблемы: наблюдателю в движущейся системе отсчета каждый вектор кажется имеющим дополнительный член в своей производной по времени, тогда как на самом деле изменяется сама система отсчета .Отсюда вполне естественно следуют уравнения Эйлера. Пусть $\mathbf{T}$ — крутящий момент на теле, а $\underline{\mathbf{I}}\boldsymbol{\omega}$ — угловой момент тела, где $\underline{\mathbf{ I}}$ — тензор момента инерции. Ключевым моментом является то, что при измерении в $K’$ тензор момента инерции постоянен . (В $K$ это неверно, так как распределение массы тела относительно базиса $\mathbf{e}_i$ меняется со временем.) Используя уравнение (2), это означает, что \начать{выравнивать} \left(\frac{\text{d}}{\text{d}t}\right)_{K’}\underline{\mathbf{I}}\boldsymbol{\omega} «=» \ underline{\ mathbf{I}}\left(\frac{\text{d}}{\text{d}t}\right)_{K’}\boldsymbol{\omega} &&\underline{\mathbf{I}}~\text{константа в}~ K’ \\ «=» \ underline{\ mathbf{I}}\left[\left(\frac{\text{d}}{\text{d}t}\right)_{K}\boldsymbol{\omega}-\underbrace{\ boldsymbol{\omega}\times\boldsymbol{\omega}}_{\mathbf{0}}\right] &&\текст{по уравнению~2} \\ «=» \ underline{\ mathbf{I}}\left(\frac{\text{d}}{\text{d}t}\right)_{K}\boldsymbol{\omega}.
&&
\тег{$\звезда$}
\end{выравнивание}
Наконец, скорость изменения углового момента тела равна приложенному крутящему моменту:
\начать{выравнивать}
\mathbf{T}
&= \left(\frac{\text{d}\underline{\mathbf{I}}\boldsymbol{\omega} }{\text{d}t}\right)_{K}
\\
«=»
\left(\frac{\text{d}\underline{\mathbf{I}}\boldsymbol{\omega}}{\text{d}t}\right)_{K’}+\boldsymbol{\omega} \times(\underline{\mathbf{I}}\boldsymbol{\omega})
&&\текст{по уравнению~2}
\\
«=»
\ underline{\ mathbf{I}}\left(\frac{\text{d}\boldsymbol{\omega}} {\text{d}t}\right)_{K}+\boldsymbol{\omega}\ раз (\ underline{\ mathbf{I}}\boldsymbol{\omega}).
&&\underline{\mathbf{I}}~\text{константа в} ~K’
\end{выравнивание}
Это уравнение Эйлера! Это верно с точки зрения инерциальной системы отсчета, но получено с использованием базисных векторов неинерциальной системы отсчета. Осталось только доказать уравнение (1). Для этого лучше всего забыть о каркасе тела $K’$ и думать о $\mathbf{e}’_j$ просто как о наборе векторов, которые движутся относительно $\mathbf{e}.
\top_{kj}\,\mathbf{e}’_k
&&\текст{по уравнению. 3}
\\
&= \epsilon_{ikm}\,\omega’_m \mathbf{e}’_k
\\
&= \epsilon_{ikm}(\boldsymbol{\omega}\cdot\mathbf{e}’_m)\mathbf{e}’_k\\
&= \frac{1}{2} \epsilon_{ikm}(\boldsymbol{\omega}\cdot\mathbf{e}’_m)\mathbf{e}’_k — \frac{1}{2}\epsilon_ {ikm} (\boldsymbol{\omega}\cdot\mathbf{e}’_k)\mathbf{e}’_m\\
&=\frac{1}{2}\epsilon_{ikm}\boldsymbol{\omega}\times(\mathbf{e}’_k\times\mathbf{e}’_m)\\
&=\frac{1}{2}\epsilon_{ikm}\boldsymbol{\omega}\times(\epsilon_{kml}\mathbf{e}’_l)\\
&=\delta_il\boldsymbol{\omega}\times\mathbf{e}’_l\\
&=\boldsymbol{\omega}\times\mathbf{e}’_i(t).\tag{2}
\end{выравнивание}
Таким образом, как видно из инерциальной системы отсчета, существует мгновенный вектор угловой скорости $\boldsymbol{\omega}$, вокруг которого вращаются штрихованные базисные векторы $\mathbf{e}’_i(t)$.Наконец, вот альтернативный вывод уравнения Эйлера, который мне особенно нравится. Поступим непосредственно, дифференцируя тензор момента инерции. Для этого совместим $\mathbf{e}’_i$ с главными осями тела.
Обозначим главный момент тела вдоль оси $\mathbf{e}’_i$ как $I_i$. Поскольку тело жесткое, главные моменты являются постоянными, поэтому мы можем явно записать момент тензора инерции как
$$
\ underline{\ mathbf{I}} = \sum_i I_i \mathbf{e}’_i \otimes \mathbf{e}’_i
$$
(условие суммирования здесь не используется).
Тогда производная по времени от $\underline{\mathbf{I}}$ (в $K$) равна
$$
\left(\frac{\text{d}}{\text{d}t}\right)_{K} \underline{\mathbf{I}} = \sum_i I_i\left[\dot{\mathbf{e }}’_i\otimes\mathbf{e}’_i+\mathbf{e}’_i\otimes\dot{\mathbf{e}}’_i\right] = \sum_i I_i\left[(\boldsymbol{\omega} \times\mathbf{e}’_i)\otimes\mathbf{e}’_i+\mathbf{e}’_i\otimes(\boldsymbol{\omega}\times\mathbf{e}’_i)\right].
$$
Пусть теперь $\mathbf{b}$ и $\mathbf{c}$ — произвольные векторы, а $\underline{\mathbf{A}}$ — линейный оператор. Используя определение тензорного произведения, имеем
$$
\left[(\underline{\mathbf{A}}\mathbf{b})\otimes\mathbf{c}\right]_{ij}=\left(\underline{\mathbf{A}}\mathbf{b }\right)_i c_j = A_{ik}b_k c_j = \left(\underline{\mathbf{A}}\right)_{ik}\left(\mathbf{b}\otimes\mathbf{c}\right )_{kj} = \left[\underline{\mathbf{A}}(\mathbf{b}\otimes\mathbf{c})\right]_{ij}
$$
и
$$
\left[\mathbf{b}\otimes(\underline{\mathbf{A}}\mathbf{c})\right]_{ij}=b_i\left(\underline{\mathbf{A}}\mathbf{ c}\right)_j = b_i A_{jk} c_k = \left(\mathbf{b}\otimes\mathbf{c}\right)_{ik}\left(\underline{\mathbf{A}}^T \right)_{kj} = \left[(\mathbf{b}\otimes\mathbf{c})\underline{\mathbf{A}}^T\right]_{ij}. T\right]\\
&=[\boldsymbol{\omega}\times]\underline{\mathbf{I}}-\underline{\mathbf{I}}[\boldsymbol{\omega}\times]
\end{выравнивание}
где $[\boldsymbol{\omega}\times]$ — оператор, определенный в предыдущем разделе, а в последней строке я указал, что этот оператор антисимметричен.
Таким образом, производная момента импульса по времени равна
\начать{выравнивать}
\mathbf{T} &= \left(\frac{\text{d}}{\text{d}t}\right)_{K} (\underline{\mathbf{I}}\boldsymbol{\omega} ) \\
&= \underline{\mathbf{I}}\left(\frac{\text{d}}{\text{d}t}\right)_{K} \boldsymbol{\omega}+\boldsymbol{\omega }\left(\frac{\text{d}}{\text{d}t}\right)_{K} \underline{\mathbf{I}}\\
&=\underline{\mathbf{I}}\left(\frac{\text{d}}{\text{d}t}\right)_{K} \boldsymbol{\omega} + [\boldsymbol{\ omega}\times]\underline{\mathbf{I}}\boldsymbol{\omega}-\underline{\mathbf{I}}\underbrace{[\boldsymbol{\omega}\times]\boldsymbol{\omega}} _{\boldsymbol{\omega}\times\boldsymbol{\omega}=\mathbf{0}}\\
&=\underline{\mathbf{I}}\left(\frac{\text{d}}{\text{d}t}\right)_{K} \boldsymbol{\omega} + \boldsymbol{\omega }\times(\underline{\mathbf{I}}\boldsymbol{\omega})
\end{выравнивание}
как прежде.
3$)
$$
\mathbf{A} = \sum_i A_i\mathbf{e}_i = \sum_j A’_j\mathbf{e}’_j.
$$
&&\текст{линейность}
\end{выравнивание}
Таким образом, мы пишем, что
$$
\left(\frac{\text{d}\mathbf{A}}{\text{d}t}\right)_{K’} = \left(\frac{\text{d}\mathbf{A} {\text{d}t}\right)_{K} — \boldsymbol{\omega}\times\mathbf{A}. \тег{2}
$$
В этом суть проблемы: наблюдателю в движущейся системе отсчета каждый вектор кажется имеющим дополнительный член в своей производной по времени, тогда как на самом деле изменяется сама система отсчета .
&&
\тег{$\звезда$}
\end{выравнивание}
Наконец, скорость изменения углового момента тела равна приложенному крутящему моменту:
\начать{выравнивать}
\mathbf{T}
&= \left(\frac{\text{d}\underline{\mathbf{I}}\boldsymbol{\omega} }{\text{d}t}\right)_{K}
\\
«=»
\left(\frac{\text{d}\underline{\mathbf{I}}\boldsymbol{\omega}}{\text{d}t}\right)_{K’}+\boldsymbol{\omega} \times(\underline{\mathbf{I}}\boldsymbol{\omega})
&&\текст{по уравнению~2}
\\
«=»
\ underline{\ mathbf{I}}\left(\frac{\text{d}\boldsymbol{\omega}} {\text{d}t}\right)_{K}+\boldsymbol{\omega}\ раз (\ underline{\ mathbf{I}}\boldsymbol{\omega}).
&&\underline{\mathbf{I}}~\text{константа в} ~K’
\end{выравнивание}
Это уравнение Эйлера! Это верно с точки зрения инерциальной системы отсчета, но получено с использованием базисных векторов неинерциальной системы отсчета. 
\top_{kj}\,\mathbf{e}’_k
&&\текст{по уравнению. 3}
\\
&= \epsilon_{ikm}\,\omega’_m \mathbf{e}’_k
\\
&= \epsilon_{ikm}(\boldsymbol{\omega}\cdot\mathbf{e}’_m)\mathbf{e}’_k\\
&= \frac{1}{2} \epsilon_{ikm}(\boldsymbol{\omega}\cdot\mathbf{e}’_m)\mathbf{e}’_k — \frac{1}{2}\epsilon_ {ikm} (\boldsymbol{\omega}\cdot\mathbf{e}’_k)\mathbf{e}’_m\\
&=\frac{1}{2}\epsilon_{ikm}\boldsymbol{\omega}\times(\mathbf{e}’_k\times\mathbf{e}’_m)\\
&=\frac{1}{2}\epsilon_{ikm}\boldsymbol{\omega}\times(\epsilon_{kml}\mathbf{e}’_l)\\
&=\delta_il\boldsymbol{\omega}\times\mathbf{e}’_l\\
&=\boldsymbol{\omega}\times\mathbf{e}’_i(t).\tag{2}
\end{выравнивание}
Таким образом, как видно из инерциальной системы отсчета, существует мгновенный вектор угловой скорости $\boldsymbol{\omega}$, вокруг которого вращаются штрихованные базисные векторы $\mathbf{e}’_i(t)$.
Обозначим главный момент тела вдоль оси $\mathbf{e}’_i$ как $I_i$. Поскольку тело жесткое, главные моменты являются постоянными, поэтому мы можем явно записать момент тензора инерции как
$$
\ underline{\ mathbf{I}} = \sum_i I_i \mathbf{e}’_i \otimes \mathbf{e}’_i
$$
(условие суммирования здесь не используется).
Тогда производная по времени от $\underline{\mathbf{I}}$ (в $K$) равна
$$
\left(\frac{\text{d}}{\text{d}t}\right)_{K} \underline{\mathbf{I}} = \sum_i I_i\left[\dot{\mathbf{e }}’_i\otimes\mathbf{e}’_i+\mathbf{e}’_i\otimes\dot{\mathbf{e}}’_i\right] = \sum_i I_i\left[(\boldsymbol{\omega} \times\mathbf{e}’_i)\otimes\mathbf{e}’_i+\mathbf{e}’_i\otimes(\boldsymbol{\omega}\times\mathbf{e}’_i)\right].
$$
Пусть теперь $\mathbf{b}$ и $\mathbf{c}$ — произвольные векторы, а $\underline{\mathbf{A}}$ — линейный оператор. Используя определение тензорного произведения, имеем
$$
\left[(\underline{\mathbf{A}}\mathbf{b})\otimes\mathbf{c}\right]_{ij}=\left(\underline{\mathbf{A}}\mathbf{b }\right)_i c_j = A_{ik}b_k c_j = \left(\underline{\mathbf{A}}\right)_{ik}\left(\mathbf{b}\otimes\mathbf{c}\right )_{kj} = \left[\underline{\mathbf{A}}(\mathbf{b}\otimes\mathbf{c})\right]_{ij}
$$
и
$$
\left[\mathbf{b}\otimes(\underline{\mathbf{A}}\mathbf{c})\right]_{ij}=b_i\left(\underline{\mathbf{A}}\mathbf{ c}\right)_j = b_i A_{jk} c_k = \left(\mathbf{b}\otimes\mathbf{c}\right)_{ik}\left(\underline{\mathbf{A}}^T \right)_{kj} = \left[(\mathbf{b}\otimes\mathbf{c})\underline{\mathbf{A}}^T\right]_{ij}.
T\right]\\
&=[\boldsymbol{\omega}\times]\underline{\mathbf{I}}-\underline{\mathbf{I}}[\boldsymbol{\omega}\times]
\end{выравнивание}
где $[\boldsymbol{\omega}\times]$ — оператор, определенный в предыдущем разделе, а в последней строке я указал, что этот оператор антисимметричен.
Таким образом, производная момента импульса по времени равна
\начать{выравнивать}
\mathbf{T} &= \left(\frac{\text{d}}{\text{d}t}\right)_{K} (\underline{\mathbf{I}}\boldsymbol{\omega} ) \\
&= \underline{\mathbf{I}}\left(\frac{\text{d}}{\text{d}t}\right)_{K} \boldsymbol{\omega}+\boldsymbol{\omega }\left(\frac{\text{d}}{\text{d}t}\right)_{K} \underline{\mathbf{I}}\\
&=\underline{\mathbf{I}}\left(\frac{\text{d}}{\text{d}t}\right)_{K} \boldsymbol{\omega} + [\boldsymbol{\ omega}\times]\underline{\mathbf{I}}\boldsymbol{\omega}-\underline{\mathbf{I}}\underbrace{[\boldsymbol{\omega}\times]\boldsymbol{\omega}} _{\boldsymbol{\omega}\times\boldsymbol{\omega}=\mathbf{0}}\\
&=\underline{\mathbf{I}}\left(\frac{\text{d}}{\text{d}t}\right)_{K} \boldsymbol{\omega} + \boldsymbol{\omega }\times(\underline{\mathbf{I}}\boldsymbol{\omega})
\end{выравнивание}
как прежде.
Leave A Comment