Конденсатор в цепи переменного тока
Мы знаем, что конденсатор не пропускает через себя постоянного тока. Поэтому в электрической цепи, в которой последовательно с источником тока включен конденсатор, постоянный ток протекать не может.
Совершенно иначе ведет себя конденсатор в цепи переменного тока (Рис 1,а).
Рисунок 1. Сравнение конденсатора в цепи переменного тока с пружиной, на которую воздействует внешняя сила.
В течение первой четверти периода, когда переменная ЭДС нарастает, конденсатор заряжается, и поэтому по цепи проходит зарядный электрический ток i, сила которого будет наибольшей вначале, когда конденсатор не заряжен. По мере приближения заряда к концу сила зарядного тока будет уменьшаться. Заряд конденсатора заканчивается и зарядный ток прекращается в тот момент, когда переменная ЭДС пе-рестает нарастать, достигнув своего амплитудного значения. Этот момент соответствует концу первой четверти периода.
После этого переменная ЭДС начинает убывать, одновременно с чем конденсатор начинает разряжаться. Следовательно, в течение второй четверти периода по цепи будет протекать разрядный ток. Так как убывание ЭДС происходит вначале медленно, а затем все быстрее и быстрее, то и сила разрядного тока, имея в начале второй четверти периода небольшую величину, будет постепенно возрастать.
Итак, к концу второй четверти периода конденсатор разрядится, ЭДС будет равна нулю, а ток в цепи достигнет наибольшего, амплитудного, значения.
С началом третьей четверти периода ЭДС, переменив свое направление, начнет опять возрастать, а конденсатор — снова заряжаться. Заряд конденсатора будет происходить теперь в обратном направлении, соответственно изменившемуся направлению ЭДС. Поэтому направление зарядного тока в течение третьей четверти периода будет совпадать с направлением разрядного тока во второй четверти, т. е. при переходе от второй четверти периода к третьей ток в цепи не изменит своего направления.
Вначале, пока конденсатор не заряжен, сила зарядного тока имеет наибольшее значение. По мере увеличения заряда конденсатора сила зарядного тока будет убывать. Заряд конденсатора закончится и зарядный ток прекратится в конце третьей четверти периода, когда ЭДС достигнет своего амплитудного значения и нарастание ее прекратится.
Итак, к концу третьей четверти периода конденсатор окажется опять заряженным, но уже в обратном направлении, т. е. на той пластине, где был прежде плюс, будет минус, а где был минус, будет плюс. При этом ЭДС достигнет амплитудного значения (противоположного направления), а ток в цепи будет равен нулю.
В течение последней четверти периода ЭДС начинает опять убывать, а конденсатор разряжаться; при этом в цепи появляется постепенно увеличивающийся разрядный ток. Направление этого тока совпадает с направлением тока в первой четверти периода и противоположно направлению тока во второй и третьей четвертях.
Из всего изложенного выше следует, что по цепи с конденсатором проходит переменный ток и что сила этого тока зависит от величины емкости конденсатора и от частоты тока. Кроме того, из рис. 1,а, который мы построили на основании наших рассуждений, видно, что в чисто емкостной цепи фаза переменного тока опережает фазу напряжения на 90°.
Кроме того, из рис. 1,а, который мы построили на основании наших рассуждений, видно, что в чисто емкостной цепи фаза переменного тока опережает фазу напряжения на 90°.
Отметим, что в цепи с индуктивностью ток отставал от напряжения, а в цепи с емкостью ток опережает напряжение. И в том и в другом случае между фазами тока и напряжения имеется сдвиг, но знаки этих сдвигов противоположны
Емкостное сопротивление конденсатора
Мы уже заметили, что ток в цепи с конденсатором может протекать лишь при изменении приложенного к ней напряжения, причем сила тока, протекающего по цепи при заряде и разряде конденсатора, будет тем больше, чем больше емкость конденсатора и чем быстрее происходят изменения ЭДС
Конденсатор, включенный в цепь переменного тока, влияет на силу протекающего по цепи тока, т. е. ведет себя как сопротивление. Величина емкостного сопротивления тем меньше, чем больше емкость и чем выше частота переменного тока. И наоборот, сопротивление конденсатора переменному току увеличивается с уменьшением его емкости и понижением частоты.
Рисунок 2. Зависимость емкостного сопротивления конденсатра от частоты.
Для постоянного тока, т. е. когда частота его равна нулю, сопротивление емкости бесконечно велико; поэтому постоянный ток по цепи с емкостью проходить не может.
Величина емкостного сопротивления определяется по следующей формуле:
где Хс — емкостное сопротивление конденсатора в ом;
f—частота переменного тока в гц;
ω — угловая частота переменного тока;
С — емкость конденсатора в ф.
При включении конденсатора в цепь переменного тока, в последнем, как и в индуктивности, не затрачивается мощность, так как фазы тока и напряжения сдвинуты друг относительно друга на 90°. Энергия в течение одной четверти периода— при заряде конденсатора — запасается в электрическом поле конденсатора, а в течение другой четверти периода — при разряде конденсатора — отдается обратно в цепь. Поэтому емкостное сопротивление, как и индуктивное, является реактивным или безваттным.
Нужно, однако, отметить, что практически в каждом конденсаторе при прохождении через него переменного тока затрачивается большая или меньшая активная мощность, обусловленная происходящими изменениями состояния диэлектрика конденсатора. Кроме того, абсолютно совершенной изоляции между пластинами конденсатора никогда не бывает; утечка в изоляции между пластинами приводит к тому, что параллельно конденсатору как бы оказывается включенным некоторое активное сопротивление, по которому течет ток и в котором, следовательно, затрачивается некоторая мощность. И в первом и во втором случае мощность затрачивается совершенно бесполезно на нагревание диэлектрика, поэтому се называют мощностью потерь.
Потери, обусловленные изменениями состояния диэлектрика, называются диэлектрическими, а потери, обусловленные несовершенством изоляции между пластинами, — потерями утечки.
Ранее мы сравнивали электрическую емкость с вместимостью герметически (наглухо) закрытого сосуда или с площадью дна открытого сосуда, имеющего вертикальные стенки.
Конденсатор в цепи переменного тока целесообразно сравнивать с гиб-костью пружины. При этом во избежание возможных недоразумений условимся под гибкостью понимать не упругость («твердость») пружины, а величину, ей обратную, т. е. «мягкость» или «податливость» пружины.
Представим себе, что мы периодически сжимаем и растягиваем спиральную пружину, прикрепленную одним концом наглухо к стене. Время, в течение которого мы будем производить полный цикл сжатия и растяжения пружины, будет соответствовать периоду переменного тока.
Таким образом, мы в течение первой четверти периода будем сжимать пружину, в течение второй четверти периода отпускать ее, в течение третьей четверти периода растягивать и в течение четвертой четверти снова отпускать.
Кроме того, условимся, что наши усилия в течение периода будут неравномерными, а именно: они будут нарастать от нуля до максимума в течение первой и третьей четвертей периода и уменьшаться от максимума до нуля в течение второй и четвертой четвертей.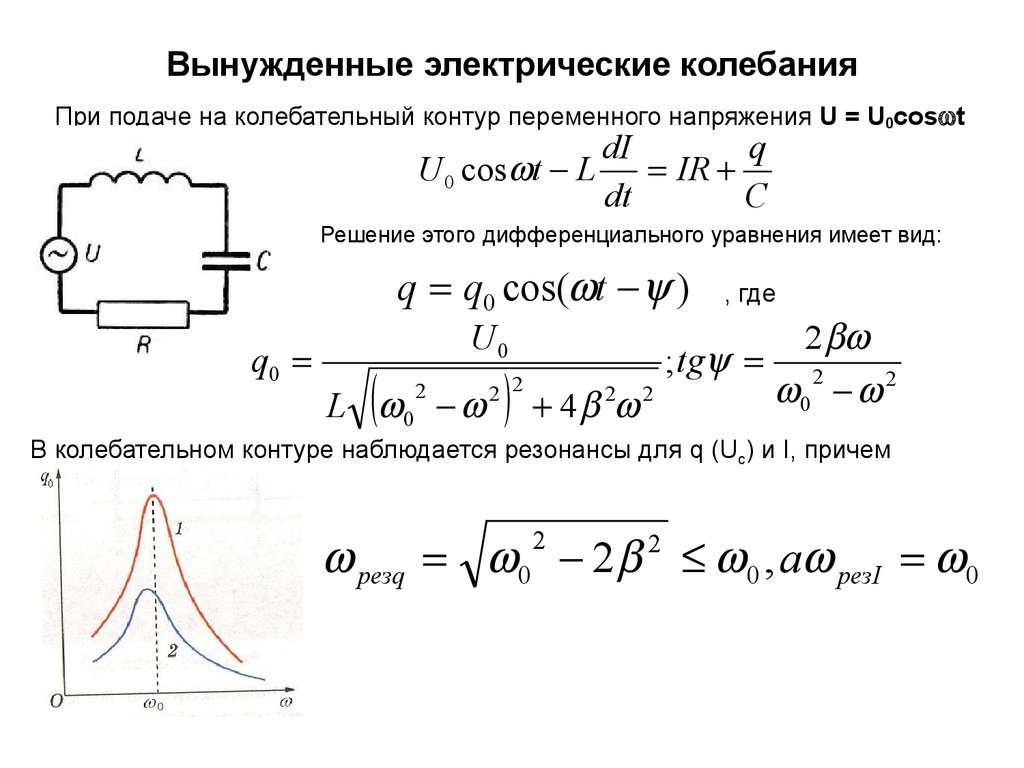
Сжимая и растягивая пружину таким образом, мы заметим, что в начале первой четверти периода незакрепленный конец пружины будет двигаться довольно быстро при сравнительно малых усилиях с нашей стороны.
В конце первой четверти периода (когда пружина сожмется), наоборот, несмотря на возросшие усилия, незакрепленный конец пружины будет двигаться очень медленно.
В продолжение второй четверти периода, когда мы будем постепенно ослаблять давление на пружину, ее незакрепленный конец будет двигаться по направлению от стены к нам, хотя наши задерживающие усилия направлены по направлению к стене. При этом наши усилия в начале второй четверти периода будут наибольшими, а скорость движения незакрепленного конца пружины наименьшей. В конце же второй четверти периода, когда наши усилия будут наименьшими, скорость движения пружины будет наибольшей и т. д.
Продолжив аналогичные рассуждения для второй половины периода (для третьей и четвертой четвертей) и построив графики (рис. 1,б) изменения наших усилий и скорости движения незакрепленного конца пружины, мы убедимся, что эти графики в точности соответствуют графикам ЭДС и тока в емкостной цепи (рис 1,а), причем график усилий будет соответствовать графику ЭДС , а график скорости — графику силы тока.
Рисунок 3. а)Процессы в цепи переменного тока с конденсатором и б)сравнение конденсатора с пружиной.
Нетрудно, заметить, что пружина, так же как и конденсатор, в течение одной четверти периода накапливает энергию, а в течение другой четверти периода отдает ее обратно.
Вполне очевидно также, что чем меньше гибкость пружины,- т е. чем она более упруга, тем большее противодействие она будет оказывать нашим усилиям. Точно так же и в электрической цепи: чем меньше емкость, тем больше будет сопротивление цепи при данной частоте.
И наконец, чем медленнее мы будем сжимать и растягивать пружину, тем меньше будет скорость движения ее незакрепленного конца. Аналогично этому, чем меньше частота, тем меньше сила тока при данной ЭДС.
При постоянном давлении пружина только сожмется и на этом прекратит свое движение, так же как при постоянной ЭДС конденсатор только зарядится и на этом прекратится дальнейшее движение электронов в цепи.
А теперь как ведет себя конденсатор в цепи переменного тока вы можете посмотреть в следующем видео:
youtube.com/embed/OwlapldZYYo» allowfullscreen=»allowfullscreen»>ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Физика Переменный ток. Активное сопротивление. Конденсатор и катушка индуктивности в цепи переменного тока
Материалы к уроку
12. Переменный ток. Активное сопротивление. Конденсатор и катушка индуктивности в цепи переменного тока.doc
55 KBСкачать12. Переменный ток. Активное сопротивление.
 Конденсатор и катушка индуктивности в цепи переменного тока.ppt2.78 MBСкачать
Конденсатор и катушка индуктивности в цепи переменного тока.ppt2.78 MBСкачать
Конспект урока
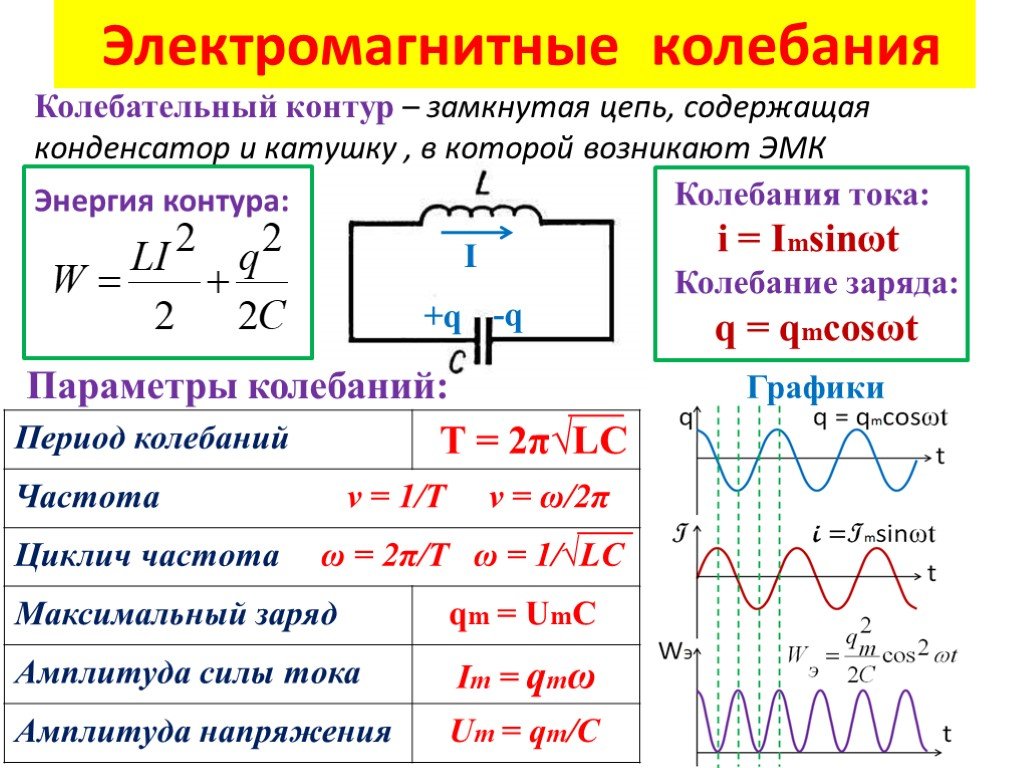
Огромное практическое значение имеют незатухающие вынужденные колебания. Свободные электромагнитные колебания в контуре быстро затухают и поэтому практически не используются. Переменный ток, используемый потребителями, представляет собой не что иное, как вынужденные электромагнитные колебания. Частота переменного тока показывает число колебаний за 1 секунду. Стандартная частота промышленного тока равна 50 Герц. Значит, на протяжении 1 с ток 50 раз течет в одну сторону и 50 раз в другую. Частота 50 Герц принята для промышленного тока во многих странах мира. Сила тока и напряжение меняются со временем по гармоническому закону. Это вытекает из следующих рассуждений. Если напряжение на концах цепи меняется по гармоническому закону, то напряженность электрического поля внутри проводников будет также меняться гармонически. Эти гармонические изменения напряженности поля вызовут гармонические колебания скорости упорядоченного движения заряженных частиц и, следовательно, гармонические колебания силы тока.
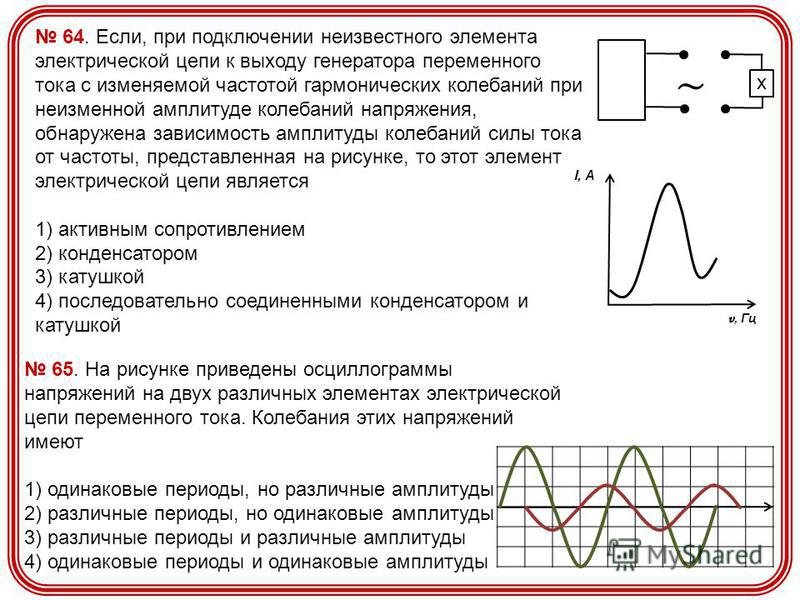



 Лампа светится ярче при постоянном напряжении. Следовательно, действующее значение силы переменного тока в рассматриваемой цепи меньше силы постоянного тока. Здесь проявляется самоиндукция. При подключении катушки к источнику постоянного напряжения сила тока в цепи нарастает постепенно. Возникающее при нарастании силы тока вихревое электрическое поле тормозит движение электронов. Лишь со временем сила тока достигает наибольшего установившегося значения, соответствующего данному постоянному напряжению. Если напряжение быстро меняется, то сила тока не будет достигать тех значений, которые оно бы приобрело с течением времени при постоянном напряжении. Следовательно, максимальное значение силы переменного тока (его амплитуда) ограничивается индуктивностью цепи и будет тем меньше, чем больше индуктивность и чем больше частота приложенного напряжения. При изменении силы тока по гармоническому закону ЭДС самоиндукции будет равна противоположному значению производной индуктивности. Так как удельная работа кулоновского поля равна напряжению на концах катушки, то напряжение на концах катушки оказывается гармонически связанным с амплитудным значением напряжения контура.
Лампа светится ярче при постоянном напряжении. Следовательно, действующее значение силы переменного тока в рассматриваемой цепи меньше силы постоянного тока. Здесь проявляется самоиндукция. При подключении катушки к источнику постоянного напряжения сила тока в цепи нарастает постепенно. Возникающее при нарастании силы тока вихревое электрическое поле тормозит движение электронов. Лишь со временем сила тока достигает наибольшего установившегося значения, соответствующего данному постоянному напряжению. Если напряжение быстро меняется, то сила тока не будет достигать тех значений, которые оно бы приобрело с течением времени при постоянном напряжении. Следовательно, максимальное значение силы переменного тока (его амплитуда) ограничивается индуктивностью цепи и будет тем меньше, чем больше индуктивность и чем больше частота приложенного напряжения. При изменении силы тока по гармоническому закону ЭДС самоиндукции будет равна противоположному значению производной индуктивности. Так как удельная работа кулоновского поля равна напряжению на концах катушки, то напряжение на концах катушки оказывается гармонически связанным с амплитудным значением напряжения контура.
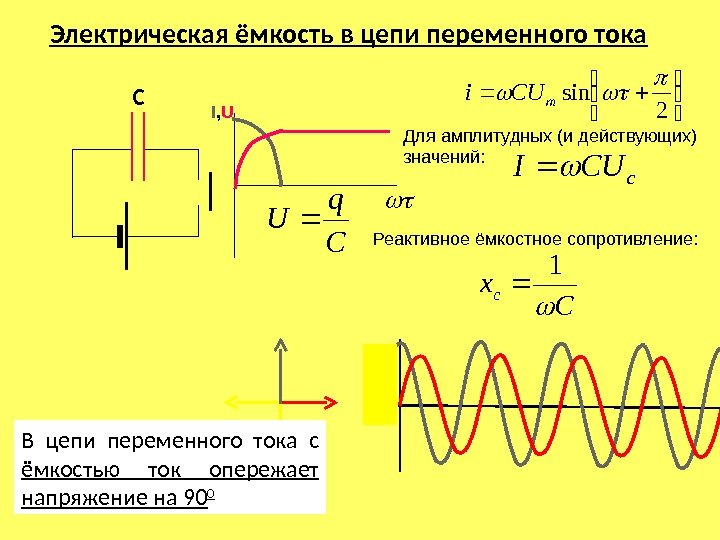 Катушка наоборот: хорошо проводит низкочастотные колебания и плохо – высокочастотные колебания. Эти свойства позволяют создать различные частотные фильтры – схемы, позволяющие выделить из всего сигнала низкочастотные и высокочастотные составляющие.
Катушка наоборот: хорошо проводит низкочастотные колебания и плохо – высокочастотные колебания. Эти свойства позволяют создать различные частотные фильтры – схемы, позволяющие выделить из всего сигнала низкочастотные и высокочастотные составляющие.Колебательный контур обладает замечательным свойством – пропускать колебания только определенной частоты, зависящей от емкости конденсатора и индуктивности катушки, под действием резонанса. Эти свойства контура широко применяются в радио- и телеприёмной и передающей аппаратуре для селекции сигналов.
Задача
Конденсатор включен в цепь переменного тока с частотой 200 Герц. Напряжение в цепи 40 Вольт, сила тока 0,64 Ампера. Какова емкость конденсатора?
Вспомнив закон Ома для цепи с колебательным контуром, выразим емкость конденсатора как отношение силы тока к напряжению и циклической частоте. Чтобы определить циклическую частоту, необходимо частоту переменного тока разделить на два-пи. Получаем результат 0,5 микрофарад есть емкость конденсатора.

Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитораОставить заявку на подбор
конденсаторы напряжения переменного тока — определение, функция и переменный ток посредством деривации конденсатора
направлении в проводнике возникает переменный ток. Электроны в электронике перемещаются от отрицательного потенциала к положительному потенциалу. Если потенциалы между двумя клеммами в фиксированный интервал времени переключаются, возникает переменный ток. Разница выражается в вольтах между положительной и отрицательной клеммами. Поэтому термин, используемый для определения значения разности потенциалов клемм при протекании переменного тока, называется напряжением переменного тока.
Электронные компоненты, используемые в цепи для накопления и высвобождения электроэнергии, известны как конденсаторы, и они имеют тенденцию пропускать переменный ток, не пропуская постоянный ток.
Конденсаторы при подключении к источнику постоянного тока заряжаются и начинают действовать как устройства временного хранения. Когда конденсаторы полностью заряжены, на их пластинах больше не будет течь электронов. Поэтому, когда конденсатор полностью заряжается, он блокирует постоянный ток.
Теперь, если переменное напряжение подать на конденсатор, то зарядка и разрядка будут происходить одновременно. Норма частоты будет определяться частотой питающего переменного напряжения. Поэтому в цепи переменного тока емкость конденсатора, который постоянно заряжается или разряжается, зависит от частоты входного сигнала.
Эта статья дает четкое представление об электрических цепях, когда используется переменное напряжение на конденсаторе. В этой схеме мы соединили конденсатор и переменное напряжение V, обозначенное символом «~».
(Изображение будет загружено в ближайшее время)
Напряжение в цепи создает разность потенциалов на ее клеммах, которая изменяется синусоидально.
Ниже приведено выражение о разности потенциалов v, или переменном напряжении:
\[ V = V_{m} sin \omega t\]
Где,
\[ V_{m} \] = амплитуда колеблющейся разности потенциалов
\[ \omega t= угловая частота \]
Мы можем рассчитать ток, который имеется в резисторе при текущем напряжении с помощью правила цикла Кирхгофа.
Вот выражение правила цикла Кирхгофа:
\[ \sum v(t) = 0 \]
На приведенной выше диаграмме поясняется источник переменного напряжения, приложенный к конденсатору.
Емкость в цепи переменного тока и емкостное реактивное сопротивление
На приведенном выше рисунке мы можем записать выражение для конденсатора:
\[ v = \frac{q}{C}\]
Как упоминалось ранее о v, мы можем переписать выражение как:
\ [ v_{m} sin \omega t = \frac{q}{C}\]
Мы можем рассчитать величину тока в цепи, используя это соотношение:
\[ i = \frac{dq}{dt }\]
\[ \Rightarrow i = \frac{d(v_{m}C sin\omega t)}{dt} = \omega Cv_{m} cos \omega t \]
\[\Rightarrow i = i_{m}sin(\omega t +\frac{\pi}{2})\]
В приведенном выше выражении используется соотношение \[ Cos\omega t = sin(\omega t +\frac{\pi }{2})\]
Также мы можем переписать амплитуду тока как:
\[ i_{m} = \omega Cv_{m} \]
Или мы можем выразить это как
\[i_{m}\] = \[\frac{v_{m}}{ \frac{1}{ω_{C}}}\]
В этом выражении \[\frac{1}{ω_{C}}\] можно принять за эквивалент сопротивления устройства.
Вот почему термин для этого выражения называется емкостным сопротивлением. \[X_{c}\] — это символ, используемый для пленного сопротивления.
\[X_{c} = \frac{1}{ω_{C}}\]
Также мы можем рассчитать амплитуду тока в цепи, используя следующее соотношение:
\[ i_{m } = \frac{v_{m}}{X_{C}} \]
Как работает конденсатор в цепи переменного тока?
В электрической цепи конденсатор обеспечивает прямую связь с переменным напряжением питания. Когда происходит изменение напряжения питания (напряжение увеличивается или уменьшается), конденсатор заряжается или разряжается в соответствии с изменением напряжения.
Когда ток проходит через цепь, он будет следовать в одном направлении, а затем в другом направлении, не позволяя фактическому току проходить через конденсатор.
Однако в цепи постоянного тока сценарий другой. Когда ток протекает через конденсатор, подключенный к цепи постоянного тока, обкладка конденсатора имеет как положительные, так и отрицательные заряды.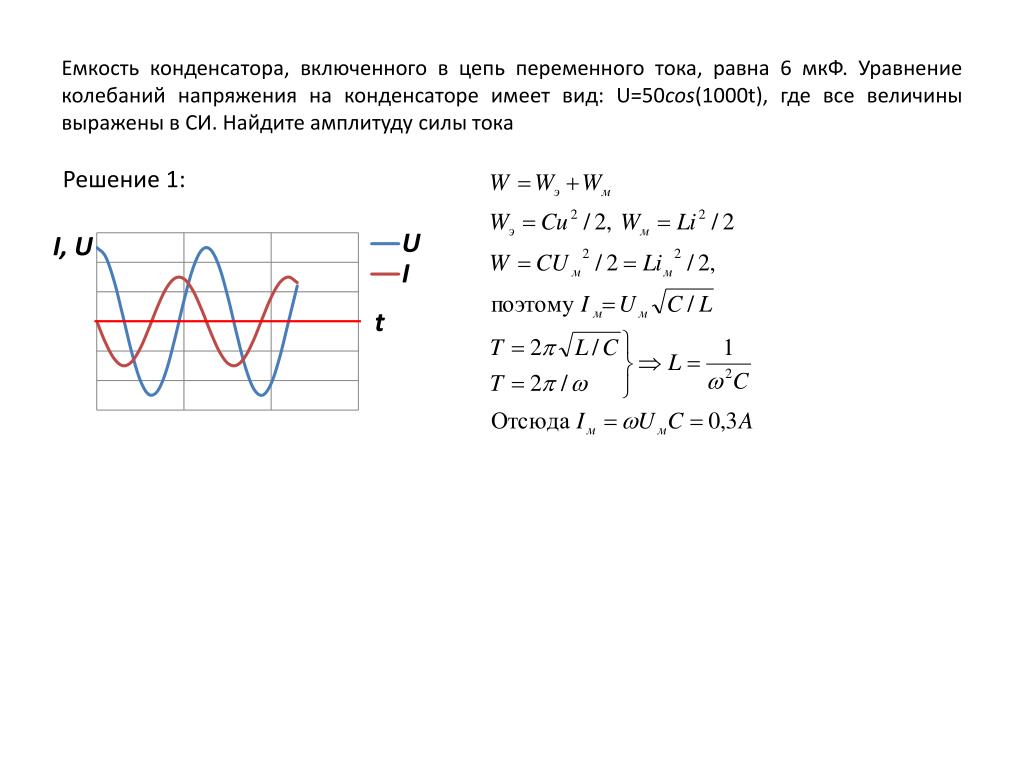
Цепи конденсаторов переменного тока
(Изображение будет загружено в ближайшее время)
Когда конденсатор подключен к цепи переменного тока, он будет последовательно заряжаться и разряжаться со скоростью, вычисляемой частотой источника питания. В цепях переменного тока емкость зависит от частоты, поскольку конденсатор постоянно заряжается и разряжается.
Какова роль конденсатора в цепи переменного и постоянного тока?
Роль конденсатора в цепи постоянного тока
В цепи постоянного тока конденсатор заряжается медленнее. Конденсатор заряжается до напряжения питания, но препятствует дальнейшему прохождению через него тока. Он блокирует протекание тока, поскольку диэлектрик конденсатора является непроводящим и изолятором.
Роль конденсатора в цепи переменного тока
Когда конденсатор используется в цепи переменного тока, он заряжается и разряжается для изменения напряжения питания.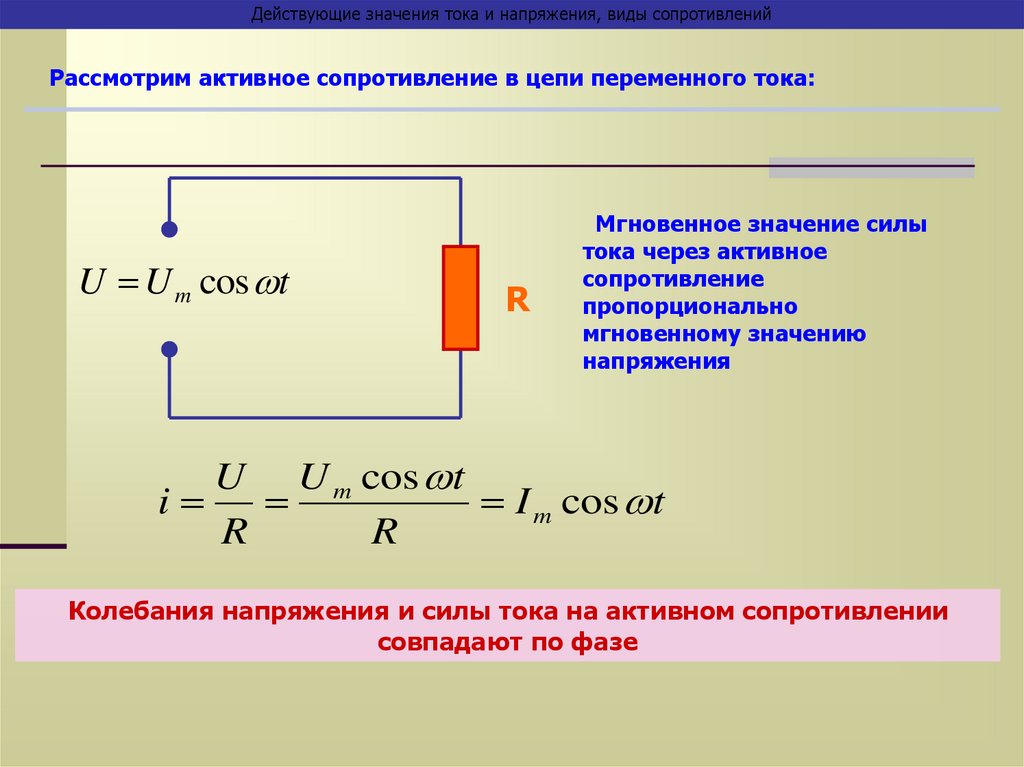 Согласно записи, ток становится прямо пропорциональным максимальному напряжению на пластинах.
Согласно записи, ток становится прямо пропорциональным максимальному напряжению на пластинах.
Конденсаторы, включенные в цепь переменного тока, блокируют подачу питания, когда они полностью заряжены. Когда в цепи есть источник питания переменного тока, конденсаторы будут заряжаться и разряжаться попеременно со скоростью, определяемой подаваемой частотой.
Функция конденсатора в цепи переменного тока
Мы знаем, что конденсаторы используются для накопления энергии на своих проводящих пластинах в виде электрического заряда.
Конденсаторы используются для повышения напряжения выше входного. Это помогает в плавных текущих колебаниях.
Самое главное, конденсаторы используются в схемах выпрямителей для выравнивания колебаний тока.
Конденсаторы также используются для блокирования статического напряжения постоянного тока и позволяют сигналам переменного тока проходить из одной области цепи в другую.
 Эти типы конденсаторов известны как конденсаторы связи.
Эти типы конденсаторов известны как конденсаторы связи.Для устранения любых сигналов переменного тока в точке смещения постоянного тока используются развязывающие конденсаторы.
Пусковой крутящий момент можно увеличить с помощью конденсаторов. Кроме того, конденсаторы хороши для одной фазы.
Также конденсаторы используются для улучшения коэффициента мощности в энергосистемах.
Переменный ток через конденсатор — вывод
Пару проводников можно назвать конденсатором, разделенным некоторой средой. Когда мы подключаем конденсатор к цепи переменного тока, мы можем найти ток, протекающий через него.
Когда мы подключаем лампу в эту цепь, лампа светится, что показывает прохождение тока в цепи переменного тока.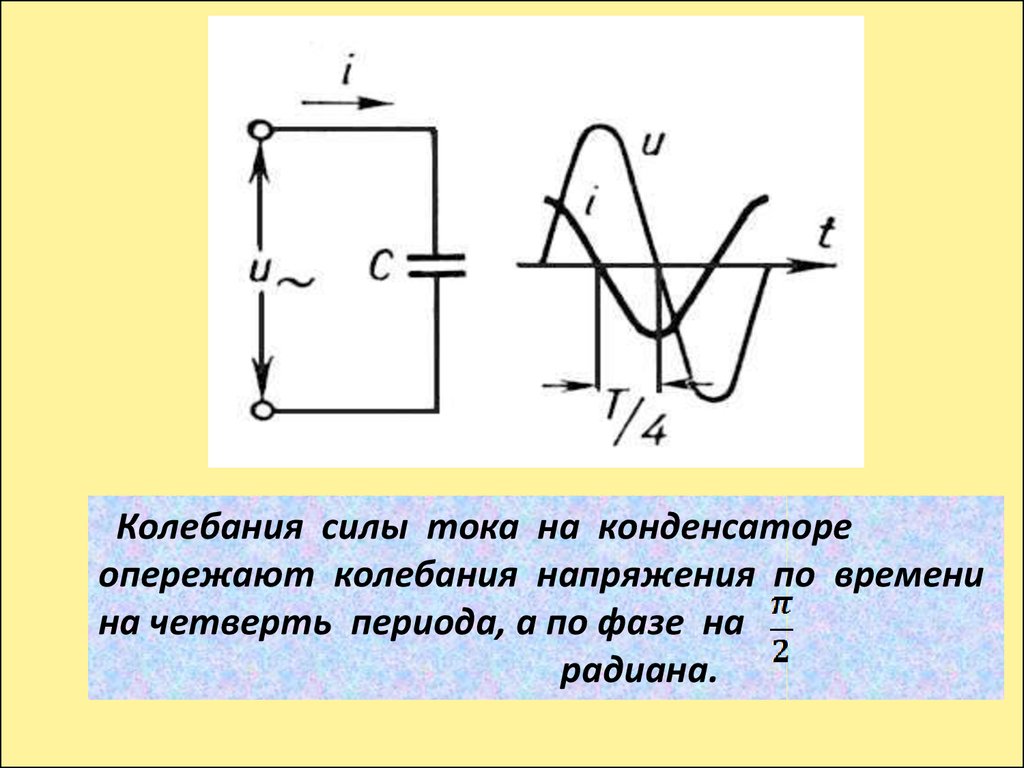 Мы пришли к выводу, что конденсатор является проводником в цепи переменного тока, но работает как изолятор в цепи постоянного тока.
Мы пришли к выводу, что конденсатор является проводником в цепи переменного тока, но работает как изолятор в цепи постоянного тока.
(Изображение будет загружено в ближайшее время)
Предположим, что в цепи источник переменного напряжения равен \[ V = V_{0} sin \omega t\], а емкость конденсатора равна C.
В любой момент времени t заряд конденсатора равен q, а текущий ток равен i.
Поскольку сопротивление отсутствует, мгновенное падение потенциала в цепи на конденсаторе будет равно \[ \frac{q}{c}\] и должно быть равно приложенному переменному напряжению. Следовательно,
\[ \frac{q}{c} = V_{0} sin \omega t \]
Мгновенный ток в цепи равен \[ i = \frac{d}{t}\], следовательно,
\[ i = \frac{dq}{dt}(CV_{0} sin \omega t) \]
\[ i = \frac{dq}{dt}(CV_{0} cos \omega t)\]
\[ i = \frac{V_{0}}{\frac{1}{\ omega C}} cos \omega t \]
\[ i = i_{0} cos \omega t \]
\[ \frac{q}{c} = i_{0} sin (\omega t + \ frac{\pi }{2})\]
, где \[i_{0} = \frac{V_{0}}{\frac{1}{\omega _{C}}}\] = пиковое значение тока
Если мы сравним пиковое значение тока с \[ V = V_{0} sin \omega t\], мы заметим, что ток опережает ЭДС в идеальном конденсаторе на фазовый угол /2.
Теперь, если мы сравним пиковое значение тока с законом Ома, мы заметим, что величина \[\frac{1}{\omega C}\] имеет размерность сопротивления, поэтому
\[X_{C } = \frac{1}{\omega C} = \frac{1}{2}\pi fC\]
Это известно как емкостное реактивное сопротивление.
Из этого уравнения видим, что при увеличении частоты тока емкостное сопротивление уменьшается, а при частоте равной нулю емкостное сопротивление бесконечно для постоянного тока.
(Изображение скоро будет загружено)
15.S: Цепи переменного тока (Резюме) — Physics LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 10311
- ОпенСтакс
- ОпенСтакс
Ключевые термины
| переменный ток | ток, который синусоидально колеблется во времени с фиксированной частотой |
| переменное напряжение | напряжение, которое синусоидально колеблется во времени с фиксированной частотой |
| переменный ток (ac) | поток электрического заряда, который периодически меняет направление |
| средняя мощность | Среднее значение мгновенной мощности за один цикл |
| пропускная способность | диапазон угловых частот, в котором средняя мощность превышает половину максимального значения средней мощности |
| емкостное реактивное сопротивление | Противодействие конденсатора изменению тока |
| постоянный ток (постоянный ток) | поток электрического заряда только в одном направлении |
| импеданс | ac аналог сопротивления в цепи постоянного тока, который измеряет комбинированный эффект сопротивления, емкостного сопротивления и индуктивного сопротивления |
| индуктивное сопротивление | противопоставление катушки индуктивности изменению тока |
| фазовый угол | Величина, на которую напряжение и ток не совпадают по фазе друг с другом в цепи |
| коэффициент мощности | величина, на которую мощность, подаваемая в цепь, меньше теоретического максимума цепи из-за того, что напряжение и ток не совпадают по фазе |
| добротность | безразмерная величина, характеризующая остроту пика полосы пропускания; высокая добротность – острый или узкий резонансный пик |
| резонансная частота | частота, при которой амплитуда тока максимальна и цепь будет колебаться, если не будет управляться источником напряжения |
| действующее значение тока | среднеквадратичное значение текущего |
| среднеквадратичное значение напряжения | среднеквадратичное значение напряжения |
| понижающий трансформатор | трансформатор, уменьшающий напряжение и увеличивающий ток |
| повышающий трансформатор | трансформатор, увеличивающий напряжение и уменьшающий ток |
| трансформатор | Устройство, преобразующее напряжение из одного значения в другое с помощью индукции |
| уравнение трансформатора | уравнение, показывающее, что отношение вторичных и первичных напряжений в трансформаторе равно отношению числа витков в их обмотках |
Ключевые уравнения
| Напряжение переменного тока | \(\displaystyle v=V_0sinωt\) |
| Переменный ток | \(\displaystyle i=I_0sinωt\) |
| емкостное реактивное сопротивление | \(\displaystyle \frac{V_0}{I_0}=\frac{1}{ωC}=X_C\) |
| среднеквадратичное напряжение | \(\displaystyle V_{rms}=\frac{V_0}{\sqrt{2}}\) |
| Действующее значение тока | \(\displaystyle I_{rms}=\frac{I_0}{\sqrt{2}}\) |
| индуктивное сопротивление | \(\displaystyle \frac{V_0}{I_0}=ωL=X_L\) |
| Фазовый угол цепи серии RLC | 92_{rms}R\)|
| Резонансная угловая частота контура | \(\ displaystyle ω_0 = \ sqrt {\ frac {1} {LC}} \) |
| Добротность цепи | \(\displaystyle Q=\frac{ω_0}{Δω}\) |
| Коэффициент качества цепи по параметрам цепи | \(\displaystyle Q=\frac{ω_0L}{R}\) |
| Уравнение трансформатора с напряжением | \(\displaystyle \frac{V_S}{V_P}=\frac{N_S}{N_P}\) |
| Уравнение трансформатора с током | \(\displaystyle I_S=\frac{N_P}{N_S}I_P\) |
Резюме
15.
 2 Источники переменного тока
2 Источники переменного тока- Постоянный ток (постоянный ток) относится к системам, в которых напряжение источника является постоянным.
- Переменный ток (ac) относится к системам, в которых напряжение источника изменяется периодически, в частности, синусоидально.
- Источник напряжения системы переменного тока выдает напряжение, рассчитанное по времени, пиковому напряжению и угловой частоте.
- В простой цепи ток находится путем деления напряжения на сопротивление. Переменный ток рассчитывается с использованием пикового тока (определяемого путем деления пикового напряжения на сопротивление), угловой частоты и времени.
15.3 Простые цепи переменного тока
- Для резисторов ток и напряжение на них совпадают по фазе.
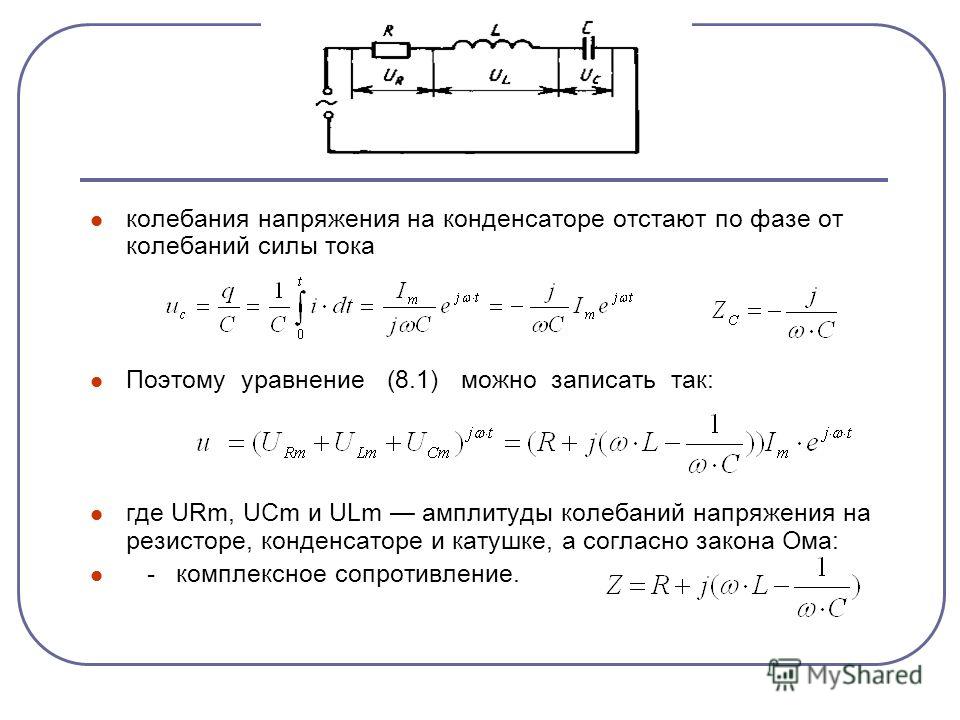
- Для конденсаторов мы обнаружили, что когда к конденсатору прикладывается синусоидальное напряжение, напряжение следует за током на одну четвертую периода. Поскольку конденсатор может останавливать ток при полной зарядке, он ограничивает ток и предлагает другую форму сопротивления переменному току, называемую емкостным реактивным сопротивлением, которое измеряется в омах.

- Для катушек индуктивности в цепях переменного тока мы обнаружили, что когда к катушке индуктивности приложено синусоидальное напряжение, напряжение опережает ток на одну четвертую периода.
- Противодействие катушки индуктивности изменению тока выражается в виде реактивного сопротивления переменного тока. Это индуктивное сопротивление, измеряемое в омах, зависит от частоты источника переменного тока.
15.4 Цепи серии RLC с переменным током
- Цепь серии RLC представляет собой последовательную комбинацию резистора, конденсатора и катушки индуктивности на источнике переменного тока.
- Один и тот же ток протекает через каждый элемент цепи серии RLC во все моменты времени.
- Аналогом сопротивления в цепи постоянного тока является импеданс, который измеряет комбинированное действие резисторов, конденсаторов и катушек индуктивности. Максимальный ток определяется версией закона Ома для переменного тока.

- Полное сопротивление измеряется в омах и определяется с помощью сопротивления, емкостного и индуктивного сопротивления.
15.5 Мощность в цепи переменного тока
- Средняя мощность переменного тока находится путем умножения среднеквадратичных значений тока и напряжения.
- Закон Ома для среднеквадратичного значения переменного тока находится путем деления среднеквадратичного значения напряжения на импеданс.
- В цепи переменного тока существует угол сдвига фаз между напряжением источника и током, который можно найти, разделив сопротивление на импеданс.
- На среднюю мощность, подаваемую в цепь RLC , влияет фазовый угол.
- Коэффициент мощности находится в диапазоне от –1 до 1.
15.6 Резонанс в цепи переменного тока
- На резонансной частоте индуктивное сопротивление равно емкостному.
- График зависимости средней мощности от угловой частоты для схемы RLC имеет пик, расположенный на резонансной частоте; резкость или ширина пика известна как ширина полосы.

- Полоса пропускания связана с безразмерной величиной, называемой добротностью. Высокое значение добротности – это острый или узкий пик.
15.7 Трансформаторы
- Электростанции передают высокое напряжение при малом токе для снижения омических потерь в многокилометровых линиях электропередачи.
- Трансформаторы используют индукцию для преобразования напряжения из одного значения в другое.
- Для трансформатора напряжения на первичной и вторичной катушках или обмотках связаны уравнением трансформатора.
- Токи в первичной и вторичной обмотках связаны количеством первичных и вторичных петель или витков в обмотках трансформатора.
- Повышающий трансформатор увеличивает напряжение и уменьшает ток, а понижающий трансформатор снижает напряжение и увеличивает ток.
Авторы и авторство
Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойолы Мэримаунт) и Билл Моебс со многими сотрудничающими авторами.

 Конденсатор и катушка индуктивности в цепи переменного тока.ppt2.78 MBСкачать
Конденсатор и катушка индуктивности в цепи переменного тока.ppt2.78 MBСкачать Эти типы конденсаторов известны как конденсаторы связи.
Эти типы конденсаторов известны как конденсаторы связи.


Leave A Comment