| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | sin((5pi)/3) | ||
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | ||
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Точные значения sin x и cos x
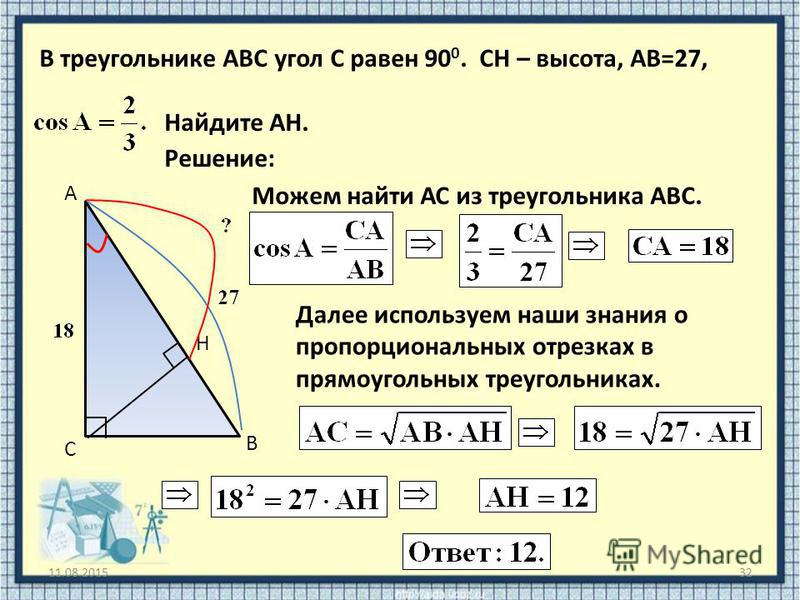
Значения синуса и косинуса для всех угловых измерений, кратных 3 градусам, могут быть представлены в терминах радикалов квадратного корня и четырех обычных арифметических операций. Эти значения можно определить геометрически с помощью трех стратегических треугольников.
В равностороннем треугольнике каждый из трех внутренних углов равен 60°. Просмотр половины треугольника дает 30-60-90 прямоугольный треугольник, гипотенуза которого равна 1, короткий катет равен 1/2, а длинный катет равен . Используя определения тригонометрии прямоугольного треугольника sin x = opp/hyp и cos x = adj/hyp, мы получаем sin 30° = 1/2 и cos 30° = . | |
Из квадрата с внутренними углами 90° проведите диагональ из одного угла в противоположный. Это образует прямоугольный треугольник, две стороны которого являются катетами треугольника, а проведенная диагональ является гипотенузой. | |
Пусть две длинные стороны равнобедренного треугольника 36-72-72 равны x , а короткая сторона равна 1. Разделите пополам один из углов 72°, продлив луч до пересечения с другой стороной треугольника. Это образует два треугольника: равнобедренный треугольник 36-36-108, обе короткие стороны которого равны 1, и меньший равнобедренный треугольник 36-72-72, длинные стороны которого равны 1, а короткая сторона равна 9.0908 x – 1, как показано на диаграммах справа: |
Два треугольника 36-72-72 пропорциональны: отношение длинных сторон x :1 такое же, как и отношение коротких сторон: 1:( x — 1). Найдите x , приравняв два отношения: x /1 = 1/( x – 1), что даст x 2 — x — 1 = 0.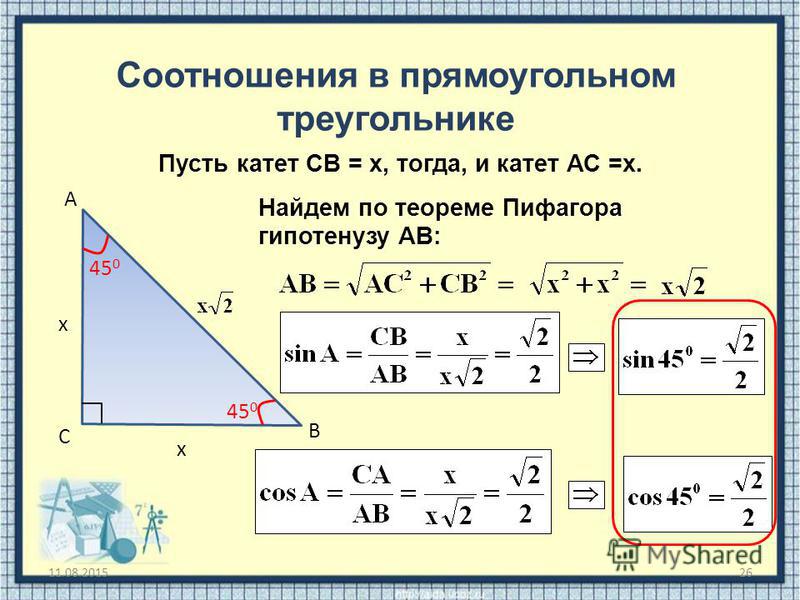 Решение для x с использованием квадратичной формулы (и игнорирование отрицательного корня) дает x = . Разделение треугольника 36-36-108 пополам образует прямоугольный треугольник, треугольник 36-54-90, с гипотенузой 1, длинным катетом x /2 и коротким катетом. Так как х = , мы имеем:
Решение для x с использованием квадратичной формулы (и игнорирование отрицательного корня) дает x = . Разделение треугольника 36-36-108 пополам образует прямоугольный треугольник, треугольник 36-54-90, с гипотенузой 1, длинным катетом x /2 и коротким катетом. Так как х = , мы имеем:
Число называется золотым сечением и обозначается греческой буквой φ (строчная фи). Таким образом, мы можем написать
Оставшиеся точные представления для углов, кратных 3°, теперь можно найти, используя тождества сумм-разностей и половинных углов. Поскольку могут использоваться разные тождества, точные представления могут «выглядеть» иначе, чем другие возможные представления, но может быть показано, что они идентичны по значению. Ниже приводится последовательность таблиц всех точных значений синуса и косинуса углов, кратных 3°, вплоть до 45°. Все радикалы были упрощены, так что ни один из них не содержал в себе частных.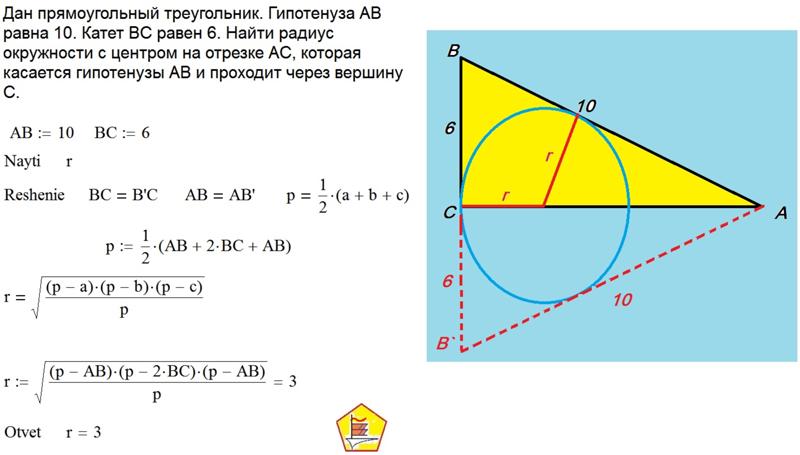 Когда это уместно, дается эквивалентное представление в терминах золотого сечения φ.
Когда это уместно, дается эквивалентное представление в терминах золотого сечения φ.
Все эти значения являются алгебраическими , что означает, что они являются корнем некоторого многочлена с целыми коэффициентами. Например, sin 90° является алгебраическим. Оно равно 1, что является корнем многочлена x – 1. Имея алгебраическое число в виде радикалов и арифметических операций, можно построить многочлен, для которого данное число является корнем. Например, мы знаем, что sin 45° = , поэтому мы устанавливаем x = sqrt(2)/2, затем возводим в квадрат обе стороны и собираем члены в одну сторону, мы получаем х 2 – 1/2 = 0. Таким образом, 2 х 2 – 1 является многочленом, для которого есть корень.
| Угол: 0° или 0 радиан | ||
| Значение: | ||
| Минимальный многочлен: |
| Угол: 3° или π/60 радиан | ||
| Десятичная аппроксимация: |  .. .. | |
| Точное представление: |
| Минимальный многочлен: | 9 x 90 7 10 + 182784 x 8 – 50176 x 6 + 7040 x 4 – 384 x 2 + 1 | (для обоих) |
| Угол: 6° или π/30 радиан | |||
| Десятичная аппроксимация: | 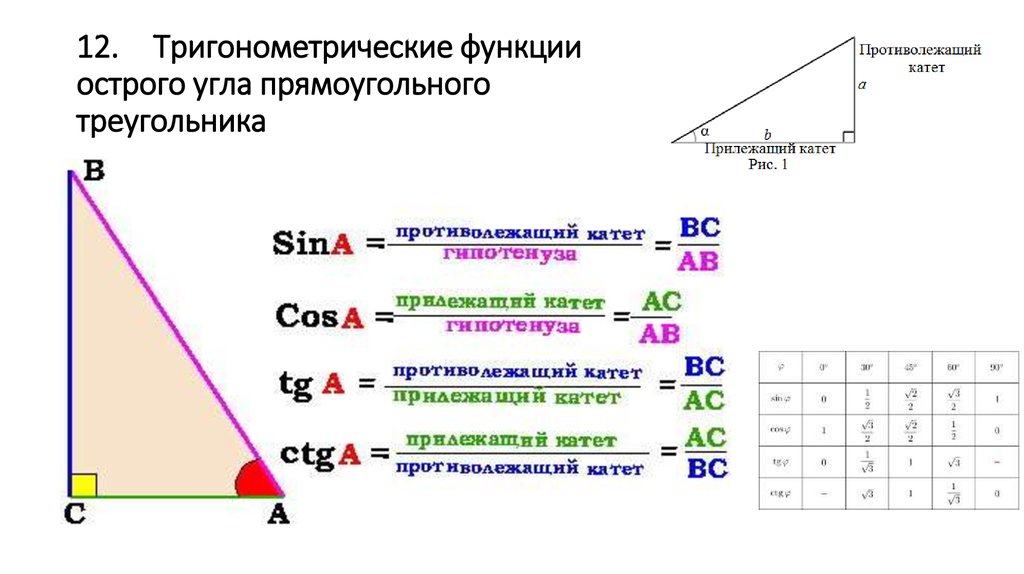 .. .. | ||
| Точное представление: | |||
| Минимальный многочлен: |
| Угол: 9° или π/20 радиан | ||
| Десятичная аппроксимация: |  .. .. | |
| Точное представление: | ||
| Точное представление в форме φ: |
| Минимальный многочлен: | |
| Минимальный многочлен в форме φ: |
| Угол: 12° или π/15 радиан | |||||||||
| Десятичная аппроксимация: |  .. .. Точное представление: | Минимальный многочлен: | |
| Угол: 15° или π/12 радиан | ||
| Десятичная аппроксимация: |  .. .. | |
| Точное представление: |
| Минимальный многочлен: | (для обоих) |
| Угол: 18° или π/10 радиан | ||
| Десятичная аппроксимация: | ||
| Точное представление: | ||
| Точное представление в форме φ: | ||
| Минимальный многочлен: |
| Угол: 21° или 7π/60 радиан | ||
| Десятичная аппроксимация: |  .. .. | |
| Точное представление: |
| Минимальный многочлен: | 9 x 90 7 10 + 182784 x 8 – 50176 x 6 + 7040 x 4 – 384 x 2 + 1 | (для обоих) |
| Угол: 24° или 2π/15 радиан | ||
| Десятичная аппроксимация: |  .. .. | |
| Точное представление: | ||
| Минимальный многочлен: |
| Угол: 27° или 3π/20 радиан | |||
| Десятичная аппроксимация: | | … |  .. .. | |
| Точное представление: | |||
| Точное представление в форме φ: |
| Минимальный многочлен: | |
| Минимальный многочлен в форме φ: |
| Угол: 30° или π/6 радиан | ||
| Десятичная аппроксимация: |  .. .. | |
| Точное представление: | ||
| Минимальный многочлен: |
| Угол: 33° или 11π/60 радиан | ||
| Десятичная аппроксимация: | ||
| Точное представление: |
| Минимальный многочлен: | 9 x 90 7 10 + 182784 x 8 – 50176 x 6 + 7040 x 4 – 384 x 2 + 1 | (для обоих) |
| Угол: 36° или π/5 радиан | ||
| Десятичная аппроксимация: |  .. .. | |
| Точное представление: | ||
| Точное представление в форме φ: | ||
| Минимальный многочлен: |
| Угол: 39° или 13π/60 радиан | ||
| Десятичная аппроксимация: |  .. .. | |
| Точное представление: |
| Минимальный многочлен: | (для обоих) |
| Угол: 42° или 7π/30 радиан | |||
| Десятичная аппроксимация: | | 06. |  .. .. | |
| Точное представление: | |||
| Минимальный многочлен: |
| Угол: 45° или π/4 радиана | ||
| Десятичная аппроксимация: |  .. .. | |
| Точное представление: | ||
| Минимальный многочлен: |
Общие минимальные многочлены
Обратите внимание, что sin 3°, cos 3°, sin 21°, cos 21°, sin 33°, cos 33°, sin 39° и cos 39° имеют одинаковый минимальный полином,
Этот полином является четным (все четные степени x ), так что он симметричен относительно оси y . Это означает, что полином можно разложить на множители как
Это означает, что полином можно разложить на множители как
График для этой функции для 0 < x < 1 приведен ниже.
Вот еще несколько:
Его график для 0 < x < 1 выглядит следующим образом:
Вот еще один:

Его график для – 1 < x < 1,
И еще один:
7 cos 2 9°)( x 2 – sin 2 27°)( x 2 – cos 2 27°).
Его график для 0 < x < 1 выглядит следующим образом:
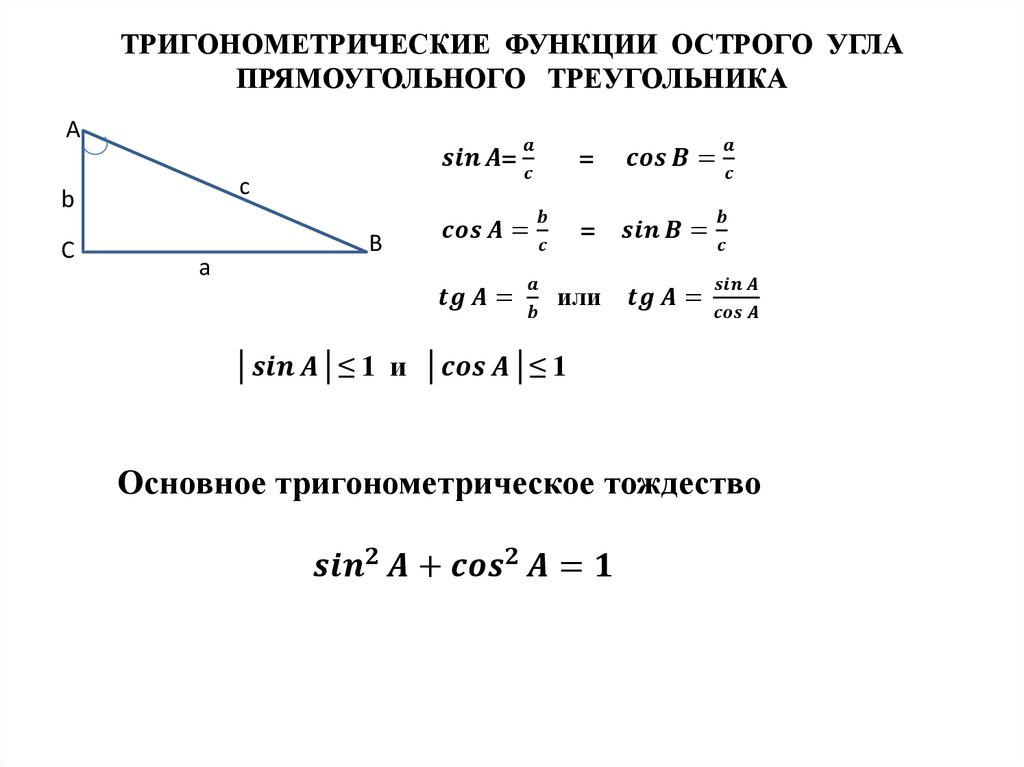
Все коэффициенты минимальных полиномов, по-видимому, состоят из степеней двойки и их суммы
Коэффициенты минимального многочлена 256 x 8 – 512 x 6 + 304 x 4 – 7 все степени 2 + 29097 , или суммы степеней 2:
512 = 2 9
304 = 2 8 + 2 5 + 2 4
48 = 2 5 + 2 4
1 = 2 0 .
Более короткие многочлены легко проверить. А как насчет того длинного выше?
262144 = 2 18
430080 = 2 18 + 2 17 + 2 15 + 2 12
372736 = 2 18 + 2 16 + 2 15 + 2 13 + 2 12
182784 = 2 17 + 2 15 + 2 14 + 2 11 + 2 9
50176 = 2 15 + 2 14 + 2 10
7040 = 2 12 + 2 11 + 2 9 + 2 8 + 2 7
384 = 2 8 + 2 7
1 = 2 0 .
Теперь все целые числа являются суммами степеней двойки, так что это не так уж глубоко при первом чтении. Однако то, что делает приведенные выше случаи (и другие) интересными, заключается в том, что, помимо конечной константы 1, коэффициенты представляют собой суммы «больших» степеней 2. Я не уверен, почему это так.
Я не уверен, почему это так.
Углы, не кратные 3°
Рассмотрим тождество синуса с тройным углом,
Полагая t = 10°, имеем
или
1/2 = – 4 sin 3 10° + 3 sin 10°.
Умножая на 2, имеем
Таким образом, многочлен 8 x 3 — 6 x + 1 = 0 имеет sin 10° в качестве корня, так что sin 10° является алгебраическим. Эквивалентно, минимальный полином для sin 10° равен 8 x 3 – 6 x + 1.
Используя тождество косинуса тройного угла и углы t = 20° и t = 40°, мы можем показать, что cos 40° и –cos 20° также являются корнями 8 x 3 – 6 x + 1 и, следовательно, алгебраических чисел.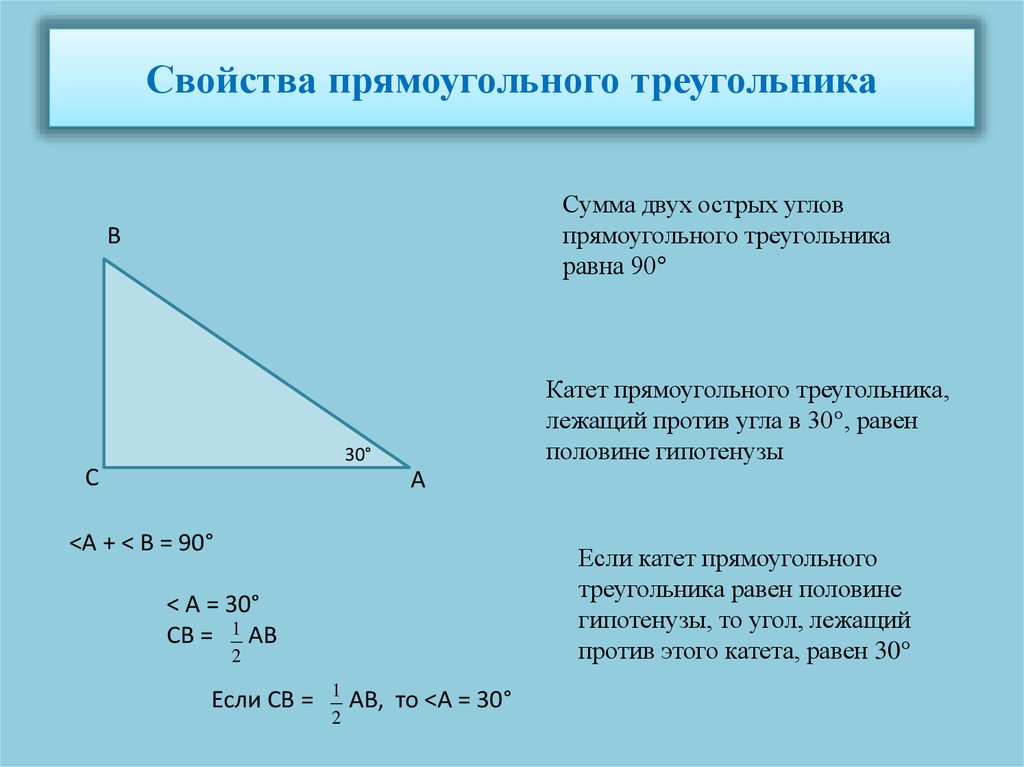 Таким образом,
Таким образом,
Аналогично, ±cos 10°, ±sin 40° и ±sin 20° являются корнями из 64 x 6 – 96 х 4 + 36 х 2 – 3. То есть,
График показан ниже:
И еще одно: ±sin 5°, ±cos 5°, ±sin 25°, ±cos 25°, ±sin 35° и ±cos 35° — все это корни

Это факторы как:
График показан ниже:
Таким образом, мы позаботились обо всех углах, кратных 5°, но не кратным 3°.
А как насчет 1°?
Следующее построение в общем случае иллюстрирует значение sin n °. Начните с равнобедренного треугольника △ABC с двумя сторонами длиной 1 и оставшейся стороной x . Пусть угол напротив x равен (2 n )°.
Продолжите построение следующим образом: начертите отрезок BD так, чтобы его длина также была x , затем начертите отрезок DE так, чтобы он пересекался с отрезком AB под прямым углом. Теперь пометьте длины следующим образом: |DE| = x cos (3 n ) и |BE| = x sin (3 n ), поэтому |AE| = 1 – x sin (3 n ). Формула Пифагора дает длины |AD| и |CD| как:
Теперь пометьте длины следующим образом: |DE| = x cos (3 n ) и |BE| = x sin (3 n ), поэтому |AE| = 1 – x sin (3 n ). Формула Пифагора дает длины |AD| и |CD| как:
Это показано на следующем рисунке
Теперь опустим перпендикуляр из А на отрезок ВС, а также перпендикуляр из В на отрезок CD. При этом мы разделили измерение угла (2 n )° в n °. Важно отметить, что треугольники △ABC и △BCD пропорциональны. Теперь мы можем определить sin ( n °) двумя способами, используя конструкцию «противоположность по гипотенузе» для прямых углов:
Соотнося два выражения, мы имеем:
Это упрощает до
После возведения в квадрат радикала уравнение принимает вид

Поскольку x = 0 дает тривиальный случай, мы игнорируем его и делим на x :
Пусть a — положительный корень этого многочлена, ближайший к 0. Следовательно, sin ( n °) = а /2, или а = 2 sin ( n °). Например, чтобы найти sin 1°, пусть n = 1, что дает x 3 – 3 x + 2 sin (3°) = 0. Калькулятор показывает, что a = 0,0349048 является корень этого многочлена. Следовательно, sin 1° = 0,0349048/2, или около 0,0174524, что также подтверждается калькулятором.
Поскольку sin 10° и sin 9° являются алгебраическими (как и cos 10° и cos 9°, что легко показать с помощью тождества Пифагора), то
Произведение и сумма/разность двух алгебраических чисел также являются алгебраическими.

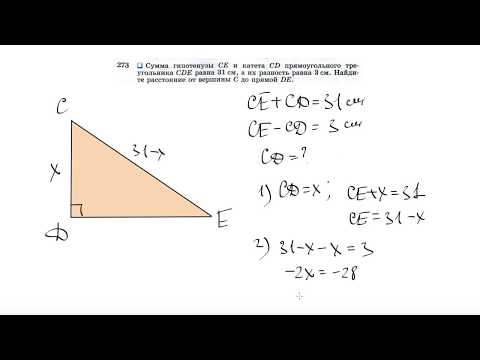 Пусть гипотенуза равна 1 единице длины. Тогда каждая из сторон имеет единицы длины. Это дает sin 45° = cos 45° = .
Пусть гипотенуза равна 1 единице длины. Тогда каждая из сторон имеет единицы длины. Это дает sin 45° = cos 45° = .
Leave A Comment