121. Геометрический и физический смысл производной

Рассмотрим график функции в декартовой системе координат (рис. 10.2). Возьмем на графике точку и точку . Проведем через эти точки прямую . Эта прямая называется Секущей. Ее уравнением будет , а угловой коэффициент этой прямой равен тангенсу угла наклона секущей:

Если то секущая MN поворачивается вокруг точки и переходит в касательную с угловым коэффициентом

Если , то секущая MN поворачивается вокруг точки М и в пределе переходит в касательную с угловым коэффициентом .

Угловой коэффициент касательной к графику функции в данной точке равен значению производной функции в этой
точке: .

Геометрический смысл производной состоит в том, что производная равна угловому коэффициенту касательной к графику функции в данной точке.

Значение производной в точке равно тангенсу угла наклона касательной (рис. 10.3).

Нормаль – это прямая, перпендикулярная к касательной в точке касания (рис.

10.3).

Уравнение касательной к кривой в точке запишем как уравнение прямой, которая проходит через заданную точку: .

Уравнение нормали к кривой в точке запишем так: .

Пример 1. Напишите уравнение касательной к графику функции в точке с абсциссой .

Решение. 1) Найдем значение функции, если : .

2) Найдем первую производную функции: .

3) Найдем значение производной, если : .

4) Запишем уравнение касательной, которая проходит через данную точку : или .

Ответ. Уравнение касательной: .

Пример 2. Напишите уравнение нормали к графику функции в точке с абсциссой .

Решение. 1) Найдем значение функции, если : .

2) Найдем первую производную функции: .

3) Найдем значение производной, если : .

4) Запишем уравнение нормали, которая проходит через данную точку : или .

Ответ. Уравнение нормали: .

Рассмотрим задачу о свободном падении тела и найдем мгновенную скорость его движения.

Из физики мы знаем, что , где H – высота падения, G – ускорение свободного падения, T – время падения.

За время тело проходит расстояние , а за время – расстояние . Приращение аргумента (времени T) будет равно , откуда .

Приращение функции будет равно:

Найдем предел отношения приращения функции к приращению ее аргумента T , если ΔT Стремится к нулю:

.

В левой части равенства мы получили значение производной функции , а в правой части значение мгновенной скорости тела в момент времени T0.

Физический смысл производной. Производная функции в точке есть мгновенная скорость изменения функции в точке , т. е. скорость протекания процесса, который описывается зависимостью .

Например, если дана функция , то ее производная будет , тогда значение производной в точке будет , а значение производной в точке будет . Это значит, что в точке функция изменяется в 4 раза быстрее аргумента , а в точке изменяется в 6 раз быстрее (т.

е. различная скорость изменения функции или протекания процесса). В этом и состоит физический смысл производной.

Операция нахождения (взятия) производной функции называется Дифференцированием функции.

Ответьте на вопросы

1. Что показывает угловой коэффициент K в уравнении прямой ?

2. Чему равен угловой коэффициент касательной к кривой в точке ?

3. Как найти угловой коэффициент нормали к кривой в точке ?

4. В чем состоит геометрический смысл производной?

5. В чем состоит физический смысл производной?

< Предыдущая   Следующая >

Геометрический смысл производной. Уравнение касательной к графику функции. Задание 7

Геометрический смысл производной. Уравнение касательной к графику функции. Задание 7.

 

Вспомним определение производной:

Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:

Исходя из этого определения, рассмотрим, каким образом производная функции  связана с графиком этой функции.

Посмотрите ВИДЕОУРОК, в котором я подробно объясняю, в чем заключается геометрический смысл производной, и как выводится уравнение касательной. А затем мы рассмотрим решение задач из Открытого банка заданий для подготовки к ЕГЭ по математике.

 

 

Итак.

Геометрический смысл производной.

Тангенс угла наклона касательной (угловой коэффициент наклона касательной), проведенной к графику функции   в точке    равен производной функции в этой точке:

Заметим, что угол  — это угол между прямой и положительным направлением оси ОХ:

Уравнение касательной к графику функции  в точке  имеет вид:

В этом уравнении:

— абсцисса точки касания,

— значение функции  в точке касания,

— значение производной функции  в точке касания.

Приведем несколько примеров решения задач из Открытого банка заданий для подготовки к ЕГЭ по математике, в которых используется знание геометрического смысла производной.

Пример 1. Задание В8 (№ 27504) На рисунке изображены график функции   и касательная к нему в точке с абcцисcой  . Найдите значение производной функции  в точке  .

Значение производной функции  в точке  равно тангенсу угла между касательной и положительным направлением оси ОХ. Чтобы его найти, выделим прямоугольный треугольник, гипотенуза которого лежит на касательной, а катеты параллельны осям координат. Обозначим точки с целыми координатами буквами  А и В — эти точки выделены на касательной:

Проведем через точку А прямую параллельно оси ОХ, а через точку В — параллельно оси OY. Получим прямоугольный треугольник ABC:

Угол А  треугольника  АВС равен углу между касательной и положительным направлением оси ОХ.

Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему.

Длины катетов считаем по количеству клеточек.

Ответ: 0,25

Пример 2. Задание В8 (№ 27506) На рисунке изображены график функции   и касательная к нему в точке с абцисоой 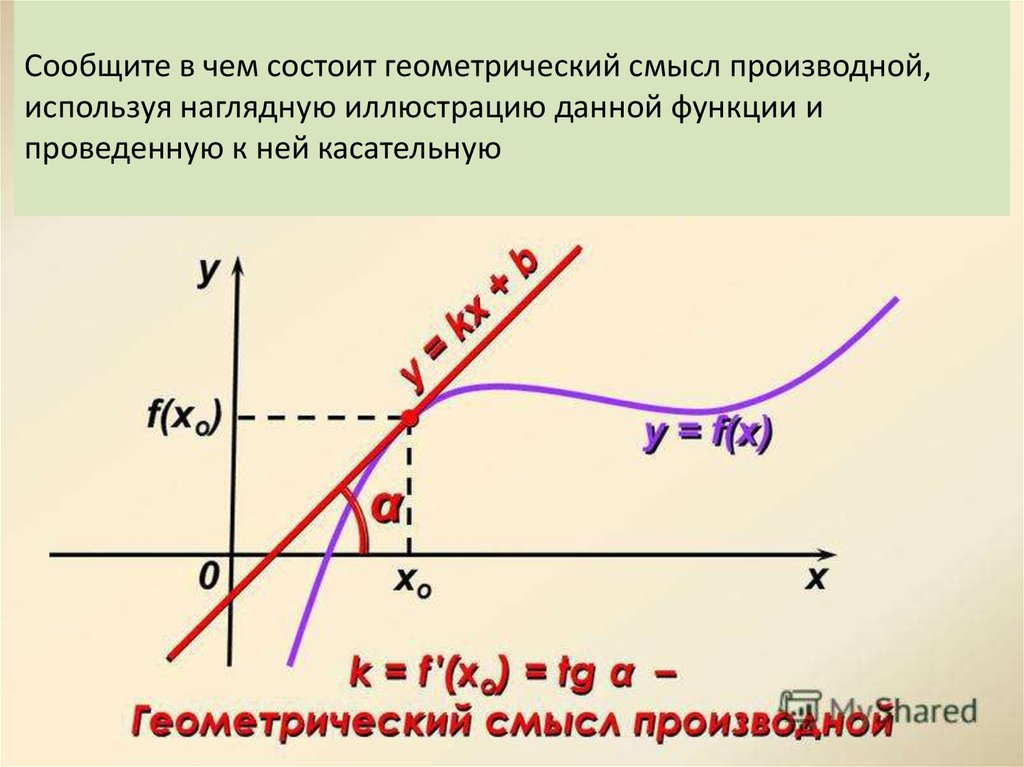 . Найдите значение производной функции  в точке .

Эта задача очень похожа на предыдущую, за исключением того, что здесь касательная  наклонена влево, и угол между касательной и положительным направлением оси ОХ расположен так:

Построим, как предыдущей задаче, прямоугольный треугольник АВС:

Угол А треугольника ABC и угол — смежные, то есть их сумма равна 180 градусов. Значит,

Запомните, если прямая наклонена влево, то коэффициент наклона прямой отрицателен.

Ответ: -0,25

Пример 3. Задание В8 (№ 40129)  На рисунке изображен график функции . Прямая, проходящая через начало координат, касается графика этой функции в точке с абсцссой 8. Найдите значение производной функции в точке .

Соединим  отрезком точку начала координат с точкой касания:

Производная функции в точке касания равна тангенсу угла  между касательной и положительным направлением оси ОХ:

Чтобы найти тангенс , рассмотрим прямоугольный треугольник АОВ:

 

Ответ: 1,25

И. В. Фельдман, репетитор по математике.

1.8: Геометрическая интерпретация производных

  1. Последнее обновление
  2. Сохранить как PDF
  • Идентификатор страницы
    25429
    • Дэн Слоутер
    • Университет Фурмана

    Напомним, что если \(y=f(x),\), то для любого действительного числа \(\Delta x\)

    \[\frac{\Delta y}{\Delta x}=\frac{f(x+\Delta x)-f(x)}{\Delta x}\] — средняя скорость изменения \(y\ ) относительно \(x\) на интервале \([x, x+\Delta x]\) (см. \((1.2.7)) .\) Теперь, если график \(y\) является прямым прямой, т. е. если \(f(x)=m x+b\) для некоторых действительных чисел \(m\) и \(b,\), то \((1.8.1)\) есть \(m, \) наклон линии. {\prime}(a)(x-a)+f(a) .\] Следовательно, касательная к графику функции \(f\) — это прямая через точку на графике \(f\), наклон которой равен наклону графика в этой точке. 9{2}(x)\] в точке \(x=\frac{\pi}{4}\).

    Ответить

    \(y=3\left(t-\frac{\pi}{4}\right)+\frac{3}{2}\)

    Эта страница под названием 1.8: Геометрическая интерпретация производных доступна в соответствии с лицензией CC BY-NC-SA 1.0 и была создана, изменена и/или курирована Дэном Слоутером посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами платформа LibreTexts; подробная история редактирования доступна по запросу.

    1. Наверх
      • Была ли эта статья полезной?
      1. Тип изделия
        Раздел или Страница
        Автор
        Дэн Слоутер
        Лицензия
        CC BY-NC-SA
        Версия лицензии
        1,0
        Показать страницу TOC
        нет
      2. Теги
        1. источник@http://www. synechism.org/wp/the-calculus-of-functions-of-several-variables

      5.2 Геометрическая интерпретация производной как наклона

      В этом разделе мы обсудим геометрическую интерпретацию производной функции в точке. Рассмотрим график функции \(y=f(x)\) и пусть \(P(x_{0},y_{0})\) — фиксированная точка на нем (рис. 1). Поскольку \(P\) находится на графике \(f\), мы знаем \(y_{0}=f(x_{0})\). Здесь мы используем нижний индекс 0, чтобы подчеркнуть, что \(x_{0}\) и \(y_{0}\) остаются постоянными в ходе обсуждения. Пусть \(Q(x_{1},y_{1})\) будет другой точкой на кривой с \(x_{1}=x_{0}+\Delta x\) и поскольку \(Q\) находится на график \(f\) \[y_{1}=f(x_{1})=f(x_{0}+\Delta x).\] Отсюда мы вычитаем \(y_{0}=f (x_{0})\) для получения. \[\Delta y=y_{1}-y_{0}=f(x_{0}+\Delta x_{0})-f(x_{0}).\] Так как \(\Delta x=PR\ ) и \(\Delta y=RQ\), \[\begin{align} \frac{\Delta y}{\Delta x} & =\frac{f(x_{0}+\Delta x)-f( x_{0})}{\Delta x}\\ & =\tan\widehat{RPQ}=\tan\phi\\ & =m _{\text{sec}}\\ & =\text{наклон секущей }PQ.

      \end{выровнено}\]

       

      Рисунок 1. Наклон секущей равен \(m_{\text{sec}}=\tan\phi=\frac{\Delta y}{\Delta x}\)

       

       

      • \(\Delta x=PR\) положительно, если \(R\) находится справа от \(P\), и отрицательно, если $R$ находится слева от \(P\). \(\Delta y=RQ\) положительно, если \(Q\) выше \(R\), и отрицательно, если \(Q\) ниже \(R\).

      • Поскольку линия, соединяющая \(P\) и \(Q\), пересекает кривую, она называется секущей. Использование секущей для этой ситуации происходит от латинского secare означает «разрезать» и не относится к функции секущей, которую мы имеем в тригонометрии.

       

      Производная от \(f\) в точке \(x=x_{0}\) равна
      \[\begin{align}
      \lim_{\Delta x\to0}\frac{\Delta y}{ \Delta x} & =\lim_{\Delta x\to0}\frac{f(x_{0}+\Delta x)-f(x_{0})}{\Delta x}\\
      & =\left .\frac{dy}{dx}\right|_{x_{0}}=f'(x_{0})\\

      &=\text{значение производной в точке }P\tag{a}
      \ end{align}\] Но когда мы позволим \(\Delta x\to0\), точка \(Q\) будет двигаться по кривой и приближаться все ближе и ближе к \(P\), секущая будет поворачиваться \ (P\) и приблизимся к касательной как к предельному положению (рис. 2), и мы получим \[\begin{align} \lim_{\Delta x\to0}\frac{\Delta y}{\Delta x} & = \lim_{Q\to P}\tan\phi=\tan\theta\\ & =\text{наклон касательной в точке }P\tag{b}\end{align}\] Следовательно, из (a) и ( б)
      \[\bbox[#F2F2F2,5px,border:2px сплошной черный]{\left.\frac{dy}{dx}\right|_{x_{0}}=f'(x_{0})=\ text{наклон касательной }.}\]
      Следовательно:

      Значение производной в любой точке кривой равно наклону линии, касательной к кривой в этой точке.

      Именно эта касательная задача привела Готфрида Вильгельма Лейбница к открытию дифференциального исчисления.

      Рисунок 2: Предел наклона секущей как \(Q\to P\) с любой стороны представляет собой наклон касательной к кривой в точке \(P\) и равен \(f'(x_{0 })\) 9{2}}}{\Delta x}\\ & =\lim _{\Delta x\to0}\frac{\bcancel{\Delta x}(2x+\Delta x)}{\bcancel{\Delta x}}\ \ & =2x.\end{выровнено}\]

      \begin{equation}
      \frac{dy}{dx}=f'(x)=2x=\text{наклон касательной в любой точке кривой.}\tag{i}
      \end{equation }

      Чтобы найти наклон касательной в вершине, подставьте \(x=0\) в (i), получив \[\left.