Глава 4
В природе, технике и быту можно часто наблюдать превращение одного вида механической энергии в другой: потенциальной в кинетическую и кинетической в потенциальную. Например, при падении воды с плотины её потенциальная энергия превращается в кинетическую. В качающемся маятнике периодически эти виды энергии переходят друг в друга.
Рис. 195. Маятник Максвелла
Явление превращения одного вида механической энергии в другой очень удобно наблюдать на приборе, изображённом на рисунке 195. Накручивая на ось нить, поднимают диск прибора. Диск, поднятый вверх, обладает некоторой потенциальной энергией. Если его отпустить, то он, вращаясь, начнёт падать. По мере падения потенциальная энергия диска уменьшается, но вместе с тем возрастает его кинетическая энергия. В конце падения диск обладает таким запасом кинетической энергии, что может опять подняться почти до прежней высоты. (Часть энергии расходуется на работу против силы трения, поэтому диск не достигает первоначальной высоты.
Превращение энергии из одного вида в другой происходит также при ударе двух каких-нибудь упругих тел, например резинового мяча о пол или стального шарика о стальную плиту.
Рис. 196. Превращение потенциальной энергии шарика в кинетическую при его падении
Если поднять над стальной плитой стальной шарик (рис. 196) и затем выпустить его из рук, то он будет падать. По мере падения шарика его потенциальная энергия убывает, а кинетическая растёт, так как увеличивается скорость движения шарика. При ударе шарика о плиту произойдёт сжатие как шарика, так и плиты. Кинетическая энергия, которой шарик обладал, превратится в потенциальную энергию сжатой плиты и сжатого шарика. Затем благодаря действию упругих сил плита и шарик примут почти первоначальную форму.
Превращение потенциальной энергии тетивы в кинетическую энергию стрелы |
Явления природы обычно сопровождаются превращением одного вида энергии в другой.
Энергия может и передаваться от одного тела к другому. Так, например, при стрельбе из лука потенциальная энергия натянутой тетивы переходит в кинетическую энергию летящей стрелы.
1. Как на опыте можно показать превращение одного вида механической энергии в другой? 2. Какие превращения энергии происходят при падении воды с плотины? 3.
1.Какие превращения одного вида энергии в другой происходят: а) при падении воды водопада; б) при бросании мяча вертикально вверх; в) при закручивании пружины механических часов; г) при открывании двери, имеющей пружину?
2.Массы падающих тел одинаковы. Одинаковы ли значения потенциальной энергии тел на одной и той же высоте и одинаковы ли значения кинетической энергии на этой высоте?
3.Приведите примеры тел, обладающих одновременно кинетической и потенциальной энергией.
Это любопытно… |
Всякое тело, поднятое над землёй, обладает потенциальной энергией. Это в равной степени относится и к воде. Например, вода объёмом 1 м3 на высоте 50 м обладает потенциальной энергией:
Еп = 9,8 •1000 •1 м3•50 м ≈ 500 000 Дж = 500 кДж.
При падении воды с этой высоты совершится работа A = 500 кДж.
Но в природе сравнительно редко встречаются большие водопады.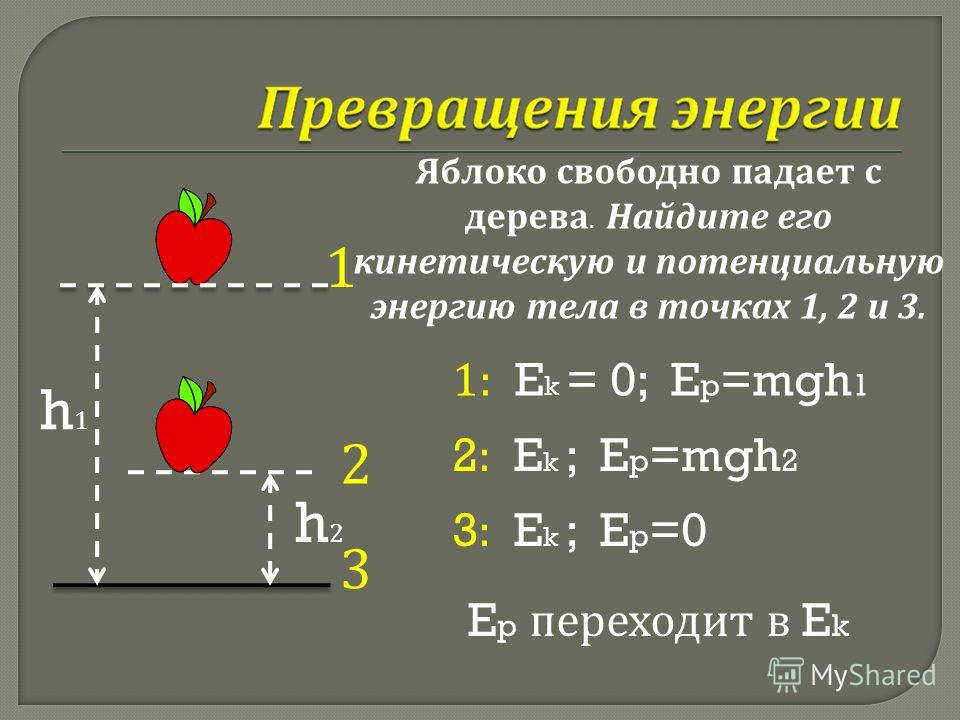 Чаще всего русла рек имеют небольшой уклон. В этих случаях для создания давления (напора), необходимого для работы гидравлических двигателей, приходится поднимать уровень воды в реке искусственно, при помощи плотин. За счёт энергии поднятой воды гидравлические двигатели могут совершать механическую работу.
Чаще всего русла рек имеют небольшой уклон. В этих случаях для создания давления (напора), необходимого для работы гидравлических двигателей, приходится поднимать уровень воды в реке искусственно, при помощи плотин. За счёт энергии поднятой воды гидравлические двигатели могут совершать механическую работу.
Один из простейших и древнейших двигателей — водяное колесо. Наиболее совершенные гидравлические двигатели — водяные турбины. В таких турбинах вода отдаёт энергию колесу, приводя в движение лопасти турбины. Рабочее колесо турбины соединено с валом электрического генератора, дающего электрический ток.
Ветряные двигатели используют энергию движущегося воздуха — ветра. Энергию ветра иногда называют энергией «голубого угля».
Рис. 197. Ветряные двигатели
Ветер представляет собой источник дешёвой энергии, но этот источник энергии обладает большим непостоянством, — в этом его неудобство.
Ветряные двигатели известны с древнейших времён. Современный довольно мощный ветряной двигатель изображён на рисунке 197.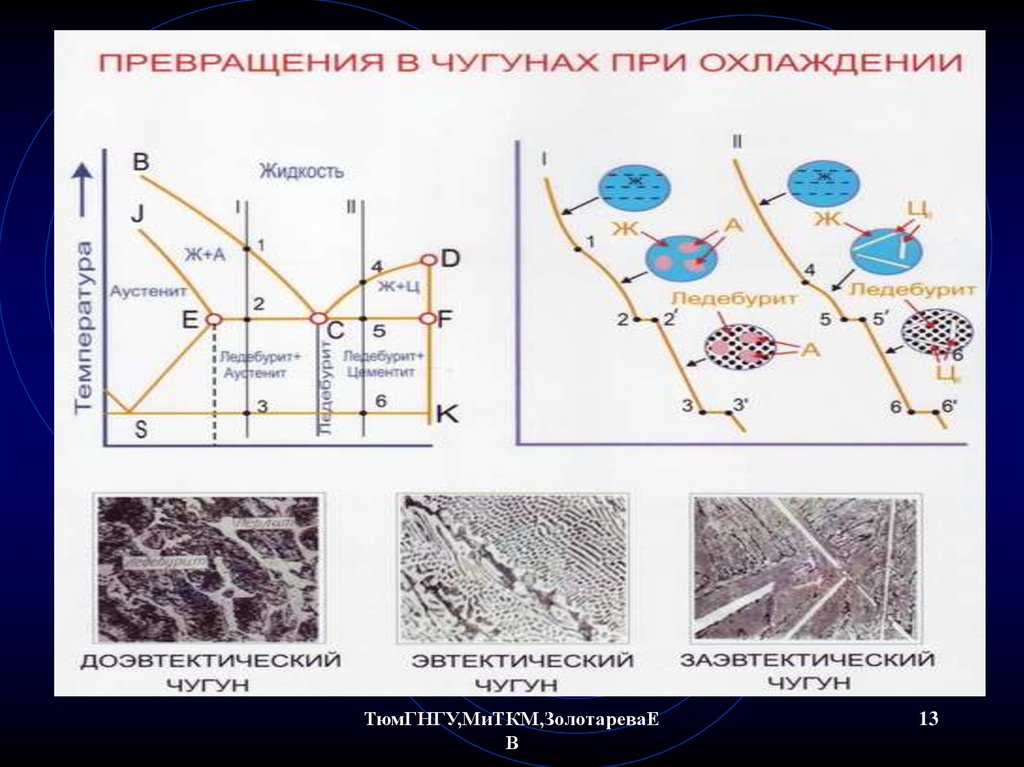 Движущиеся массы воздуха оказывают давление на наклонные плоскости крыльев ветряных двигателей и приводят их в движение. Вращательное движение крыльев при помощи системы передач передаётся механизмам, выполняющим какую-либо работу.
Движущиеся массы воздуха оказывают давление на наклонные плоскости крыльев ветряных двигателей и приводят их в движение. Вращательное движение крыльев при помощи системы передач передаётся механизмам, выполняющим какую-либо работу.
Экономически целесообразно использовать ветродвигательные установки там, где ветры дуют часто и сильно. Например, в Поволжье, на Алтае. Удобно их использовать и в отдалённых районах, куда не поступает энергия от электростанций, куда трудно подвозить топливо, например в дальних или высокогорных экспедициях. Они, как и гидравлические двигатели, имеют преимущества перед двигателями, в которых источником энергии служит топливо или радиоактивное вещество. Во-первых, водяные и воздушные двигатели, после того как они построены, уже не требуют затрат на топливо. Энергия, используемая в них, — энергия текущей воды и ветра — поставляется самой природой, возобновляется.
Во-вторых, работа этих двигателей не сопровождается выделением вредных отходов: газов, образующихся при сгорании топлива или радиоактивных отходов, т.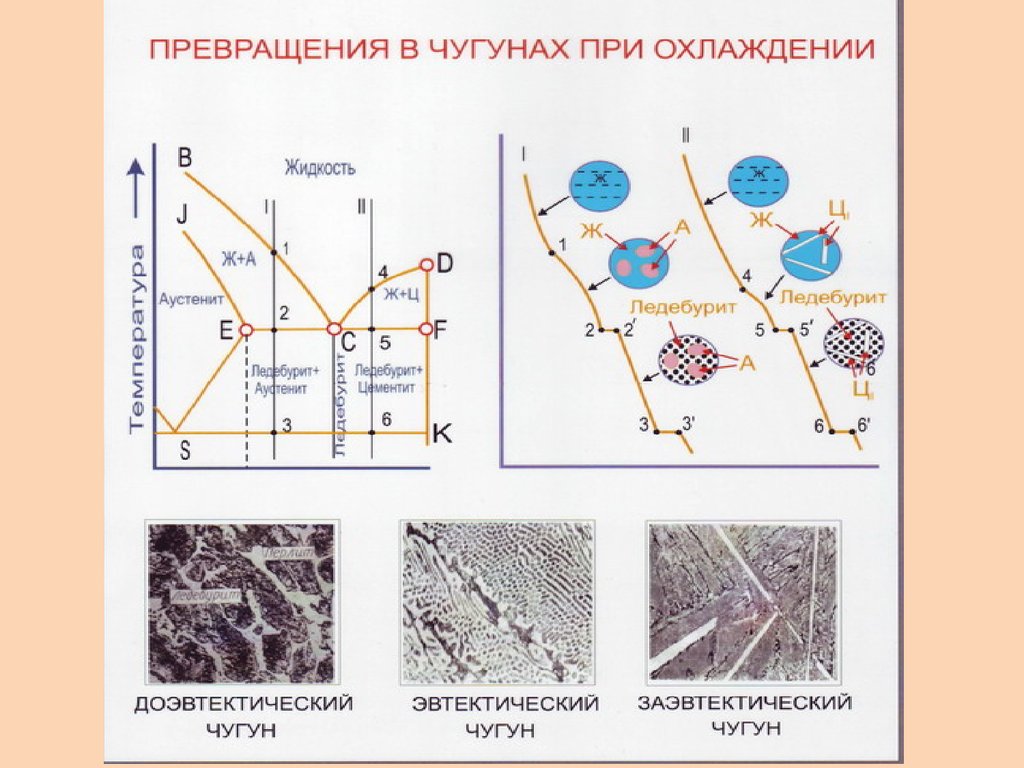
- Механическая работа совершается в том случае, когда тело движется под действием силы:
A = Fs.
- Мощность характеризует способность различных тел совершать определённую работу за некоторый промежуток времени:
.
- Рычаг — это простой механизм, представляющий собой твёрдое тело, которое может вращаться вокруг неподвижной оси.
- Рычаг будет находиться в равновесии, если
.
- Для того чтобы узнать эффективность работы механизма, вводят КПД:
η = или η = •100%.
1.Механическая работа совершается
А.если на тело действует сила и оно движется
Б.если сила тяжести равна весу тела
В.всегда, когда тело движется
2. Механическую работу вычисляют по формуле
Механическую работу вычисляют по формуле
А.A = Fs
Б.P = gm
В.
3.Мощность — это
А.отношение работы ко времени, за которое она была совершена
Б.работа, которую совершает тело
В.сила, с которой совершается работа
А.ватт (Вт)
Б.джоуль (Дж)
В.ньютон (Н)
5.Плечо силы — это
А.кратчайшее расстояние между точкой опоры и линией действия силы
Б.расстояние до точки приложения силы
6.Условие равновесия рычага
А.
Б.
В.F = gm
7.Момент силы вычисляют по формуле
А.M = Fl
Б.M = Fs
В.
8.КПД — это
А.отношение полезной работы к полной
Б.равенство полезной работы и полной
В.когда полная работа меньше полезной
Выполните задания, предложенные в электронном приложении.
Глава 5.1/ 5.1.2. Превращения в стали при нагреве — Купити в Харкові, Києві, Україні. Безкоштовне тестування
Превращения, т. е. изменение структуры (фазового состава), происходят при нагреве сплавов до критических точек — температур фазовых превращений. Именно эти температуры определяют режимы нагрева сталей и чугунов при термической обработке.
е. изменение структуры (фазового состава), происходят при нагреве сплавов до критических точек — температур фазовых превращений. Именно эти температуры определяют режимы нагрева сталей и чугунов при термической обработке.
В соответствии с диаграммой состояния Fe — Fe3C (см. рис. 4.2) выделим следующие критические точки:
- А1 — геометрическое место точек на линии PSK, т.е. для всех сплавов эта температура одинакова — 727°С. При нагреве до этой температуры происходит превращение перлита в аустенит;
- А3— геометрическое место точек на линии GS, при нагреве до этой температуры заканчивается полиморфное превращение феррита в аустенит. Для разных сплавов (сталей) эта температура неодинакова, она понижается по мере повышения содержания углерода;
- Аm — геометрическое место точек на линии SE, при нагреве до этой температуры заканчивается растворение цементита в аустените (при нагреве растворимость углерода в аустените повышается).
 Для разных сплавов (сталей) эта температура неодинакова, она повышается по мере увеличения содержания углерода.
Для разных сплавов (сталей) эта температура неодинакова, она повышается по мере увеличения содержания углерода.
Температуры превращений (критические точки) на практике несколько отличаются от равновесных температур, приведенных на диаграмме: при нагреве они несколько выше, при охлаждении — ниже. Чтобы отличить критические точки при охлаждении и нагреве, их дополнительно обозначают индексами: с при нагреве (Аc1, Ас3, Асm) и r при охлаждении (Аr1, Ar3, Аrm).
Рассмотрим стальной угол диаграммы Fe — Fe3C (рис. 5.1). Превращение перлита в аустенит (П[Ф + Ц] →А) при весьма медленном нагреве может завершиться при температуре 727 °С, т.е. в полном соответствии с диаграммой Fe — Fe3C. Этот процесс протекает в результате образования зародышей кристаллов аустенита из феррита путем изменения кристаллической решетки, или перекристаллизации (исходная ОЦК решетка феррита, конечная ГЦК решетка аустенита), их последующего роста и растворения цементита в аустените. Это превращение носит диффузионный характер и сопровождается перемещением атомов углерода.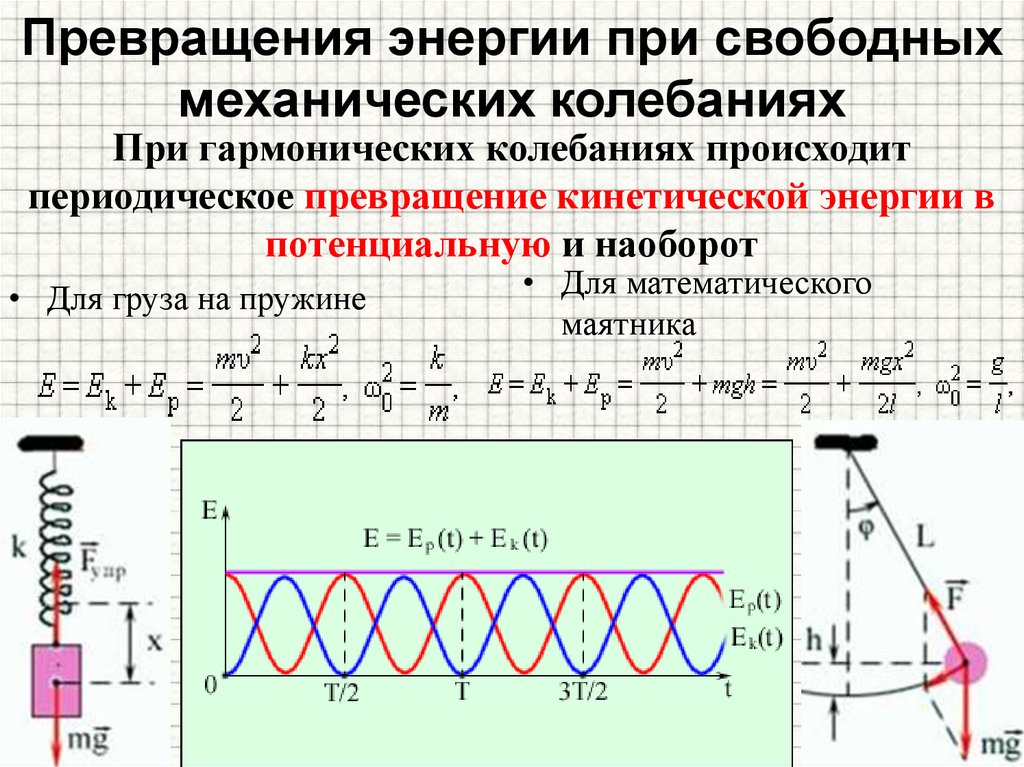
Рис. 5.1. Стальной угол диаграммы состояния сплава железо — цементит
Зародыши аустенита возникают на границах раздела кристаллов феррита и цементита (рис. 5.2). С увеличением степени перегрева относительно точки Ас1 превращение перлита в аустенит ускоряется (рис. 5.3). Так, повышение температуры с 740 до 800 °С приводит к увеличению скорости возникновения зародышей аустенита примерно в 280 раз и скорости их роста примерно в 80 раз.
Окончание процесса превращения характеризуется образованием аустенита и исчезновением перлита. Вновь образовавшийся аустенит неоднороден даже в объеме одного зерна. В тех местах, где раньше были пластинки цементита, содержание углерода значительно больше, чем в тех местах, где были пластинки феррита.
Для получения однородного (гомогенного) аустенита необходимо нагреть сталь выше Ас1 и дать выдержку для завершения диффузионных процессов. Скорость превращения перлита в аустенит зависит не только от температуры нагрева, но также от дисперсности цементита и его формы.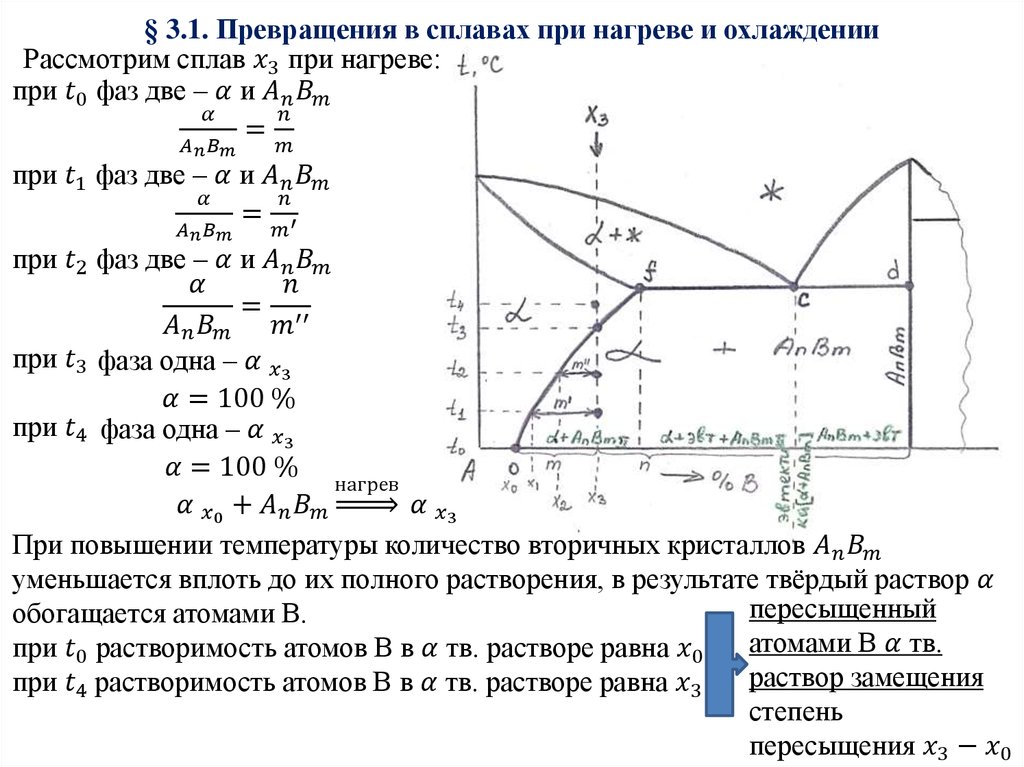 Чем мельче частицы цементита, тем быстрее протекает превращение перлита в аустенит.
Чем мельче частицы цементита, тем быстрее протекает превращение перлита в аустенит.
Рис. 5.2. Схема превращения перлита в аустенит при нагреве
Рис. 5.3. Влияние температуры нагрева на скорость превращения перлита в аустенит: t — температура; т — время; А — аустенит; П — перлит; Ц — цементит; ц и Vj — скорости нагрева; Ал — критическая точка (точка Кюри)
При нагреве доэвтектоидных сталей (С
У заэвтектоидных сталей (С > 0,8 %) при нагреве до температуры Асt (727 °С, линия PSK) также происходит превращение перлита в аустенит. Одновременно при этой температуре начинается растворение цементита в аустените (в соответствии с линией SE), которое заканчивается при температуре, соответствующей критической точке Асm, т.е. на линии SE.
Зарождение зерен аустенита происходит по границам зерен перлита. Эти границы имеют большую протяженность, поэтому превращение перлита в аустенит начинается с образования большого числа зародышей, следовательно, после окончания превращения образуется большое количество зерен аустенита малой величины (см.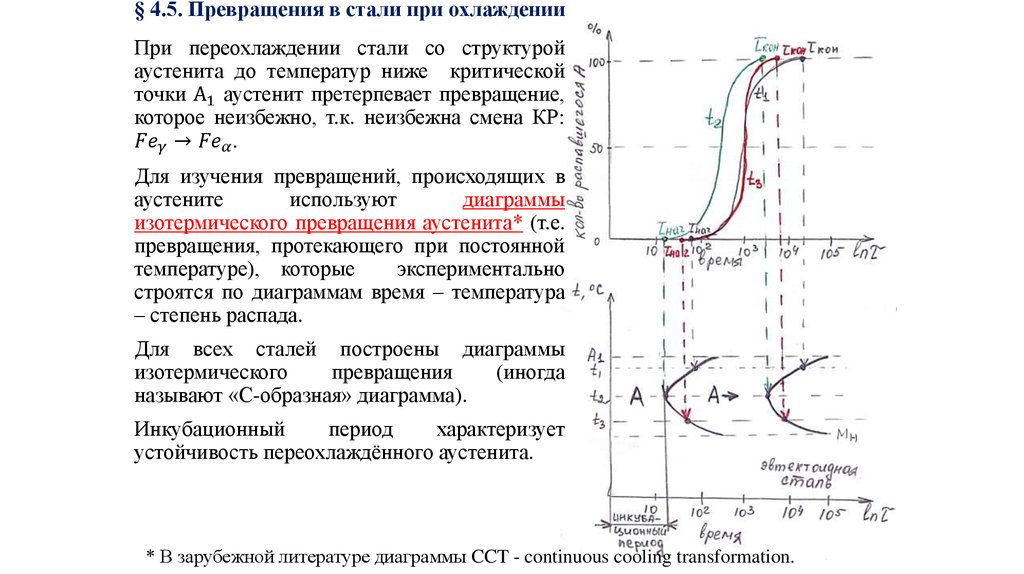 под разд. 2.7).
под разд. 2.7).
Размер аустенитного зерна по завершении превращений определяет величину начального зерна аустенита. Дальнейший нагрев или выдержка вызывают рост аустенитного зерна. Размер зерна, полученный в результате той или иной термической обработки, называется размером действительного зерна.
Различают два типа сталей: наследственно мелкозернистые и наследственно крупнозернистые. Наследственность в данном случае — это склонность к росту аустенитного зерна.
Наследственно мелкозернистые стали характеризуются малой склонностью к росту аустенитного зерна при нагреве, наследственно крупнозернистые, наоборот, — повышенной (рис, 5.4).
Рис. 5.4. Схема роста зерна стали при нагреве:
1 — наследственно мелкозернистая сталь; 2 -наследственно крупнозернистая сталь; А1 — температура превращения перлита в аустенит
Рис. 5.5. Шкала крупности зерна стали (100х): 1—8 — баллы зернистости зерна
5.5. Шкала крупности зерна стали (100х): 1—8 — баллы зернистости зерна
При переходе через критическую точку Aci получаем структуру аустенита с мелким зерном. При дальнейшем нагреве зерно аустенита наследственно мелкозернистой стали не растет до температур 950… 1000°С. У крупнозернистой стали рост зерна начинается при температуре, близкой к критической точке.
На практике наследственную зернистость определяют по шкале зернистости (рис. 5.5). Для этого сталь нагревают до таких температур, при которых у наследственно мелкозернистой стали зерно еще не растет, а у крупнозернистой уже выросло (930 °С), а после охлаждения определяют величину зерна.
У наследственно мелкозернистых сталей величина зерна соответствует баллам от 5 до 8, у наследственно крупнозернистых — от 1 до 4 баллов.
Эксплуатационные свойства стали определяются действительным размером зерна. Крупное зерно в стали не влияет на твердость, но снижает прочность и ударную вязкость.
Некоторые технологические свойства, напротив, определяются наследственным зерном. Так, наследственно мелкозернистую сталь можно прокатывать (ковать) при более высоких температурах, когда сталь обладает большей пластичностью. Наследственно мелкозернистая сталь более технологична при термической обработке — у нее более широкий интервал закалочных температур, потому что такая сталь не склонна к перегреву (см. рис. 5.4).
- Попередня
- Наступна
Типы, правила, формулы, графики, примеры
Преобразования — это изменения, выполняемые в фигурах на координатной плоскости путем поворота, отражения или перемещения. В 19 веке Феликс Кляйн предложил новую точку зрения на геометрию, известную как трансформационная геометрия. Большинство доказательств в геометрии основано на преобразованиях объектов. Мы можем изменить любое изображение в координатной плоскости с помощью преобразований. Графика, используемая в видеоиграх, лучше понимается с применением правил трансформации.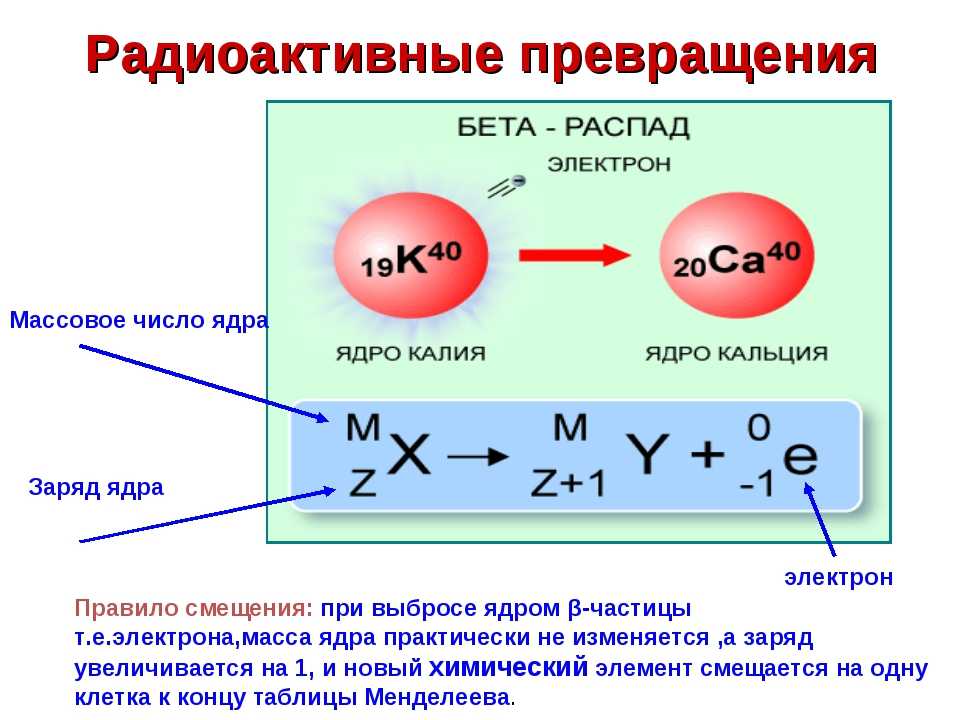 Давайте научимся идентифицировать преобразования, поймем правила преобразования функций и изучим типы преобразований.
Давайте научимся идентифицировать преобразования, поймем правила преобразования функций и изучим типы преобразований.
| 1. | Что такое трансформации? |
| 2. | Типы трансформаций |
| 3. | Правила трансформации |
| 4. | Формула Превращений |
| 5. | Часто задаваемые вопросы о преобразованиях |
Что такое преобразования в математике?
Функция f, которая отображается сама на себя, называется преобразованием, т. е. f: X → X. Прообраз X становится изображением X после преобразования. Это преобразование может быть любым или комбинацией операций, таких как перемещение, вращение, отражение и расширение. Перевод — это перемещение функции в определенном направлении, вращение — это вращение функции вокруг точки, отражение — это зеркальное отображение функции, а расширение — это масштабирование функции.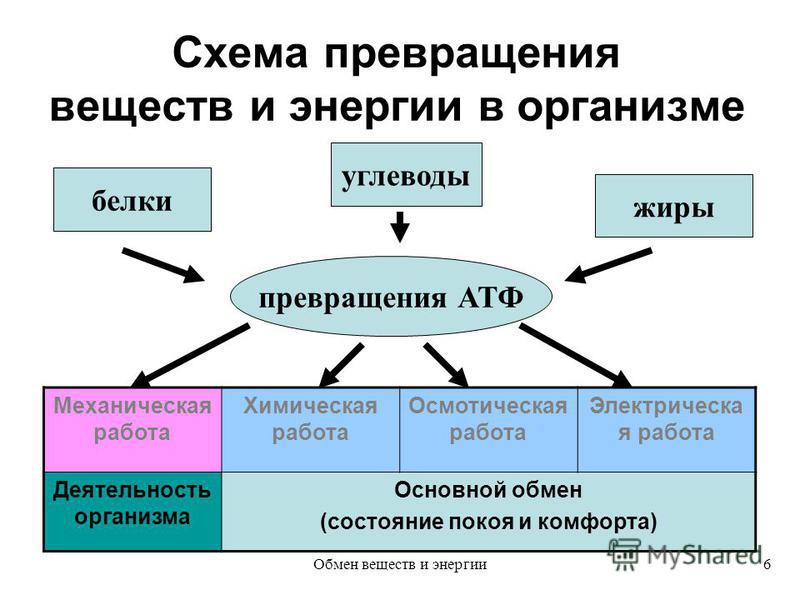 Преобразования в математике описывают, как двумерные фигуры перемещаются по координатной плоскости.
Преобразования в математике описывают, как двумерные фигуры перемещаются по координатной плоскости.
Типы трансформаций
Существует четыре распространенных типа преобразований: перемещение, вращение, отражение и расширение. Из определения преобразования у нас есть вращение вокруг любой точки, отражение по любой линии и перемещение по любому вектору. Это жесткие преобразования, при которых изображение конгруэнтно своему прообразу. Они также известны как изометрические преобразования. Расширение выполняется практически в любой точке и не является изометрическим. Здесь образ подобен своему прообразу.
| Трансформация | Функция | Результат |
|---|---|---|
| Вращение | Вращает или поворачивает прообраз вокруг оси | Без изменения размера или формы |
| Отражение | Переворачивает предварительное изображение и создает зеркальное изображение | Без изменений размера, формы или ориентации |
| Перевод | Скользит или перемещает прообраз | Без изменения размера или формы; Изменяет только направление формы |
| Расширение | Растягивает или сжимает прообраз | Расширяет или сужает форму |
Правила трансформаций
Рассмотрим функцию f(x). На координатной сетке мы используем оси x и y для измерения движения. Вот правила преобразования функций, которые можно применить к графикам функций. Преобразования могут быть представлены алгебраически и графически. Преобразования обычно встречаются в алгебраических функциях. Мы можем использовать формулу преобразований в графических функциях, чтобы получить график, просто преобразуя базовую или родительскую функцию, и тем самым перемещать график, а не табулировать значения координат. Преобразования помогают нам визуализировать и изучать уравнения в алгебре.
На координатной сетке мы используем оси x и y для измерения движения. Вот правила преобразования функций, которые можно применить к графикам функций. Преобразования могут быть представлены алгебраически и графически. Преобразования обычно встречаются в алгебраических функциях. Мы можем использовать формулу преобразований в графических функциях, чтобы получить график, просто преобразуя базовую или родительскую функцию, и тем самым перемещать график, а не табулировать значения координат. Преобразования помогают нам визуализировать и изучать уравнения в алгебре.
Преобразование перемещения
Перемещение двумерной формы вызывает скольжение этой формы. Чтобы описать положение синей фигуры относительно красной фигуры, давайте посмотрим на взаимное расположение их вершин. Нам нужно найти позиции A′, B′ и C′, сравнивая их положение относительно точек A, B и C. Мы находим, что A′, B′ и C′ равны:
- 8 единиц слева от A, B и C соответственно.
- На 3 единицы ниже A, B и C соответственно.

Этот перевод можно алгебраически перевести как 8 единиц влево и 3 единицы вниз. то есть (x, y) → (x-8, y-3)
Преобразование квадратичных функций
Мы можем применить правила преобразования к графикам квадратичных функций. Этот прообраз в первой функции показывает функцию f(x) = x 2 . Преобразование f(x) = (x+2) 2 сдвигает параболу на 2 шага вправо.
Трансформация отражения
Тип преобразования, происходящего при отражении каждой точки фигуры от линии, называется отражением. Когда точки отражаются над линией, изображение находится на том же расстоянии от линии, что и прообраз, но с другой стороны линии. Каждая точка (p, q) отражается на точку изображения (q, p). Если точка A находится на расстоянии 3 единиц от линии отражения справа от линии, то точка A’ будет на расстоянии 3 единиц от линии отражения слева от линии. Таким образом, линия отражения действует как серединный перпендикуляр между соответствующими точками изображения и прообраза.
Вот график квадратичной функции, показывающий преобразование отражения. Функция f(x) = x 3 . Преобразование f(x) есть g(x) = — x 3 , то есть отражение f(x) относительно оси x.
Преобразование вращения
Преобразование, которое поворачивает каждую точку фигуры на определенное число градусов вокруг этой точки, называется вращением. Фигура вращается против часовой стрелки, если число градусов положительное, и по часовой стрелке, если число градусов отрицательное. Общее правило преобразования вращения вокруг начала координат следующее.
Повернуть на 90º: (x,y) → (-y, x)
Повернуть на 180º (x,y) → (-x,-y)
Повернуть на 270º (x,y) → (y, -x)
На приведенном ниже графике функции мы наблюдаем преобразование вращения, при котором прообраз поворачивается на 180º в центре вращения в точке (0,1). Давайте проследим, как здесь применяется правило поворота от (x, y) к каждой вершине. Здесь происходит преобразование из (x,y) → (-x, 2-y)
(-2,4) →(2,-2), (-3,1) → (3,1 ) и (0,1 ) → (0,1)
Преобразование расширения
Преобразование, которое заставляет двухмерную фигуру растягиваться или сжиматься по вертикали или горизонтали с постоянным коэффициентом, называется расширением. Вертикальное растяжение задается уравнением y = a.f(x). Если a > 1, функция растягивается относительно оси y. Если a < 1, функция сжимается по оси y. Горизонтальное растяжение определяется как y = f.(ax). Если a > 1, функция сжимается по оси x. Если a < 1, функция растягивается относительно оси x.
Вертикальное растяжение задается уравнением y = a.f(x). Если a > 1, функция растягивается относительно оси y. Если a < 1, функция сжимается по оси y. Горизонтальное растяжение определяется как y = f.(ax). Если a > 1, функция сжимается по оси x. Если a < 1, функция растягивается относительно оси x.
Рассмотрим родительскую функцию y = x 2 +x. После горизонтального сжатия в 5 раз измененная функция становится равной 5x 2 +5x в точке (1/5x, y). После горизонтального растяжения с коэффициентом 1/5 преобразованная функция становится равной 1/5 x 2 +1/5 x в точке (5x,y). После вертикального сжатия в 5 раз измененная функция становится равной 5x 2 +5x в точке (x, 5y). После вертикального растяжения в 1/5 преобразованная функция принимает вид 1/5 x 2 +1/5 x в точке (x, 1/5y).
Формула превращений
Рассмотрим граф f(x) = x 2
- Допустим, нам нужно построить график f(x) = x 2 -3, сдвинем вершину на 3 единицы вниз.

- Допустим, нам нужно построить график f(x) = 3x 2 + 2, сдвинем вершину на две единицы вверх и растянем по вертикали в три раза.
- Допустим, нам нужно построить график f(x) = 2(x-1) 2 , сдвинем вершину на единицу вправо и растянем по вертикали в 2 9 раз0108
- Таким образом, мы получаем общую формулу преобразований в виде
f(x) =a(bx-h) n +k
где k — вертикальное смещение,
h — горизонтальное смещение,
a — вертикальное растяжение и
b — горизонтальная растяжка.
Аналогично, f(x) можно преобразовывать разными способами. В этой таблице показан результирующий график после применения преобразования к f(x).
| Преобразование f(x) | Преобразование графа | Изменить (х, у) на |
|---|---|---|
| -ф(х) | отражает f(x) по оси x | (х, у) |
| ф(-х) | отражает f(x) по оси Y | (-х, у) |
| ф(х)+а | сдвиг f(x) вверх на единицу | (х, у+а) |
| ф(х) — а | сдвиг f(x) вниз на единицу | (х, у-а) |
| ф(х+а) | сдвиг f(x) влево на единицу | (х-а, у) |
| ф(х-а) | сдвиг f(x) вправо на единицу | (х+а,у) |
а. ф(х) ф(х) | растягивание/сжатие f(x) по вертикали | (х, ау) |
| ф(акс) | растягивание/сжатие f(x) по горизонтали | (х/а,у) |
Важные замечания по преобразованиям
- Преобразования в геометрии можно комбинировать. Форма может быть отражена или повернута, перемещена или расширена, или может иметь комбинацию этих преобразований.
- Преобразования выражаются алгебраически в функциях графика.
☛ Связанные темы:
- Графические функции
Часто задаваемые вопросы о преобразованиях
Что такое трансформации?
Преобразования — это изменения, выполняемые с функцией путем перемещения, отражения, поворота и расширения. Исходное изображение, известное как предварительное изображение, изменяется, чтобы получить изображение.
Какие существуют 4 типа трансформации?
Перевод, отражение, вращение и расширение — это 4 типа преобразований. Перевод — это перемещение формы в определенном направлении, отражение — создание зеркального отображения формы, вращение переворачивает форму относительно точки в градусах, а расширение — растяжение или сжатие формы на постоянный коэффициент.
Перевод — это перемещение формы в определенном направлении, отражение — создание зеркального отображения формы, вращение переворачивает форму относительно точки в градусах, а расширение — растяжение или сжатие формы на постоянный коэффициент.
Почему в математике важны преобразования?
Математика предназначена для выявления закономерностей и понимания взаимосвязей между понятиями для выработки решения проблемы. Преобразования важны в математике, чтобы в основном знать конгруэнтность и подобие фигур на плоскости. Мы могли бы изменить положение точки, линии или двумерной фигуры, используя 4 преобразования.
Как построить отражение и какие трансформации происходят?
Когда мы отражаем точку по оси x, координата y преобразуется, а координата x остается прежней. x-координата будет иметь тот же знак, но изменится знак y-координаты.
Какова формула трансформации?
Общая формула преобразований: f(x) =a(bx-h) n +k
где k — вертикальное смещение,
h — горизонтальное смещение,
a — вертикальное растяжение
b — горизонтальная вытяжка.
Как работают трансформации?
Преобразования позволяют нам изменить график функции, чтобы скользить, растягиваться или сжиматься, вращаться.
Как выполнять преобразования на графике?
При преобразовании графа необходимо выполнить следующие шаги.
- Найдите родительскую функцию f(x) и определите последовательность необходимых преобразований.
- Определите, должно ли оно отражаться по оси x или оси y, смещаться по вертикали или по горизонтали, поворачиваться на градусы в точке или растягиваться или сжиматься вокруг осей, используя коэффициент масштабирования.
- Введите координаты родительской функции, следуя правилам преобразования.
- Постройте преобразованную функцию соответствующим образом.
Каково правило трансформации?
Предположим, что родительской функцией является f(x), f(x)+a сдвигает f(x) вверх на a единиц, f(x+a) сдвигает f(x) влево на a единиц, -f(x) отражает f(x) по оси x, f(-x) отражает f(x) по оси y, a. f(x) растягивает или сжимает f(x) по вертикали, а f(a.x) растягивает или сжимает f(x) по горизонтали. Это несколько правил преобразования графов.
f(x) растягивает или сжимает f(x) по вертикали, а f(a.x) растягивает или сжимает f(x) по горизонтали. Это несколько правил преобразования графов.
Преобразования в математике — определение, типы и примеры
Автор:
Малкольм МакКинзи
Проверено
Пол Маццола 85 это процесс, который манипулирует многоугольником или другим двумерным объектом. на плоскости или в системе координат. Математические преобразования описывают, как двумерные фигуры перемещаются по плоскости или системе координат.
прообраз или прообраз — это двумерная форма до любого преобразования. image – фигура после преобразования.
Типы преобразований
В математике существует пять различных преобразований:
Расширение — Изображение представляет собой увеличенную или уменьшенную версию прообраза; «уменьшение» или «увеличение».

Отражение — Изображение является зеркальным прообразом; «флип».
Вращение — Изображение представляет собой прообраз, вращающийся вокруг фиксированной точки; «поворот».
Сдвиг — Все точки вдоль одной стороны прообраза остаются фиксированными, а все остальные точки прообраза перемещаются параллельно этой стороне пропорционально расстоянию от данной стороны; «перекос.,»
Перевод — Изображение смещено на постоянную величину от прообраза; «слайд.»
Расширение
Расширение прообраза любого многоугольника выполняется путем дублирования его внутренних углов при пропорциональном увеличении каждой стороны. Вы можете думать о расширении как об изменении размера. Какое изображение треугольника, желтое или синее, является расширением оранжевого прообраза?
Преобразование расширения — определение и примеры Желтый треугольник, расширение, увеличено по сравнению с прообразом в 3 раза.
Отражение
Представьте, что вы вырезаете прообраз, поднимаете его и кладете обратно лицевой стороной вниз. Это отражение или флип. Образ отражения – это зеркальное отображение прообраза. Какое изображение трапеции, красное или пурпурное, является отражением зеленого прообраза?
Преобразование отражения – определение и примерыИзображение пурпурной трапеции было отражено вдоль оси x, но вам не нужно использовать ось координатной плоскости для отражения.
Вращение
Используя начало координат, (0, 0) , как точку, вокруг которой вращается двумерная фигура, вы можете легко увидеть вращение на всех этих рисунках:
Преобразование вращения – определение и примерыФигура делает не должны зависеть от происхождения для вращения.
Сдвиг
Вот квадратный прообраз. Чтобы срезать его, вы «искажаете его», создавая изображение ромба:
Определение преобразования сдвига Когда фигуру срезают, ее площадь не изменяется. Стрижка не растягивает размеры; он меняет внутренние углы.
Перемещение
Перемещение перемещает фигуру из исходного положения на координатной плоскости без изменения ее ориентации. Какое изображение восьмиугольника ниже, розовое или голубое, является переводом желтого прообраза?
Определение трансформации переводаСиний восьмиугольник — это перевод, а розовый восьмиугольник повернулся.
Жесткие преобразования
Жесткое преобразование не изменяет размер или форму прообраза при создании изображения. Три преобразования являются жесткими.
К жестким преобразованиям относятся отражение, вращение и перемещение. Изображение от этих преобразований не изменит свой размер или форму.
Нежесткие преобразования
Нежесткое преобразование может изменить размер или форму, или и размер, и форму прообраза.
Два преобразования, растяжение и сдвиг, нежесткие. Изображение, полученное в результате преобразования, изменит свой размер, форму или и то, и другое.
Жесткие и нежесткие трансформацииПримеры трансформации
Существует пять различных типов трансформации, и трансформацию форм можно комбинировать.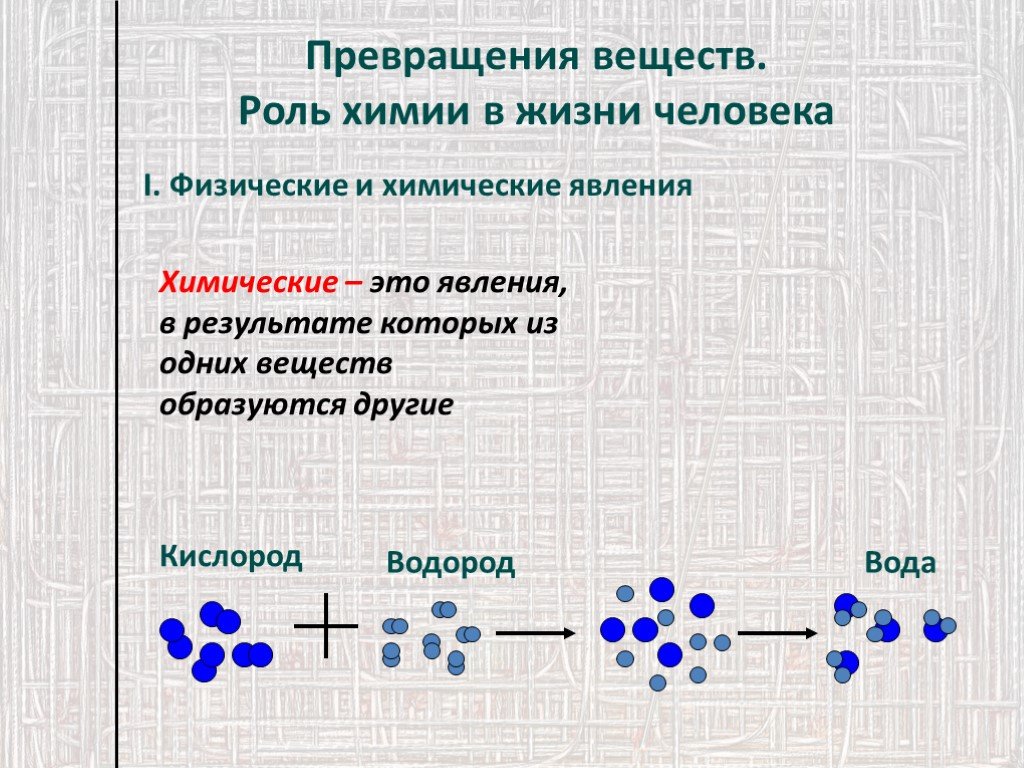 Многоугольник может быть отражен 90 482 и 90 483 перемещен, поэтому изображение кажется отделенным и зеркальным от своего прообраза. Прямоугольник можно увеличить и разрезать, чтобы он выглядел как параллелограмм большего размера.
Многоугольник может быть отражен 90 482 и 90 483 перемещен, поэтому изображение кажется отделенным и зеркальным от своего прообраза. Прямоугольник можно увеличить и разрезать, чтобы он выглядел как параллелограмм большего размера.
Вот прообраз и образ. Какие два преобразования были проведены над ним?
Пример комбинированных преобразованийПрообраз был повернут и расширен (сжат) для создания изображения.
Преобразования в координатной плоскости
В координатной сетке вы можете использовать оси x и y для измерения каждого перемещения. Линии также помогают рисовать многоугольники и плоские фигуры. Сосредоточьтесь на координатах вершин фигуры, а затем соедините их, чтобы сформировать изображение.
Вот высокий синий прямоугольник, нарисованный в квадранте III.
Пример преобразования переводаНас просят перевести в новые координаты. Математически инструкции по построению графика выглядят так:
Это говорит нам добавить 9 к каждому x для каждой вершины, а затем соедините новые точки в квадрантах II и IV.
Вращение с использованием координатной сетки также легко выполняется с помощью осей x и y: значение умножить на -1 и поменять местами значения x и y)
Повернуть на 180° : (x, y)→(−x, −y) make(умножить значение y и x -значение умножить на -1)
Чтобы повернуть на 270° : (x, y)→ (y, −x) (умножить значение x на -1 и поменять местами x- и y- значений)
Отражение многоугольник через линию отражения означает подсчет расстояния от каждой вершины до линии, а затем подсчет такого же расстояния от линии в другом направлении. Если фигура имеет вершину в (-5, 4) и вы используете ось Y в качестве линии отражения, то отраженная вершина будет в (5, 4).
Сдвиг под фигурой понимается фиксация одной линии многоугольника и перемещение всех остальных точек и линий в определенном направлении пропорционально их удалению от заданной фиксированной линии. Курсивные буквы на компьютере являются примерами сдвига.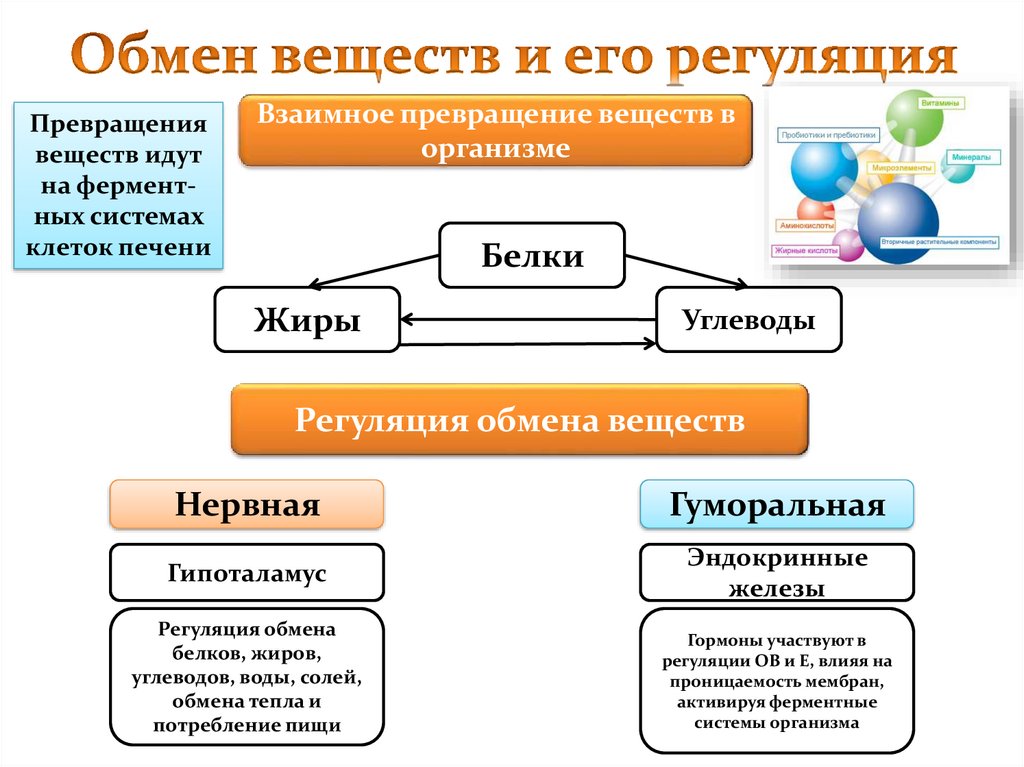

 Для разных сплавов (сталей) эта температура неодинакова, она повышается по мере увеличения содержания углерода.
Для разных сплавов (сталей) эта температура неодинакова, она повышается по мере увеличения содержания углерода.


Leave A Comment