Параллелограмм
- Определение параллелограмма
- Свойства параллелограмма
- Признаки параллелограмма
- Теоремы параллелограмма
- Углы параллелограмма
- Свойства диагоналей параллелограмма
- Как вычислить площадь параллелограмма?
- Как вписать параллелограмм в окружность?
- Как вписать окружность в параллелограмм?
- Как начертить параллелограмм?
- Трапеция — это параллелограмм?
- Средняя линия параллелограмма
- Параллелограмм, у которого все стороны равны
- Ось симметрии параллелограмма
Определение параллелограмма
С этой фигурой знакомы все, освоившие курс школьной программы. Впервые с понятием «параллелограмм» встречаются в 8 классе на уроках геометрии.
Параллелограмм — геометрическая фигура, являющаяся разновидностью четырехугольника.
Противоположные стороны параллельны.
Стоит отметить, что всем известные фигуры, такие как квадрат, ромб, прямоугольник, являются параллелограммами. Исходя из этого, им можно дать следующие определения:
- Квадрат — параллелограмм с равными сторонами, пересекающимися под углом 90 градусов.
- Ромб — параллелограмм с равными между собой сторонами, не пересекающимися под углом 90 градусов.
- Прямоугольник — параллелограмм с неравными между собой сторонами, но пересекающимися под прямым углом.
Свойства параллелограмма
Для того чтобы определить параллелограмм, нужно обладать знанием о его свойствах. Рассмотрим их на примере четырехугольника MNPK.
- Длина противоположных сторон фигуры одинакова.
MK=NP, MN=PK
- Противоположные стороны параллельны.
MK||NP, MN||PK
- Углы, являющиеся противоположными, равны.
∠NMK=∠NPK, ∠MNP=∠MKP
- Сумма всех четырех углов составляет 360 градусов.

∠NMK+∠NPK +∠MNP+∠MKP = 360°
- Сумма двух соседних углов равна 180 градусов.
∠NMK+∠MNP=∠NPK+∠MKP=
- Диагонали разделяют параллелограмм на два треугольника, равные между собой.
- При пересечении диагоналей образуется точка пересечения, представляющая собой центр симметрии.
- Диагонали пересекаются и точка их пересечения разделяет каждую диагональ пополам.
- Биссектриса, проведенная из любого угла, отделает от четырехугольника равнобедренный треугольник.
Признаки параллелограмма
Четырехугольник MNPK можно называть параллелограммом при выполнении минимум одного условия:
- Противоположные стороны равны парами: MK=NP, MN=PK.
- Противоположные углы равны парами: ∠NMK=∠NPK, ∠MNP=∠MKP.
- Диагонали пересекаются, и точка их пересечения разделяет каждую диагональ пополам.
- Противоположные стороны равны и параллельны между собой: MK=NP, MN|PK.

- Сумма квадратов двух диагоналей равняется сумме квадратов четырех его сторон: MP²+NK²=MN²+NP²+PK²+MK².
Теоремы параллелограмма
Все существующие теоремы доказывают свойства параллелограмма и исходят из определения о том, что это четырехугольник с противоположно расположенными параллельными сторонами.
Основные теоремы доказывают, что:
- параллелограммом является выпуклый четырехугольник;
- противоположные стороны попарно равны;
- углы, являющиеся противоположными, попарно равны;
- точка пересечения диагоналей разделает их пополам.
Параллелограммом является выпуклый четырехугольник
Многоугольник признается выпуклым при условии отсутствия продления до прямой хотя бы одной из сторон, а все оставшиеся стороны будут располагаться по одну сторону от этой прямой.
Пусть дан параллелограмм MNPK, сторона MN противоположна PK, а MK противоположна NP. Следовательно, исходя из определения, следует вывод о том, что MN || PK, а MK || NP.
Параллельные отрезки общих точек соприкосновения не имеют. Следовательно, PK находится со стороной MN по одну сторону. Отрезок NP соединяет точку N отрезка MN с точкой P отрезка PK. Противоположный отрезок MK соединяет оставшиеся две точки отрезков, что дает право утверждать о нахождении отрезков NP и MK по одну сторону от прямой MN. Исходя из всего вышесказанного, можно сделать вывод о том, что три стороны PK, NP и MK располагаются по одну сторону от отрезка MN.
Аналогичный алгоритм доказательства предположения о нахождении трех других сторон по одну сторону относительно остальных.
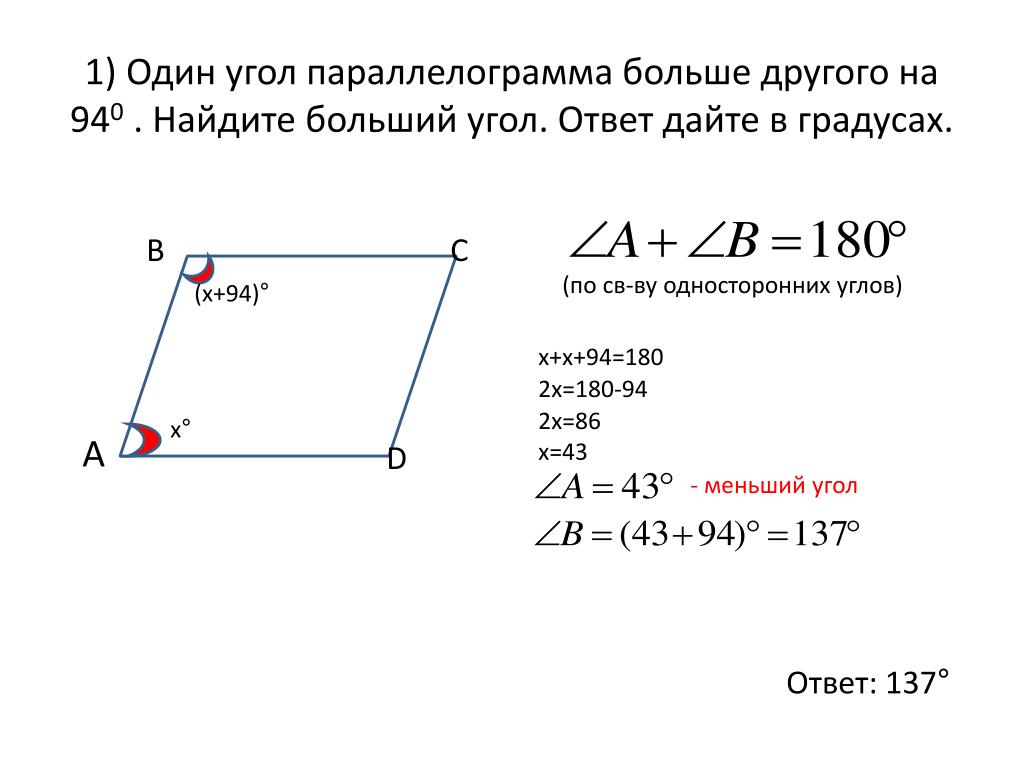
Противоположные стороны и углы попарно равны
Имеется четырехугольник MNPK, у которого MK=NP, MN=PK, ∠NMK=∠NPK, ∠MNP=∠MKP.
Параллелограмм — это, как мы знаем, четырехугольник. Следовательно, имеет 2 диагонали. Зная о том, что это выпуклая фигура, делаем вывод о делении фигуры на два треугольника. В нашем случае образовались треугольники MNP и MKP.
У треугольников имеется общее — сторона MP. ∠NPM=∠PMK, а ∠NMP=∠MPK, так как накрест лежащие углы, пересекая параллельные прямые, равны.
∠NPM=∠PMK, а ∠NMP=∠MPK, так как накрест лежащие углы, пересекая параллельные прямые, равны.
Следовательно, ΔMNP=ΔMKP, так как одна общая сторона и два равных смежных угла. Отсюда NP=MK, MN=PK.
∠NMP=∠NMP+∠PMK
∠NPK=∠NPM+∠MPK
∠NPM=∠PMK и ∠NMP=∠MPK
Из равенств следует, что ∠NMK=∠NPK.
Таким образом, теорема о равенстве противоположных углов и сторон доказана.
Точка пересечения диагоналей разделяет их пополам
Зная, что параллелограмм представляет собой выпуклый четырёхугольник, можно сказать о наличии двух пересекающихся диагоналей.
Есть четырехугольник MNPK с диагоналями NK и PM, пересекающимися в точке O. Возьмем два полученных треугольника MNO и PKO.
Из свойства противоположно лежащих сторон параллелограмма следует равенство MN=PK. Угол MNO и угол OKP — накрест лежащие, следовательно, они равны. Аналогично, два других угла — NMO и OPK — являются равными. Делаем вывод о равенстве треугольников MNO и PKO по стороне и двум углам.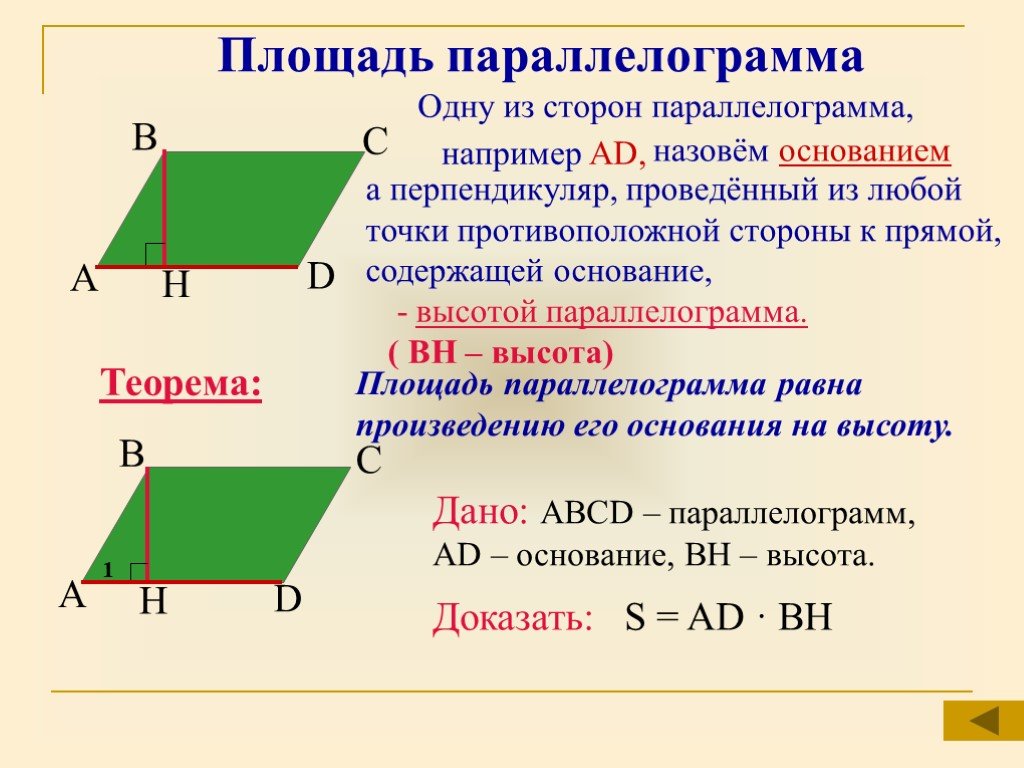
Из рисунка видно, что углы MON и KOP вертикальные, а значит, они равны.
Зная о равенстве образовавшихся треугольников, можно утверждать и о равенстве всех соответствующих элементов. Сторона MO равна стороне PO, как и сторона NO=OK. Каждая из пар вместе представляет собой диагональ параллелограмма.
Таким образом, теорема о делении диагоналей пополам доказана.
Углы параллелограмма
Для углов действует правило, согласно которому смежные углы в сумме дают 180 градусов, а два противоположных равны друг другу. Основываясь на этих утверждениях, значения остальных углов находятся по формуле:
∠α=180°-β
Свойства диагоналей параллелограмма
- Точка пересечения диагоналей разделяет их пополам.
- Любая диагональ разделяет фигуру на два треугольника, равные друг другу.
- Сумма квадратов его диагоналей равняется сумме квадратов всех его сторон.
- Площадь фигуры находится путем умножения длины диагоналей на синус угла, расположенного между ними, разделённый на 1/2.

Как вычислить площадь параллелограмма?
Существует несколько вариантов нахождения площади:
- По основанию и высоте: S=a*h.
- Зная значение двух смежных сторон и угла между ними: S=a*b*sin(α)°.
- По длине диагоналей и углу между ними: S=1/2*d1*d2*sin α.
Разберем подробнее последнюю формулу площади на примере. Дан параллелограмм с диагоналями АС и BD. Точка пересечения — О. Угол пересечения диагоналей в точке O = 60°. Отрезки AO=6 см и OD=5 см Площадь находится по формуле:
S=1/2*d1*d2*sin α
Зная свойство деления диагоналей точкой пересечения пополам, получаем:
AC=AO*2=12 см и DB=OD*2=10 см
Подставляем полученные значения в формулу:
S=1/2 * 12*10*1/2√3=51,962 см2
Как вписать параллелограмм в окружность?
Вписанный параллелограмм — это когда фигура находится внутри окружности.
Не каждый параллелограмм можно поместить внутрь окружности. Эту манипуляцию можно проделать с той фигурой, у которой два противоположных угла в сумме составляют 180 градусов.
Эту манипуляцию можно проделать с той фигурой, у которой два противоположных угла в сумме составляют 180 градусов.
Из этого можно прийти к выводу, что у вписанного в окружность параллелограмма все четыре угла равны 90°. Параллелограмм бывает трех видов: квадрат, ромб, прямоугольник. Следовательно вписать в окружность можно прямоугольник, квадрат.
Алгоритм построения:
- Начертить окружность.
- Найти ее центр, обозначить буквой O.
- Выбрать любую точку на окружности и назвать ее точкой A.
- Если вписываем квадрат, то нужно построить два диаметра с углом между ними в 90 градусов. Точки пересечения диагоналей с окружностью соединить прямыми линиями.
- Для прямоугольника нужно иметь значения угла между диагоналями или размеры сторон. Зная размеры сторон по теореме Пифагора, высчитываем угол между диагоналями. Проведя один диаметр, обозначить точки пересечения с окружностью. От точки O (центр окружности и середина диагонали) отмерить угол между диагоналями.
 Провести второй диаметр через центр и новую полученную точку. Соединить полученные точки прямыми.
Провести второй диаметр через центр и новую полученную точку. Соединить полученные точки прямыми.
Как вписать окружность в параллелограмм?
В окружность можно вписать параллелограмм при условии равнозначных сумм противолежащих сторон. Из трех вариантов параллелограмма сумма противоположных сторон одинакова только у ромба. Следовательно, если в параллелограмм вписана окружность, то этот параллелограмм является ромбом.
Алгоритм действий:
- Начертить ромб можно, зная длину минимум одной стороны и одного угла.
- Провести горизонтальную линию, равную длине стороны.
- Транспортиром отмерить известный угол и провести луч.
- На луче отмерить тот же самый размер стороны.
- Оставшиеся две стороны нарисовать параллельно имеющимся.
- Согласно свойству ромба и вписанной окружности, проводим две биссектрисы из смежных углов (они же диагонали в ромбе).
- Пересечение биссектрис отметить точкой О.

- Точка О будет центром окружности.
- Вписанная окружность должна касаться всех сторон параллелограмма. Следовательно, стороны ромба будут касательными к окружности.
- Касательные перпендикулярны радиусу, который проходит к точке касания. Таким образом, из центра окружности (точки О) надо опустить перпендикуляр к любой стороне ромба.
- Иголку циркуля поставить в точку О, а ножку — на точку касания перпендикуляра со стороной ромба.
- Начертить окружность.
- Правильно начерченная фигура будет соприкасаться со всеми сторонами ромба.
Как начертить параллелограмм?
Рассмотрим схему построения каждого вида по отдельности.
Алгоритм построения квадрата
- Узнать размер одной стороны. Этого достаточно, так как все стороны в квадрате равны.
- Один из признаков квадрата — все углы равны 90 градусов.
- Чертим прямую, равную длине одной стороны.

- С каждой стороны проводим перпендикулярную линию.
- На перпендикулярах отмечаем нужную длину и ставим точку.
- Соединяем две точки, построенные на перпендикулярных прямых.
Построение ромба
- Начертить ромб можно, зная длину минимум одной стороны и одного угла.
- Провести горизонтальную линию, равную длине стороны.
- Транспортиром отмерить известный угол и провести луч.
- На луче отмерить тот же самый размер стороны.
- Оставшиеся две стороны нарисовать параллельно имеющимся.
Как построить прямоугольник
- Нужно знать значения длины и ширины.
- Начертить прямую, равную длине.
- Провести два перпендикуляра с обеих сторон отрезка.
- Отметить на перпендикулярных линиях отрезок равный ширине прямоугольника.
- Соединить полученные два отрезка.
- При правильном построении полученная линия должны быть перпендикулярна длине (первой начерченной линии).

Трапеция — это параллелограмм?
Обе фигуры являются четырехугольниками с двумя противоположными сторонами, которые равны. Трапеция по определению имеет 2 непараллельные стороны. В параллелограмме все 4 стороны попарно параллельны.
Таким образом, трапеция не является параллелограммом.
Средняя линия параллелограмма
Под этим термином понимается отрезок, соединяющий середины противоположных сторон параллелограмма.
Средняя линия всегда равна параллельной ей стороне
Свойства средней линии в параллелограмме:
- точка пересечения диагоналей является точкой пересечения средних линий;
- точка пересечения делит средние линии пополам;
- точка пересечения выступает центром симметрии параллелограмма.
Параллелограмм, у которого все стороны равны
Все четыре стороны имеют равное значение в двух разновидностях фигуры — ромбе и квадрате.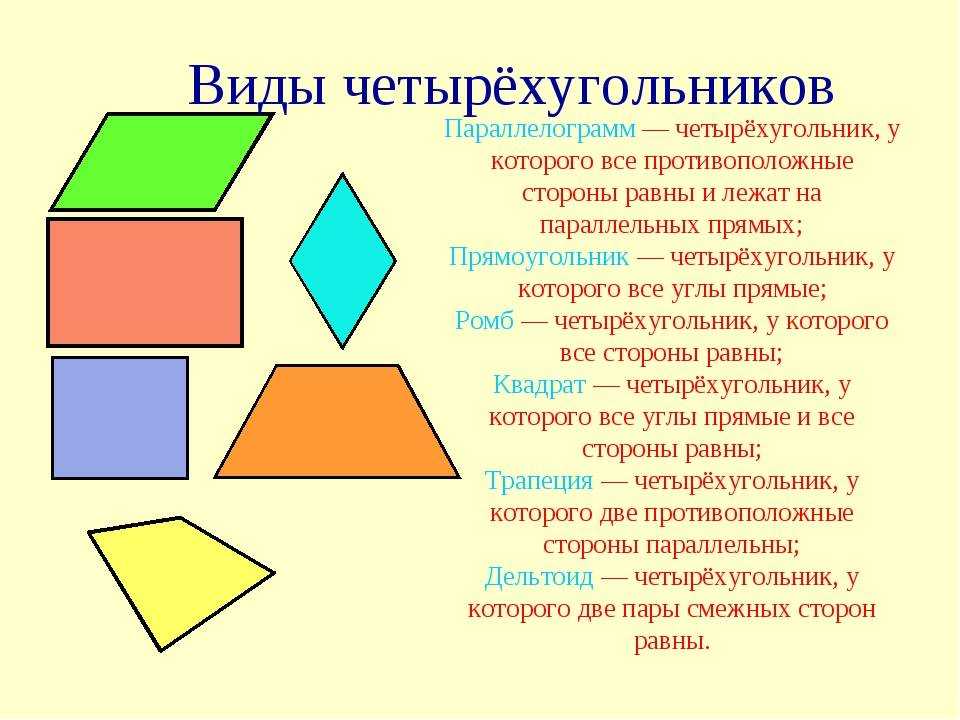
Ось симметрии параллелограмма
Под осью симметрии понимается прямая, разделяющая фигуру на две зеркально равные фигуры.
В прямоугольнике осью симметрии являются прямые, которые проходят через середину противоположной стороны.
В ромбе оси симметрии представляют собой его 2 диагонали.
Квадрат, объединяя в себе две предыдущие фигуры, имеет 4 оси симметрии: 2 диагонали и 2 средние линии.
Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Коля, Дима и Саша собрали. ..
..
Скажите пожалуйста правильный ответ на такое уравнение: 3-3х6+2=?
Через точку О,не лежащую между…
за 3 корочки хлеба и 2 кружки молока надо заплатить 20 монет. Сколько стоит 1 корочка хлеба, если она дешевле 1 кружки молока на 5 монет
Решено
В прямоугольном треугольнике АВС угол С равен 90 градусов, AB = 4, tg А=0.75 . Найдите АС.
Пользуйтесь нашим приложением
Обнаружение формул для площади – Элементарная математика
Формулы площади
Учащиеся, у которых есть неформальное представление о том, что площадь – это «количество двумерных «вещей»», содержащихся внутри области, могут изобрести для себя большинство формул, которые они часто используют попросил просто запомнить. Каждая формула, которую они заново изобретают, помогает укрепить их понимание (и память) о других формулах, которые они знают.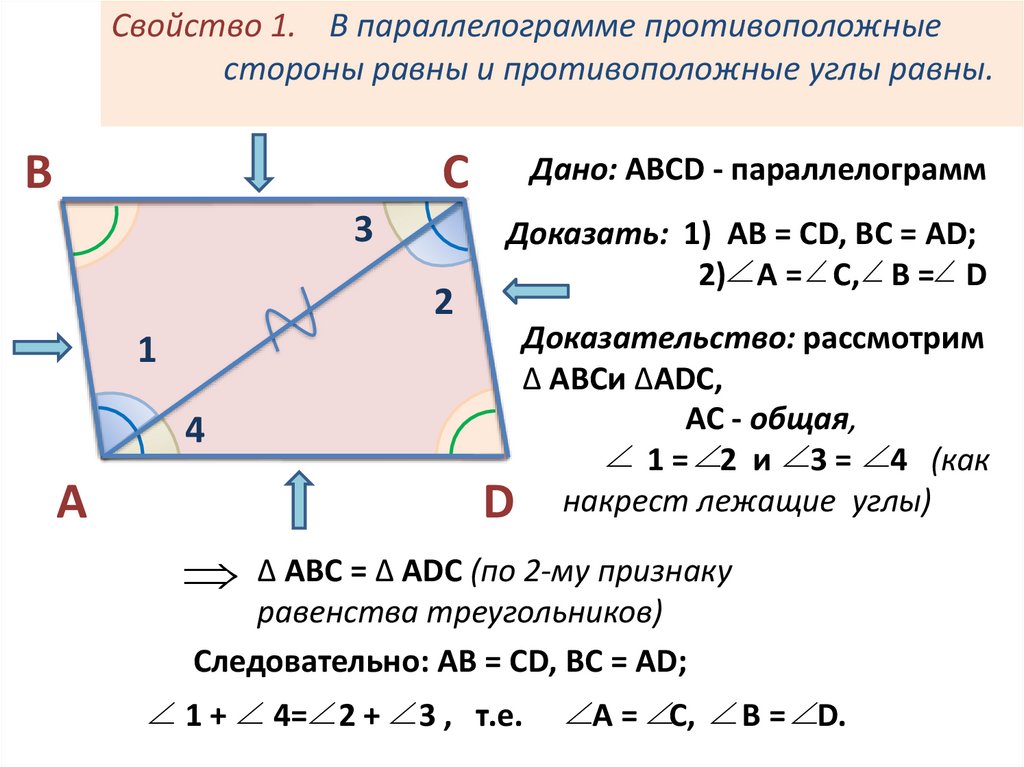 (См. также площадь поверхности.)
(См. также площадь поверхности.)
Площадь прямоугольников
Выбирая квадрат в качестве единицы площади, мы получаем интуитивное представление о площади прямоугольников. Если мы решим, что площадь этого квадрата равна 1, то прямоугольник, длина которого в 7 раз больше, будет иметь площадь 7 × 1.
Прямоугольник, который в два раза больше высоты, будет иметь вдвое большую площадь, поэтому площадь равна 2 × 7 единиц площади. Мы можем сосчитать два ряда по семь квадратов. Точно так же имеет 3 строки по 7 квадратов (или 7 столбцов по 3 квадрата), всего 7 × 3 квадрата, поэтому его площадь составляет 21 квадратную единицу.
Количество квадратов в одном ряду равно длине прямоугольника. Количество строк равно высоте прямоугольника. Итак, площадь равна длине × высоте.
Поскольку прямоугольник можно нарисовать под наклоном, «высота» определяется как «направление, перпендикулярное основанию», а «основание» определяется как любая сторона, которую вы выберете.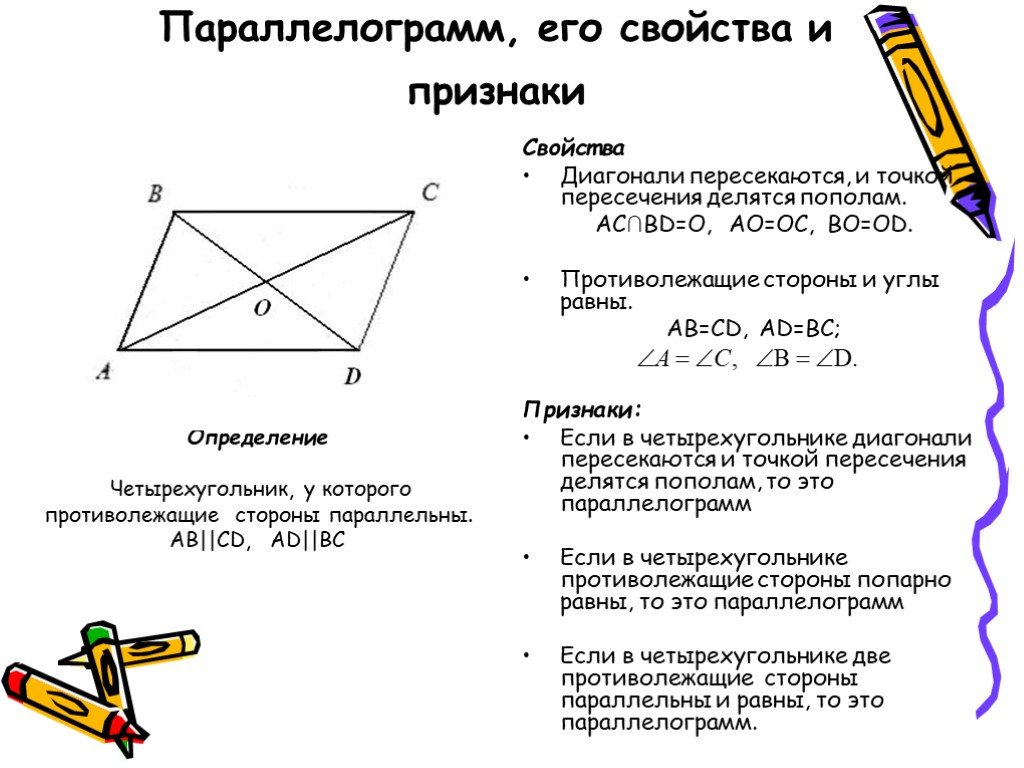
Подходит для подсчета чисел. Это работает даже для дробей. Синий прямоугольник, показанный здесь, имеет высоту в половину единицы длины и ширину в пять с половиной единиц длины. Если мы выберем соответствующий квадрат в качестве нашей единицы площади, мы увидим, что синий прямоугольник содержит пять половинных единиц площади и одну четверть единицы площади, или всего две и три четверти единицы площади. (Розовые части показывают завершение каждой квадратной единицы площади.)
Чтобы включить все чисел, мы определить площадь прямоугольника как основание × высоту (где «основание» и «высота» означают длины этих сторон, измеренные в тех же единицах ).
Площадь параллелограмма
Появление идеи
Мы можем вычислить формулу площади параллелограмма, разрезав параллелограмм и переставив части так, чтобы получился прямоугольник. Поскольку параллелограмм и прямоугольник состоят из одних и тех же частей, они обязательно имеют одинаковую площадь.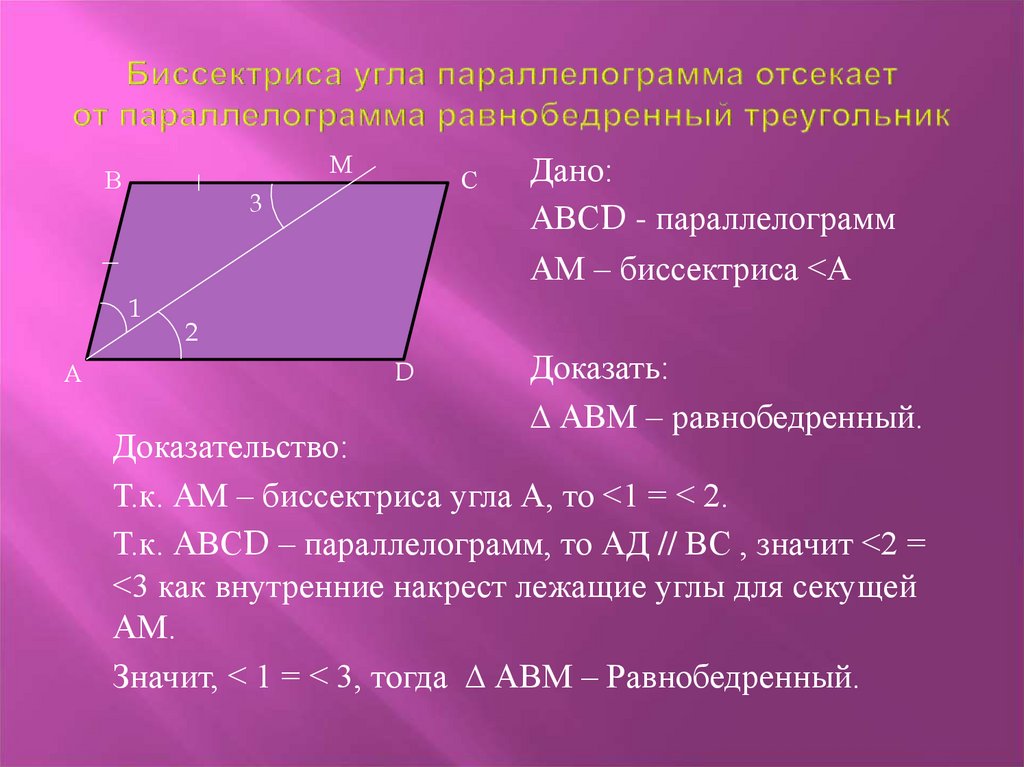 (См. определение площади, чтобы узнать, почему эти области одинаковы.)
(См. определение площади, чтобы узнать, почему эти области одинаковы.)
Мы видим, что они и имеют точно такую же длину основания (синий) и точно такую же высоту (зеленый). Поскольку Основание × Высота дает площадь прямоугольника, мы можем использовать те же измерения на параллелограмме для вычисления его площади: База × HEIST 44444444444444444444444444444444444444444444444444444444444444444444444 (Как и раньше, «высота» измеряется перпендикулярно основанию, а «основание» — это сторона, которую вы выбрали первой. См. параллелограмм.)
На разрезе, показанном выше, легко увидеть, что длина основания не изменилась. На самом деле перпендикулярный разрез можно сделать в любом месте вдоль основания.
Укрепление дыр
Интуиция и доказательство
Это рассечение дает интуитивное понимание формулы площади параллелограмма, причины того, что он должен быть таким, какой он есть. Но мы не задавались вопросом, действительно ли рассечение «работает». То есть, когда мы разрезаем параллелограмм и переставляем его части, мы ожидать получить и результат, безусловно, выглядит так. Но внешность может быть обманчива. Что гарантирует нам, что при перемещении этого треугольника в результате получится прямоугольник? Что, если это больше похоже (хотя и менее преувеличено)? Если результатом не всегда является идеальный прямоугольник, мы не можем использовать наши знания формулы площади прямоугольника для разработки формулы параллелограмма. В старших классах учащиеся смогут доказать, что две части параллелограмма, если их правильно собрать, образуют прямоугольник. В классах К-8 учащиеся по большей части должны опираться на визуальный эксперимент и получать интуитивное ощущение. Узнайте больше о том, почему эти рассечения работают.
Но мы не задавались вопросом, действительно ли рассечение «работает». То есть, когда мы разрезаем параллелограмм и переставляем его части, мы ожидать получить и результат, безусловно, выглядит так. Но внешность может быть обманчива. Что гарантирует нам, что при перемещении этого треугольника в результате получится прямоугольник? Что, если это больше похоже (хотя и менее преувеличено)? Если результатом не всегда является идеальный прямоугольник, мы не можем использовать наши знания формулы площади прямоугольника для разработки формулы параллелограмма. В старших классах учащиеся смогут доказать, что две части параллелограмма, если их правильно собрать, образуют прямоугольник. В классах К-8 учащиеся по большей части должны опираться на визуальный эксперимент и получать интуитивное ощущение. Узнайте больше о том, почему эти рассечения работают.
Что, если мы выберем короткую сторону в качестве основания?
Мы вольны выбрать любую сторону в качестве базы; «высота» измеряется перпендикулярно стороне, которую мы выбрали в качестве основания.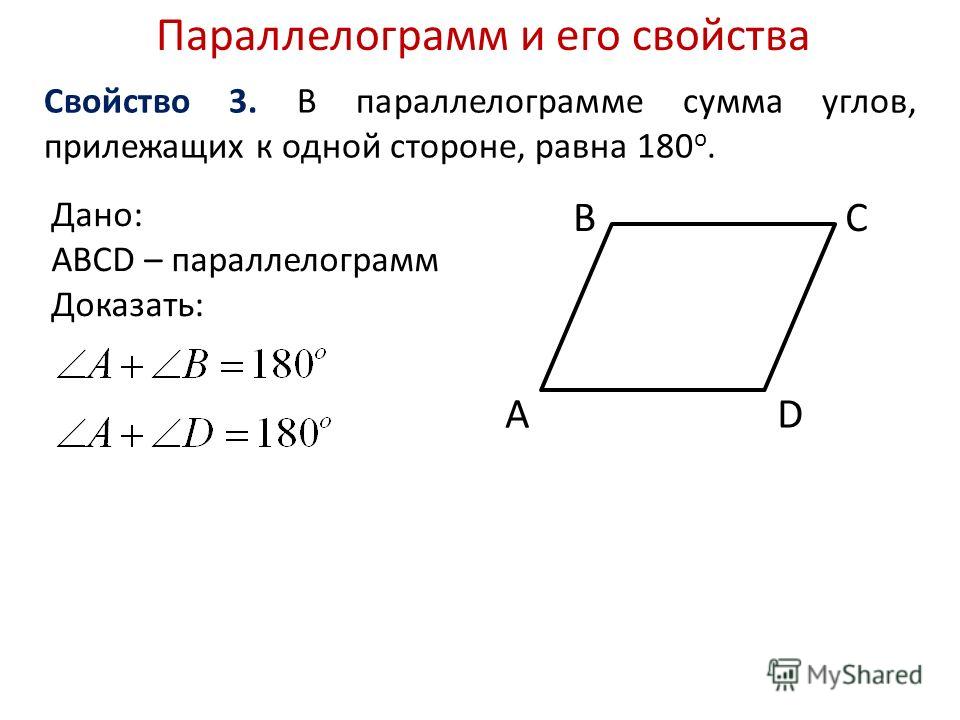 Если мы возьмем короткую сторону (синюю) за основу, показанное выше рассечение будет не таким убедительным. Разрезание по этой высоте и перестановка частей оставляет беспорядок:
Если мы возьмем короткую сторону (синюю) за основу, показанное выше рассечение будет не таким убедительным. Разрезание по этой высоте и перестановка частей оставляет беспорядок:
В этом конкретном примере мы можем спасти беспорядок, сделав еще один разрез, но что, если бы параллелограмм был еще длиннее и тоньше?
Получается, что любой параллелограмм, каким бы длинным и тонким он ни был, можно разрезать таким образом, чтобы части — возможно, многие из них — можно было переставить в прямоугольник. Но требуется больше работы, чтобы показать, что это всегда можно сделать. Нам нужна другая идея.
Несколько иная идея вскрытия значительно облегчает жизнь в этом случае. (Сами можете показать, что это работает и в исходном случае.)
- Заключите параллелограмм в прямоугольник.
- Две части прямоугольника, равные , а не внутри параллелограмма, являются конгруэнтными треугольниками.
- Сдвиньте один из этих треугольников к другому, пока они не сойдутся в прямоугольник.
 Поскольку общая площадь внешнего прямоугольника не изменилась (это тот же прямоугольник, что и раньше) и желтая область не изменилась (фигуры просто переместились), разница между ними — фиолетовыми областями — должна быть одинаковой. Как и прежде, мы также можем видеть, что размеры прямоугольной фиолетовой области — это основание и высота исходного параллелограмма.
Поскольку общая площадь внешнего прямоугольника не изменилась (это тот же прямоугольник, что и раньше) и желтая область не изменилась (фигуры просто переместились), разница между ними — фиолетовыми областями — должна быть одинаковой. Как и прежде, мы также можем видеть, что размеры прямоугольной фиолетовой области — это основание и высота исходного параллелограмма.
Интуиция и доказательство, повторение: Опять же, рассечение дает существенное понимание, но требуется немного больше усилий, чтобы убедиться, что два желтых треугольника, которые, безусловно, выглядят так, как если бы они совмещались, образуя прямоугольник, на самом деле подходят точно, а не только почти .
Почему так важно быть осторожным?
Когда мы будем строить другие формулы площади (см. ниже), мы захотим использовать наш способ нахождения площади параллелограмма, и поэтому мы хотим иметь возможность полагаться на найденное нами правило. Мы может быть уверенным, что перестановка частей не изменит площадь: в конце концов, именно так мы определяем площадь. Но мы также должны быть уверены, что детали подходят друг к другу так, как мы заявляем о , иначе мы не можем полагаться на сделанные нами измерения. И мы должны быть уверены, что правило основания × высоты не зависит от удачного выбора основания.
Но мы также должны быть уверены, что детали подходят друг к другу так, как мы заявляем о , иначе мы не можем полагаться на сделанные нами измерения. И мы должны быть уверены, что правило основания × высоты не зависит от удачного выбора основания.
В большинстве учебных программ учащиеся не имеют достаточно систематической базы геометрических знаний до 8 класса, чтобы убедительно доказать, что эти рассечения работают. Но интуитивного понимания достаточно для объяснения и обоснования формул, а также хорошей основы для последующего изучения геометрии.
Площадь треугольника
Знание того, как найти площадь параллелограмма, поможет нам найти площадь треугольника.
Разрез треугольника
Мы можем разрезать треугольник на две части — одну на треугольник и одну на трапецию — разрезав его параллельно основанию. Если мы разрежем высоту ровно пополам с помощью этого среза, две части соединятся вместе, чтобы получить параллелограмм с тем же основанием , но наполовину меньше высоты .
Итак, основание × половина высоты дает площадь треугольника. Аналогичный разрез показывает полубаза × высота . Любой из них сводится к bh .
Удвоение треугольника с последующим делением полученной площади пополам
Другой способ мышления: две копии треугольника образуют параллелограмм с тем же основанием и той же высотой , что и треугольник.
Площадь параллелограмма равна основание × высота , но это вдвое больше площади треугольника, поэтому площадь треугольника равна основания × высоты , как мы видели с методом рассечения.
(Как всегда, выберите «основание» и измерьте высоту, перпендикулярную этому основанию, от основания до противоположной вершины.)
Площадь трапеции
Удвоение трапеции, а затем уменьшение полученной площади пополам
Как и было с помощью треугольника две копии трапеции можно сложить вместе, чтобы получился параллелограмм.
Высота параллелограмма равна высоте трапеции, но его основание равно сумме двух оснований трапеции. Таким образом, площадь параллелограмма равна высоты × ( основание1 + основание2 ). Но эта площадь равна двум трапециям, поэтому нам нужно разрезать ее пополам, чтобы получить площадь трапеции.
Разрез трапеции
Мы также можем разрезать трапецию так же, как разрезали треугольник, с одним срезом, сокращающим ее высоту пополам. Две части соединяются вместе, образуя параллелограмм, основание которого равно сумме двух оснований трапеции, а высота равна половине высоты трапеции.
В случае трапеции основания нельзя выбирать произвольно. Две параллельных сторон являются основаниями, а высота, как всегда, является перпендикулярным расстоянием от одного основания до противоположного.
Площадь этого параллелограмма равна его высоте (половина высоты трапеции), умноженной на его основание (сумма оснований трапеции), поэтому его площадь равна полувысоты × ( основание1 + основание2 ). Поскольку параллелограмм состоит из того же «материала», что и трапеция, это тоже площадь трапеции.
Поскольку параллелограмм состоит из того же «материала», что и трапеция, это тоже площадь трапеции.
В любом случае площадь трапеции равна × высота × ( основание1 + основание2 ) .
Площадь других специальных четырехугольников
Площадь ромба
Площадь ромба можно найти, разрезав и переставив части так, чтобы получился параллелограмм. Это можно сделать несколькими способами:
- Разрежьте более короткую диагональ (а), чтобы сформировать два конгруэнтных треугольника. Переместите нижнюю половину треугольника рядом с верхней половиной, чтобы сформировать параллелограмм. Более короткая диагональ (a) становится основанием параллелограмма, а половина большей диагонали (b) становится высотой параллелограмма. Таким образом, площадь ромба равна a * b или произведению диагоналей, что является стандартной формулой для ромба.
- Другой подобный способ состоит в том, чтобы разрезать ромб на четыре конгруэнтных треугольника и перестроить их в прямоугольник с более короткой диагональю в качестве основания и половиной большей диагонали в качестве высоты.

- Разрезав ромб на два конгруэнтных треугольника, мы можем вычислить площадь одного из треугольников, которая равна * основание (а) * высота (b) = ab. Затем умножьте на два, так как их два: 2 * ab = ab.
Площадь воздушного змея
Площадь воздушного змея можно найти аналогично площади ромба. Если пересечь более длинную диагональ, получится два равных треугольника. Если мы переставим их, мы можем сформировать параллелограмм с большей диагональю (b) в качестве основания и половиной меньшей диагонали (a) в качестве высоты. Таким образом, площадь становится b * a = ab. Более сложный подход включает в себя немного алгебры. Разрежьте воздушного змея по более короткой диагонали, чтобы сформировать два треугольника с более короткой диагональю (а) в качестве основания. Таким образом, площадь первого треугольника равна * волнистой линии, где волнистая линия — высота. Площадь второго треугольника равна a * (b — волнистая линия), где (b — волнистая линия) — оставшаяся часть большей диагонали. Таким образом, общая площадь становится ( a * волнистой) + ( a * (b — волнистой)). Выделив a, мы имеем a (волнистый + b – волнистый) = ab.
Таким образом, общая площадь становится ( a * волнистой) + ( a * (b — волнистой)). Выделив a, мы имеем a (волнистый + b – волнистый) = ab.
Ну, что ты знаешь. По сути, вам нужно знать только формулу площади параллелограмма, а затем вывести формулы для остальных.
геометрия — Максимальный прямоугольник внутри параллелограмма
@Gabrielek на самом деле дал действительно хорошее начало, которое, я считаю, можно улучшить, и я попробую это сделать. Дайте мне знать, если есть ошибка с ним. Я не против критики, так как эта проблема меня действительно интересует. (И я уже давно не посещал уроки математики.)
Чтобы вписать прямоугольник в параллелограмм, существует более одного решения. Два, вероятно, простых случая — принять противоположные стороны за «авторитетные» и отрезать остаток, чтобы получился прямоугольник.
Но сколько еще существует решений? Если бы прямоугольник не нужно было максимизировать, мы все легко могли бы представить, что существует бесконечное множество решений. Но это все равно может быть бесконечное число, когда мы идем на максимальную площадь прямоугольника. Просто попадание в один из максимумов было бы удовлетворительным для меня.
Но это все равно может быть бесконечное число, когда мы идем на максимальную площадь прямоугольника. Просто попадание в один из максимумов было бы удовлетворительным для меня.
Поскольку мы вписываем прямоугольник в параллелограмм, я предполагаю, что вершины прямоугольника должны быть по одной на каждом из четырех ребер параллелограмма. @Gabrielek сказал, что есть угол $\alpha$, описывающий, насколько прямоугольник повернут по отношению к параллелограмму. При увеличении угла вершины прямоугольника должны блуждать по краям параллелограмма.
Думаю, достаточно посмотреть на поворот на 90°, так как после этого найденные решения будут повторяться. В течение этих 90°, вершины не будут проходить через одно полное ребро, так как есть позиции, в которых они не могут существовать. Например, на моей картине это левый нижний угол.
Итак, давайте тщательно выберем возможное значение, возможно, в середине нижнего края. На данный момент меня волнует расположение вершины, а не угол. Из-за симметрии вершина на верхнем ребре также должна быть в середине верхнего ребра. Знание одной вершины сразу же устанавливает положение для другой. Осталось всего два очка.
Из-за симметрии вершина на верхнем ребре также должна быть в середине верхнего ребра. Знание одной вершины сразу же устанавливает положение для другой. Осталось всего два очка.
Также для них у нас есть некоторые ограничения: Они должны быть на левом и правом краях. И для обеих наших известных вершин, глядя на одну из неизвестных, а затем поворачиваясь к другой, мы должны получить угол 90°. Также для двух неизвестных вершин известные должны располагаться под углом 90°.
Я пытался нарисовать это, но почему-то не получилось. Итак, я начинаю верить, что два неизвестных не обязательно должны быть частью краев, но ограничение 90° остается, так как я все-таки ищу прямоугольник.
Редактировать: я продвинулся вперед в своей работе по рисованию и теперь убежден, что не все прямоугольники могут иметь все свои вершины на ребрах параллелограмма. Но в то же время я ясно вижу, что прямоугольник не может быть таким же большим, как тот, который я нарисовал в качестве левого решения.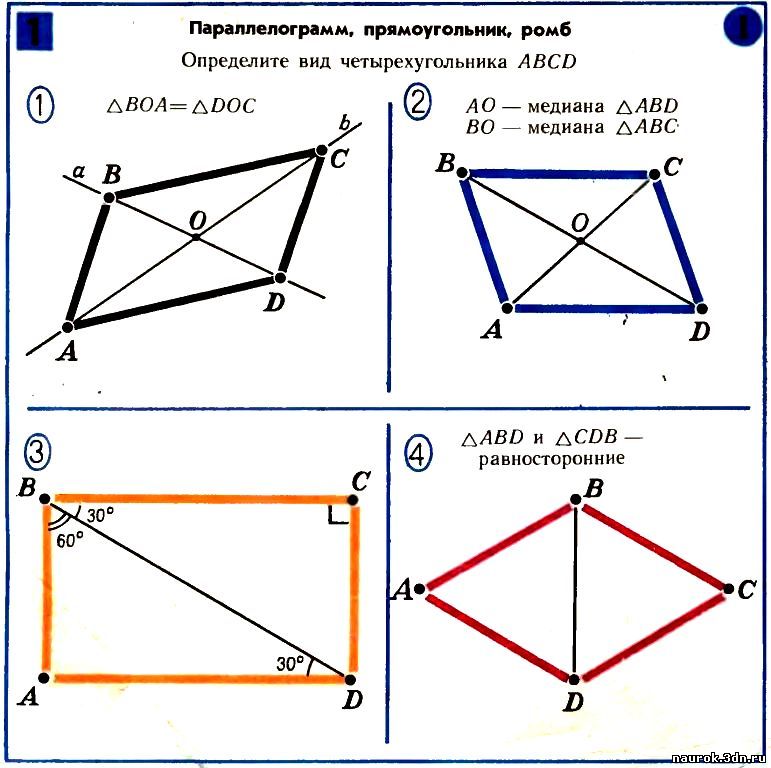
И с достаточно длинным параллелограммом это будет означать, что прямоугольник будет касаться только двух сторон и может перемещаться внутри параллелограмма — для этого потребуется смещение x, чтобы точно описать, на какой прямоугольник я смотрю. Что доказывает, что @Gabrielek всегда был прав. Я принял его ответ как правильный.
Покажу, с чем столкнулся: У меня есть параллелограмм и я выбираю одну вершину. Из-за симметрии противоположная вершина также имеет известное положение. Я провожу линию через обе известные точки. Это одна из диагоналей моего предполагаемого прямоугольника. Обе половины прямоугольника являются прямоугольными треугольниками. Таким образом, создав круг вокруг середины диагонали, я знаю все возможности для оставшихся двух вершин — и получить их, просто выбрав другую линию, проходящую через центральную точку, которая пересекает круг в пределах границ параллелограмма.
Какую бы линию я ни выбрал, она будет иметь ту же длину, что и первая диагональ.



 Провести второй диаметр через центр и новую полученную точку. Соединить полученные точки прямыми.
Провести второй диаметр через центр и новую полученную точку. Соединить полученные точки прямыми.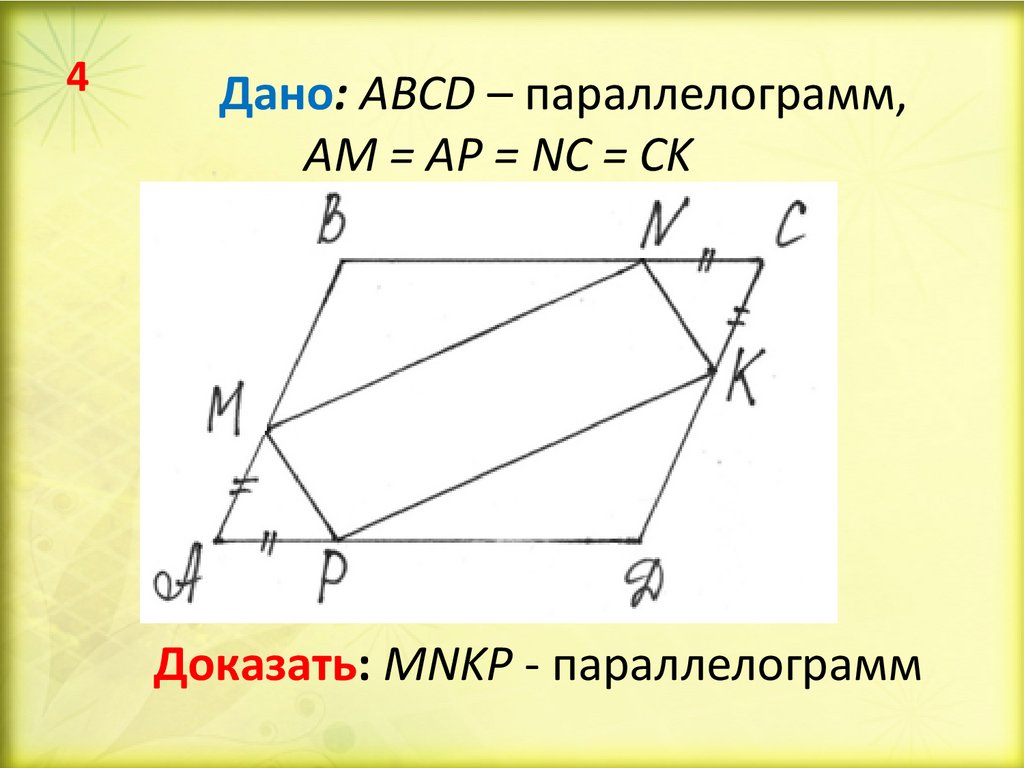

 11.17
11.17 Поскольку общая площадь внешнего прямоугольника не изменилась (это тот же прямоугольник, что и раньше) и желтая область не изменилась (фигуры просто переместились), разница между ними — фиолетовыми областями — должна быть одинаковой. Как и прежде, мы также можем видеть, что размеры прямоугольной фиолетовой области — это основание и высота исходного параллелограмма.
Поскольку общая площадь внешнего прямоугольника не изменилась (это тот же прямоугольник, что и раньше) и желтая область не изменилась (фигуры просто переместились), разница между ними — фиолетовыми областями — должна быть одинаковой. Как и прежде, мы также можем видеть, что размеры прямоугольной фиолетовой области — это основание и высота исходного параллелограмма.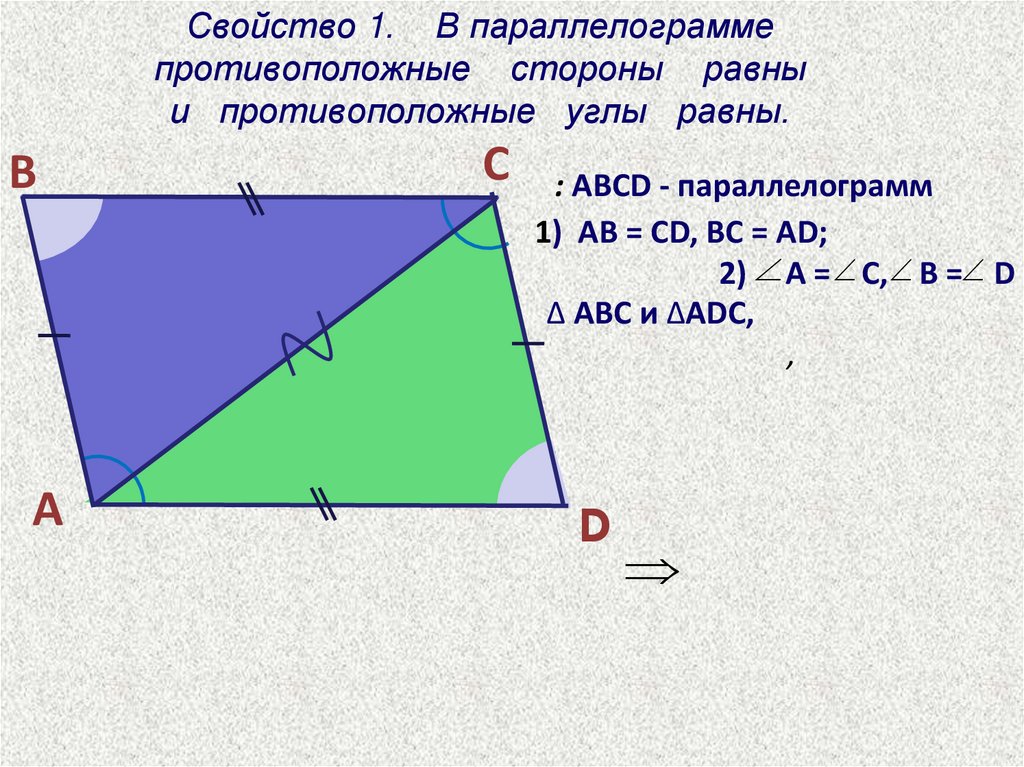
Leave A Comment