Page not found — Сайт skobelevserg!
- Главная
- Информатика
- Практикумы
- Подготовка к ОГЭ
- Рабочие программы
- Используемая литература
- Об авторах
Unfortunately the page you’re looking doesn’t exist (anymore) or there was an error in the link you followed or typed. This way to the home page.
- Главная
- Информатика
- 5 класс (ФГОС)
- Информация вокруг нас
- Компьютер — универсальная машина для работы с информацией
- Ввод информации в память компьютера
- Управление компьютером
- Хранение информации
- Передача информации
- Кодирование информации
- Текстовая информация
- Представление информации в виде таблиц
- Наглядные формы представления информации
- Компьютерная графика
- Обработка информации
- 6 класс (ФГОС)
- Объекты окружающего мира
- Компьютерные объекты
- Отношения объектов и их множеств
- Разновидности объектов и их классификация
- Системы объектов
- Персональный компьютер как система
- Как мы познаем окружающий мир
- Понятие как форма мышления
- Информационное моделирование
- Знаковые информационные модели
- Табличные информационные объекты
- Графики и диаграммы
- Схемы
- Что такое алгоритм
- Исполнители вокруг нас
- Формы записи алгоритмов
- Типы алгоритмов
- Управление исполнителем Чертежник
- Компьютерный практикум
- 7 класс (ФГОС)
- Информация и информационные процессы
- Компьютер универсальное устройство для работы с информацией
- Обработка графической информации
- Обработка текстовой информации
- Технология мультимедиа
- 8 класс (ФГОС)
- Математические основы информатики
- Основы алгоритмизации
- Начала программирования
- 9 класс (ФГОС)
- Моделирование и формализация
- Алгоритмизация и программирование
- Обработка числовой информации в электронных таблицах
- Коммуникационные технологии
- 10 класс (ФГОС)
- Информация и информационные процессы
- Компьютер и его программное обеспечение
- Представление информации в компьютере
- Элементы теории множеств и алгебры логики
- Современные технологии создания и обработки информационных объектов
- 11 класс (ФГОС)
- Обработка информации в электронных таблицах
- Алгоритмы и элементы программирования
- Информационное моделирование
- Сетевые информационные технологии
- Основы социальной информатики
- Практикумы
- Google формы
- Основы работы в Microsoft PowerPoint
- Создание анимации в презентациях
- Основы работы в Microsoft Word
- Основы работы в Microsoft Excel
- Создание простейшей базы данных
- Практикум по MS Excel
- Подготовка к ОГЭ
- Рабочие программы
- Используемая литература
- Об авторах
- Блоги
- Сайты
Построение таблиц истинности для логических выражений
- org/Person»>
Федосеева Марина Сергеевна, учитель информатики
Разделы: Информатика
Цель урока: сформировать умения строить и заполнять таблицы истинности
Задачи:
- Обучающие: изучить последовательность действий построения таблиц истинности, сформировать умение применять алгоритм заполнения таблиц истинности, научить находить значение логических выражений посредством построения таблиц истинности.
- Развивающие: развивать логическое мышление и познавательный интерес к предмету, развивать внимание, память, речь учащихся.
- Воспитательные: воспитывать культуру общения, взаимопомощь учащихся, формировать интеллектуальную и эмоциональную активность учащихся, воспитывать чувства ответственности за результаты своего труда, учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве.

Тип урока: урок изучения и первичного закрепления новых знаний.
Формы работы учащихся:фронтальная, групповая, индивидуальная.
План урока:
- Организационный момент (2 мин.)
- Повторение материала предыдущего урока (8 мин.)
- Объяснение нового материала (12 мин.)
- Закрепление разбор примера (5 мин.)
- задания для самостоятельной работы (15 мин.)
- Обобщение урока, домашнее задание (3 мин.)
Оборудование и программный материал:
- белая доска;
- мультимедийный проектор;
- демонстрация презентации. Приложение 1
- карточки с заданиями.
ХОД УРОКА
I. Организационный момент
Мы продолжаем изучение темы «Основы логики». На предыдущем уроке мы увидели, что логика достаточно крепко связана с нашей повседневной жизнью, а также увидели, что почти любое высказывание можно записать в виде формулы. Познакомились с тремя основными логическими операциями.
Познакомились с тремя основными логическими операциями.
II. Повторение материала предыдущего урока
Давайте вспомним основные определения и понятия:
Ответ | |
1. Что называется высказыванием? (Пример) | Повествовательное предложение, в котором что-либо утверждается или отрицается |
2. На какие виды делятся высказывания по своей структуре? (примеры) | Простые и сложные |
3. Что связывает переменные в формулах алгебры высказываний? | Логические операции |
4. На слайдах (2, 3, 4) представлены логические операции. Назовите их и дайте определение. | Дизъюнкция (сложение) |
5. 1 ряд – инверсия | Ответы |
6. Запишите формулы для следующих суждений: *«Прозрачный лес один чернеет, и ель сквозь иней зеленеет, и речка подо льдом блестит». *«Рыбу ловят сачком или ловят крючком, или мухой приманивают, или червячком». |
F= A/\B/\C F= ¬A/\¬B |
III. Объяснение нового материала
Хорошо, повторили пройденный материал, переходим к новой теме.
На прошлом уроке мы находили значение составного высказывания путем подстановки исходных значений входящих логических переменных. А сегодня мы узнаем, что можно построить таблицу истинности, которая определяет истинность или ложность логического выражения при всех возможных комбинациях исходных значений простых высказываний (логических переменных) и, что можно определить значения исходных логических переменных, зная какой нам нужен результат.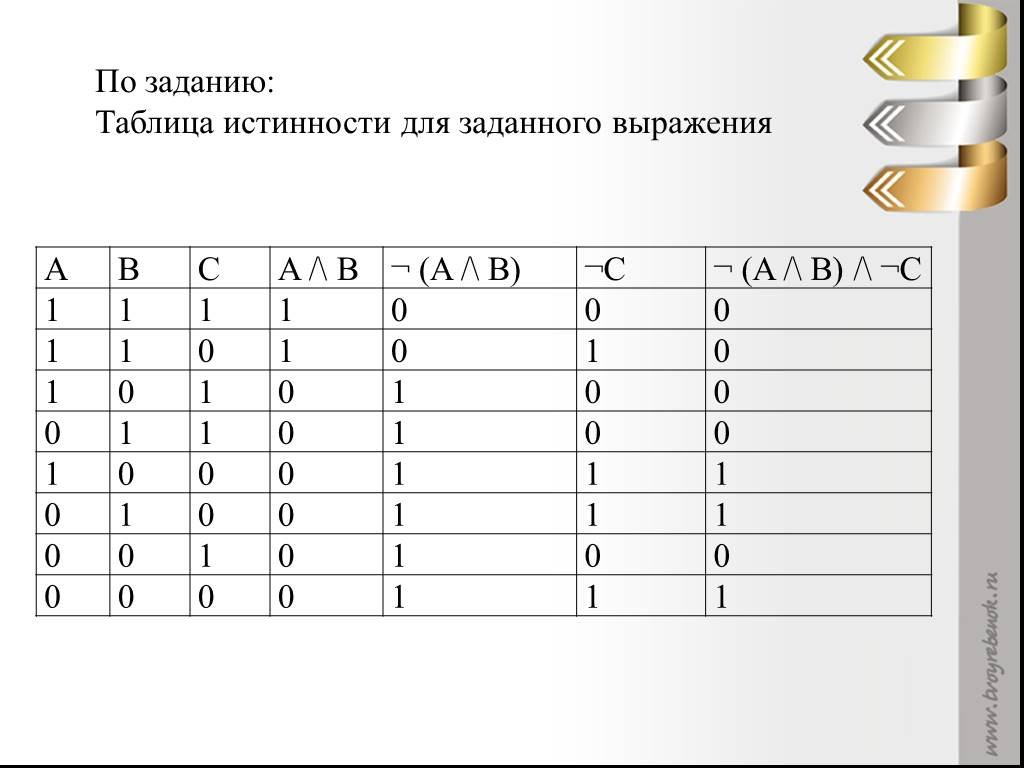
Понятие таблицы истинности (слайд 5): таблица истинности — это таблица, в которой перечислены все возможные значения входящих логических переменных и соответствующие им значения функции.
При построении таблиц истинности есть определенная последовательность действий. У вас на столах находится памятка с этими правилами (Приложение 2), вклейте ее в тетрадь. На доске я продемонстрирую вам, как благодаря этим действиям строится таблица истинности для логической функции
IV. Закрепление разбор примера
Построить таблицу истинности для составного высказывания:
F = (AvB)/\(¬Av¬B) (слайд 7)
Теперь мы можем определить значение логической функции для любого набора значений логических переменных.
V. Задания для самостоятельной работы
1. Работа по карточкам в парах. Кто быстрее заполнит таблицу истинности. (Приложение 3).
2. Индивидуальные задания (Приложение 4).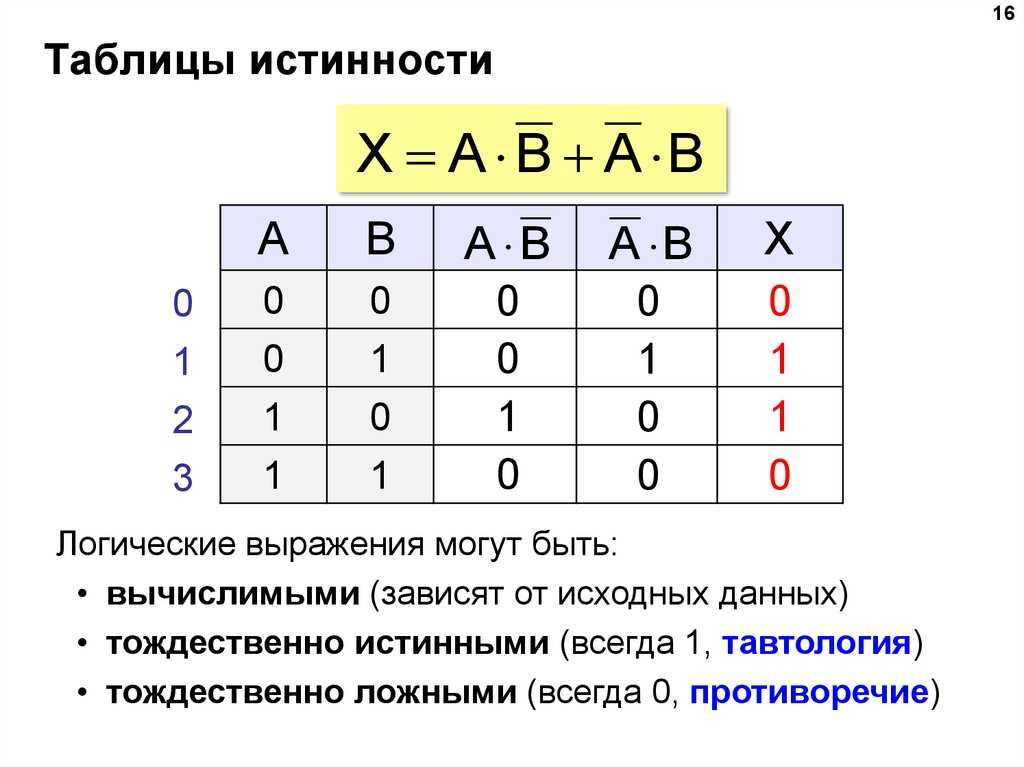 Задания разного уровня сложности распечатаны на листах разного цвета (красный – простой уровень, желтый – средний, зеленый – сложный). Ребята сами выбирают задания.
Задания разного уровня сложности распечатаны на листах разного цвета (красный – простой уровень, желтый – средний, зеленый – сложный). Ребята сами выбирают задания.
VI. Обобщение урока, домашнее задание
Сегодня на уроке мы научились определять истинность составных высказываний, но больше с математической точки зрения, так как вам были даны не сами высказывания, а формулы, отображающие их. На следующих уроках мы закрепим эти умения и постараемся их применить к решению логических задач.
Домашнее задание: §1.3, стр. 39 задание 8 примеры 2, 3, 4. (учебник Л.Л. Босовой Информатика 8 класс. ФГОС).
Булева логика и таблицы истинности
Последнее изменение: 09 августа 2021 г.
И используется, чтобы найти, где несколько условий верны
ИЛИ используется, чтобы найти, где хотя бы одно из нескольких условий верно
Если говорить более подробно, булева логика — это способ представления того, как обрабатываются биты в компьютере.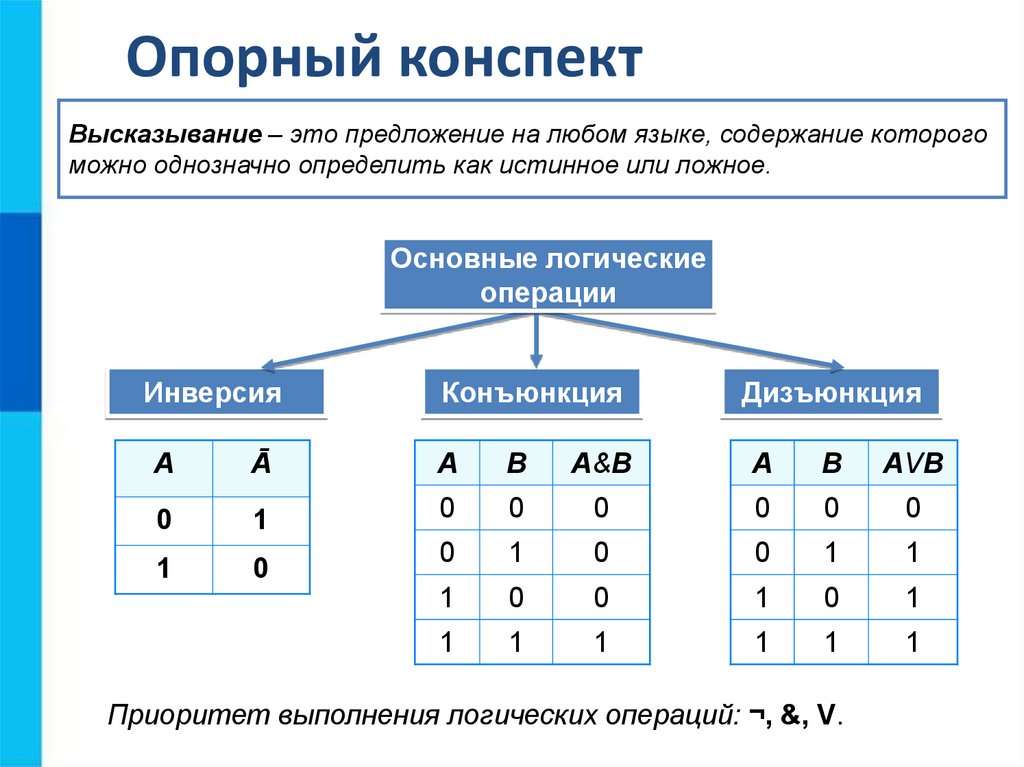 Давайте больше изучим эти условные операторы (например, операторы if-else, where или case-when) с таблицами истинности, чтобы понять, как именно работает логическая логика.
Давайте больше изучим эти условные операторы (например, операторы if-else, where или case-when) с таблицами истинности, чтобы понять, как именно работает логическая логика.
Таблицы истинности
Например, давайте посмотрим на следующее условное выражение:
Если: А и В
Затем: С
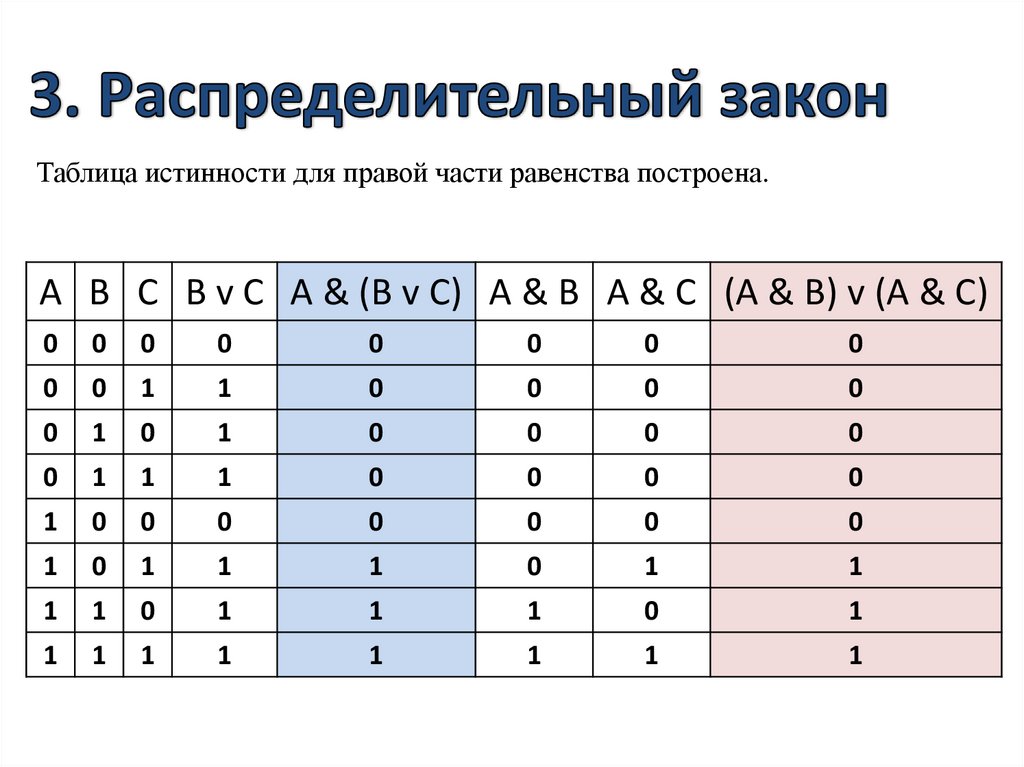
Возвращает значение C, если значения A и B верны. Мы можем представить это с помощью так называемой таблицы истинности. Таблица истинности — это способ представления всех возможных входных данных и соответствующих им выходных данных. Таблица истинности для этого оператора AND выглядит так:
.| А | Б | С |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
В таблице истинности 1 соответствует истине, а 0 представляет ложь. Глядя на эту таблицу, становится очевидным, что единственный случай, когда С истинно, — это когда истинны и А, и В.
Глядя на эту таблицу, становится очевидным, что единственный случай, когда С истинно, — это когда истинны и А, и В.
Существует также оператор ИЛИ. Оператор ИЛИ верен, когда верно A OR B:
Если: А или В
Затем: С
Таблица истинности:
| А | Б | С |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Эта таблица истинности может немного отличаться от ожидаемой. Это связано с тем, что оператор ИЛИ является ложным только тогда, когда оба входных значения (A и B) имеют значение False.
Создание таблицы правды 93 или 8 ряд.
Далее нам нужно решить, сколько столбцов использовать.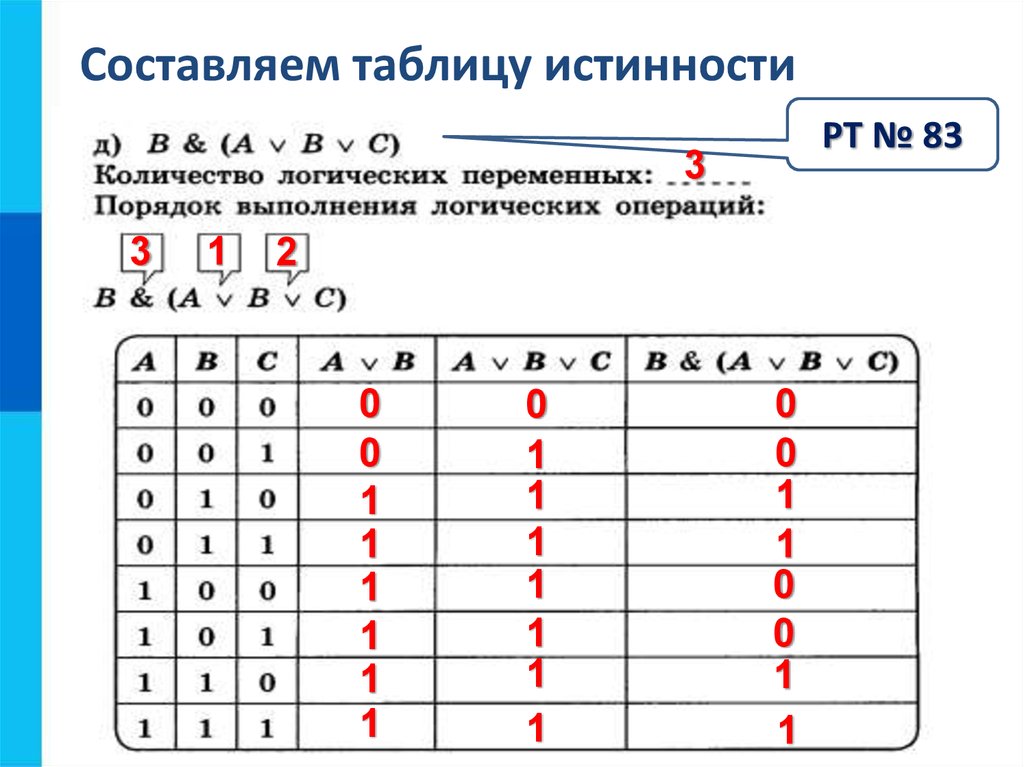 В этом случае у нас будет один столбец для каждого входа, один для вывода и один для значений A и B. Таблица истинности будет выглядеть так:
В этом случае у нас будет один столбец для каждого входа, один для вывода и один для значений A и B. Таблица истинности будет выглядеть так:
| А | Б | С | А или В | Д |
| 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 |
Как и ожидалось, когда таблица заполнена, единственный верный результат — это когда верны все 3 входа.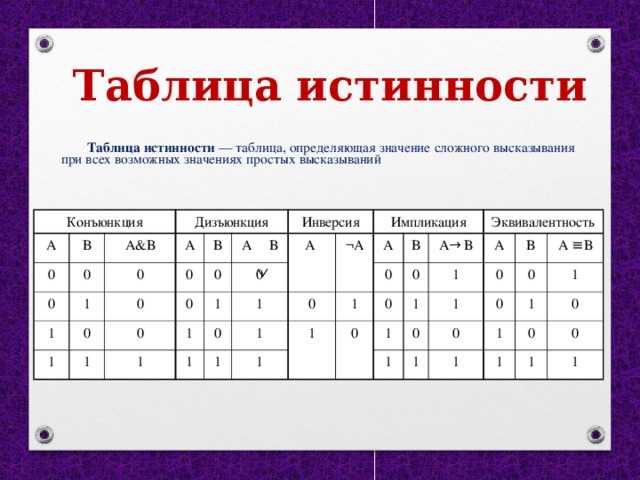
Логика короткого замыкания
Из-за того, как работает логика И и ИЛИ , языки программирования могут использовать так называемую «логику короткого замыкания». Это когда оцениваются не все входные данные, потому что компьютер может угадать ответ по первому проверенному вводу. Чтобы увидеть, как это работает, снова взгляните на таблицу истинности AND:
| А | Б | С |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
Обратите внимание, что, когда A имеет значение False ( 0 ), C также всегда имеет значение False. Это связано с тем, что C истинно только тогда, когда оба входа истинны, поэтому одно ложное значение C ложно.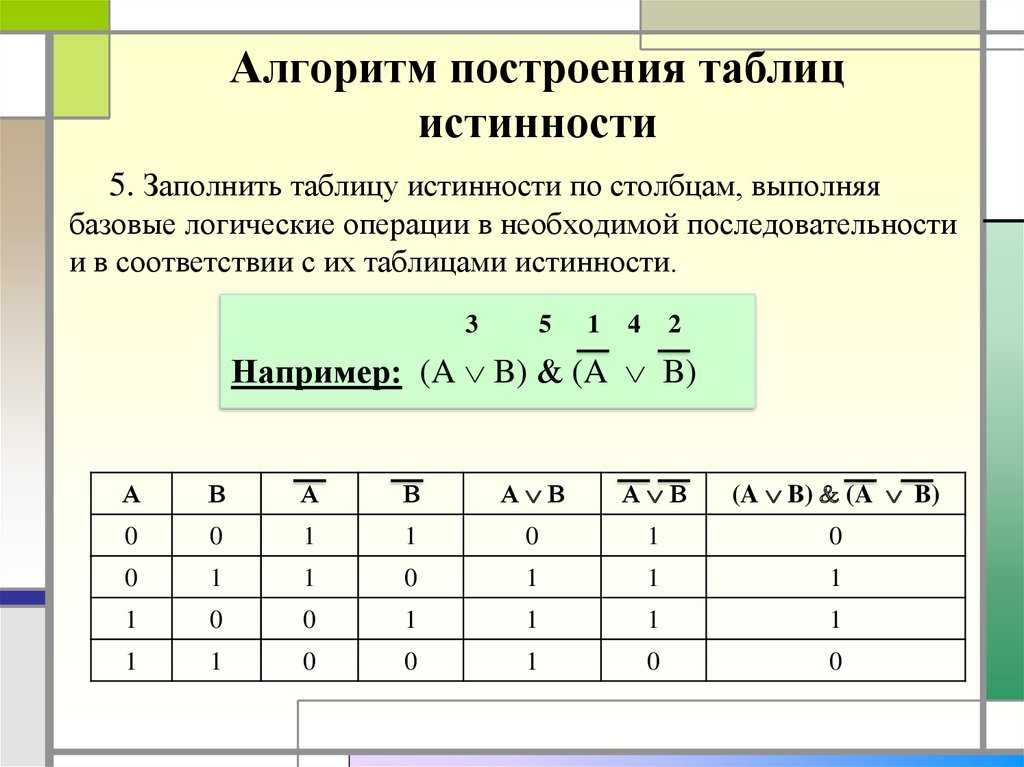
Если компьютер использует условие И и первое входное значение ложно, то второе входное значение B никогда не будет проверяться. ИЛИ будет оцениваться как истина без проверки второго ввода, когда первый ввод верен. Эта способность компьютера аннулировать более поздние шаги логической логики может сэкономить много ненужной вычислительной мощности для вашего запроса.
Примеры в SQL
Пример условия WHERE :
ВЫБЕРИТЕ * ИЗ [таблицы] ГДЕ [столбец A]=5 И [столбец B]=22;
Пример оператора CASE-WHEN
СЛУЧАЙ КОГДА [столбец A]=21 ИЛИ [столбец B]=7 ТО [Действие] КОНЕЦ
Резюме
- Булева логика И/ИЛИ может быть визуализирована с помощью таблицы истинности
- Таблицы истинности две по количеству входных строк в них
- 1 — верно
- 0 — ложь
- Логика короткого замыкания
- Если первый ввод гарантирует конкретный результат, то второй вывод не будет прочитан
- И — первый ввод false приведет к короткому замыканию на false
- ИЛИ — первый ввод true приведет к короткому замыканию на true
Написано:
Мэтью Лейн
Отзыв:
Мэтт Дэвид
Оставьте отзыв о нашем Документе Google Далее – Условная логика
- Дом
- Веб-книги
- Авторы
- Миссия
- Пожертвовать
- Slack-сообщество
Наши веб-книги
- Обмен данными
- Управление облачными данными
- Как спроектировать панель мониторинга
- Как учить людей SQL
- Изучите SQL
- Избегайте искажения данных
- Оптимизация SQL
- Основы анализа
Логические вентили и таблицы истинности
Видео
Вступительное видео
https://www. youtube.com/watch?v=gI-qXk7XojAВидео не может быть загружено, так как отключен JavaScript: Булева логика и логические вентили: ускоренный курс Информатика №3 (https://www.youtube.com/watch?v=gI-qXk7XojA)
youtube.com/watch?v=gI-qXk7XojAВидео не может быть загружено, так как отключен JavaScript: Булева логика и логические вентили: ускоренный курс Информатика №3 (https://www.youtube.com/watch?v=gI-qXk7XojA)
НЕ
Элементы НЕ
Элементы НЕ являются простейшей формой логических элементов. Он просто берет один вход и инвертирует сигнал.
| Таблица истинности шлюза NOT | |
| Вход А | Выход |
| 0 | 1 |
| 1 | 0 |
И
Элементы И
Элемент И — это элемент, который производит выход только в том случае, если оба входа включены.
| И Таблица истинности шлюзов | ||
| Вход А | Вход Б | Выход |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
ИЛИ
Элементы ИЛИ
Элементы ИЛИ — это тип элемента, который производит выход, если один (или оба) входа включены.
| Таблица истинности шлюза ИЛИ | ||
| Вход А | Вход Б | Выход |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
NAND
NAND Gates
NAND Gate — это вентиль, который отключает оба, только если оба входа включены, в противном случае он остается включенным. Он состоит из вентиля И, входящего в вентиль НЕ.
| Таблица истинности шлюза NAND | ||
| Вход А | Вход Б | Выход |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
НО
НО Ворота
Логический элемент НЕ-ИЛИ включается, только если оба входа отключены. Он состоит из вентиля ИЛИ, входящего в вентиль НЕ.
Он состоит из вентиля ИЛИ, входящего в вентиль НЕ.
| Таблица истинности шлюза NOR | ||
| Вход А | Вход Б | Выход |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
XOR
XOR Gates
AN XOR Gate включается только в том случае, если один (но не оба) входы включены.
| Таблица истинности шлюза NOR | ||
| Вход А | Вход Б | Выход |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Практика
Упражнение 1
Попробуйте соединить несколько логических вентилей, чтобы посмотреть, что произойдет, используя симулятор ниже. Можете ли вы разработать входы и выходы для следующих примеров.
Можете ли вы разработать входы и выходы для следующих примеров.
https://academo.org/demos/logic-gate-simulator/
Пример 1
Пример 2
Пример 3
Пример 4
. по ссылке ниже, посмотрите, сможете ли вы создать следующие системы:
Симулятор приложений Logic Gates
Система 1 — Вентиляторная система охлаждения.
Если главный выключатель системы включен, то вентилятор будет работать, когда:
- Каждые 5 секунд
- При нажатии кнопки ручного управления.
Система 2 – Базовая система сигнализации
Создайте систему, в которой при срабатывании любого из 3 датчиков (используйте 3 переключателя для обозначения датчиков) индикатор тревоги будет мигать КРАСНЫМ.
Система 3 – Расширенная система сигнализации
Настройте систему так, чтобы:
- Тревога не срабатывала, если система не была поставлена на охрану (используйте для этого другой переключатель)
- Тревога должна попеременно мигать красным и включать сирену каждую 1 секунду.


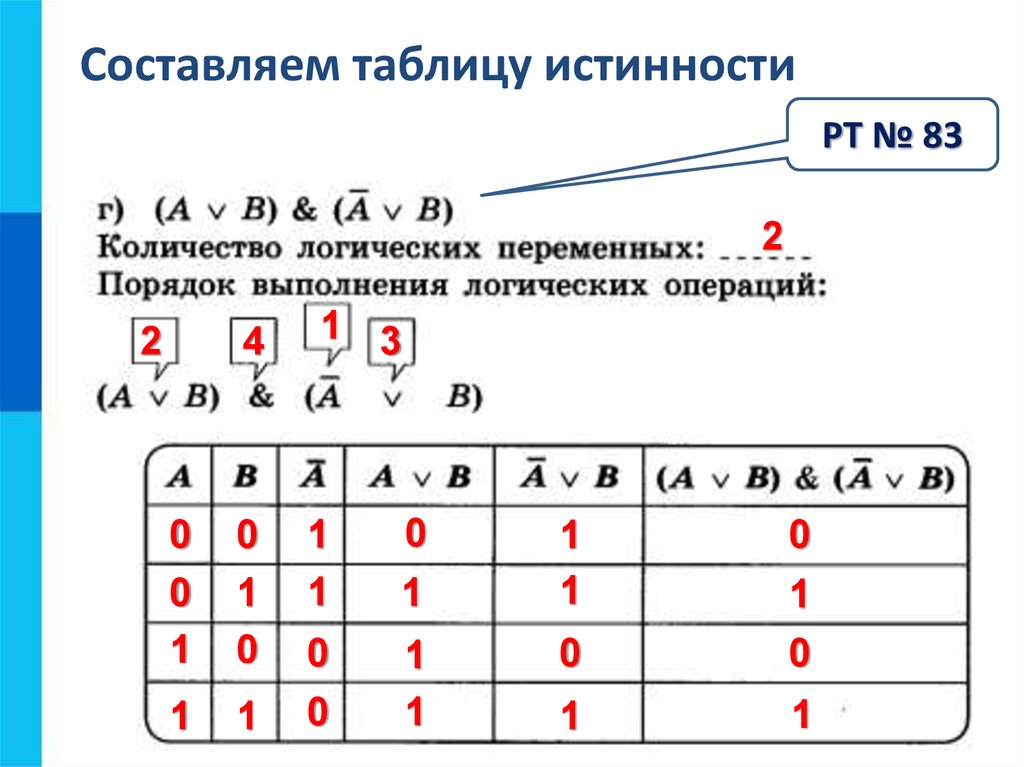 Придумать составное высказывание с логическими связками:
Придумать составное высказывание с логическими связками:
Leave A Comment