Как найти ускорение на графике скорости и времени: задачи и примеры —
В этой статье мы узнаем, как найти ускорение на графике скорости от времени, используя несколько примеров, и решим некоторые задачи.
Ускорение — это разность скоростей, изменяющаяся во времени; следовательно, по графику скорость-время мы можем найти ускорение, измерив наклон графика.
График скорости во времени для положительного ускоренияДавайте посмотрим, как найти ускорение по графику скорость-время. Ниже приводится график зависимости скорости от времени.
График зависимости скорости от времени для положительного ускоренияПо оси x отложено время в секундах, а по оси y отложена скорость объекта в разное время. Наклон графика определяется выражением m=Δy/Δt. Здесь наклон графика скорость-время дает ускорение объекта.
а = м = ΔV/ΔT = v2-v1/t2-t1
Из приведенного выше графика ускорение будет положительным, если V2>V1 то есть, если скорость объекта увеличивается со временем. То же самое будет отрицательным, если V2<V1, то есть если скорость объекта уменьшается со временем. Это тот случай, когда объект замедляется. Так и в том случае, даже когда объект движется в противоположном направлении от направления его движения.
То же самое будет отрицательным, если V2<V1, то есть если скорость объекта уменьшается со временем. Это тот случай, когда объект замедляется. Так и в том случае, даже когда объект движется в противоположном направлении от направления его движения.
Подробнее о Как найти ускорение с постоянной скоростью: факты и примеры задач.
1 задачи: Рассмотрим объект круглой формы, покоящийся на вершине холма. К объекту прикладывают силу, чтобы сместить его с места. При приложении силы объект ускоряется вниз к подножию холма. Скорость объекта увеличивается до 4 м/с после прохождения расстояния 16 метров. Постройте график для того же, а затем рассчитайте ускорение объекта, учитывая начальную скорость объекта 2 м/с в определенный момент времени.
Решение: Изменение скорости объекта определяется как.
V1= 2 м / с
V2= 4 м / с
Скорость, равная 4 м/с, наблюдалась после того, как объект прошел расстояние 16 метров. Следовательно, время, затрачиваемое на перемещение 16 м и ускорение тела, равно
Следовательно, время, затрачиваемое на перемещение 16 м и ускорение тела, равно
2м/с=16м/т
t=16м/2м/с=8с
Следовательно, скорость объекта в момент времени t = 8 секунд была 4 м/с. Теперь мы можем построить график для того же, что и ниже.График скорости-времени
Судя по графику, скорость v1=2 м/с при t1=4 сек и скорость v2=4 м/с при t1=8 сек.
Следовательно, ускорение объекта между временными интервалами от 4 до 8 секунд равно
а = v2-v1/t2-t1 = 4-2/8-4 = 2/4 = 1/2 = 0.5 м/с2
Ускорение тела равно 0.5 м/с.2.
График зависимости скорости от времени для нулевого ускоренияПриведенный ниже график показывает, что скорость объекта не меняется со временем и остается постоянной. Это означает, что между этими интервалами времени ускорения объекта не было.График зависимости скорости от времени для Постоянная скорость
Приведенный выше график показывает, что скорость объекта остается неизменной все время, поэтому мы получаем прямую линию на графике зависимости скорости от времени. Это ясно указывает на то, что в этом случае график зависимости скорости от времени не дает наклона. Поскольку наклон графика отсутствует, ускорение, равное наклону, равно нулю.
Это ясно указывает на то, что в этом случае график зависимости скорости от времени не дает наклона. Поскольку наклон графика отсутствует, ускорение, равное наклону, равно нулю.
Это означает, что перемещение объекта одинаково для разных интервалов времени, следовательно, скорость постоянна.
2 задачи:Скорость объекта, движущегося по плоской поверхности, оказалась равной 0.5 м/с. Через 5 минут другой наблюдатель обнаружил, что скорость равна 0.5 м/с. Тогда каково ускорение объекта на основе наблюдения?
Решение: V1=0.5 м/с; В2=0.5 м/с, временной интервал t=5 минут=300 секунд.
а=в2-v1/t2-t1= 0.5-0.5/300 =0
Поскольку изменений скорости объекта не наблюдалось, ускорение объекта равно нулю.
Подробнее о ускорение.
График зависимости скорости от времени для отрицательного ускоренияЕсли объект замедляется со временем, то наклон графика скорость-время будет отрицательным.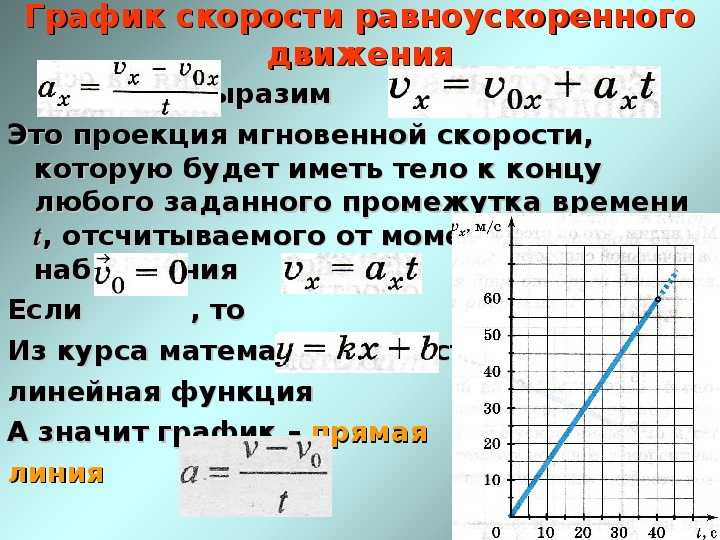 Это показано на приведенном ниже графике зависимости скорости от времени.График зависимости скорости от времени для отрицательного ускорения
Это показано на приведенном ниже графике зависимости скорости от времени.График зависимости скорости от времени для отрицательного ускорения
Поскольку разница между конечной и начальной рассматриваемой точкой по оси ординат отрицательна, наклон графика ускорения объекта будет отрицательным.
3 задачи: Рассмотрим объект, замедляющийся со временем, как показано на графике ниже.
График скорости-времениВычислите ускорение тела на пути от А до В.
Решение: Скорость объекта в точке А в момент времени t1= 2 секунды v1=10 м/с и в момент времени t2= 5 секунд v2=4м/с. Поэтому ускорение тела равно
а = v2-v1/t2-t1 = 4-10/5-2= -6/3= -2m/s2
Поскольку скорость объекта со временем уменьшается, ускорение объекта отрицательно и равно -2 м/с.2.
Подробнее о График постоянного отрицательного ускорения: что, как, примеры.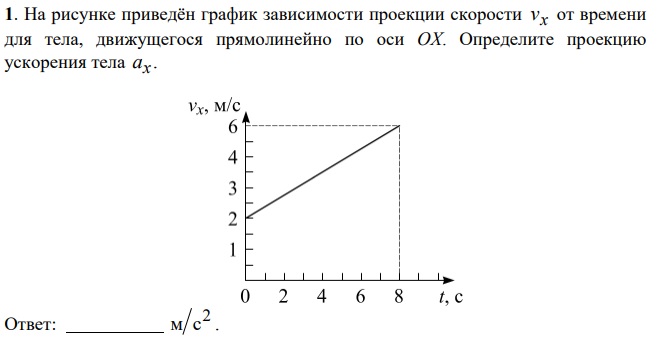
Когда объект удаляется от точки назначения по отрицательной оси, смещение объекта принимается как отрицательное по отрицательной оси Y. Если положение объекта отклоняется от направления его движения, то считается, что смещение объекта происходит в отрицательном направлении.Отрицательная скорость В/с График времени
Выше приведен график зависимости скорости от времени для отрицательного ускорения. Видно, что скорость со временем уменьшается, наклон графика оказывается отрицательным, а значит, и ускорение отрицательное.
График отрицательной скорости во времени для положительного ускоренияНиже приведен график зависимости отрицательной скорости от времени в секунду, который дает положительное ускорение.Отрицательный график зависимости скорости от времени
Поскольку замедляющийся объект однажды начинает ускоряться обратно за счет какого-то внешнего силы, то ускорение, равное наклону График зависимости скорости от времени положителен, потому что скорость объекта продолжает расти со временем.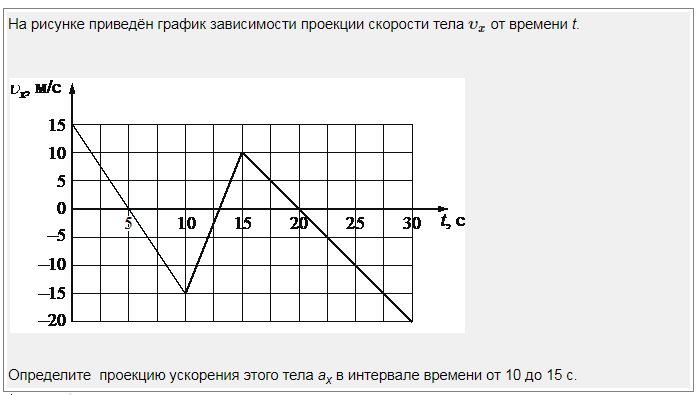
Подробнее о Отрицательная скорость и нулевое ускорение: как, когда, пример и проблемы.
Часто задаваемые вопросыQ1. Из приведенного ниже графика вычислите ускорение объекта из точки О в А, из А в В и из В в С; а затем вычислить среднее ускорение объекта от O до C.График скорости-времениРешение: От О до А, v1=0 при t1=0; в2=8 м/с при t2= 4s
Следовательно, ускорение тела из точки О в точку А равно
а = v2-v1/t2-t1=8-0/4-0=8/4=2m/s2
От А до Б, в1=8 м/с при t1=4с; в2=5 м/с при t2= 8s
Следовательно, ускорение тела из точки А в точку В равно
а=в2-v1/t2-t1=5-8/8-4=-3/4=-0.75m/s2
От B до C, v1=5 м/с при t1=8с; в2=5 м/с при t2= 12s
Следовательно, ускорение тела из точки В в С равно
а=в2-v1/t2-t1=5-5/12-8=0/4=0
Среднее ускорение графика от O до C равно
Aсредний= aoa+aab+abc/3
=2-0.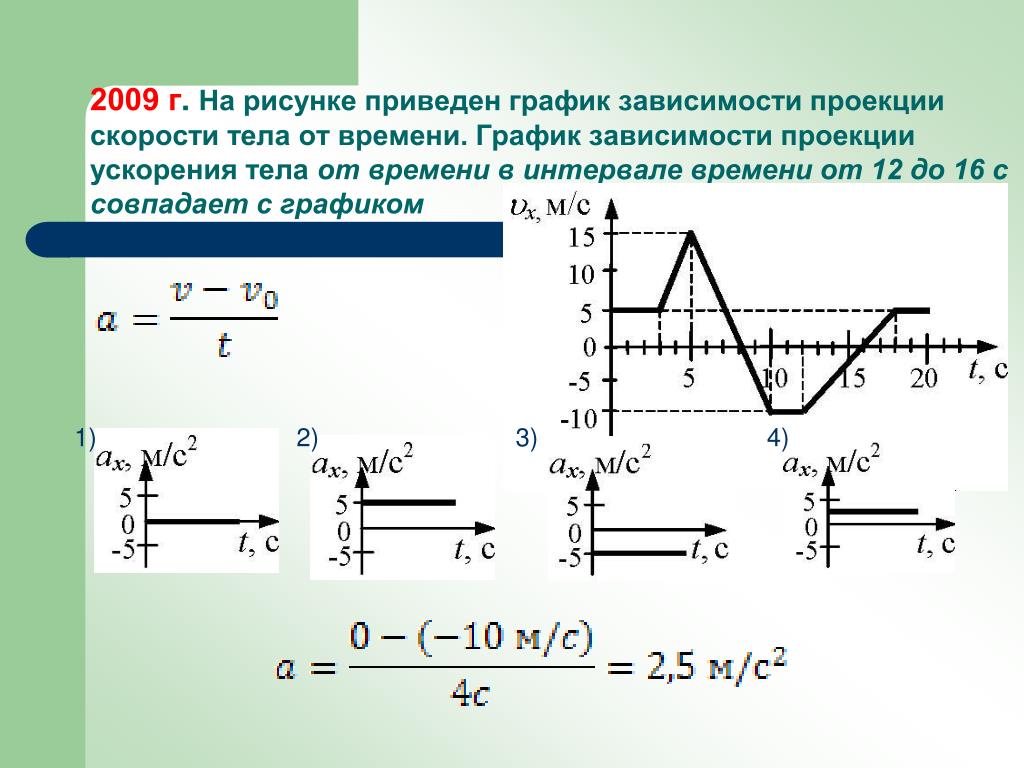 75+0/3=1.25/3=0.42m/s2
75+0/3=1.25/3=0.42m/s2
Следовательно, среднее ускорение тела от О до А равно 0.42 м/с.2.
Почему ускорение является векторной величиной?Ускорение имеет величину и направление.
Направление ускорения такое же, как и направление скорости после изменения; следовательно, это векторная величина.
Скорость прямолинейного равноускоренного движения. График скорости
Тема: Скорость прямолинейного равноускоренного движения. График скорости
Цели урока: Расширить взгляды учащихся на природу механического движения. Научиться строить график скорости от времени. Развитие навыков самостоятельной работы.
Ход урока
Повторение. Проверка домашнего задания
Дайте определение мгновенной скорости.
Каков физический смысл мгновенной скорости?
Что такое ускорение?
Назовите единицы ускорения.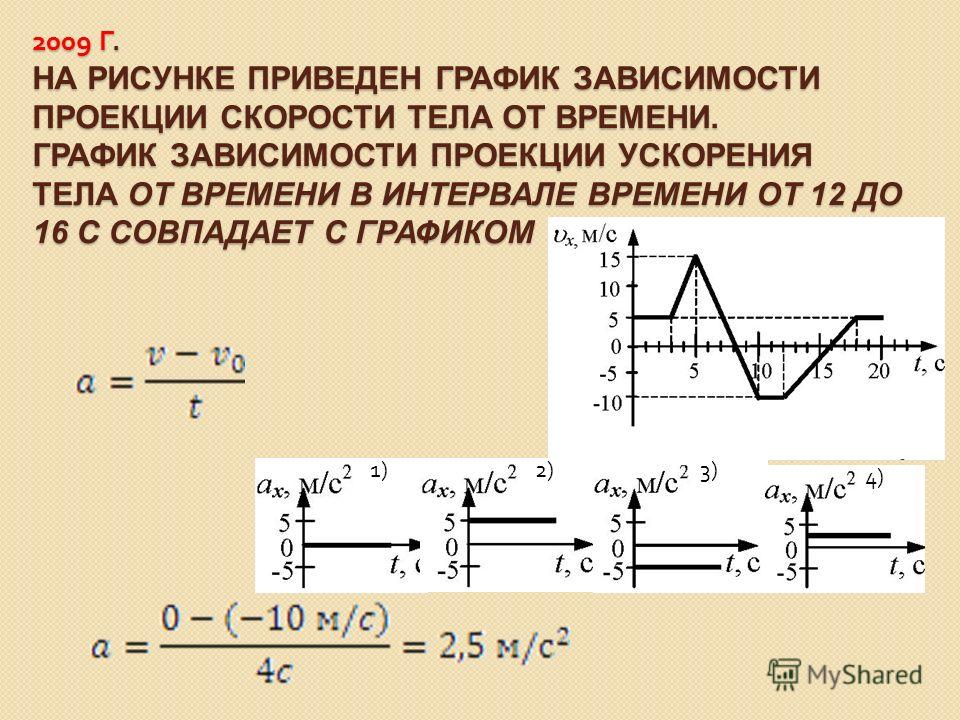
Как рассчитывается мгновенная скорость при равноускоренном движении?
Чем отличаются векторные величины от скалярных?
Что показывает модуль вектора ускорения?
Каковы правила сложения векторных величин?
Какое движение называют равноускоренным?
По какой формуле находится ускорение?
Что характеризует ускорение?
С целью повторения материала можно предложить учащимся ряд простых устных задач по изученной теме:
Какой путь пройдет велосипедист за 2 ч, если его средняя скорость 15 км/ч?
Чему равна мгновенная скорость камня, брошенного вертикально вверх, в верхней точке траектории?
О какой скорости — средней или мгновенной — идет речь в следующих случаях:
а) пуля вылетает из винтовки со скоростью 800 м/с;
б) самолет летит из Киева в Москву со скоростью 800 км/ч;
в) скоростемер на тепловозе показывает 75 км/ч?
Работа по карточкам
Карточка № 1
При равноускоренном движении скорость тела за 5 с увеличилась на 4 м/с. Найдите ускорение тела.
Найдите ускорение тела.
Если при равноускоренном движении скорость тела за 2 с изменилась на 4 м/с, то за последующие 3 с она изменится на .
Карточка № 2
Если при равноускоренном движении скорость тела за 3 с изменилась на 6 м/с, то изменение скорости на 4 м/с произойдет за .
За 5 с до финиша скорость велосипедиста равнялась 18 км/ч, а на финише 25,2 км/ч. Определите ускорение, с которым финишировал велосипедист.
Карточка № 3
При подходе к станции поезд уменьшил скорость от 90 км/ч в течение 25 с. Определите ускорение поезда.
Если при равноускоренном движении скорость тела за 4 с изменилась на 8 м/с, то за следующую секунду она изменится на .
Изучение нового материала
План изложения нового материала:
Вычисление скорости при равноускоренном движении.
Построение графиков зависимости скорости от времени.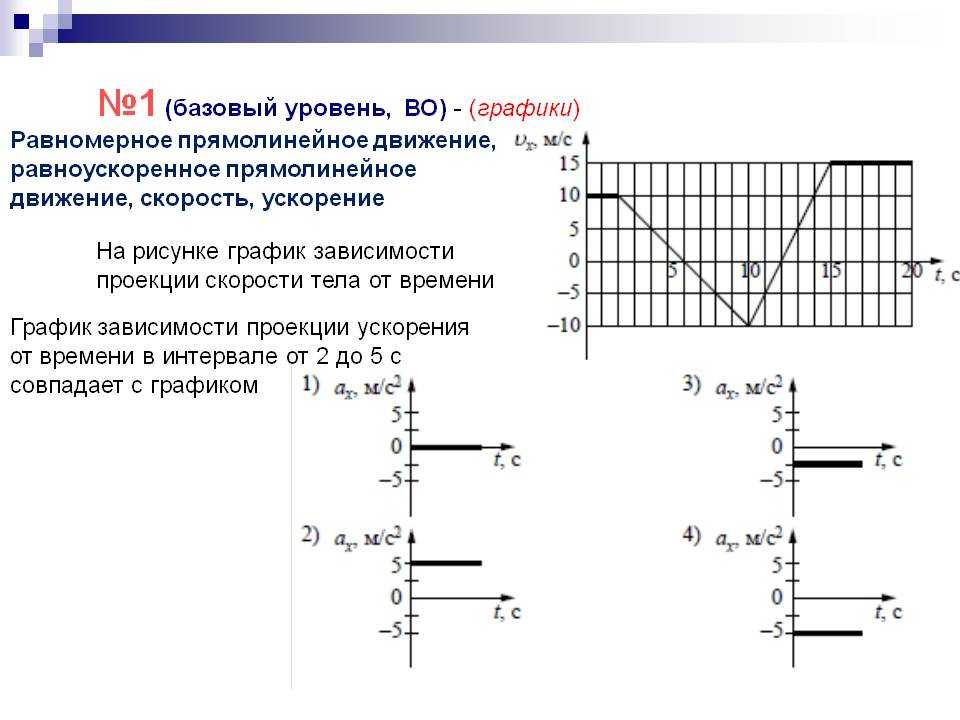
Средняя скорость движения.
Скорость при равноускоренном движении
Теория равноускоренного движения была разработана Галилео Галилеем. Галилей впервые дал определение равноускоренного движения, доказал ряд теорем, которые описывали закономерности этого движения.
Изучение равноускоренного движения опирается на основное соотношение, которое определяет ускорение тела: = , из этой формулы выразим скорость прямолинейного равноускоренного движения: = + ·t.
Если тело начинает равноускоренное движение из состояния покоя, т. е. = 0, то скорость тела в любой момент времени определяется так: = ·t.
Построение графиков зависимости скорости от времени
Наглядно движение тела можно представлять в виде графиков.
Зависимость скорости тела от времени называют законом изменения скорости, а графическое представление этого закона — графиком скорости. Чтобы построить график скорости, оси прямоугольной системы координат обозначаются так: по оси х откладывают время, а по оси у — значения скорости тела.
Чтобы построить график скорости, оси прямоугольной системы координат обозначаются так: по оси х откладывают время, а по оси у — значения скорости тела.
— На рис. 1 представлены два графика равноускоренного движения из состояния покоя. Ускорение первого тела равно = 1 м/с2, а второго — = 3 м/с2.
— На рис. 2 показаны графики равнозамедленного движения: ускорение первого тела равно = — м/с2, а второго — =-1 м/с2.
— При помощи графика скорости мы всегда можем найти скорость тела в любой момент времени. По виду графика скорости можно судить о характере движения тела.
Средняя скорость движения
Из графика скорости вытекает, что при = 0 в равноускоренном движении средняя скорость на отрезке времени t всегда равна половине достигнутой скорости (рис. 3), т. е.: =
— При равнозамедленном движении средняя скорость определяется так: =
— При условии, что конечная скорость тела = 0.
Закрепление изученного материала
— Учитель строит возможные варианты графиков и комментирует их (рис.).
По графику зависимости скорости от времени можно найти ускорение: =
Задание 1
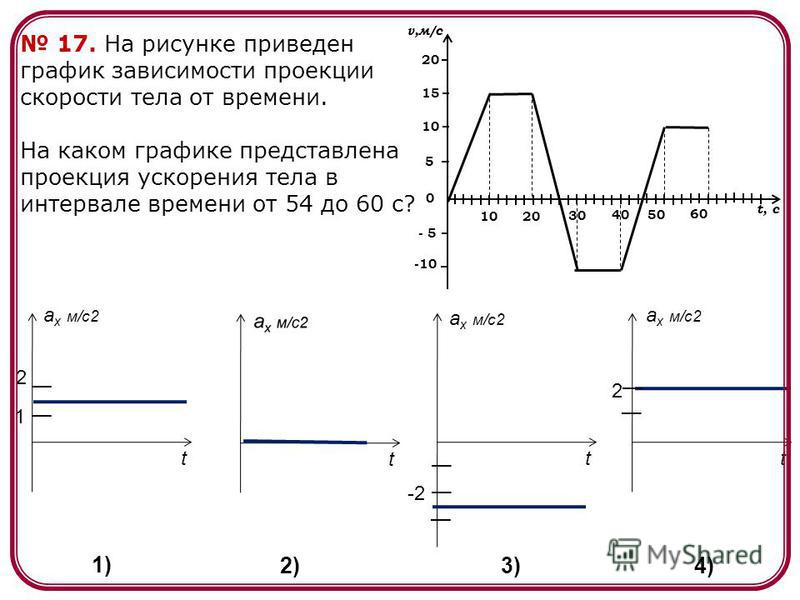
Записать уравнение скорости от времени (t) для каждого участка графика на рисунке.
Решение:
Участок ОА: = 0, а = = 20 м/ . Уравнение = 20t;
Участок АВ: = = 60, а = 0. Уравнение = 60;
Участок BD: = 60 м/с, = — 60 м/с, а = = — 60 м/ .
Уравнение = 60 — 60t;
Участок DF: = = — 60, а = 0. Уравнение = — 60.
Задание 2
На рис. показаны тела, их скорости и ускорения. Запишите уравнения скорости для каждого тела и определите скорость через 5 с после начала движения.
= 2t; через 5 с: = 10 м/с;
= 8 + 2t через 5 с: = 8 м/с + 5 с · 2 = 18 м/с;
= 8t; через 5 с: = 8 м/с — 5 с · 2 = 2 м/с;
= — 8 — 2t; через 5 с: = — 8 м/с — 2 · 5 с = — 18 м/с; Модуль скорости = | | = 18 м/с;
= 1; через 2 с: = 1 м/с.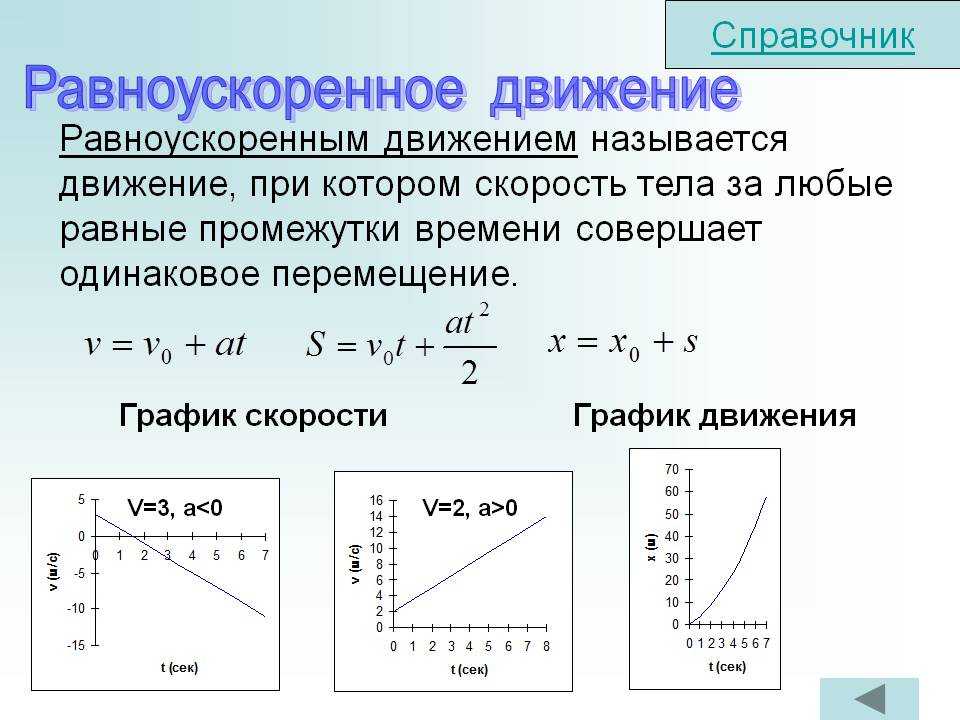
— Постройте график зависимости от t для пятого тела. Что будет графиком функции?
(Прямая, параллельная оси t.)
— А что будет графиком зависимости для остальных четырех тел? (Прямая.)
В данном случае имеем линейную зависимость.
З адание 3
По графику скорости I определить ускорение тела и скорость тела через 6 с, 10 с.
По графику скорости II определить ускорение и скорость тела через 4 с.
По графику скорости III определить ускорение и скорость тела через 16 с.
Задание 4 (Работа с таблицей)
Вид графиков зависимости проекции вектора скорости от времени при равноускоренном движении | ||
Векторы . | Векторы | |
Вид графиков | ||
По графикам (t) можно определить: | ||
Начальную скорость | = 1 м/с | = 4 м/с |
Скорость в любой момент времени | (2с) = 3 м/с | (2с) = 2,5 м/с |
Найти ускорение, с которым движется тело = | = = 1 м/ | = = — 0,75 м/ |
Составить уравнение зависимости (t): = + ·t | = 1 + 1t = 1 + t | = 4 — 0,75t |
Решение задач
Задача 1
В одитель нажимает на тормоз в тот момент, когда спидометр показывает 72 км/ч.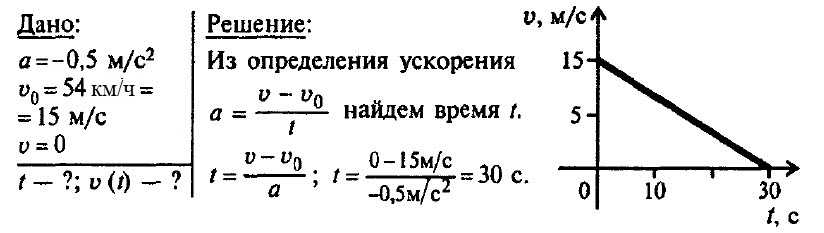 Через какое время автомобиль остановится, если он двигался с ускорением 2 м/с2?
Через какое время автомобиль остановится, если он двигался с ускорением 2 м/с2?
Домашнее задание: §6; упр. 6. Сборник № 150
Как найти ускорение с помощью графика зависимости скорости от времени
Что такое ускорение
- Скорость изменения скорости называется ускорением. Это векторная величина
\(т.е. \text{ }a=\frac{v-u}{t}\)
, где u — начальная скорость объекта, v — его конечная скорость, а t — затраченное время. - Единица ускорения = м/с 2 или мс -2
- Если скорость тела уменьшается, то оно испытывает отрицательное ускорение, которое называется замедлением или замедлением.
- На рисунке показан автомобиль, движущийся по прямой. Спидометр автомобиля показывает, что он движется с возрастающей скоростью. Автомобиль ускоряется.
- Мы говорим, что объект испытывает замедление или замедление, когда он замедляется. Тогда скорость изменения скорости объекта имеет отрицательное значение.
 На рисунке показано торможение автомобиля. Спидометр автомобиля показывает, что он движется с уменьшающейся скоростью.
На рисунке показано торможение автомобиля. Спидометр автомобиля показывает, что он движется с уменьшающейся скоростью.
Равномерное ускорение: Если тело движется прямолинейно и его скорость увеличивается на равные величины за равные промежутки времени, говорят, что оно находится в состоянии равномерного ускорения.
напр. движение свободно падающего тела.
Неравномерное ускорение: Тело имеет неравномерное ускорение, если его скорость увеличивается на неравные величины за равные промежутки времени.
Мгновенное ускорение: Ускорение тела в любой момент называется его мгновенным ускорением.
Ускорение определяется наклоном графика время-скорость.
\(\tan \theta =\frac{dv}{dt}\)
- Если график скорости времени представляет собой прямую линию, ускорение остается постоянным .
- Если наклон прямой линии положительный, возникает положительное ускорение.

- Если наклон прямой линии отрицательный, отрицательный происходит ускорение или замедление.
Анализ движения
- На рисунке показана установка аппарата для анализа движения в лаборатории.
- (a) Тикер-таймер — это устройство, которое обеспечивает постоянную запись движения для дальнейшего анализа. При подключении к источнику питания переменного тока (обычно 12 В) он вибрирует с частотой 50 Гц.
(b) Тикерный таймер делает серию точек со скоростью 50 точек в секунду на ленте бегущей строки, протягиваемой тележкой через таймер. Таким образом, временной интервал точки и следующей точки, который также известен как один тик равен 1/50 или 0,02 с.
(c) Расстояние между двумя точками равно расстоянию, пройденному тележкой за промежуток времени между точками.
(d) Тикерную ленту можно анализировать для определения времени, смещения, средней скорости, ускорения и типа движения объекта.
- Тикерную ленту можно разрезать на полосы одинакового времени (равное количество тактов) и склеить вместе, чтобы сформировать диаграмму для анализа движения тележки.
- На рисунке показаны три графика, сформированные из полос бегущей строки, каждая из которых состоит из десяти тиков.
- Для движения с равномерным ускорением или замедлением его значение может быть определено путем анализа графика. На рисунке показан график, сформированный из полос бегущей строки по десять тиков в каждой.
Решение: Начальная скорость, u = 10 мс -1
Конечная скорость, v = 20 мс -1
Затраченное время, t = 2,5 с
Пример 2. Автомобиль, движущийся со скоростью 24 м с -1 притормозил, когда загорелся красный сигнал светофора. После равномерного торможения в течение 4 с он остановился перед светофором. Вычислите ускорение автомобиля.
После равномерного торможения в течение 4 с он остановился перед светофором. Вычислите ускорение автомобиля.
Решение: Начальная скорость, u = 24 мс -1
Конечная скорость, v = 0 мс -1
Затраченное время, t = 4 с
Пример 3. График зависимости скорости тела от времени показан на рисунке. Найдите его ускорение в м/с 2 .
Решение: Как видно из рисунка,
При t = 0 с, v = 20 м/с
При t = 4 с, v = 80 м/с
\(поэтому \text{Ускорение,} a=\frac{\text{Изменение}\,\text{in}\,\text{скорость}}{\text{Timeint}\,\text{erval}} \)
\( =\frac{\Delta v}{\Delta t}=\frac{{{v}_{2}}-{{v}_{1}}}{{{t}_{2}}-{{t}_{1} }} \) 9{\text{2}}} \)
Пример 4. График время-скорость частицы показан на рисунке. Найти его мгновенное ускорение через следующие промежутки времени
(i) при t = 3 с
(ii) при t = 6 с
(iii) при t = 9 с
Решение: (i) Мгновенное ускорение при t = 3 с, равно определяется как
a = наклон линии AB = ноль
(ii) Мгновенное ускорение в момент t = 6 с определяется как a = наклон линии BC
\( =\frac{CM}{BM}=\frac{ 100-60}{8-4}=\text{ }10\text{ м/}{{\text{s}}^{\text{2}}} \) 9{\text{2}}} \)
Пример 5. Начав с отдыха, Дипак разгоняет свой велосипед до скорости 6 м/с за 30 секунд, затем он нажимает на тормоза, чтобы скорость велосипеда снизилась. до 4 м/с в следующие 5 секунд. Вычислите ускорение велосипеда в обоих случаях.
Начав с отдыха, Дипак разгоняет свой велосипед до скорости 6 м/с за 30 секунд, затем он нажимает на тормоза, чтобы скорость велосипеда снизилась. до 4 м/с в следующие 5 секунд. Вычислите ускорение велосипеда в обоих случаях.
Решение: (i) Начальная скорость, u = 0, конечная скорость,
v = 6 м/с, время, t = 30 с
Используя уравнение v = u + at, имеем
\( a =\frac{v-u}{t} \) 9{\текст{2}}}\текст{; }\!\!~\!\!\text{ } \)
, что является задержкой.
Примечание: Ускорение в случае (i) положительное, а в случае (ii) отрицательное.
Пример 6. Тележка протягивала бегущую ленту через бегущую строку таймера при движении вниз по наклонной плоскости. На рис. 2.10 показана полученная бегущая лента.
Определить среднюю скорость тележки.
Решение:
Пример 7. На рисунке показаны бегущие строки, полученные при движении тележки.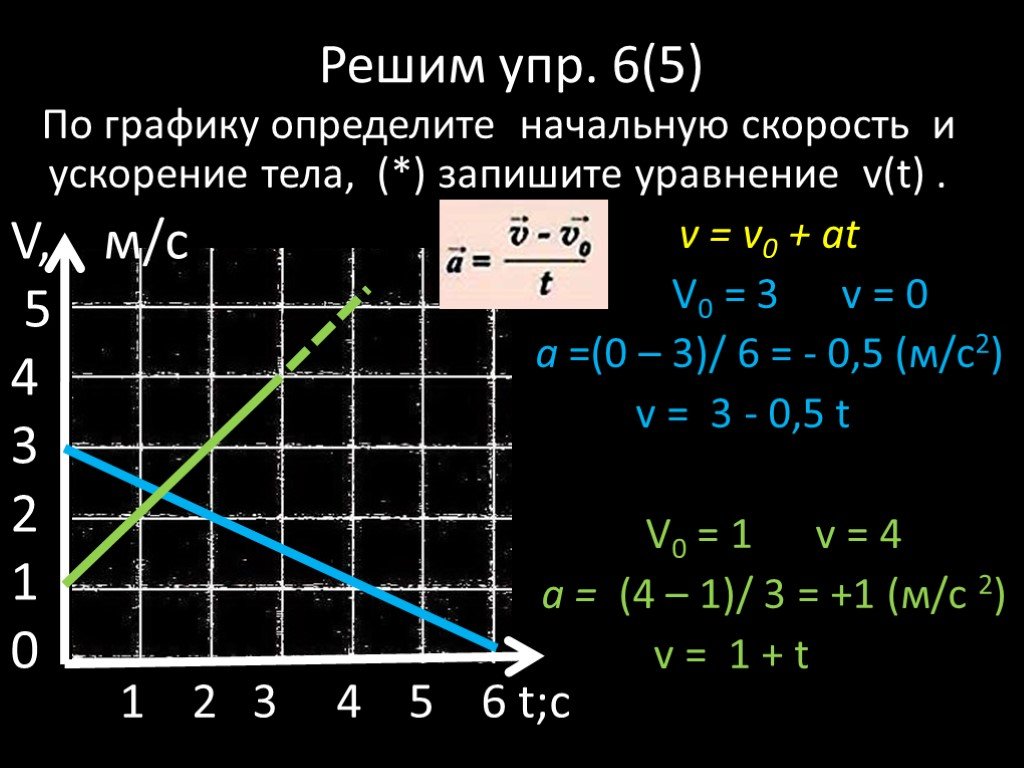
Опишите тип движения тележки для каждой бегущей строки.
Решение:
(a) Расстояния между двумя соседними точками одинаковы на всей ленте. Следовательно, тележка двигалась с равномерной скоростью.
(b) Расстояния между двумя соседними точками увеличиваются. Следовательно, тележка двигалась с возрастающей скоростью. Тележка ускорялась.
(c) Расстояния между двумя соседними точками уменьшаются. Поэтому тележка двигалась с уменьшающейся скоростью. Тележка тормозила.
Пример 8. На рисунке показан график движения тележки с равноускорением.
Определить его ускорение.
Решение:
Пример 9. Тележка двигалась по наклонной плоскости, тянущейся за бегущую ленту. На рисунке показан график, сформированный путем разрезания и размещения бегущей строки на полосы по десять тиков в каждой.
Определить ускорение тележки.
Решение:
Пример 10.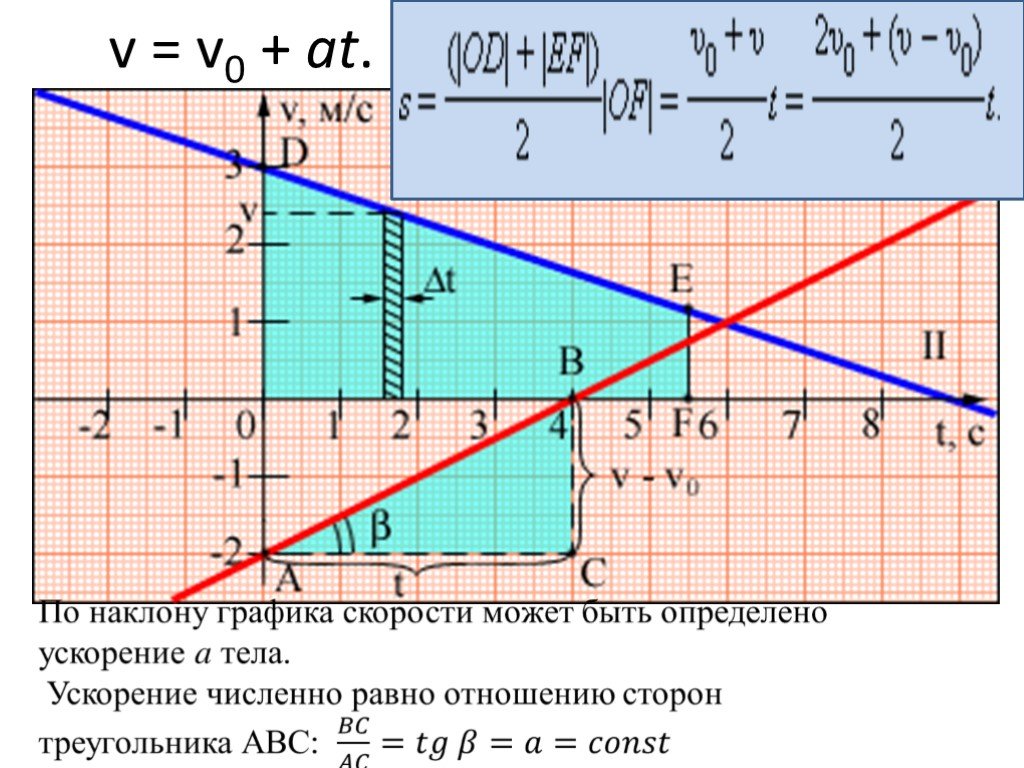 На рисунке показана полоса бегущей строки, изображающая движение игрушечной машинки с равномерным ускорением.
На рисунке показана полоса бегущей строки, изображающая движение игрушечной машинки с равномерным ускорением.
Определите ускорение игрушечной машинки.
Решение:
Скорость и ускорение: формулы и графики
Что такое скорость? Чем она отличается от скорости? Какой смысл в ускорении, если мы уже знаем скорость, с которой движется объект? На эти вопросы вы сможете ответить в конце этой статьи. Сначала мы пройдемся по определениям и уравнениям для скорости и ускорения. Затем мы смотрим на их графики во времени и, наконец, работаем над несколькими примерами, чтобы лучше понять эти концепции. Приятного обучения!
Формула скорости и ускорения
Скорость объекта – это его скорость в заданном направлении. Скорость является векторной величиной.
Скорость против скорости, Nidhish Gokuldas StudySmarter originals
Скорость объекта определяется следующим уравнением: n
Где Δs изменение рабочего объема ( расстояние в определенном направлении ) объекта и t — это время , необходимое для прохождения этого перемещения . Скорость измеряется в м/с.
Скорость измеряется в м/с.
Основное различие между скоростью и скоростью состоит в том, что скорость является скалярной величиной, а скорость является векторной величиной . Это означает, что скорость имеет только величину, а скорость имеет не только величину, но и направление. Например, 25 м/с — это скорость, а 25 м/с — это скорость, где юг — это направление, в котором движется рассматриваемый объект.
Ускорение — это скорость изменения скорости с по отношению ко времени.
Ускорение и торможение; когда водитель нажимает ногу на педаль газа, автомобиль ускоряется за счет силы, с которой двигатель воздействует на колеса автомобиля. ускорение,
мы можем вычислить ускорение объекта, если мы знаем, насколько его скорость изменяется за период времени . Задается следующим уравнением:a=∆vt,
или прописью
id=»2821967″ role=»math» ускорение=changeinvelocitytimetaken.
Ускорение измеряется в м/с2. Ускорение может быть положительным или отрицательным. Отрицательное ускорение называется замедлением. Ускорение и скорость являются векторами, поскольку они имеют величину и направление .
Разность скорости и ускорения
Скорость измеряет скорость изменения смещения движущегося объекта. Ускорение измеряет скорость изменения скорости движущегося объекта. Различия между скоростью и ускорением перечислены ниже, чтобы сделать различие между ними более четким.
| Скорость | Ускорение |
| Скорость измеряется в м/с | Ускорение измеряется в м/с2 |
| Скорость означает, что объект покрывает расстояние в один метр каждую секунду. | Ускорение в 1 м/с2 означает, что скорость объекта увеличивается на 1 м в секунду. |
Давайте теперь посмотрим на соотношение между скоростью и ускорением, когда объект движется по прямой .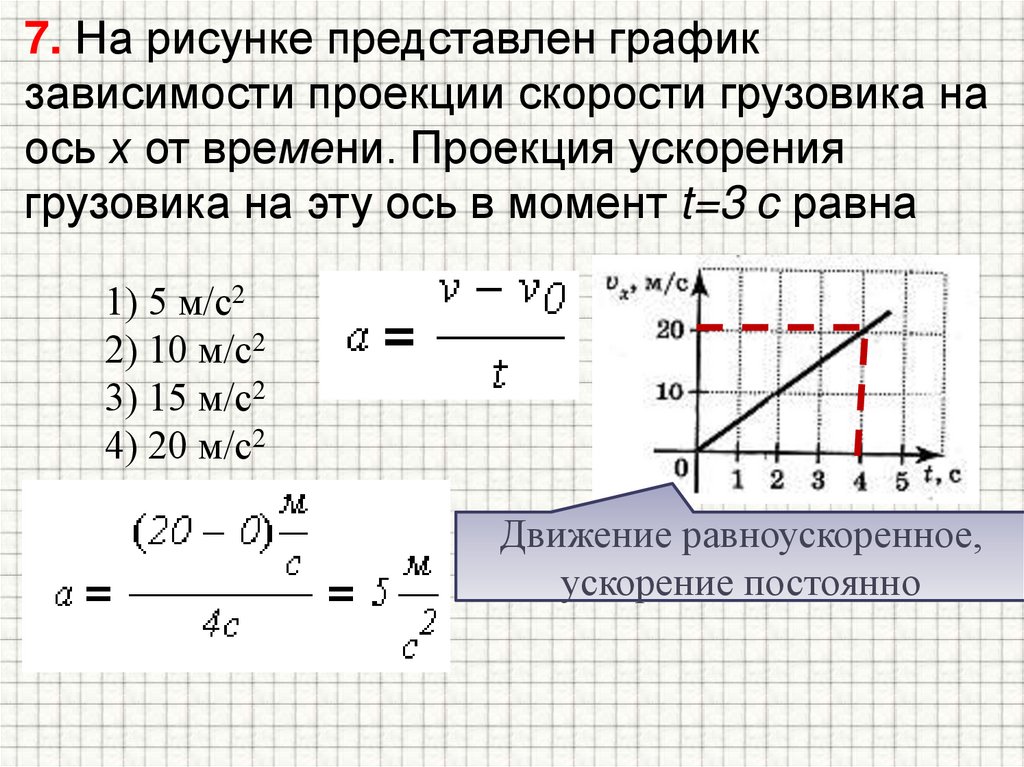
Связь между скоростью и ускорением
Глядя на уравнение ускорения, мы видим, что оно прямо пропорционально изменению скорости и обратно пропорционально времени, необходимому для ускорения или замедления.
Если скорость объекта увеличивается (начальная скорость < конечной скорости) , то он имеет положительное ускорение в направлении скорости.
Если скорость уменьшается, то ускорение будет отрицательным и в направлении, противоположном скорости.
Если скорость постоянна, то ускорение равно нулю. Это потому, что ускорение определяется скоростью изменения скорости. Если скорость не меняется, то ускорение должно быть равно нулю.
a=∆vt=v-ut
Если v=u, то ускорение тела равно
a=0m/st=0m/s2
Теперь представим взаимосвязь между скоростью и ускорением движущихся объектов используя графики.
Графики скорости и ускорения во времени
Скорость и ускорение движущегося объекта можно визуализировать с помощью графика скорость-время . На приведенном ниже графике показан график зависимости скорости от времени объекта, движущегося по прямой линии.
График зависимости скорости от времени для объекта, который начинает ускоряться, затем движется с постоянной скоростью, прежде чем, наконец, замедлится, оригиналы StudySmarter
- Наклон вверх оранжевой линии указывает на то, что скорость увеличивается во времени. Это означает, что объект имеет положительное ускорение.
- Горизонтальная зеленая линия означает, что скорость постоянна, а ускорение равно нулю.
- Синяя линия представляет собой наклон вниз, показывающий уменьшение скорости, что указывает на отрицательное замедление. Чтобы вычислить ускорение в любой точке, нам нужно найти наклон кривой скорости.
градиент=y2-y1x2-x1
где (x1,x2) — координаты начальной точки на графике и (x2, y2) — координаты конечной точки.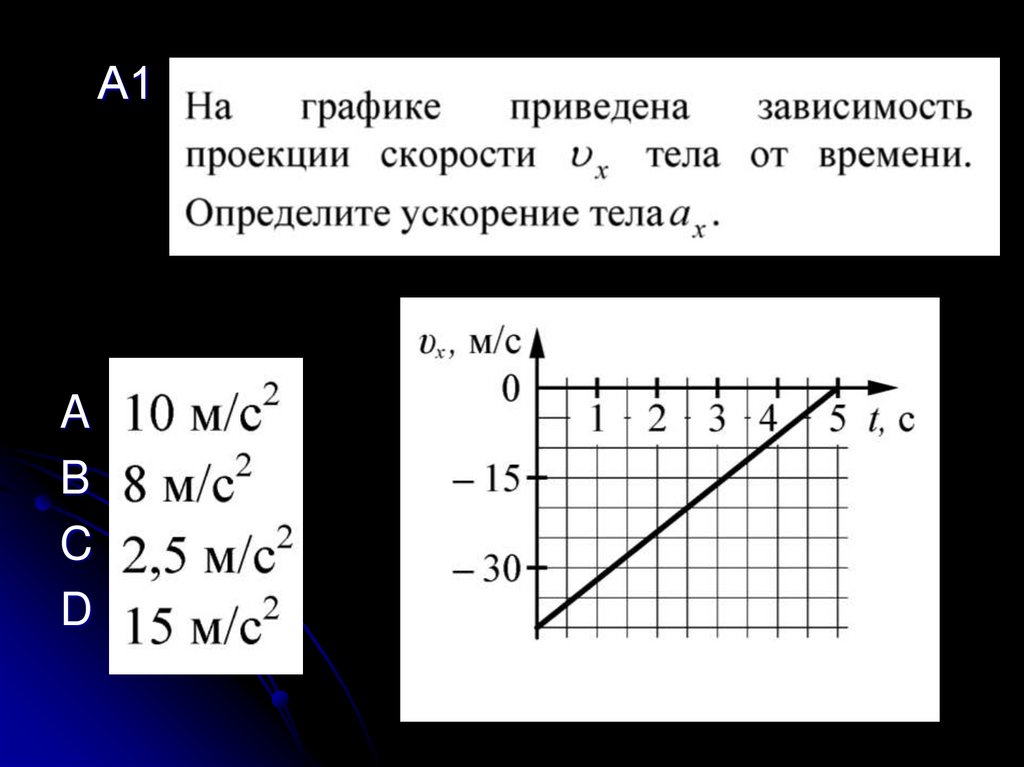

 На рисунке показано торможение автомобиля. Спидометр автомобиля показывает, что он движется с уменьшающейся скоростью.
На рисунке показано торможение автомобиля. Спидометр автомобиля показывает, что он движется с уменьшающейся скоростью.
Leave A Comment