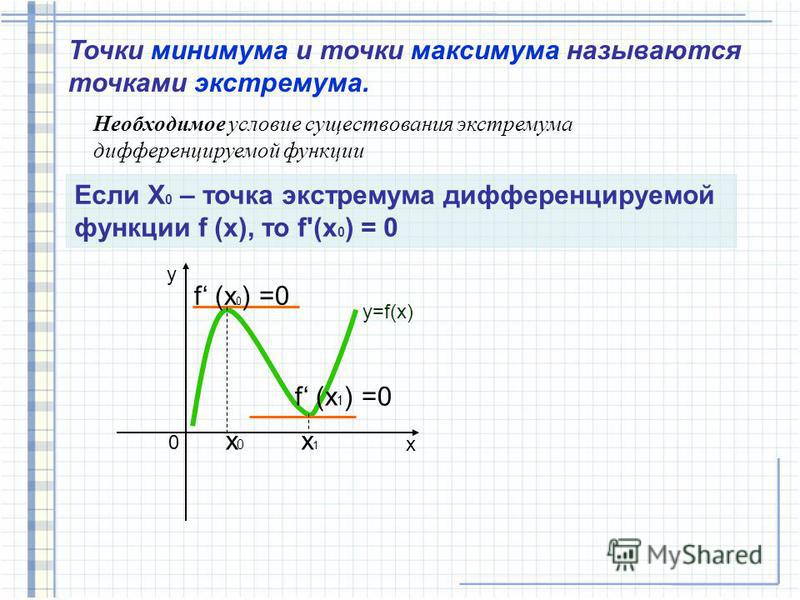
Как определить точку минимума и максимума функции: Урок 16. экстремумы функции - Алгебра и начала математического анализа - 11 класс

Точки экстремума функции, необходимые и достаточные условия экстремума

Содержание:

Определение

Точка $x_{0}$ называется точкой локального максимума функции $f(x)$, если существует такая окрестность этой точки, что для всех $x$ из этой окрестности выполняется неравенство: $f(x) \leq f\left(x_{0}\right)$.

Точка $x_{0}$ называется точкой локального минимума функции $f(x)$, если существует такая окрестность этой точки, что для всех $x$ из этой окрестности $f(x) \geq f\left(x_{0}\right)$.

Значение функции в точке максимума называется локальным максимумом, значение функции в точке минимума — локальным минимумом данной функции. Локальные максимум и минимум функции называются локальными экстремумами.

Точка $x_{0}$ называется точкой строгого локального максимума функции $y=f(x)$, если для всех $x$ из окрестности этой точки будет справедливо строгое неравенство $f(x) \lt f\left(x_{0}\right)$.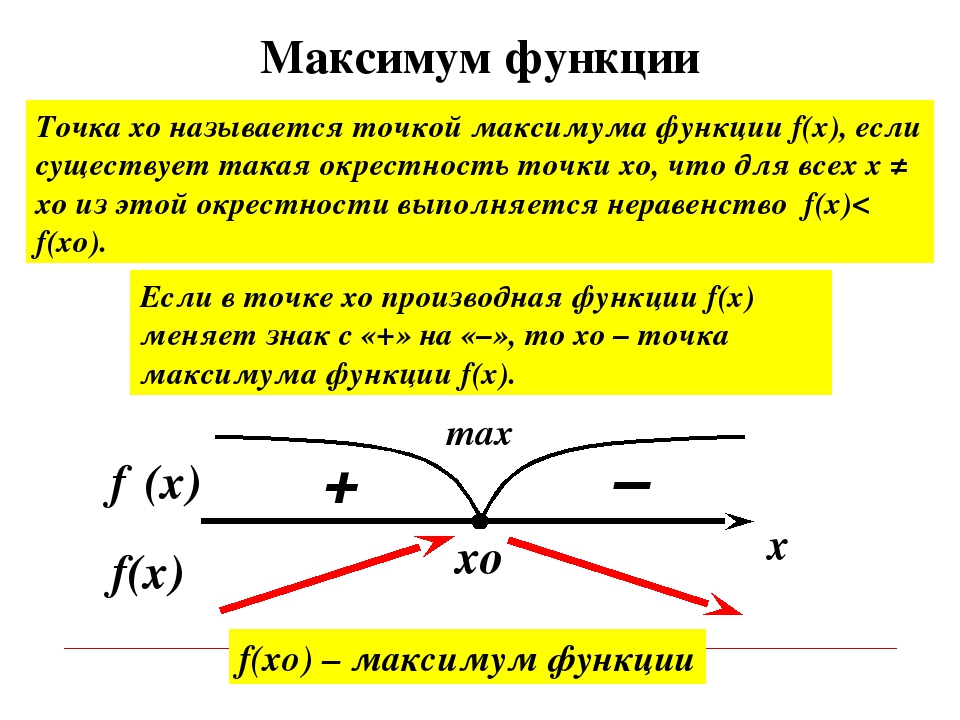

2+7х–5.

Пришло время в данном разделе рассмотреть степенные функции. На блоге уже представлены задания на нахождение точек максимума и минимума различных функций, а именно: функций с числом е, с логарифмами, тригонометрические, рациональные.

Алгоритм нахождения данных точек оговаривался уже неоднократно, кратко повторюсь:

1. Находим производную функции.

2. Находим нули производной (приравниваем производную к нулю и решаем уравнение).

3. Далее строим числовую ось, на ней отмечаем найденные точки и определяем знаки производной на полученных интервалах. *Это делается путём подстановки произвольных значений из интервалов в производную.

4. Далее делаем вывод.

Если вы совсем не знакомы со свойствами производной для исследования функций, то обязательно изучите статью «Исследование функций. Это нужно знать!».Также повторите таблицу производных и правила дифференцирования (имеются в этой же статье). Рассмотрим задачи:

77431. Найдите точку максимума функции у = х³–5х²+7х–5.

Найдём производную функции:

Найдем нули производной:

3х² – 10х + 7 = 0

Решая квадратное уравнение получим:

*Это точки возможного максимума (минимума) функции.

Определяем знаки производной функции на интервалах и отметим их на эскизе. Подставляем произвольное значение из каждого интервала в выражение производной:

у(0)’ = 3∙0² – 10∙0 + 7 = 7 > 0

у(2)’ = 3∙2² – 10∙2 + 7 = – 1< 0

у(3)’ = 3∙3² – 10∙3 + 7 = 4 > 0

В точке х = 1 производная меняет свой знак с положительного на отрицательный, значит это есть искомая точка максимума.

Ответ: 1

77432. Найдите точку минимума функции у = х³+5х

2+7х–5.

Найдём производную функции:

Найдем нули производной:

3х² + 10х + 7 = 0

Решая квадратное уравнение получим:

у(–3)’ = 3∙(–3)² + 10∙(–3) + 7 = 4 > 0

у(–2)’= 3∙(–2)² + 10∙(–2) + 7 = –1 < 0

у(0)’= 3∙0² – 10∙0 + 7 = 7 > 0

В точке х = –1 производная меняет свой знак с отрицательного на положительный, значит это есть искомая точка минимума.

Ответ: –1

77435. Найдите точку максимума функции у = 7+12х–х³

Найдём производную функции:

Найдем нули производной:

12 – 3х² = 0

х² = 4

Решая уравнение получим:

*Это точки возможного максимума (минимума) функции.

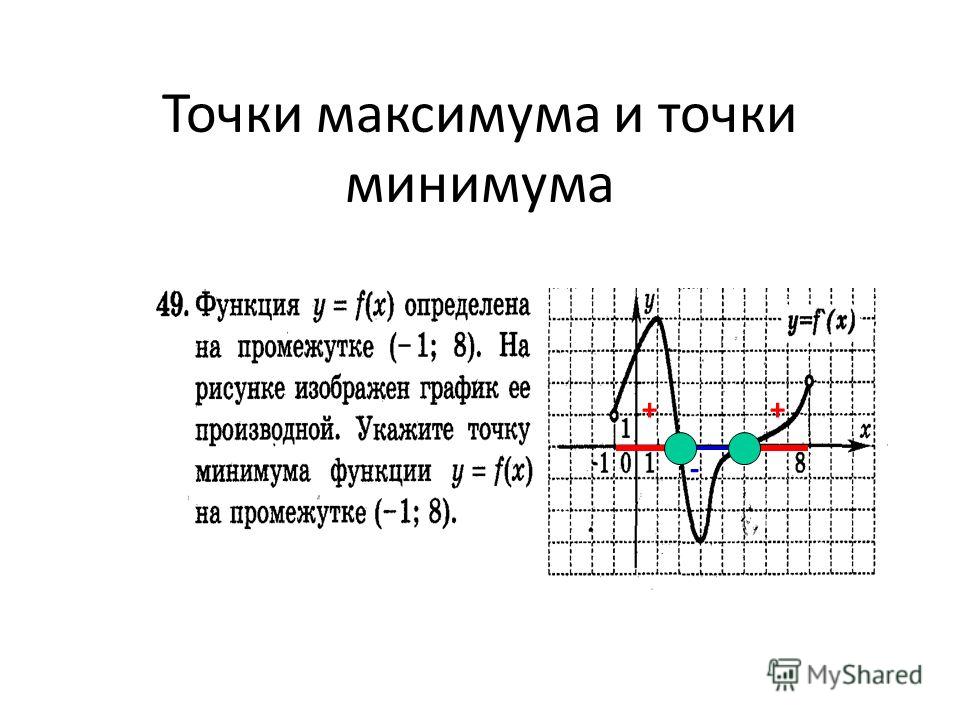
у(–3)’=12 – 3∙(–3)² = –15 < 0

у(0)’=12 – 3∙0²

= 12 > 0

у(3)’=12 – 3∙3² = –15 < 0

В точке х = 2 производная меняет свой знак с положительного на отрицательный, значит это есть искомая точка максимума.

Ответ: 2

*Для этой же функции точкой минимума является точка х = – 2.

77439. Найдите точку максимума функции у = 9х²– х³.

Найдём производную функции:

Найдем нули производной:

18х –3х² = 0

3х(6 – х) = 0

Решая уравнение получим:

у(–1)’=18 (–1) –3 (–1)² = –21< 0

у(1)’=18∙1 –3∙1² = 15 > 0

у(7)’=18∙7 –3∙7² = –1< 0

В точке х = 6 производная меняет свой знак с положительного на отрицательный, значит это есть искомая точка максимума.

Ответ: 6

*Для этой же функции точкой минимума является точка х = 0.

77443. Найдите точку максимума функции у = (х³/3)–9х–7.

Найдём производную функции:

Найдем нули производной:

х² – 9 = 0

х² = 9

Решая уравнение получим:

у(–4)’= (–4)² – 9 > 0

у(0)’= 0² – 9 < 0

у(4)’= 4² – 9 > 0

В точке х = – 3 производная меняет свой знак с положительного на отрицательный, значит это есть искомая точка максимума.

Ответ: – 3

*Для этой же функции точкой минимума является точка х = 3.

77443. Найдите точку максимума функции у = 5+9х– (х³/3).

Найдём производную функции:

Найдем нули производной:

9 – х² = 0

х² = 9

Решая уравнение получим:

у(–4)’= 9 – (–4)²

< 0

у(0)’= 9 – 0² > 0

у(4)’= 9 – 4² < 0

В точке х = 3 производная меняет свой знак с положительного на отрицательный, значит это есть искомая точка максимума.

Ответ: 3

*Для этой же функции точкой минимума является точка х = – 3.

77419. Найдите точку максимума функции у = х³– 48х+17. Решение.

77423. Найдите точку максимума функции у = х³–3х²+2. Решение.

77427. Найдите точку максимума функции у = х³+2х²+х+3. Решение.

На этом всё. Успеха вам!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Алгебра – 10 класс. Точки экстремумов функций

Дата публикации: 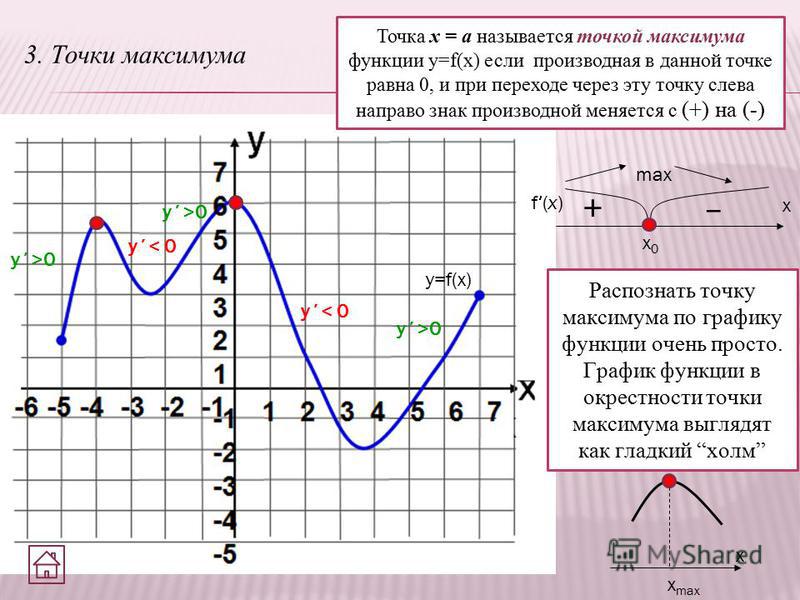09 апреля 2017.

Что будем изучать:
1. Введение.
2. Точки минимума и максимума.
3. Экстремум функции.
4. Как вычислять экстремумы?
5. Примеры.

Введение в экстремумы функций

Ребята, давайте посмотрим на график некоторой функции:

Заметит, что поведение нашей функции y=f (x) во многом определяется двумя точками x1 и x2. Давайте внимательно посмотрим на график функции в этих точках и около них. До точки x2 функция возрастает, в точке x2 происходит перегиб, и сразу после этой точки функция убывает до точки x1. В точке x1 функция опять перегибается, и после этого — опять возрастает. Точки x1 и x2 пока так и будем называть точками перегиба. Давайте проведем касательные в этих точках:

Касательные в наших точках параллельны оси абсцисс, а значит, угловой коэффициент касательной равен нулю. Это значит, что и производная нашей функции в этих точках равна нулю.

Посмотрим на график вот такой функции:

Касательные в точках x2 и x1 провести невозможно. Значит, производной в этих точках не существует. Теперь посмотрим опять на наши точки на двух графиках. Точка x2 — это точка, в которой функция достигает наибольшего значения в некоторой области (рядом с точкой x2). Точка x1 — это точка, в которой функция достигает своего наименьшего значения в некоторой области (рядом с точкой x1).

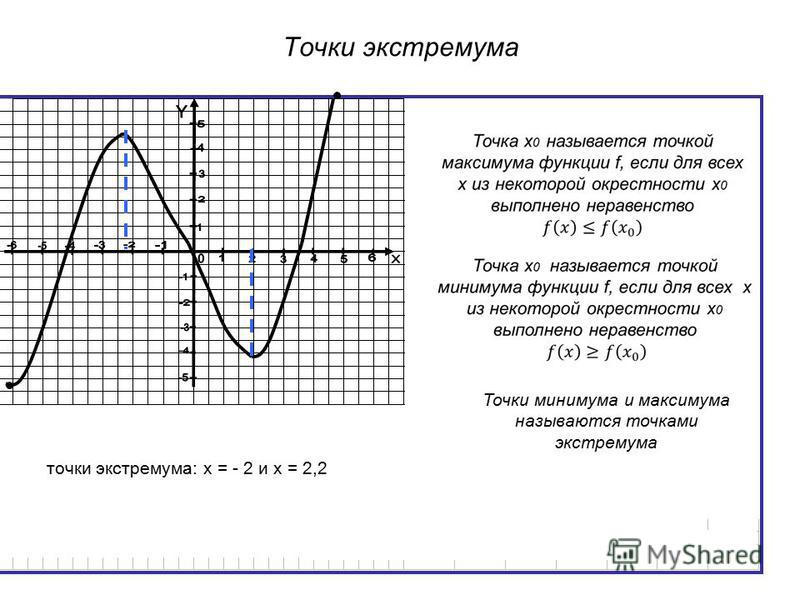
Точки минимума и максимума

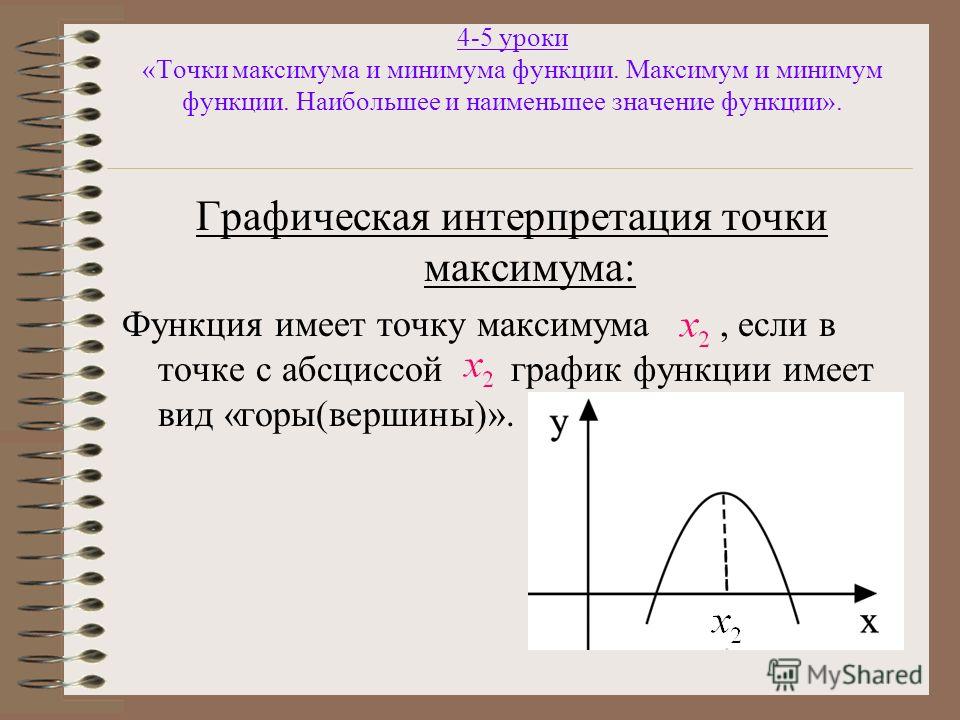
Определение: Точку x= x0 называют точкой минимума функции y=f(x), если существует окрестность точки x0, в которой выполняется неравенство: f(x) ≥ f(x0).

Определение: Точку x=x0 называют точкой максимума функции y=f(x), если существует окрестность точки x0, в которой выполняется неравенство: f(x) ≤ f(x0).

Ребята, а что такое окрестность?

Определение: Окрестность точки — множество точек, содержащее нашу точку, и близкие к ней.

Окрестность мы можем задавать сами. Например, для точки x=2, мы можем определить окрестность в виде точек 1 и 3.

Вернемся к нашим графикам, посмотрим на точку x2, она больше всех других точек из некоторой окрестности, тогда по определению — это точка максимума. Теперь посмотрим на точку x1, она меньше всех других точек из некоторой окрестности, тогда по определению — это точка минимума.

Ребята, давайте введем обозначения:

y_min — точка минимума,
y_max — точка максимума.

Важно! Ребята, не путайте точки максимума и минимума с наименьшим и наибольшим значение функции. Наименьшее и наибольшее значения ищутся на всей области определения заданной функции, а точки минимума и максимума в некоторой окрестности.

Экстремумы функции

Для точек минимума и максимума есть общей термин – точки экстремума.

Экстремум (лат. extremum – крайний) – максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума.

Соответственно, если достигается минимум – точка экстремума называется точкой минимума, а если максимум – точкой максимума.

Как же искать экстремумы функции?

Давайте вернемся к нашим графикам. В наших точках производная либо обращается в нуль (на первом графике), либо не существует (на втором графике).

Тогда можно сделать важное утверждение: Если функция y= f(x) имеет экстремум в точке x=x0, то в этой точке производная функции либо равна нулю, либо не существует.

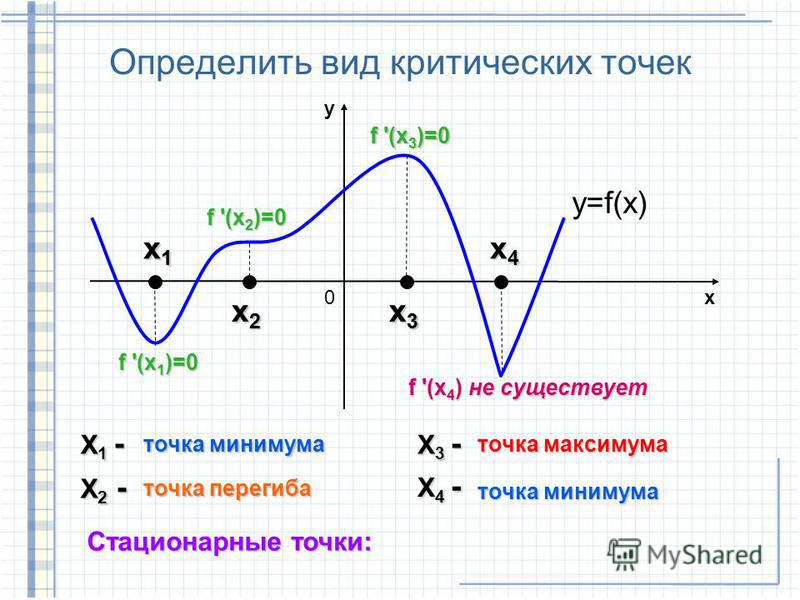
Точки, в которых производная равна нулю называются стационарными.

Точки, в которых производной функции не существует, называются критическими.

Как вычислять экстремумы?

Ребята, давайте опять вернемся к первому графику функции:

Анализируя этот график, мы говорили: до точки x2 функция возрастает, в точке x2 происходит перегиб, и после этой точки функция убывает до точки x1. В точке x1 у функции опять перегибается, и после этого функция опять возрастает.

На основании таких рассуждений, можно сделать вывод, что функция в точках экстремума меняет характер монотонности, а значит и производная функция меняет знак. Вспомним: если функция убывает, то производная меньше либо равно нулю, а если функция возрастает, то производная больше либо равна нулю.

Обобщим полученные знания утверждением:

Теорема: Достаточное условие экстремума: пусть функция y=f(x) непрерывна на некотором промежутке Х и имеет внутри промежутка стационарную или критическую точку x= x0. Тогда:

Если у этой точки существует такая окрестность, в которой при x x0 выполняется f’(x)>0, то точка x0 – точка минимума функции y= f(x).
Если у этой точки существует такая окрестность, в которой при x 0, а при x> x0 выполняется f’(x)Если у этой точки существует такая окрестность, в которой и слева и справа от точки x0 знаки производной одинаковы, то в точке x0 экстремума нет.

Для решении задач запомните такие правила: Если знаки производных определены то:

Алгоритм исследования непрерывной функции y= f(x) на монотонность и экстремумы:

Найти производную y’.
Найти стационарные(производная равна нулю) и критические точки (производная не существует).
Отметить стационарные и критические точки на числовой прямой и определить знаки производной на получившихся промежутках.
По указанным выше утверждениям сделать вывод о характере точек экстремума.

Примеры нахождения точки экстремумов

1) Найти точки экстремума функции и определить их характер: y= 7+ 12*x — x³

Решение: Наша функция непрерывна, тогда воспользуемся нашим алгоритмом:
а) y’= 12 — 3x²,
б) y’= 0, при x= ±2,
в) отметим стационарные точки на числовой прямой и определим знаки производной:
г) посмотрим на наш рисунок, где изображены правила определения экстремумов.

Точка x= -2 — точка минимума функции, точка x= 2 — точка максимума функции.
Ответ: x= -2 — точка минимума функции, x= 2 — точка максимума функции.

2) Найти точки экстремума функции и определить их характер.

Решение: Наша функция непрерывна. Воспользуемся нашим алгоритмом:
а) б) в точке x= 2 производная не существует, т.к. на нуль делить нельзя, Область определения функции: [2; +∞], в этой точки экстремума нет, т.к. окрестность точки не определена. Найдем значения, в которой производная равна нулю: в) Отметим стационарные точки на числовой прямой и определим знаки производной: г) посмотрим на наш рисунок, где изображены правила определения экстремумов.
Точка x= 3 — точка минимума функции.
Ответ: x= 3 — точка минимума функции.

3) Найти точки экстремума функции y= x — 2cos(x) и определить их характер, при -π ≤ x ≤ π.

Решение: Наша функция непрерывна, воспользуемся нашим алгоритмом:
а) y’= 1 + 2sin(x),
б) найдем значения в которой производная равна нулю: 1 + 2sin(x)= 0, sin(x)= -1/2,
т.

к. -π ≤ x ≤ π, то: x= -π/6, -5π/6,
в) отметим стационарные точки на числовой прямой и определим знаки производной: г) посмотрим на наш рисунок, где изображены правила определения экстремумов.
Точка x= -5π/6 — точка максимума функции.
Точка x= -π/6 — точка минимума функции.
Ответ: x= -5π/6 — точка максимума функции, x= -π/6 — точка минимума функции.

4) Найти точки экстремума функции и определить их характер:

Решение: Наша функция имеет разрыв только в одной точке x= 0. Воспользуемся алгоритмом:
а) б) найдем значения в которой производная равна нулю: y’= 0 при x= ±2,
в) отметим стационарные точки на числовой прямой и определим знаки производной:
г) посмотрим на наш рисунок, где изображены правила определения экстремумов.
Точка x= -2 точка минимума функции.
Точка x= 2 — точка минимума функции.
В точке x= 0 функция не существует.
Ответ: x= ±2 — точки минимума функции.

Задачи для самостоятельного решения

а) Найти точки экстремума функции и определить их характер: y= 5x³ — 15x — 5.

б) Найти точки экстремума функции и определить их характер:
в) Найти точки экстремума функции и определить их характер: y= 2sin(x) — x при π ≤ x ≤ 3π.
г) Найти точки экстремума функции и определить их характер:

Задание 12 Профильного ЕГЭ по математике. Готовимся правильно

Задание 12 первой части Профильного ЕГЭ по математике — это нахождение точек максимума и минимума функции, а также наибольших и наименьших значений функции с помощью производной.

Вот какие типы задач могут встретиться в этом задании:

Нахождение точек максимума и минимума функций

Исследование сложных функций

Нахождение наибольших и наименьших значений функций на отрезке

Нахождение точек максимума и минимума функций

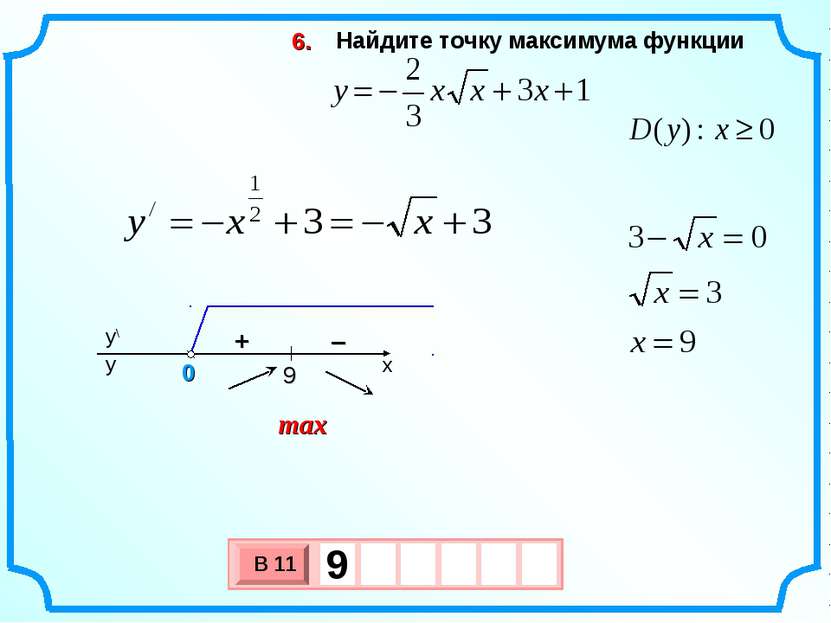
1. Найдите точку максимума функции

Найдем производную функции.

Приравняем производную к нулю. Получим:

Исследуем знаки производной.

В точке производная меняет знак с «плюса» на «минус». Значит, — точка максимума функции

Ответ: 17.

2. Найдите точку минимума функции

Найдем производную функции.

Приравняем производную к нулю.

Определим знаки производной.

В точке производная меняет знак с «минуса» на «плюс». Значит, — точка минимума функции

Ответ: 1.

Исследование сложных функций

3. Найдите точку максимума функции

Перед нами сложная функция Возможно, вы знаете формулы производной сложной функции. Но вообще-то их изучают на первом курсе вуза, поэтому мы решим задачу более простым способом.

Так как функция монотонно возрастает, точка максимума функции .будет при том же , что и точка максимума функции А ее найти легко.

при . В точке производная меняет знак с «плюса» на «минус». Значит, — точка максимума функции .

Заметим, что точку максимума функции можно найти и без производной.

Графиком функции является парабола ветвями вниз, и наибольшее значение достигается в вершине параболы, то есть при

Ответ: — 4.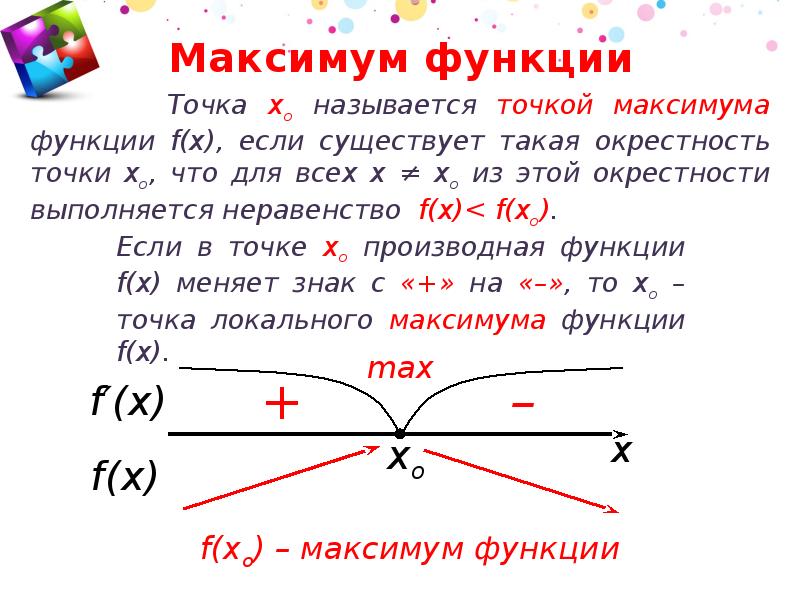

4. Найдите абсциссу точки максимума функции

Напомним, что абсцисса — это координата по

Снова сложная функция. Применяем тот же прием, что и в предыдущей задаче.

Так как функция монотонно возрастает, точка максимума функции является и точкой максимума функции

Это вершина квадратичной параболы

Нахождение наибольших и наименьших значений функций на отрезке

5. Найдите наибольшее значение функции на отрезке

Мы помним, что наибольшее значение функции на отрезке может достигаться либо в точке максимума, либо на конце отрезка. Эти случаи показаны на рисунке.

Будем искать точку максимума функции с помощью производной. Найдем производную и приравняем ее к нулю.

Найдем знаки производной.

В точке производная равна нулю и меняет знак с «+» на «-«. Значит, x = — 2 — точка максимума функции . Поскольку при функция убывает, В этой задаче значение функции на концах отрезка искать не нужно.

Ответ: 12

6. Найдите наименьшее значение функции на отрезке

Найдем производную функции и приравняем ее к нулю.

при

Найдем знаки производной.

Точка — точка минимума функции . Точка не лежит на отрезке Поэтому

и Значит, наименьшее значение функции на отрезке достигается при Найдем это значение.

Ответ: -11.

7. Найдите наименьшее значение функции на отрезке

Иногда перед тем, как взять производную, формулу функции полезно упростить.

Мы применили формулу для логарифма произведения. при

Если то Если , то

Значит, — точка минимума функции . В этой точке и достигается наименьшее значение функции на отрезке

Ответ: 4

8. Найдите наибольшее значение функции на отрезке

Найдем производную функции

Приравняем производную к нулю:

. Поскольку если

Найдем знаки производной на отрезке

При знак производной меняется с «плюса» на «минус». Значит, — точка максимума функции

Мы нашли точку максимума, но это еще не все. Сравним значения функции в точке максимума и на конце отрезка, то есть при и

Мы нашли, что

Заметим, что если вам попадется такая задача в первой части ЕГЭ по математике, то находить значение функции при не обязательно. Как мы видим, это значение — число иррациональное. А в первой части ЕГЭ по математике ответом может быть только целое число или конечная десятичная дробь.

Ответ: 4

9. Найдите наименьшее значение функции на отрезке [0;2].

Снова сложная функция. Запишем полезные формулы:

Найдем производную функции

если Тогда

При знак производной меняется с «минуса» на «плюс». Значит, — точка минимума функции

10. Найдите наибольшее значение функции на отрезке

Как всегда, возьмем производную функции и приравняем ее к нулю.

По условию, . На этом отрезке условие выполняется только для Найдем знаки производной слева и справа от точки

В точке производная функции меняет знак с «плюса» на «минус». Значит, точка — точка максимума функции . Других точек экстремума на отрезке функция не имеет, и наибольшее значение функции на отрезке достигается при

Ответ: 12.

11.Найдите наименьшее значение функции на отрезке

Найдем производную функции и приравняем ее к нулю. — нет решений.

Что это значит? Производная функции не равна нулю ни в какой точке. Это значит, что знак производной в любой точке одинаков, а функция не имеет экстремумов и является монотонной.

Поскольку , получим, что для всех , и функция монотонно возрастает при

Значит, наименьшее свое значение функция принимает в левом конце отрезка , то есть при

Ответ: 6

Краткие сведения из теории оптимизации

Интеллектуальные информационные системы

Лекции

13. КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ОПТИМИЗАЦИИ

13.1. Основные сведения.

13.2. Классическая теория оптимизации.

13.3. Математическое программирование (исследование операций).

13.4. Имитационное моделирование.

13.5. Эвристический подход к оптимизации.

Вопросы для самопроверки.

13.1. Основные сведения

В последующих лекциях методы, на которых базируются интеллектуальные информационные системы, будут рассматриваться применительно к решению оптимизационных задач. В связи с этим в лекции приводятся краткие сведения из теории оптимизации.

Оптимизация (в математике, информатике и исследовании операций) — задача нахождения экстремума (минимума или максимума) целевой функции в некоторой области конечномерного векторного пространства, ограниченной набором линейных и/или нелинейных равенств и/или неравенств.

Оптимизация — процесс приведения системы в наилучшее (оптимальное) состояние.

Для того, чтобы выбрать наилучший вариант или привести систему в оптимальное состояние необходимо выполнить процедуру поиска этого варианта или состояния из множества возможных.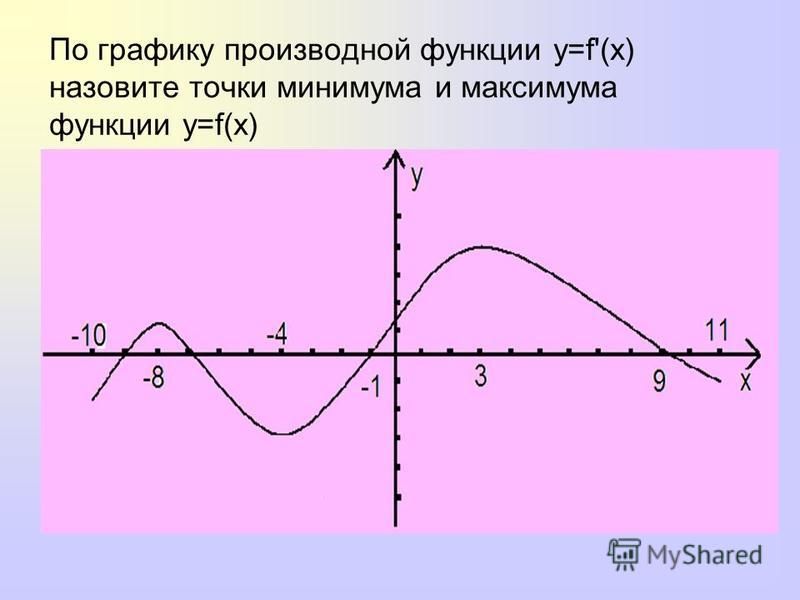

В задачах оптимизации имеется целевая функция, зависящая от одной или нескольких переменных. Требуется найти такие значения переменных, при которых функция примет оптимальное (наилучшее) значение. При этом на переменные могут накладываться различные ограничения.

Наилучшее значение функции достигается в так называемых точках минимума или максимума (экстремальных точках).

Рис.13.1. Пример функции одной переменной

Для функции одной переменной математически экстремальную точку (экстремум) можно определить следующим образом:

— точка x₀ является точкой максимума функции f(x), если соблюдается неравенство

f(x₀ — ∆x) ≤ f(x₀) ≥ f(x₀ + ∆x),

где ∆x – достаточно малое приращение значения переменной x.

— точка x₀ является точкой минимума функции f(x), если соблюдается неравенство

f(x₀ — ∆x) ≥ f(x₀) ≤ f(x₀ + ∆x).

На рис.13.1 для интервала [a, b] точки x₁, x₂, x₃, x₄ и x₆ являются экстремальными точками.

Значение f(x₆) называется глобальным или абсолютным максимумом, а значения f(x₁) и f(x₃) — локальными или относительными максимумами. Аналогично, f(x₂) – глобальный минимум и f(x₄) – локальный минимум.

Заметим, что хотя точка х₁, являясь точкой максимума функции f(x), отличается от остальных локальных максимумов f(x) т.к. по крайней мере в одной точке ее окрестности значение функции f(x) совпадает с f(x₁). Точка х₁ по этой причине называется нестрогим (слабым) максимумом функции, а точки х₃ и x₆ — строгими максимумами. Нестрогий максимум, следовательно, подразумевает наличие (бесконечного количества) различных точек, которым соответствует одно и то же максимальное значение функции.

13.2. Классическая теория оптимизации

Классическая теория оптимизации базируется на аппарате дифференциального исчисления (математического анализа).

На рис.13.1 легко заметить, что первая производная функции f(x) (тангенс угла наклона касательной к графику функции) равна 0 во всех ее экстремальных точках. Однако это условие выполняется и в точках перегиба и седловых точках (x₅).

Т.о. x_i, являющиеся решениями уравнения f’(x) = 0, – это либо точки экстремума либо точки перегиба. Условие f’(x) = 0 называют необходимым условием наличия экстремума.

Исследование производных высших порядков позволяет убедиться, что точка x_i – экстремум и более того, является она точкой максимума или минимума. Для этого необходимо найти вторую производную f”(x) и в нее подставить значения x_i, полученные при решении уравнения f’(x) = 0:

— если f”(x_i) > 0 – то в точке x_i минимум функции;

— если f”(x_i) < 0 – то в точке x_i максимум функции;

— если f”(x_i) = 0 – то необходимо исследовать следующие производные. В этом случае, если первые (n-1) производных равны 0 и f⁽ⁿ⁾(x_i) <> 0, то в точке x_i функция имеет:

— точку перегиба, если n – нечетное;

— минимум, если n – четное и f⁽ⁿ⁾(x_i) > 0;

— максимум, если n – четное и f⁽ⁿ⁾(x_i) < 0.

Эти условия называются достаточными.

Таблица 13.1

Примеры определения экстремумов функции

№ п/п	Функция	Экстремумы	График функции
1	y = f(x) = x²	f’(x) = 2x 2x = 0 x₀ = 0 – точка экстремума или перегиба. f”(x) = 2 → 2 > 0 x₀ = 0 – точка минимума.
2	y = f(x) = x³ – 2x² + x + 1	f’(x) = 3x² — 4x + 1 3x² — 4x + 1 = 0 x₁ = 1/3 и x₂ = 1 – точки экстремума или перегиба. 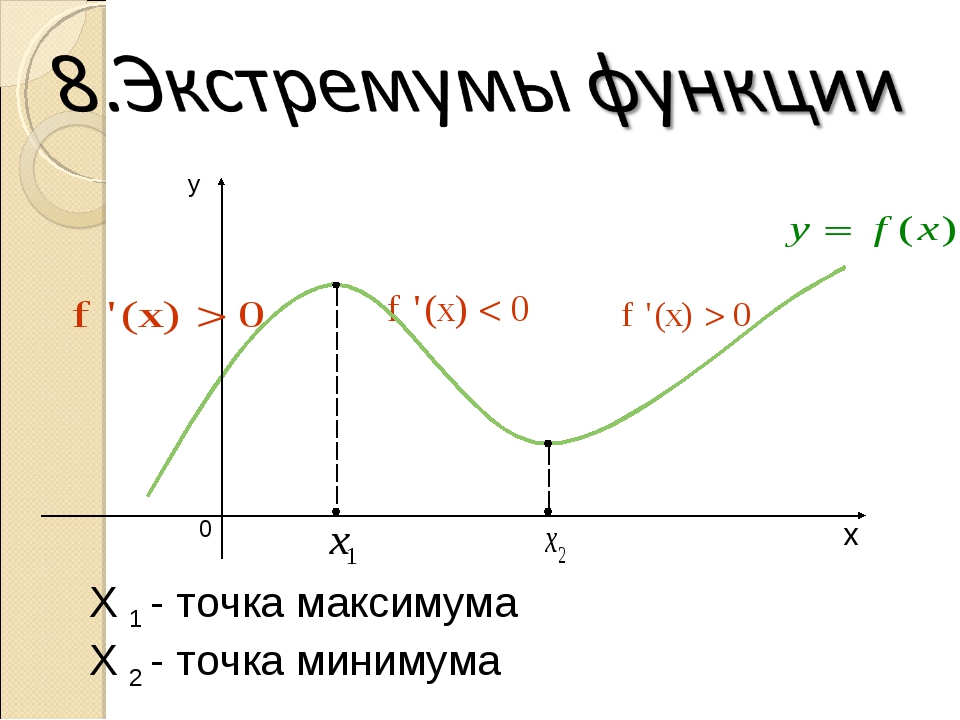f”(x) = 6x — 4 → f”(x₁) = 6 * 1/3 – 4 = -2 f”(x₁) < 0 x₁ = 0 – точка максимума; f”(x₂) = 6 * 1 – 4 = 2 f”(x₂) > 0 x₂ = 0 – точка минимума.
3	y = f(x) = 2x⁴	f’(x) = 8x³ 8x³ = 0 x₀ = 0 – точка экстремума или перегиба. f”(x) = 24x² f”(x₀) = 24 * 0² = 0. f⁽³⁾(x) = 48x f⁽³⁾(x₀)=48 * 0 = 0. f⁽⁴⁾(x) = 48 48 > 0 и n = 4 – четное x₀ = 0 – точка минимума.
4	y = f(x) = 2x³	f’(x) = 6x² 6x² = 0 x₀ = 0 – точка экстремума или перегиба. f”(x) = 12x f”(x₀) = 12 * 0² = 0. f⁽³⁾(x) = 12 n = 3 – нечетное x₀ = 0 – точка перегиба.

При наличии ограничений, помимо точек экстремума проверяют граничные значения функции. Например, для функции из 2-ого примера f(x) = x³ – 2x² + x + 1 требуется найти максимум при ограничениях x ≥ -2 и x ≤ 3. Тогда помимо точек экстремума x₁ = 1/3 (f(x₁) = 1.15) и x₂ = 1 (f(x₂) = 1), проверяем значения функции в точках x₃ = -2 (f(x₃) = -17) и x₄ = 3 (f(x₄) = 13). Таким образом, искомое оптимальное значение функции в точке x₄ = 3.

13.3. Математическое программирование (исследование операций)

Если исходная функция не имеет первой производной (не дифференцируема), невозможно найти корни уравнения f’(x) = 0 или система ограничений имеет сложный вид, то на помощь может прийти математическое программирование.

Наиболее известными и эффективными методами математического программирования являются методы линейного программирования, когда целевая функция и все ограничения являются линейными функциями. Для решения математических моделей других типов предназначены методы дискретного программирования (если все переменные должны принимать только дискретные или целочисленные значения), динамического программирования (когда исходную задачу можно разбить на меньшие подзадачи) и нелинейного программирования (когда целевая функция и/или ограничения являются нелинейными функциями). Перечисленные методы составляют только часть из большого количества самых разнообразных доступных методов исследования операций.

Практически все методы математического программирования не позволяют получить решение в замкнутой форме (в виде формул). Напротив, они порождают вычислительные алгоритмы, которые являются итерационными по своей природе. Это означает, что задача решается последовательно (итерационно), когда на каждом шаге (итерации) получаем решения, постепенно сходящиеся к оптимальному. Итерационная природа алгоритмов обычно приводит к объемным однотипным вычислениям. В этом и заключается причина того, что эти алгоритмы разрабатываются, в основном, для реализации с помощью вычислительной техники [4].

13.4. Имитационное моделирование

Несмотря на впечатляющие достижения математического программирования, многие реальные ситуации невозможно адекватно представить с помощью соответствующих математических моделей. Часто в этом «виновата» определенная «жесткость» математики как языка описания и представления событий и явлений. Но даже если существует возможность формализовать рассматриваемую жизненную ситуацию посредством построения математической модели, полученная на ее основе задача оптимизации может быть слишком сложной для современных алгоритмов решения задач этого класса. Альтернативой математическому моделированию сложных систем может служить имитационное моделирование. Различие между математической и имитационной моделями заключается в том, что в последней отношение между «входом» и «выходом» может быть явно не задано. Вместо явного математического описания взаимоотношения между входными и выходными переменными математической модели, при имитационном моделировании реальная система разбивается на ряд достаточно малых (в функциональном отношении) элементов или модулей. Затем поведение исходной системы имитируется как поведение совокупности этих элементов, определенным образом связанных (путем установки соответствующих взаимосвязей) в единое целое. Вычислительная реализация такой модели начинается с входного элемента, далее проходит по всем элементам, пока не будет достигнут выходной элемент.

Имитационные модели значительно гибче в представлении реальных систем, чем их математические «конкуренты», но за гибкость приходится платить высокими требованиями к потребляемым временным и вычислительным ресурсам. Поэтому реализация некоторых имитационных моделей даже на современных быстрых и высокопроизводительных компьютерах может быть очень медленной [35].

13.5. Эвристический подход к оптимизации

Некоторые модели могут быть такими сложными, что их невозможно решить никакими доступными методами оптимизации. В этом случае остается только эвристический подход: поиск подходящего «хорошего» решения вместо оптимального. Эвристический подход предполагает наличие эмпирических правил, в соответствии с которыми ведется поиск подходящего решения [35].

Вопросы для самопроверки

1. Дайте определение понятиям: «оптимизация» и «экстремум».

2. Назовите отличия глобального максимума от локального и строго от нестрогого.

3. В чем заключается суть классической теории оптимизации?

4. Назовите необходимое условие наличия экстремума.

5. Перечислите основные методы математического программирования.

6. В каком случае применяется эвристический подход к оптимизации?

Экстремумы функции (Лекция №9)

Рассмотрим график непрерывной функции y=f(x), изображенной на рисунке.

Значение функции в точке x₁ будет больше значений функции во всех соседних точках как слева, так и справа от x₁. В этом случае говорят, что функция имеет в точке x₁ максимум. В точке x₃ функция, очевидно, также имеет максимум. Если рассмотреть точку x₂, то в ней значение функции меньше всех соседних значений. В этом случае говорят, что функция имеет в точке x₂ минимум. Аналогично для точки x₄.

Функция y=f(x) в точке x₀ имеет максимум, если значение функции в этой точке больше, чем ее значения во всех точках некоторого интервала, содержащего точку x₀, т.е. если существует такая окрестность точки x₀, что для всех x≠x₀, принадлежащих этой окрестности, имеет место неравенство f(x)<f(x₀).

Функция y=f(x) имеет минимум в точке x₀, если существует такая окрестность точки x₀, что для всех x≠x₀, принадлежащих этой окрестности, имеет место неравенство f(x)>f(x₀.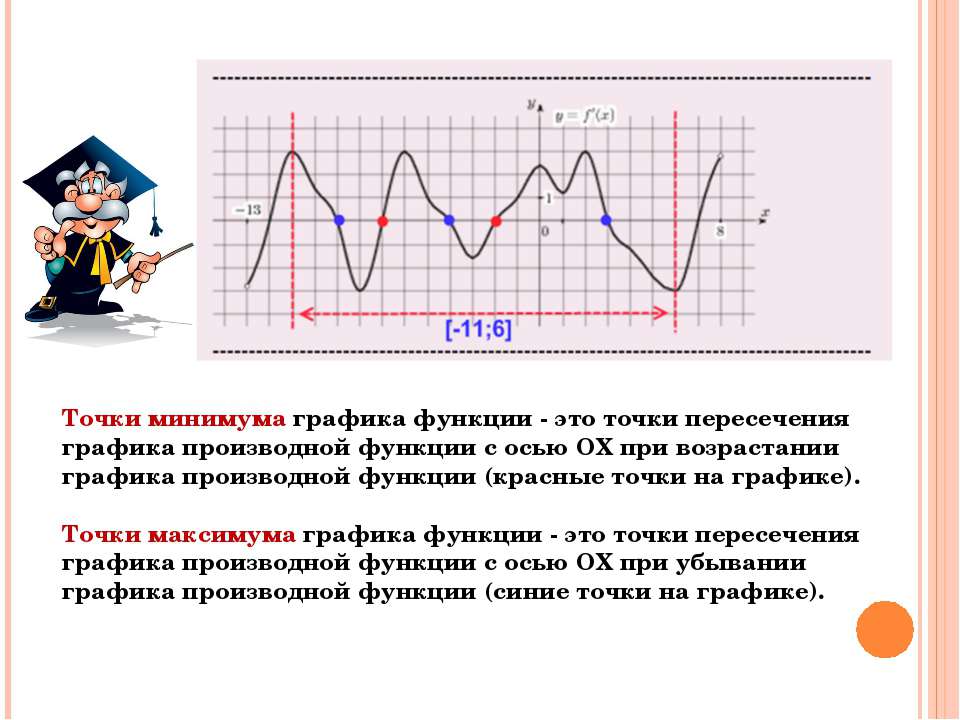

Точки, в которых функция достигает максимума и минимума, называются точками экстремума, а значения функции в этих точках экстремумами функции.

Обратим внимание на то, что функция, определенная на отрезке, может достигать максимума и минимума только в точках, заключенных внутри рассматриваемого отрезка.

Отмети, что если функция имеет в точке максимум, то это не означает, что в этой точке функция имеет наибольшее значение во всей области определения. На рисунке, рассмотренном выше, функция в точке x₁ имеет максимум, хотя есть точки, в которых значения функции больше, чем в точке x₁. В частности, f(x₁) < f(x₄) т.е. минимум функции больше максимума. Из определения максимума следует только, что это самое большое значение функции в точках, достаточно близкихк точке максимума.

Теорема 1. (Необходимое условие существования экстремума. ) Если дифференцируемая функция y=f(x) имеет в точке x= x₀ экстремум, то ее производная в этой точке обращается в нуль.

Доказательство. Пусть для определенности в точке x₀ функция имеет максимум. Тогда при достаточно малых приращениях Δx имеем f(x₀+ Δx)<f(x₀), т.е. Но тогда

Переходя в этих неравенствах к пределу при Δx→ 0 и учитывая, что производная f ‘(x₀) существует, а следовательно предел, стоящий слева, не зависит от того как Δx → 0, получаем: при Δx → 0 – 0 f’(x₀) ≥ 0 а при Δx → 0 + 0 f’(x₀) ≤ 0. Так как f ‘(x₀) определяет число, то эти два неравенства совместны только в том случае, когда f ‘(x₀) = 0.

Доказанная теорема утверждает, что точки максимума и минимума могут находиться только среди тех значений аргумента, при которых производная обращается в нуль.

Мы рассмотрели случай, когда функция во всех точках некоторого отрезка имеет производную. Как же обстоит дело в тех случаях, когда производная не существует? Рассмотрим примеры.

Примеры.

y=|x|.
Функция не имеет производной в точке x=0 (в этой точке график функции не имеет определенной касательной), но в этой точке функция имеет минимум, так как y(0)=0, а при всех x≠ 0y > 0.

Функция не имеет производной при x=0, так как обращается в бесконечность приx=0. Но в этой точке функция имеет максимум.

Функция не имеет производной при x=0, так как при x→0. В этой точке функция не имеет ни максимума, ни минимума. Действительно, f(x)=0 и при x<0f(x)<0, а при x>0f(x)>0.

Таким образом, из приведенных примеров и сформулированной теоремы видно, что функция может иметь экстремум лишь в двух случаях: 1) в точках, где производная существует и равна нулю; 2) в точке, где производная не существует.

Однако, если в некоторой точке x₀ мы знаем, что f ‘(x₀)=0, то отсюда нельзя делать вывод, что в точке x₀ функция имеет экстремум.

Например. .

Но точка x=0 не является точкой экстремума, поскольку слева от этой точки значения функции расположены ниже оси Ox, а справа выше.

Значения аргумента из области определения функции, при которых производная функции обращается в нуль или не существует, называются критическими точками.

Из всего вышесказанного следует, что точки экстремума функции находятся среди критических точек, и, однако, не всякая критическая точка является точкой экстремума. Поэтому, чтобы найти экстремум функции, нужно найти все критические точки функции, а затем каждую из этих точек исследовать отдельно на максимум и минимум. Для этого служит следующая теорема.

Теорема 2. (Достаточное условие существования экстремума.) Пусть функция непрерывна на некотором интервале, содержащем критическую точку x₀, и дифференцируема во всех точках этого интервала (кроме, быть может, самой точки x₀). Если при переходе слева направо через эту точку производная меняет знак с плюса на минус, то в точке x = x₀ функция имеет максимум. Если же при переходе через x₀ слева направо производная меняет знак с минуса на плюс, то функция имеет в этой точке минимум.

Таким образом, если
1. f ‘(x)>0 при x<x₀ и f ‘(x)<0 при x> x₀, то x₀ – точка максимума;
2. при x<x₀ и f ‘(x)>0 при x> x₀, то x₀ – точка минимума.
Доказательство. Предположим сначала, что при переходе через x₀ производная меняет знак с плюса на минус, т.е. при всех x, близких к точке x₀f ‘(x)>0 для x< x₀, f ‘(x)<0 для x> x₀. Применим теорему Лагранжа к разности f(x) — f(x₀) = f ‘(c)(x- x₀), где c лежит между x и x₀.
1. Пусть x < x₀. Тогда c< x₀ и f ‘(c)>0. Поэтомуf ‘(c)(x- x₀)<0и, следовательно,
  f(x) — f(x₀)<0,т.е. f(x)< f(x₀).
2. Пусть x > x₀. Тогда c> x₀ и f ‘(c)<0. Значитf ‘(c)(x- x₀)<0. Поэтому f(x) — f(x₀)<0,т.е.f(x) < f(x₀).
Таким образом, для всех значений x достаточно близких к x₀f(x) < f(x₀). А это значит, что в точке x₀ функция имеет максимум.

Аналогично доказывается вторая часть теоремы о минимуме.

Проиллюстрируем смысл этой теоремы на рисунке. Пусть f ‘(x₁)=0 и для любых x, достаточно близких к x₁, выполняются неравенства

f ‘(x)<0 при x< x₁, f ‘(x)>0 при x> x₁.

Тогда слева от точки x₁ функция возрастает, а справа убывает, следовательно, при x = x₁ функция переходит от возрастания к убыванию, то есть имеет максимум.

Аналогично можно рассматривать точки x₂ и x₃.

Схематически все вышесказанное можно изобразить на картинке:

Правило исследования функции y=f(x) на экстремум
1. Найти область определения функции f(x).
2. Найти первую производную функции f ‘(x).
3. Определить критические точки, для этого:
  1. найти действительные корни уравнения f ‘(x)=0;
  2. найти все значения x при которых производная f ‘(x) не существует.
4. Определить знак производной слева и справа от критической точки. Так как знак производной остается постоянным между двумя критическими точками, то достаточно определить знак производной в какой-либо одной точке слева и в одной точке справа от критической точки.
5. Вычислить значение функции в точках экстремума.
Примеры. Исследовать функции на минимум и максимум.
1. . Область определения функции D(y)=R.
  Найдем производную заданной функции
  
  Определим критические точки . Производная не существует при х₂= 0. Следовательно, критические точки: 0 и 2/5. Нанесем их на числовую ось и определим знак производной на каждом из полученных промежутков.
2. Критическая точка функции x =3. Точка x= –1 не входит в область определения функции.
НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ ФУНКЦИИ НА ОТРЕЗКЕ

Наибольшим значением функции на отрезке называется самое большое из всех ее значений на этом отрезке, а наименьшим – самое маленькое из всех ее значений.

Рассмотрим функцию y=f(x) непрерывную на отрезке [a, b]. Как известно, такая функция достигает своего наибольшего и наименьшего значений, либо на границе отрезка, либо внутри него. Если наибольшее или наименьшее значение функции достигается во внутренней точке отрезка, то это значение является максимумом или минимумом функции, то есть достигается в критических точках.

Таким образом, получаем следующее правило нахождения наибольшего и наименьшего значений функции на отрезке[a, b]:
1. Найти все критические точки функции в интервале (a, b) и вычислить значения функции в этих точках.
2. Вычислить значения функции на концах отрезка при x = a, x = b.
3. Из всех полученных значений выбрать наибольшее и наименьшее.
Примеры.
1. Найти наибольшее и наименьшее значения функции на отрезке [–2; –0,5].
  Найдем критические точки функции.
  
  Вычислим значения функции в найденной точке и на концах заданного отрезка.
  
  Итак,
2. Найти наибольшее и наименьшее значения функцииy=x-2·ln x на [1; e].
3. Чему равна наименьшая площадь боковой поверхности прямого кругового конуса объема 3π?
  
  По теореме Пифагора
  
  .
  
  Следовательно, .
  
  .
  
  Найдем критические точки функции S: S‘ = 0, т.е.
  
  Покажем, что при найденном значении h функция S_бок достигает минимума.
  
  .
4. Найти радиус основания и высоту цилиндра наибольшего объема, который можно вписать в шар радиусом R.
  
  Пусть r – радиус основания цилиндра, h – высота.
  
  Нам нужно максимизировать объем цилиндра .
  
  Используя условие задачи, найдем связь между r и h. По теореме Пифагора из треугольника ABC следует, что . Отсюда .
  
  , по смыслу задачи 0≤h≤2R.
  
  .
  
  Покажем, что при найденном значении h функция V принимает наибольшее значение.

Локальный экстремум функции.

Примеры

Отыскание локальных максимумов и минимумов не обходится без дифференцирования и является необходимым при исследовании функции и построении ее графика.

Точка называется точкой локального максимума (или минимума) функции , сли существует такой окрестность этой точки, принадлежащий области определения функции, и для всех из этого окрестности выполняется неравенство (или ).

Точки максимума и минимума называются точками экстремума функции, а значения функции в экстремальных точках — ее экстремальными значениями.

НЕОБХОДИМОЕ УСЛОВИЕ ЛОКАЛЬНОГО ЭКСТРЕМУМА:

Если функция имеет в точке локальный экстремум, то либо производная равна нулю , либо не существует.

Точки которые удовлетворяют выписанным выше требованиям называют критическими точками.

Однако в каждой критической точке функция имеет экстремум. Ответ на вопрос: будет критическая точка точкой экстремума дает следующая теорема.

ДОСТАТОЧНОЕ УСЛОВИЕ СУЩЕСТВОВАНИЯ ЭКСТРЕМУМА ФУНКЦИИ

Теорема І. Пусть функция непрерывна в некотором интервале, содержащем критическую точку и дифференцированная во всех точках этого интервала (за исключением, возможно, самой точки ).

Тогда для точки функция имеет максимум, если для аргументов выполняется условие, что производная больше нуля , а для условие — производная меньше нуля .

Если же для производная меньше нуля , а для больше нуля , то для точки функция имеет минимум.

Теорема ІІ. Пусть функция дважды дифференцируема в окрестности точки и производная равна нулю . Тогда в точке функция имеет локальный максимум, если вторая производная меньше нуля и локальный минимум, если наоборот .

Если же вторая производная равна нулю , то точка может и не быть точкой экстремума.

При исследовании функций на экстремумы используют обе теоремы. Первая на практике проще, поскольку не требует нахождения второй производной.

ПРАВИЛА НАХОЖДЕНИЯ ЕКСТРЕМУМОВ (МАКСИМУМОВ И МИНИМУМОВ) С ПОМОЩЬЮ ПЕРВОЙ ПРОИЗВОДНОЙ

1) найти область определения ;

2) найти первую производную ;

3) найти критические точки;

4) исследовать знак производной на интервалах, которые получили от разбиения критическими точками области определения .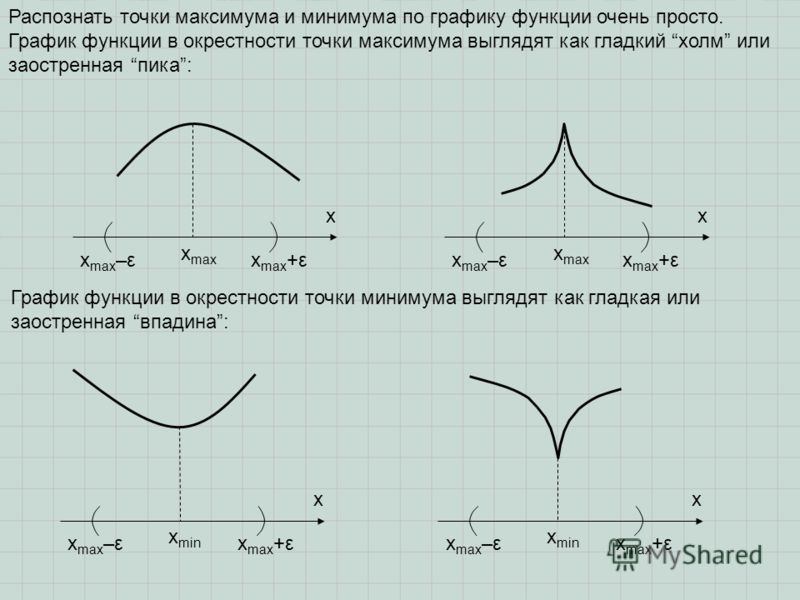

При этом критическая точка является точкой минимума, если при переходе через нее слева направо производная меняет знак с отрицательного на положительный , в противном случаэ является точкой максимума.

Вместо данного правила можно определять вторую производную и исследовать согласно второй теоремы.

5) вычислить значения функции в точках экстремума.

Рассмотрим теперь исследование функции на экстремумы на конкретных примерах.

————————————

Примеры.

Сборник В.Ю. Клепко, В.Л. Голец «Высшая математика в примерах и задачах»

1. (4.53.7)

1) Областью определения будет множество действительных чисел

;

2) Находим производную

3) Вычисляем критические точки

Они разбивают область определения на следующие интервалы

4) Исследуем знак производной на найденных интервалах методом подстановки значений

Таким образом первая точка является точкой минимума, а вторая — точкой максимума.

5) Вычисляем значение функции

——————————

2. (4.53.9)

1) Областью определения будет множество действительных чисел , так корень всегда больше единицы

и функция арктангенс определена на всей действительной оси.

2) Находим производную

3) С условия равенства производной нулю находим критическую точку

Она разбивает область определения на два интервала

4) Определим знак производной в каждой из областей

Таким образом находим, что в критической точке функция принимает минимальное значение.

5) Вычислим экстремум функции

——————————

3. (4.53.13)

1) Функция определена когда знаменатель не превращается в ноль

Из этого следует, что область определения состоит из трех интервалов

2) Вычисляем производную

3) Приравниваем производную к нулю и находим критические точки.

4) Устанавливаем знак производной в каждой из областей, подстановкой соответствующих значений.

Таким образом точка является точкой локального максимума, а локального минимума. В имеем перегиб функции, но о нем будет больше материала в следующих статьях.

5) Находим значение в критических точках

Несмотря на то, что значение функции , первая точка является точкой локального максимума, а дуга — минимума. Не бойтесь, если у Вас выйдут подобные результаты, при определении локальных экстремумов такие ситуации допустимы.

———————————————-

Посмотреть материалы:

Как найти максимальное и минимальное значение функции

КАК НАЙТИ МАКСИМАЛЬНОЕ И МИНИМАЛЬНОЕ ЗНАЧЕНИЕ ФУНКЦИИ

Значение функции в точке максимума называется максимальным значением функции, а значение функции в точке минимума называется минимальным значением функции.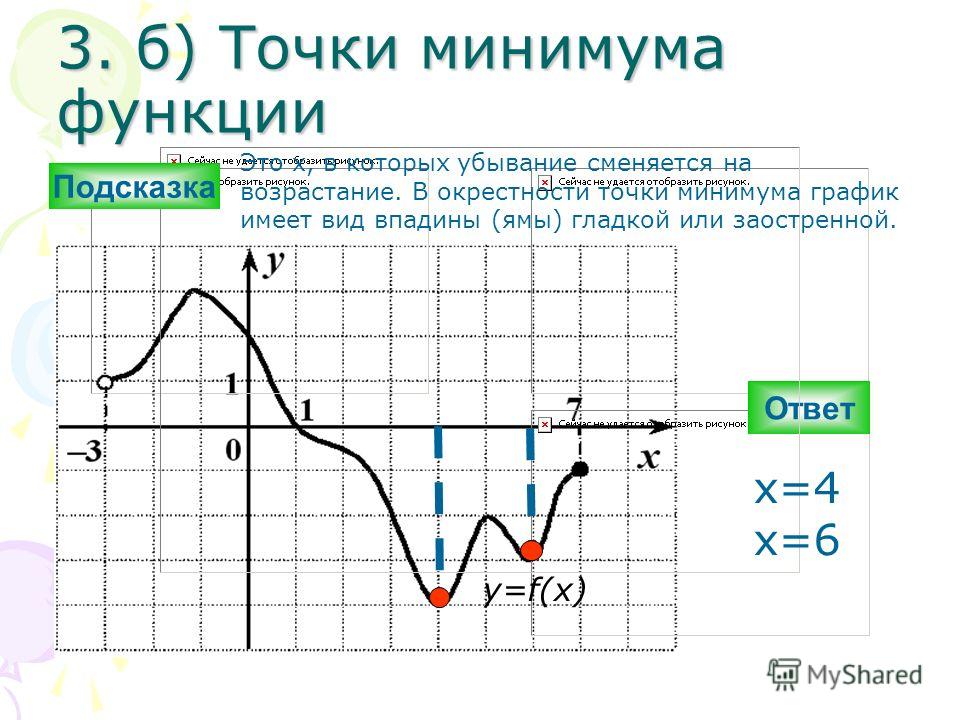

Различить данную функцию.
пусть f ‘(x) = 0 и найдите критические числа
Затем найдите вторую производную f’ ‘(x).
Примените эти критические числа во второй производной.
Функция f (x) максимальна, когда f » (x) <0
Функция f (x) минимальна, когда f » (x)> 0
Чтобы найти максимальное и минимальное значение, нам нужно применить эти значения x в исходной функции.

Примеры

Пример 1:

Определите максимальные значения функций

y = 4x — x ² + 3

Решение:

f (x) = y = 4x — x ² + 3

Сначала найдем первую производную

f ‘(x) = 4 (1) — 2x + 0

f’ (x) = 4 — 2x

Пусть f ‘(x) = 0

4 — 2x = 0

2 (2 — x) = 0

2 — x = 0

x = 2

Теперь найдем вторую производную

f » (x) = 0 — 2 (1 )

f » (x) = -2 <0 Максимум

Чтобы найти максимальное значение, мы должны применить x = 2 в исходной функции.

f (2) = 4 (2) — 2 ² + 3

f (2) = 8-4 + 3

f (2) = 11-4

f (2) = 7

Следовательно, максимальное значение равно 7 при x = 2. Теперь давайте проверим это на графике.

Проверка:

y = 4x — x ² + 3

Данная функция является уравнением параболы.

y = -x² + 4 x + 3

y = — (x² — 4 x — 3)

y = — {x² — 2 (x) (2) + 2² — 2² — 3}

y = — {(x — 2) ² — 4 — 3}

y = — {(x — 2) ² — 7}

y = — (x — 2) ² + 7

y — 7 = — (x — 2) ²

(y — k) = -4a (x — h) ²

Здесь (h, k) равно (2, 7) и парабола открыта вниз.

Пример 2:

Найдите максимальное и минимальное значение функции

2x ³ + 3x ² — 36x + 1

Решение:

Пусть y = f (x) = 2x ³ + 3x ² — 36x + 1

f ‘(x) = 2 (3x ²) + 3 (2x) — 36 (1) + 0

f’ (x) = 6x ² + 6x — 36

установить f ‘(x) = 0

6x² + 6x — 36 = 0

÷ на 6 => x² + x — 6 = 0

(x — 2) (x + 3) = 0

х — 2 = 0

х = 2

х + 3 = 0

х = -3

f ‘(x) = 6x² + 6x — 36

f’ ‘(x) = 6 (2x) + 6 (1) — 0

f’ ‘(x) = 12x + 6

Положим x = 2

f » (2) = 12 (2) + 6

= 24 + 6

f » (2) = 30> 0 Минимум

Чтобы найти минимальное значение, применим x = 2 в исходная функция

f (2) = 2 (2) ³ + 3 (2) ² — 36 (2) + 1

= 2 (8) + 3 (4) — 72 + 1

= 16 + 12-72 + 1

= 29-72

f (2) = -43

Положим x = -3

f » (- 3) = 12 (-3) + 6

= -36 + 6

f » (- 3) = -30> 0 Максимум

Чтобы найти максимальное значение, применим x = -3 в исходной функции

f (-3) = 2 (-3) ³ + 3 (-3) ² — 36 (-3) + 1

= 2 (-27) + 3 (9) + 108 + 1

= -54 + 27 + 109

= — 54 + 136

= 82

Следовательно, минимальное значение -4 3 и максимальное значение 82.

Кроме того, что описано в этом разделе, если вам нужны другие математические данные, воспользуйтесь нашим пользовательским поиском Google здесь.

Если у вас есть отзывы о наших математических материалах, напишите нам:

[email protected]

Мы всегда ценим ваши отзывы.

Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.

ЗАДАЧИ СО СЛОВАМИ

Задачи со словами HCF и LCM

Задачи со словами на простых уравнениях

Задачи со словами на линейных уравнениях

Задачи со словами на квадратных уравнениях

000

Проблемы со словами

Проблемы со словами в поездах

Проблемы со словами по площади и периметру

Проблемы со словами при прямом и обратном изменении

Проблемы со словами по цене за единицу

Проблемы со словом при скорости единицы

Задачи по сравнению ставок

Преобразование обычных единиц Word задачи

Преобразование метрических единиц Word задачи

Word задачи по простому проценту

Word задачи по сложным процентам

Word задачи по типам ngles

Проблемы с дополнительными и дополнительными углами в словах

Проблемы со словами с двойными фактами

Проблемы со словами в тригонометрии

Проблемы со словами в процентах

Проблемы со словами

прибыли и убытки Задачи

Задачи с десятичными словами

Задачи со словами о дробях

Задачи со словами о смешанных фракциях

Одношаговые задачи с уравнениями со словами

Проблемы со словами с линейным неравенством

Задачи

Проблемы со временем и рабочими словами

Задачи со словами на множествах и диаграммах Венна

Проблемы со словами на возрастах

Проблемы со словами в теореме Пифагора

Процент числового слова проблемы

Проблемы со словами при постоянной скорости

Проблемы со словами при средней скорости

Проблемы со словами на сумме углов треугольника 180 градусов

ДРУГИЕ ТЕМЫ

Сокращения прибыли и убытков

Сокращение в процентах

Сокращение в таблице времени

Сокращение времени, скорости и расстояния

Сокращение соотношения и пропорции

Область и диапазон рациональных функций

Область и диапазон рациональных функций функции с отверстиями

График рациональных функций

График рациональных функций с отверстиями

Преобразование повторяющихся десятичных дробей в дроби

Десятичное представление рациональных чисел

видение

Л. Метод CM для решения временных и рабочих задач

Преобразование задач со словами в алгебраические выражения

Остаток при делении 2 в степени 256 на 17

Остаток при делении в степени 17 на 16

Сумма всех трехзначных чисел, делимых на 6

Сумма всех трехзначных чисел, делимых на 7

Сумма всех трехзначных чисел, делимых на 8

Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4

Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами

Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3

Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6

Расчет минимальных и максимальных значений Часть I

Одно из наиболее важных применений исчисления — определение минимума и максимума. значения.Это находит применение в производстве, финансах, машиностроении и множество других отраслей. Прежде чем мы рассмотрим реальный пример, мы должны научиться вычислять такие ценности.
Давайте использовать для нашего первого примера уравнение 2X ² -5X -7 = 0

Это квадратное уравнение с одной переменной. То есть это уравнение формы: ax ² + bx + c = 0
С уравнениями этого типа мы знаем что, когда член «а» положительный, график кривой будет «вогнутым вверх» (U-образный) и, следовательно, уравнение будет иметь минимальное значение, но не максимальное. значение (хорошо — технически максимальное значение бесконечно).Глядя на график мы видим, что точка минимума примерно равна X = 1,5 и Y = -10. Есть ли способ определения минимальной точки без построения графика уравнения и получить точное значение ? Да, есть !
Посмотрите на график. Если значения наклона были рассчитаны для точек на левой стороне кривой, вы могли видеть, что наклон всегда был бы отрицательным , но он становится «менее отрицательный», чем ближе кривая приближается к минимуму (внизу). Если бы наклон был рассчитан вдоль правой стороны кривой, значение будет всегда положительным и значения наклона будут тем больше, чем дальше в стороне от «низа» точки были.
Итак, логично думать, что наклон равен нулю в этой «нижней» точке. и, следовательно, производная в этой точке также равна нулю .
Итак, возьмем производную 2X ² -5X -7 = 0, которая равна:
4X — 5 Когда 4X -5 равно нулю, X = 1.25, что означает, что на данный момент минимум значение существует. Что касается значения Y, мы переходим к исходному уравнению и вводим значение X как 1,25. Y = 2X ² -5X -7 Y = 2 * (1,25) ²-5 * 1,25 -7 Y = -10,125 Итак, в точке X = 1,25, Y = -10,125 существует минимальное значение.
В этом примере мы знали, что получаем минимальное значение, потому что мы изобразили это. Также мы заявили, что «правило» для квадратных уравнений таково: что, когда член «а» положителен, кривая будет «вогнутой вверх».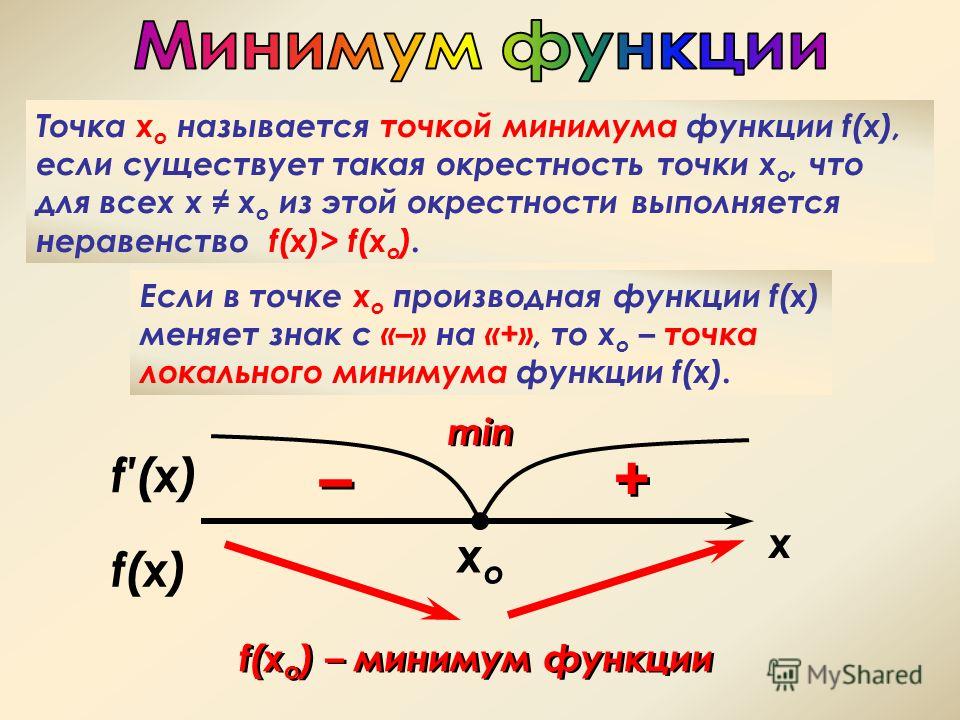 Есть еще третий метод определения того, является ли точка максимальным или минимальным значением.
Если мы возьмем вторую производную , и если это значение будет положительным , то мы будем имея дело с минимальным значением .
В этом примере, взяв производную от производной , мы имеют положительное значение 4, поэтому мы знаем, что это минимум.
Для уравнений типа aX ² + bX + c = 0 удобным инструментом для использования является Калькулятор квадратного уравнения.Это не только вычисляет корни уравнения, он также покажет производную и точку, в которой существует максимум или минимум.
Второй пример, который мы рассмотрим, очень похож на предыдущий, за исключением что он «вогнутый вниз», а не «вогнутый вверх». Если вы думаете, что понимаете концепции, представленные до сих пор, затем перейдите к Части II
Хорошо, давайте рассмотрим это уравнение:
-4X ² + 4X + 13 = 0 Поскольку это квадратное уравнение от одной переменной с отрицательным членом ‘a’, мы знаем, что график кривая будет иметь форму «вогнутой вниз» (в форме ∩) и будет иметь максимальное значение, но не минимальное значение (хорошо, если вы хотите быть техническим, его минимальное значение — отрицательная бесконечность. Теперь ты счастлив?).
Из первого примера мы узнали, что способ вычисления максимума (или минимума) точка — найти точку, в которой производная уравнения равна нулю . Производная этого уравнения: -8X + 4 а когда -8X + 4 = 0, тогда X = 0,5, и именно в той точке, где максимум кривой расположен. Что касается значения Y, мы подставляем 0,5 в исходное уравнение и получаем: Y = -4 * (. 5 * .5) ² + 4 * .5 + 13 Y = 14 Итак, в точке X = 0,5, Y = 14 существует максимальное значение.
Взяв вторую производную от -8X + 4, мы получаем -8. Поскольку это отрицательно, это означает, что мы нашли максимальное значение.
Пришло время перейти ко второй части.
Как вычислить максимумы, минимумы и точки перегиба в функции
В этом уроке я научу вас вычислять максимумов, минимумов и точек перегиба функции, когда у вас нет ее графика.
Относительные крайние значения функции — это максимумы, минимумы и точки перегиба (точка, где функция переходит от вогнутой к выпуклой и наоборот).
Как получить максимумы, минимумы и точки перегиба с производными
Относительные экстремумы (максимумы, минимумы и точки перегиба) могут быть точками, которые делают первую производную функции равной нулю:
Эти точки будут кандидатами на роль максимума, минимума, точки перегиба, но для этого они должны соответствовать второму условию, которое я указываю в следующем разделе.
Как узнать, является ли точка максимальной, минимальной или точкой перегиба
После того, как мы получили точки, для которых первая производная функции равна нулю, для каждой точки мы должны проверить следующее:
Если значение второй производной в этой точке больше нуля, то эта точка минимальна:
Если значение второй производной в этой точке меньше нуля, то эта точка является максимальной:
Если вторая производная в этой точке равна нулю, то эта точка является точкой перегиба, если третья производная в этой точке отлична от нуля:
Давайте посмотрим на примере все, что было объяснено до сих пор.
Решенное упражнение по вычислению максимумов, минимумов и точек перегиба
Получим относительные экстремумы следующей функции:
Во-первых, мы собираемся получить возможные относительные экстремумы, получив первую производную функции и приравняв ее к 0.
Первая производная функции:
Мы приравниваем его к нулю, чтобы получить баллы, соответствующие этому условию:
Чтобы решить уравнение, мы ранее упростили его:
Поскольку это уравнение третьей степени, я разбиваю его на множители по правилу Руффини:
Чьи решения:
Это соответствует возможным максимумам, минимумам или точкам перегиба.
Теперь проверим, чему соответствует каждая точка, изучая знак второй производной. Для этого получаем вторую производную функции:
И мы вычисляем значение второй производной для каждого из значений, которые мы только что вычислили и которые делают первую производную равной нулю (x = -2, x = -1 и x = 1).
Начнем с вычисления значения второй производной для x = -2:
Результат больше нуля, поэтому в x = -2 есть минимум:
Мы вычислили значение f ”(x) для x = -1:
Результат меньше нуля, поэтому в x = -1 есть максимум
И, наконец, вычисляем значение второй производной для x = 1:
Чье значение больше нуля, поэтому в x = 1 есть минимум:
При значениях x, полученных при приравнивании первой производной к нулю, у нас не было значения f ”(x), равного нулю, то есть мы не нашли ни одной точки перегиба.
Следовательно, мы собираемся вычислить точки, которые делают вторую производную равной 0:
.
Приравниваем вторую производную к 0:
И решаем уравнение, результат которого:
Эти два значения являются возможными точками перегиба, если они соответствуют третьей производной для этих точек, отличной от нуля.
Вычисляем третью производную функции:
И находим значение третьей производной для x = 0. 2 — 12x + 3 $.
Я знаю, что локальный максимум и локальный минимум указывают наибольшее и наименьшее значение функции …
Фактически, локальный максимум или минимум возникает, соответственно, в точке, где функция достигает своего максимального или минимального значения в открытом интервале.
Определение. Говорят, что функция $ f $ имеет относительный (или локальный ) максимум в точке $ c $ в открытом интервале $ (a, b) $, если $ f (x) \ leq f ( в) $ для каждого $ x \ in (a, b) $.Говорят, что функция $ f $ имеет относительный (или локальный ) минимум в точке $ c $ на открытом интервале $ (a, b) $, если $ f (x) \ geq f (c ) $ для каждого $ x \ in (a, b) $. Относительный максимум или минимум называется относительным экстремумом функции.
Функция не обязательно достигает своего максимального или минимального значения при относительном экстремуме.
Например, функция
$$ g (x) = x + \ frac {1} {x} $$
имеет относительный максимум при $ x = -1 $, поскольку $ g (x) \ leq g (-1) = -2 $ для $ x \ in (- \ infty, 0) $, и относительный минимум при $ x = 1 $, поскольку $ g (x) \ geq g (1) = 2 $ для $ x \ in (0, \ infty) $.Поскольку $ g (-1) g (-1) $, относительный минимум $ x = 1 $ не является абсолютным (глобальным) минимумом функции $ g $.
… Я не понимаю, как найти точки из уравнения.
Относительные экстремумы функции $ f $ возникают в точках, где $ f ‘(x) = 0 $ или $ f’ (x) $ не существует. Точки, в которых $ f ‘(x) = 0 $, называются критическими точками .2 + х — 2) \\ & = 6 (х + 2) (х — 1) \ end {align *}
Поскольку $ f ‘$ — полиномиальная функция, производная определена всюду. Установка производной равной нулю дает критические точки $ x = -2 $ или $ x = 1 $.
Когда производная в интервале положительна, функция увеличивается в этом интервале. Когда производная отрицательна в интервале, функция убывает в этом интервале.
Поскольку производная $ f ‘(x) = 6 (x + 2) (x — 1) $ является квадратичным многочленом, она непрерывна.Таким образом, он может изменить знак только в точке, где он равен нулю. Таким образом, производная может менять знак только в критических точках $ x = -2 $ и $ x = 1 $.
В интервале $ (- \ infty, -2) $, $ f ‘(x) = 6 (x + 2) (x — 1)> 0 $, как вы можете определить, заменив контрольную точку $ -3 $ на $ x $. Следовательно, функция $ f $ возрастает на интервале $ (- \ infty, -2] $.
В интервале $ (- 2, 1) $, $ f ‘(x) <0 $, как вы можете определить, заменив $ x $ контрольной точкой $ 0 $. Следовательно, функция $ f $ убывает на интервале $ [- 2, 1] $.
В интервале $ (1, \ infty) $ $ f ‘(x) = 6 (x + 2) (x — 1)> 0 $, как вы можете определить, заменив контрольную точку $ 2 $ на $ x $. Таким образом, функция $ f $ возрастает на интервале $ [1, \ infty) $.
Выше мы показали, что $ f $ возрастает на $ (- \ infty, -2] $ и убывает на $ [- 2, 1] $. Поскольку функция возрастает слева от $ -2 $, она определена в $ x = -2 $ и уменьшается вправо от $ -2 $, функция имеет относительный максимум при $ x = -2 $.
Выше мы показали, что $ f $ убывает на интервале $ [- 2, 1] $ и растет на $ [1, \ infty) $.Поскольку $ f $ убывает слева от $ 1 $, определено в $ x = 1 $ и увеличивается вправо от $ 1 $, $ f $ имеет относительный минимум при $ x = 1 $.
Мы применили Первый производный тест.
Первый производный тест. Пусть $ f $ — функция, непрерывная на $ [a, b] $ и дифференцируемая на $ (a, b) $, кроме, возможно, точки $ c $.
(a) Если $ f ‘(x)> 0 $ для всех $ x c $, то $ f $ имеет относительный максимум в $ c $.
(b) Если $ f ‘(x) <0 $ для всех $ x 0 $ для всех $ x> c $, то $ f $ имеет относительный минимум в $ c $.
С $$ \ lim_ {x \ to \ infty} f (x) = \ infty $$ и $$ \ lim_ {x \ to — \ infty} f (x) = — \ infty $$ относительные экстремумы не являются абсолютными экстремумами.
Как найти минимальное и максимальное значения функции?
Как найти минимальное и максимальное значения функции?

Максимумы и минимумы
(1) Говорят, что функция f (x) достигает максимума при x = a, если существует окрестность (a — δ, a + δ) такая, что f (x) ⇒ f (x) — f (a) <0 для всех x ∈ (a - δ, a + δ), x ≠ a
В таком случае f (a) называется максимальным значением f (x) при x = a.
(2) Говорят, что функция f (x) достигает минимума при x = a, если существует такое nbd (a — δ, a + δ), что f (x)> f (a) для всех x ∈ (a — δ, a + δ), x ≠ a
⇒ f (x) — f (a)> 0 для всех x ∈ (a — δ, a + δ), x ≠ a
В таком случае f (a) называется минимальным значением f (x) при x = a. Точки, в которых функция достигает максимальных или минимальных значений, называются крайними точками или поворотными точками, а максимальное и минимальное значения f (x) называются экстремальными или экстремальными значениями.
Таким образом, функция достигает экстремального значения при x = a, если f (a) является максимальным или минимальным значением. Следовательно, в крайней точке a, f (x) — f (a) сохраняет один и тот же знак для всех значений x в удаленном nbd элемента a.
Необходимое условие для экстремальных значений
Необходимым условием для того, чтобы f (a) было экстремальным значением функции f (x), является то, что f ’(a) = 0, если он существует.
Примечание:
Этот результат утверждает, что если производная существует, она должна быть равна нулю в крайних точках.Однако функция может достигать экстремального значения в точке, но в которой ее не выводить.
Например, функция f (x) = | x | достигает минимального значения в начале координат, даже если оно не дифференцируется при x = 0.
Это условие является лишь необходимым условием для того, чтобы точка x = a была крайней точкой. Недостаточно , т.е. f ’(a) = 0 не обязательно означает, что x = a является крайней точкой. Есть функции, для которых производные обращаются в нуль в точке, но не имеют там экстремального значения на e.г . f (x) = x ³ при x = 0 не достигает экстремального значения при x = 0 и f ‘(0) = 0.
Геометрически вышеупомянутое условие означает, что касательная к кривой y = f (x) в точке, где максимальная или минимальная ордината параллельна оси x .
Значения x , для которых f ’(x) = 0, называются стационарными значениями или критическими значениями x , а соответствующие значения f (x) называются стационарными или поворотными значениями f (x).
Точки, в которых функция достигает максимума (или минимума), также известны как точки локального максимума (или локального минимума), а соответствующие значения f (x) называются локальными максимальными (или локальными минимальными) значениями.
Достаточные критерии для экстремальных значений (тест производной 1
^st)
Пусть f (x) будет функцией, дифференцируемой при x = a.
Тогда (a) x = a является точкой локального максимума f (x), если
f ‘(a) = 0 и
f’ (a) меняет знак с положительного на отрицательный, когда x проходит через а я.е., f ‘(x)> 0 в каждой точке в левой окрестности (a — δ, a) a и f’ (x) <0 в каждой точке в правой окрестности (a, a + δ ) от до .
(b) x = a — точка локального минимума f (x), если
f ‘(a) = 0 и
f’ (a) меняет знак с отрицательного на положительный при прохождении x через a, , т.е. ., f ‘(x) <0 в каждой точке в левой окрестности (a - δ, a) a и f’ (x)> 0 в каждой точке в правой окрестности (a, a + δ) из a .
(c) Если f ‘(a) = 0, но f’ (a) не меняет знак, то есть имеет тот же знак во всей окрестности a , то a не является ни точкой ни локальный максимум, ни точка локального минимума.
Рабочее правило для определения крайних значений функции f (x)

Если dy / dx меняет знак с положительного на отрицательный, когда x проходит через c ₁, тогда функция достигает локального максимума в точке x = c ₁.Если dy / dx меняет свой знак с отрицательного на положительный, когда x проходит через c ₁, тогда функция достигает локального минимума при x = c ₁. В случае отсутствия смены знака x = c ₁ не является ни точкой локального максимума, ни точкой локального минимума.
Тест производной высшего порядка
Найдите f ’(x) и приравняйте его к нулю. Решите f ’(x) = 0, пусть его корни равны x = a ₁, a ₂… ..
Найдите f’ ’(x) и при x = a ₁;
Если f ’’ (₁) положительно, то f (x) минимально при x = a ₁.
Если f ’’ (₁) отрицательно, то f (x) является максимальным при x = a ₁.
Если f » (a ₁) = 0, перейдите к шагу 3.
Если при x = a ₁, f » (a ₁) = 0, тогда найдите f » ‘(Икс). Если f ’’ ’(a ₁) ≠ 0, то f (x) не является ни максимальным, ни минимальным при x = a ₁.
Если f ’’ ’(a ₁) = 0, найти f ^iv (x).
Если f ^iv (x) равно + ve (минимальное значение)
f ^iv (x) равно — ve (максимальное значение)
Если при x = a ₁, f ^iv (a ₁) = 0, затем найдите f ^v (x) и действуйте аналогично.
Свойства максимумов и минимумов
Максимумы и минимумы возникают попеременно, то есть между двумя максимумами есть один минимум, и наоборот.
Если f (x) → ∞ при x → a или b и f ‘(x) = 0 только для одного значения x (скажем, c) между a и b, то f (c) обязательно является минимальным и наименьшим ценить.
Если f (x) → -∞ при x → a или b, то f (c) обязательно является максимальным и наибольшим значением.
Наибольшее и наименьшее значения функции, определенной на интервале [a, b]
По максимальному (или минимальному) или локальному максимальному (или локальному минимуму) значению функции f (x) в точке c ∈ [a , b] мы имеем в виду наибольшее (или наименьшее) значение в непосредственной окрестности x = c.Это не означает наибольший или абсолютный максимум (или наименьший или абсолютный минимум) f (x) в интервале [a, b].
Функция может иметь несколько локальных максимумов или локальных минимумов в заданном интервале, и даже локальный минимум может быть больше относительного максимума.
Таким образом, локальное максимальное значение не может быть наибольшим (абсолютным максимумом), а локальное минимальное значение может не быть наименьшим (абсолютным минимумом) значением функции в любом заданном интервале.
Однако, если функция f (x) непрерывна на отрезке [a, b], то она достигает абсолютного максимума (абсолютного минимума) в критических точках или в конечных точках интервала [a, b] . Таким образом, чтобы найти абсолютное максимальное (абсолютное минимальное) значение функции, мы выбираем наибольшее и наименьшее среди чисел f (a), f (c ₁), f (c ₂),… .f ( c _n), f (b) где x = c ₁, c ₂,… .., c _n — критические точки.
Максимальные и минимальные проблемы с решениями
1.

Решение:

2.

Решение:

3.

Решение:

4.

Решение:

5.

Решение:

6.

967 Решение: 9

9675
Решение:

8.

Решение:

9.

Решение:

10.

Решение:
67 9.

Решение:
Мин., Макс., Критические точки
Определение кривой вогнутости вверх: f (x) — «вогнутая вверх» при x ₀ тогда и только тогда, когда f ‘(x) увеличивается при x ₀
Определение вогнутой вниз кривой: f (x) — «вогнутая вниз» at x ₀ тогда и только тогда, когда f ‘(x) убывает при x ₀
Тест второй производной: Если существует f » (x) в x ₀ и положительно, тогда f » (x) вогнутая вверх в x ₀.Если f » (x ₀) существует и отрицательна, то f (x) вогнута вниз при x ₀. Если f » (x) не существует или равен нулю, тогда тест не пройден.
Локальный (относительный) экстремум
Определение локальных максимумов: Функция f (x) имеет локальный максимум at x ₀ тогда и только тогда, когда существует некоторый интервал I, содержащий x ₀ такой, что f (x ₀)> = f (x) для всех x в I.
Определение локальных минимумов: Функция f (x) имеет локальный минимум at x ₀ тогда и только тогда, когда существует некоторый интервал I, содержащий x ₀ такой, что f (x ₀) <= f (x) для всех x в I.
Возникновение локальных экстремумов: Все локальные экстремумы возникают в критических точки, но не все критические точки находятся в локальных экстремумах.
Тест первой производной для локальных экстремумов: Если f (x) увеличивается (f ‘(x)> 0) для всех x в некотором интервале (a, x ₀] и f (x) убывает (f ‘(x) <0) для всех x в некоторой интервал [x ₀, b), то f (x) имеет локальный максимум в x ₀. Если f (x) убывает (f ‘(x) <0) для всех x в некотором интервал (a, x ₀] и f (x) увеличивается (f ‘(x) > 0) для всех x в некотором интервале [x ₀, b), то f (x) имеет локальный минимум в x ₀.
Тест второй производной для локальных экстремумов: Если f ‘(x ₀) = 0 и f » (x ₀)> 0, то f (x) имеет локальный минимум при x ₀. Если f ‘(x ₀) = 0 и f » (x ₀) <0, то f (x) имеет локальный максимум при x ₀.
Абсолютные экстремумы
Определение абсолютных максимумов: y ₀ — «абсолютный максимум «f (x) на I тогда и только тогда, когда y ₀> = f (x) для всех х на I.
Определение абсолютных минимумов: y ₀ — «абсолютный минимум «f (x) на I тогда и только тогда, когда y ₀ <= f (x) для всех х на I.
Теорема об экстремальном значении: Если f (x) непрерывна в замкнутом интервале I, то f (x) имеет хотя бы один абсолютный максимум и один абсолютный максимум. минимум в I.
Возникновение абсолютных максимумов: Если f (x) непрерывна в замкнутом интервале I, то абсолютный максимум f (x) в I является максимальным значением функции f (x) на всех локальных максимумах и концах на I.
Возникновение абсолютных минимумов: Если f (x) непрерывна в замкнутом интервале I, то абсолютный минимум f (x) в I является минимальным значением функции f (x) на всех локальных минимумах и концах на I.
Альтернативный метод поиска экстремумов: Если f (x) непрерывно на отрезке I, то абсолютные экстремумы f (x) в I встречаются в критических точках и / или на концах I.
(Это менее конкретная форма вышеперечисленного.)
Определение возрастающей функции: Функция f (x) «увеличивается» в точке x ₀ тогда и только тогда, когда существует интервал I, содержащий x ₀ такой, что f (x ₀)> f (x) для всех x в I слева от x ₀ и f (x ₀) < f (x) для всех x в I справа от x ₀.
Определение убывающей функции: Функция f (x) «убывающая» в точке x ₀ тогда и только тогда, когда существует некоторый интервал I содержащий x ₀ такой, что f (x ₀) 0 и f (x ₀)> f (x) для все x в I справа от x ₀.
Тест первой производной: Если f ‘(x ₀) существует и положительно, то f ‘(x) возрастает при x ₀.Если f ‘(x) существует и отрицательно, то f (x) убывает при x ₀. Если f ‘(x ₀) не существует или равен нулю, тогда тест говорит об ошибке.
Минимумы и максимумы | Блог по математике ∞
Функции имеют области, которые снова и снова перемещаются вверх и вниз. В точках изменения обычно есть очень маленькое плато. Эти плато могут быть максимумами или минимумами (максимальное или минимальное число во множественном числе), в зависимости от того, где они находятся на графике.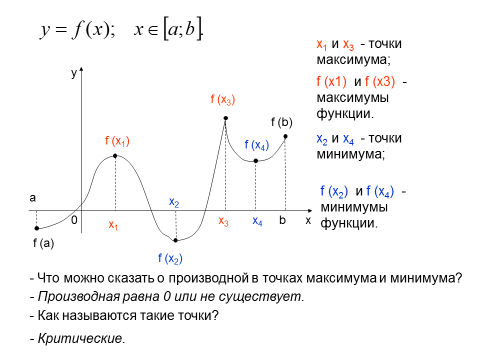 Вместе они составляют крайности. Граф также может иметь локальные и глобальные экстремумы. Локальное значение — это максимум или минимум для небольшого пространства на графике, а глобальное — это максимум или минимум для всего графа, включая части, которые могут не отображаться, потому что вся функция слишком велика для рисования на одном графике.
Как найти максимумы и минимумы
Экстремумы — это точки, в которых функция на мгновение выравнивается. Их расположение на графике легко увидеть, но необходимо найти точные числа, определив, где наклон равен нулю.Когда наклон равен нулю, линия является горизонтальной, даже если она проходит всего на одну точку, прежде чем снова начнет подниматься или опускаться. Чтобы найти, где наклон равен нулю, могут помочь производные.
Наклон и производные
Наклон функции — это просто изменение y, деленное на изменение x. В одной точке наклон будет нулевым, потому что точка не идет ни в каком направлении.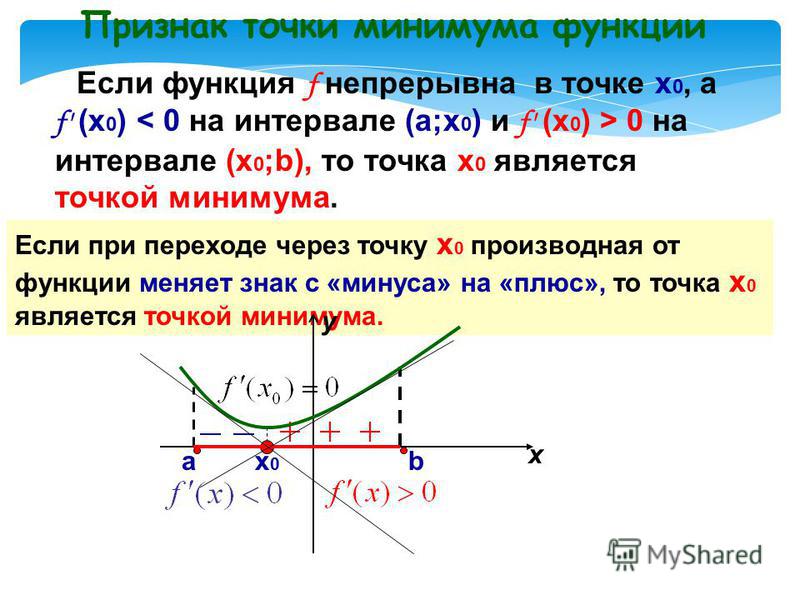 Однако производные можно использовать, чтобы узнать, каков наклон очень небольшой области вокруг точки, что может помочь определить наклон в точке.
Понимание правил деривативов может облегчить определение наклона точки. Как только наклон известен, можно определить, является ли точка максимумом или минимумом, посмотрев, становится ли число меньше или больше. Это делается путем выполнения второй производной, на этот раз крутизны, где наклон функции равен нулю в точке x. Когда вторая производная в x меньше 0, это максимум. Когда он больше нуля, это минимум.
Когда вторая производная равна нулю
Есть много плато с нулевым наклоном на графике, но не все они являются точками максимума или минимума.Важно знать, когда точка — это просто плоская точка на графике (также называемая седловой точкой), а когда — максимум или минимум. Чтобы сказать, необходимо найти первую производную функции, чтобы получить наклон, а затем производную наклона в точке x. Если он выше или ниже нуля, это означает максимум или минимум.