Глупо конечно было брать, что z=\frac{x}{2}, и тут я в ступоре. Вообще идей нет, как найти z
2 лайка
Zhanibek1 (Zhanibek Rassululy)
2
если я правильно понимаю, под z вы имеете ввиду расстояние от вершины основания тетраэдра до точки пересечения высоты тетраэдра с основанием. Попробуйте представить это как нахождение расстояния между вершиной равностороннего треугольника и его центром. Стоит посмотреть на бисектрисы основания.
2 лайка
Mendy (Adilzhan)
3
Для начала, там к сожалению z не равен \frac{x}{2}.
2}{4}\cdot\sqrt{2}=\frac{\sqrt{2}}{\sqrt{3}}a= \frac{\sqrt{6}}{3}a
В самом конце я умножил на \sqrt{3} и числитель и знаменатель.
6 лайков
Vera (Vera Korableva)
4
z=\frac{2x}{3} по правилу подобия треугольников KHA и BKC. Маленький катет относится к гипотенузе как 1:2.
1 лайк
Madsoul (Madiyar Kassymaly)
5
Вообще, попробуй построить куб, и обозначить четыре точки в кубе так, чтобы получился тетраэдр. Так легче будет визуализировать и делать какие-либо расчеты (просто на будущее).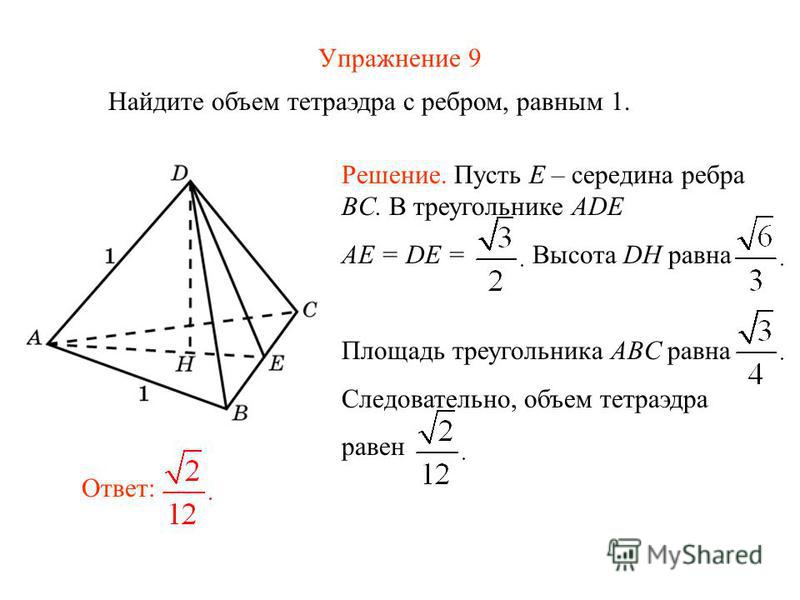
1 лайк
Высота — тетраэдр — Большая Энциклопедия Нефти и Газа, статья, страница 1
Cтраница 1
Высота тетраэдра служит осью конуса, вершина которого совпадает с вершиной тетраэдра, а окружность основания касается его боковых граней. Найти объем конуса, если эта окружность пересекает: 1) остальные высоты тетраэдра; 2) прямые, соединяющие середины скрещивающихся ребер тетраэдра. [1]
Рассмотреть треугольник, образованный высотой тетраэдра, одним из боковых ребер и проекцией этого ребра на плоскость основания, а также подобный ему треугольник, в котором участвует искомый радиус. [2]
Доказать, что если две высоты тетраэдра пересекаются, то и две другие высоты также пересекаются. [3]
Оси третьего порядка совпадают с высотами тетраэдра; кажда из осей второго порядка служит общим перпендикуляром к двум противоположным ребрам тетраэдра. [4]
Объем АК / 3 A5n, где h — высота тетраэдра, опущенная из его вершины О на наклонную грань ABC.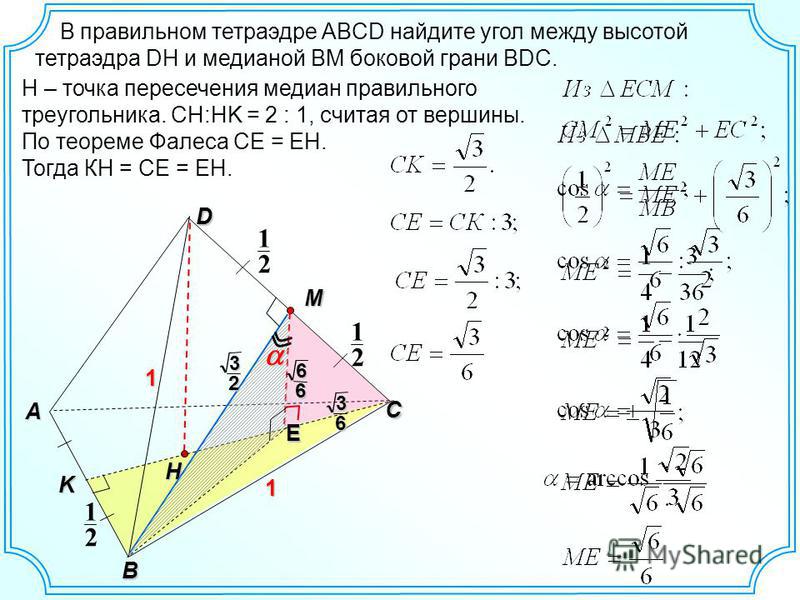
Поделим обе части ( 5) на Д5 и перейдем к пределу, устремив высоту тетраэдра h к нулю.
[5]
Объем АК1 / 3 / гА5, где h — высота тетраэдра, опущенная из его вершины О на наклонную грань ABC. Поделим обе части ( 5) на А5 и перейдем к пределу, устремив высоту тетраэдра h к нулю. [6]
Рассматриваются сечения правильного тетраэдра ABCD, параллельные ребру АВ и
Объем AF1 / 3 / zAS I1, где h — высота тетраэдра, опущенная из его вершины О на наклонную грань ABC. Поделим обе части ( 5) на ASn и перейдем к пределу, устремив высоту тетраэдра h к нулю. [8]
Объем Al / 1 / s / iASn, где / г — высота тетраэдра, опущенная из его вершины О на наклонную грань ABC. Поделим обе части ( 5) на А5П и перейдем к пределу, устремив высоту тетраэдра h к нулю. [9]
В правильном тетраэдре его центр удален от каждой грани на расстояние, равное Я / 4, где Н — высота тетраэдра.
Следовательно, центр вписанной в правильный тетраэдр сферы совпадает с центром тетраэдра.
[10]
В правильном тетраэдре его центр удален от каждой грани на расстояние, равное Я / 4, где Я — высота тетраэдра. Следовательно, центр вписанной в правильный тетраэдр сферы совпадает с центром тетраэдра. [11]
Два правильных тетраэдра ABCD и MNPQ расположены так, что плоскости BCD и NPQ совпадают, вершина М лежат на высоте АС первого тетраэдра, а плоскость MNP проходит через центр грани ABC и середину ребра BD. [12]
Два правильных тетраэдра ABCD и MNPQ расположены так, что плоскости BCD и NPQ совпадают, вершина М лежит на высоте АО первого тетраэдра, а плоскость MNP проходит через центр грани ABC и середину ребра BD. [13]
Два правильных тетраэдра ABCD и MNPQ расположены так, что плоскости BCD и NPQ совпадают, вершина М лежит на высоте АО первого тетраэдра, а плоскость MNP проходит через центр грани ABC и середину ребра BD, Найти отношение длин ребер тетраэдров.
[14]
На тетраэдр АВСМ будут действовать поверхностные силы p dS, и padS, а также массовая сила dk — Fdm pFdV pF j h dS, где dm — масса в объеме тетраэдра dV, h — высота тетраэдра. [15]
Страницы: 1 2 3
Тетраэдр
|
Что такое тетраэдр?
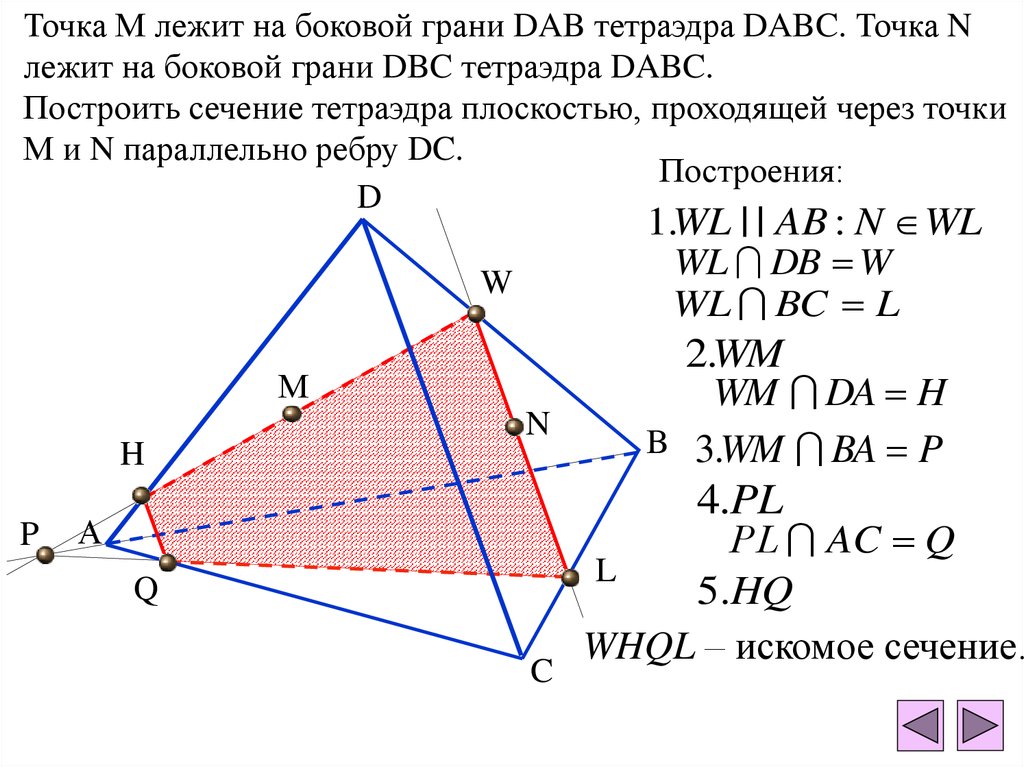Если поднять три треугольника (1), получится тетраэдр
вид сверху (2). Обычно это показано в перспективе (3).Если вы посмотрите на слово тетраэдр (тетраэдр означает «с четырьмя плоскостями»), вы могли бы назвать каждую пирамиду с треугольником основание тетраэдра.
Однако тетраэдр – это прямой правильный треугольник
пирамида на этом сайте.
Высота и площадь бокового треугольника
Четыре равносторонних треугольника образуют тетраэдр.
| … | Выбран треугольник: три высоты пересекаются друг друга в одной точке, как и в каждом треугольнике. Это центр г. треугольник. Высота может быть рассчитана по стороне a как h=sqr(3)/2*a, используя теорема Пифагора. |
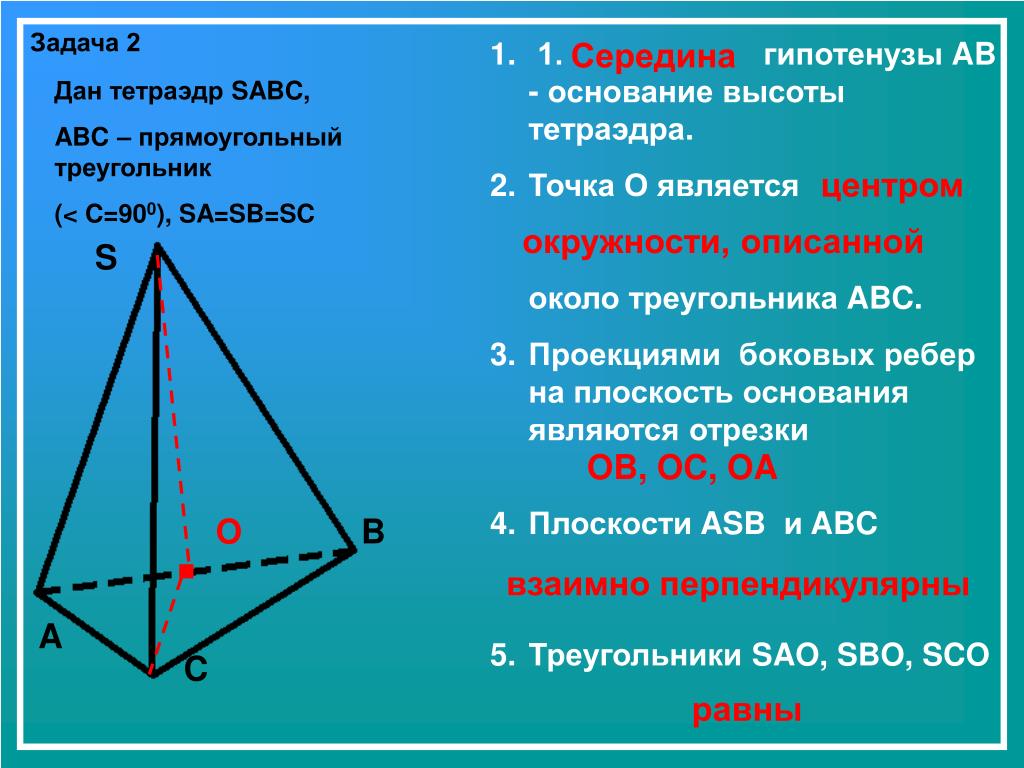
Площадь треугольника равна A=sqr(3)/4*a².
Пространственная высота
Центр, Ограниченный Сфера и вписанная сфера
| … | Вы получаете две формулы для r и R с помощью
Теорема Пифагора (1) и H=R+r (2): |
Уголок
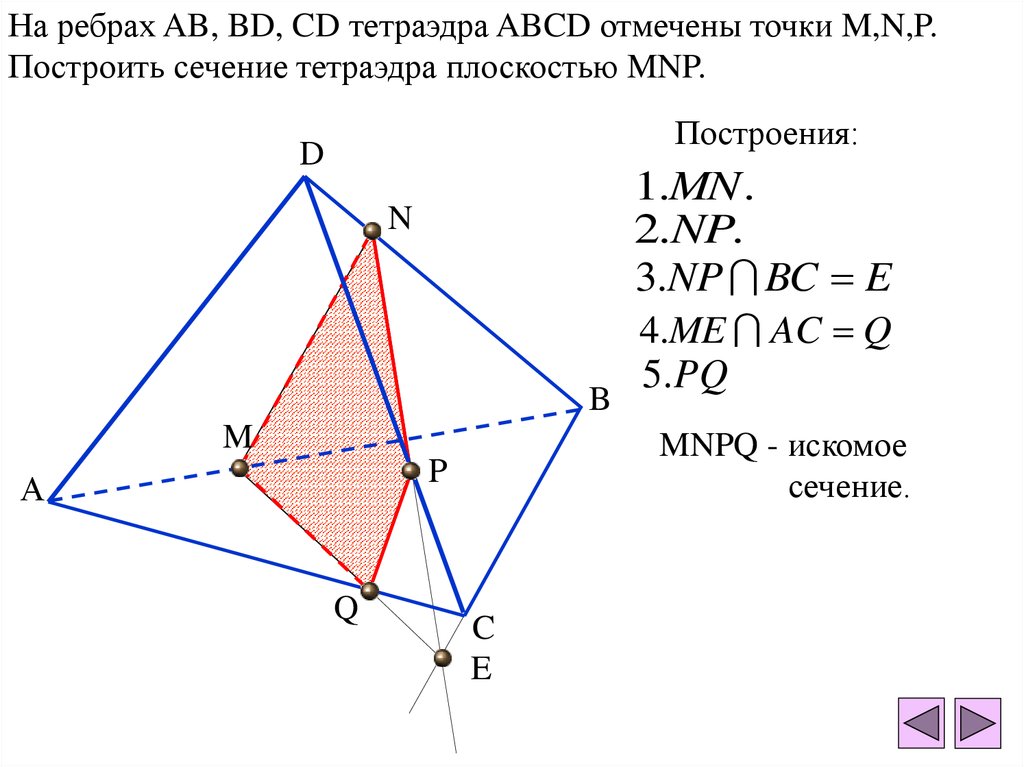. ….. | Угол наклона (краевой угол) между боковыми
треугольник, а основание видно в желтом опорном треугольнике. Есть 70,5°. |
Поверхность
| …….. | Площадь основания и боковых граней образуют поверхность O. Существует O=4*A (треугольник) = sqr(3)a². |
Объем
Если поставить призму (1) с объемом A(треугольник)*H вокруг
тетраэдра и переместите вершину в углы призмы три раза
(2,3,4), вы получите три кривые треугольные пирамиды с одинаковым объемом.
Они заполняют призму (5).
Таким образом, объем треугольной пирамиды равен (1/3)*A(треугольник)*H.
Для тетраэдра V=sqr(2)/12*a³.
Четырехгранные числа топ
| …… | Вы можете построить тетраэдр из слоев сфер.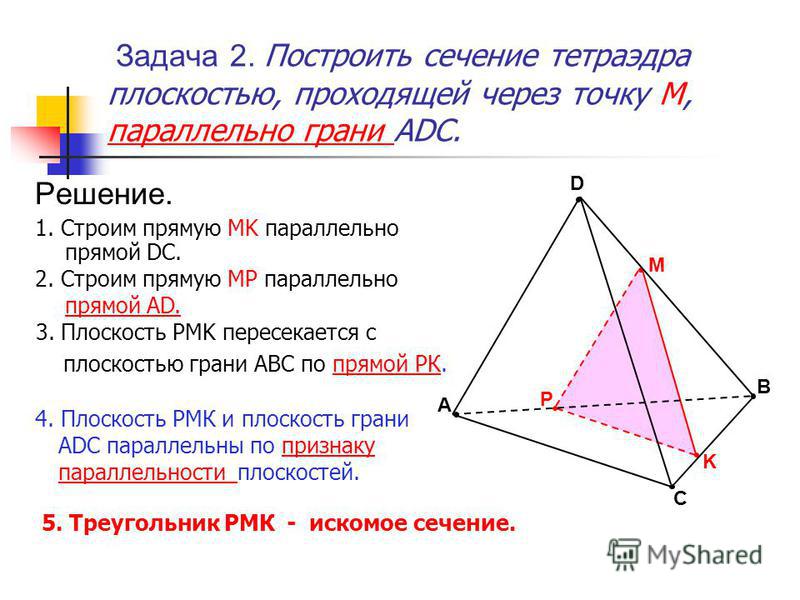 количество сфер в одном слое 1,3,6,10…, обычно n(n+1)/2. Если добавлять сферы слой за слоем, получится тетраэдр числа 1,4,10,20,…, обычно 1+3+6+10+…+n(n+1)/2=n(n+1)(n+2)/6. |
| …… | Если склеить 20 шариков в две группы по четыре и два с шестью, вы получаете известную головоломку: вы должны построить пирамиду из четырех куски. |
Тетраэдр в
топ Cube
Шесть диагоналей граней образуют в кубе тетраэдр.
Если вы знаете 3D-просмотр, вы можете трехмерно
посмотрите на следующие две пары кубов.
Если нарисовать второй тетраэдр и линии пересечения, вы получаете проникновение двух тетраэдров.
Фигура состоит из лицевых диагоналей и соединительных
линии центров боковых квадратов исходного куба.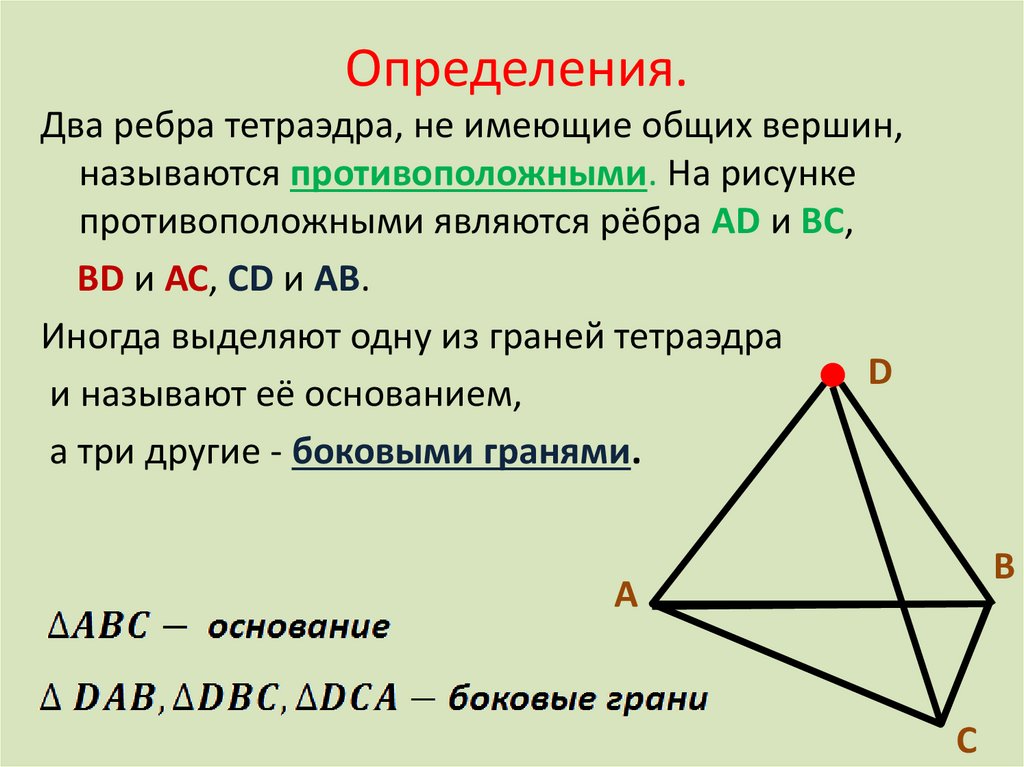
Последний
они образуют октаэдр.
Кольца тетраэдров топ
Можно сделать тетраэдры из бумаги и наклеить четное число
из них в кольцо. Кольцо может постоянно вращаться внутрь или наружу через
центр. Это красивая игрушка. — Эти кольца еще называют калейдоциклами.
Вы найдете больше на моей веб-странице Kaleidocycles.
Тетраэдры в Интернете топ
немецкий
Кристоф Вебер
Был
шляпа dieser Körper mit Kugeln zu tun? (Reuleaux’sche Tetraeder)
Альберт Клюге
Эйн
rotierender Tetraeder как Java-Applet
ФАЗ
Tetraederpackung:
Eins geht noch
Георг Буркхард
Пирамида
де Цестий, Рим (ua)
Герд Мюллер
Платонище
Кёрпер в Stereodarstellung
H.B.Meyer (Polyeder aus Flechtstreifen)
Тетраэдер
LANDRAT-LUCAS-GYMNASIUM Леверкузен
Серпинский
тетраэдер
рур-проводник
Тетраэдер
Ботроп
Википедия
Тетраэдер,
Тетраэдер (Ботроп),
Тетрапод, Тетрадерцаль
Английский
Эрик В.
Вайсштейн (Мир математики)
Тетраэдр
H.B.Meyer (Polyeder aus Flechtstreifen)
Тетраэдр
Джойс Фрост и Пег Кейгл (mathforum)
Ан
Удивительный, заполняющий пространство, неправильный тетраэдр
Википедия
Тетраэдр,
тетрапод
(структура), Тетраэдрический
число
Обратная связь: Адрес электронной почты на моей главной странице
Это страница также доступна на немецком языке.
URL-адрес
моя домашняя страница:
http://www.mathematische-bastelien.de/
© 2001 Юрген Келлер
Как найти высоту тетраэдра?
Геометрия Тригонометрия Тетраэдр 3d высота Высота тетраэдра Пифагор Как найти высоту тетраэдра 3d Пифагор 3d Тригонометрия
Талия М.
спросил 09/09/14 Правильный тетраэдр имеет ребра по 5 см каждое.
Насколько это высоко?
Объясните, пожалуйста, как найти ответ на этот вопрос. Спасибо 🙂
Подписаться І 3
Подробнее
Отчет
2 ответа от опытных наставников
Лучший Новейшие Самый старыйАвтор: Лучшие новыеСамые старые
Эмили Б. ответил 09/09/14
Репетитор
4.7 (136)
Эмили Б. — Учитель математики
Смотрите таких репетиторов
Смотрите таких репетиторов
В правильном тетраэдре высота будет перпендикулярна основанию (и в его центре).
Подумайте о треугольнике, образованном высотой, линией, проведенной от места, где высота встречается с основанием, к одной стороне, а затем высотой этой стороны тетраэдра.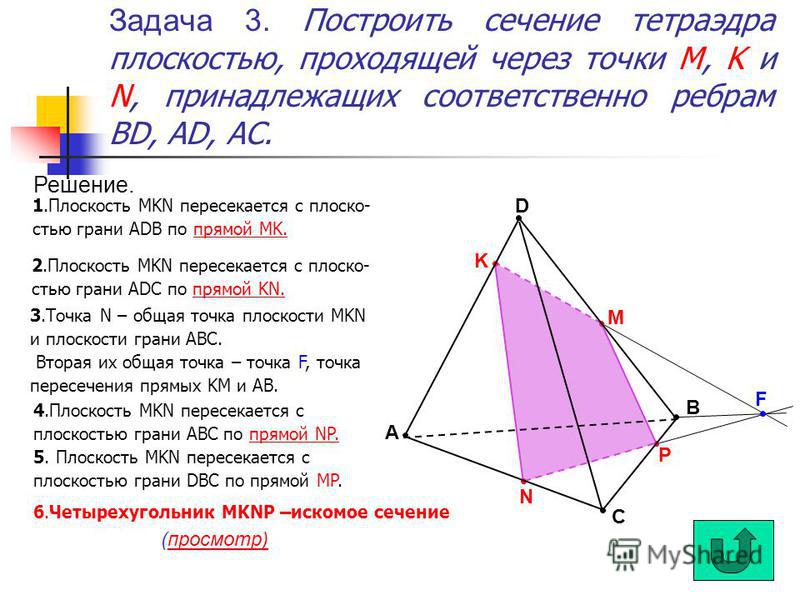
Это прямоугольный треугольник. 92). В этом случае гипотенуза будет равна 5 см, сторона внизу будет 1/2 от 5 см или 2,5 см. Сможете ли вы найти третью сторону? Я бы назвал эту длину L.
Теперь у нас есть одна сторона нашего треугольника, которая включает высоту тетраэдра (гипотенузу).
Сторона внизу должна быть 1/2 высоты стороны или 1/2 L.
Исправление: Сторона внизу не 1/2L — центр находится в центре основания треугольник, но не на 1/2 высоты. Использование 30-60-92=225/16 игнорировать это сейчас
h=15/4 игнорировать — см. исправления Голосовать за 1 Голосовать против Подробнее Отчет Филипп Р.
ответил 09.09.14 Репетитор Новое в Византе Высшее репетиторство по математике и естественным наукам от Brown Univ Grad См. Смотрите таких репетиторов формула: высота h = (√6/3)a, где a = длина ребра h = (5√6)/3 Как мы получаем этот ответ. У нас получится два прямоугольных треугольника. Первый лежит плоско в основании пирамиды с одной ногой = 1/2 ребра и одной ногой, проведенной от середины ребра к центру треугольного основания. Гипотенуза проведена из угла (вершины) в центр. Угол при вершине равен 30 градусов, так что это 30-60-90 треугольник. Гипотенуза равна x = (1/2)a / cos 30 = √3a/3 Нет, мы рисуем еще один прямой угол с гипотенузой вверху как один из катетов, а гипотенуза — это ребро, идущее вверх из того же угла (вершины). Тогда высота пирамиды h равна другому ребру. Using the Pythagorean theorem (√3a/3) 2 + h 2 = a 2 a 2 /3 + h 2 = a 2 ч 2 = 2а 2 /3 ч = √(2а 2 /3) = √2а/√3 = √2√3а / 3 = √3 Итак, в этом примере a = 5, и мы снова имеем (5√6)/3 Голосовать за 1 Голосовать против Подробнее Отчет
таких репетиторов Все еще ищете помощи? Получите правильный ответ, быстро.
Leave A Comment