Найти высоту равнобедренной трапеции если известны основания. Особенности равнобедренной трапеции. Как быть, если известны координаты вершин трапеции
Геометрия – одна из наук, с применением которой на практике человек сталкивается практически ежедневно. Среди многообразия геометрических фигур отдельного внимания заслуживает и трапеция. Она представляет собой выпуклую фигуру с четырьмя сторонами, из которых две параллельны между собой. Последние называются основаниями, а оставшиеся две – боковыми сторонами. Отрезок, перпендикулярный основаниям и определяющий величину промежутка между ними, и будет высотой трапеции. Каким же образом можно вычислить его длину?
Найти высоту произвольной трапеции
Базируясь на исходных данных, определение высоты фигуры возможно несколькими способами.
Известна площадь
Если длина параллельных сторон известна, а также указана площадь фигуры, то для определения искомого перпендикуляра можно воспользоваться следующим соотношением:
S=h*(a+b)/2,
h – искомая величина (высота),
S – площадь фигуры,
a и b – стороны, параллельные друг другу.
Из приведенной формулы следует, что h=2S/(a+b).
Известна величина средней линии
Если среди исходных данных помимо площади трапеции (S) известна, и длина ее линии средины (l), то для вычислений пригодится другая формула. Прежде стоит уточнить, что такое средняя линия для данного вида четырехугольника. Термин определяет часть прямой, соединяющей средины боковых сторон фигуры.
Исходя из свойства трапеции l=(a+b)/2,
l – линия средины,
a, b – стороны-основания четырехугольника.
Поэтому h=2S/(a+b)=S/l.
Известны 4 стороны фигуры
В данном случае поможет теорема Пифагора. Опустив перпендикуляры на большую сторону-основание, воспользуйтесь ею для двух получившихся прямоугольных треугольников. Итоговое выражение будет иметь вид:
h=√c 2 -(((a-b) 2 +c 2 -d 2)/2(a-b)) 2 ,
c и d – 2 другие стороны.
Углы в основании
При наличии данных об углах при основании, воспользуйтесь тригонометрическими функциями.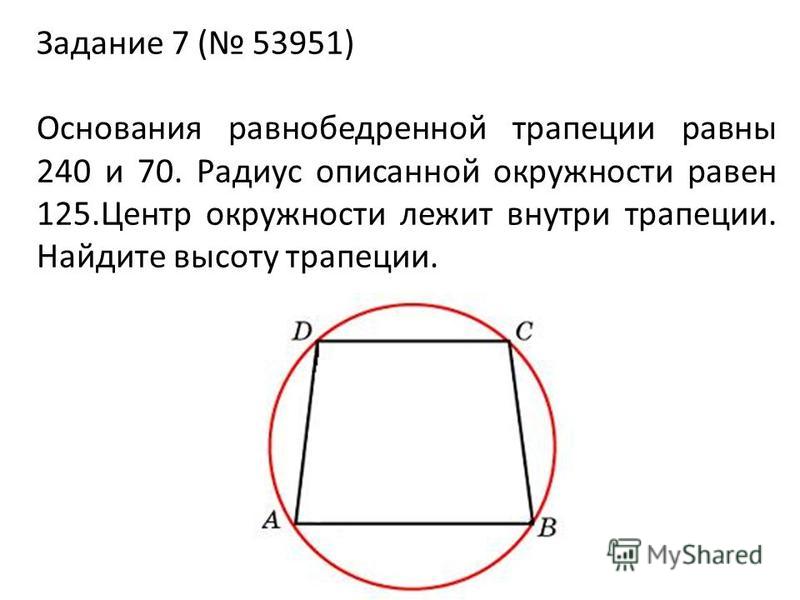
h = c* sinα = d*sinβ,
α и β – углы в основании четырехугольника,
c и d – его боковые стороны.
Диагонали фигуры и углы, которые пересекаясь они образуют
Длина диагонали – длина отрезка, соединяющего противоположные вершины фигуры. Обозначим данные величины символами d1 и d2, а углы между ними γ и φ. Тогда:
h = (d1*d2)/(a+b) sin γ = (d1*d2)/(a+b) sinφ,
h = (d1*d2)/2l sin γ = (d1*d2)/2l sinφ,
a и b – стороны-основания фигуры,
d1 и d2 – диагонали трапеции,
γ и φ – углы между диагоналями.
Высота фигуры и радиус окружности, которая в нее вписана
Как следует из определения такого рода окружности, она касается каждого основания в 1 точке, которые являются частью одной прямой. Поэтому расстояние между ними – диаметр – искомая высота фигуры. А так как диаметр – удвоенный радиус, то:
h = 2 * r,
r – радиус окружности, которую вписали в данную трапецию.
Найти высоту равнобедренной трапеции
- Как и следует из формулировки, отличительной характеристикой равнобедренной трапеции является равенство ее боковых сторон.
 Поэтому для нахождения высоты фигуры воспользуйтесь формулой для определения данной величины в случае, когда известны стороны трапеции.
Поэтому для нахождения высоты фигуры воспользуйтесь формулой для определения данной величины в случае, когда известны стороны трапеции.
Итак, если с = d, то h=√c 2 -(((a-b) 2 +c 2 -d 2)/2(a-b)) 2 = √c 2 -(a-b) 2 /4,
a, b – стороны-основания четырехугольника,
c = d – его боковые стороны.
- При наличии величины углов, образованных двумя сторонами (основанием и боковой), высоту трапеции определяет следующее соотношение:
h = c* sinα,
h = с * tgα *cosα = с * tgα * (b — a)/2c = tgα * (b-a)/2,
α – угол в основании фигуры,
a, b (a
c = d – его боковые стороны.
- Если даны величины диагоналей фигуры, то выражение для нахождения высоты фигуры видоизменится, т.к. d1 = d2:
h = d1 2 /(a+b)*sinγ = d1 2 /(a+b)*sinφ,
h = d1 2 /2*l*sinγ = d1 2 /2*l*sinφ.
Многоликая трапеция… Она может быть произвольной, равнобедренной или прямоугольной. И в каждом случае нужно знать, как найти площадь трапеции. Конечно, проще всего запомнить основные формулы. Но иногда проще воспользоваться той, которая выведена с учетом всех особенностей конкретной геометрической фигуры.
Но иногда проще воспользоваться той, которая выведена с учетом всех особенностей конкретной геометрической фигуры.
Несколько слов о трапеции и ее элементах
Любой четырехугольник, у которого две стороны параллельны, можно назвать трапецией. В общем случае они не равны и называются основаниями. Большее из них — нижнее, а другое — верхнее.
Две другие стороны оказываются боковыми. У произвольной трапеции они имеют различную длину. Если же они равны, то фигура становится равнобедренной.
Если вдруг угол между любой боковой стороной и основанием окажется равным 90 градусам, то трапеция является прямоугольной.
Все эти особенности могут помочь в решении задачи о том, как найти площадь трапеции.
Среди элементов фигуры, которые могут оказаться незаменимыми в решении задач, можно выделить такие:
- высота, то есть отрезок, перпендикулярный обоим основаниям;
- средняя линия, которая имеет своими концами середины боковых сторон.
По какой формуле вычислить площадь, если известны основания и высота?
Это выражение дается основным, потому что чаще всего можно узнать эти величины, даже когда они не даны явно.
Если обозначить основания буквами а 1 и а 2 , высоту — н, то формула для площади будет выглядеть так:
S = ((а 1 + а 2)/2)*н.
Формула, по которой вычисляется площадь, если даны ее высота и средняя линия
Если посмотреть внимательно на предыдущую формулу, то легко заметить, что в ней явно присутствует значение средней линии. А именно, сумма оснований, деленная на два. Пусть средняя линия будет обозначена буквой l, тогда формула для площади станет такой:
S = l * н.
Возможность найти площадь по диагоналям
S = ((д 1 * д 2)/2) * sin &alpha-.
В этом выражении можно легко заменить &alpha- на &beta-. Результат не изменится.
Как узнать площадь, если известны все стороны фигуры?
Бывают и такие ситуации, когда в этой фигуре известны именно стороны. Эта формула получается громоздкой и ее сложно запомнить. Но возможно. Пусть боковые стороны имеют обозначение: в 1 и в 2 , основание а 1 больше, чем а 2 . Тогда формула площади примет такой вид:
S = ((а 1 + а 2) / 2) * &radic- {в 1 2 — [(а 1 — а 2) 2 + в 1 2 — в 2 2) / (2 * (а 1 — а 2))] 2 }.
Способы вычисления площади равнобедренной трапеции
Первый связан с тем, что в нее можно вписать окружность. И, зная ее радиус (он обозначается буквой r), а также угол при основании — &gamma-, можно воспользоваться такой формулой:
S = (4 * r 2) / sin &gamma-.
Последняя общая формула, которая основана на знании всех сторон фигуры, существенно упростится за счет того, что боковые стороны имеют одинаковое значение:
S = ((а 1 + а 2) / 2) * &radic- {в 2 — [(а 1 — а 2) 2 / (2 * (а 1 — а 2))] 2 }.
Методы вычисления площади прямоугольной трапеции
Понятно, что подойдет любой из перечисленных для произвольной фигуры. Но иногда полезно знать об одной особенности такой трапеции. Она заключается в том, что разность квадратов длин диагоналей равна разности, составленной из квадратов оснований.
Часто формулы для трапеции забываются, в то время как выражения для площадей прямоугольника и треугольника помнятся. Тогда можно применить простой способ. Разделить трапецию на две фигуры, если она прямоугольная, или три. Одна точно будет прямоугольником, а вторая, или две оставшиеся, треугольниками. После вычисления площадей этих фигур останется их только сложить.
Это достаточно простой способ того, как найти площадь прямоугольной трапеции.
Как быть, если известны координаты вершин трапеции?
В этом случае потребуется воспользоваться выражением, которое позволяет определить расстояние между точками. Его можно применить три раза: для того, чтобы узнать оба основания и одну высоту.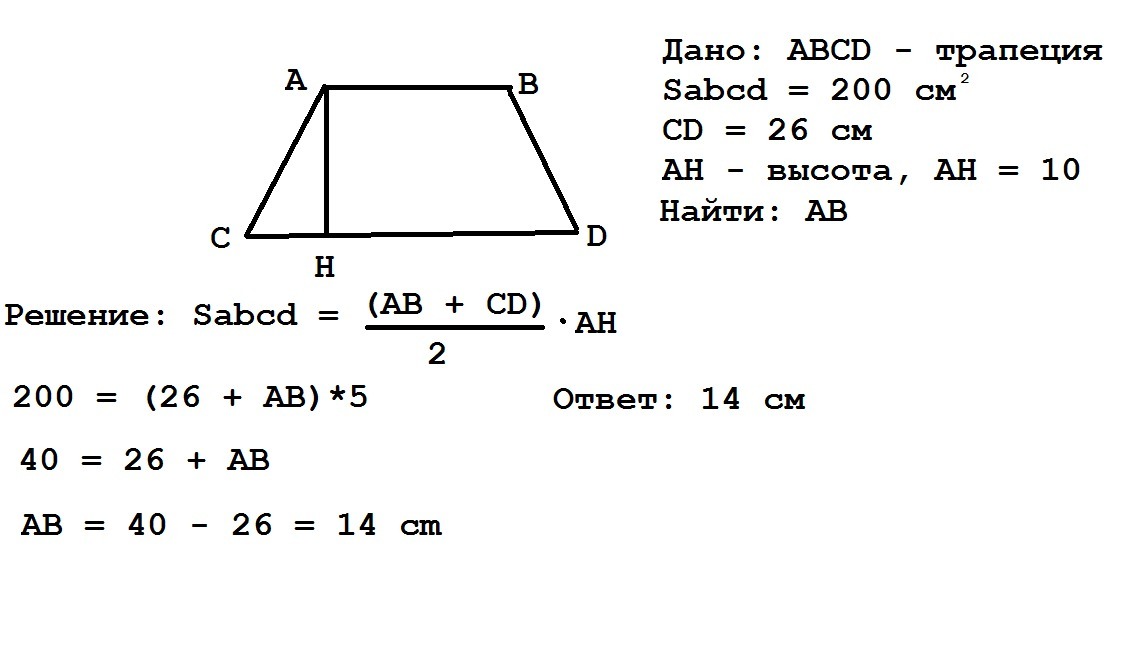 А потом просто применить первую формулу, которая описана немного выше.
А потом просто применить первую формулу, которая описана немного выше.
Для иллюстрации такого метода можно привести такой пример. Даны вершины с координатами А(5- 7), В(8- 7), С(10- 1), Д(1- 1). Нужно узнать площадь фигуры.
До того как найти площадь трапеции, по координатам нужно вычислить длины оснований. Потребуется такая формула:
длина отрезка = &radic-{(разность первых координат точек) 2 + (разность вторых координат точек) 2 }.
Верхнее основание обозначено АВ, значит, его длина будет равна &radic-{(8-5) 2 + (7-7) 2 } = &radic-9 = 3. Нижнее — СД = &radic- {(10-1) 2 + (1-1) 2 } = &radic-81 = 9.
Теперь нужно провести высоту из вершины на основание. Пусть ее начало будет в точке А. Конец отрезка окажется на нижнем основании в точке с координатами (5- 1), пусть это будет точка Н. Длина отрезка АН получится равной &radic-{(5-5) 2 + (7-1) 2 } = &radic-36 = 6.
Осталось только подставить получавшиеся значения в формулу площади трапеции:
S = ((3 + 9) / 2) * 6 = 36.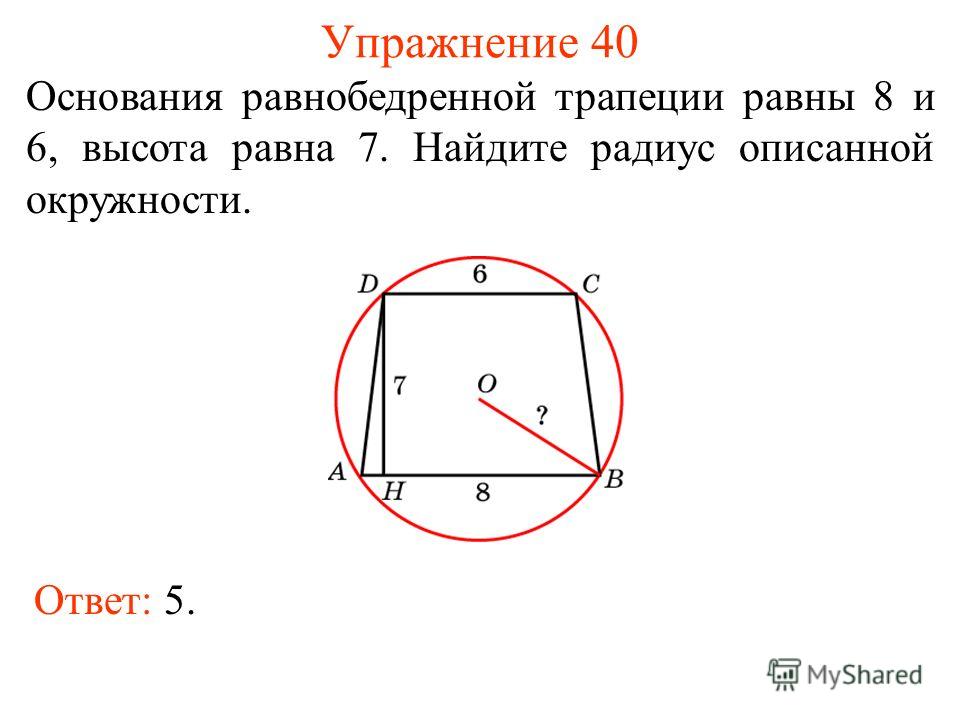
Задача решена без единиц измерения, потому что не указан масштаб координатной сетки. Он может быть как миллиметр, так и метр.
Примеры задач
№ 1. Условие. Известен угол между диагоналями произвольной трапеции, он равен 30 градусам. Меньшая диагональ имеет значение 3 дм, а вторая больше ее в 2 раза. Необходимо посчитать площадь трапеции.
Решение. Для начала нужно узнать длину второй диагонали, потому что без этого не удастся сосчитать ответ. Вычислить ее несложно, 3 * 2 = 6 (дм).
Теперь нужно воспользоваться подходящей формулой для площади:
S = ((3 * 6) / 2) * sin 30º- = 18/2 * ½- = 4,5 (дм 2). Задача решена.
Ответ: площадь трапеции равна 4,5 дм 2 .
№ 2. Условие. В трапеции АВСД основаниями являются отрезки АД и ВС. Точка Е — середина стороны СД. Из нее проведен перпендикуляр к прямой АВ, конец этого отрезка обозначен буквой Н. Известно, что длины АВ и ЕН равны соответственно 5 и 4 см. Нужно вычислить площадь трапеции.
Решение. Для начала нужно сделать чертеж. Поскольку значение перпендикуляра меньше стороны, к которой он проведен, то трапеция будет немного вытянутой вверх. Так ЕН окажется внутри фигуры.
Чтобы отчетливо увидеть ход решения задачи, потребуется выполнить дополнительное построение. А именно, провести прямую, которая будет параллельна стороне АВ. Точки пересечения этой прямой с АД — Р, а с продолжением ВС — Х. Получившаяся фигура ВХРА — параллелограмм. Причем его площадь равна искомой. Это связано с тем, что треугольники, которые получились при дополнительном построении, равны. Это следует из равенства стороны и двух прилежащих к ней углов, один — вертикальный, другой — накрест лежащий.
Найти площадь параллелограмма можно по формуле, которая содержит произведение стороны и высоты, опущенной на нее.
Таким образом, площадь трапеции равна 5 * 4 = 20 см 2 .
Ответ: S = 20 см 2 .
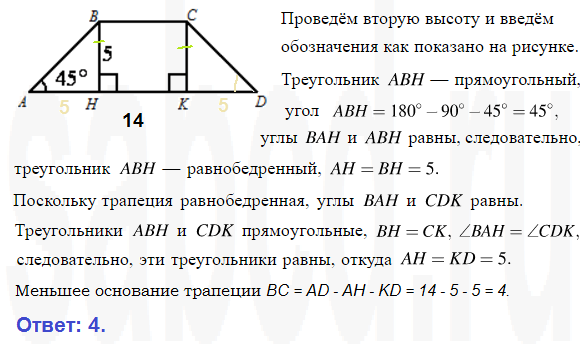
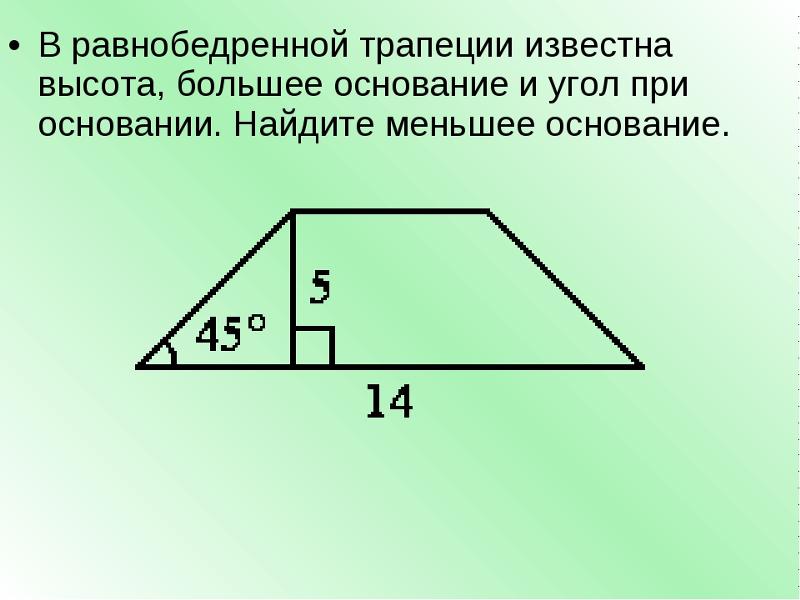
№ 3. Условие. Элементы равнобедренной трапеции имеют такие значения: нижнее основание — 14 см, верхнее — 4 см, острый угол — 45º-. Нужно вычислить ее площадь.
Нужно вычислить ее площадь.
Решение. Пусть меньшее основание имеет обозначение ВС. Высота, проведенная из точки В, будет называться ВН. Поскольку угол 45º-, то треугольник АВН получится прямоугольный и равнобедренный. Значит, АН=ВН. Причем АН очень легко найти. Она равна половине разности оснований. То есть (14 — 4) / 2 = 10 / 2 = 5 (см).
Основания известны, высота сосчитана. Можно пользоваться первой формулой, которая здесь была рассмотрена для произвольной трапеции.
S = ((14 + 4) / 2) * 5 = 18/2 * 5 = 9 * 5 = 45 (см 2).
Ответ: Искомая площадь равна 45 см 2 .
№ 4. Условие. Имеется произвольная трапеция АВСД. На ее боковых сторонах взяты точки О и Е, так что ОЕ параллельна основанию АД. Площадь трапеции АОЕД в пять раз больше, чем у ОВСЕ. Вычислить значение ОЕ, если известны длины оснований.
Решение. Потребуется провести две параллельные АВ прямые: первую через точку С, ее пересечение с ОЕ — точка Т- вторую через Е и точкой пересечения с АД будет М.
Пусть неизвестная ОЕ=х. Высота меньшей трапеции ОВСЕ — н 1 , большей АОЕД — н 2 .
Поскольку площади этих двух трапеций соотносятся как 1 к 5, то можно записать такое равенство:
(х + а 2) * н 1 = 1/5 (х + а 1) * н 2
н 1 /н 2 = (х + а 1) / (5(х + а 2)).
Высоты и стороны треугольников пропорциональны по построению. Поэтому можно записать еще одно равенство:
н 1 /н 2 = (х — а 2) / (а 1 — х).
В двух последних записях в левой части стоят равные величины, значит, можно написать, что (х + а 1) / (5(х + а 2)) равно (х — а 2) / (а 1 — х).
Здесь требуется провести ряд преобразований. Сначала перемножить крест накрест. Появятся скобки, которые укажут на разность квадратов, после применения этой формулы получится короткое уравнение.
В нем нужно раскрыть скобки и перенести все слагаемые с неизвестной «х» в левую сторону, а потом извлечь
Ответ : х = &radic- {(а 1 2 + 5 а 2 2) / 6}.
ДРУГОЕ
Для того чтобы чувствовать себя на уроках геометрии уверенно и успешно решать задачи, недостаточно выучить формулы. Их…
Их…
Математика — школьный предмет, который изучается всеми, независимо от профиля класса. Однако она не всеми любима. Порой…
Математика — это удивительная наука. Однако такая мысль приходит только тогда, когда ее понимаешь. Чтобы этого достичь,…
Школьная программа предусматривает обучение детей геометрии с раннего возраста. Одно из самых базовых знаний этой…
Периметр любого треугольника — это длина линии, ограничивающей фигуру. Чтобы его вычислить, нужно узнать сумму всех…
Куб — удивительная фигура. Он одинаковый со всех сторон. Любая его грань может вмиг стать основанием или боковой. И от…
После изучения темы про прямоугольные треугольники ученики часто выбрасывают из головы всю информацию о них. В том…
Часто ученики возмущенно спрашивают: «Как мне в жизни это пригодится?». На любую тему каждого предмета. Не…
Самый простой многоугольник, который изучается в школе — это треугольник. Он более понятен для учащихся и встречает…
На простой вопрос «Как найти высоту трапеции?» существует несколько ответов, и все потому, что могут быть…
Найти площадь равностороннего треугольника можно по любой формуле для произвольной фигуры данного типа или…
Часто на просторах интернета можно найти насмешки по поводу того, как знания по математике — интегралы, дифференциалы,…
В нашей жизни очень часто приходится сталкиваться с применением геометрии на практике, например, в строительстве. Среди наиболее часто встречающихся геометрических фигур есть и трапеция. И для того, чтобы проект был успешным и красивым, необходим правильный и точный расчет элементов для такой фигуры.
Среди наиболее часто встречающихся геометрических фигур есть и трапеция. И для того, чтобы проект был успешным и красивым, необходим правильный и точный расчет элементов для такой фигуры.
Что собой представляет выпуклый четырехугольник, который имеет пару параллельных сторон, именуемых основаниями трапеции. Но есть еще две другие стороны, соединяющие эти основания. Их называют боковыми. Один из вопросов, касающийся данной фигуры, это: «Как найти высоту трапеции?» Сразу необходимо обратить внимание, что высота — это отрезок, определяющий расстояние от одного основания до другого. Существует несколько способов для определения этого расстояния, в зависимости от известных величин.
1. Известны величины обоих оснований, обозначим их b и k, а так же площадь данной трапеции. Используя известные величины, найти высоту трапеции в этом случае очень легко. Как известно из геометрии, вычисляется, как произведение половины суммы оснований и высоты. Из этой формулы можно легко вывести искомую величину. Для этого необходимо площадь разделить на половину суммы оснований. В виде формул это будет выглядеть так:
Для этого необходимо площадь разделить на половину суммы оснований. В виде формул это будет выглядеть так:
S=((b+k)/2)*h, отсюда h=S/((b+k)/2)=2*S/(b+k)
2. Известна длина средней линии, обозначим ее d, и площадь. Для тех, кто не знает, средней линией называю расстояние между серединами боковых сторон. Как найти высоту трапеции в этом случае? Согласно свойству трапеции, средняя линия соответствует половине суммы оснований, то есть d=(b+k)/2. Опять же прибегаем к формуле площади. Заменив половину суммы оснований на величину средней линии, получим следующее:
Как видим из полученной формулы очень легко вывести высоту. Разделив площадь на величину средней линии, мы найдем искомую величину. Запишем это формулой:
3. Известна длина одной боковой стороны (b) и угол, образующийся между этой стороной и наибольшим основанием. Ответ на вопрос, как найти высоту трапеции, есть и в этом случае. Рассмотрим трапецию ABCD, где AB и CD являются боковыми сторонами, причем AB=b. Наибольшим основанием является AD. Угол, образованный AB и AD обозначим α. Из точки B опустим высоту h на основание AD. Теперь рассмотрим полученный треугольник ABF, который является прямоугольным. Сторона AB является гипотенузой, а BF-катетом. Из свойства прямоугольного треугольника отношение значения катета и значению гипотенузы соответствует синусу угла, противолежащего катету (BF). Поэтому, исходя из вышеизложенного, для вычисления высоты трапеции перемножаем значение известной стороны и синус угла α. В виде формулы это выглядит следующим образом:
Угол, образованный AB и AD обозначим α. Из точки B опустим высоту h на основание AD. Теперь рассмотрим полученный треугольник ABF, который является прямоугольным. Сторона AB является гипотенузой, а BF-катетом. Из свойства прямоугольного треугольника отношение значения катета и значению гипотенузы соответствует синусу угла, противолежащего катету (BF). Поэтому, исходя из вышеизложенного, для вычисления высоты трапеции перемножаем значение известной стороны и синус угла α. В виде формулы это выглядит следующим образом:
4. Аналогично рассматривается случай, если известны размер боковой стороны и угол, обозначим его β, образующийся между этой стороной и меньшим основанием. При решении такой задачи величина угла между известной боковой стороной и проведенной высотой будет 90°- β. Из свойства треугольников — отношение длины катета и гипотенузы соответствует косинусу угла, расположенного между ними. Из этой формулы легко вывести величину высоты:
h = b *cos(β-90°)
5. Как найти высоту трапеции, если известен лишь радиус вписанной окружности? Из определения окружности, она касается одной точкой каждого основания.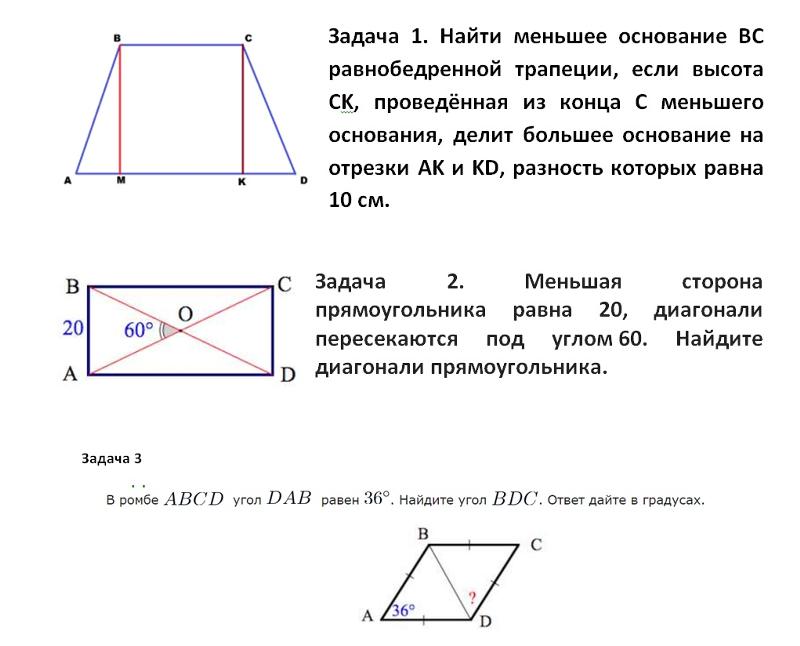 Кроме того, эти точки находятся на одной линии с центром окружности. Из этого следует, что расстояние между ними является диаметром и, в то же время, высотой трапеции. Выглядит так:
Кроме того, эти точки находятся на одной линии с центром окружности. Из этого следует, что расстояние между ними является диаметром и, в то же время, высотой трапеции. Выглядит так:
6. Часто встречаются задачи, в которых необходимо найти высоту равнобедренной трапеции. Напомним, что трапеция, имеющая равные боковые стороны, называется равнобедренной. Как найти высоту равнобедренной трапеции? При перпендикулярных диагоналях высота равна половине суммы оснований.
Но, что делать, если диагонали не перпендикулярны? Рассмотрим равнобедренную трапецию ABCD. Согласно ее свойствам, основания параллельны. Из этого следует, что углы при основаниях также будут равны. Проведем две высоты BF и CM. Исходя из вышесказанного, можно утверждать, что треугольники ABF и DCM равны, то есть AF= DM = (AD — BC)/2 = (b-k)/ 2. Теперь, исходя из условия задачи, определимся с известными величинами, а уж потом находим высоту, учитывая все свойства равнобедренной трапеции.
Как найти высоту трапеции.
В этой статье мы постараемся насколько возможно полно отразить свойства трапеции. В частности, речь пойдет про общие признаки и свойства трапеции, а также про свойства вписанной трапеции и про окружность, вписанную в трапецию. Затронем мы и свойства равнобедренной и прямоугольной трапеции.
Пример решения задачи с использованием рассмотренных свойств поможет вам разложить по местам в голове и лучше запомнить материал.
Трапеция и все-все-все
Для начала коротко вспомним, что такое трапеция и какие еще понятия с ней связаны.
Итак, трапеция – фигура-четырехугольник, две из сторон которой параллельны друг другу (это основания). И две не параллельны – это боковые стороны.
В трапеции может быть опущена высота – перпендикуляр к основаниям. Проведены средняя линия и диагонали. А также из любого угла трапеции возможно провести биссектрису.
Про различные свойства, связанные со всеми эти элементами и их комбинациями, мы сейчас и поговорим.
Свойства диагоналей трапеции
Чтобы было понятнее, пока читаете, набросайте себе на листке трапецию АКМЕ и проведите в ней диагонали.
- Если вы найдете середины каждой из диагоналей (обозначим эти точки Х и Т) и соедините их, получится отрезок. Одно из свойств диагоналей трапеции заключается в том, что отрезок ХТ лежит на средней линии. А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2 .
- Перед нами все та же трапеция АКМЕ. Диагонали пересекаются в точке О. Давайте рассмотрим треугольники АОЕ и МОК, образованные отрезками диагоналей вместе с основаниями трапеции. Эти треугольники – подобные. Коэффициент подобия k треугольников выражается через отношение оснований трапеции: k = АЕ/КМ.
Отношение площадей треугольников АОЕ и МОК описывается коэффициентом k 2 . - Все та же трапеция, те же диагонали, пересекающиеся в точке О. Только в этот раз мы будем рассматривать треугольники, которые отрезки диагоналей образовали совместно с боковыми сторонами трапеции. Площади треугольников АКО и ЕМО являются равновеликими – их площади одинаковые.
- Еще одно свойство трапеции включает в себя построение диагоналей.
 Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Если мы теперь продлим прямую ХТ, то она соединит вместе точку пересечения диагоналей трапеции О, точку, в которой пересекаются продолжения боковых сторон и середины оснований Х и Т. - Через точку пересечения диагоналей проведем отрезок, который соединит основания трапеции (Т лежит на меньшем основании КМ, Х – на большем АЕ). Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЕ .
- А теперь через точку пересечения диагоналей проведем параллельный основаниям трапеции (a и b) отрезок. Точка пересечения разделит его на две равных части. Найти длину отрезка можно по формуле 2ab/(a + b) .
Свойства средней линии трапеции
Среднюю линию проведите в трапеции параллельно ее основаниям.
- Длину средней линии трапеции можно вычислить, если сложить длины оснований и разделить их пополам: m = (a + b)/2 .
- Если провести через оба основания трапецию любой отрезок (высоту, к примеру), средняя линия разделит его на две равных части.
Свойство биссектрисы трапеции
Выберите любой угол трапеции и проведите биссектрису. Возьмем, например, угол КАЕ нашей трапеции АКМЕ. Выполнив построение самостоятельно, вы легко убедитесь – биссектрисой отсекается от основания (или его продолжения на прямой за пределами самой фигуры) отрезок такой же длины, что и боковая сторона.
Свойства углов трапеции
- Какую бы из двух пар прилежащих к боковой стороне углов вы не выбрали, сумма углов в паре всегда составляет 180 0: α + β = 180 0 и γ + δ = 180 0 .
- Соединим середины оснований трапеции отрезком ТХ. Теперь посмотрим на углы при основаниях трапеции. Если сумма углов при любом из них составляет 90 0 , длину отрезка ТХ легко вычислить исходя из разности длин оснований, разделенной пополам: ТХ = (АЕ – КМ)/2 .

- Если через стороны угла трапеции провести параллельные прямые, те разделят стороны угла на пропорциональные отрезки.
Свойства равнобедренной (равнобокой) трапеции
- В равнобедренной трапеции равны углы при любом из оснований.
- Теперь снова постройте трапецию, чтобы проще было представить, о чем речь. Посмотрите внимательно на основание АЕ – вершина противоположного основания М проецируется в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки проекции вершины М и средняя линия равнобедренной трапеции – равны.
- Пару слов о свойстве диагоналей равнобедренной трапеции – их длины равны. А также одинаковы углы наклона этих диагоналей к основанию трапеции.
- Только около равнобедренной трапеции можно описать окружность, поскольку сумма противолежащих углов четырехугольника 180 0 – обязательное условие для этого.
- Из предыдущего пункта следует свойство равнобедренной трапеции – если возле трапеции можно описать окружность, она является равнобедренной.

- Из особенностей равнобедренной трапеции вытекает свойство высоты трапеции: если ее диагонали пересекаются под прямым углом, то длина высоты равна половине суммы оснований: h = (a + b)/2 .
- Снова проведите отрезок ТХ через середины оснований трапеции – в равнобедренной трапеции он является перпендикуляром к основаниям. И одновременно ТХ – ось симметрии равнобедренной трапеции.
- На этот раз опустите на большее основание (обозначим его a) высоту из противолежащей вершины трапеции. Получится два отрезка. Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2 . Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим на два: (a – b)/2 .
Свойства трапеции, вписанной в окружность
Раз уже речь зашла о вписанной в окружность трапеции, остановимся на этом вопросе подробней. В частности на том, где находится центр окружности по отношению к трапеции. Тут тоже рекомендуется не полениться взять карандаш в руки и начертить то, о чем пойдет речь ниже. Так и поймете быстрее, и запомните лучше.
Так и поймете быстрее, и запомните лучше.
- Расположение центра окружности определяется углом наклона диагонали трапеции к ее боковой стороне. Например, диагональ может выходить из вершины трапеции под прямым углом к боковой стороне. В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ).
- Диагональ и боковая сторона могут встречаться и под острым углом – тогда центр окружности оказывается внутри трапеции.
- Центр описанной окружности может оказаться вне пределов трапеции, за большим ее основанием, если между диагональю трапеции и боковой стороной – тупой угол.
- Угол, образованный диагональю и большим основанием трапеции АКМЕ (вписанный угол) составляет половину того центрального угла, который ему соответствует:МАЕ = ½МОЕ .
- Коротко про два способа найти радиус описанной окружности. Способ первый: посмотрите внимательно на свой чертеж – что вы видите? Вы без труда заметите, что диагональ разбивает трапецию на два треугольника.
 Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ . Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.
Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ . Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников. - Способ второй: находим радиус описанной окружности через площадь треугольника, образованного диагональю, боковой стороной и основанием трапеции: R = АМ*МЕ*АЕ/4*S АМЕ .
Свойства трапеции, описанной около окружности
Вписать окружность в трапецию можно, если соблюдается одно условие. Подробней о нем ниже. И вместе эта комбинация фигур имеет ряд интересных свойств.
- Если в трапецию вписана окружность, длину ее средней линии можно без труда найти, сложив длины боковых сторон и разделив полученную сумму пополам: m = (c + d)/2 .
- У трапеции АКМЕ, описанной около окружности, сумма длин оснований равна сумме длин боковых сторон: АК + МЕ = КМ + АЕ .
- Из этого свойства оснований трапеции вытекает обратное утверждение: окружность можно вписать в ту трапецию, сумма оснований которой равна сумме боковых сторон.

- Точка касания окружности с радиусом r, вписанной в трапецию, разбивает боковую сторону на два отрезка, назовем их a и b. Радиус окружности можно вычислить по формуле: r = √ab .
- И еще одно свойство. Чтобы не запутаться, этот пример тоже начертите сами. У нас есть старая-добрая трапеция АКМЕ, описанная около окружности. В ней проведены диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и боковыми сторонами треугольники АОК и ЕОМ – прямоугольные.
Высоты этих треугольников, опущенные на гипотенузы (т.е. боковые стороны трапеции), совпадают с радиусами вписанной окружности. А высота трапеции – совпадает с диаметром вписанной окружности.
Свойства прямоугольной трапеции
Прямоугольной называют трапецию, один из углов которой является прямым. И ее свойства проистекают из этого обстоятельства.
- У прямоугольной трапеции одна из боковых сторон перпендикулярна основаниям.
- Высота и боковая сторона трапеции, прилежащая к прямому углу, равны.
 Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2 ) не только через высоту, но и через боковую сторону, прилежащую к прямому углу.
Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2 ) не только через высоту, но и через боковую сторону, прилежащую к прямому углу. - Для прямоугольной трапеции актуальны уже описанные выше общие свойства диагоналей трапеции.
Доказательства некоторых свойств трапеции
Равенство углов при основании равнобедренной трапеции:
- Вы уже наверное и сами догадались, что тут нам снова потребуется трапеция АКМЕ – начертите равнобедренную трапецию. Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).
Полученный четырехугольник АКМТ – параллелограмм (АК || МТ, КМ || АТ). Поскольку МЕ = КА = МТ, ∆ МТЕ – равнобедренный и МЕТ = МТЕ.
АК || МТ, следовательно МТЕ = КАЕ, МЕТ = МТЕ = КАЕ.
Откуда АКМ = 180 0 — МЕТ = 180 0 — КАЕ = КМЕ.
Что и требовалось доказать.
Теперь на основании свойства равнобедренной трапеции (равенства диагоналей) докажем, что трапеция АКМЕ является равнобедренной :
- Для начала проведем прямую МХ – МХ || КЕ.
 Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).
Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).
∆АМХ – равнобедренный, поскольку АМ = КЕ = МХ, а МАХ = МЕА.
МХ || КЕ, КЕА = МХЕ, поэтому МАЕ = МХЕ.
У нас получилось, что треугольники АКЕ и ЕМА равны между собой, т.к АМ = КЕ и АЕ – общая сторона двух треугольников. А также МАЕ = МХЕ. Можем сделать вывод, что АК = МЕ, а отсюда следует и что трапеция АКМЕ – равнобедренная.
Задача для повторения
Основания трапеции АКМЕ равны 9 см и 21 см, боковая сторона КА, равная 8 см, образует угол 150 0 с меньшим основанием. Требуется найти площадь трапеции.
Решение: Из вершины К опустим высоту к большему основанию трапеции. И начнем рассматривать углы трапеции.
Углы АЕМ и КАН являются односторонними. А это значит, в сумме они дают 180 0 . Поэтому КАН = 30 0 (на основании свойства углов трапеции).
Рассмотрим теперь прямоугольный ∆АНК (полагаю, этот момент очевиден читателям без дополнительных доказательств). Из него найдем высоту трапеции КН – в треугольнике она является катетом, который лежит напротив угла в 30 0 . Поэтому КН = ½АВ = 4 см.
Поэтому КН = ½АВ = 4 см.
Площадь трапеции находим по формуле: S АКМЕ = (КМ + АЕ) * КН/2 = (9 + 21) * 4/2 = 60 см 2 .
Послесловие
Если вы внимательно и вдумчиво изучили эту статью, не поленились с карандашом в руках начертить трапеции для всех приведенных свойств и разобрать их на практике, материал должен был неплохо вами усвоиться.
Конечно, информации тут много, разнообразной и местами даже запутанной: не так уж сложно перепутать свойства описанной трапеции со свойствами вписанной. Но вы сами убедились, что разница огромна.
Теперь у вас есть подробный конспект всех общих свойств трапеции. А также специфических свойств и признаков трапеций равнобедренной и прямоугольной. Им очень удобно пользоваться, чтобы готовиться к контрольным и экзаменам. Попробуйте сами и поделитесь ссылкой с друзьями!
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Геометрия – одна из наук, с применением которой на практике человек сталкивается практически ежедневно. Среди многообразия геометрических фигур отдельного внимания заслуживает и трапеция. Она представляет собой выпуклую фигуру с четырьмя сторонами, из которых две параллельны между собой. Последние называются основаниями, а оставшиеся две – боковыми сторонами. Отрезок, перпендикулярный основаниям и определяющий величину промежутка между ними, и будет высотой трапеции. Каким же образом можно вычислить его длину?
Среди многообразия геометрических фигур отдельного внимания заслуживает и трапеция. Она представляет собой выпуклую фигуру с четырьмя сторонами, из которых две параллельны между собой. Последние называются основаниями, а оставшиеся две – боковыми сторонами. Отрезок, перпендикулярный основаниям и определяющий величину промежутка между ними, и будет высотой трапеции. Каким же образом можно вычислить его длину?
Найти высоту произвольной трапеции
Базируясь на исходных данных, определение высоты фигуры возможно несколькими способами.
Известна площадь
Если длина параллельных сторон известна, а также указана площадь фигуры, то для определения искомого перпендикуляра можно воспользоваться следующим соотношением:
S=h*(a+b)/2,
h – искомая величина (высота),
S – площадь фигуры,
a и b – стороны, параллельные друг другу.
Из приведенной формулы следует, что h=2S/(a+b).
Известна величина средней линии
Если среди исходных данных помимо площади трапеции (S) известна, и длина ее линии средины (l), то для вычислений пригодится другая формула. Прежде стоит уточнить, что такое средняя линия для данного вида четырехугольника. Термин определяет часть прямой, соединяющей средины боковых сторон фигуры.
Прежде стоит уточнить, что такое средняя линия для данного вида четырехугольника. Термин определяет часть прямой, соединяющей средины боковых сторон фигуры.
Исходя из свойства трапеции l=(a+b)/2,
l – линия средины,
a, b – стороны-основания четырехугольника.
Поэтому h=2S/(a+b)=S/l.
Известны 4 стороны фигуры
В данном случае поможет теорема Пифагора. Опустив перпендикуляры на большую сторону-основание, воспользуйтесь ею для двух получившихся прямоугольных треугольников. Итоговое выражение будет иметь вид:
h=√c 2 -(((a-b) 2 +c 2 -d 2)/2(a-b)) 2 ,
c и d – 2 другие стороны.
Углы в основании
При наличии данных об углах при основании, воспользуйтесь тригонометрическими функциями.
h = c* sinα = d*sinβ,
α и β – углы в основании четырехугольника,
c и d – его боковые стороны.
Диагонали фигуры и углы, которые пересекаясь они образуют
Длина диагонали – длина отрезка, соединяющего противоположные вершины фигуры. Обозначим данные величины символами d1 и d2, а углы между ними γ и φ. Тогда:
Обозначим данные величины символами d1 и d2, а углы между ними γ и φ. Тогда:
h = (d1*d2)/(a+b) sin γ = (d1*d2)/(a+b) sinφ,
h = (d1*d2)/2l sin γ = (d1*d2)/2l sinφ,
a и b – стороны-основания фигуры,
d1 и d2 – диагонали трапеции,
γ и φ – углы между диагоналями.
Высота фигуры и радиус окружности, которая в нее вписана
Как следует из определения такого рода окружности, она касается каждого основания в 1 точке, которые являются частью одной прямой. Поэтому расстояние между ними – диаметр – искомая высота фигуры. А так как диаметр – удвоенный радиус, то:
h = 2 * r,
r – радиус окружности, которую вписали в данную трапецию.
Найти высоту равнобедренной трапеции
- Как и следует из формулировки, отличительной характеристикой равнобедренной трапеции является равенство ее боковых сторон. Поэтому для нахождения высоты фигуры воспользуйтесь формулой для определения данной величины в случае, когда известны стороны трапеции.
Итак, если с = d, то h=√c 2 -(((a-b) 2 +c 2 -d 2)/2(a-b)) 2 = √c 2 -(a-b) 2 /4,
a, b – стороны-основания четырехугольника,
c = d – его боковые стороны.
- При наличии величины углов, образованных двумя сторонами (основанием и боковой), высоту трапеции определяет следующее соотношение:
h = c* sinα,
h = с * tgα *cosα = с * tgα * (b – a)/2c = tgα * (b-a)/2,
α – угол в основании фигуры,
a, b (a
c = d – его боковые стороны.
- Если даны величины диагоналей фигуры, то выражение для нахождения высоты фигуры видоизменится, т.к. d1 = d2:
h = d1 2 /(a+b)*sinγ = d1 2 /(a+b)*sinφ,
h = d1 2 /2*l*sinγ = d1 2 /2*l*sinφ.
Трапецией называется такой четырехугольник, две стороны у которого параллельны (это основания трапеции, обозначенные на рисунке a и b), а другие две — нет (на рисунке АД и CB). Высота трапеции — это отрезок h, проведенный перпендикулярно к основаниям.
Как найти высоту трапеции при известных величинах площади трапеции и длин оснований?
Для вычисления площади S трапеции ABCD, воспользуемся формулой:
S = ((a+b) × h)/2.
Здесь отрезки a и b — это основания трапеции, h — это высота трапеции.
Преобразуя эту формулу, можем записать:
Используя эту формулу, получим значение h, если известны величина площади S и величины длин оснований a и b.
Пример
Если известно, что площадь трапеции S равна 50 см², длина основания a составляет 4 см, длина основания b составляет 6 см, то, чтобы найти высоту h, используем формулу:
Подставляем в формулу известные величины.
h = (2 × 50)/(4+6) = 100/10 = 10 см
Ответ: высота трапеции составляет 10 см.
Как находить высоту трапеции, если даны величины площади трапеции и длина средней линии?
Воспользуемся формулой вычисления площади трапеции:
Здесь m — средняя линия, h — высота трапеции.
Если возникает вопрос, как найти высоту трапеции, формула:
h = S/m, будет ответом.
Таким образом, можем найти величину высоты трапеции h, имея известные величины площади S и отрезка средней линии m.
Пример
Известна длина средней линии трапеции m, которая составляет 20 см, и площадь S, которая равна 200 см². Найдем значение величины высоты трапеции h.
Найдем значение величины высоты трапеции h.
Подставив значения S и m, получим:
h = 200/20 = 10 см
Ответ: высота трапеции составляет 10 см
Как найти высоту прямоугольной трапеции?
Если трапеция — это четырехугольник, с двумя параллельными сторонами (основаниями) трапеции. То диагональ — это отрезок, который соединяющий две противоположные вершины углов трапеции (отрезок АС на рисунке). Если трапеция прямоугольная, с помощью диагонали, найдем величину высоты трапеции h.
Прямоугольной трапецией называется такая трапеция, где одна из боковых сторон перпендикулярна основаниям. В этом случае ее длина (АД) совпадает с высотой h.
Итак, рассмотрим прямоугольную трапецию ABCD, где AD — это высота, DC — это основание, AC — это диагональ. Воспользуемся теоремой Пифагора. Квадрат гипотенузы AC прямоугольного треугольника ADC равен сумме квадратов его катетов AB и BC.
Тогда можно записать:
AC² = AD² + DC².
AD — это катет треугольника, боковая сторона трапеции и, в то же время, ее высота. Ведь отрезок АД перпендикулярен основаниям. Его длина составит:
Ведь отрезок АД перпендикулярен основаниям. Его длина составит:
AD = √(AC² — DC²)
Итак, имеем формулу для вычисления высоты трапеции h = AD
Пример
Если длина основания прямоугольной трапеции(DC) равна 14 см, а диагональ (AC) составляет 15 см, для получения значения высоты(AD -боковой стороны) воспользуемся теоремой Пифагора.
Пусть х — это неизвестный катет прямоугольного треугольника(AD), тогда
AC² = AD² + DC² можно записать
15² = 14² + х²,
х = √(15²-14²) = √(225-196) = √29 см
Ответ: высота прямоугольной трапеции (АВ) составит √29 см, что приблизительно составит, 5.385 см
Как найти высоту равнобедренной трапеции?
Равнобедренной трапецией, называют трапецию, у которой длины боковых сторон равны между собой. Прямая, проведенная через середины оснований такой трапеции будет осью симметрии. Частным случаем является трапеция, диагонали которой перпендикулярны друг другу, тогда высота h, будет равна полусумме оснований.
Рассмотрим случай, если диагонали не перпендикулярны друг другу. В равнобочной (равнобедренной) трапеции равны углы при основаниях и длины диагоналей равны. Также известно, что все вершины равнобокой трапеции касаются линии окружности, проведенной вокруг этой трапеции.
Рассмотрим рисунок. ABCD- равнобедренная трапеция. Известно, что основания трапеции параллельны, значит, BC = b параллельно AD = a, сторона AB = CD = c, значит, углы при основаниях соответственно равны, можно записать угол BAQ = CDS = α, и угол ABC = BCD = β. Таким образом, делаем вывод о равенстве треугольника ABQ треугольнику SCD, значит, отрезок
AQ = SD = (AD — BC)/2 = (a — b)/2.
Имея по условию задачи величины оснований a и b, и длину боковой стороны с, найдем высоту трапеции h, равную отрезку BQ.
Рассмотрим прямоугольный треугольник ABQ. ВО — высота трапеции, перпендикулярна основанию AD, значит и отрезку AQ. Сторону AQ треугольника ABQ, найдем, воспользовавшись выведенной нами ранее формулой:
Имея значения двух катетов прямоугольного треугольника, найдем гипотенузу BQ= h.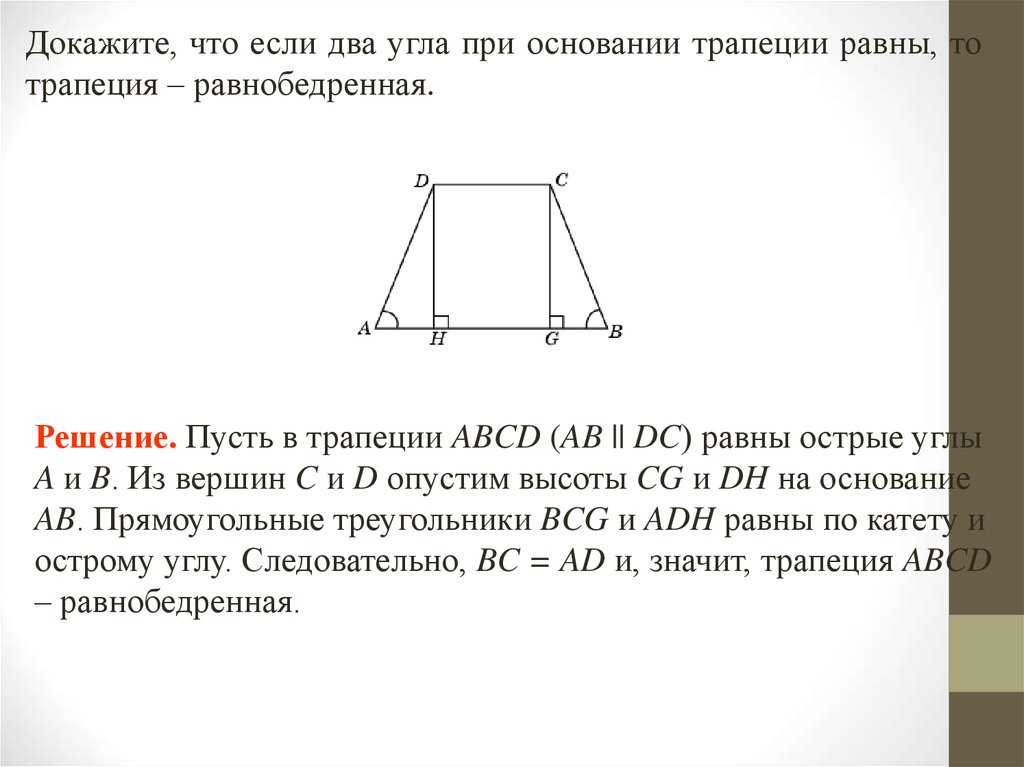 Используем теорему Пифагора.
Используем теорему Пифагора.
AB²= AQ² + BQ²
Подставим данные задачи:
c² = AQ² + h².
Получим формулу для нахождения высоты равнобедренной трапеции:
h = √(c²-AQ²).
Пример
Дана равнобедренная трапеция ABCD, где основание AD = a = 10см, основание BC = b = 4см, а боковая сторона AB = c = 12см. При таких условиях, рассмотрим на примере, как найти трапеции высоту, равнобедренной трапеции АВСД.
Найдем сторону AQ треугольника ABQ, подставив известные данные:
AQ = (a — b)/2 = (10-4)/2=3см.
Теперь подставим значения сторон треугольника в формулу теоремы Пифагора.
h = √(c²- AQ²) = √(12²- 3²) = √135 = 11.6см.
Ответ. Высота h равнобедренной трапеции ABCD составляет 11.6 см.
Калькулятор высоты трапеции
Создано Komal Rafay
Отзыв от Davide Borchia
Последнее обновление: 02 февраля 2023 г.
Содержание:- Формула высоты трапеции
- калькулятор высоты трапеции пезоид
- Часто задаваемые вопросы
Калькулятор высоты трапеции Omni — удобный инструмент, позволяющий определить высоту трапеции, но вы уже знаете это, потому что так говорит название.
Здесь вы не только узнаете, как найти высоту трапеции по формуле высоты трапеции, но и как ее вычислить, не зная площади.
Формула высоты трапеции
Высота трапеции – это расстояние между ее основаниями. А основания — параллельные стороны трапеции.
Существует два различных метода вычисления высоты трапеции, когда площадь известна и когда площадь неизвестна.
Давайте углубимся в детали этих методов и посмотрим на их формулы:
При расчете высоты трапеции с использованием площади необходимо также измерить основания aaa и bbb в сантиметрах.
Еще одна важная вещь, которую нужно знать, это то, что формула высоты трапеции выводится из формулы площади трапеции , а именно:
A=(a+b)2⋅h A = \frac {(a+b)}{ 2\cdot h}A=2⋅h(a+b)
Перемешаем эту формулу, чтобы получить желаемую высоту формулы трапеции.
h=(a+b)2⋅Ah = \frac {(a+b)}{2\cdot A}h=2⋅A(a+b)
где:
- hhh — Высота трапеции;
- ААА — Площадь трапеции;
- ааа — 1ˢᵗ основание трапеции; и
- bbb — 2ⁿᵈ основания трапеции.

Мы знаем, что высота трапеции играет роль в определении площади. В свою очередь площадь поможет определить высоту трапеции.
Но что, если у нас нет площади и нужно определить высоту? Вы можете оказаться в затруднительном положении, но мы вас прикроем.
Есть два способа оценить высоту трапеции без учета площади. В них используются ножки и углы трапеции. Катеты трапеции являются непараллельными сторонами и называются ccc и ddd.
Использование катета c и ∠α
Первая формула использует катет c\text{leg}\ cleg c и ∠α∠α∠α для определения высоты трапеции. Формула:
h=c×sin∠αh = c × \sin{ \angleα}h=c×sin∠αгде:
- hhh — Высота трапеции;
- ccc — Непараллельная ветвь c; и
- sinsinsin — Синусоидальная функция.
Используя катет и ∠δ
Вторая формула использует катет d\text{leg}\ dleg d и ∠δ∠δ∠δ для определения высоты трапеции. Формула:
Формула:
h=d×sin∠δh = d × \sin{\angleδ}h=d×sin∠δгде:
- ddd — Непараллельная ветвь d.
Калькулятор высоты трапеции
Наш калькулятор высоты трапеции представляет собой простой в использовании инструмент, позволяющий рассчитать высоту трапеции тремя различными способами. Независимо от того, знаете ли вы этот район или нет, мы обеспечим вас.
Первый метод использует отрезок и угол. Здесь у вас есть возможность ввести ключ clegc\text{leg}c и ∠α∠α∠α. В результате у вас есть высота трапеции в сантиметрах.
Например, если вы введете 10 см10\ \text{см}10 см в ccc и 75°75°75° в качестве ∠α∠α∠α, ваш рост будет равен 9.6 см9,6\ \text{см}9,6 см.
Второй метод очень похож на первый. Он также использует ногу и другой угол. Здесь legd\text{leg} dlegd используется в сочетании с ∠δ\angleδ∠δ и в результате получается высота трапеции.
Итак, давайте предположим, что вы ввели 22см22см22см в legd\text{leg} dlegd и ∠δ\угол\дельта∠δ равно 95°95°95°, тогда высота будет 21,916 см21,916\ \text{см}21,916 см.
Эти два метода не зависят от области . Теперь, если бы у вас была площадь трапеции, вы могли бы использовать 9264 см2, что дает высоту 3,2 см3,2\ \text{см}3,2 см.
Это должно развеять любые сомнения относительно того, как найти высоту трапеции или как использовать инструмент. Просто попробуйте.
Интересные калькуляторы о трапециях
Трапеции — интересные фигуры, поэтому вокруг них мы создали так много интересных калькуляторов.
Проверьте их!
- Калькулятор трапеций
- Калькулятор площади трапеции
- Калькулятор периметра трапеции
- Калькулятор стороны трапеции
- Калькулятор угла трапеции
- Средняя часть трапеции
- Калькулятор равнобедренной трапеции
- Калькулятор площади равнобедренной трапеции
- Калькулятор правой трапеции
- Калькулятор площади правой трапеции
- Калькулятор площади неправильной трапеции
Часто задаваемые вопросы
Как найти высоту трапеции?
Существует три метода расчета высоты трапеции.
Первые два метода используют непараллельные стороны и углы трапеции для определения ее высоты. Они таковы:
-
h = c × sin ∠α -
ч = d × sin ∠δ
где:
-
h— высота трапеции; -
c— Непараллельная ветвь c; -
d— Непараллельная ветвь d; и -
sin— Функция синуса.
Третий метод использует основание a и b вместе с площадью трапеции для определения ее высоты.
3. h = (a+b) / 2A
где:
-
a— Параллельное основание a; -
б— База параллельная б; и -
A— Площадь трапеции.
Является ли трапеция прямоугольником?
Нет, но каждый прямоугольник является трапецией . Это то же самое, что каждый квадрат является прямоугольником , но каждый прямоугольник не является квадратом .
Трапеция представляет собой четырехугольник, по крайней мере, с парой параллельных сторон. Другая пара сторон может быть или не быть параллельной.
Если 2 пары четырехугольников параллельны, то это прямоугольник.
Параллельные стороны трапеции называются основаниями и обозначаются как a и b . Непараллельные стороны известны как ножки и обозначаются как c и d .
Какова высота трапеции, если c = 15 см и α = 65?
Высота h = 13,595 см если ножка c = 15 см и α = 65° .
Высоту трапеции можно оценить по формуле:
h = c × sin ∠α
где:
-
h— высота трапеции; -
c— Непараллельная ветвь c; и -
sin— Функция синуса.
Komal Rafay
С помощью ножки и α
c (ножка)
Высота (h)
Использование ножки и δ
d (ножка)
Угол4
Высота (h)
Площадь и основания
b2a (основание) 90 )
Площадь (A)
Высота (h)
Посмотреть 23 похожих калькулятора 2d геометрии 📏
ПлощадьПлощадь прямоугольникаПлощадь полумесяца… Еще 20 и периметр в виде равнобедренной трапеции с основаниями 120м, 95м, высота 50м.
Правильный ответ:
S = 5375 м 2o = 318,0776 м
Пошаговое объяснение: )/2⋅ h=(120+95)/2⋅ 50=5375 м2
x=(a−c)/2=(120−95)/2=225=12,5 м b=h3+x2
=502+12,52
≐51,5388 м о=а+с+2⋅ b=120+95+2⋅ 51,5388=318,0776 м
Нашли ошибку или неточность? Не стесняйтесь
написать нам. Спасибо!
Советы по использованию связанных онлайн-калькуляторов
См. также наш калькулятор прямоугольного треугольника.
Расчет равнобедренного треугольника.
См. также наш калькулятор тригонометрического треугольника.
Для решения этой словесной задачи по математике необходимо знать следующие знания:
- алгебра
- выражение переменной из формулы 0009 прямоугольный треугольник
- площадь фигуры
- периметр
- треугольник
- трапеция
Уровень задачи:
- практика для 13-летних
- практика для 14-летних 307 7 1010 9009
- Рассчитать 20643
Рассчитать площадь и периметр участка под застройку в форме равнобедренной трапеции с основанием 120 м, 95 м, а высота 50 м.
- Основания
Основания равнобедренной трапеции ABCD имеют длину 10 см и 6 см. Его плечи образуют угол α = 50˚ с более длинным основанием. Вычислите длину окружности и площадь трапеции ABCD. - Равнобедренная трапеция
Основания равнобедренной трапеции относятся как 5:3. Руки имеют длину 5 см и высоту = 4,8 см. Вычислите длину окружности и площадь трапеции. - Длина окружности 1608
Основания равнобедренной трапеции равны 110 м и 50 м. Расстояние между базами 40м. Вычислите его окружность. - Четырехугольник 24161
Вычислите объем четырехугольника, основанием которого является равнобедренная трапеция с основаниями 10 см и 4 см на расстоянии 6 см друг от друга. Высота призмы 25 см. Как можно вычислить площадь поверхности? - Длина IT
Найдите длину (окружность) равнобедренной трапеции, у которой длины оснований а, с и высота h заданы: а = 8 см, с = 2 см, h = 4 см. - Равнобедренная трапеция
Вычислить площадь равнобедренной трапеции, основания которой относятся как 4:3; ножка b = 13 см и высота = 12 см.
- Что такое
Какова длина окружности равнобедренной трапеции площадью 106,75 см²? Длины сторон находятся в соотношении 1:3:2:1, а основания отстоят друг от друга на 6,1 см. - Трапеция ISO v2
Основания равнобедренной трапеции равны 20 см и 4 см, а периметр 55 см. Чему равна площадь трапеции? - Равнобедренная трапеция
Вычислите длину окружности и площадь равнобедренной трапеции, если известны размеры оснований 8 и 12 см, а размер плеч 5 см. - Длина окружности 66134
Площадь равнобедренной трапеции ABCD равна 36 см². Одно из его оснований в два раза длиннее другого. Высота 4 см. Вычислите длину окружности трапеции. - Четыре призмы
Вопрос №1: Призма имеет размеры a = 2,5 см, b = 100 мм, c = 12 см. Каков его объем? а) 3000 см² б) 300 см² в) 3000 см³ г) 300 см³ Вопрос №2: Основанием призмы является ромб со стороной 30 см и высотой 27 см. Высота т - Рассмотрим 3
Рассмотрим равнобедренную трапецию PQRS. Базы |PQ|=120 мм, |RS|=62 мм и плечо s=48 мм.
Мы рекомендуем вам посмотреть это руководство видео по математической задаче: видео1 видео2

 Поэтому для нахождения высоты фигуры воспользуйтесь формулой для определения данной величины в случае, когда известны стороны трапеции.
Поэтому для нахождения высоты фигуры воспользуйтесь формулой для определения данной величины в случае, когда известны стороны трапеции.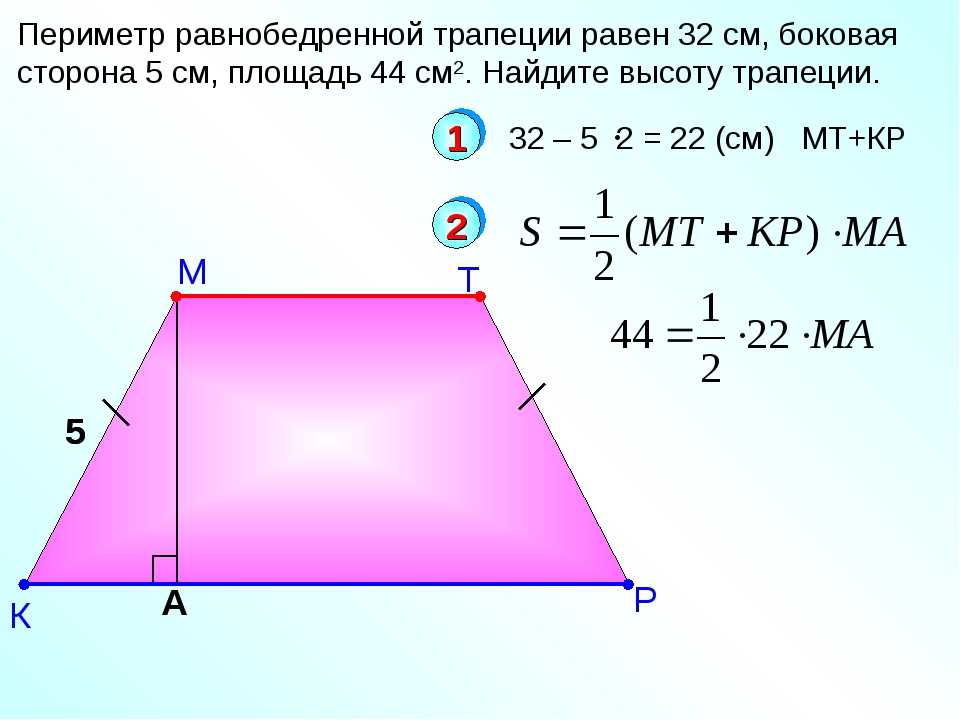 Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.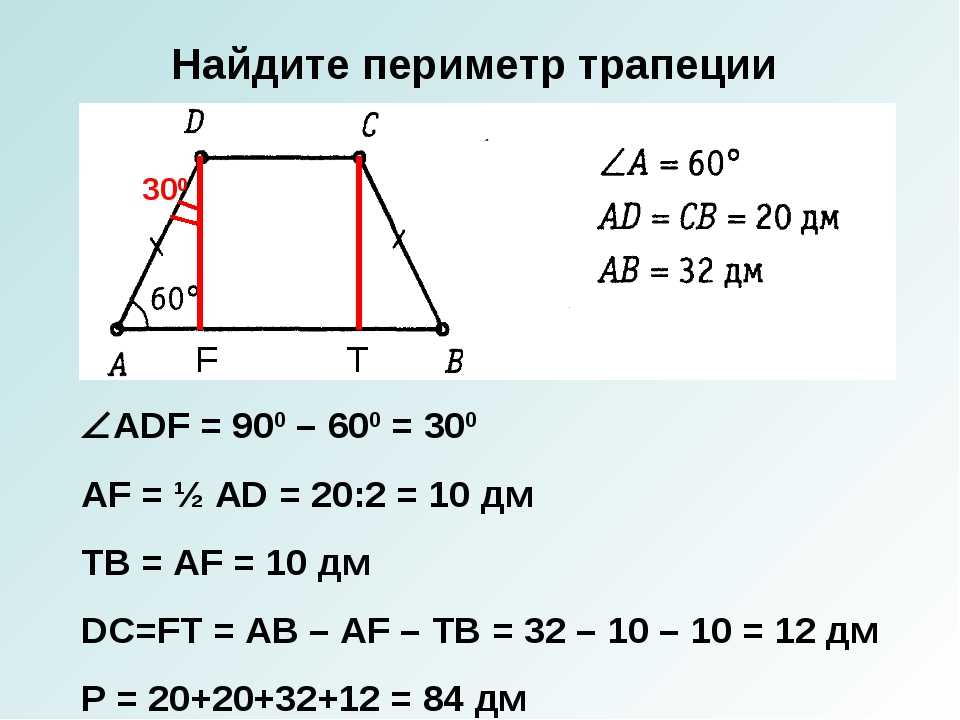
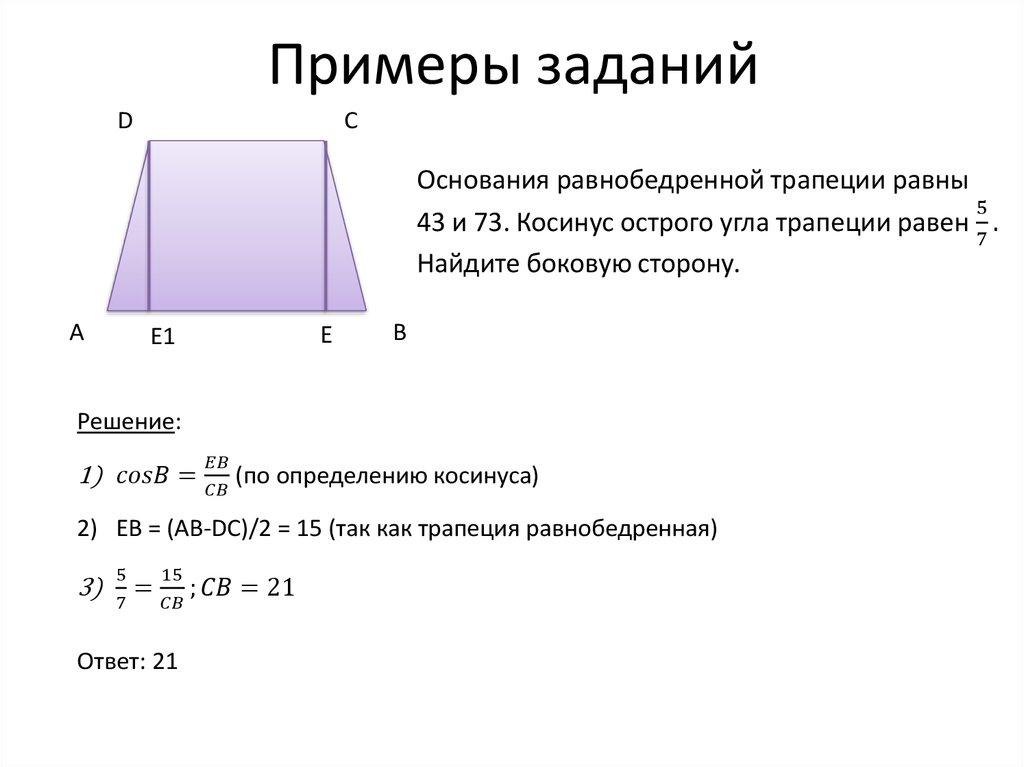
 Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ . Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.
Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ . Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.
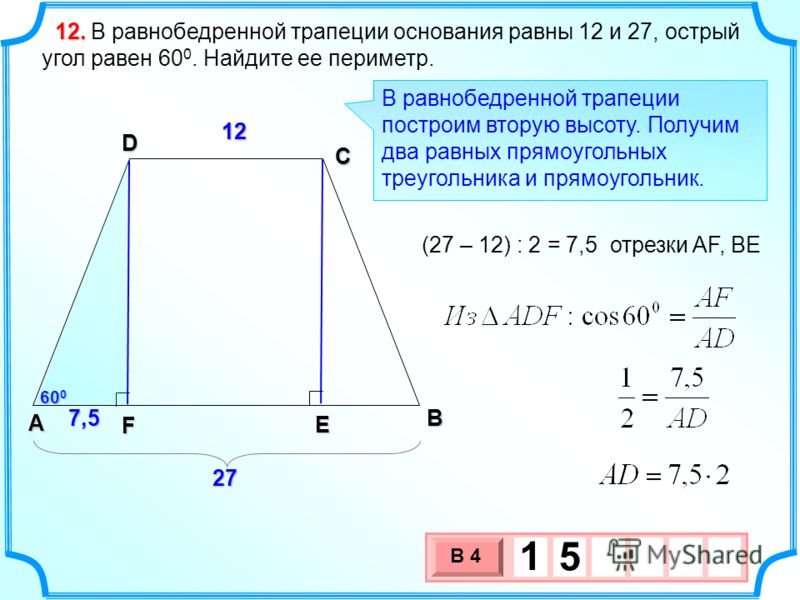 Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2 ) не только через высоту, но и через боковую сторону, прилежащую к прямому углу.
Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2 ) не только через высоту, но и через боковую сторону, прилежащую к прямому углу. Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).
Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).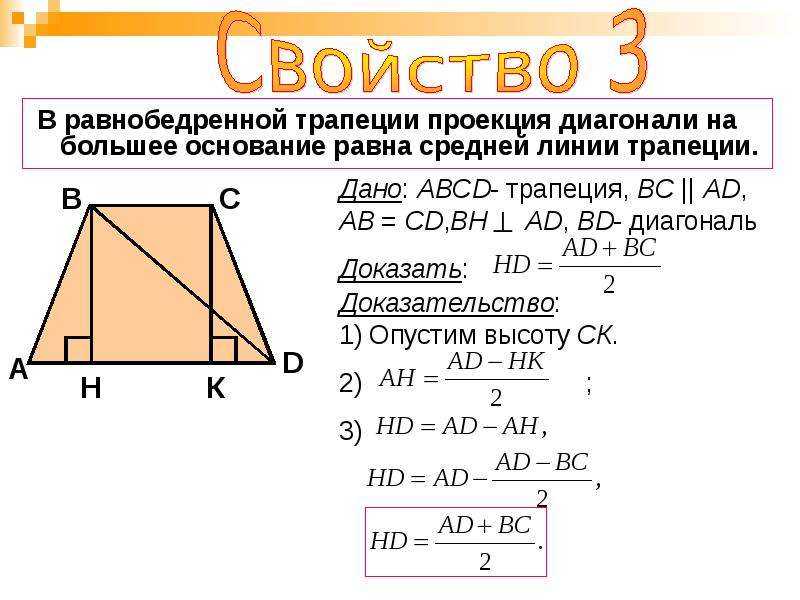
 Формула:
Формула: 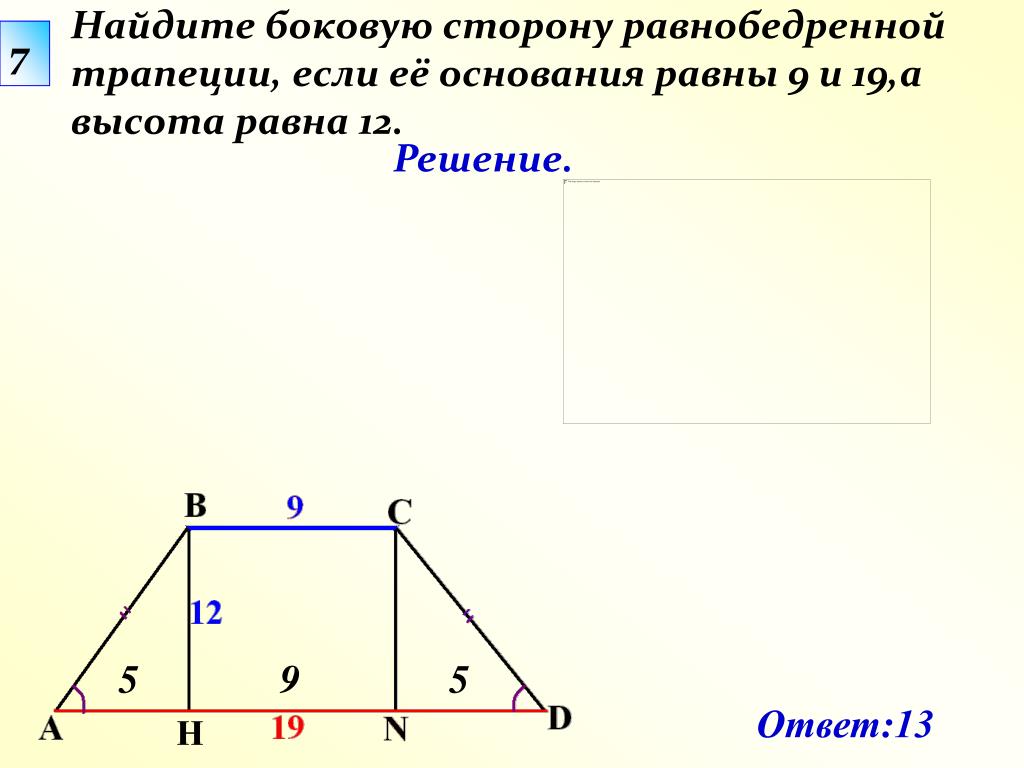

Leave A Comment