2} — это формула площади круга, а в нашем случае — площадь основания. Поэтому формулу объема цилиндра можно записать через площадь основания и высоту:

S (б.п.) = hP = 2πrh

— Если известна площадь бок. поверхности S (б.п.) и высота h цилиндра, радиус будет равен частному от деления S (б.п.) на произведение 2пи на высоту:

Формула вычисления объема цилиндра

1. Через площадь основания и высоту

Объем (V) цилиндра равняется произведению его высоты и площади основания.

V = S ⋅ H

2. Через радиус основания и высоту

Как мы знаем, в качестве оснований цилиндра (равны между собой) выступает круг, площадь которого вычисляется так: S = π ⋅ R2. Следовательно, формулу для вычисления объема цилиндра можно представить в виде:

V = π ⋅ R2 ⋅ H

Примечание: в расчетах значение числа π округляется до 3,14. 2.

Расшифровать формулу просто:

  • V – объем цилиндра;
  • π – 3,14;
  • R – радиус цилиндра;
  • D – диаметр.

То есть получается, что, если разделить объем на площадь основания, получится высота цилиндра.

Можно поступить проще. Для этого нам придется вычислить площадь боковой поверхности искомого цилиндра. Это легко сделать по формуле: S=2πRH. Слегка изменив формулу, получаем: H=S/2πR.

Таким образом, есть уже два способа, которые помогли вспомнить, как найти высоту цилиндра. Это нетрудно, когда перед глазами стройные формулы.

Способ расчета радиуса цилиндра:

Высота: Объем:

Высота: Площадь боковой поверхности:

Высота: Площадь полной поверхности:

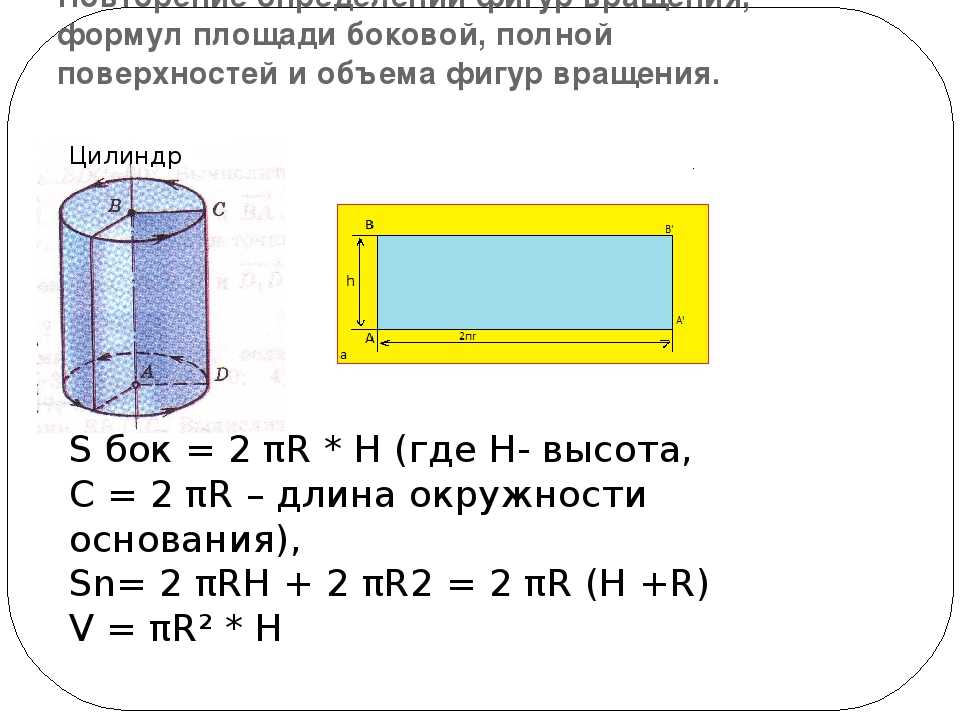
Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее.

Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Формула радиуса цилиндра:
где V – объем цилиндра, h – высота

Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.

Формула радиуса цилиндра:
где Sb – площадь боковой поверхности, h – высота

Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее.

Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Формула радиуса цилиндра:
где S – площадь полной поверхности, h – высота

S (п.п.) = S (б.п.) + 2S (осн.) = 2πrh + πr2=πr (2h+r)

Площадь боковой поверхности равняется длине окружности основания умноженной на высоту:

R = √V / πh

где V — объем цилиндра, h — высота.
Полная площадь поверхности цилиндра складывается из сумм площадей его боковой поверхности и двух оснований:

Примеры задач

Задание 1
Высота цилиндра равняется 5 см, а объем – 141,3 см3. Вычислите его радиус.

Решение:
Воспользуемся соответствующей формулой, подставив в нее известные по условиям задачи значения:

Задание 2
Найдите радиус цилиндра, если площадь его боковой поверхности равна 175,84 см2, а высота составляет 7 см.

Решение:
Применим формулу, в которой задействованы заданные величины:

Задание 3
Рассчитайте радиус цилиндра, если полная площадь его поверхности – 602,88 см2, а высота – 10 см.

Решение:
Используем третью формулу для нахождения неизвестной величины:

Через площадь боковой поверхности

Радиус цилиндра считается таким образом:

Sбок. – площадь боковой поверхности цилиндра; равна произведению длины окружности (2πR), являющейся основанием фигуры, на его высоту:

S = 2πRh

Площадь полной поверхности цилиндра через радиус основания и высоту

{S = 2pi r (h+r)}

Формула для нахождения полной поверхности цилиндра через высоту и радиус основания:

{S = 2pi r (h+r)}, где π — число Пи (3,14159…), r

— радиус основания цилиндра, h — высота цилиндра.

Источники

  • https://mnogoformul.ru/obem-cilindra
  • https://infofaq.ru/radius-cilindra.html
  • https://MicroExcel.ru/obyom-tsilindra/
  • https://www.calc.ru/radius-tsilindra.html
  • https://MicroExcel.ru/radius-tsilindra/
  • https://mnogoformul.ru/ploshhad-poverkhnosti-cilindra

Как найти высоту цилиндра? – Обзоры Вики

Значения радиуса и объема помещаются в формулу для получения объема цилиндра. Следовательно, высота цилиндра рассчитывается по формуле: V / πr2.

Точно так же, каково значение числа пи? Вкратце, пи, которое записывается как греческая буква р или π, представляет собой отношение длины окружности любого круга к диаметру этого круга. Независимо от размера круга, это отношение всегда будет равно числу пи. В десятичной форме значение числа пи равно приблизительно 3.14.

Как посчитать литры в цилиндре? ИЛИ литров

  1. Баллоны имеют объем в литрах.
  2. Чтобы рассчитать объем цилиндра, используйте следующее уравнение V = πr²h. 3.
  3. Чтобы перевести в миллилитры, разделите на 1000 (1000 мл = 1 литр).

Как вычислить Пи вручную?

В некотором смысле Pi (π) — действительно простое число — вычислить Pi просто включает в себя разделение окружности на диаметр любого круга.. … На самом деле, если долго искать среди цифр числа Пи (π), можно найти любое число, включая день рождения.

тогда что такое формула Пи? Формула Пи) Для вычисления значения π используется формула Пи, которая выглядит следующим образом: π = (окружность/диаметр) Теперь π = 3.14159 = 22/7.

Почему Пи 22 делится на 7? Дробное значение числа Пи равно 22/7. Так как пи является иррациональным числом, т.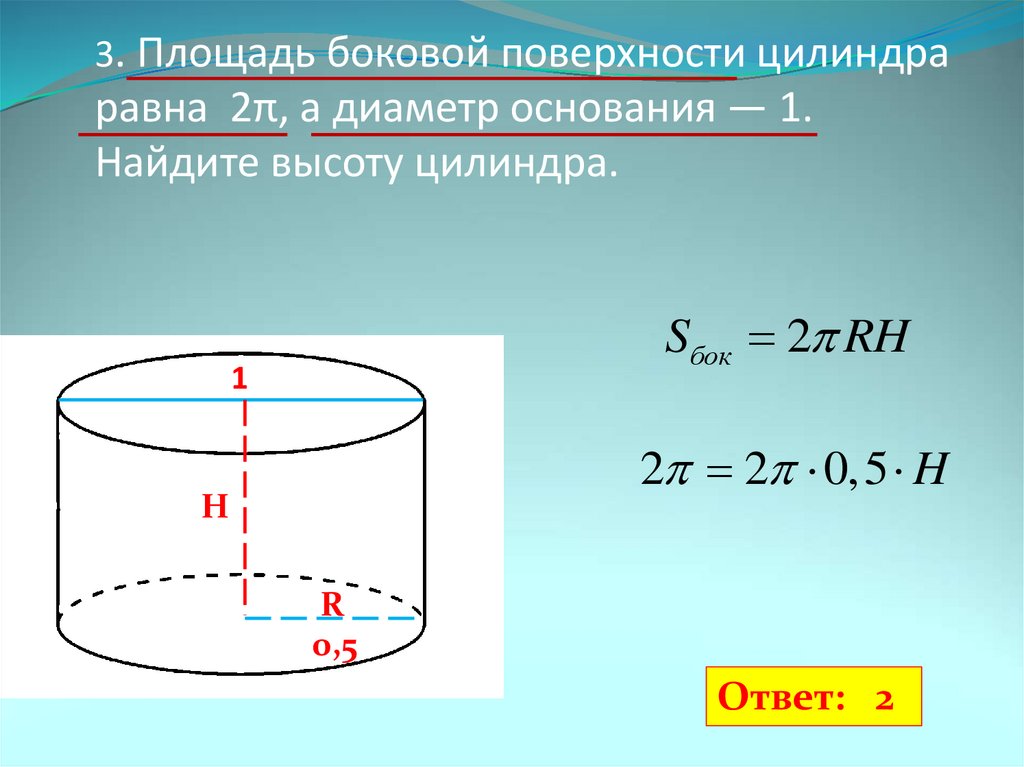 е. цифры после запятой никогда не заканчиваются и не заканчиваются, т.е. 3.1415926 … и так далее. Вот почему 22/7 используется для расчетов.

Сколько мл в цилиндре?

Градуированные цилиндры обычно имеют размер от От 5 мл до 500 мл. Некоторые могут даже вместить объемы более литра.

Как измеряются миллилитры? Миллилитр, сокращенно мл или мл, является единицей объема в метрической системе. Один миллилитр равен одной тысячной литра., или 1 кубический сантиметр. В имперской системе это небольшая сумма:. 004 чашки.

Каковы 3 размера цилиндра?

Цилиндр — это трехмерная фигура, имеющая две круглые грани, одну вверху и одну внизу, а одна изогнутая поверхность. Цилиндр имеет высоту и радиус. Высота цилиндра — это перпендикулярное расстояние между верхней и нижней гранями.

Какова длина ширина и высота цилиндра?

Как найти высоту цилиндра без радиуса?

Как изначально рассчитывалось число Пи?

Древние вавилоняне рассчитали площадь круга, если взять в 3 раза больше квадрата его радиуса, что дало значение pi = 3. … Первое вычисление π было сделано Архимедом Сиракузским (287–212 до н. э.), одним из величайших математиков древнего мира.

Как мы нашли пи?

Древние вавилоняне рассчитали площадь круга, умножив на 3 квадрат его радиуса, что дало значение пи = 3. … Первое вычисление π было сделано Архимедом Сиракузским (287–212 до н.э.), один из величайших математиков древнего мира.

Является ли 0 действительным числом? На самом деле реальные числа — это практически любые числа, которые только можно придумать. … Действительные числа могут быть положительными или отрицательными, и включить число ноль. Их называют действительными числами, потому что они не являются мнимыми, а это другая система чисел.

Пи бесконечно?

Значение числа пи

Пи — это иррациональное число, что означает, что это действительное число, которое не может быть выражено простой дробью. Это потому, что математики называют «бесконечной десятичной дробью» — цифры после десятичной точки идут вечно.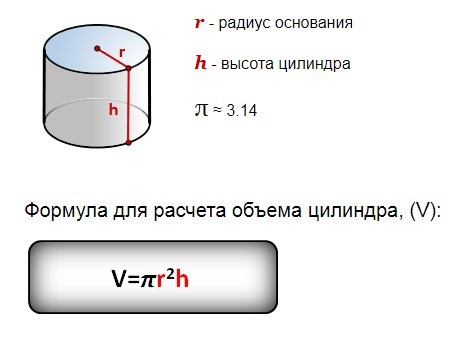

Является ли 3.14 рациональным числом? 3.14 можно записать в виде дроби двух целых чисел: 314100 и поэтому рационально. π нельзя записать в виде дроби от двух целых чисел.

Калькулятор высоты цилиндра

Этот калькулятор высоты цилиндра быстро находит высоту прямого кругового цилиндра десятью различными способами . Интересно, как найти высоту цилиндра? Просто выберите два известных параметра, введите указанные значения и вычислите высоту.

Продолжайте читать, если хотите узнать, какова возможная высота цилиндра. В большинстве случаев вы можете оценить его, зная только две из следующих величин:

  • Радиус ;
  • Том ;
  • Самая длинная диагональ ;
  • Площадь основания ;
  • Площадь боковой поверхности ; или
  • Общая площадь поверхности .

Наш калькулятор высоты цилиндра представляет собой удобный инструмент, предназначенный для правильного кругового цилиндра .

Этот тип цилиндра состоит из двух конгруэнтных окружностей (называемых основаниями ). Они лежат точно одна над другой, и поэтому мы называем это 9.0003 правый цилиндр. С другой стороны, если одно из оснований сдвинуто, то цилиндр косой . Термин круговой более очевиден — основания имеют форму кругов. Вы должны помнить, что слово цилиндр может соответствовать разным формам (обобщенный цилиндр), но обычно мы имеем в виду правильный круговой цилиндр.

Калькулятор отвечает на вопрос как найти высоту цилиндра . Если вы хотите оценить другие параметры, ознакомьтесь с нашим расчетом правильного цилиндра! 92 — \frac{2}{\pi}A_\mathrm{b}}h=d2−π2​Ab​

​

  1. Даны боковая площадь и общая площадь :

h=Al2π(A−Al)\quad h = \frac{A_\mathrm{l}}{\sqrt{2 \pi (A — A_\mathrm{l})}}h=2π(A−Al ​)

​Al​​

Вас интересуют расчеты прямоугольного цилиндра? Вам обязательно нужно проверить калькулятор объема цилиндра и калькулятор площади поверхности цилиндра!

Как найти высоту цилиндра

Калькулятор высоты цилиндра очень удобен для решения самых разных задач.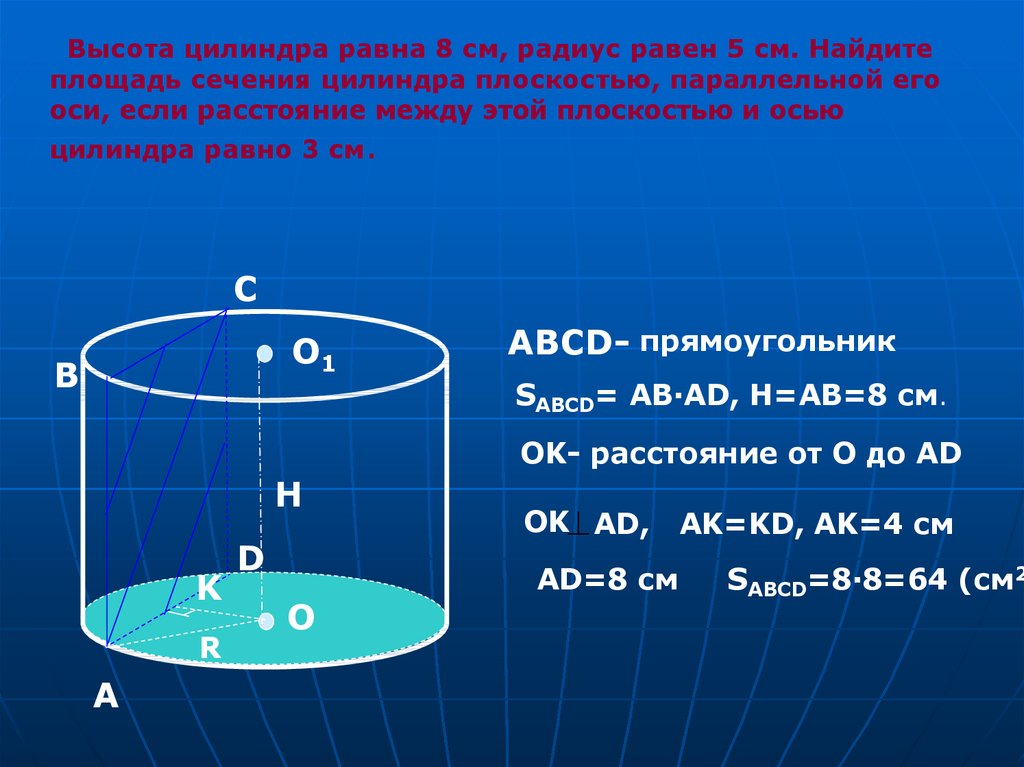

Иногда вы знаете объем и площадь основания цилиндра, но не знаете его высоту. В другой раз у вас будут указаны только площади поверхности. Если вы когда-либо сталкивались с такой проблемой, используйте этот калькулятор, чтобы оценить высоту в три простых шага:

  1. Определите , какие параметры цилиндра вы знаете. Их нужно иметь как минимум два.
  2. Введите значения выбранных переменных.
  3. Считать результат вычислений.

Помните, что с помощью калькулятора высоты цилиндра вы можете выбрать единицы измерения любого параметра. Обязательно ознакомьтесь с конвертером длины и инструментами преобразования объема. Они могут быть очень полезны во многих вычислениях.

Часто задаваемые вопросы

Как найти высоту цилиндра по площади его поверхности?

Чтобы найти высоту цилиндра по его общей площади поверхности и радиусу, выполните следующие действия:

  1. Умножьте квадрат радиуса на 2π и вычтите значение из общей площади поверхности .

  2. Разделите результат шага 1 на значение 2π × радиус

    .

  3. Поздравляем! Вы вычислили высоту цилиндра.

Как рассчитать высоту цилиндра по объему и радиусу?

Чтобы рассчитать высоту цилиндра по его объему и радиусу, следуйте приведенным инструкциям:

  1. Возьмите квадрат радиуса и умножьте это на π .

  2. Разделить объем цилиндра на результат шага 1 .

  3. Вы получите высоту цилиндра.

Какова высота цилиндра радиусом 5 см и объемом 900 см³?

11,46 см . Формула для расчета высоты цилиндра с учетом его объема и радиуса: высота = объем / (π × радиус²) .

Подставляя значения в формулу получаем, высота = 900 см³ / (π × 5 см × 5 см) = 11,46 см

Чему равна высота цилиндра, имеющего радиус 8 см и боковую поверхность площадь 1005,5 см²?

20 см .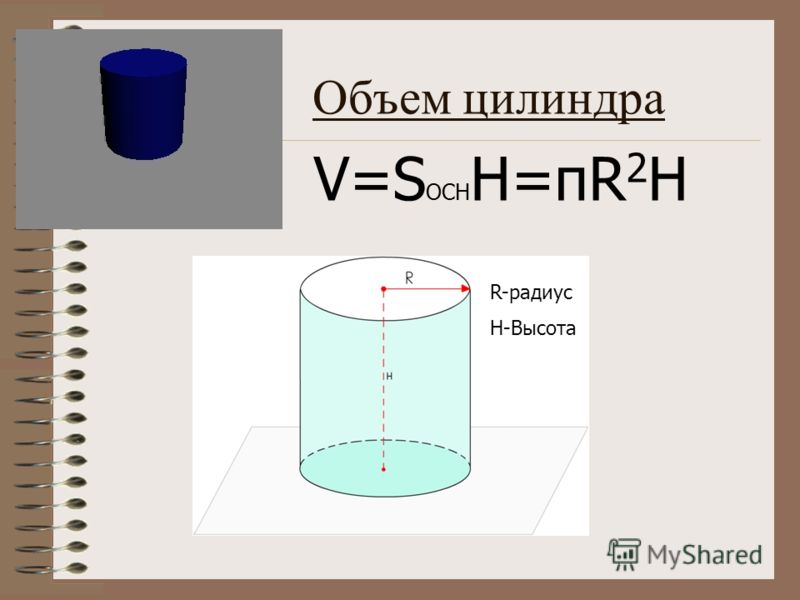 Для нахождения высоты цилиндра воспользуемся формулой высота = площадь боковой поверхности / (2π × радиус) .

Следовательно, высота цилиндра будет высоты = 1005,5 см² / (2π × 8 см) = 20 см .

Калькулятор высоты цилиндра

‘ Калькулятор высоты цилиндра ‘ — это бесплатный онлайн-инструмент, который помогает рассчитать высоту цилиндра с заданным радиусом и объемом.

Какова высота цилиндра Калькулятор?

В калькуляторе высоты цилиндра введите значения радиуса и объема, чтобы найти высоту цилиндра за несколько секунд.

Калькулятор высоты цилиндра

ПРИМЕЧАНИЕ: Введите радиус до трех цифр и объем до пяти цифр.

Как пользоваться калькулятором высоты цилиндра?

Выполните шаги, указанные ниже, чтобы использовать калькулятор и найти высоту цилиндра:

  • Шаг 1: Введите радиус и объем цилиндра в соответствующие поля ввода.
  • Шаг 2: Нажмите кнопку  «Рассчитать» , чтобы найти высоту цилиндра.
  • Шаг 3:  Нажмите кнопку «Сброс» , чтобы очистить поля и ввести новые значения.

Как найти высоту цилиндра?

Чтобы найти высоту цилиндра, нам нужны входные значения радиуса и объема цилиндра. Объем цилиндра — это вместимость цилиндра или мера занимаемого им пространства. Он рассчитывается по формуле πr 2 h , , где r — радиус круглого основания, h — высота цилиндра, а π(Pi) — математическая константа с приблизительным значением 3.14. Значения радиуса и объема подставляются в формулу для получения объема цилиндра.

Таким образом, высота цилиндра рассчитывается по формуле V/ πr 2 .

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.

Записаться на бесплатный пробный урок

Решенные примеры расчета высоты цилиндра

Пример 1:

Цилиндр имеет радиус 4 единицы и объем 251,33 кубических единицы. Найдите высоту цилиндра и проверьте ее с помощью калькулятора высоты цилиндра.

Решение:

Формула для нахождения объема цилиндра = πr 2

ч. Радиус = 4 единицы, объем = 251,33 куб. Итак, подставим значения:

Объем цилиндра = πr 2 h

высота цилиндра = V/ πr 2 .

= 251,33 / 3,14 × 4 2

= 251,33 / 50,24  

= 5,002 ед.

Следовательно, высота цилиндра = 5,002 единицы.

Пример 2:

Цилиндр имеет радиус 7 единиц и объем 300 кубических единиц. Найдите высоту цилиндра и проверьте ее с помощью калькулятора высоты цилиндра.

Решение:

Формула для нахождения объема цилиндра = πr 2 ч.