Ромб. Формулы, признаки и свойства ромба

Ромб. Формулы, признаки и свойства ромба

Навигация по странице: Определение ромба Признаки ромба Основные свойства ромба Стороны ромба Диагонали ромба Периметр ромба Площадь ромба Окружность вписанная в ромб

Определение.

Ромб — это параллелограмм, который имеет равные стороны. Если у ромба все углы прямые, тогда он называется квадратом.

Ромбы отличаются между собой размером стороны и размером углов.

Рис.1 Рис.2

Признаки ромба

Параллелограмм ABCD будет ромбом, если выполняется хотя бы одно из следующих условий:

1. Две его смежные стороны равны (отсюда следует, что все стороны равны):

АВ = ВС = СD = AD

2.

Его диагонали пересекаются под прямым углом:

AC┴BD

3. Одна из диагоналей (биссектриса) делит содержащие её углы пополам:

∠BAC = ∠CAD или ∠BDA = ∠BDC

4. Если все высоты равны:

BN = DL = BM = DK

5. Если диагонали делят параллелограмм на четыре равных прямоугольных треугольника:

Δ ABO = Δ BCO = Δ CDO = Δ ADO

6. Если в параллелограмм можно вписать круг.


Основные свойства ромба

1. Имеет все свойства параллелограмма

2. Диагонали перпендикулярны:

AC┴BD

3. Диагонали являются биссектрисами его углов:

∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC

4. Сумма квадратов диагоналей равна квадрату стороны умноженному на четыре:

AC2 + BD2 = 4AB2

5. Точка пересечения диагоналей называется центром симметрии ромба.

6. В любой ромб можно вписать окружность.

7. Центром окружности вписанной в ромб будет точка пересечения его диагоналей.


Сторона ромба

Формулы определения длины стороны ромба:

1. Формула стороны ромба через площадь и высоту:

a = S
ha

2. Формула стороны ромба через площадь и синус угла:

a = √S
√sinα
a = √S
√sinβ

3. Формула стороны ромба через площадь и радиус вписанной окружности:

a = S
2r

4. Формула стороны ромба через две диагонали:

a = √d12 + d22
2

5.

Формула стороны ромба через диагональ и косинус острого угла (cos α) или косинус тупого угла (cos β):
a = d1
√2 + 2 cosα
a = d2
√2 — 2 cosβ

6. Формула стороны ромба через большую диагональ и половинный угол:

a = d1
2cos(α/2)
a = d1
2sin(β/2)

7. Формула стороны ромба через малую диагональ и половинный угол:
a = d2
2cos(β/2)
a = d2
2sin(α/2)

8. Формула стороны ромба через периметр:

a = Р
4


Диагонали ромба

Определение.

Диагональю ромба называется любой отрезок соединяющий две вершины противоположных углов ромба.

Ромб имеет две диагонали — длинную d1, и короткую — d2

Формулы определения длины диагонали ромба:

1. Формулы большой диагонали ромба через сторону и косинус острого угла (cosα) или косинус тупого угла (cosβ)

d1 = a√2 + 2 · cosα

d1 = a√2 — 2 · cosβ

2. Формулы малой диагонали ромба через сторону и косинус острого угла (cosα) или косинус тупого угла (cosβ)

d2 = a√2 + 2 · cosβ

d2 = a√2 — 2 · cosα

3. Формулы большой диагонали ромба через сторону и половинный угол:

d1 = 2a · cos(α/2)

d1 = 2a · sin(β/2)

4. Формулы малой диагонали ромба через сторону и половинный угол:

d2 = 2a · sin(α/2)

d2 = 2a · cos(β/2)

5. Формулы диагоналей ромба через сторону и другую диагональ:

d1 = √4a2 — d22

d2 = √4a2 — d12

6. Формулы диагоналей через тангенс острого tgα или тупого tgβ угла и другую диагональ:

d1 = d2 · tg(β/2)

d2 = d1 · tg(α/2)

7. Формулы диагоналей через площадь и другую диагональ:

d1 = 2S
d2
d2 = 2S
d1

8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:

d1 = 2r
sin(α/2)
d2 = 2r
sin(β/2)

Периметр ромба

Определение.

Периметром ромба называется сумма длин всех сторон ромба.

Длину стороны ромба можно найти за формулами указанными выше.

Формула определения длины периметра ромба:

Формула периметра ромба через сторону ромба:

P = 4a


Площадь ромба

Определение.

Площадью ромба называется пространство ограниченное сторонами ромба, т.е. в пределах периметра ромба.

Формулы определения площади ромба:

1. Формула площади ромба через сторону и высоту:

S = a · ha

2. Формула площади ромба через сторону и синус любого угла:

S = a2 · sinα

3. Формула площади ромба через сторону и радиус:

S = 2a · r

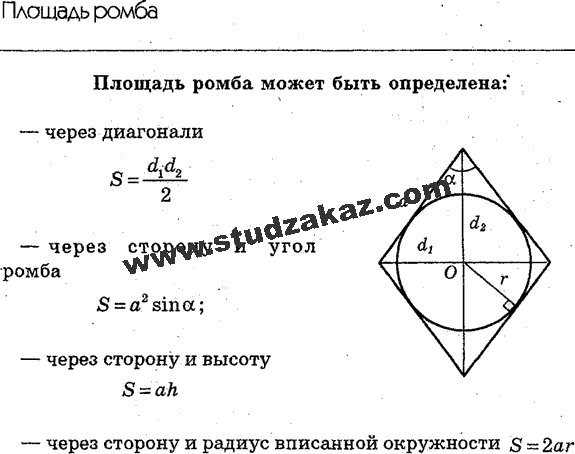
4. Формула площади ромба через две диагонали:

S = 1d1d2
2

5. Формула площади ромба через синус угла и радиус вписанной окружности:

S = 4r2
sinα

6. Формулы площади через большую диагональ и тангенс острого угла (tgα) или малую диагональ и тангенс тупого угла (tgβ):

S = 1d12 · tg(α/2)
2
S = 1d22 · tg(β/2)
2

Окружность вписанная в ромб

Определение.

Кругом вписанным в ромб называется круг, который примыкает ко всем сторонам ромба и имеет центр на пересечении диагоналей ромба.

Формулы определения радиуса круга вписанного в ромб:

1. Формула радиуса круга вписанного в ромб через высоту ромба:

r = h
2

2.

Формула радиуса круга вписанного в ромб через площадь и сторону ромба:

r = S
2a

3. Формула радиуса круга вписанного в ромб через площадь и синус угла:

r = √S · sinα
2

4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:

r = a · sinα
2
r = a · sinβ
2

5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:

r = d1 · sin(α/2)
2
r = d2 · sin(β/2)
2

6. Формула радиуса круга вписанного в ромб через две диагонали:

r = d1 · d2
2√d12 + d22

7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:

r = d1 · d2
4a

Все таблицы и формулы

Площади ромба. Формула площади ромба через диагонали. Формула нахождения площади ромба.

  • Альфашкола
  • Статьи
  • Площади ромба

                 Возьмем любую сторону, проведем к ней высоту, перемножим  \(a\) и  \(h:\)

 

\(S=a*h\)

              где  \(a\) — длина стороны ромба, \(h\) — длина высоты ромба

 

Сторона ромба:

Высота, проведенная к стороне ромба:

 

Также площадь ромба можно найти по стороне и острому углу:

 

\(S=a^2*sinα \)


\(α \)- угол между сторонами ромба,
\(a\) — длина стороны ромба,

 

         Cторона ромба:

 

Угол между сторонами в градусах:

 

 

Площадь ромба можно найти по двум диагоналям:


\(S=\frac{1}{2}d_1d_2\)


            где \(d_1,d_2\) — длины диагоналей.

         Первая диагональ ромба:

 

Вторая диагональ ромба:

 

 

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Сергей Александрович Москвин

Репетитор по математике

Стаж (лет)

Образование:

Костромской государственный университет им. Н.А. Некрасова

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Анастасия Александровна Белая

Репетитор по математике

Стаж (лет)

Образование:

Могилёвский государственный университет имени А. А.Кулешова

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Ольга Яновна Савинова

Репетитор по математике

Стаж (лет)

Образование:

Гродненский государственный университет имени Янки Купалы

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Предметы

  • Математика
  • Репетитор по физике
  • Репетитор по химии
  • Репетитор по русскому языку
  • Репетитор по английскому языку
  • Репетитор по обществознанию
  • Репетитор по истории России
  • Репетитор по биологии
  • Репетитор по географии
  • Репетитор по информатике

Специализации

  • Подготовка к ЕГЭ по математике (базовый уровень)
  • Репетитор для подготовки к ОГЭ по физике
  • Репетитор по русскому языку для подготовки к ОГЭ
  • Репетитор по грамматике русского языка
  • Репетитор по грамматике английского языка
  • Репетитор для подготовки к ОГЭ по истории
  • ВПР по физике
  • Репетитор для подготовки к ОГЭ по обществознанию
  • Репетитор по биологии для подготовки к ЕГЭ
  • Репетитор по географии для подготовки к ОГЭ

Похожие статьи

  • Особенности решения текстовых задач
  • Задача по планиметрии
  • Решаем ОГЭ по математике. Задание №5. 1
  • Задачи с логарифмическими уравнениями и неравенствами
  • Топ-5 книг, которые помогут полюбить математику
  • Наводим красоту: топ-10 простых и красивых причесок для девушек (разного возраста)
  • Первая школьная любовь и как помочь подростку пережить ее?
  • Как использовать материнский капитал на образование: полная инструкция для родителей

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Текст с ошибкой:

Расскажите, что не так

Диагональ ромба – формула, свойства, примеры

Диагональ ромба – это отрезок, соединяющий любые две несмежные вершины ромба. У ромба есть две диагонали, которые пересекают друг друга под прямым углом пополам, поэтому они образуют 4 прямоугольных треугольника, которые конгруэнтны. Давайте узнаем больше о диагонали ромба в этой статье.

1. Какие диагонали у ромба?
2. Диагональ ромба Свойства
3. Диагональ ромба Формула
4. Вывод диагонали ромба Формула
5. Часто задаваемые вопросы о диагонали ромба

Какие диагонали у ромба?

При соединении противоположных вершин ромба они образуют диагонали ромба. У ромба две диагонали пересекаются под углом 9.0°. Обратите внимание на следующий ромб, чтобы определить его диагонали и их свойства, перечисленные в следующем разделе.

Диагональ ромба Свойства

Диагонали ромба — это отрезки, проведенные между противоположными вершинами ромба. Свойства диагоналей ромба перечислены ниже.

  • Диагонали ромба делятся пополам под прямым углом.
  • Диагонали ромба могут не совпадать.
  • Две диагонали делят ромб на четыре равных прямоугольных треугольника.
  • Длину диагоналей можно рассчитать различными методами, например, с помощью теоремы Пифагора или с помощью площади ромба.

Диагональ ромба Формула

Формула для диагоналей ромба основана на площади диагоналей и выражается как p = (2 × Площадь)/q, где «p» и «q» — две диагонали ромба. Мы знаем, что обе диагонали делят друг друга пополам под прямым углом, а две диагонали делят ромб на четыре конгруэнтных прямоугольных треугольника. Теперь, используя эти свойства, давайте поймем, как выводится формула для нахождения диагонали ромба.

Вывод диагонали ромба по формуле

Формула диагонали ромба выводится через площадь ромба. Другими словами, если даны площадь и одна из диагоналей, то другую диагональ можно вычислить по формуле p = (2 × площадь)/q, где «p» и «q» — две диагонали ромб. Вывод формулы можно понять, если вывести формулу площади ромба. Поскольку мы знаем, что диагонали ромба делят его на 4 равных прямоугольных треугольника, площадь ромба будет равна площади всех четырех треугольников вместе взятых. Обратите внимание на следующий ромб, чтобы увидеть 4 конгруэнтных прямоугольных треугольника, которые могут быть сформированы в нем.

Математически это можно представить следующим образом:

Площадь ромба = 4 × площадь одного треугольника

Площадь ромба = 4 × (1/2 × основание × высота). Теперь, если мы возьмем диагонали ромба равными «p» и «q» соответственно, то основание и высоту в этой формуле можно заменить как p/2 и q/2 соответственно, поскольку мы знаем, что диагонали делят друг друга пополам. .

Площадь ромба = 4 × (1/2 × p/2 × q/2)

Площадь ромба = 4 × (1/8 × p × q)

Площадь ромба = 1/2 × p × q

Теперь, когда получена эта формула, из нее можно вывести формулу для неизвестной диагонали. Например, если в качестве неизвестной диагонали взять p, формула будет следующей: p = (2 × площадь)/q

Важные замечания о диагонали ромба

  • Диагонали ромба делят друг друга пополам справа углы.
  • Диагонали ромба делят его на четыре равных прямоугольных треугольника.
  • Диагональ ромба не может быть равна другой диагонали.

Похожие статьи

  • Диагонали
  • Диагональ квадрата
  • Ромб

 

Примеры использования диагонали ромба

  1. Пример 1: Найдите длину диагонали ромба, если площадь 54 единицы 2 , а одна диагональ равна 6 единицам.

    Решение:

    Площадь ромба = 54 кв. одна диагональ (q) = 6 единиц

    Мы будем использовать формулу для диагонали ромба, p = (2 × Площадь)/q, где «p» и «q» две диагонали ромба. Подставляя значения, p = (2 × 54)/6 = 18 единиц.

    Ответ:  Следовательно, длина неизвестной диагонали равна 18 единицам.

  2. Пример 2: Найдите длину второй диагонали ромба, если периметр равен 56 единицам, а одна диагональ 18 единицам.

    Решение:

    Неизвестную диагональ ромба можно вычислить, используя периметр ромба, равный 56 квадратным единицам; одна диагональ (p) = 18 единиц, половина этой диагонали = 18 ÷ 2 = 9 единиц

    Поскольку все стороны ромба равны, каждая сторона составляет 56 ÷ 4 = 14 единиц. Мы знаем, что диагонали ромба пересекаются под прямым углом пополам. Итак, половина каждой диагонали и сторона ромба образуют прямоугольный треугольник. Используя теорему Пифагора, можно вычислить длину неизвестной диагонали ромба.

    Половина неизвестной диагонали = √(14 2 — 9 2 ) = √(196 — 81) = √115 = 10,72 единицы. Поскольку это половина диагонали, полная длина неизвестной диагонали равна 10,72 + 10,72 = 21,44 единицы.

    Ответ:  Следовательно, длина неизвестной диагонали равна 21,44 единицы.

перейти к слайдуперейти к слайду

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, что стоит за математикой, с нашими сертифицированными экспертами

Записаться на бесплатный пробный урок

Практические вопросы по диагонали ромба

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о диагонали ромба

Что такое диагональ ромба в математике?

Диагональ ромба — это отрезок, соединяющий две противоположные вершины ромба. В ромбе есть две диагонали, которые делят друг друга пополам под прямым углом.

Что такое формула диагонали ромба?

Диагонали ромба имеют разную длину. Они могут быть рассчитаны различными методами. Давайте посмотрим, как найти диагональ ромба, если известна площадь ромба. Например, если известны площадь и одна из диагоналей, другую диагональ можно рассчитать по формуле: p = (2 × Площадь)/q, где «p» и «q» — две диагонали ромба.

Как рассчитать диагональ ромба?

Диагональ ромба можно вычислить различными способами.

  • Если даны площадь и одна диагональ, мы используем формулу p = (2 × площадь)/q, где p и q — две диагонали ромба.
  • Если известны периметр и одна диагональ, найдем сторону ромба, разделив периметр на 4, так как все стороны ромба равны. Поскольку диагонали ромба делят друг друга пополам под прямым углом, половина каждой диагонали и сторона ромба образуют прямоугольный треугольник. Используя теорему Пифагора, можно вычислить длину неизвестной диагонали.

Как найти диагональ ромба, зная периметр?

Если периметр ромба дан вместе с одной диагональю, то неизвестную диагональ можно вычислить по теореме Пифагора. Например, если периметр ромба равен 100 единицам, а одна из его диагоналей равна 40 единицам, нам нужно найти другую диагональ. Мы знаем, что все стороны ромба равны по длине, а периметр равен 100 единицам, значит, длина каждой стороны 100 ÷ 4 = 25 единиц. Поскольку диагонали ромба делят друг друга пополам под прямым углом, следовательно, мы имеем прямоугольный треугольник, две стороны которого известны, а третью сторону мы можем найти по теореме Пифагора. Половина неизвестной диагонали = √(25 2 — 20 2 ) = √(625 — 400) = √225 = 15 единиц. Поскольку это половина диагонали, полная длина неизвестной диагонали равна 15 + 15 = 30 единиц.

Как найти диагональ ромба, если дана сторона?

Мы знаем, что диагонали ромба делят друг друга пополам под прямым углом. Итак, половина каждой диагонали и сторона ромба образуют прямоугольный треугольник. Используя теорему Пифагора, можно вычислить длину неизвестной диагонали.

Как найти другую диагональ ромба?

Если известна одна диагональ ромба и площадь ромба, то другую диагональ можно рассчитать по формуле p = (2 × площадь)/q, где p и q — две диагонали ромба. Заданные значения площади и одной диагонали можно подставить, чтобы получить длину другой диагонали. Например, если площадь ромба составляет 48 квадратных единиц, а одна диагональ (q) равна 12 единицам, то другую диагональ (p) можно рассчитать по формуле p = (2 × площадь)/q. Подставляя значения, p = (2 × 48)/12 = 8 единиц. Следовательно, длина другой диагонали равна 8 единицам.

Скачать БЕСПЛАТНЫЕ учебные материалы

Диагональ ромба

Как найти площадь ромба

Все ресурсы по продвинутой геометрии

6 Диагностические тесты 57 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 3 4 5 Следующая →

Расширенная справка по геометрии » Плоская геометрия » Четырехугольники » ромбы » Как найти площадь ромба

Какая из следующих фигур является ромбом?

Возможные ответы:

Правильный ответ:

Пояснение:

Ромб – это четырехгранная фигура, все стороны которой прямые и равны по длине. Все противоположные стороны параллельны. Квадрат считается ромбом.

Сообщить об ошибке

Предположим, что четырехугольник — ромб. Если диагональ  и диагональ , какова площадь ромба 

Возможные ответы:

Правильный ответ:

Пояснение:

Чтобы найти площадь ромба, нужно знать уравнение для нахождения площади ромба. Уравнение , где и – две диагонали ромба. Поскольку оба эти значения даны нам в исходной задаче, нам просто нужно подставить эти значения в уравнение, чтобы получить:

Таким образом, площадь ромба равна квадратным единицам.

Сообщить об ошибке

Какова площадь ромба выше?

Возможные ответы:

Правильный ответ:

Объяснение:

Формула площади ромба по диагоналям равна половине произведения диагоналей, или в математических терминах:

 где  и  длины диагоналей.

Подстановка наших значений дает, 

Сообщить об ошибке

Вверху ромб, наложенный на прямоугольник. Чему равна площадь ромба?

Возможные ответы:

Правильный ответ:

Объяснение:

Одна из формул для ромба: основание умножить на высоту,

Поскольку стороны ромба равны, основание равно 5, а высота ромба равна высоте прямоугольника, 4.

Подставляя в эти значения получаем следующее:

Сообщить об ошибке

Предположим, что четырехугольник — ромб. Периметр равен , а длина одной из его диагоналей равна . Какова площадь?

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы найти площадь ромба , мы должны использовать уравнение , где  и  – диагонали ромба. Поскольку периметр ромба равен , а по определению все 4 стороны ромба имеют одинаковую длину, мы знаем, что длина каждой стороны равна . Мы можем найти длину другой диагонали, если узнаем, что две диагонали вместе с боковым ребром образуют прямоугольный треугольник. Длина гипотенузы равна , а каждый катет треугольника равен половине каждой диагонали. Таким образом, мы можем составить уравнение, использующее теорему Пифагора, следующим образом:

, где  равно половине длины неизвестной диагонали.

Таким образом, мы можем найти следующее:

 равно 8, а наша другая диагональ равна 16. Теперь мы можем использовать обе диагонали, чтобы найти площадь ромба:

Площадь ромба поэтому равно 

Сообщить об ошибке

Какова площадь ромба с длинами диагоналей  и ?

Возможные ответы:

Правильный ответ:

Пояснение:

Площадь ромба указана ниже. Подставь диагонали и найди площадь.

Сообщить об ошибке

Найдите площадь ромба, если длины диагоналей равны  и .

Возможные ответы:

Правильный ответ:

Пояснение:

Площадь ромба указана ниже. Подставляем диагонали в формулу.

Сообщить об ошибке

Найдите площадь ромба, если длины его диагоналей равны и .

Возможные ответы:

Правильный ответ:

Пояснение:

Напишите уравнение площади ромба.

Подставьте диагонали и оцените площадь.

Сообщить об ошибке

Найдите площадь ромба, если обе его диагонали имеют длину .

Возможные ответы:

Правильный ответ:

Пояснение:

Напишите формулу площади ромба.