Найдите площадь поверхности прямой призмы
Заключительная статья про параллелепипеды. По крайней мере, на данный момент рассмотрены все задания, которые имеются в открытом банке заданий ЕГЭ. Здесь представлены две задачи, связанные с площадью поверхности прямого параллелепипеда.
Это взаимообратные задачи: в одной даны диагонали ромба лежащего в основании и боковое ребро, требуется найти площадь поверхности параллелепипеда; в другой задаче дана площадь поверхности, диагонали ромба лежащего в основании и требуется найти боковое ребро. Напомню формулы. Площадь поверхности прямой призмы:
Так же для нахождения площади ромба будет использована формула площади четырёхугольника:
Понятно, что диагонали ромба пересекаются под углом 900. Известно, что синус этого угла равен единице, поэтому формула примет вид:
Рассмотрим задачи:
Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 9 и 40, и боковым ребром, равным 55.
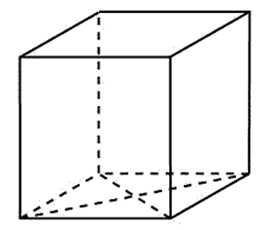
Площадь поверхности данной призмы равна сумме площадей оснований и четырёх боковых граней:
Основание призмы – ромб, его площадь мы найдём по формуле:
Значит:
Так как призма прямая, то её высота равна боковому ребру:
Используя теорему Пифагора можем выразить сторону ромба через его диагонали d1 и d2 как:
Значит:
Тогда площадь поверхности призмы равна:
Ответ: 4870
В основании прямой призмы лежит ромб с диагоналями, равными 15 и 36. Площадь ее поверхности равна 2100. Найдите боковое ребро этой призмы.
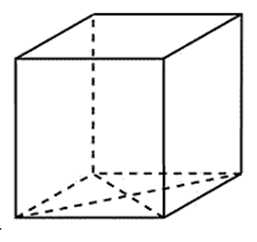
Данная задача является обратной предыдущей. Здесь известна площадь поверхности и требуется найти боковое ребро. У прямой призмы боковое ребро равно её высоте.
Запишем формулу площади поверхности призмы:
Площадь поверхности известна, значит нам необходимо найти площадь ромба лежащего в основании и его сторону.
Площадь ромба:
Используя теорему Пифагора можем выразить сторону ромба через его диагонали d1 и d2 как:
Значит:
Таким образом:
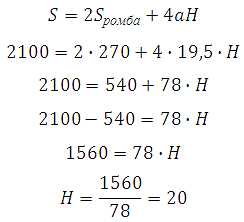
Ответ: 20
27062. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10.

Посмотреть решение
27148. В основании прямой призмы лежит ромб с диагоналями, равными 6 и 8. Площадь ее поверхности равна 248. Найдите боковое ребро этой призмы.

Посмотреть решение
В будущем вас ожидают задачи с пирамидами, не пропустите! На этом всё. Успеха вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
matematikalegko.ru
Площадь поверхности и обьём призмы — урок. Геометрия, 11 класс.
Площадь полной поверхности призмы — сумма площадей всех граней призмы.
Она состоит из площади боковой поверхности и площади оснований
Sполн.=Sбок.+2⋅Sосн.
Все грани куба — квадраты, поэтому рациональнее использовать формулу
Sполн. пов. куба=6⋅a2
Объём прямой призмы находится по формуле:
V=Sосн.⋅H
Для прямоугольного параллелепипеда можно использовать формулу \(V = abc\) , где \(a\), \(b\), \(c\) — измерения прямоугольного параллелепипеда (длина, ширина, высота).
Для куба используется формула V=a3, где \(a\) — ребро куба.
Основанием призмы может быть любой \(n\)-угольник, поэтому важно знать формулы вычисления их площадей.
Важные формулы нахождения площади \(n\)-угольников
| квадрат | a2 | ||
| прямоугольник | a⋅b | ||
| ромб | a⋅b⋅sinα | a⋅h | d1⋅d22 |
| параллелограмм | a⋅b⋅sinα | a⋅h | |
| равносторонний треугольник | a234 | ||
| прямоугольный треугольник | a⋅b2 | a⋅h3 | |
| произвольный треугольник | a⋅b⋅sinα2 | a⋅h3 | p⋅p−ap−bp−c |
| трапеция | a+b2⋅h |
Формула нахождения площади правильного шестиугольника
Правильный шестиугольник состоит из 6 правильных треугольников.
Sправ. ш.=6⋅a234, где \(a\) — сторона шестиугольника. |
Призма [wiki.eduVdom.com]
Призма — многогранник, две параллельные грани которого (основания) n−угольники, а остальные n граней (боковые) — параллелограммы. Очевидно, что все боковые ребра призмы равны, и в основаниях — равные n−угольники с соответственно параллельными сторонами.
Призма является многогранником.
Боковыми ребрами называются отрезки, соединяющие соответствующие вершины оснований.
Высотой призмы называется расстояние между плоскостями ее оснований.
Призма называется прямой, если ее боковое ребро перпендикулярно плоскости основания.
См.
Рис.1
Призма называется наклонной, если боковое ребро призмы не перпендикулярно плоскости основания. См.Рис.2
Рис.2
Правильная призма — прямая призма, основания которой являютя правильными многоугольниками.
Площадь полной поверхности призмы — сумма площадей всех её граней. Площадь полной поверхности (Sполн) выражается через площадь боковой поверхности (Sбок) и площадь основания призмы формулой:
Площадь боковой поверхности призмы (Sбок) — сумма площадей её боковых граней.
Имеют место формулы : Sбок = Pl; V = Sосн · H , где Sбок — площадь боковой поверхности призмы, P — периметр перпендикулярного сечения, l — длина бокового ребра, V — объем, Sосн — площадь основания, H — высота призмы.
Теорема о площади боковой поверхности прямой призмы. Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.
Сечение, образованное плоскостью, перпендикулярной к боковому ребру призмы, называется нормальным (ортогональным) сечением призмы.
Призма называется параллелепипедом, если её основания — параллелограммы.
Пример 1. Найдите объём многогранника, вершинами которого являются точки A, B, C, A1, B1, C1 правильный шестиугольник призмы ABCDEFA1B1C1D1E1F1 , площадь основания которой равна 6, а боковое ребро равно 3.
Видео-решение.
Пример №2
Пример №3
Пример №4
www.wiki.eduvdom.com
Площадь поверхности прямой призмы: формулы и пример задачи
Объем и площадь поверхности — это две важные характеристики любого тела, имеющего конечные размеры в трехмерном пространстве. В данной статье рассмотрим известный класс многогранников — призмы. В частности, будет раскрыт вопрос, как найти площадь поверхности прямой призмы.
Что собой представляет призма?
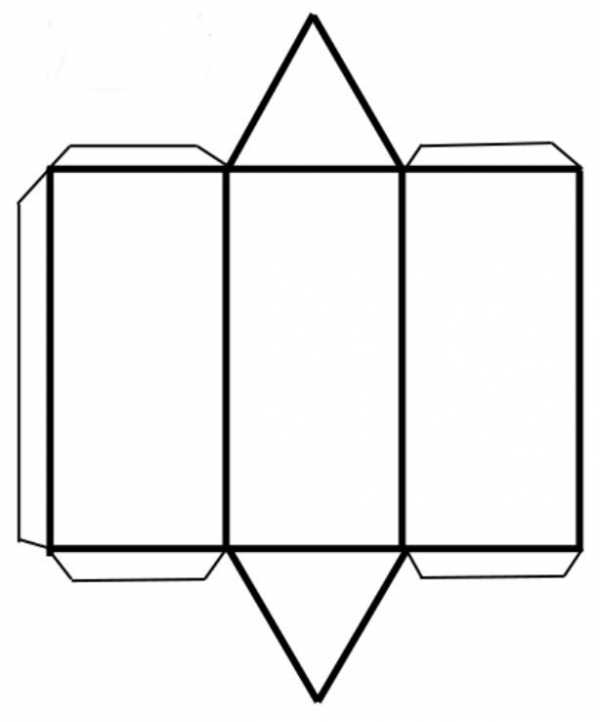
Призмой называется любой многогранник, который ограничен несколькими параллелограммами и двумя одинаковыми многоугольниками, расположенными в параллельных плоскостях. Эти многоугольники считают основаниями фигуры, а ее параллелограммы — это боковые стороны. Количество сторон (углов) основания определяет название фигуры. Например, на рисунке ниже изображена пятиугольная призма.
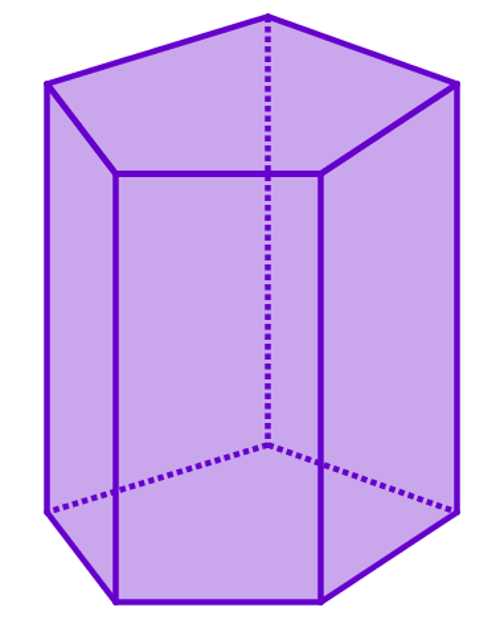
Расстояние между основаниями называется высотой фигуры. Если высота равна длине любого бокового ребра, то такая призма будет прямой. Вторым достаточным признаком для прямой призмы является то, что у нее все боковые стороны представляют собой прямоугольники или квадраты. Если же хотя бы одна боковая сторона является параллелограммом общего вида, то фигура будет наклонной. Ниже можно посмотреть, как визуально отличаются прямая и наклонная призмы на примере четырехугольных фигур.
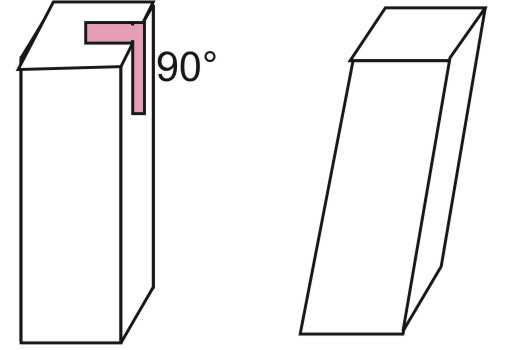
Площадь поверхности прямой призмы
Если геометрическая фигура имеет n-угольное основание, тогда она состоит из n+2 граней, n из которых являются прямоугольниками. Обозначим длины сторон основания символом ai, где i = 1,2,…,n, а высоту фигуры, которая равна длине бокового ребра, обозначим h. Чтобы определить площадь (S) поверхности всех граней, необходимо сложить площадь So каждого из оснований и все площади боковых сторон (прямоугольников). Таким образом, формулу для S в общем виде можно записать так:
S = 2*So + Sb
Где Sb — площадь боковой поверхности.
Поскольку основанием прямой призмы может быть совершенно любой плоский многоугольник, то единой формулы для вычисления So привести нельзя, и для определения этой величины в общем случае следует проводить геометрический анализ. Например, если основание представляет собой правильный n-угольник со стороной a, тогда его площадь вычисляется по формуле:
So = n/4*ctg(pi/n)*a2
Что касается величины Sb, то выражение для ее вычисления привести можно. Площадь боковой поверхности прямой призмы равна:
Sb = h*∑i=1n(ai)
То есть величина Sb вычисляется как произведение высоты фигуры на периметр ее основания.
Пример решения задачи
Применим полученные знания для решения следующей геометрической задачи. Дана призма, основание которой представляет собой прямоугольный треугольник со сторонами при прямом угле 5 см и 7 см. Высота фигуры составляет 10 см. Необходимо найти площадь поверхности прямой призмы треугольной.
Для начала вычислим гипотенузу треугольника. Она будет равна:
c = √(52 + 72) = 8,6 см
Теперь сделаем еще одну подготовительную математическую операцию — рассчитаем периметр основания. Он составит:
P = 5 + 7 + 8,6 = 20,6 см
Площадь боковой поверхности фигуры вычисляется как произведение величины P на высоту h=10 см, то есть Sb = 206 см2.
Чтобы найти площадь всей поверхности, к найденной величине следует добавить две площади основания. Поскольку площадь прямоугольного треугольника определяется половиной произведения катетов, то получаем:
2*So = 2*5*7/2 = 35 см2
Тогда получаем, что площадь поверхности прямой призмы треугольной составляет 35 + 206 = 241 см2.
fb.ru
Призма. Формулы и свойства призмы
Определение.
Призма — это многогранная объемная фигура, которая состоит из двух одинаковых плоских многоугольников (основ), находящихся в двух параллельных плоскостях, а другие грани (боковые грани) — параллелограммы, что имеют общие стороны с этими многоугольниками.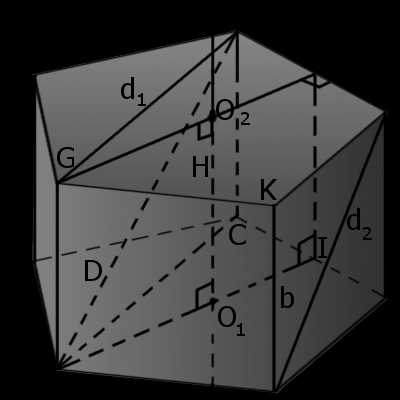 |
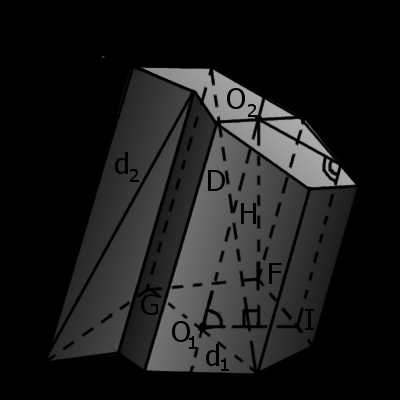 |
|
| Рис.1 | Рис.2 |
Определение. Основы призмы — две грани, которые являются равными параллельными плоскими многоугольниками (ABCEF, GMNJK).
Определение. Боковые грани призмы — все остальные грани за исключением основ.
Определение. Боковая поверхность призмы — совокупность всех боковых граней призмы.
Определение. Поверхность призмы — это совокупность поверхностей двух оснований и боковой поверхности.
Определение. Боковое ребро призмы — общая сторона двух боковых граней.
Определение. Высота — это перпендикуляр, который соединяет две основы призмы под прямым углом.
Определение. Диагональ основания призмы — это отрезок, соединяющий две не соседние вершины, принадлежащие этой же основе.
Определение. Диагональ боковой грани призмы — это отрезок, соединяющий две противоположные вершины, лежащие на одной боковой грани однако принадлежат различным основам.
Определение. Диагональ призмы (AN) — это отрезок, соединяющий две вершины, лежащие на разных основаниях, но не лежат на одной боковой стороне.
Определение. Диагональное сечение — это пересечение призмы плоскостью, проходящей через диагональ основания призмы и боковое ребро. Треугольная призма (в основе призмы треугольники) не имеет диагональных сечений.
Определение. Перпендикулярное сечение — это пересечение призмы плоскостью, пересекающей боковые ребра призмы под прямым углом.
Определение. Прямая призма — это призма, в которой все боковые грани перпендикулярны к основанию. Высота равна длине бокового ребра.
Определение.
Определение. Правильная призма — это призма, в которой основы являются правильными многоугольниками. Правильная призма может быть, как прямой, так и наклонной.
Определение. Усечённая призма — это призма, в которой две основы не параллельны (рис. 2). Усечённая призма может быть, как прямой, так наклонной.
Объём призмы
Формула. Объём призмы через площадь основания и высоту:V = SоснH
Формула. Объём наклонной призмы через площадь перпендикулярного сечения и длину бокового ребра:V = SпL
Формула. Объём правильной прямой призмыПлощадь поверхности призмы
Формула. Площадь боковой поверхности призмы через периметр основания и высоту:Sb = P·h
Формула. Площадь поверхности призмы через площадь основания, периметр основания и высоту:S = 2Soсн + P·h
Формула. Площадь поверхности правильной призмы через высоту (h), длину стороны (a) и количество сторон (n):Основные свойства призмы
Основы призмы — равные многоугольники.
Боковые грани призмы — параллелограммы.
Боковые ребра призмы параллельны и равны между собой.
Перпендикулярное сечение перпендикулярно всем боковым ребрам и боковым граням.
Высота прямой призмы равна длине бокового ребра.
Высота наклонной призмы всегда меньше длины ребра.
В прямой призме гранями могут быть прямоугольниками или квадратами.
ru.onlinemschool.com
Основанием прямой треугольной призмы
Для вас ещё несколько несложных задачек на решение призмы. Рассмотрим прямую призму с прямоугольным треугольником в основании. Ставится вопрос о нахождении объёма или площади поверхности. Формула объёма призмы:
Формула площади поверхности призмы (общая):
*У прямой призмы боковая поверхность состоит из прямоугольников и равна она произведению периметра основания и высоты призмы. Необходимо помнить формулу площади треугольника. В данном случае, имеем прямоугольный треугольник – его площадь равна половине произведения катетов. Рассмотрим задачи:
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 10 и 15, боковое ребро равно 5. Найдите объем призмы.
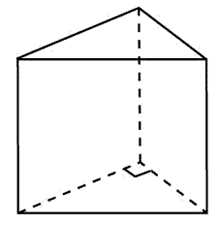
Площадь основания это площадь прямоугольного треугольника. Она равна половине площади прямоугольника со сторонами 10 и 15).
Таким образом, искомый объём равен:
Ответ: 375
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 20 и 8. Объем призмы равен 400. Найдите ее боковое ребро.

Задача обратная предыдущей.
Объем призмы:
Площадь основания это площадь прямоугольного треугольника:
Таким образом
Ответ: 5
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 5 и 12, высота призмы равна 8. Найдите площадь ее поверхности.

Площадь поверхности призмы складывается из площадей всех граней – это два равных по площади основания и боковая поверхность.
Для того, чтобы найти площади всех граней необходимо найти третью сторону основания призмы (гипотенузу прямоугольного треугольника).
По теореме Пифагора:
Теперь мы можем найти площадь основания и площадь боковой поверхности. Площадь основания равна:
Площадь боковой поверхности призмы с периметром основания равна:
*Можно обойтись без формулы и просто сложить площади трёх прямоугольников:
Полная площадь поверхности призмы:
Ответ: 300
27082. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.
Посмотреть решение
27132. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности.
Посмотреть решение
27151. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8. Площадь ее поверхности равна 288. Найдите высоту призмы.
На этом всё. Успеха вам!
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
matematikalegko.ru
Формулы площади поверхности тел
Площадь поверхности геометрической фигуры измеряется в квадратных единицах. Очень часто используется в повседневной жизни, в строительстве, на производствах. Например, нужно вам покрасить комнату, зная сколько краски используется на кв. метр, и площади стен комнаты легко можно вычислить, сколько всего вам нужно купить краски.
Различают два вида площадей поверхности тел: Sбок — площадь боковой поверхности тела, и Р — площадь полной поверхности тела, которая равна сумме площадей боковой поверхности и основания тела.
Содержание статьи:
Формула площади поверхности призмы
Площадь боковой поверхности прямой призмы равна периметру основания умноженному на высоту призмы (высота=боковому ребру).
Sбок = ph=pl
р — периметр основания;
h — высота;
l — боковое ребро.
Формула площади поверхности куба
Площадь боковой поверхности куба равна числу боковых граней умноженному на квадрат ребра.
Sбок = 4a2
Площадь полной поверхности куба равна числу всех граней куба умноженному на квадрат ребра.
P = 6a2
а — ребро куба.
Формула площади поверхности пирамиды
1) Правильная пирамида:
Sбок = 1/2pA
p — периметр основания;
A — апофема.
Sбок = S/cos φ
S — площадь основания;
φ — угол между боковой гранью и основанием пирамиды.
Sбок = Sгр n
Sгр — площадь одной боковой грани;
n — количество боковых граней пирамиды.
2) Правильная усеченная пирамида:
Sбок = 1/2(p1 + p2)A
p1 ,p2— периметры оснований;
A — апофема.
Р = Sбок + S1 + S2
Р — площадь полной поверхности правильной усеченной пирамиды;
Sбок— площадь боковой поверхности правильной усеченной пирамиды;
S1 + S2 — площади оснований.
Формула площади поверхности цилиндра
Sбок = 2πrh = πdh
P = 2πr2+2πrh = 2π(r+h)
P — площадь полной поверхности цилиндра;
r — радиус цилиндра;
d — диаметр цилиндра;
h — высота цилиндра.
Формула площади поверхности конуса
1) Прямой круговой конус:
Sбок = πrl = 1/2 πdl
P = πr2 + πrl= πr(r+l)
P — площадь полной поверхности конуса;
r -радиус конуса;
d -диаметр конуса;
l — образующая конуса.
2) Усеченный прямой круговой конус:
Sбок = πl(r1 + r2) = 1/2πl(d1 + d2)
P = πl(r1 + r2) + π(r1 + r2)
P — площадь полной поверхности усеченного конуса;
r1, r2— радиусы оснований усеченного конуса;
d1, d2— диаметры оснований усеченного конуса;
l — образующая усеченного конуса.
Формула площади поверхности шара (сферы)
Шар — тело, созданное вращением полукруга вокруг диаметра.
Сфера — поверхность шара.
P = 4πR2 = πD2
Формула площади поверхности сферического сегмента
Сферический сегмент — часть сферы, что отсекается от сферы плоскостью.
Sсф. сегм. = 2πRh = π(a2 + h2)
Формула площади поверхности шарового сегмента
Шаровой сегмент — часть шара, что отсекается от шара плоскостью, и ограничивается кругом (основание шарового сегмента) и сферическим сегментом.
Sшар. сегм. = π(2Rh+a2)=π(h2+2a2)
R — радиус шара;
D — диаметр шара;
h — высота сегмента;
a — радиус основания сегмента.
Материалы по теме:
Поделиться с друзьями:
Загрузка…matemonline.com

Leave A Comment