Площадь многоугольника по координатам онлайн
|
|
|
|||||||||||||||||||||||||||||||
Как найти длину фигуры по координатам вершин.
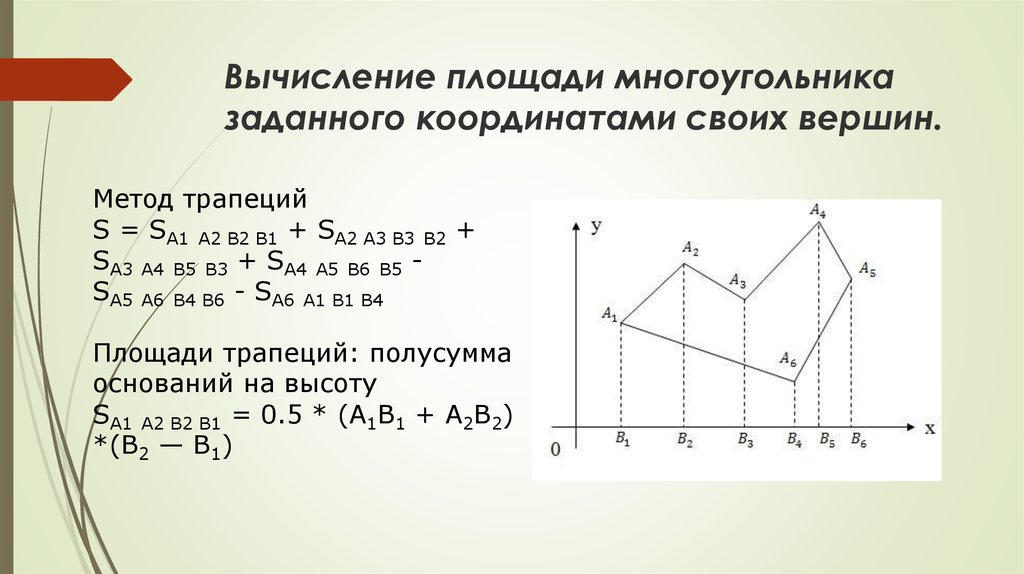
 Вычисление площади многоугольника по координатам его вершин
Вычисление площади многоугольника по координатам его вершинМетод координат, предложенный в XVII веке французскими математиками Р. Декартом (1596-1650) и П. Ферма (1601-1665), является мощным аппаратом, позволяющем переводить геометрические понятия на алгебраический язык. В основе этого метода лежит понятие — система координат. Мы будем рассматривать вычисление площади многоугольника по координатам его вершин в прямоугольной системе координат.
Площадь треугольника
Теорема 1 . Если — площадь треугольника
то справедливо равенство
будем называть определителем площади треугольника.
Доказательство. Пусть вершины треугольника расположены в первой координатной четверти. Возможны два случая.
Случай 1 . Направление (или, или) расположения вершин треугольника совпадает с направлением движения конца часовой стрелки (рис. 1.30).
Так как фигура — трапеция.
Аналогично находим, что
Выполнив алгебраические преобразования
получим, что:
В равенстве (1.
Покажем, что. Действительно, здесь
(площадь прямоугольника с основанием и высотой больше суммы площадей прямоугольников с основаниями, и высотами, ; (рис. 1.30), откуда
Случай 2 . Указанные направления в случае 1 противоположны направлению движения конца часовой стрелки (рис. 1.31)
так как фигура — трапеция, а
где. Действительно, здесь
Теорема доказана, когда вершины треугольника расположены в первой координатной четверти.
Воспользовавшись понятием модуля, равенства (1.9) и (1.10) можно записать так:
Замечание 1 . Мы вывели формулу (1.8), рассматривая простейшее расположение вершин, изображённое на рисунках 1.30 и 1.31; однако формула (1.8) верна при любом расположении вершин.
Рассмотрим случай, изображённый на рисунке 1.32.
Поэтому, выполнив несложные геометрические преобразования:
получим снова, что, где
Площадь n-угольника
Многоугольник может быть выпуклым или невыпуклым, порядок нумерации вершин считается отрицательным, если вершины нумеруются по направлению движения конца часовой стрелки. Многоугольник, не имеющий самопересечения сторон, будем называть простым. Для простого именно
Многоугольник, не имеющий самопересечения сторон, будем называть простым. Для простого именно
Теорема 2 . Если — площадь простого n -угольника, где, то справедливо равенство
будем называть определителем площади простого n -угольника.
Доказательство. Возможны два случая.
Случай 1 . n -угольник — выпуклый. Докажем формулу (1.11) методом математической индукции.
Для она уже доказана (теорема 1). Предположим, что она справедлива для n -угольника; докажем, что она остаётся справедливой и для выпуклого (n +1)-угольника.
Добавим к многоугольнику ещё одну вершину (рис. 1.33).
Таким образом, формула справедлива для (n +1)-угольника, и, значит, условия математической индукции выполнены, т. е. формула (1.11) для случая выпуклого n -угольника доказана.
Случай 2 . n -угольник — невыпуклый.
В любом невыпуклом n -угольнике можно провести диагональ, лежащую внутри него, и поэтому доказательство случая 2 для невыпуклого n -угольника аналогична доказательству для выпуклого n -угольника.
Замечание 2 . Выражения для запоминаются нелегко. Поэтому, для вычисления его значений удобно выписать в столбец координаты первой, второй, третьей, …, n -й и снова первой вершин n -угольника и провести умножение по схеме:
Знаки в столбце (1.12) надо расставить так, как указано в схеме (1.13).
Замечание 3 . При составлении столбца (1.12) для треугольника можно начать с любой вершины.
Замечание 4 . При составлении столбца (1.12) для n -угольника () необходимо соблюдать последовательность выписывания координат вершин n -угольника (с какой вершины начинать обход безразлично). Поэтому вычисление площади n -угольника следует начинать с построения «грубого» чертежа.
Треугольник — это одна из самых распространенных геометрических фигур, с которой мы знакомимся уже в начальной школе. С вопросом, как найти площадь треугольника, сталкивается каждый школьник на уроках геометрии. Так, какие же особенности нахождения площади данной фигуры можно выделить? В данной статье мы рассмотрим основные формулы, необходимые для выполнения такого задания, а также разберем виды треугольников.
Виды треугольников
Найти площадь треугольника можно абсолютно разными способами, потому что в геометрии выделяется не один вид фигур, содержащих три угла. К таким видам относятся:
- Тупоугольный.
- Равносторонний (правильный).
- Прямоугольный треугольник.
- Равнобедренный.
Рассмотрим подробнее каждый из существующих типов треугольников.
Такая геометрическая фигура считается наиболее распространенной при решении геометрических задач. Когда возникает необходимость начертить произвольный треугольник, на помощь приходит именно этот вариант.
В остроугольном треугольнике, как понятно по названию, все углы острые и в сумме составляют 180°.
Такой треугольник также очень распространен, однако встречается несколько реже остроугольного. Например, при решении треугольников (т. е. известно несколько его сторон и углов и нужно найти оставшиеся элементы) иногда требуется определить, является угол тупым или нет. Косинус — это отрицательное число.
В величина одного из углов превышает 90°, поэтому оставшиеся два угла могут принимать маленькие значения (например, 15° или вовсе 3°).
Чтобы найти площадь треугольника данного типа, необходимо знать некоторые нюансы, о которых мы поговорим дальше.
Правильный и равнобедренный треугольники
Правильным многоугольником называется фигура, включающаяся в себя n углов, у которой все стороны и углы равны. Таким и является правильный треугольник. Так как сумма всех углов треугольника составляет 180°, то каждый из трех углов равен 60°.
Правильный треугольник, благодаря его свойству, также называют равносторонней фигурой.
Стоит также отметить, что в правильный треугольник можно вписать только одну окружность и около него можно описать только одну окружность, причем их центры расположены в одной точке.
Помимо равностороннего типа, можно также выделить равнобедренный треугольник, несильно от него отличающийся. В таком треугольнике две стороны и два угла равны между собой, а третья сторона (к которой прилегают равные углы) является основанием.
На рисунке показан равнобедренный треугольник DEF, углы D и F которого равны, а DF является основанием.
Прямоугольный треугольник
Прямоугольный треугольник назван так потому, что один из его углов прямой, то есть равен 90°. Другие же два угла в сумме составляют 90°.
Самая большая сторона такого треугольника, лежащая против угла в 90° является гипотенузой, остальные же две его стороны — это катеты. Для данного типа треугольников применима теорема Пифагора:
Сумма квадратов длин катетов равна квадрату длины гипотенузы.
На рисунке изображен прямоугольный треугольник BAC с гипотенузой AC и катетами AB и BC.
Чтобы найти площадь треугольника с прямым углом, нужно знать числовые значения его катетов.
Перейдем к формулам нахождения площади данной фигуры.
Основные формулы нахождения площади
В геометрии можно выделить две формулы, которые подходят для нахождения площади большинства видов треугольников, а именно для остроугольного, тупоугольного, правильного и равнобедренного треугольников.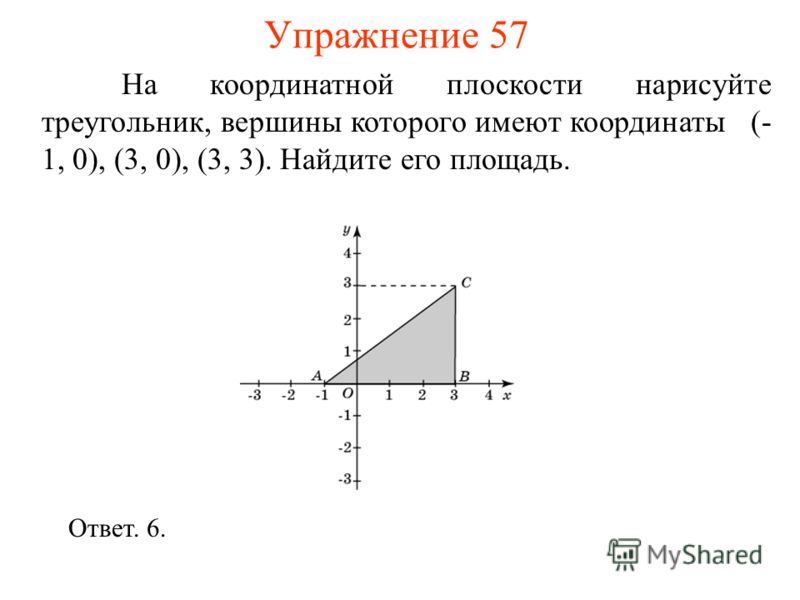 Разберем каждую из них.
Разберем каждую из них.
По стороне и высоте
Данная формула является универсальной для нахождения площади, рассматриваемой нами фигуры. Для этого достаточно знать длину стороны и длину проведенной к ней высоты. Сама формула (половина произведения основания на высоту) выглядит следующим образом:
где A — сторона данного треугольника, а H — высота треугольника.
Например, чтобы найти площадь остроугольного треугольника ACB, нужно умножить его сторону AB на высоту CD и разделить получившееся значение на два.
Однако не всегда бывает легко найти площадь треугольника таким способом. Например, чтобы воспользоваться этой формулой для тупоугольного треугольника, необходимо продолжить одну из его сторон и только после этого провести к ней высоту.
На практике данная формула применяется чаще остальных.
По двум сторонам и углу
Данная формула, как и предыдущая подходит для большинства треугольников и по своему смыслу является следствием формулы нахождения площади по стороне и высоте треугольника.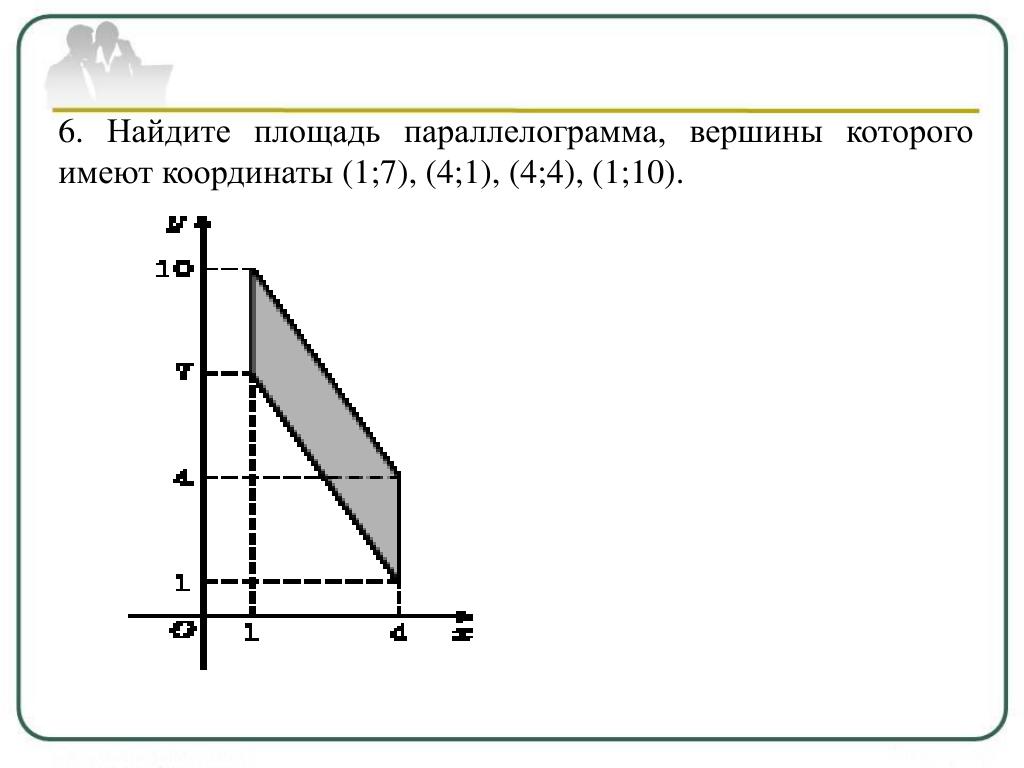 То есть рассматриваемую формулу можно легко вывести из предыдущей. Ее формулировка выглядит так:
То есть рассматриваемую формулу можно легко вывести из предыдущей. Ее формулировка выглядит так:
S = ½*sinO*A*B,
где A и B — это стороны треугольника, а O — угол между сторонами A и B.
Напомним, что синус угла можно посмотреть в специальной таблице, названной в честь выдающегося советского математика В. М. Брадиса.
А теперь перейдем к другим формулам, подходящим только для исключительных видов треугольников.
Площадь прямоугольного треугольника
Помимо универсальной формулы, включающей в себя необходимость проводить высоту в треугольнике, площадь треугольника, содержащего прямой угол, можно найти по его катетам.
Так, площадь треугольника, содержащего прямой угол, — это половина произведения его катетов, или:
где a и b — катеты прямоугольного треугольника.
Правильный треугольник
Данный вид геометрических фигур отличается тем, что его площадь можно найти при указанной величине лишь одной его стороны (так как все стороны правильного треугольника равны).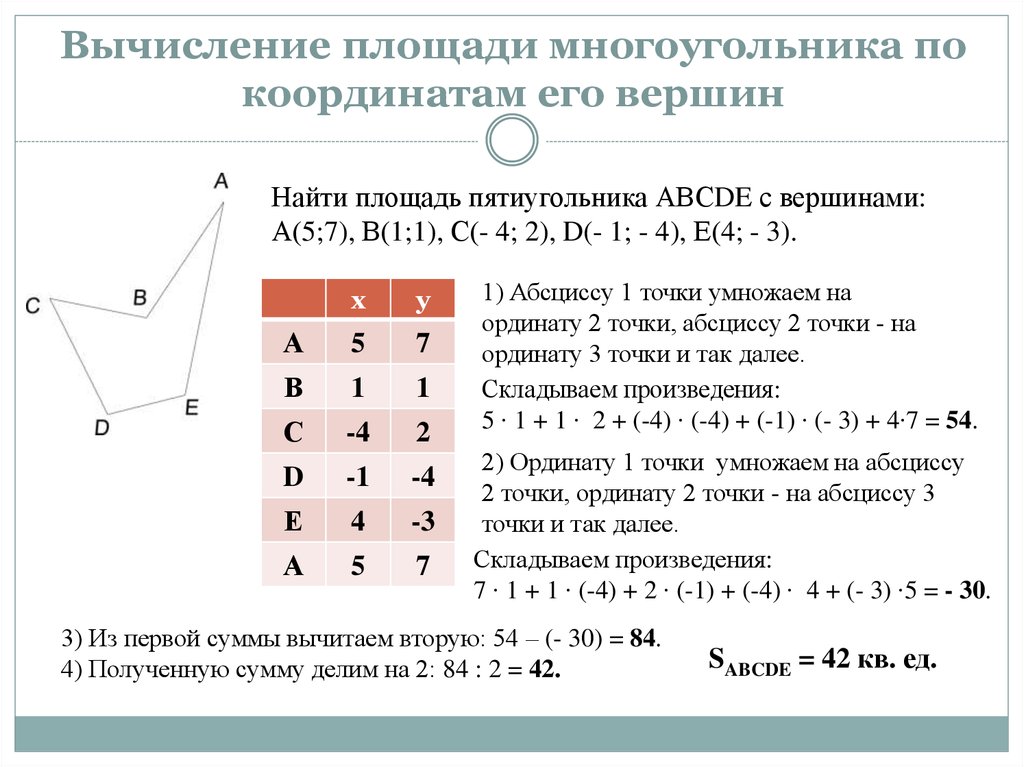 Итак, встретившись с задачей «найти площадь треугольника, когда стороны равны», нужно воспользоваться следующей формулой:
Итак, встретившись с задачей «найти площадь треугольника, когда стороны равны», нужно воспользоваться следующей формулой:
S = A 2 *√3 / 4,
где A — это сторона равностороннего треугольника.
Формула Герона
Последний вариант для нахождения площади треугольника — это формула Герона. Для того чтобы ею воспользоваться, необходимо знать длины трех сторон фигуры. Формула Герона выглядит так:
S = √p·(p — a)·(p — b)·(p — c),
где a, b и c — это стороны данного треугольника.
Иногда в задаче дано: «площадь правильного треугольника — найти длину его стороны». В данном случае нужно воспользоваться уже известной нам формулой нахождения площади правильного треугольника и вывести из нее значение стороны (или ее квадрата):
A 2 = 4S / √3.
Экзаменационные задачи
В задачах ГИА по математике встречаются множество формул. Помимо этого, достаточно часто необходимо найти площадь треугольника на клетчатой бумаге.
В данном случае удобнее всего провести высоту к одной из сторон фигуры, определить по клеткам ее длину и воспользоваться универсальной формулой для нахождения площади:
Итак, после изучения представленных в статье формул, у вас не возникнут проблемы при нахождении площади треугольника любого вида.
Калькулятор площади треугольника с координатами
Создано Krishna Nelaturu
Отзыв от Rijk de Wet
Последнее обновление: 02 февраля 2023 г.
Содержание:- Формула площади треугольника с вершинами 0 9 площадь треугольника с координатами?
- Как вычислить периметр треугольника с помощью точек?
- Как использовать этот калькулятор площади треугольника с координатами
- Другие связанные калькуляторы
- Часто задаваемые вопросы
Если вы хотите рассчитать площадь треугольника с вершинами , то этот калькулятор площади треугольника с координатами — правильный инструмент для вас! Вы также можете использовать этот калькулятор, чтобы найти периметра треугольника с вершинами . В этой статье вы узнаете:
- Какова формула площади треугольника с вершинами?
- Как найти площадь треугольника с координатами?
- Как вычислить периметр треугольника с помощью точек?
- Как определить, лежат ли три заданные точки на одной прямой?
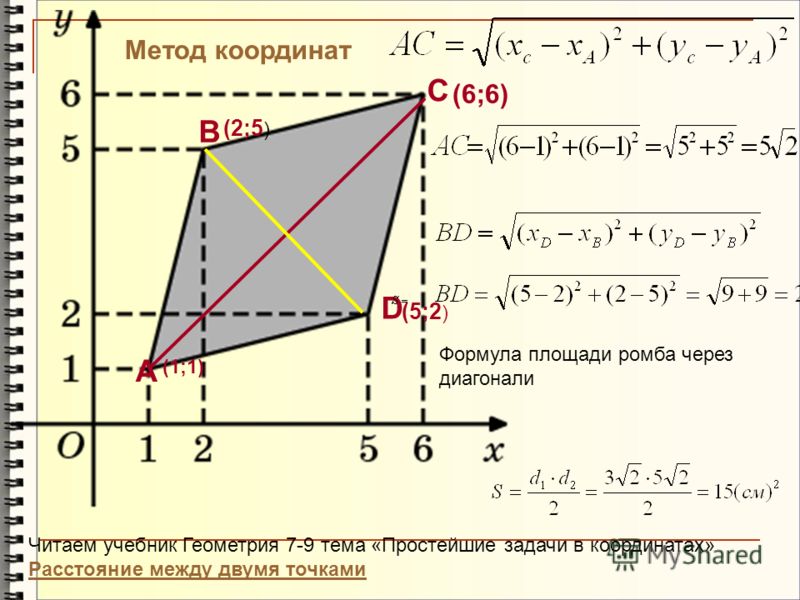
Формула площади треугольника с вершинами
Треугольник, образованный тремя точками A(x1,y1)A(x_1, y_1)A(x1,y1), B(x2,y2)B(x_2, y_2)B( x2,y2) и C(x3,y3)C(x_3, y_3)C(x3,y3).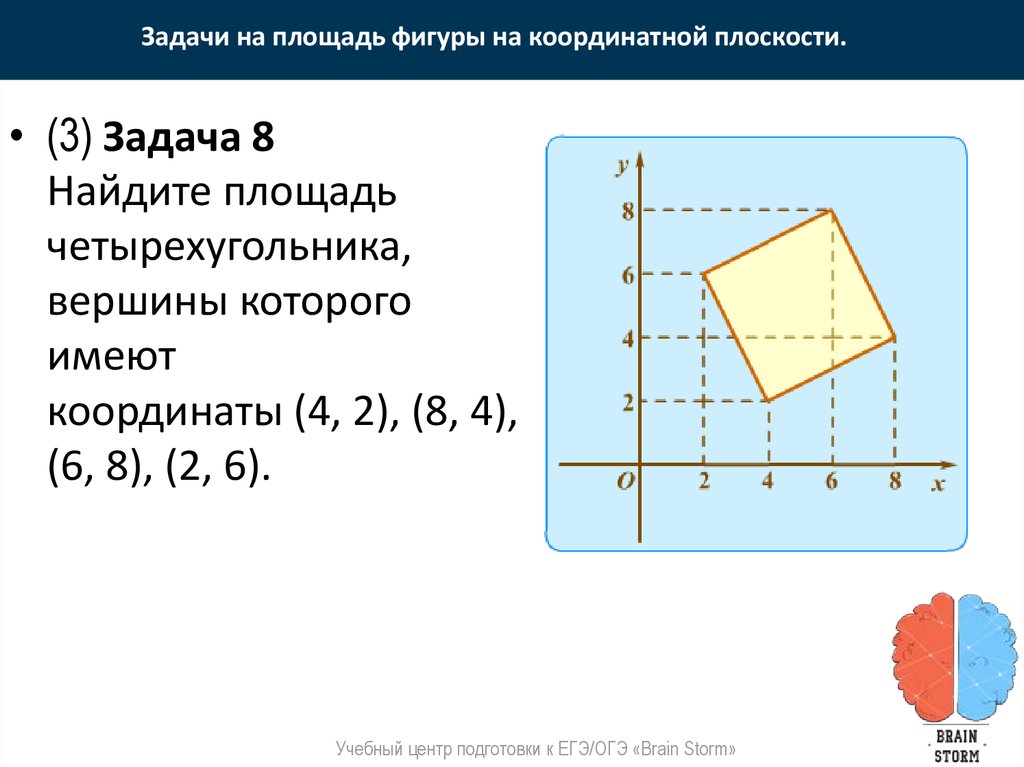
Формула для площади треугольника из его трех вершин задается следующим образом: \начать{выравнивать*} \text{Площадь} = \frac{1}{2} &\big\lvert x_1(y_2-y_3) + x_2(y_3-y_1) \\ &+ x_3(y_1-y_2) \big\rvert \end{align*}Area=21∣
∣x1(y2−y3)+x2(y3−y1)+x3(y1−y2)∣
∣
где:
- Area\text{ Area}Площадь равна площади треугольника ABCABCABC;
- (x1,y1)(x_1,y_1)(x1,y1) — координаты вершины AAA;
- (x2,y2)(x_2,y_2)(x2,y2) — координаты вершины BBB; и
- (x3,y3)(x_3,y_3)(x3,y3) — координаты вершины CCC;
Эта простая формула удобна для вычисления площади треугольника по трем координатам. Другой способ выразить эту же формулу через с помощью определителя . Чтобы вычислить площадь треугольника по 3 точкам:
Area=12∣111x1x2x3y1y2y3∣\text{Area} = \frac{1}{2} \begin{vmatrix} 1 и 1 и 1\\ х_1 и х_2 и х_3 \\ у_1 и у_2 и у_3 \end{vmatrix}Area=21∣
∣1×1y11×2y21×3y3∣
∣
Как найти площадь треугольника с координатами?
Чтобы вычислить площадь треугольника с его вершинами A(x 1 , y 1 ), B(x 2 , y 2 ) и C(x 3 , y 3 ) , выполните следующие простые действия: значение выражения |x 1 (y 2 -y 3 ) + x 2 (y 3 -y 1 ) + x 3 09 3 (y 19093 92 2 )| .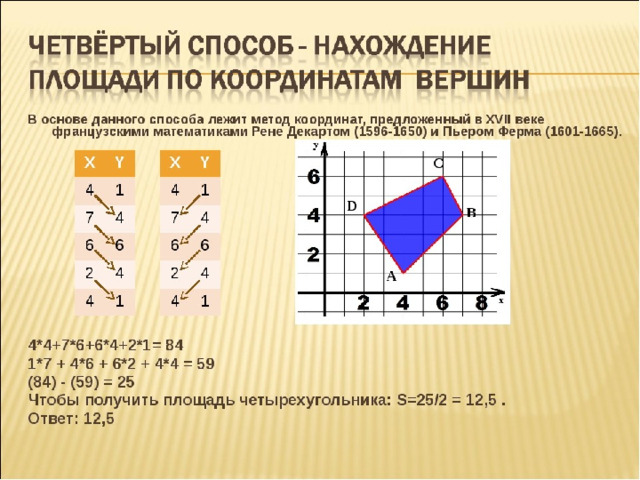
Как вычислить периметр треугольника с помощью точек?
Чтобы вычислить и найти периметр треугольника с его вершинами A(x 1 , y 1 ), B(x 2 , y 2 ) , и 903 9020 C(x , y 3 ) , выполните следующие простые шаги:
- Рассчитайте длину стороны AB , используя формулу расстояния AB = √(x 909 x 3 2 1 ) 2 + (у 2 − у 1 ) 2 .
- Аналогично, найти длины сторон BC и AC , используя формулу расстояния .
- Добавьте длин трех сторон , чтобы получить периметр треугольника ABC.

- Проверьте этот результат, используя нашу площадь треугольника с калькулятором координат.
Как использовать эту площадь треугольника с калькулятором координат
Этот калькулятор может выполнять две функции одновременно:
- Вычислять площадь треугольника по трем точкам.
- Вычислите (или найдите) периметр треугольника с точками.
Просто введите координаты вершин треугольника, а все остальное сделает этот калькулятор.
У нас есть еще калькуляторы треугольников для вас:
- Калькулятор площади треугольника;
- Калькулятор подобных треугольников;
- Калькулятор площади трехстороннего треугольника; Калькулятор
- квадратных футов треугольника;
- Калькулятор площади разностороннего треугольника;
- Калькулятор площади тупоугольного треугольника;
- Калькулятор площади косоугольного треугольника; и
- Площадь треугольника Калькулятор SAS.
Часто задаваемые вопросы
Как определить, лежат ли три точки на одной прямой?
Чтобы определить, являются ли любые три точки A(x 1 , y 1 ), B(x 2 , y 2 ) и C(x 3 , y 3 ) коллинеарны, выполните следующие шаги:
- Оцените значение выражения | 93 ) + x 2 (y 3 −y 1 ) + x 3 (y 1 −y 2 )| .

- Если это значение равно нулю , точки коллинеарны . Если это значение ненулевое , точки неколлинеарны .
Какова площадь треугольника, образованного A(1,2), B(-1,1) и C(0,5)?
3,5 шт. Чтобы вычислить это значение самостоятельно, выполните следующие действия:
- Вычислите абсолютное значение выражения |(1)×(1−5)+(−1)×(5−2)+(0)×( 2−1)| = |−4−3+0| = 7 .
- Разделите это значение на 2 , чтобы получить 7/2 = 3,5 .
- Проверьте этот результат, используя нашу площадь треугольника с калькулятором координат.
Кришна Нелатуру
Площадь треугольника с вершинами A(x₁, y₁), B(x₂, y₂), C(x₃, y₃)
Периметр
Посмотреть 18 подобных калькуляторов треугольников 60 5 9
3 45 90 треугольникПлощадь прямоугольного треугольника… Еще 15
Математическая задача: Многоугольник — координаты площади
Найти периметр и площадь многоугольника с заданными вершинами.
T (2,7), U (2,9), V (5,9), W (5,7)
Правильный ответ:
p = 10S = 6
Пошаговое объяснение:
T=(2,7) U=(2,9) V=(5,9) W=(5,7) TU ∣∣ VW ∣∣y UV ∣∣ TW ∣∣ x UT ⊥ UV a=Uy−Ty=9−7=2 b=Vx−Tx=5−2=3 p=2⋅ (a+b)= 2⋅ (2+3)=10
S=a⋅ b=2⋅ 3=6
Нашли ошибку или неточность? Не стесняйтесь
написать нам. Спасибо!
Чтобы решить эту математическую задачу, вам необходимо знать следующие знания:
- геометрия
- аналитическая геометрия
- арифметика
- абсолютное значение
- планиметрия
- многоугольник
- периметр
- 0 прямоугольник 30 1052100 Единица измерения s физических величин:
- площадь
Класс задачи:
- Практика для 13-летних
- Практика для 14-летних
Рекомендуем посмотреть это обучающее видео по этой математической задаче: видео1
- Построить 8
Построить задачу аналитической геометрии, где требуется найти вершины треугольника ABC: Вершинами этого треугольника являются точки A (1,7), B (-5,1) C (5, — 11). В указанной задаче следует использовать понятия расстояния от точки до прямой, рати
В указанной задаче следует использовать понятия расстояния от точки до прямой, рати - Прямоугольный 66344
Из квадрата со стороной 4 см вырежем четыре прямоугольных равнобедренных треугольника с прямыми углами в вершинах квадрата и с нахлестом √2 см. Получаем восьмиугольник. Вычислите его периметр, если площадь восьмиугольника равна 14 см². - Прямоугольник 39
Найдите периметр и площадь прямоугольника с вершинами (-1, 4), (0,4), (0, -1) и (-4, 4) - Прямоугольный треугольник 2
LMN — прямоугольный треугольник с вершинами в точках L(1,3), M(3,5) и N(6,n). Данный угол LMN равен 90° найти n - Координаты шестиугольника
Дан правильный шестиугольник ABCDEF. Точка А имеет координаты [1; 3], а точка D имеет координаты [4; 7]. Вычислите сумму координат центра его описанной окружности. - Координаты
Координаты (5, 2) и (-6, 2) являются вершинами шестиугольника. Объясните, как найти длину отрезка, образованного этими концами. Какова длина сегмента? - Окружность 7143
Петя начертил правильный шестиугольник, вершины которого лежат на окружности длиной 16 см. Затем для каждой вершины этого шестиугольника он нарисовал окружность с центром в этой вершине, проходящую через две ее соседние вершины. Блок получился как на картинке. Найдите ci
Затем для каждой вершины этого шестиугольника он нарисовал окружность с центром в этой вершине, проходящую через две ее соседние вершины. Блок получился как на картинке. Найдите ci - Шестиугольная призма
Основание призмы представляет собой правильный шестиугольник, состоящий из шести треугольников со стороной a = 12 см и высотой va = 10,4 см. Высота призмы 5 см. Найдите объем и поверхность призмы. - Додекагон
Найдите площадь правильного двенадцатиугольника (n=12), если радиус описанной окружности равен 5 см. - Пятиугольник
Найдите периметр пятиугольника, стороны которого равны 11/2 см, 7/4 см, 3 1/3 см, 2 1/3 см и 2 1/12 см. - MO Z8–I–6 2018
Трапеция KLMN, KL имеет основание 40 см и MN 16 см. Точка P лежит на прямой KL так, что отрезок NP делит трапецию на две части одинаковой площади. Найдите длину линии КП. - Четырехугольник 78874
Дан четырехугольник ABCD, вписанный в окружность, диагональ АС которого равна диаметру окружности. Расстояние между точкой В и диаметром 15 см, а между точкой D и диаметром 18 см. Вычислить радиус окружности и перим
Расстояние между точкой В и диаметром 15 см, а между точкой D и диаметром 18 см. Вычислить радиус окружности и перим - Определить
Определить тип четырехугольника ABCD и найти его периметр, если известны координаты вершин: A/2,4/, B/-2,1/, C/-2 , -2 /, Д/2, -5 /. - N точек сбоку
У равностороннего треугольника A, B и C на каждой из его внутренних сторон лежит N=13 точек. Найдите количество всех треугольников, вершины которых лежат в данных точках по разные стороны. - Проценты 80164
Мне дали квадрат ABCD 4,2 см. Найдите множество всех точек, отстоящих от одной из его вершин на расстояние меньше или равное 2 см и лежащих внутри этого квадрата. Укажите, какую часть квадрата занимает эта площадь в процентах. - Прямоугольник 5
Прямоугольник OABC имеет одну вершину в точке O, центре круга, а вторая вершина A находится на расстоянии 2 см от края круга, как показано на рисунке. Вершина А также находится на расстоянии 7 см от С. Точки В и С лежат на окружности окружности.


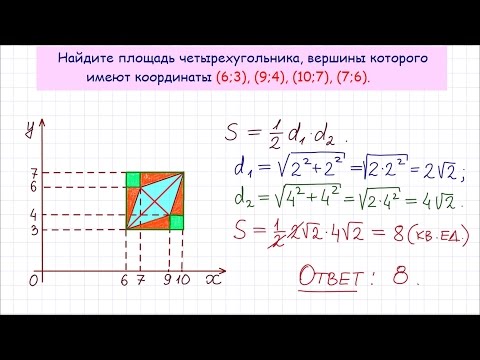
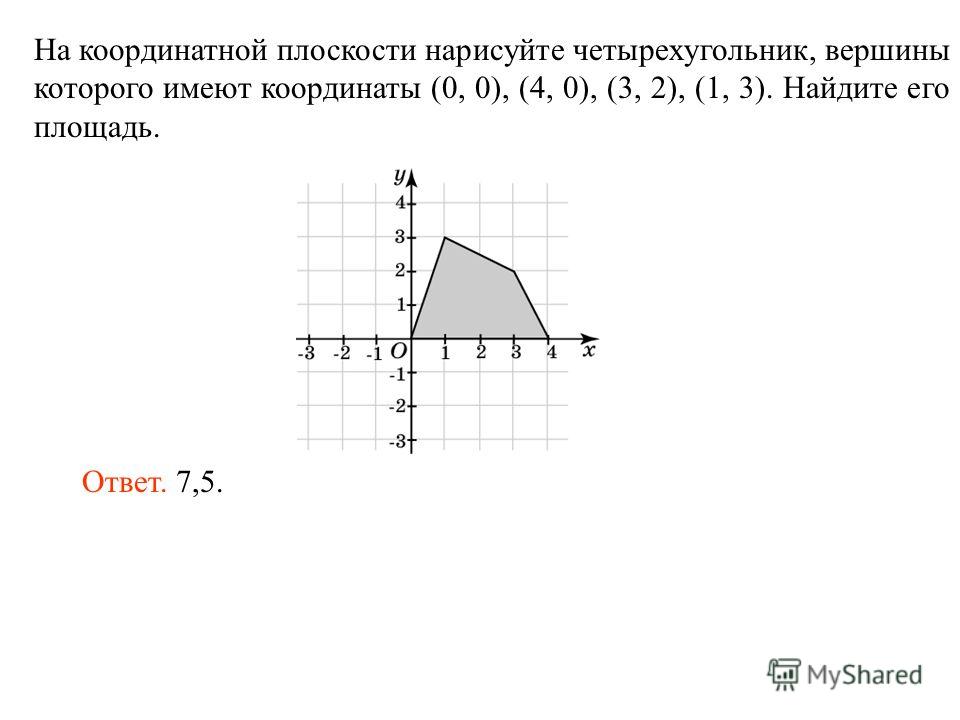 Угол между ними.
Угол между ними.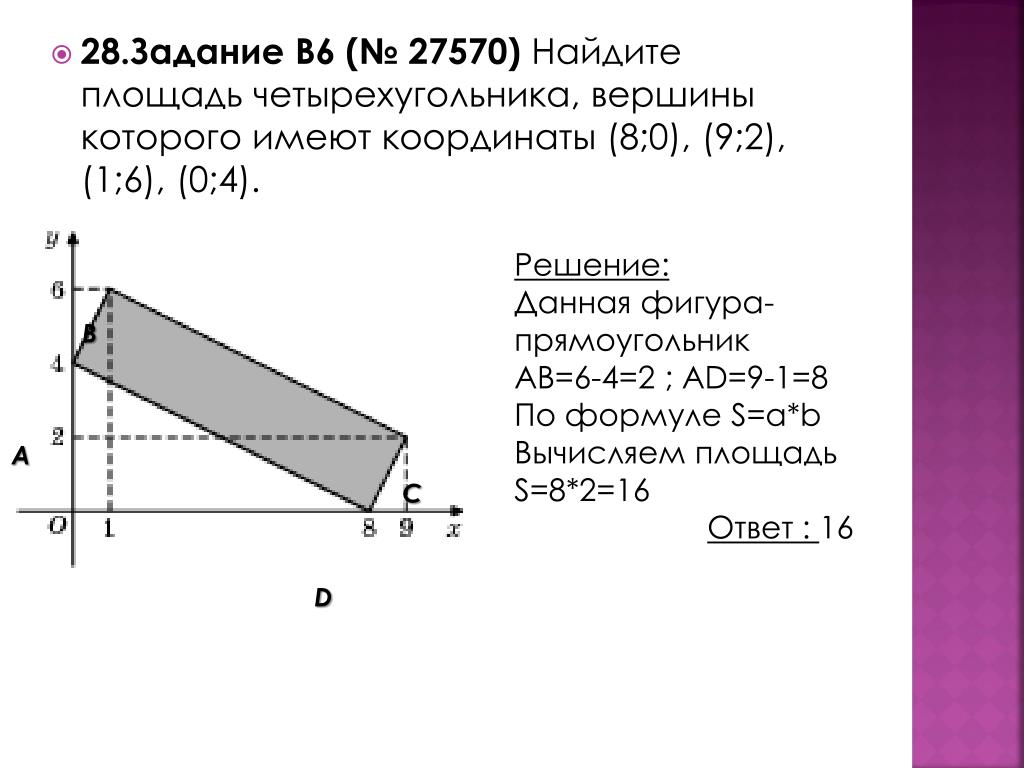 Матрица смежности онлайн
Матрица смежности онлайн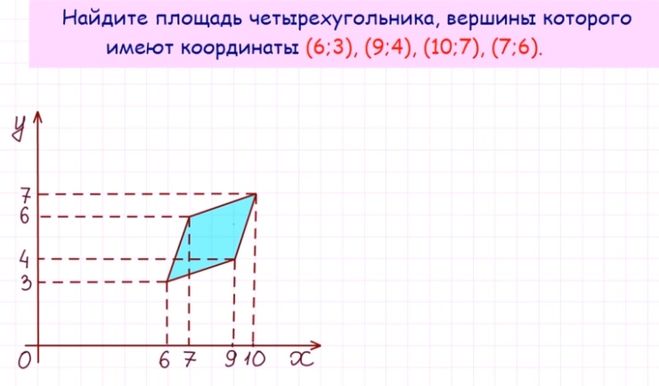

 В указанной задаче следует использовать понятия расстояния от точки до прямой, рати
В указанной задаче следует использовать понятия расстояния от точки до прямой, рати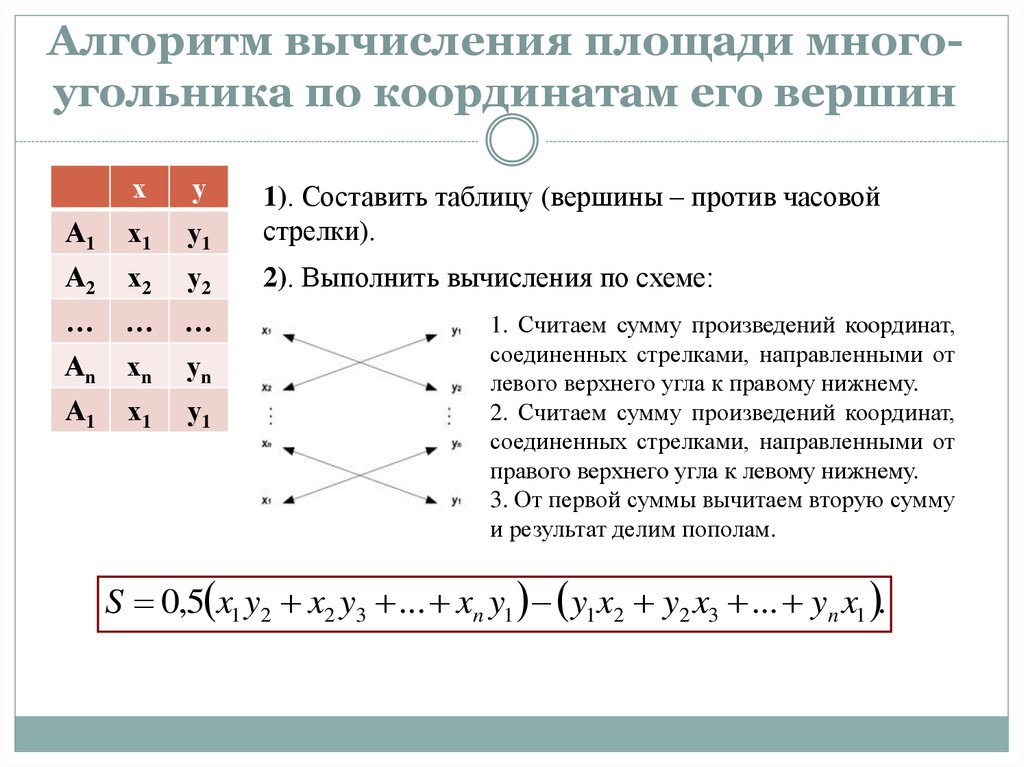 Затем для каждой вершины этого шестиугольника он нарисовал окружность с центром в этой вершине, проходящую через две ее соседние вершины. Блок получился как на картинке. Найдите ci
Затем для каждой вершины этого шестиугольника он нарисовал окружность с центром в этой вершине, проходящую через две ее соседние вершины. Блок получился как на картинке. Найдите ci Расстояние между точкой В и диаметром 15 см, а между точкой D и диаметром 18 см. Вычислить радиус окружности и перим
Расстояние между точкой В и диаметром 15 см, а между точкой D и диаметром 18 см. Вычислить радиус окружности и перим
Leave A Comment