Помогите. Найти квадрат длины вектора с началом в точке А(3,1,0) и концом в точке В(2,2,2) — вопрос №2173237 — Учеба и наука

Лучший ответ по мнению автора

Оксана

Вектор АВ имеет координаты (2-3,2-1,2_0)=(-1,1,2)
Квадрат длины равен сумме квадратов координат: 1+1+4=6

21. 10.16
Лучший ответ по мнению автора

Ответ понравился автору вопроса

Другие ответы

Координаты вектора АВ(2-3; 2-1; 2-0)=(-1; 1; 2)
|АВ|^2=(-1)^2 +1^2 +2^2=1+1+4=6

21. 2 = 1 + 1 + 4 = 6

23.10.16

Михаил Александров
Читать ответы

Андрей Андреевич
Читать ответы

Eleonora Gabrielyan
Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Математика

Похожие вопросы

Решено

на трёх полках стояли книги . 2 — 2x — 3. Найдите: а)наименьшее значение функции; б) значения x, при которых значение функции равно 5; в) значение…

Пользуйтесь нашим приложением

вектор длина

Вы искали вектор длина? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычисление длины вектора, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «вектор длина».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает.

Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как вектор длина,вычисление длины вектора,вычисление длины вектора по его координатам,вычисление длины вектора по его координатам доказательство,вычислить длину вектора,длина вектор,длина вектора,длина вектора c,длина вектора в пространстве,длина вектора как найти,длина вектора как обозначается,длина вектора модуль вектора,длина вектора определение,длина вектора по двум точкам,длина вектора по его координатам,длина вектора по координатам,длина вектора по координатам начала и конца,длина вектора по координатам точек,длина вектора по координатам формула,длина вектора равна,длина вектора равна квадратному корню из суммы его координат,длина вектора формула,длина вектора формула по координатам,длина вектора через координаты,длина вектора это,длина векторов,длина векторов по координатам,длина через координаты вектора,длину вектора,длины векторов,длины векторов как найти,как в прямоугольнике найти длины векторов,как вычислить длину вектора,как вычислить длину вектора по координатам,как зная координаты вектора найти его длину,как зная координаты найти длину вектора,как найти длина вектора,как найти длину вектора,как найти длину вектора ав,как найти длину вектора если известны его координаты,как найти длину вектора если известны координаты вектора,как найти длину вектора зная его координаты,как найти длину вектора зная его координаты начала и конца,как найти длину вектора зная координаты,как найти длину вектора зная координаты его начала и конца,как найти длину вектора и координаты,как найти длину вектора по двум точкам,как найти длину вектора по его координатам,как найти длину вектора по координатам,как найти длину вектора по координатам двух точек,как найти длину вектора по координатам начала и конца,как найти длину вектора формула,как найти длину вектора через координаты,как найти длину векторов,как найти длину и координаты вектора,как найти длины векторов,как найти длины векторов по координатам,как найти квадрат длины вектора,как найти координаты вектора если известна длина вектора,как найти координаты вектора зная длину,как найти координаты вектора зная его длину,как найти координаты вектора зная его длину и координаты начала,как найти координаты вектора и длину,как найти координаты вектора через длину,как найти координаты и длину вектора,как находить длину вектора,как обозначается длина вектора,как определить длину вектора,как определить длину вектора по координатам,как узнать длину вектора,как узнать длину вектора по координатам,квадрат длины вектора формула,координаты вектора длина вектора,модуль вектора длина вектора,модуль вектора определение,найдите длину и координаты вектора,найдите длины векторов,найти длину вектора,найти длину вектора по координатам,найти длину вектора по координатам точек,найти длину и координаты вектора,найти длину по координатам точек вектора,найти длины векторов,найти координаты вектора и длину,найти координаты и длину вектора,нахождение длины вектора,нахождение длины вектора по его координатам,определение вектора длина вектора,определение вектора длины,определение вектора длины вектора,определение длина вектора,определение длины вектора,определение модуль вектора,по координатам точек найти длину вектора,формула вычисления длины вектора,формула вычисления длины вектора по его координатам,формула длина вектора,формула длины вектора,формула длины вектора по его координатам,формула для вычисления длины вектора по его координатам,формула для нахождения длины вектора,формула как найти длину вектора,формула квадрат длины вектора,формула модуля вектора,формула нахождения длины,формула нахождения длины вектора,формула нахождения длины вектора по его координатам,чему равна длина вектора,что такое длина вектора.
На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и вектор длина. Просто введите задачу в окошко и нажмите «решить» здесь (например, вычисление длины вектора по его координатам).

Решить задачу вектор длина вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

MathScene — Векторы — Урок 3

MathScene — Векторы — Урок 3

2008 Расмус Эф и Джанн Сак

Урок 3

Векторы в системе координат

 

Пример 1

точка А имеет координаты (2, 2), а точка В — координаты (6, 5) (см.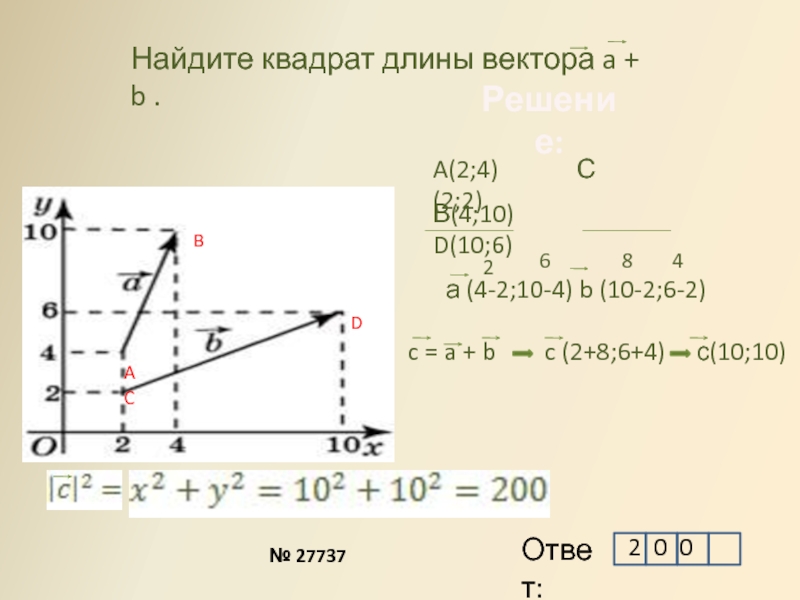 схему). Координаты вектора

Мы можно использовать формулу расстояния между двумя точками, чтобы найти расстояние между A и B, то есть длина вектора
(см. Правило Пифагора в уроке 2). Формула выглядит следующим образом:

Подставляя заданные координаты в формулу получаем:

Мы видим, что числа под квадратным корнем — это просто координаты вектор. Это, конечно, потому, что длина вектора — это просто гипотенуза в прямоугольном треугольнике с более короткими сторонами 3 и 4.

Формула длины вектора, начинающегося в точке
A = (x 1 , y 1 ) и заканчивается на B = (x 2 , у 2 ) равно:

Если координаты вектора то имеем следующее правило:


Пример 2

Найдите вектор что параллельно и который имеет длину 2 единицы (видеть диаграмму).

Два треугольника на диаграмме подобны, поэтому соответствующие стороны находятся в одинаковом соотношении.
|| = т∙||. Число t есть отношение между соответствующими сторонами. Отношение такое.
Мы можем найти координаты  как следует:

Если векторы и являются параллельно, то существует число t такое, что:

= т∙

Пример 3

Какие из следующих векторов параллельны и .

Если векторы и являются параллельно, то существует число t такое, что    = т∙. Если векторы и являются параллельно существует число r такое, что «=» р∙.

Мы можно найти числа t и r, используя координаты x, а затем проверить, чтобы увидеть найдены ли те же значения, когда мы используем координаты y.

= т∙

3 = t∙13 дает t = 3/13 = 2/9

4 = t∙18 также дает t = 4/18 = 2/9

векторы  и  есть параллель .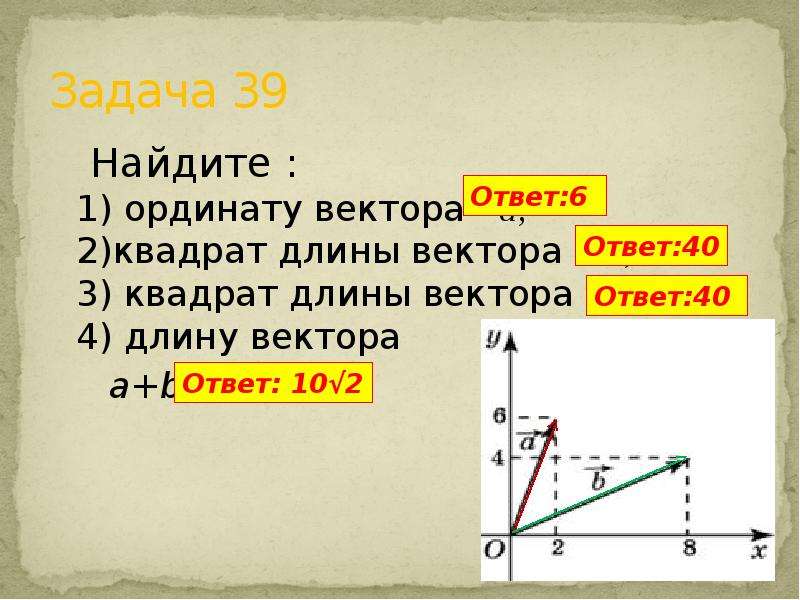

= р∙

3 = r∙6 дает r =

4 = r∙9 дает r = 4/9

векторы  и  есть не параллельно (Это значит, что и являются тоже не параллельно).

 

Вектор на диаграмме имеет координаты . вектор начинается в точке (0, 0) и заканчивается в (3, 2), поэтому координаты конечная точка совпадает с координатами самого вектора. Это относится к все векторы, которые начинаются в начале системы координат, то есть в точка (0, 0).

Вектор, который начинается в точке (0, 0), имеет те же координаты, что и его конечная точка. Этот вектор называется вектором положения для A.

Каждая точка в системе координат может быть представлена ​​своим вектором положения. Координаты точки и вектор ее положения совпадают. Это может быть очень полезно при просмотре переводов в системе координат.

Пример 4

Треугольник, показанный на диаграмме, должен быть переведен вектором .

Мы используем векторы положения вершинных точек (−3, 0),
(2, −2) и (3, 1) и добавляем вектор каждому из них.

Это дает нам новый вектор положения каждой вершины. Диаграмма ниже показывает перевод.

Пример 5

Теперь мы будем использовать векторы положения, чтобы найти середину отрезка AB, если А = (1, 2) и В = (4, 3).

Как обычно, точка O является началом системы координат. Если M середина AB тогда:

«=» + ∙

Вектор является вектор положения точки M и, следовательно, имеет те же координаты, что и точку М, которую мы хотим вычислить. Вектор – это вектор положения A. Чтобы достичь середины M, нам нужно добавить половину вектор . Нарисуйте схему, чтобы увидеть это.

Сначала нам нужно найти вектор .

Теперь мы можем найти .

«=» + ∙

Координаты M такие же, как у вектора положения или (2, 2) .

Легко найти формулу, по которой можно найти координаты точки. середина отрезка АВ.

Из диаграммы видно, что в середину М можно попасть из двух направлениях, от O через A до M и от O через B до M.

Таким образом, мы можем написать два векторных уравнения для .

«=» + ∙

«=» — ∙

Складывая эти два уравнения вместе, мы получаем

2 = + ∙ + — ∙

Мы видим, что вектор положения середины отрезка представляет собой своего рода среднее значение векторов положения конечных точек. Поэтому мы можем найти координаты средней точки, найдя среднее значение координат x и y координаты соответственно.
Это приводит нас к правилу, которое мы называем правилом средней точки.

Середина M отрезка AB задается правилом:

При использовании координат правило:

Пример 6

Вершинами треугольника ABC являются A = (1, 2), B = (4, 3) и C = (3, 0).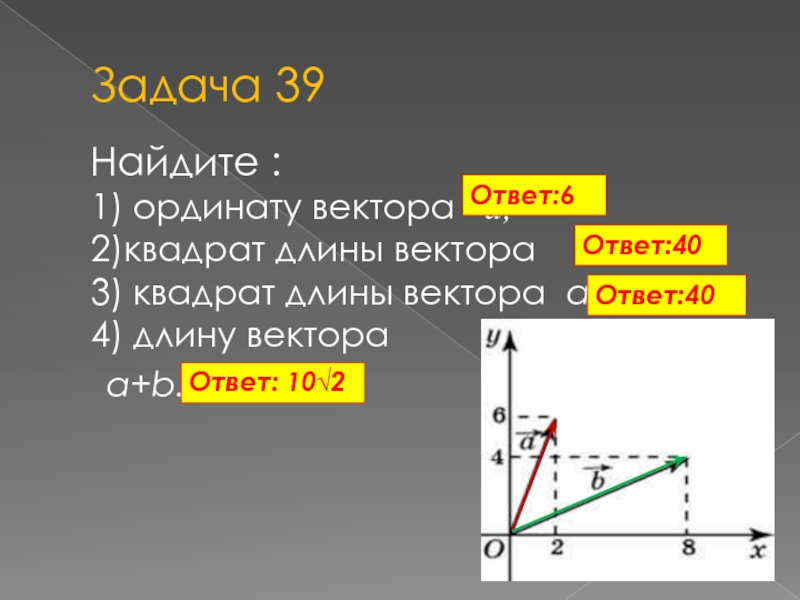

Найдите длину прямой, проведенной от А до середины стороны ВС (медиану стороны ВС). треугольник АВС).

Мы начнем с нахождения середины BC, используя приведенное выше правило.

Назовем середину M и найдем ее вектор положения (видеть схему).

= ∙ + ∙

Следовательно, M, середина ВС, имеет координаты
М = (3, 1).

Далее находим координаты вектора .

Наконец, мы можем найти длину вектора как необходимый.

           ≈ 2,55

Три медианы треугольника пересекаются в одной точке, называемой центр треугольника (обозначен Т на диаграмме). Если мы знаем координаты вершин треугольника можно найти координаты T по простой формуле. Эта формула находится аналогично Правило средней точки.

Мы можем достичь T через все три вершины треугольника, тогда мы добавляем три векторных выражения вместе.

В уроке 2 о треугольниках мы видели, что все медианы пересекаются в одной точке. точки, делящие друг друга в соотношении 2:1 или 2/1. Отсюда мы знаем, что длина вектора в два раза больше, чем и поэтому

«=» ∙ и «=» −∙. Используя это, мы можем написать три уравнения:

= + ∙ 

= + ∙ — ∙

= — ∙ — ∙

Когда мы сложим их вместе, выходит и мы получаем:

3= + +

Чтобы найти координаты T, мы берем среднее значение x и y координаты вершин соответственно.

Таким образом, мы находим точку пересечения T медиан треугольника путем нахождения своего рода среднего векторов положения вершины. Таким образом, это правило является расширением правила средней точки.

Пример 7

Найдите точку пересечения Т медиан треугольника АВС ( центр ) при условии, что A = (1, 2), B = (4, 3) и C = (3, 0) (см. схему).

Центр Т = (2, 1) .

Попробуйте Викторина 3 на Векторы.
Не забывайте использовать контрольный список, чтобы отслеживать свою работу.

 

 

 

 

 

 

 

 

 

Точечный продукт

Вектор имеет величины (длина) и направления :

Вот два вектора:

Они могут быть умножены на с использованием » Скалярного произведения » (см. также Перекрестное произведение).

Расчет

Скалярный продукт записывается с использованием центральной точки:

a · b
Это означает скалярное произведение a и б

Мы можем вычислить скалярное произведение двух векторов следующим образом:

а · б = | и | × | б | × cos(θ)

Где:
| и | величина (длина) вектора a
| б | модуль (длина) вектора b
θ угол между a и b

Итак, мы умножаем длину на a умножить на длину b , затем умножить на косинус угла между a и b

 

ИЛИ мы можем рассчитать это так:

a · b = a x x b x + a y x b y

Итак, мы умножаем x, умножаем y, а затем складываем.

Оба метода работают!

И результат номер (называемый «скаляром», чтобы показать, что это не вектор).

Пример: вычислить скалярное произведение векторов

a и b :

a · b = | и | × | б | × cos(θ)

a · b = 10 × 13 × cos(59,5°)

a · b = 10 × 13 × 0,5075…

a · b 9035 3 = 65,98… = 66 (округлено)

ИЛИ мы можем вычислить это так:

a · b = a x × b x + a y × b y

a · b = -6 × 5 + 8 × 12

90 352 а · б = -30 + 96

a · b = 66

Оба метода дали одинаковый результат (после округления)

Также обратите внимание, что мы использовали минус 6 для x (оно движется в отрицательном направлении x)

Примечание: вы можете использовать векторный калькулятор чтобы помочь вам.

Почему cos(θ) ?

Хорошо, чтобы умножить два вектора, имеет смысл перемножить их длины вместе , но только тогда, когда они указывают в одном направлении .

Итак, мы делаем одну «точку в том же направлении», что и другая, умножая на cos(θ):

   
Возьмем компонент a
, лежащий рядом с b 		  Как пролить свет, чтобы увидеть
где лежит тень

ТОГДА умножаем!

Это работает точно так же, если мы «проецируем» b рядом с a , а затем умножаем:

Потому что не имеет значения, в каком порядке мы делаем умножение:

| и | × | б | × потому что (θ) = | и | × соз (θ) × | б |

Прямоугольные

Когда два вектора расположены под прямым углом друг к другу, скалярное произведение равно нулю .

Пример: рассчитать скалярный продукт для:

a · b = | и | × | б | × cos(θ)

а · б = | и | × | б | × cos(90°)

а · б = | и | × | б | × 0

a · b = 0

или можно вычислить так:

a · b = a x x b x + a y x b y

a · b = -12 x 1 2 + 16 × 9

а · б = -144 + 144

а · б = 0

Это может быть удобным способом узнать, находятся ли два вектора под прямым углом.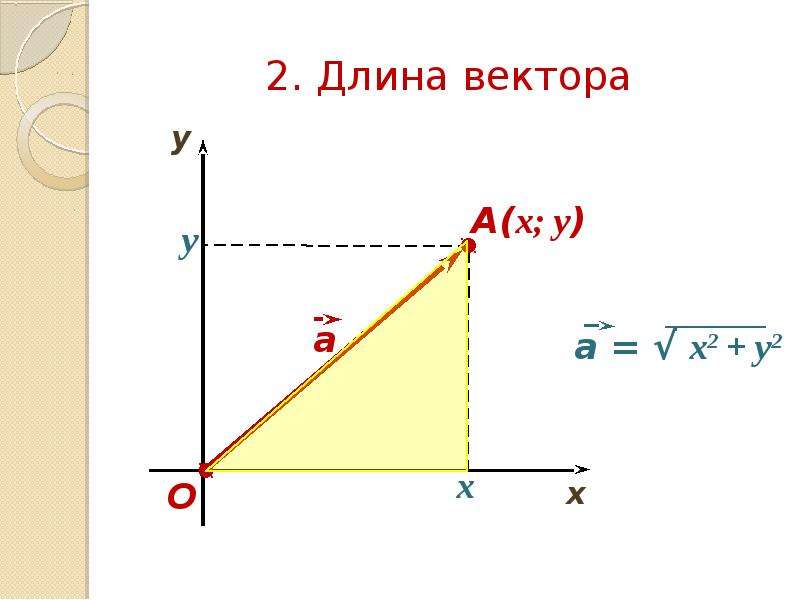

Три или более размеров

Все это прекрасно работает и в 3-х (или более) измерениях.

И действительно может быть очень полезным!

Пример: Сэм измерил концы двух полюсов и хочет узнать

угол между ними :

У нас есть 3 измерения, поэтому не забудьте z-компоненты:

a · b = a x x b x + a 90 042 г × б y + a z × b z

a · b = 9 × 4 + 2 × 8 + 7 × 10

a · b = 3 6 + 16 + 70

а · b = 122

 

Теперь другая формула:

a · b = | и | × | б | × cos(θ)

Но что такое | и | ? Это величина или длина вектора a . Мы можем использовать Pythagoras:

  • | и | = √(4 2 + 8 2 + 10 2 )
  • | и | = √(16 + 64 + 100)
  • | и | = √180

Аналогично для | б |:

  • | б | = √(9 2 + 2 2 + 7 2 )
  • | б | = √(81 + 4 + 49)
  • | б | = √134

И мы знаем из вычислений выше, что a · b = 122, поэтому:

a · b = | и | × | б | × cos(θ)

122 = √180 × √134 × cos(θ)

cos(θ) = 122 / (√180 × √134)

cos(θ) = 0,7855.