Площадь четырехугольника формула. Формула площади четырехугольника по диагоналям. Площадь произвольного четырехугольника.
- Альфашкола
- Статьи
- Площадь произвольного четырехугольника
Дарим в подарок бесплатный вводный урок!
Предметы
- Математика
- Репетитор по физике
- Репетитор по химии
- Репетитор по русскому языку
- Репетитор по английскому языку
- Репетитор по истории России
- Репетитор по биологии
- Репетитор по географии
- Репетитор по информатике
Специализации
- Подготовка к ЕГЭ по математике (базовый уровень)
- Репетитор по геометрии
- Репетитор для подготовки к ОГЭ по физике
- Подготовка к олимпиадам по физике
- Репетитор по английскому языку для подготовки к ЕГЭ
- Репетитор по английскому языку для подготовки к ОГЭ
- Подготовка к олимпиадам по английскому языку
- Репетитор по английскому для взрослых
- Репетитор по биологии для подготовки к ОГЭ
- Репетитор по информатике для подготовки к ОГЭ
Площадь произвольного четырехугольника можно найти перемножив диагонали данного четырехугольника, полученный результат разделить на \(2\) и умножить результат на синус угла.
\(S=\frac{1}{2} AC⋅BD \ sin\ φ\)
Первая диагональ четырехугольника:
Вторая диагональ четырехугольника:
Угол между диагоналями:
Больше уроков и заданий по всем школьным предметам в онлайн-школе «Альфа». Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Карина Рафаэльевна Сайфулина
Репетитор по математике
Стаж (лет)
Образование:
Крымский федеральный университет им.
Вернадского
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Юлия Игоревна Ярош
Репетитор по математике
Стаж (лет)
Образование:
Брестский государственный университет имени А. С. Пушкина
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Галина Федоровна Захарина
Репетитор по математике
Стаж (лет)
Образование:
Гомельский государственный университет имени Ф.
Скорины
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Похожие статьи
- Площадь цилиндра
- Средняя линия треугольника
- Разряды : сотни, десятки, единицы
- Графики кубических функций
- ЕГЭ по математике, профильный уровень. Рациональные уравнения
- Наводим красоту: топ-10 простых и красивых причесок для девушек (разного возраста)
- Отпусти меня, мама, я уже взрослый
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
| Справочник по математике | Геометрия (Планиметрия) | Четырехугольники |
| Формулы для площадей четырехугольников |
| Вывод формул для площадей четырехугольников |
| Вывод формулы Брахмагупты для площади вписанного четырехугольника |
В данном разделе рассматриваются только выпуклые фигуры, и считается известной формула:
S = ab,
которая позволяет найти площадь прямоугольникапрямоугольника с основанием a и высотой b.
Формулы для площадей четырехугольников
| Четырехугольник | Рисунок | Формула площади | Обозначения |
| Прямоугольник | S = ab | a и b – смежные стороны | |
Посмотреть вывод формулы | d – диагональ, | ||
S = 2R2 sin φ Получается из верхней формулы подстановкой d=2R | R – радиус описанной окружности, | ||
| Параллелограмм | S = a ha Посмотреть вывод формулы | a – сторона, | |
S = absin φ Посмотреть вывод формулы | a и b – смежные стороны, | ||
Посмотреть вывод формулы | d1, d2 – диагонали, φ – любой из четырёх углов между ними | ||
| Квадрат | S = a2 | a – сторона квадрата | |
| S = 4r2 | r – радиус вписанной окружности | ||
Посмотреть вывод формулы | d – диагональ квадрата | ||
S = 2R2 Получается из верхней формулы подстановкой d = 2R | R – радиус описанной окружности | ||
| Ромб | S = a ha Посмотреть вывод формулы | a – сторона, | |
S = a2 sin φ Посмотреть вывод формулы | a – сторона, | ||
Посмотреть вывод формулы | d1, d2 – диагонали | ||
S = 2ar Посмотреть вывод формулы | a – сторона, | ||
Посмотреть вывод формулы | r – радиус вписанной окружности, | ||
| Трапеция | Посмотреть вывод формулы | a и b – основания, | |
| S = m h | m – средняя линия, | ||
Посмотреть вывод формулы | d1, d2 – диагонали, φ – любой из четырёх углов между ними | ||
Посмотреть вывод формулы | a и b – основания, | ||
| Дельтоид | S = ab sin φ | a и b – неравные стороны, | |
a и b – неравные стороны, | |||
S = (a + b) r Посмотреть вывод формулы | a и b – неравные стороны, | ||
Посмотреть вывод формулы | d1, d2 – диагонали | ||
| Произвольный выпуклый четырёхугольник | Посмотреть вывод формулы | d1, d2 – диагонали, φ – любой из четырёх углов между ними | |
| Вписанный четырёхугольник | , Посмотреть вывод формулы Брахмагупты | a, b, c, d – длины сторон четырёхугольника, Формулу называют «Формула Брахмагупты» |
| Прямоугольник | |
S = ab где | |
где Посмотреть вывод формулы | |
S = 2R2 sin φ где Формула получается из верхней формулы подстановкой d = 2R | |
| Параллелограмм | |
S = a ha где Посмотреть вывод формулы | |
S = absin φ где Посмотреть вывод формулы | |
где φ – любой из четырёх углов между ними Посмотреть вывод формулы | |
| Квадрат | |
| S = a2 где | |
| S = 4r2 где | |
где Посмотреть вывод формулы | |
S = 2R2 где Получается из верхней формулы подстановкой d = 2R | |
| Ромб | |
S = a ha где Посмотреть вывод формулы | |
S = a2 sin φ где Посмотреть вывод формулы | |
где Посмотреть вывод формулы | |
S = 2ar где Посмотреть вывод формулы | |
где Посмотреть вывод формулы | |
| Трапеция | |
где Посмотреть вывод формулы | |
S = m h где | |
где φ – любой из четырёх углов между ними Посмотреть вывод формулы | |
где Посмотреть вывод формулы | |
| Дельтоид | |
S = ab sin φ где | |
где | |
S = (a + b) r где Посмотреть вывод формулы | |
где Посмотреть вывод формулы | |
| Произвольный выпуклый четырёхугольник | |
где φ – любой из четырёх углов между ними Посмотреть вывод формулы | |
| Вписанный четырёхугольник | |
, где Формулу называют «Формула Брахмагупты» Посмотреть вывод формулы Брахмагупты | |
| Прямоугольник |
S = ab где |
где Посмотреть вывод формулы |
S = 2R2 sin φ где Формула получается из верхней формулы подстановкой d = 2R |
| Параллелограмм |
S = a ha где Посмотреть вывод формулы |
S = absin φ где Посмотреть вывод формулы |
где φ – любой из четырёх углов между ними Посмотреть вывод формулы |
| Квадрат |
S = a2 где |
S = 4r2 где |
где Посмотреть вывод формулы |
S = 2R2 где Получается из верхней формулы подстановкой d = 2R |
| Ромб |
S = a ha где Посмотреть вывод формулы |
S = a2 sin φ где Посмотреть вывод формулы |
где Посмотреть вывод формулы |
S = 2ar где Посмотреть вывод формулы |
где Посмотреть вывод формулы |
| Трапеция |
где Посмотреть вывод формулы |
S = m h где |
где φ – любой из четырёх углов между ними Посмотреть вывод формулы |
где Посмотреть вывод формулы |
| Дельтоид |
S = ab sin φ где |
где |
S = (a + b) r где Посмотреть вывод формулы |
где Посмотреть вывод формулы |
| Произвольный выпуклый четырёхугольник |
где φ – любой из четырёх углов между ними Посмотреть вывод формулы |
| Вписанный четырёхугольник |
где Формулу называют «Формула Брахмагупты» Посмотреть вывод формулы Брахмагупты |
Вывод формул для площадей четырехугольников
Утверждение 1.
Площадь выпуклого четырёхугольника можно найти по формуле
где d1 и d2 – диагонали четырёхугольника, а φ – любой из четырёх углов между ними (рис. 1).
Рис. 1
Доказательство. В соответствии с рисунком 1 справедливо равенство:
что и требовалось доказать.
Утверждение 2. Площадь параллелограммапараллелограмма можно найти по формуле
S = a ha ,
где a – сторона параллелограмма, а ha – высотавысотавысота, опущенная на эту сторону (рис. 2).
Рис. 2
Доказательство. Поскольку прямоугольный треугольник DFC равен прямоугольному треугольнику AEB (рис.26), то четырёхугольник AEFB – прямоугольник. Поэтому
SABCD = SAEFD = a ha ,
что и требовалось доказать.
Утверждение 3.Площадь параллелограмма параллелограмма можно найти по формуле
S = ab sin φ,
где a и b – смежные стороны параллелограмма, а φ – угол между ними (рис. 3).
Рис. 3
Доказательство. Поскольку
ha = b sin φ,
то, в силу утверждения 2, справедлива формула
S = a ha = ab sin φ,
что и требовалось доказать.
Утверждение 4. Площадь ромбаромба можно найти по формуле
,
где r – радиус вписанной в ромб окружности, а φ – любой из четырёх углов ромба (рис.4).
Рис. 4
Доказательство. Поскольку каждая из диагоналей ромба является биссектрисой угла, а каждая точка биссектрисы угла равноудалена от сторон угла, то точка пересечения диагоналей ромба равноудалена от всех сторон ромба и является центром вписанной в ромб окружности.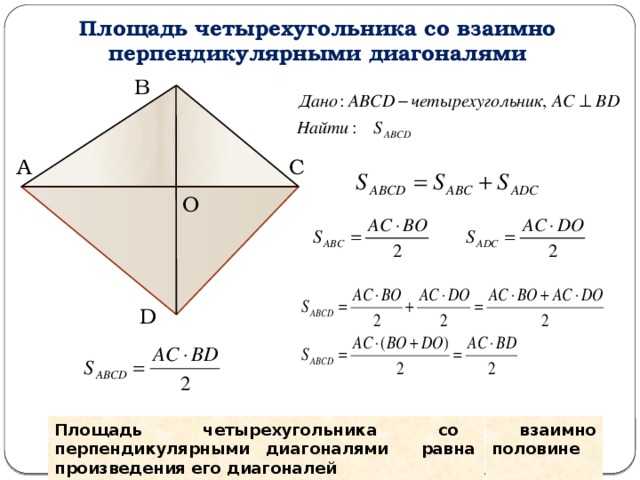
Отсюда следует, в частности, что высота ромба в 2 раза больше радиуса вписанной окружности (рис.4). Поэтому
что и требовалось доказать.
Утверждение 5. Площадь трапеции можно найти по формуле
,
где a и b – основания трапеции, а h – высотавысотавысота (рис.5).
Рис. 5
Доказательство. Проведём прямую BE через вершину B трапеции и середину E боковой стороны CD. Точку пересечения прямых AD и BE обозначим буквой F (рис. 5). Поскольку треугольник BCE равен треугольнику EDF (по стороне и прилежащим к ней углам), то площадь трапеции ABCD равна площади треугольника ABF. Поэтому
что и требовалось доказать.
Утверждение 6. Площадь трапеции трапеции можно найти по формуле
,
где a и b – основания, а c и d – боковые стороны трапеции,
(рис.
6).
Рис. 6
Доказательство. Воспользовавшись теоремой Пифагора, составим следующую систему уравнений с неизвестными x, y, h (рис. 6):
Следовательно,
где
,
что и требовалось доказать.
Утверждение 7. Площадь дельтоида, дельтоида, можно найти по формуле:
S = (a + b) r,
где a и b – неравные стороны дельтоида, а r – радиус вписанной в дельтоид окружности (рис.7).
Рис. 7
Доказательство. Докажем сначала, что в каждый дельтоид можно вписать окружность. Для этого заметим, что треугольники ABD и BCD равны в силу признака равенства треугольников «По трём сторонам» (рис. 7). Отсюда вытекает, что диагональ BD является биссектрисой углов B и D, а биссектрисы углов A и C пересекаются в некоторой точке O, лежащей на диагонали BD.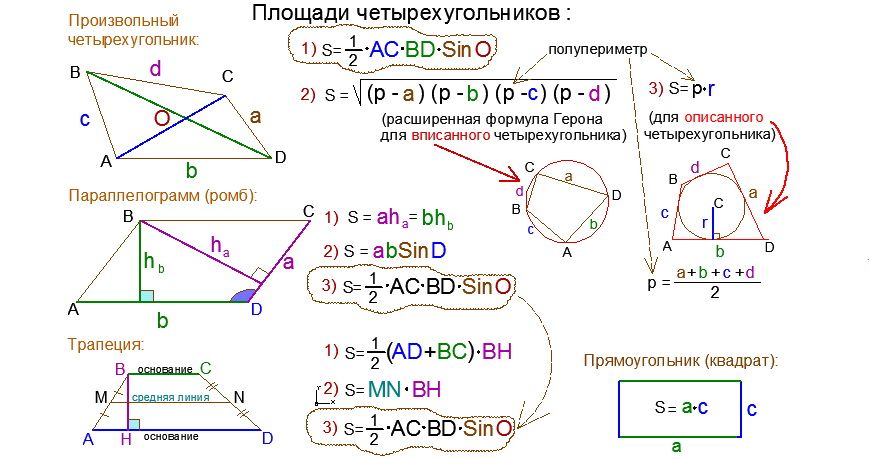
Точка O и является центром вписанной в дельтоид окружности.
Если r – радиус вписанной в дельтоид окружности, то
что и требовалось доказать.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Как найти площадь четырехугольника? Определение, примеры, факты
Четырехугольник — это многоугольник, который получается путем соединения четырех вершин, и он имеет четыре стороны и четыре угла. Есть два типа четырехугольников — правильные и неправильные четырехугольники. Некоторыми примерами четырехугольников являются квадрат, прямоугольник, ромб, трапеция и параллелограмм. Площадь многоугольника относится к пространству, занимаемому плоской формой. Это сумма площадей правильного и неправильного треугольников внутри.
Чтобы оценить площадь четырехугольника, мы разделим его на две основные геометрические фигуры, например треугольники. Затем мы находим площади двух отдельных треугольников, используя формулу, и складываем эти площади, чтобы найти площадь четырехугольника.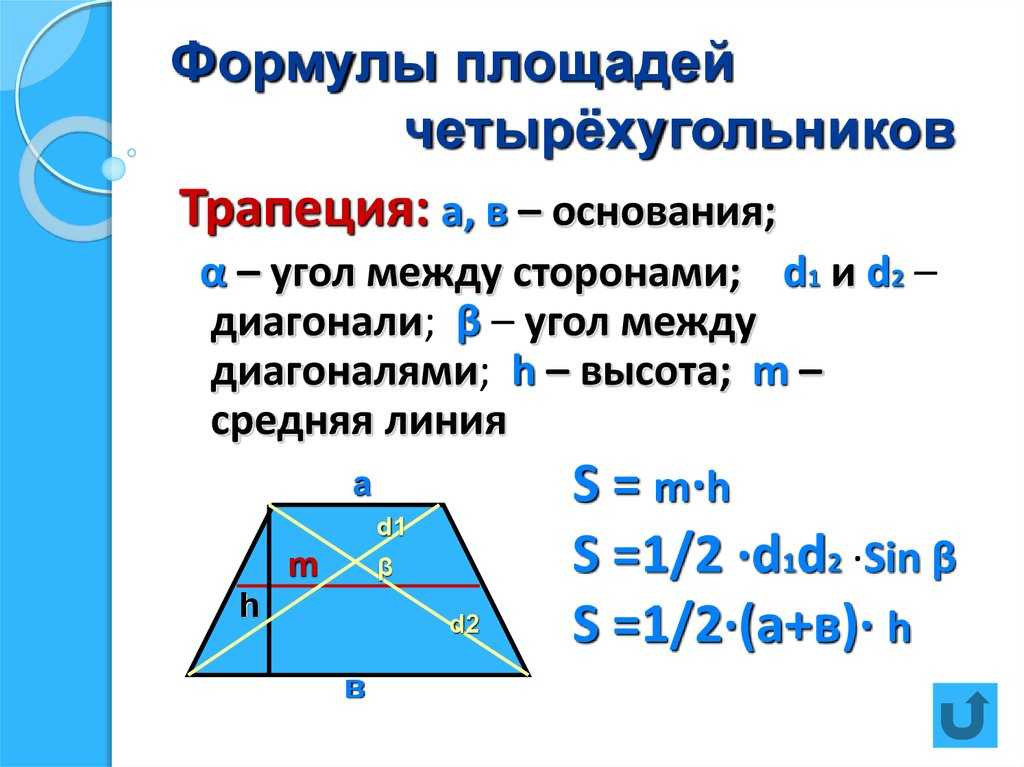
Мы можем вычислить площади различных типов четырехугольников, используя данную формулу. Для четырехугольника ABCD, если мы используем сантиметр в качестве единицы измерения, единицей измерения площади будет см 2 .
Чтобы вычислить площадь параллелограмма, проведите перпендикуляр из одной из вершин к основанию. Этот перпендикуляр и есть высота. Таким образом, площадь будет произведением основания и высоты.
Чтобы найти площадь ромба, мы разделим четырехугольник на два равных равнобедренных треугольника, используя две диагонали. В данном ромбе ABCD точкой пересечения этих диагоналей является E. Таким образом, площадь ромба равна:
Площадь прямоугольника с использованием приведенной выше формулы даст произведение двух его смежных сторон, основания и высоты. Мы представляем это как:
Реальное применение четырехугольников и их площади очень полезно в области дизайна, сельского хозяйства и архитектуры. Эта концепция очень полезна при расширенном проектировании навигационных карт, масштабированных с точностью до фактических расстояний и областей.
Площадь четырехугольника, образованного соединением четырех различных точек на карте
1 Площадь параллелограмма с основанием в 5 единиц равна 30 квадратных единиц. Какова высота параллелограмма?3 единицы 6 единиц 10 единиц 12 единиц Правильный ответ: 6 единиц 2 Площадь ромба с диагональю 8 см равна 24 кв.см. Какова длина другой диагонали?2 см 3 см 4 см 6 см Правильный ответ: 6 см 3 Какова площадь параллелограмма с основанием 7 см и высотой 8 см? 15 кв. 28 кв. см 30 кв. см 56 кв. см Правильный ответ: 56 кв. см 4 Какова площадь ромба с диагоналями 6 единиц и 9 единиц?15 квадратных единиц 27 квадратных единиц 30 квадратных единиц 54 квадратных единиц Правильный ответ: 27 квадратных единиц |
смКак найти площадь четырехугольника?
Чтобы найти площадь четырехугольника, разделите его диагональю на два треугольника. Затем вычислите площадь каждого треугольника и сложите их.
По какой формуле найти площадь четырехугольника?
Площадь четырехугольника = (1/2) × d × (h2 + h3). Здесь d = диагональ четырехугольника, h2, h3 = высоты треугольников, образованных по обе стороны от диагонали (d)
Какова единица площади четырехугольника?
Единица площади четырехугольника такая же, как и у других фигур, т.
е. квадратные единицы длины (квадратный метр, квадратный дюйм и т. д.)
По какой формуле найти площадь особых четырехугольников?
Вот формулы для нахождения площади особых четырехугольников: – Площадь квадрата = сторона × сторона – Площадь прямоугольника = длина × ширина – Площадь параллелограмма = основание × высота – Площадь трапеции = 1/ 2 × (основание1 + основание2) × высота – Площадь ромба = 1/2 × диагональ1 × диагональ2 – Площадь воздушного змея = 1/2 × диагональ1 × диагональ2
Площадь четырехугольника – формула, определение и примеры
Площадь четырехугольника – это площадь области внутри него. Вспомним, что такое четырехугольник. Четырехугольник — это замкнутая фигура, ограниченная четырьмя отрезками. Четырехугольник может быть правильным и неправильным. Правильный четырехугольник – это четырехугольник, у которого все стороны имеют одинаковую длину. Четырехугольник, который не является правильным, называется неправильным четырехугольником.
- квадратный
- прямоугольник
- параллелограмм
- трапеция
- ромб
- воздушный змей
На этой странице мы увидим, как найти площадь четырехугольника, разделив его на два треугольника, и как найти площадь четырехугольника, используя его 4 стороны. Кроме того, мы изучим формулы для нахождения площади каждого из этих различных типов четырехугольников.
| 1. | Что такое площадь четырехугольника? |
| 2. | Формула площади четырехугольника путем деления на два треугольника |
| 3. | Формула площади четырехугольника с использованием сторон |
| 4. | Формулы площади четырехугольников различных типов |
| 5. | Площадь четырехугольника по формуле Герона |
| 6. | Площадь четырехугольника с использованием координат |
7. | Часто задаваемые вопросы о площади четырехугольника |
Какова площадь четырехугольника?
Площадь четырехугольника есть не что иное, как область, ограниченная сторонами четырехугольника. Она измеряется в квадратных единицах, таких как м 2 , 2 см , 2 см и т. Д. Процесс нахождения площади четырехугольника зависит от его типа и информации, доступной о четырехугольнике. Если четырехугольник не принадлежит ни к одному из упомянутых выше типов, то его площадь можно найти либо разбив его на два треугольника, либо воспользовавшись формулой (которая называется формулой Бретшнейдера) нахождения площади четырехугольника используя четыре стороны. Здесь вы можете увидеть формулы для нахождения площади четырехугольника, который не принадлежит ни к одному из стандартных типов.
Давайте узнаем больше об этих формулах в следующих разделах.
Формула площади четырехугольника путем деления на два треугольника
Рассмотрим четырехугольник ABCD, длина диагонали BD которого известна как «d».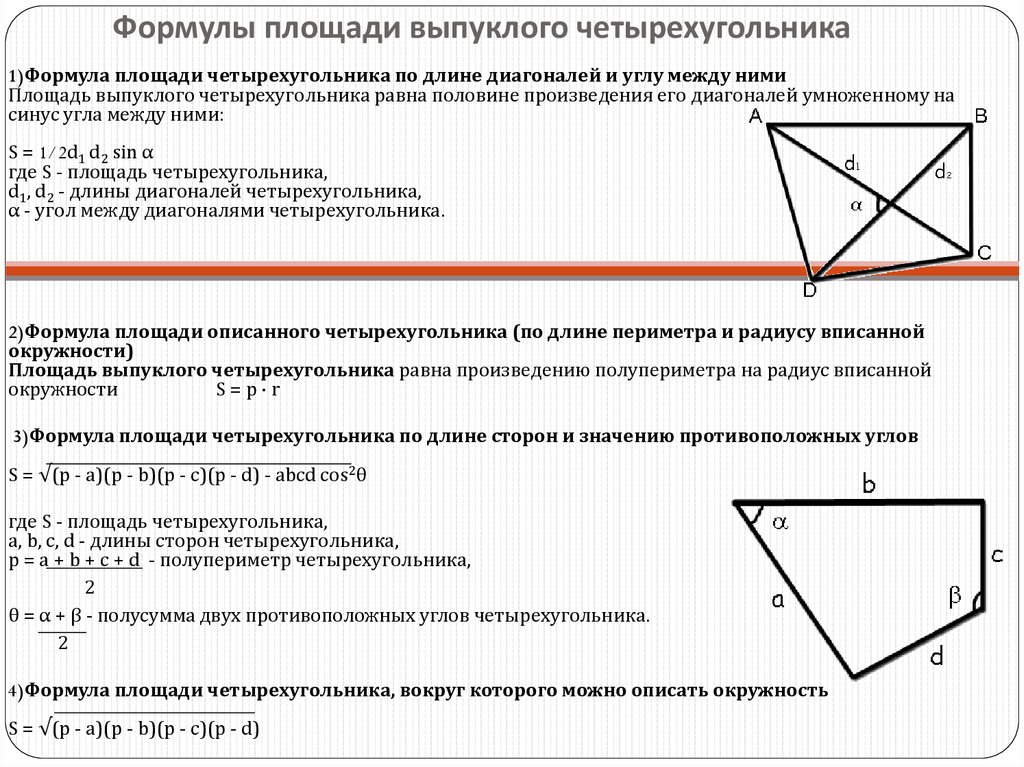
ABCD можно разделить на два треугольника диагональю BD. Чтобы найти его площадь, нужно знать высоты треугольников ABD и BCD. Предположим, что высоты треугольников BCD и ABD равны \(h_1\) и \(h_2\) соответственно. Найдем площадь четырехугольника ABCD, сложив площади треугольников BCD и ABD.
Здесь площадь треугольника BCD = (1/2) × d × \(h_1\).
Площадь треугольника ABD = (1/2) × d × \(h_2\).
На приведенном выше рисунке площадь четырехугольника ABCD = площадь ΔBCD + площадь ΔABD.
Таким образом, площадь четырехугольника ABCD = (1/2) × d × \(h_1\) + (1/2) × d × \(h_2\) = (1/2) × d × (\( h_1+h_2\)).
Таким образом, формула, используемая для нахождения площади четырехугольника, когда даны одна из его диагоналей и высоты треугольников (образованных данной диагональю),
Площадь = (1/2) × Диагональ × (Сумма высот)
Формула площади четырехугольника с использованием сторон
Зная стороны четырехугольника и два его противоположных угла, мы можем найти его площадь по формуле Бретшнайдера.
{2} \frac{\theta}{2}}\), где
- s = полупериметр четырехугольника = (a + b + c + d)/2
- θ = θ\(_1\) + θ\(_2\)
Площадь четырехугольника по формуле Герона
По формуле Герона площадь треугольника с тремя сторонами a, b и c равна \(\sqrt{s(s-a)(s-b)(s-c)}\), где ‘s’ — полупериметр треугольника. треугольник, т. е. s = (a + b + c)/2. Чтобы найти площадь четырехугольника по формуле Герона,
- Разделите его на два треугольника с помощью диагонали (используйте диагональ, длина которой известна).
- Примените формулу Герона к каждому треугольнику, чтобы найти его площадь.
- Сложите площади двух треугольников, чтобы получить площадь четырехугольника.
Формулы площади четырехугольников различных типов
Мы уже узнали, что существует 6 типов четырехугольников: квадрат, прямоугольник, параллелограмм, трапеция, ромб и воздушный змей. У нас есть специальная формула для нахождения площади каждого из этих четырехугольников.
Давайте посмотрим на них.
Площадь четырехугольника с использованием координат
Площадь четырехугольника можно вычислить, если известны координаты его вершин. Рассмотрим четырехугольник в координатной плоскости, как показано ниже:
. (_2\)), C(x\(_3\), y\(_3\)) и D(x\(_4\), y\(_4\)) — вершины.
Чтобы найти площадь четырехугольника ABCD, возьмем вершины A(x\(_1\), y\(_1\)), B(x\(_2\), y\(_2\)), C( x\(_3\), y\(_3\)) и D(x\(_4\), y\(_4\)) четырехугольника ABCD и запишите их, как показано ниже,
Сложите диагональные произведения x\(_1\)y\(_2\), x\(_2\)y\(_3\), x\(_3\)y\(_4\) и x\( _4\)y\(_1\) , которые показаны синими стрелками на изображении выше.
(х\(_1\)у\(_2\) + х\(_2\)у\(_3\) + х\(_3\)у\(_4\) + х\(_4\)у \(_1\)) → (1)
Складываем диагональные произведения x\(_2\)y\(_1\), x\(_3\)y\(_2\), x\(_4\)y\ (_3\) и x\(_1\)y\(_4\), которые показаны оранжевыми стрелками.
(х\(_2\)у\(_1\) + х\(_3\)у\(_2\) + х\(_4\)у\(_3\) + х\(_1\) у\(_4\)) → (2)
Вычтите (2) из (1) и умножьте разницу на 1/2, чтобы получить площадь четырехугольника ABCD.
Итак, площадь четырехугольника ABCD определяется как
A = (1/2) ⋅ {(x\(_1\)y\(_2\) + x\(_2\)y\(_3\) + х\(_3\)у\(_4\) + х\(_4\)у\(_1\)) — (х\(_2\)у\(_1\) + х\(_3\) y\(_2\) + x\(_4\)y\(_3\) + x\(_1\)y\(_4\))}
Примечание: Мы также можем вычислить площадь четырехугольника используя координаты вершин, разделив его на два треугольника и добавив их соответствующие площади. Давайте разберемся с этой техникой на примере, приведенном ниже,
Пример: Рассмотрим следующие четыре точки: A(−3, 1), B(−1, 4), C(3, 2), D(1, −2). Эти четыре точки являются вершинами четырехугольника:
Здесь мы разделим четырехугольник на два треугольника (используя любую из диагоналей), вычислим (положительное значение) площади каждого треугольника и добавим эти значения к получить общую площадь. На следующем рисунке четырехугольник ABCD разделен на ΔABD и ΔADC.
Теперь вычислим площади двух треугольников по отдельности.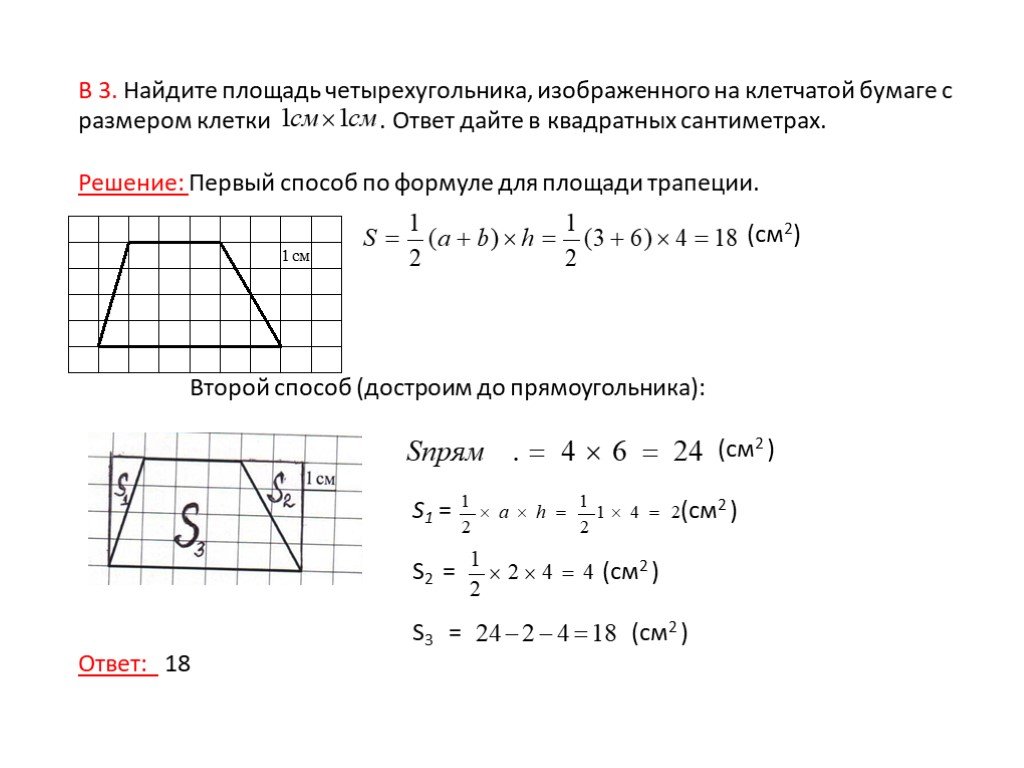
Площадь треугольника ABC:
= (1/2) |−3 × (4 − 2) + (−1) × (2 − 1) + 3 × (1 − 4)| = (1/2) |−6−1−9| = (1/2) × 16 = 8 квадратных единиц
Площадь треугольника ACD:
= (1/2) |−3 × (−2 − 2) + 1 × (2 − 1) + 3 × (1 −(−2))|
= (1/2)|12 + 1 + 9| = (1/2) × 22 = 11 квадратных единиц
Площадь четырехугольника ABCD:
Площадь (ABCD) = площадь (ΔABC) + площадь (ΔADC) = 8 + 11 = 19 квадратных единиц
Ниже перечислены некоторые темы, связанные с площадью четырехугольников.
- Типы четырехугольников
- Периметр четырехугольника
- 2D-фигуры
- 3D-фигуры
Площадь четырехугольника Примеры
Пример 1: Найдите площадь прямоугольника, длина которого 10 дюймов, а ширина 15 дюймов.
Решение:
Длина прямоугольника l = 10 дюймов. = 15 дюймов.
Используя формулы площади четырехугольника, площадь (A) данного прямоугольника равна,
А = l × b = 10 × 15 = 150 в 2 .
Ответ: Площадь данного прямоугольника = 150 в 2 .
Пример 2: Найдите площадь воздушного змея, диагонали которого составляют 18 единиц и 15 единиц.
Решение:
Диагонали данного воздушного змея равны, d\(_1\) = 18 единиц и d\(_2\) = 15 единиц.
Используя формулы площади четырехугольника, площадь (A) данного воздушного змея составляет,
A = (1/2) × d\(_1\) × d\(_2\) = (1/2) × 18 × 15 = 135 квадратных единиц.
Ответ: Площадь данного воздушного змея = 135 квадратных единиц.
Пример 3: Найдите площадь следующего четырехугольника. Округлите ответ до двух знаков после запятой.
Решение:
Стороны данного четырехугольника равны,
а = 15; б = 12; с = 8; и d = 10,
Его полупериметр равен s = (a + b + c + d)/2 = (15 + 12 + 8 + 10)/2 = 22,5. 9{2} \frac{180}{2}}\) ≈ 119,47
Ответ: Площадь данного четырехугольника = 119,47 квадратных единиц.
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций с помощью Cuemath.
Запись на бесплатный пробный урок
Практические вопросы по площади четырехугольника
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о площади четырехугольника
Какова площадь четырехугольника в математике?
Площадь четырехугольника – это площадь, заключенная в нем. Он измеряется в квадратных единицах, таких как 2 , см 2 , м 2 и т. д.
Что такое площадь четырехугольника?
Площадь четырехугольника можно найти, разделив его на два треугольника диагональю. Когда длина диагонали и высоты двух треугольников известны, площадь (A) четырехугольника равна A = (1/2) × Диагональ × (Сумма высот).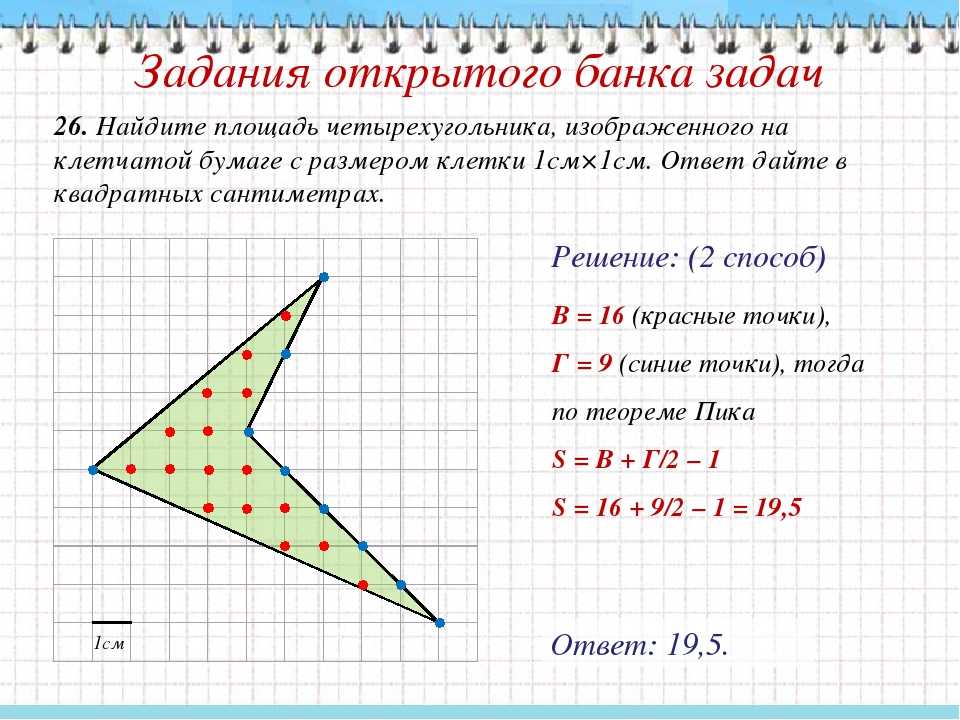
9{2} \frac{\theta}{2}}\), где s – полупериметр четырехугольника. т. е. s = (a + b + c + d)/2.
Как найти площадь четырехугольника по формуле Герона?
Мы знаем, что площадь четырехугольника можно найти, разделив его диагональю на два треугольника. Кроме того, мы знаем, что площадь треугольника с тремя сторонами можно найти по формуле Герона. По формуле Герона площадь треугольника со сторонами a, b и c определяется выражением \(\sqrt{s(s-a)(s-b)(s-c)}\), где s – полупериметр треугольника. треугольник. т. е. s = (a + b + c)/2. Используя эту формулу, мы можем найти площади двух треугольников (которые образованы четырехугольником) и сложить их, чтобы получить площадь четырехугольника.
Какие существуют формулы для нахождения площадей четырехугольников различных типов?
Существуют разные формулы, используемые для нахождения площадей четырехугольников разных типов. Вот они:
- Площадь квадрата со стороной x равна x 2 .
- Площадь прямоугольника с размерами ‘l’ и ‘b’ равна l × b.
Leave A Comment