Многовариантная самостоятельная работа по теме «ЭДС. Закон Ома для полной цепи». Физика 10 класс (базовый и повышенный уровень)
Многовариантная самостоятельная работа по теме
«Электродвижущая сила. Закон Ома для полной цепи».
Физика 10 класс («А» — базовый уровень, «Б» — повышенный уровень)
Самостоятельная работа
«Электродвижущая сила. Закон Ома для полной цепи»
Вариант 1А
1.Найдите внутреннее сопротивление гальванического элемента, если его ЭДС 1,2 В и при внешнем сопротивлении 5 Ом ток в цепи 0,2 А.
2.Аккумулятор мотоцикла имеет ЭДС 6 В и внутреннее сопротивление 0,5 Ом. К нему подключен реостат сопротивлением 5,5 Ом. Найдите силу тока в реостате.
3.При сопротивлении внешней цепи 1 Ом напряжение на зажимах источника 1,5 В, а при сопротивлении 2 Ом напряжение 2 В.
4*.ЭДС источника 100 В. При замыкании на внешнее сопротивление 49 Ом сила тока в цепи равна 2 А. Каково внутреннее сопротивление источника тока и сила тока короткого замыкания?
Самостоятельная работа
«Электродвижущая сила. Закон Ома для полной цепи»
Вариант 2А
1.ЭДС источника тока равна 5 В. какой суммарный заряд должен быть перемещён от
отрицательного полюса источника к положительному, чтобы работа сторонних сил
составила 0,2 мДж.
0,5 Ом. К аккумулятору подключили реостат сопротивлением 7,5 Ом. Найдите силу тока в реостате и напряжение на клеммах аккумулятора?
3.При замыкании источника тока на резистор сопротивлением 3,9 Ом сила тока в цепи 0,5 А, а при замыкании источника тока на резистор сопротивлением 1,9 Ом сила тока в цепи 1 А. найдите ЭДС источника и его внутреннее сопротивление.
найдите ЭДС источника и его внутреннее сопротивление.
4*.Определите силу тока при коротком замыкании батарейки с ЭДС 9
замыкании её на внешнее сопротивление 3 Ом ток в цепи равен 2 А.
Самостоятельная работа
«Электродвижущая сила. Закон Ома для полной цепи»
Вариант 3А
1.Определите силу тока в цепи при нагрузке сопротивлением 6 Ом, если ЭДС источ-
ника равна 8 В, а его внутреннее сопротивление 0,4 Ом. Чему равны падения напряжения внешнем и внутреннем участках цепи?
2.К генератору, ЭДС которого 120 В, присоединили нагревательный элемент сопротивлением 38 Ом. Определите внутреннее сопротивление генератора и напряжение на его зажимах, если сила тока в цепи
3.При подключении к батареи гальванических элементов резистора сопротивлением 18 Ом сила тока в цепи была 1 А, а при подключении резистора сопротивлением 8 Ом сила тока стала 1,8 А. Найдите ЭДС и внутреннее сопротивление батареи.
Найдите ЭДС и внутреннее сопротивление батареи.
4*.В проводнике сопротивлением 2 Ом, подключенном к источнику тока с ЭДС равной 1,1 В, сила тока 0,5 А. Какова сила тока короткого замыкания.
Самостоятельная работа
«Электродвижущая сила. Закон Ома для полной цепи»
Вариант 4А
1.ЭДС батарейки равна 6 В, внутреннее сопротивление 2 Ом. Батарейка замкнута на сопротивление 10 Ом. Какова сила тока в резисторе? Какое напряжение на зажимах
батарейки?
2.При замыкании гальванического элемента на сопротивление 4 Ом, сила тока в цепи 0,2 А, а при замыкании на сопротивление 7 Ом, то ток в цепи равен 0,14 А. Найдите ЭДС элемента и его внутреннее сопротивление.
3.ЭДС батареи 3 В. Внешнее сопротивление цепи 12 Ом, а внутреннее сопротивление батареи
 Какова сила тока в цепи?
Какова сила тока в цепи?4*.При подключенной внешней цепи напряжение на полюсах источника тока, имею-щего ЭДС 15 В, равно 9 В, а сила тока в цепи 1,5 А. Каково внутреннее сопротивление источника тока?
Самостоятельная работа
«Электродвижущая сила. Закон Ома для полной цепи»
Вариант 5А
1.К источнику с ЭДС 12 В и внутренним сопротивлением 1 Ом подключен реостат,
сопротивление которого 5 Ом. Найдите силу тока в цепи и напряжение на зажимах
источника.
2.Определите ЭДС и внутреннее сопротивление аккумулятора, если известно, что при замыкании его на внешнее сопротивление 1 Ом, напряжение на зажимах аккумулятора 2 В, а при замыкании на сопротивление 2 Ом напряжение на зажимах аккумулятора
2,4 В.
3.Батарея аккумуляторов подключена для зарядки к источнику с напряжением 12 В. Внутреннее сопротивление батареи 1 Ом. Найдите ЭДС батареи, если ток зарядки
Внутреннее сопротивление батареи 1 Ом. Найдите ЭДС батареи, если ток зарядки
500 мА?
4*.При подключении лампочки к источнику тока с ЭДС
напряжение на лампочке 4 В, а амперметр – силу тока 0,25 А. Каково внутреннее
сопротивление источника тока?
Самостоятельная работа
«Электродвижущая сила. Закон Ома для полной цепи»
Вариант 6А
1.Каково внутреннее сопротивление элемента, если его ЭДС 1,2 В и при внешнем
сопротивлении 5 Ом сила тока в цепи 0,2 А?
2.При замыкании батарейки на сопротивление 4,5 В ток в цепи 0,2 А, а при замыкании на сопротивление
3.Гальванический элемент с ЭДС 1,5 В и внутренним сопротивлением 2 Ом, замкнут на резистор сопротивлением 3 Ом. Определите силу тока в цепи.
Определите силу тока в цепи.
4*.ЭДС батареи 6 В. При замыкании её на внешнее сопротивление 1 Ом она даёт ток
3 А. Какова сила тока короткого замыкания?
Самостоятельная работа
«Электродвижущая сила. Закон Ома для полной цепи»
1.К источнику тока с ЭДС 8 В и внутренним сопротивление 3,2 Ом подключен нагреватель сопротивление 4,8 Ом. Какова сила тока в цепи? Какое напряжение на зажимах нагревателя?
2.При замыкании гальванического элемента на сопротивление 1,5 Ом, сила тока в
цепи 0,6 А, а при замыкании на сопротивление 2,5 Ом, то ток в цепи равен 0,4 А.
Найдите ЭДС элемента и его внутреннее сопротивление.
3.Каково внутреннее сопротивление элемента, если его ЭДС 1,2 В и если при внешнем сопротивлении 5 Ом сила тока равна 0,2 А?
4*.
Самостоятельная работа
«Электродвижущая сила. Закон Ома для полной цепи»
Вариант 8А
1.ЭДС элемента 1,5 В, а внутреннее сопротивлением 0,5 Ом. Какова сила тока в цепи, если внешнее сопротивление цепи 2 Ом. Найдите напряжение на полюсах источника.
2.Определите ЭДС и внутреннее сопротивление аккумулятора, если при внешнем сопротивление 3,9 Ом сила тока в цепи
3.Определите силу тока при коротком замыкании батареи с ЭДС 12 В, если при замыкании её на внешний резистор сопротивлением 4 Ом сила тока в цепи 2 А.
4*.Аккумулятор подключен для зарядки к сети напряжением 12,5 В.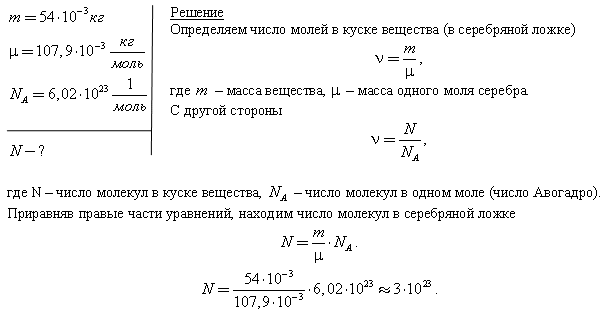 Внутреннее
Внутреннее
сопротивление аккумулятора 1 Ом. Чему равна ЭДС, если при зарядке через неё проходит ток силой 0,5 А?
Самостоятельная работа
«Электродвижущая сила. Закон Ома для полной цепи»
Вариант 9А
1.ЭДС источника тока 1 В, сопротивление внешнего участка цепи 4 Ом, сила тока в цепи 0,2 А. Определите внутреннее сопротивление источника.
2. ЭДС аккумуляторной батареи на электрокаре 100 В, её внутреннее сопротивление
1 Ом. Определите сопротивление электрического двигателя и напряжение, под которым он работает, если потребляемый ток 4 А.
3.Гальванический элемент с ЭДС 1,5 В и внутренним сопротивлением 2 Ом, замкнут на резистор сопротивлением 3 Ом. Определите силу тока в цепи.
4*.ЭДС источника тока 1 В, сопротивление внешнего участка цепи 4 Ом, сила тока
в цепи 0,2 А.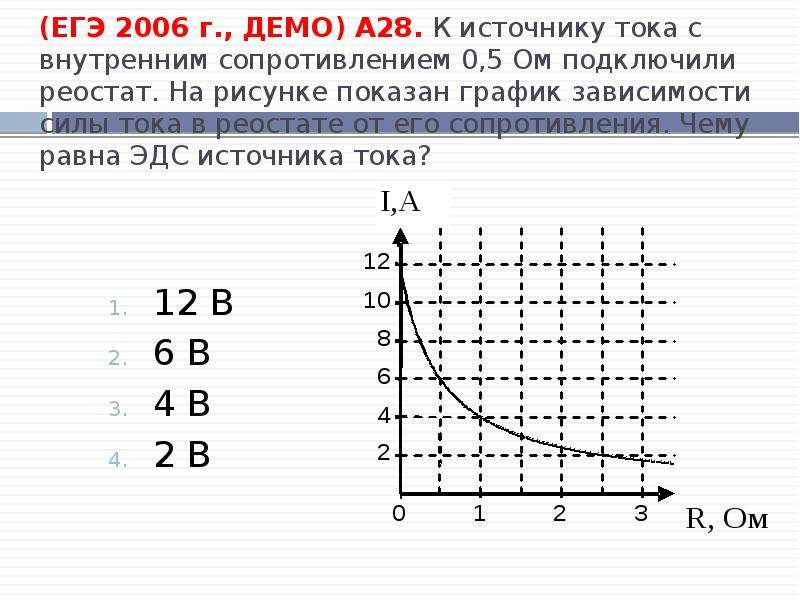 Определите внутреннее сопротивление источника.
Определите внутреннее сопротивление источника.
Самостоятельная работа
«Электродвижущая сила. Закон Ома для полной цепи»
Вариант 1Б
1.Проводник какого сопротивления надо включить во внешнюю цепь генератора с ЭДС 220 В и внутренним сопротивлением 0,1 Ом, чтобы на его зажимах напряжение оказалось равным 210 В?
2.Определите силу тока при коротком замыкании батарейки с ЭДС 9 В, если при замыкании её на внешнее сопротивление 3 Ом ток а цепи 2 А?
3.Определите ЭДС и внутреннее сопротивление источника тока, если при включении резистора сопротивлением 1,5 Ом по цепи проходит ток силой 0,6 А, а при включении резистора сопротивлением 2,5 Ом в цепи сила тока 0,4 А?
4*.ЭДС источника тока равна 100 В. При замыкании на внешнее сопротивление
49 Ом сила тока в цепи равна 2 А. Каково внутреннее сопротивление источника тока и сила тока короткого замыкания?
Каково внутреннее сопротивление источника тока и сила тока короткого замыкания?
Самостоятельная работа
«Электродвижущая сила. Закон Ома для полной цепи»
Вариант 2Б
1.При подключении к источнику тока резистора сопротивлением 10 Ом напряжение на зажимах источника было 10 В, а при подключении резистора сопротивлением 20 Ом напряжение стало 12 В. Определите ток короткого замыкания.
2.ЭДС аккумулятора 2,8 В, его внутреннее сопротивление 0,4 Ом, сопротивление
внешнего участка цепи 1 Ом. Найдите напряжение на клеммах аккумулятора?
3.Определите работу сторонних сил за 1 мин, если напряжение на зажимах источника тока 10 В, сопротивление нагрузки 10 Ом, внутреннее сопротивление 1 Ом.
4*.Ток короткого замыкания от источника с ЭДС 1,45 В равен 2,4 А.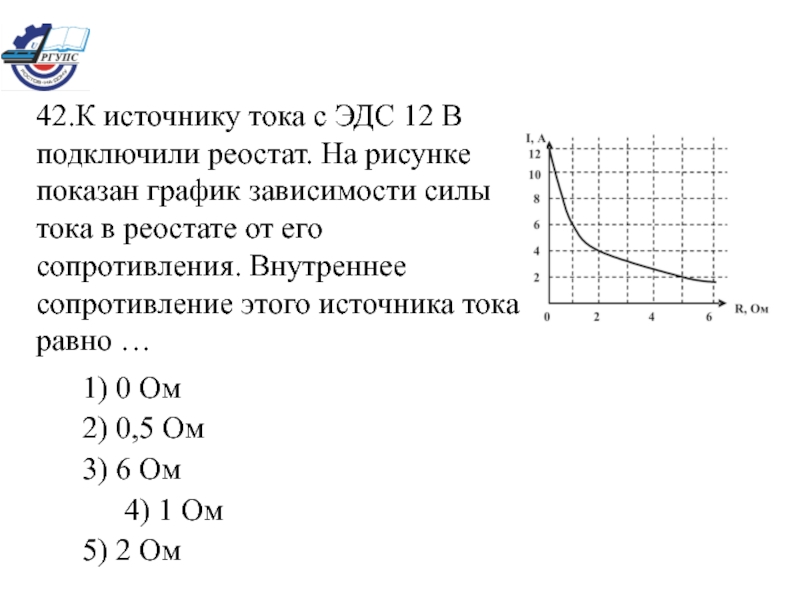 При каком внещнем сопротивлении ток в цепи будет равен 0,5 А?
При каком внещнем сопротивлении ток в цепи будет равен 0,5 А?
Самостоятельная работа
«Электродвижущая сила. Закон Ома для полной цепи»
Вариант 3Б
1.Внутреннее сопротивление источника 0,5 Ом, а напряжение на его зажимах 220 В.
Найдите ЭДС этого источника и силу тока, если внешнее сопротивление 10 Ом.
2.ЭДС аккумуляторной батареи на электрокаре 80 В, её внутреннее сопротивление
2 Ом. Определите сопротивление электрического двигателя и напряжение, под которым он работает, если потребляемый ток 2 А.
3.Реостат подключен к источнику тока. При изменении сопротивления реостата от
4 Ом до 9,5 Ом сила тока в цепи изменяется от 8 А до 3,6 А. Найдите ЭДС источника тока и его внутреннее сопротивление.
4*.При замыкании элемента на резистор сопротивлением 2,3 Ом в цепи протекает ток
силой 0,56 А, а при замыкании на резистор сопротивлением 1,8 Ом ток в цепи 0,7 А.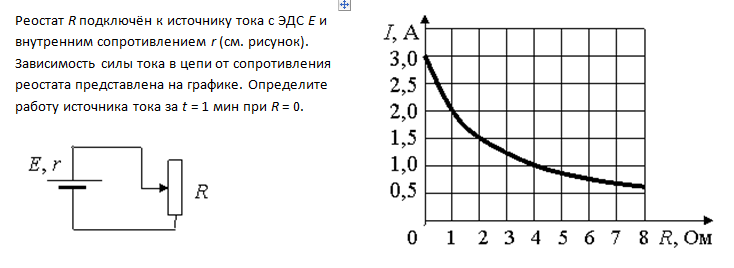
Чему равен ток короткого замыкания?
Самостоятельная работа
«Электродвижущая сила. Закон Ома для полной цепи»
Вариант 4Б
1.ЭДС источника тока 6 В. При внешнем сопротивлении 1,1 Ом сила тока в цепи 3 А. Определите падение напряжения внутри источника и его сопротивление.
2.Когда аккумулятор заряжали током 1 А, напряжение на её зажимах было 19 В, а
когда тот же аккумулятор заряжали током 0,5 А, напряжение на её зажимах равнялось
20 В. Определите ЭДС и внутреннее сопротивление аккумулятора.
3.ЭДС аккумуляторной батареи 6 В. При замыкании её на внешнее сопротивление
1 Ом в цепи течёт ток силой 3 А. Рассчитайте силу тока при коротком замыкании
батареи.
4*.При подключении внешнего участка цепи разность потенциалов на полюсах аккумуляторной батареи составляет 9 В, а сила тока в цепи 1,5 А. Каково внутреннее сопротивление батареи и сопротивление внешнего участка, если ЭДС аккумуляторной батареи 15 В?
Каково внутреннее сопротивление батареи и сопротивление внешнего участка, если ЭДС аккумуляторной батареи 15 В?
Самостоятельная работа
«Электродвижущая сила. Закон Ома для полной цепи»
Вариант 5Б
1.Определите падение напряжение внутри источника тока и его ЭДС, если падение напряжения на внешнем участке цепи 1,2 В, сопротивление внешнего участка 1,5 Ом, а внутреннее сопротивление источника 0,3 Ом.
2.При подключении к источнику электрического тока двух одинаковых резисторов сопротивлением по 6 Ом, соединённых последовательно, напряжение на зажимах
источника было 24 В. При подключении этих резисторов, соединённых параллельно, напряжение на зажимах стало 15 В. Определите ЭДС и внутреннее сопротивление
источника.
3.Аккумулятор имеет ЭДС 12 В. Сила тока в цепи 5 А, напряжение на зажимах аккумулятора 11 В. Определите ток короткого замыкания.
Определите ток короткого замыкания.
4*.Батарея элементов с ЭДС 21 В и внутренним сопротивлением 0,5 Ом подключена к внешней цепи, состоящей из трёх параллельно соединенных проводников сопротивлениями 2 Ом, 6 Ом и 12 Ом. Определите силу тока в цепи и силу тока в каждом резисторе.
Самостоятельная работа
«Электродвижущая сила. Закон Ома для полной цепи»
Вариант 6Б
1.Найдите ЭДС и внутреннее сопротивление батареи элементов, если при силе тока
15 А, напряжение на клеммах батареи 9 В, а при силе токе в цепи 6 А, напряжение
стало 10,8 В.
2.При подключении внешней цепи напряжение на полюсах аккумулятора стало 9 В, а сила тока в цепи установилась в 1,5 А. Каково внутреннее сопротивление источника и сопротивление внешней цепи? ЭДС аккумулятора 15 В. 2)/2 — кинетическая энергия снаряда
2)/2 — кинетическая энергия снаряда
x= E2/E1
Проекции на ось 0у вверх: ma= Fтяги-mg, Fтяги=15*(1+10)= 165 Н
По формуле изображений получаемых при различных углах меэ плоских зеркал
. Подставляем и вычисляем:
Ответ: 5 изображений
Сопроивление проводника зависит от длинны, удельного сопротивления и поперечного сечения проволника: R = ро(удельное сопротивление)*L(длинна)/S(поперечное сечение)удельное сопротивление меди = 0,017 (Ом*мм^2)/м
m = ро1(плотность)*V(объём) = ро1*L*S
выразим например S
S= m/(ро1*L)
подставим в формулу сопротивления: R =ро*L/ (m/(ро1*L)) = ро*ро1*L^2/m
подставит числа получим L = 5,8 м
S = 0,0000426 м^2 = 42,6 мм^2
Находим период маятника по формуле
T=t/n
T=60/36=1,67c. 2
2
Физика 10 класс Постоянный ток Закон Ома для полной цепи Задание
Решение задач
Тема: «Закон Ома для полной цепи»
Дескриптор:
• записывает в дано физические величины в СИ
• записывает закон Ома для полной цепи
• записывает формулу ЭДС
• выражает неизвестную величину
• выполняет математические расчеты
• записывает ответ
1. К источнику с ЭДС 12 В и внутренним сопротивлением 1 Ом подключен реостат, сопротивление которого 5 Ом. Найти силу тока в цепи и напряжение на зажимах источника.
2. При
подключении лампочки к батарее элементов с ЭДС 4,5 В вольтметр показал
напряжение на лампочке 4 В, а амперметр — силу тока 0,25 А. Каково внутреннее
сопротивление батареи?
Каково внутреннее
сопротивление батареи?
3. В проводнике сопротивлением 2 Ом, подключенном к элементу с ЭДС 1,1 В, сила тока равна 0,5 А. Какова сила тока при коротком замыкании элемента?
4. Для определения ЭДС и внутреннего сопротивления источника тока к его выходу подключили реостат. При одном положении движка реостата сила тока в цепи была I1=1,5 A, а напряжение U1=4,5 B. При другом положении движка получены значения I2=2 A, U2=3 B. Найдите ЭДС источника и его внутреннее сопротивление.
Задачи с решением
1. К источнику с ЭДС 12 В и внутренним сопротивлением 1 Ом подключен реостат, сопротивление которого 5 Ом. Найти силу тока в цепи и напряжение на зажимах источника.
Решение:
Ответ: 10 В.
2.
При подключении лампочки к батарее элементов с ЭДС 4,5 В вольтметр
показал напряжение на лампочке 4 В, а амперметр — силу тока 0,25 А. Каково
внутреннее сопротивление батареи?
Каково
внутреннее сопротивление батареи?
Решение:
Ответ: 2 Ом.
3. В проводнике сопротивлением 2 Ом, подключенном к элементу с ЭДС 1,1 В, сила тока равна 0,5 А. Какова сила тока при коротком замыкании элемента?
Решение:
Ответ: 5,5 А.
4. Для определения ЭДС и внутреннего сопротивления источника тока к его выходу подключили реостат. При одном положении движка реостата сила тока в цепи была I1=1,5 A, а напряжение U1=4,5 B. При другом положении движка получены значения I2=2 A, U2=3 B. Найдите ЭДС источника и его внутреннее сопротивление.
Решение:
Ответ: 9В; 3 Ом.
Задачи к контрольной работе по теме «Законы постоянного тока». 10 класс
Задачи к контрольной работе «Законы постоянного тока»
При питании лампочки от гальванического элемента с ЭДС ξ =9 В. При этом за время 0,5 мин сторонними силами в гальваническом элемента совершается работа 0, 54 кДж. Определите значение силы тока.
При этом за время 0,5 мин сторонними силами в гальваническом элемента совершается работа 0, 54 кДж. Определите значение силы тока.
При питании лампочки от гальванического элемента с ЭДС ξ сила тока в цепи равна 3 А. При этом за время 2 мин сторонними силами в гальваническом элемента совершается работа 4,3 кДж. Определите значение ЭДС.
При питании лампочки от гальванического элемента с ЭДС ξ =4,5В сила тока в цепи равна 1,5 А. При этом сторонними силами в гальваническом элемента совершается работа 0,4 кДж. Определите время совершения работы.
При питании лампочки от гальванического элемента с ЭДС ξ =9 В сила тока в цепи равна 2 А. При этом за время 2 мин сторонними силами в гальваническом элемента совершается работа. Определите работу сторонних сил.
При питании лампочки от гальванического элемента с ЭДС ξ =4,5 В. При этом за время 1 мин сторонними силами в гальваническом элемента совершается работа 0, 81кДж. Определите значение силы тока.
При питании лампочки от гальванического элемента с ЭДС ξ сила тока в цепи равна 1,5 А. При этом за время 0,5 мин сторонними силами в гальваническом элемента совершается работа 0,4 кДж. Определите значение ЭДС.
При питании лампочки от гальванического элемента с ЭДС ξ =12 В сила тока в цепи равна 3 А. При этом сторонними силами в гальваническом элемента совершается работа 4,3 кДж. Определите время совершения работы.
При питании лампочки от гальванического элемента с ЭДС ξ =4,5 В сила тока в цепи равна 1,5 А. При этом за время 1,5 мин сторонними силами в гальваническом элемента совершается работа. Определите работу сторонних сил.
При питании лампочки от гальванического элемента с ЭДС ξ =12 В. При этом за время 2 мин сторонними силами в гальваническом элемента совершается работа 2,2 кДж. Определите значение силы тока.
При питании лампочки от гальванического элемента с ЭДС ξ сила тока в цепи равна 2 А. При этом за время 1,5 мин сторонними силами в гальваническом элемента совершается работа 0,81 кДж. Определите значение ЭДС.
Определите значение ЭДС.
При питании лампочки от гальванического элемента с ЭДС ξ =9 В сила тока в цепи равна 3 А. При этом сторонними силами в гальваническом элемента совершается работа 8,1 кДж. Определите время совершения работы.
П ри питании лампочки от гальванического элемента с ЭДС ξ =12 В сила тока в цепи равна 2 А. При этом за время 0,5 мин сторонними силами в гальваническом элемента совершается работа. Определите работу сторонних сил.
На рисунке изображена схема соединения одинаковых резисторов, сопротивление которых равно 2 кОм. Напряжение 10 В подано на клеммы DF. Вычислите сопротивление цепи, напряжение на каждом из резисторов и силу тока в нем, мощность, выделяющуюся в цепи.
Н а рисунке изображена схема соединения одинаковых резисторов, сопротивление которых равно 3 кОм. Напряжение 15 В подано на клеммы ВF. Вычислите сопротивление цепи, напряжение на каждом из резисторов и силу тока в нем, мощность, выделяющуюся в цепи.
На рисунке изображена схема соединения одинаковых резисторов, сопротивление которых равно 5 кОм. Напряжение 25 В подано на клеммы АК. Вычислите сопротивление цепи, напряжение на каждом из резисторов и силу тока в нем, м ощность, выделяющуюся в цепи.
На рисунке изображена схема соединения одинаковых резисторов, сопротивление которых равно 6 кОм. Напряжение 30 В подано на клеммы ЕК. Вычислите сопротивление цепи, напряжение на каждом из резисторов и силу тока в нем, мощность, выделяющуюся в цепи.
Н а рисунке изображена схема соединения одинаковых резисторов, сопротивление которых равно 8 кОм. Напряжение 20 В подано на клеммы АВ. Вычислите сопротивление цепи, напряжение на каждом из резисторов и силу тока в нем, мощность, выделяющуюся в цепи.
Н а рисунке изображена схема соединения одинаковых резисторов, сопротивление которых равно 10 кОм. Напряжение 25 В подано на клеммы АЕ. Вычислите сопротивление цепи, напряжение на каждом из резисторов и силу тока в нем, мощность, выделяющуюся в цепи.
Н а рисунке изображена схема соединения одинаковых резисторов, сопротивление которых равно 1 кОм. Напряжение 10 В подано на клеммы АF. Вычислите сопротивление цепи, напряжение на каждом из резисторов и силу тока в нем, мощность, выделяющуюся в цепи.
Н а рисунке изображена схема соединения одинаковых резисторов, сопротивление которых равно 2 кОм. Напряжение 10 В подано на клеммы ВD. Вычислите сопротивление цепи, напряжение на каждом из резисторов и силу тока в нем, мощность, выделяющуюся в цепи.
Н а рисунке изображена схема соединения одинаковых резисторов, сопротивление которых равно 2 кОм. Напряжение 10 В подано на клеммы DE. Вычислите сопротивление цепи, напряжение на каждом из резисторов и силу тока в нем, мощность, выделяющуюся в цепи.
Н а рисунке изображена схема соединения одинаковых резисторов, сопротивление которых равно 1 кОм. Напряжение 5 В подано на клеммы ВК. Вычислите сопротивление цепи, напряжение на каждом из резисторов и силу тока в нем, мощность, выделяющуюся в цепи.
Вычислите сопротивление цепи, напряжение на каждом из резисторов и силу тока в нем, мощность, выделяющуюся в цепи.
Н а рисунке изображена схема соединения одинаковых резисторов, сопротивление которых равно 1 кОм. Напряжение 5 В подано на клеммы ЕF. Вычислите сопротивление цепи, напряжение на каждом из резисторов и силу тока в нем, мощность, выделяющуюся в цепи.
На рисунке изображена схема соединения одинаковых резисторов, сопротивление которых равно 10 кОм. Напряжение 40 В подано на клеммы KD. Вычислите сопротивление цепи, напряжение на каждом из резисторов и силу тока в нем, мощность, выделяющуюся в цепи.
Под действием электрического поля напряженностью Е=8 мВ/м электроны перемещаются в проводнике со скоростью 30·10-6 м/с. Концентрация свободных электронов 6·1028 м-3 . Определить удельное сопротивление проводника. Заряд электрона 1, 6 ·10 -19 Кл.
Под действием электрического поля электроны перемещаются в проводнике со скоростью 60·10-6 м/с. Концентрация свободных электронов 6,3·1028 м-3 . Удельное сопротивление проводника 5,5 ·10-8 Ом·м. Заряд электрона 1, 6 ·10 -19 Кл. Определить напряженность электрического поля.
Концентрация свободных электронов 6,3·1028 м-3 . Удельное сопротивление проводника 5,5 ·10-8 Ом·м. Заряд электрона 1, 6 ·10 -19 Кл. Определить напряженность электрического поля.
Под действием электрического поля напряженностью Е=27 мВ/м электроны перемещаются в проводнике. Концентрация свободных электронов 8,4·1028 м-3 . Удельное сопротивление проводника 1,7 ·10-8 Ом·м. Определить скорость электронов. Заряд электрона 1, 6 ·10 -19 Кл.
Под действием электрического поля напряженностью Е=78 мВ/м электроны перемещаются в проводнике со скоростью 7 0·10-6 м/с. Удельное сопротивление проводника 21 ·10-8 Ом·м. Определить концентрацию электронов. Заряд электрона 1, 6 ·10 -19 Кл.
Под действием электрического поля напряженностью Е=7,4 мВ/м электроны перемещаются в проводнике со скоростью 50·10-6 м/с. Концентрация свободных электронов 5,8·1028 м-3 . Определить удельное сопротивление проводника. Заряд электрона 1, 6 ·10 -19 Кл.
Определить удельное сопротивление проводника. Заряд электрона 1, 6 ·10 -19 Кл.
Под действием электрического поля электроны перемещаются в проводнике со скоростью 40·10-6 м/с. Концентрация свободных электронов 8,4·1028 м-3 . Удельное сопротивление проводника 9,8·10-8 Ом·м. Заряд электрона 1, 6 ·10 -19 Кл. Определить напряженность электрического поля.
Под действием электрического поля напряженностью Е=20 мВ/м электроны перемещаются в проводнике. Концентрация свободных электронов 6,4·1028 м-3 . Удельное сопротивление проводника 5,7 ·10-8 Ом·м. Определить скорость электронов. Заряд электрона 1, 6 ·10 -19 Кл.
Под действием электрического поля напряженностью Е=110 мВ/м электроны перемещаются в проводнике со скоростью 75·10-6 м/с. Удельное сопротивление проводника 10 ·10-8 Ом·м. Определить концентрацию электронов. Заряд электрона 1, 6 ·10 -19 Кл.
Под действием электрического поля напряженностью Е=61 мВ/м электроны перемещаются в проводнике со скоростью 90·10-6 м/с. Концентрация свободных электронов 3,7·1028 м-3 . Определить удельное сопротивление проводника. Заряд электрона 1, 6 ·10 -19 Кл.
Под действием электрического поля электроны перемещаются в проводнике со скоростью 80·10-6 м/с. Концентрация свободных электронов 4·1028 м-3 . Удельное сопротивление проводника 95,8·10-8 Ом·м. Заряд электрона 1, 6 ·10 -19 Кл. Определить напряженность электрического поля.
Под действием электрического поля напряженностью Е=39 мВ/м электроны перемещаются в проводнике. Концентрация свободных электронов 8,2·1028 м-3 . Удельное сопротивление проводника 2,7 ·10-8 Ом·м. Определить скорость электронов. Заряд электрона 1, 6 ·10 -19 Кл.
Под действием электрического поля напряженностью Е=62 мВ/м электроны перемещаются в проводнике со скоростью 100·10-6 м/с. Удельное сопротивление проводника 5,9·10-8 Ом·м. Определить концентрацию электронов. Заряд электрона 1, 6 ·10 -19 Кл.
Удельное сопротивление проводника 5,9·10-8 Ом·м. Определить концентрацию электронов. Заряд электрона 1, 6 ·10 -19 Кл.
К источнику тока с ЭДС ξ и внутренним сопротивлением r=2 Ом подключен электрический чайник. Когда вода в нем кипит, то из носика площадью поперечного сечения S=1,2 см2 пар вырывается со скоростью ϑ = 2, 5 м/с. КПД источника η=90 %. Определить ЭДС.
К источнику тока с ЭДС ξ=110 В и внутренним сопротивлением подключен электрический чайник. Когда вода в нем кипит, то из носика площадью поперечного сечения S=2 см2 пар вырывается со скоростью ϑ = 1, 4 м/с. КПД источника η=95 %. Определить внутреннее сопротивление.
К источнику тока с ЭДС ξ=70 В и внутренним сопротивлением r=1 Ом подключен электрический чайник. Когда вода в нем кипит, то из носика площадью поперечного сечения S=2,5 см2 пар вырывается со скоростью ϑ = 0,9 м/с. Определить КПД η .
К источнику тока с ЭДС ξ =90 В и внутренним сопротивлением r=1 Ом подключен электрический чайник. Когда вода в нем кипит, то из носика площадью поперечного сечения пар вырывается со скоростью ϑ = 1, 5 м/с. КПД источника η=90 %. Определить площадь поперечного сечения .
Когда вода в нем кипит, то из носика площадью поперечного сечения пар вырывается со скоростью ϑ = 1, 5 м/с. КПД источника η=90 %. Определить площадь поперечного сечения .
К источнику тока с ЭДС ξ =50 В и внутренним сопротивлением r=2 Ом подключен электрический чайник. Когда вода в нем кипит, то из носика площадью поперечного сечения S=1 см2 пар вырывается. КПД источника η=95 %. Определить скорость вырывания пара.
К источнику тока с ЭДС ξ и внутренним сопротивлением r=2 Ом подключен электрический чайник. Когда вода в нем кипит, то из носика площадью поперечного сечения S=3 см2 пар вырывается со скоростью ϑ = 4,1 м/с. КПД источника η=93 %. Определить ЭДС.
К источнику тока с ЭДС ξ=120 В и внутренним сопротивлением подключен электрический чайник. Когда вода в нем кипит, то из носика площадью поперечного сечения S=2,5 см2 пар вырывается со скоростью ϑ = 3,6 м/с. КПД источника η=90 %. Определить внутреннее сопротивление.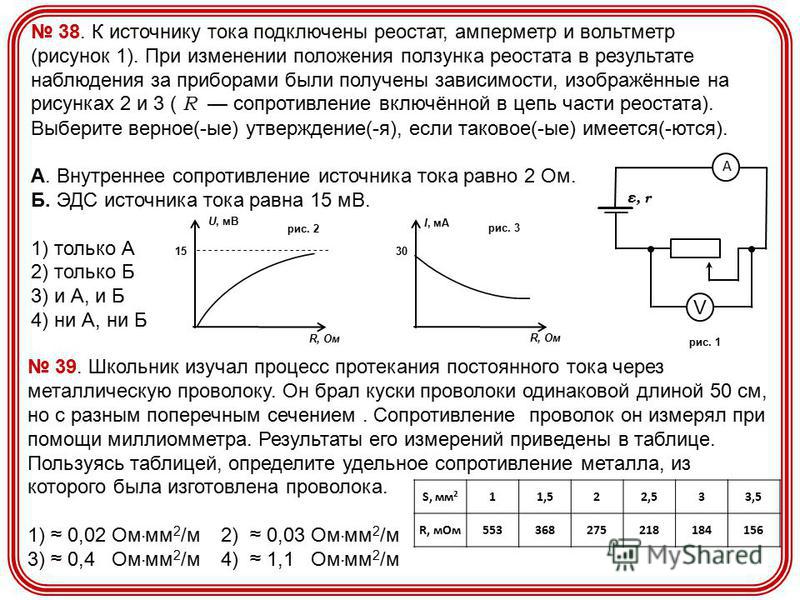
К источнику тока с ЭДС ξ=100 В и внутренним сопротивлением r=3 Ом подключен электрический чайник. Когда вода в нем кипит, то из носика площадью поперечного сечения S=1 см2 пар вырывается со скоростью ϑ = 1,7 м/с. Определить КПД η .
К источнику тока с ЭДС ξ =90 В и внутренним сопротивлением r=1,5 Ом подключен электрический чайник. Когда вода в нем кипит, то из носика площадью поперечного сечения пар вырывается со скоростью ϑ = 1, 3 м/с. КПД источника η=95 %. Определить площадь поперечного сечения .
К источнику тока с ЭДС ξ =220 В и внутренним сопротивлением r=2 Ом подключен электрический чайник. Когда вода в нем кипит, то из носика площадью поперечного сечения S=1,5 см2 пар вырывается. КПД источника η=98 %. Определить скорость вырывания пара.
К источнику тока с ЭДС ξ и внутренним сопротивлением r=1,4 Ом подключен электрический чайник. Когда вода в нем кипит, то из носика площадью поперечного сечения S=1,5 см2 пар вырывается со скоростью ϑ = 5,6 м/с. КПД источника η=90 %. Определить ЭДС.
КПД источника η=90 %. Определить ЭДС.
К источнику тока с ЭДС ξ=90 В и внутренним сопротивлением подключен электрический чайник. Когда вода в нем кипит, то из носика площадью поперечного сечения S=2 см2 пар вырывается со скоростью ϑ =1 м/с. КПД источника η=96 %. Определить внутреннее сопротивление.
Закон Ома для замкнутой цепи
336.При питании лампочки от элемента с ЭДС 1,5 В сила тока в цепи равна 0,2 А. Найти работу сторонних сил в элементе за 1 мин.
337.К источнику с ЭДС 12 В и внутренним сопротивлением 1 Ом подключен реостат, сопротивление которого 5 Ом. Найти силу тока в цепи и напряжение на зажимах источника.
338.Каково напряжение на полюсах источника с ЭДС, равной ε, когда сопротивление внешней части цепи равно внутреннему сопротивлению источника?
339.При подключении лампочки к батарее элементов с ЭДС 4,5 В вольтметр показал напряжение на лампочке 4 В, а амперметр – силу тока 0,25 А. Каково внутреннее сопротивление батареи?
340. При подключении электромагнита к источнику с ЭДС 30 В и внутренним сопротивлением 2 Ом напряжение на зажимах источника стало 28 В. Найти силу тока в цепи. Какую работу совершают сторонние силы источника за 5 мин? Какова работа тока во внешней и внутренней частях цепи за то же время?
При подключении электромагнита к источнику с ЭДС 30 В и внутренним сопротивлением 2 Ом напряжение на зажимах источника стало 28 В. Найти силу тока в цепи. Какую работу совершают сторонние силы источника за 5 мин? Какова работа тока во внешней и внутренней частях цепи за то же время?
341.В проводнике сопротивлением 2 Ом, подключенном к элементу с ЭДС 1,1 В, сила тока равна 0,5 А. Какова сила тока при коротком замыкании элемента?
342.При подключении к батарее гальванических элементов резистора сопротивлением 16 Ом сила тока в цепи была 1 А, а при подключении резистора сопротивлением 8 Ом сила тока стала 1,8 А. Найти ЭДС и внутреннее сопротивление батареи.
343.Найти внутреннее сопротивление и ЭДС источника тока, если при силе тока 30 А мощность во внешней цепи равна 180 Вт, а при силе тока 10 А эта мощность равна 100 Вт.
344.Вольтметр, подключенный к зажимам источника тока, показал 6 В. Когда к тем же зажимам подключили резистор, вольтметр стал показывать 3 В. Что покажет вольтметр, если вместо одного подключить два таких же резистора, соединенных последовательно? параллельно?
Что покажет вольтметр, если вместо одного подключить два таких же резистора, соединенных последовательно? параллельно?
345.От генератора с ЭДС 40 В и внутренним сопротивлением 0,04 Ом ток поступает по медному кабелю площадью поперечного сечения 170 мм2 к месту электросварки, удаленного от генератора на 50 м. Найти напряжение на зажимах генератора и на сварочном аппарате, если сила тока в цепи равна 200 А. Какова мощность сварочной дуги?
346.Лампочки, сопротивления которых 3 и 12 Ом, поочередно подключенные к некоторому источнику тока, потребляют одинаковую мощность. Найти внутреннее сопротивление источника и КПД цепи в каждом случае.
347.Источник тока с ЭДС 9 В и внутренним сопротивлением 1 Ом питает через реостат три параллельно соединенные лампочки, рассчитанные на напряжение 6,3 В и силу тока 0,3 А. Реостат поставлен в такое положение, что лампочки работают в номинальном режиме. Одна из лампочек перегорела. Во сколько раз изменилась мощность каждой из двух оставшихся лампочек по сравнению с номинальной, если считать, что сопротивление каждой лампочки осталось прежним?
348. Источник тока с внутренним сопротивлением r и ЭДС ε замкнут на три резистора с сопротивлением 3r каждый, соединенные последовательно. Во сколько раз изменяется сила тока в цепи, напряжение на зажимах источника и полезная мощность, если резисторы соединить параллельно?
Источник тока с внутренним сопротивлением r и ЭДС ε замкнут на три резистора с сопротивлением 3r каждый, соединенные последовательно. Во сколько раз изменяется сила тока в цепи, напряжение на зажимах источника и полезная мощность, если резисторы соединить параллельно?
349.Ламповый реостат состоит из пяти электрических ламп, включенных параллельно. Найти сопротивление реостата, если: а) горят все лампы, б) вывинтили одну, в) вывинтили две, г) вывинтили три лампы.
350.Сколько витков нихромовой проволоки нужно намотать на фарфоровый цилиндр радиусом 2,5 см, чтобы получить печь, сопротивлением 40 Ом?
351.Сколько электронов проходит за 1 с через 1 мм2 поперечного сечения железного проводника длиной 10 м при напряжении на его концах 6 В?
352.Резистор 5 кОм и вольтметр, соединенные последовательно, подключили к сети напряжением 120 В. При этом вольтметр показал 80 В. Когда резистор поменяли другим, вольтметр показал 50 В. Определить сопротивление второго резистора.
353.ЭДС батареи 12 В. Максимальная сила тока от этой батареи 6 А. Определить максимальную мощность, которая может быть получена на внешнем участке цепи.
354.Резистор и амперметр, соединенные последовательно, подключили к источнику тока. К концам резистора подключили вольтметр, сопротивление которого 2 кОм. При этом вольтметр показал 100 В, амперметр 0,25 А. Определить сопротивление резистора. Какой будет относительная погрешность, если не учесть сопротивление вольтметра?
355.ЭДС батареи 8 В. При силе тока 2 А к.п.д. батареи равна 0,75. Определить ее внутреннее сопротивление.
356.При внешнем сопротивлении 3 Ом сила тока в цепи 0,3 А, а при сопротивлении 5 Ом сила тока 0,2 А. Определить силу тока короткого замыкания.
357. Элемент с ЭДС 1,1 В и внутренним сопротивлением 1 Ом замкнут на внешнее сопротивление 9 Ом. Найти: 1) силу тока в цепи, 2) падение потенциала во внешней цепи, 3) падение потенциала внутри элемента, 4) с каким к. п.д. работает элемент.
п.д. работает элемент.
358.Сопротивление одного из последовательно включенных проводников в n раз больше другого. Во сколько раз изменится сила тока в цепи (напряжение постоянно), если эти проводники включить параллельно?
359.На схеме, приведенной на рис. 40, все сопротивления равны R = 10 Ом. Определить заряд на конденсаторе, если его емкость С = 10 мФ, напряжение источника U0 = 10 В.
360.Какова ЭДС источника напряжения, если напряженность стороннего электрического поля Е = 24 В/м, а расстояние, проходимое электрическим зарядом вдоль действия сил стороннего поля, равно r = 0,05 м?
361.На баллоне электрической лампы написано 220 В, 100 Вт. Для измерения сопротивления нити накала в холодном состоянии на лампу подали напряжение U = 2 В, при этом сила тока была I = 54 мА. Найти температуру накала T вольфрамовой нити.
362.К источнику тока с ЭДС ε = 1,5 В присоединили катушку с сопротивлением R = 0,1 Ом. Амперметр показал силу тока, равную I1 = 0,5 А. Когда к источнику тока присоединили последовательно еще один источник тока с такой же ЭДС, то сила тока I в той же катушке оказалось равной 0,4 А. Определить внутренние сопротивления и первого и второго источника.
Когда к источнику тока присоединили последовательно еще один источник тока с такой же ЭДС, то сила тока I в той же катушке оказалось равной 0,4 А. Определить внутренние сопротивления и первого и второго источника.
363.Сила тока в проводнике сопротивлением R = 12 Ом равномерно убывает от I0 = 5 A до I = 0 в течение времени t = 10 с. Какое количество теплоты Q выделяется в этом проводнике за указанный промежуток времени?
364.Элемент, сопротивление и амперметр соединены последовательно. Элемент имеет ЭДС ε = 2 В и внутреннее сопротивление r = 0,4 Ом. Амперметр показывает ток I = 1 А. С каким КПД работает элемент?
365.Катушка из медной проволоки имеет сопротивление R = 10,8 Ом. Масса медной проволоки m = 3,41кг. Какой длины l и какого диаметра d проволока намотана на катушке?
366.Напряжение на зажимах источника, нагруженного сопротивлением R = 250 Ом, U = 4,5 В. Напряжение на зажимах того же источника без нагрузки 4,77 В. Определить внутреннее сопротивление источника.
367.Найти падение напряжения в проводнике, если за время t = 1 мин по нему прошел электрический заряд, равный Q = 80 Кл, а его сопротивление R = 1,5 Ом.
368.Элемент с ЭДС 2 В имеет внутреннее сопротивление r = 0,5 Ом. Найти падение потенциала Ur внутри элемента при силе тока I = 0,25 A. Каково внешнее сопротивление R цепи при этих условиях?
369.Какова ЭДС источника, если сторонние силы совершают 20 Дж работы при перемещении 10 Кл электричества внутри щеточника от одного полюса к другому?
370.ЭДС источника равна 12 В. Какую работу совершают сторонние силы при перемещении 50 Кл электричества внутри источника от одного полюса к другому?
371.ЭДС элемента 1,5 В, а внутреннее сопротивление 0,50 Ом. Какую наибольшую силу тока можно получить от этого элемента? Какой будет сила тока, если сопротивление внешней цепи равно: 0,50 Ом, 1,0 Ом, 2,0 Ом?
372.Каково внутреннее сопротивление элемента, если его ЭДС равна 1,2 В и при внешнем сопротивлении 5,0 Ом сила тока равна 0,20 А?
373. ЭДС батарейки от карманного фонаря равна 3/7:В, а внутреннее сопротивление 1,5 Ом. Батарейка замкнута на сопротивление 11,7 Ом. Каково напряжение на зажимах батарейки?
ЭДС батарейки от карманного фонаря равна 3/7:В, а внутреннее сопротивление 1,5 Ом. Батарейка замкнута на сопротивление 11,7 Ом. Каково напряжение на зажимах батарейки?
374.ЭДС батареи 6,0 В, ее внутреннее сопротивление 0,5 Ом, сопротивление внешней цепи 11,5 Ом. Найти силу тока в цепи, напряжение на зажимах батареи и падение напряжения внутри батареи.
375.К источнику тока, внутреннее сопротивление которого 2 Ом, подключены параллельно две лампочки сопротивлением 80м каждая. Амперметр в неразветвленной части цепи показывает 2 А. Что покажет амперметр, если; одна, из ламп перегорит?
376.При подключенной внешней цепи напряжение на полюсах источника равно 9 В а сила тока в цепи 1,5 А. Каково внутреннее сопротивление источника и сопротивление внешней цепи? ЭДС источника 15 В.
377.К полюсам источника с ЭДС 2,0 В и внутренним сопротивлением 0,80.0м присоединен кусок никелиновой проволоки длиной 2,1 м и сечением 0,21. мм2. Каково напряжение на зажимах, источника?
378. Какой длины нужно взять кусок стальной проволоки сечением 0,20 мм2 чтобы, присоединив его к полюсами элемента с ЭДС 120 В и внутренним сопротивлением 1,2 Ом, получить в цепи силу тока 250 мА?
Какой длины нужно взять кусок стальной проволоки сечением 0,20 мм2 чтобы, присоединив его к полюсами элемента с ЭДС 120 В и внутренним сопротивлением 1,2 Ом, получить в цепи силу тока 250 мА?
379.К полюсам источника тока, присоединяют поочередно резисторы сопротивлением 45 Ом и 10 Ом. При этом сила тока в цепи оказывается равной 0,2 и 0,1 А соответственно. Найти ЭДС источника и его внутреннее сопротивление.
380.При сопротивлении внешней цепи 1 Ом напряжение на зажимах источника 1,5 В, а при сопротивлении 2 Ом напряжение 2 В. Найти ЭДС и внутреннее сопротивление источника.
381.При зарядке батареи аккумуляторов сила тока равна 2,5 А, а напряжение на зажимах батарей 12,5 В. ЭДС батареи 12,0 В. Каково внутреннее сопротивление батареи?
382.Батарея аккумуляторов подключена для зарядки к источнику с напряжением 12 В. Внутреннее сопротивление батареи 1,0 Ом. Какова ЭДС батареи, если при зарядке сила тока равна 500 мА?
383. ЭДС источника 2,0 В, его внутреннее сопротивление 1,0 Ом. Какая сила тока в цепи, если мощность тока во внешней цепи 0,75 Вт? Объяснить смысл двух ответов.
ЭДС источника 2,0 В, его внутреннее сопротивление 1,0 Ом. Какая сила тока в цепи, если мощность тока во внешней цепи 0,75 Вт? Объяснить смысл двух ответов.
384.К полюсам элемента присоединяют поочередно проволочные спирали сопротивлением 4 Ом и 9 Ом. В обоих случаях мощность электрического тока в спиралях оказывается одинаковой. Определить внутреннее сопротивление элемента.
385.Три элемента, каждый из которых имеет ЭДС 2 В и внутреннее сопротивление 0,35 Ом, соединены в батарею последовательно. К полюсам подключены два проводника сопротивлением 2,0 и 8,0 Ом, соединенные между собой параллельно. Определить напряжение на зажимах батареи и силу тока в каждом из проводников.
386.Два элемента, каждый из которых имеет внутреннее сопротивление 0,50 Ом и ЭДС по 4 В, соединены в батарею параллельно. К полюсам батареи подключены два проводника сопротивлением 1,0 и 3,0 Ом, соединенные между собой параллельно. Найти силу тока в каждом из проводников, если сопротивление соединительных проводников (считая от узлов параллельного соединения) 4,0 Ом.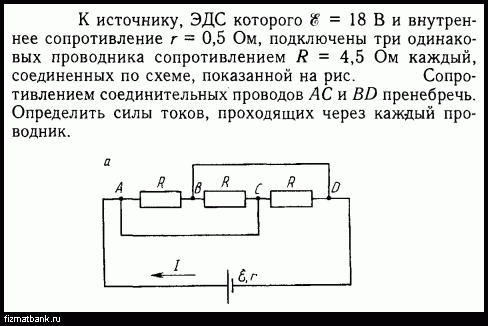
387.Э.д.с. элемента 1,6 В и внутреннее его сопротивление 0,5 Ом. Чему равен к.п.д. элемента при силе тока 2,4 А?
388.
В цепи, как показано на схеме (рис. 41) сопротивления R1 = R2 = R3 = 200 Ом, сопротивление вольтметра Rv = 1 кОм. Вольтметр показывает разность потенциалов U = 100 B. Найти ЭДС батареи.
389.Какая разность потенциалов получается на зажимах двух элементов, включенных параллельно, если их ЭДС равны соответственно = 1,4 В и = 1,2 В и внутренние сопротивления r1 = 0,6 Ом и r2 = 0,4 Ом?
390.Найти показания амперметра и вольтметра в схеме, изображенной на рис. 42. ЭДС батареи ε = 110 В, сопротивление вольтметра RV = 1 кОм, сопротивления резисторов R1 = 400 Ом и R2 = 600 Ом.
391.Найти показания амперметра и вольтметра в схеме, изображенной на рис.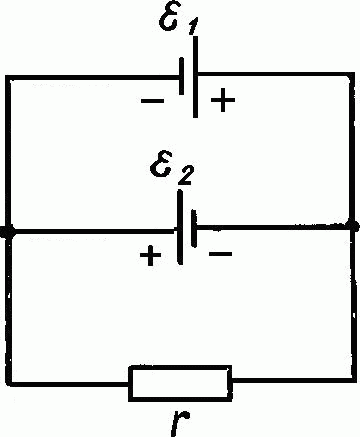 43. ЭДС батареи ε = 110 В, сопротивление вольтметра RV =1 кОм, сопротивления резисторов R1 = 400 Ом и R2 = 600 Ом.
43. ЭДС батареи ε = 110 В, сопротивление вольтметра RV =1 кОм, сопротивления резисторов R1 = 400 Ом и R2 = 600 Ом.
392.Найти показания амперметра и вольтметра в схеме, изображенной на рис. 44. ЭДС батареи ε = 110 В, сопротивление вольтметра RV =1 кОм, сопротивления резисторов R1 = 400 Ом и R2 = 600 Ом.
Законы Кирхгофа
393.Две батареи аккумуляторов (ε1 = 10 В, r1 = 1 Ом, ε2 = 8 В, r2 = 2 Ом) и реостат (R = 6 Ом) соединены, как показано на рис. 45. Найти силу тока в реостате.
394.ЭДС элементов ε = 2,1 В и ε = 1,9 В, сопротивления R1 = 45 Ом, R2 = 10 Ом и R3 = 10 Ом. Найти токи I, во всех участках цепи на схеме рис. 46.
395.
Два элемента с одинаковыми ЭДС ε1 = ε2 = 110 В и внутренними сопротивлениями r1 = 1 Ом и r2 = 2 Ом замкнуты на внешнее сопротивление R (рис.
 45). Через элемент с ЭДС течет ток I1=1A. Найти сопротивление R и ток I2 текущий через элемент с ЭДС . Какой ток I течет через сопротивление R?
45). Через элемент с ЭДС течет ток I1=1A. Найти сопротивление R и ток I2 текущий через элемент с ЭДС . Какой ток I течет через сопротивление R?396.В схеме на рис. 45 и – два элемента с одинаковой ЭДС 2 В и одинаковым внутренним сопротивлением 0,5 Ом. Найти силу тока, текущего: 1) через сопротивление R1 = 0,5 Ом, 2) через сопротивление R2 = 1,5 Ом, 3) через элемент .
397. В схеме на рис. 48 и , R1=0,5 Ом и падение потенциала на сопротивлении R2 (ток через R2 направлен сверху вниз) равно 1 В. Найти показание амперметра. Внутренним сопротивлением элементов и амперметра пренебречь.
398.Батареи имеют ЭДС и , сопротивления R1 = R2 = 100 Ом и R3 = 500 Ом. Найти показания амперметра на рис. 48.
399. В схеме, изображенной на рис. 49, токи I1 и I3 направлены справа налево, ток I2 – сверху вниз. Падения потенциалов на сопротивлениях R1, R2 и R3 равны U1 = U3 = 2U2 = 10 B. Найти ЭДС и , если ЭДС = 25 В.
Падения потенциалов на сопротивлениях R1, R2 и R3 равны U1 = U3 = 2U2 = 10 B. Найти ЭДС и , если ЭДС = 25 В.
400.Батареи имеют ЭДС , и , сопротивления R1 =4 Ом, R2 = 6 Ом, и R3 =8 Ом. Найти силу тока на каждом участке цепи по схеме (рис. 49).
401. Батареи имеют ЭДС сопротивления R1 = 20 Ом, R2 = 12 Ом. При коротком замыкании верхнего узла схемы с отрицательным зажимом батарей через замыкающий провод течет ток I = 1.6 A. Найти токи I во всех участках цепи (рис. 49) и сопротивление R3.
402.Батареи имеют ЭДС , , сопротивления R1 =1 кОм, R2 = 0,5 кОм, и R3 = 0,2 кОм, сопротивление амперметра RА = 0,2 кОм. Найти показания амперметра на схеме (рис. 50).
403.Батареи имеют ЭДС , , сопротивление R3 =1,5 кОм, сопротивление амперметра RА = 0,5 кОм. Падение потенциала на сопротивлении R2 составляет 1 В (ток через R2 направлен сверху вниз). Найти показания амперметра (рис. 50).
Падение потенциала на сопротивлении R2 составляет 1 В (ток через R2 направлен сверху вниз). Найти показания амперметра (рис. 50).
404. В цепи (рис. 51) найти силу тока в каждой ветви, если ЭДС источников тока равны ε1 = 1 В, ε2 = 3 В, ε3 = 5 В, а сопротивления R1 =2 Ом, R2 = 4 Ом, R3 = 2 Ом. Внутренним сопротивлением источников пренебречь.
Работа и мощность тока
405.Какой объем воды V можно вскипятить, затратив электрическую энергию W = 3 кВт·ч? начальная температура воды t0=10˚C.
406.ЭДС батареи 60 В, внутреннее сопротивление 4 Ом. Внешняя цепь потребляет мощность 125 Вт. Определить силу тока, напряжение на внешней цепи и его сопротивление.
407.От батареи с ЭДС 500 В необходимо передать мощность 10 кВт на расстояние 2,5 км. Определить минимальные потери мощности в медных проводниках, если их диаметр 1,5 см.
408. Элемент, ЭДС которого и внутреннее сопротивление r, замкнут на внешнее сопротивление R. Наибольшая мощность во внешней цепи равно 9 Вт. Сила тока, текущего при этих условиях по цепи равна 3 А. Найти и r.
Элемент, ЭДС которого и внутреннее сопротивление r, замкнут на внешнее сопротивление R. Наибольшая мощность во внешней цепи равно 9 Вт. Сила тока, текущего при этих условиях по цепи равна 3 А. Найти и r.
409.Мощность электрочайника 2 кВт∙ч. Определить силу тока в спирали и время нагревания чайником двух литров воды, взятых при температуре 18˚C до кипения, если при этом 5% воды обратилось в пар.
410.Найти работу тока в течение 1 мин. и мощность тока, если:
а) сопротивление щели 2;0 Ом, а сила тока 100 мА;
б) сила тока 5,0 А, а напряжение на концах цепи 0,10 кВ;
в) сопротивление цепи 0,10 кОм, а напряжение 100 В.
411.Два проводника сопротивлением 10 и 28 0м включены в сеть напряжением 100 В. Какое количество теплоты выделится в каждую секунду в каждом проводнике, если их соединить: а) последовательно; 2) параллельно?
412.Какова должна быть сила тока в нагревателе сопротивлением 100 Ом, чтобы в течение 1 с расплавился 1,0 г тающего льда? нагрелся 1,0 г воды от точки плавления до точки кипения? превратился в пар 100 г кипящей воды?
413. Какой длины и какого поперечного сечения необходимо взять нихромовую проволоку для изготовления электрического кипятильника на 120 В, 480 Вт? Допустимая плотность тока 100 А/мм2.
Какой длины и какого поперечного сечения необходимо взять нихромовую проволоку для изготовления электрического кипятильника на 120 В, 480 Вт? Допустимая плотность тока 100 А/мм2.
Достаточный уровень
Энергетика Достаточный уровень
просмотров — 339
Средний уровень
ЗАКОН ОМА ДЛЯ ПОЛНОЙ ЦЕПИ
Достаточный уровень
322.Два резистора сопротивлением 6 Ом и 10 Ом включены в цепь последовательно. Какое количество теплоты выделится в каждом резисторе за 2 мин, если напряжение на втором равно 20 В?
323.Два резистора сопротивлением 3 Ом и 6 Ом включены в цепь параллельно. В первом течет ток силой 2 А. Какое количество теплоты выделится обоими резисторами за 10 с?
324.Три проводника соединены последовательно. Первый имеет сопротивление 2 Ом, второй — 6 Ом, а в третьем за 1 мин выделилось 2,4 кДж теплоты.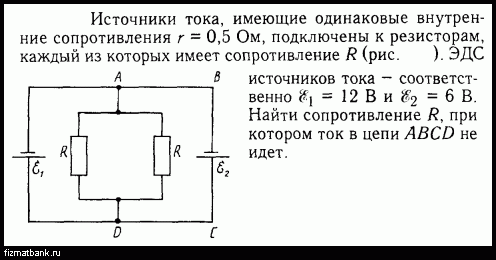 Каково сопротивление третьего проводника, если напряжение на втором равно 12В?
Каково сопротивление третьего проводника, если напряжение на втором равно 12В?
325.Два проводника соединены параллельно. В первом за 1 мин выделилось 3,6 кДж теплоты, а во втором за то же время — 1,2 кДж. Вычислите сопротивление второго проводника, если сопротивление первого равно 2 Ом.
326.Сколько теплоты выделится за 40 мин в медных проводниках с поперечным сечением 1,5 мм2 и длиной 3 м, подводящих электрический ток к плитке, если сила тока в спирали 5 А?
327.Аккумулятор мотоцикла имеет ЭДС 6 В и внутреннее сопротивление 0,5 Ом. К нему подключен реостат сопротивлением 5,5 Ом. Найдите силу тока в реостате.
328.ЭДС батарейки карманного фонарика равна 3,7 В, внутреннее сопротивление 1,5 Ом. Батарейка замкнута на сопротивление 11,7 Ом. Каково напряжение на зажимах батарейки?
329.К источнику с ЭДС 12 В и внутренним сопротивлением 1 Ом подключен реостат, сопротивление которого 5 Ом. Найдите силу тока в цепи и напряжение на зажимах источника.
Найдите силу тока в цепи и напряжение на зажимах источника.
330.ЭДС батареи 6 В. Внешнее сопротивление цепи равно 11,5 Ом, а внутреннее — 0,5 Ом. Найдите силу тока в цепи и напряжение на зажимах батареи.
331.Проводник какого сопротивления нужно включить во внешнюю цепь генератора с ЭДС 220 В и внутренним сопротивлением 0,1 Ом, чтобы на его зажимах напряжение оказалось равным 210 В?
332.При подключении внешней цепи напряжение на полюсах источника равно 9 В, а сила тока в цепи — 1,5 А. Каково внутреннее сопротивление батареи и сопротивление внешней цепи? ЭДС источника 15 В.
333.Определите силу тока при коротком замыкании батарейки с ЭДС 9 В, если при замыкании ее на внешнее сопротивление 3 Ом ток в цепи равен 2 А.
334.Источник тока с ЭДС 2 В и внутренним сопротивлением 0,8 Ом замкнут никелиновой проволокой длиной 2,1 м и сечением 0,21 мм2. Определите напряжение на зажимах источника тока.
335.Напряжение на зажимах генератора 36 В, а сопротивление внешней цепи в 9 раз больше внутреннего сопротивления. Какова ЭДС генератора?
336.При подключении к батареи гальванических элементов резистора сопротивлением 18 Ом сила тока в цепи была 1 А, а при подключении резистора сопротивлением 8 Ом сила тока стала 1,8 А. Найдите ЭДС и внутреннее сопротивление батареи.
337.Какова ЭДС элемента͵ если при измерении напряжения на его зажимах вольтметром, внутреннее сопротивление которого 20 Ом, мы получаем напряжение 1,37 В, а при замыкании элемента на сопротивление 10 Ом получаем ток 0,132 А?
Читайте также
Средний уровень.
ПРЯМОЛИНЕЙНОЕ РАВНОУСКОРЕНОЕ ДВИЖЕНИЕ.
Высокий уровень.
Достаточный уровень
Средний уровень
ПРЯМОЛИНЕЙНОЕ РАВНОМЕРНОЕ ДВИЖЕНИЕ.
ЗАДАЧ ПО
СБОРНИК
ФИЗИКЕ
РАЗДЕЛ 1. МЕХАНИКА1.Велосипедист за 40 мин проехал 10 км…. [читать подробенее]
МЕХАНИКА1.Велосипедист за 40 мин проехал 10 км…. [читать подробенее]
КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ ГРАФИЧЕСКОЕ ИЗОБРАЖЕНИЕ РАВНОУСКОРЕНОГО ДВИЖЕНИЯ. 19.По данным графики скорости построить графики для координаты и ускорения. а б 20. а б По данным графикам ускорения построить графики для координаты и скорости. … [читать подробенее]
Достаточный уровень Средний уровень. 54.Под действием какой силы пружина, имеющая жесткость 10000 Н/м, сжалась на 4 см? 55.Чему равна жесткость латунного стержня, если под действием груза 1000 Н он удлинился на 1 мм? 56.Определите удлинение пружины, если на нее действует… [читать подробенее]
ИНТЕРФЕРЕНЦИЯ СВЕТА.
Достаточный уровень
Средний уровень
469.На каком расстоянии от собирающей линзы с фокусным расстоянием 20 см получится изображение предмета, если сам предмет находится от линзы на расстоянии 15 см?
470. Определите фокусное расстояние… [читать подробенее]
Определите фокусное расстояние… [читать подробенее]
ПОТЕНЦИАЛЬНАЯ И КИНЕТИЧЕСКАЯ ЭНЕРГИЯ. Достаточный уровень Средний уровень МОЩНОСТЬ. Средний уровень. МЕХАНИЧЕСКАЯ РАБОТА. 73.Какую работу совершает сила тяжести, действующая на дождевую каплю массой 20 мг, при ее падении с высоты 2 км? 74.Груженая… [читать подробенее]
СОЕДИНЕНИЕ КОНДЕНСАТОРОВ. Средний уровень 216.В паспорте конденсатора указано: «150 мкФ, 200 В». Какой наибольший допустимый электрический заряд можно сообщить данному конденсатору? 217.Если проводнику сообщить заряд 10 -8 Кл, то его электрический потенциал… [читать подробенее]
Средний уровень.
ПЕРВАЯ КОСМИЧЕСКАЯ СКОРОСТЬ.
ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ.
Достаточный уровень.
Средний уровень.
31.С каким ускорением движется при разбеге реактивный самолет массой 60 т, если сила тяги двигателей 90 кН?
32. Какая сила сообщает телу массой 5 кг… [читать подробенее]
Какая сила сообщает телу массой 5 кг… [читать подробенее]
Средний уровень ЗАКОН ОМА ДЛЯ ПОЛНОЙ ЦЕПИ Достаточный уровень 322.Два резистора сопротивлением 6 Ом и 10 Ом включены в цепь последовательно. Какое количество теплоты выделится в каждом резисторе за 2 мин, если напряжение на втором равно 20 В? 323.Два резистора… [читать подробенее]
КВАНТОВЫЕ ПОСТУЛАТЫ БОРА. Средний уровень Средний уровень ФОТОЭФФЕКТ. 505.Определите наибольшую длину волны света. При которой может происходить фотоэффект для платины. 506.Наибольшая длина волны света, при которой наблюдается фотоэффект для калия 6,2 • 10 -5 см…. [читать подробенее]
284.Вычислите сопротивление цепи, состоящей из электрической лампочки сопротивлением 9,5 Ом, реостата сопротивлением 12 Ом и медных проводов длиной 4 м и сечением 0,4 мм2, соединенных последовательно. 285.В электрическую сеть с напряжением 120 В включены последовательно три… [читать подробенее]
285.В электрическую сеть с напряжением 120 В включены последовательно три… [читать подробенее]
«Законы Ома». Для этого вам предлагается ответить самостоятельно на следующие вопросы и заполнить пропущенные места в предложениях
Практическая работа №9
Изучение закона Ома для полной цепи
Подготовительная часть.
Для выполнения работы необходимо вспомнить теоретический материал по теме «Законы Ома». Для этого вам предлагается ответить самостоятельно на следующие вопросы и заполнить пропущенные места в предложениях.
Электрический ток – это…
Для возникновения и существования в веществе постоянного электрического тока необходимо, чтобы:
а) имелись в веществе;
б) напряженность электрического поля в проводнике была ;
в) цепь постоянного тока ;
г) на свободные электрические заряды, кроме кулоновских сил, должны действовать
.
Если сила тока со временем не меняется, то ток называют . Сила тока зависит от
, который переносит каждая частица, частиц, их направленного движения и проводника.
Впервые зависимость силы тока от напряжения и сопротивления установил в 1827 г. Немецкий ученый Георг Симон Ом (1787 – 1854). Экспериментально установленный закон Ома для участка цепи имеет вид:
Графическую зависимость силы тока от напряжения называют .
Согласно закону Ома, для проводника с сопротивлением R такая зависимость .
I
U
На
внешнем участке цепи электрические
заряды движутся под действием
электрического поля, поскольку здесь
ток проходит от высшего потенциала к
низшему, т. е. от знака «…» к «…». На
внутренней части цепи ток проходит
внутри самого источника тока, и здесь
заряды перемещаются от низшего потенциала
к высшему, т.е. от знака «…» к «…».
е. от знака «…» к «…». На
внутренней части цепи ток проходит
внутри самого источника тока, и здесь
заряды перемещаются от низшего потенциала
к высшему, т.е. от знака «…» к «…».
Работу по перемещению зарядов электрическое поле выполнять не может, ее должны выполнять сторонние силы – силы неэлектрического происхождения. Природа сторонних сил может быть различной. Это могут быть силы.
Закон Ома для полной цепи имеет вид:
При значительном уменьшении сопротивления внешнего участка цепи () ток достигает максимального для источника значения и закон Ома для полной цепи примет вид:
Такой случай называют , а соответствующее значение тока —
Напряжение на внешнем сопротивлении замкнутого круга всегда ЭДС и равно:
Заполните таблицу.

Название величины | Обозначение величины | Единица измерения | Значение | Связь с другими величинами |
Электрический заряд | ||||
Элементарный заряд | ||||
Сила Кулона | ||||
Напряженность электрического тока | ||||
Потенциал электрического поля | ||||
Напряжение | ||||
Электроемкость проводников | ||||
Сила тока | ||||
Электрическое сопротивление | ||||
Удельное сопротивление | ||||
Проводимость | ||||
Электродвижущая сила | ||||
Работа тока | ||||
Мощность тока | ||||
Количество теплоты, выделяемое током при прохождении по проводнику |
Практическая часть.

Выберите правильный ответ.
Какой заряд проходит через поперечное сечение проводника за 2 с при силе тока 3 А?
А. 2 Кл
Б. 6 Кл
В. 1,5 Кл
Г. 1 Кл
Какая сила тока в проводнике сопротивлением 2 Ом, напряжение на нем 5 В?
А. 2 А
Б. 2,5 А
В. 10 А
Г. 0,4 А
Как называется физическая величина, характеризующая работу сторонних сил по разделению заряда 1 Кл внутри источника тока?
А. Напряжение
Б. Сила тока
В. Электродвижущая сила
Г. Работа электрического тока
Какое из приведенных ниже выражений характеризует работу сторонних сил по перемещению заряда внутри источника тока?
А. E
E
Б.
В.
Г.
Какая физическая величина определяется отношением работы, совершаемой сторонними силами при перемещении заряда по всей замкнутой электрической цепи, к значению этого заряда?
А. Сила тока
Б. Электродвижущая сила
В. Напряжение
Г. Мощность электрического тока
Какая физическая величина определяется отношением ЭДС в цепи к полному сопротивлению этой цепи?
А. Напряжение
Б. Работа электрического тока
В. Сила тока
Г. Мощность электрического тока
Какое количество теплоты выделилось в резисторе сопротивлением 10 Ом за 30 с при силе тока 0,2 А?
А. 12 Дж
Б. 60 Дж
В. 6 Дж
Г. 8 Дж
Чему равно электрическое сопротивление медного проводника длиной 100 м с помощью поперечного сечения 0,25 ?
А. 4,25 мОм
4,25 мОм
Б. 0,68 мОм
В. 6,8 мОм
Г. 68 Ом
Шкала вольтметра имеет 150 делений. Вольтметр рассчитан на измерение напряжения до 3 В. Стрелка прибора отклоняется на 50 делений при прохождении через него тока 1 мА. Чему равно электрическое сопротивление прибора?
А. 0,5 кОм
Б. 1 кОм
В. 1,5 кОм
Г. 2 кОм
Источник тока с ЭДС 12 В имеет внутреннее сопротивление 1 Ом, подключен к резистору сопротивлением 5 Ом. Найдите силу тока.
А. 0,5 А
Б. 1 А
В. 2 А
Г. 3 А
Решите задачи, выбрав подходящий уровень сложности. Выполнение всех задач среднего уровня соответствует оценке «3», выполнение всех задач достаточного уровня – оценке «4».
 Дополнительно к
ним можно выполнить задания высокого
уровня, тем самым повысив оценку на 1
балл (до «4», до «5»).
Дополнительно к
ним можно выполнить задания высокого
уровня, тем самым повысив оценку на 1
балл (до «4», до «5»).
Средний уровень:
Аккумулятор мотоцикла имеет ЭДС 6 В и внутреннее сопротивление 0,5 Ом. К нему подключен реостат сопротивлением 5,5 Ом. Найти силу тока в реостате.
ЭДС батарейки карманного фонарика равна 3,7 В, внутреннее сопротивление 1,5 Ом. Батарейка замкнута на сопротивление 11,7 Ом. Каково напряжение на зажимах батарейки?
К источнику с ЭДС 12 В и внутренним сопротивлением 1 Ом подключен реостат, сопротивление которого 5 Ом. Найти силу тока в цепи и напряжение на зажимах источника.
ЭДС батареи 6 В. Внешнее сопротивление цепи равно 11,5 Ом, а внутреннее – 0,5 Ом.
 Найти силу тока в цепи и напряжение на
зажимах батареи.
Найти силу тока в цепи и напряжение на
зажимах батареи.
Проводник какого сопротивления надо включить во внешнюю цепь генератора с ЭДС 220 В и внутренним сопротивлением 0,1 Ом, чтобы на его зажимах напряжение оказалось равным 210 В?
При подключении внешней цепи напряжение на полюсах источника равно 9 В, а сила тока в цепи – 1,5 А. Каково внутреннее сопротивление батареи и сопротивление внешней цепи? ЭДС источника 15 В.
Достаточный уровень
Определите силу тока при коротком замыкании батарейки с ЭДС 9 В, если при замыкании ее на внешнее сопротивление 3 Ом ток в цепи равен 2 А.
Источник тока с ЭДС 2 В и внутренним сопротивлением 0,8 Ом замкнут никелиновой проволокой длиной 2,1 м и сечением 0,21 .
 Определите
напряжение на зажимах источника тока.
Определите
напряжение на зажимах источника тока.
Напряжение на зажимах генератора 36 В, а сопротивление внешней цепи в 9 раз больше внутреннего сопротивления. Какова ЭДС генератора?
При подключении к батареи гальванических элементов резистора сопротивлением 18 Ом сила тока в цепи была 1 А, а при подключении резистора сопротивлением 8 Ом сила тока стала 1,8 А. Найти ЭДС и внутреннее сопротивление батареи.
Какова ЭДС элемента, если при измерении напряжения на его зажимах вольтметром, внутреннее сопротивление которого 20 Ом, мы получаем напряжение 1,37 В, а при замыкании элемента на сопротивление 10 Ом получаем ток 0,132 А?
Гальванический элемент дает на внешнее сопротивление 4 Ом ток 0,2 А. если же внешнее сопротивление 7 Ом, то элемент дает ток 0,14 А.
 Какой ток даст элемент, если его замкнуть
накоротко?
Какой ток даст элемент, если его замкнуть
накоротко?
Определить внутреннее сопротивление аккумулятора, если известно, что при замыкании его на внешнее сопротивление 1 Ом напряжение на зажимах аккумулятора 2 В, а при замыкании на сопротивление 2 Ом напряжение на зажимах 2,4 В. Сопротивлением подводящих проводов пренебречь.
Батарея аккумуляторов с общим внутренним сопротивлением 1 Ом замкнута на сопротивление . Вольтметр, подключенный к зажимам батареи, показывает напряжение 20 В. Когда параллельно присоединяется такое же сопротивление, показания вольтметра уменьшаются до 15 В. Определить , считая, что сопротивление вольтметра намного больше . Сопротивлением подводящих проводов пренебречь.
Высокий уровень
Два элемента соединены параллельно. Первый элемент имеет ЭДС 2 В и внутреннее сопротивление 0,6 Ом.
 Второй имеет ЭДС 1,5 В и внутреннее сопротивление 0,4 Ом.
Определите напряжение на зажимах
батареи.
Второй имеет ЭДС 1,5 В и внутреннее сопротивление 0,4 Ом.
Определите напряжение на зажимах
батареи.
Вольтметр, подключенный к зажимам источника тока, показал 6 В. Когда к тем же зажимам подключили резистор, вольтметр стал показывать 3 В. Что покажет вольтметр, если вместо одного подключить два таких же резистора, соединенных параллельно?
Два элемента, ЭДС которых 1,9 В и 1,1 В, внутренние сопротивления 0,8 Ом и 0,1 Ом, замкнуты параллельно на внешнее сопротивление 10 Ом. Определите силу тока во внешней цепи.
Элементы с ЭДС 1,8 и 2 В и внутренними сопротивлениями 0,3 и 0,2 Ом соединены в батарею так, что во внешней цепи с сопротивлением 0,2 Ом идет ток 4 А. как в этом случае соединены элементы?
Домашнее задание.

В ходе лабораторной работы (рис 9.1 и 9.2), целью которой являлось измерить ЭДС и внутреннее сопротивление источника тока, были получены данные, которые занесены в таблицу. Выполните необходимые расчёты и заполните таблицу до конца.
Экспериментальная установка изображена на рис 9.1. К источнику тока 1 подключается резистор 2 сопротивлением 2 Ом, амперметр 3 и ключ 4. ЭДС источника тока непосредственно измеряется вольтметром 5.
Рис 9.1
Электрическая схема данной цепи приведена на рис 9.2.
Рис 9.2
Согласно закону Ома сила тока I в замкнутой цепи с одним источником определяется выражением (1). Отсюда (2). Из формулы (2) можно найти внутреннее сопротивление r источника тока, ЭДС которого предварительно измеряют вольтметром:
Сила
тока I в цепи измеряется амперметром.
№ | E =U, В | E, В | E, В | E E, В | I, А | I, А | r, Ом | r, Ом | r, Ом | rr, Ом |
1. | 2,42 | 1,05 | ||||||||
2. | 2,38 | 0,98 | ||||||||
3. | 2,37 | 0,97 | ||||||||
Общий результат | ||||||||||
Опишите использование постоянного тока в медицине.

Биогенератор
Электрографический метод регистрации биопотенциалов
Электрокардиограф
Гальванизация
Электрофорез
Оценка внутреннего сопротивления в цепях | Электрические цепи
Рабочий пример 7: Внутреннее сопротивление в цепи с последовательно включенными резисторами
Для следующей схемы рассчитайте:
разности потенциалов \ (V_ \ text {1} \), \ (V_ \ text {2} \) и \ (V_ \ text {3} \) на резисторах \ (R_ \ text {1} \), \ (R_ \ text {2} \) и \ (R_ \ text {3} \)
.сопротивление \ (R_ \ text {3} \).
сопротивление \ (R_ \ text {3} \).
Если внутреннее сопротивление равно \ (\ text {0,1} \) \ (\ text {Ω} \), какова ЭДС батареи и какая мощность рассеивается внутренним сопротивлением батареи?
Примечание
Это очень похожий на то, что вы видели ранее. Это чтобы выделить
Дело в том, что подход при работе с внутренним сопротивлением строится все же на
принципы, с которыми вы уже работали.
Определите, как подойти к проблеме
Нам дана разность потенциалов в ячейке и ток в цепи, а также сопротивления двух из трех резисторов.Мы можем использовать закон Ома для расчета разности потенциалов на известных резисторах. Поскольку резисторы включены в последовательную цепь, разность потенциалов равна \ (V = V_ \ text {1} + V_ \ text {2} + V_ \ text {3} \), и мы можем вычислить \ (V_ \ text {3} \). Теперь мы можем использовать эту информацию, чтобы найти разность потенциалов на неизвестном резисторе \ (R_ \ text {3} \).
Вычислить разность потенциалов на \ (R_ \ text {1} \)
Используя закон Ома: \ begin {align *} R_ \ text {1} & = \ frac {V_ \ text {1}} {I} \\ I \ cdot R_ \ text {1} & = I \ cdot \ frac {V_ \ text {1}} {I} \\ V_ \ text {1} & = {I} \ cdot {R_ \ text {1}} \\ & = 2 \ cdot 1 \\ V_ \ текст {1} & = \ текст {2} \ текст {V} \ end {align *}
Вычислить разность потенциалов на \ (R_ \ text {2} \)
Снова используя закон Ома: \ begin {align *} R_ \ text {2} & = \ frac {V_ \ text {2}} {I} \\ I \ cdot R_ \ text {2} & = I \ cdot \ frac {V_ \ text {2}} {I} \\ V_ \ text {2} & = {I} \ cdot {R_ \ text {2}} \\ & = 2 \ cdot 3 \\ V_ \ текст {2} & = \ текст {6} \ текст {V} \ end {align *}
Вычислить разность потенциалов на \ (R_ \ text {3} \)
Так как разность потенциалов на всех резисторах вместе взятых должна быть такой же, как разность потенциалов на ячейке в последовательной цепи, мы можем найти \ (V_ \ text {3} \), используя: \ begin {align *} V & = V_ \ text {1} + V_ \ text {2} + V_ \ text {3} \\ V_ \ text {3} & = V — V_ \ text {1} — V_ \ text {2} \\ & = 23 — 2 — 6 \\ V_ \ текст {3} & = \ текст {15} \ текст {V} \ end {align *}
Найдите сопротивление \ (R_ \ text {3} \)
Нам известна разность потенциалов на \ (R_ \ text {3} \) и ток через нее, поэтому мы можем использовать закон Ома для вычисления значения сопротивления: \ begin {align *} R_ \ text {3} & = \ frac {V_ \ text {3}} {I} \\ & = \ frac {\ text {15}} {\ text {2}} \\ R_ \ text {3} & = \ text {7,5} ~ \ Omega \ end {align *}
Разница потенциалов на внутреннем сопротивлении батареи
Значение ЭДС можно рассчитать по разности потенциалов нагрузки и разности потенциалов на внутреннем сопротивлении. 2} {R} \), и мы знаем ток в цепи, внутреннее сопротивление и разность потенциалов в ней, поэтому мы можем использовать любую форму уравнения для мощности:
2} {R} \), и мы знаем ток в цепи, внутреннее сопротивление и разность потенциалов в ней, поэтому мы можем использовать любую форму уравнения для мощности:
Напишите окончательный ответ
- \ (V_ \ text {1} = \ text {2,0} \ text {V} \)
- \ (V_ \ text {2} = \ text {6,0} \ text {V} \)
- \ (V_ \ text {3} = \ text {10,0} \ text {V} \)
- \ (R_ \ text {3} = \ text {7,5} \ Omega \)
- \ (\ mathcal {E} = \ text {23,2} \ text {V} \)
- \ (P_r = \ text {0,4} \ text {W} \)
Рабочий пример 8: Внутреннее сопротивление и резисторы параллельно
Разность потенциалов на батарее составляет 18 В, когда она подключена к двум параллельным резисторам \ (\ text {4,00} \) \ (\ Omega \) и \ (\ text {12,00} \) \ ( \ Omega \) соответственно.Рассчитайте ток через ячейку и через каждый из резисторов. Если внутреннее сопротивление батареи \ (\ text {0,375} \) \ (\ text {Ω} \), какова ЭДС батареи?
Если внутреннее сопротивление батареи \ (\ text {0,375} \) \ (\ text {Ω} \), какова ЭДС батареи?
Сначала нарисуйте схему, прежде чем производить какие-либо вычисления
Определите, как подойти к проблеме
Нам нужно определить ток через ячейку и каждый из параллельных резисторов. Нам дана разность потенциалов на ячейке и сопротивления резисторов, поэтому мы можем использовать закон Ома для расчета тока.
Рассчитать ток через ячейку
Чтобы рассчитать ток через ячейку, нам сначала нужно определить эквивалентное сопротивление остальной части цепи. Резисторы включены параллельно и поэтому: \ begin {align *} \ frac {\ text {1}} {R} & = \ frac {\ text {1}} {R_ \ text {1}} + \ frac {\ text {1}} {R_ \ text {2}} \ \ & = \ frac {\ text {1}} {\ text {4}} + \ frac {\ text {1}} {\ text {12}} \\ & = \ frac {3 + 1} {\ text {12}} \\ & = \ frac {\ text {4}} {\ text {12}} \\ R & = \ frac {\ text {12}} {\ text {4}} = \ text {3,00} \ \ Omega \ end {выровнять *} Теперь, используя закон Ома, чтобы найти ток через ячейку: \ begin {align *} R & = \ frac {V} {I} \\ I & = \ frac {V} {R} \\ & = \ frac {\ text {18}} {\ text {3}} \\ I & = \ text {6,00} \ text {A} \ end {align *}
Теперь определите ток через один из параллельных резисторов
Мы знаем, что для чисто параллельной конфигурации резисторов разность потенциалов на ячейке такая же, как и разность потенциалов на каждом из параллельных резисторов. Для этой схемы:
\ begin {align *}
V & = V_ \ text {1} = V_ \ text {2} = \ text {18} \ text {V}
\ end {выровнять *}
Начнем с вычисления тока через \ (R_ \ text {1} \) по закону Ома:
\ begin {align *}
R_ \ text {1} & = \ frac {V_ \ text {1}} {I_ \ text {1}} \\
I_ \ text {1} & = \ frac {V_ \ text {1}} {R_ \ text {1}} \\
& = \ frac {\ text {18}} {\ text {4}} \\
I_ \ text {1} & = \ text {4,50} \ text {A}
\ end {align *}
Для этой схемы:
\ begin {align *}
V & = V_ \ text {1} = V_ \ text {2} = \ text {18} \ text {V}
\ end {выровнять *}
Начнем с вычисления тока через \ (R_ \ text {1} \) по закону Ома:
\ begin {align *}
R_ \ text {1} & = \ frac {V_ \ text {1}} {I_ \ text {1}} \\
I_ \ text {1} & = \ frac {V_ \ text {1}} {R_ \ text {1}} \\
& = \ frac {\ text {18}} {\ text {4}} \\
I_ \ text {1} & = \ text {4,50} \ text {A}
\ end {align *}
Рассчитайте ток через другой параллельный резистор
Мы можем снова использовать закон Ома, чтобы найти ток в \ (R_ \ text {2} \):
\ begin {align *}
R_ \ text {2} & = \ frac {V_ \ text {2}} {I_ \ text {2}} \\
I_ \ text {2} & = \ frac {V_ \ text {2}} {R_ \ text {2}} \\
& = \ frac {\ text {18}} {\ text {12}} \\
I_ \ text {2} & = \ text {1,50} \ text {A}
\ end {выровнять *} Альтернативный метод вычисления \ (I_ \ text {2} \) заключался бы в использовании того факта, что токи через каждый из параллельных резисторов должны складываться в общий ток через ячейку: \ begin {align *}
I & = I_ \ text {1} + I_ \ text {2} \\
I_ \ text {2} & = I — I_ \ text {1} \\
& = 6 — 4. 5 \\
I_ \ text {2} & = \ text {1,5} \ text {A}
\ end {align *}
5 \\
I_ \ text {2} & = \ text {1,5} \ text {A}
\ end {align *}
Определить ЭДС
Этот полный ток через батарею — это ток через внутреннее сопротивление батареи. Знание силы тока и сопротивления позволяет нам использовать закон Ома для определения разности потенциалов на внутреннем сопротивлении и, следовательно, ЭДС батареи.
Используя закон Ома, мы можем определить разность потенциалов на внутреннем сопротивлении:
\ begin {align *} V & = I \ cdot r \\ & = \ текст {6} \ cdot \ text {0,375} \\ & = \ текст {2,25} \ текст {V} \ end {выровнять *}Мы знаем, что ЭДС аккумулятора — это разность потенциалов на клеммах, суммированная с разностью потенциалов на внутреннем сопротивлении, так:
\ begin {align *} \ mathcal {E} & = V + Ir \\ & = \ text {18} + \ text {2,25} \\ & = \ текст {20,25} \ текст {V} \ end {align *}Напишите окончательный ответ
Ток через ячейку равен \ (\ text {6,00} \) \ (\ text {A} \).
Ток через резистор \ (\ text {4,00} \) \ (\ Omega \) равен \ (\ text {4,50} \) \ (\ text {A} \).
Ток через резистор \ (\ text {12,00} \) \ (\ Omega \) равен \ (\ text {1,50} \) \ (\ text {A} \).
ЭДС батареи равна \ (\ text {20,25} \) \ (\ text {V} \).
Рабочий пример 9: Мощность в последовательной и параллельной сетях резисторов
Учитывая следующую схему:
Ток, выходящий из батареи, равен \ (\ text {1,07} \) \ (\ text {A} \), общая мощность, рассеиваемая во внешней цепи, равна \ (\ text {6,42} \) \ ( \ text {W} \), отношение полных сопротивлений двух параллельных сетей \ (R_ {P \ text {1}}: R_ {P \ text {2}} \) равно 1: 2, соотношение \ (R_ \ text {1}: R_ \ text {2} \) равно 3: 5 и \ (R_ \ text {3} = \ text {7,00} \ text {Ω} \).
Определите:
- разность потенциалов АКБ,
- мощность, рассеиваемая в \ (R_ {P \ text {1}} \) и \ (R_ {P \ text {2}} \), и
- , если батарея имеет ЭДС, равную \ (\ text {6,50} \) \ (\ text {V} \), каково значение сопротивления каждого резистора и мощность, рассеиваемая в каждом из них.

Что требуется
В этом вопросе вам дается различная информация и предлагается определить мощность, рассеиваемую каждым резистором и каждой комбинацией резисторов.Обратите внимание, что данная информация в основном относится ко всей цепи. Это подсказка, которую вы должны начать с общей схемы и двигаться вниз к более конкретным элементам схемы.
Расчет разности потенциалов аккумулятора
В первую очередь остановимся на аккумуляторе. Нам дана мощность всей цепи, а также ток, покидающий батарею. Мы знаем, что разность потенциалов на клеммах аккумулятора — это разность потенциалов в цепи в целом.
Мы можем использовать соотношение \ (P = VI \) для всей цепи, потому что разность потенциалов такая же, как разность потенциалов на клеммах батареи: \ begin {align *} P & = VI \\ V & = \ frac {P} {I} \\ & = \ frac {\ text {6,42}} {\ text {1,07}} \\ & = \ текст {6,00} \ текст {V} \ end {align *}
Разность потенциалов на батарее равна \ (\ text {6,00} \) \ (\ text {V} \).
Мощность, рассеиваемая в \ (R_ {P \ text {1}} \) и \ (R_ {P \ text {2}} \)
Помните, что мы работаем от общих деталей схемы вниз к деталям отдельных элементов, это противоположно тому, как вы относились к этой схеме ранее.
Мы можем рассматривать параллельные сети как эквивалентные резисторы, поэтому схема, с которой мы сейчас работаем, будет выглядеть так:
Мы знаем, что ток через два элемента схемы будет одинаковым, потому что это последовательная цепь и что сопротивление всей цепи должно быть: \ (R_ {Ext} = R_ {P \ text {1}} + R_ {P \ text {2}} \). Мы можем определить полное сопротивление по закону Ома для цепи в целом: \ begin {align *} V_ {батарея} & = IR_ {Ext} \\ R_ {Ext} & = \ frac {V_ {battery}} {I} \\ & = \ frac {\ text {6,00}} {\ text {1,07}} \\ & = \ текст {5,61} \ текст {Ω} \ end {align *}
Мы знаем, что соотношение между \ (R_ {P \ text {1}}: R_ {P \ text {2}} \) равно 1: 2, что означает, что мы знаем: \ begin {align *} R_ {P \ text {1}} & = \ frac {\ text {1}} {\ text {2}} R_ {P \ text {2}} \ \ \ text {и} \\ R_T & = R_ {P \ text {1}} + R_ {P \ text {2}} \\ & = \ frac {\ text {1}} {\ text {2}} R_ {P \ text {2}} + R_ {P \ text {2}} \\ & = \ frac {\ text {3}} {\ text {2}} R_ {P \ text {2}} \\ (\ text {5,61}) & = \ frac {\ text {3}} {\ text {2}} R_ {P \ text {2}} \\ R_ {P \ text {2}} & = \ frac {\ text {2}} {\ text {3}} (\ text {5,61}) \\ R_ {P \ text {2}} & = \ text {3,74} \ text {Ω} \ end {выровнять *} и поэтому: \ begin {align *} R_ {P \ text {1}} & = \ frac {\ text {1}} {\ text {2}} R_ {P \ text {2}} \\ & = \ frac {\ text {1}} {\ text {2}} (3.2 (\ text {3,74}) \\ & = \ текст {4,28} \ текст {W} \ end {выровнять *} Эти значения будут в сумме с исходным значением мощности, которое у нас было для внешней цепи. Если бы они не мы бы сделали ошибку в расчетах.
Расчет параллельной сети 1
Теперь мы можем приступить к детальному расчету первого набора параллельных резисторов.
Мы знаем, что соотношение между \ (R _ {\ text {1}}: R _ {\ text {2}} \) составляет 3: 5, что означает, что мы знаем \ (R _ {\ text {1}} = \ frac {\ text {3}} {\ text {5}} R _ {\ text {2}} \).Нам также известно общее сопротивление двух параллельных резисторов в этой сети. это \ (\ text {1,87} \) \ (\ text {Ω} \). Мы можем использовать соотношение между значениями двух резисторов, а также формула для общей сопротивление (\ (\ frac {\ text {1}} {R_PT} = \ frac {\ text {1}} {R_ \ text {1}} + \ frac {\ text {1}} {R_ \ text {2) }} \)) чтобы найти номиналы резисторов: \ begin {align *} \ frac {\ text {1}} {R_ {P \ text {1}}} & = \ frac {\ text {1}} {R_ \ text {1}} + \ frac {\ text {1}} { R_ \ text {2}} \\ \ frac {\ text {1}} {R_ {P \ text {1}}} & = \ frac {\ text {5}} {3R_ \ text {2}} + \ frac {\ text {1}} { R_ \ text {2}} \\ \ frac {\ text {1}} {R_ {P \ text {1}}} & = \ frac {\ text {1}} {R_ \ text {2}} (\ frac {\ text {5}} { \ text {3}} + 1) \\ \ frac {\ text {1}} {R_ {P \ text {1}}} & = \ frac {\ text {1}} {R_ \ text {2}} (\ frac {\ text {5}} { \ text {3}} + \ frac {\ text {3}} {\ text {3}}) \\ \ frac {\ text {1}} {R_ {P \ text {1}}} & = \ frac {\ text {1}} {R_ \ text {2}} \ frac {\ text {8}} {\ текст {3}} \\ R_ \ text {2} & = R_ {P \ text {1}} \ frac {\ text {8}} {\ text {3}} \\ & = (\ text {1,87}) \ frac {\ text {8}} {\ text {3}} \\ & = \ текст {4,99} \ текст {Ω} \ end {выровнять *} Мы также можем вычислить \ (R _ {\ text {1}} \): \ begin {align *} R _ {\ text {1}} & = \ frac {\ text {3}} {\ text {5}} R _ {\ text {2}} \\ & = \ frac {\ text {3}} {\ text {5}} (\ text {4,99}) \\ & = \ текст {2,99} \ текст {Ω} \ end {align *}
Чтобы определить мощность, нам нужно рассчитанное нами сопротивление и либо разность потенциалов, либо ток. 2} {\ text {4,99}} \\ & = \ текст {0,80} \ текст {W} \ end {align *}
Параллельная сеть 2 вычисления
Теперь мы можем приступить к детальному расчету второго набора параллельных резисторов.
Нам дано \ (R_ \ text {3} = \ text {7,00} \ text {Ω} \), и мы знаем \ (R_ {P \ text {2}} \), поэтому мы можем вычислить \ (R_ \ text {4} \) из: \ begin {align *} \ frac {\ text {1}} {R_ {P \ text {2}}} & = \ frac {\ text {1}} {R_ \ text {3}} + \ frac {\ text {1}} { R_ \ text {4}} \\ \ frac {\ text {1}} {\ text {3,74}} & = \ frac {\ text {1}} {\ text {7,00}} + \ frac {\ text {1}} {R_ \ текст {4}} \\ R_ \ text {4} & = \ text {8,03} \ text {Ω} \ end {align *}
Мы можем вычислить разность потенциалов во второй параллельной сети, вычтя разность потенциалов первой параллельной сети из разности потенциалов батареи, \ (V_ {P \ text {2}} = \ text {6,00} — \ text {2,00} = \ text {4,00} \ text {V} \).2} {\ text {8,03}} \\ & = \ текст {1,99} \ текст {W} \ end {align *}
Внутреннее сопротивление
Мы знаем, что ЭДС батареи равна \ (\ text {6,5} \) \ (\ text {V} \), но что разность потенциалов, измеренная на клеммах, составляет всего \ (\ text {6} \) \ (\ текст {V} \). Разница — это разность потенциалов на внутреннем сопротивлении батареи, и мы можем использовать известный ток и закон Ома для определения внутреннего сопротивления:
\ begin {align *} V & = I \ cdot R \\ R & = \ frac {V} {I} \\ & = \ frac {\ text {0,5}} {\ text {1,07}} \\ & = \ text {0,4672897} \\ & = \ текст {0,47} \ текст {Ω} \ end {выровнять *}Мощность, рассеиваемая на внутреннем сопротивлении батареи:
\ begin {align *} P & = VI \\ & = \ текст {0,5} \ cdot \ text {1,07} \\ & = \ текст {0,535} \ текст {W} \ end {align *}Рабочий пример 10: Внутреннее сопротивление и фары [NSC 2011 Paper 1]
Фара и два ИДЕНТИЧНЫХ задних фонаря скутера подключены параллельно к аккумулятору с неизвестным внутренним сопротивлением, как показано на упрощенной принципиальной схеме ниже.Фара имеет сопротивление \ (\ text {2,4} \) \ (\ text {Ω} \) и управляется переключателем \ (\ textbf {S} _1 \). Задние фонари управляются переключателем \ (\ textbf {S} _2 \). Сопротивлением соединительных проводов можно пренебречь.
График рядом показывает разность потенциалов на клеммах батареи до и после включения переключателя \ (\ textbf {S} _1 \) (пока переключатель \ (\ textbf {S} _2 \) открыт). Переключатель \ (\ textbf {S} _1 \) закрывается в момент \ (\ textbf {t} _1 \).
Используйте график, чтобы определить ЭДС аккумулятора.
(1 балл)
ПРИ ТОЛЬКО ВЫКЛЮЧАТЕЛЬ \ (\ textbf {S} _1 \) ЗАКРЫТО, вычислите следующее:
Ток через фару
(3 балла)
Внутреннее сопротивление \ (r \) батареи
(3 балла)
ОБЕ ПЕРЕКЛЮЧАТЕЛИ \ (\ textbf {S} _1 \) И \ (\ textbf {S} _2 \) ТЕПЕРЬ ЗАКРЫТЫ.В течение этого периода батарея обеспечивает ток \ (\ text {6} \) \ (\ text {A} \).
Рассчитайте сопротивление каждого заднего фонаря.
(5 баллов)
Как повлияет на показания вольтметра, если фара перегорит? (Оба переключателя \ (\ textbf {S} _1 \) и \ (\ textbf {S} _2 \) все еще закрыты.)
Запишите только УВЕЛИЧИВАЕТ, УМЕНЬШАЕТСЯ или ОСТАЕТСЯ ОДИН ТО ЖЕ.
Дайте объяснение.
(3 балла)
Вопрос 1
\ (\ text {12} \) \ (\ text {V} \)
(1 балл)
Вопрос 2.1
Вариант 1:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {9,6}} {\ text {2,4}} \\ & = \ текст {4 A} \ end {выровнять *}Вариант 2:
\ begin {align *} \ text {emf} & = IR + Ir \\ 12 & = I (\ text {2,4}) + \ text {2,4} \\ \ поэтому I & = \ text {4 A} \ end {выровнять *}(3 балла)
Вопрос 2.2
Вариант 1:
\ begin {align *} \ text {emf} & = IR + Ir \\ 12 & = \ text {9,4} + 4r \\ r & = \ текст {0,6} \ \ Omega \ end {выровнять *}Вариант 2:
\ begin {align *} V_ {потеряно} & = Ir \\ \ text {2,4} & = \ text {4} r \\ \ поэтому r & = \ text {0,6} \ \ Omega \ end {выровнять *}Вариант 3:
\ begin {align *} \ text {emf} & = I (R + r) \\ \ text {12} & = \ text {4} (\ text {2,4} + r) \\ \ поэтому r & = \ text {0,6} \ \ Omega \ end {выровнять *}(3 балла)
Вопрос 3
Вариант 1:
\ begin {align *} \ text {emf} & = IR + Ir \\ \ text {12} & = \ text {6} (R + \ text {0,6}) \\ R _ {\ text {ext}} & = \ text {1,4} \ \ Omega \ end {align *} \ begin {align *} \ frac {1} {R} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ \ frac {1} {\ text {1,4}} & = \ frac {1} {\ text {2,4}} + \ frac {1} {R} \\ R & = \ текст {3,36} \ \ Omega \ end {выровнять *}Каждый задний фонарь: \ (R = \ text {1,68} \ \ Omega \)
Вариант 2:
\ begin {align *} \ text {Emf} & = V _ {\ text {terminal}} + Ir \\ 12 & = V _ {\ text {терминал}} + 6 (\ text {0,6}) \\ \ поэтому V _ {\ text {terminal}} & = \ text {8,4} \ text {V} \ end {align *} \ begin {align *} I _ {\ text {2,4} \ \ Omega} & = \ frac {V} {R} \\ & = \ frac {\ text {8,4}} {\ text {2,4}} \\ & = \ text {3,5 A} \ end {align *} \ begin {align *} I _ {\ text {задние фонари}} & = 6 — \ text {3,5} \\ & = \ текст {2,5} \ текст {A} \\ R _ {\ text {задние фонари}} & = \ frac {V} {I} \\ & = \ frac {\ text {8,4}} {\ text {2,5}} \\ & = \ текст {3,36} \ \ Omega \\ R _ {\ text {задний фонарь}} & = \ text {1,68} \ \ Omega \ end {выровнять *}Вариант 3:
\ begin {align *} V & = IR \\ \ text {12} & = \ text {6} (R) \\ R _ {\ text {ext}} & = 2 \ \ Omega \ end {align *} \ begin {align *} R _ {\ text {parallel}} & = 2 — \ text {0,6} \\ & = \ текст {1,4} \ \ Omega \\ \ frac {1} {R} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ \ frac {1} {\ text {1,4}} & = \ frac {1} {\ text {2,4}} + \ frac {1} {R} \\ R & = \ текст {3,36} \ \ Omega \ end {выровнять *}Каждый задний фонарь: \ (R = \ text {1,68} \ \ Omega \)
Вариант 4:
Для параллельной комбинации: \ (I_ {1} + I_ {2} = 6 \ text {A} \)
\ begin {align *} \ поэтому \ frac {V} {\ text {2,4}} + \ frac {V} {R _ {\ text {задние фонари}}} & = \ text {6} \\ \ text {8,4} \ left (\ frac {1} {\ text {2,4}} + \ frac {1} {R _ {\ text {задние фонари}}} \ right) & = \ text {6 } \\ \ поэтому R _ {\ text {задние фонари}} & = \ text {3,36} \ \ Omega \\ R _ {\ text {задний фонарь}} & = \ text {1,68} \ \ Omega \ end {выровнять *}(5 баллов)
Вопрос 4
Увеличивается
Сопротивление увеличивается, а ток уменьшается.Таким образом, \ (Ir \) (потерянное вольт) должно уменьшаться, что приводит к увеличению напряжения.
(3 балла)
[ИТОГО: 15 баллов]
ЗаконОма: сопротивление и простые схемы
Цели обучения
К концу этого раздела вы сможете:
- Объясните происхождение закона Ома.
- Рассчитывайте напряжения, токи или сопротивления по закону Ома.
- Объясните, что такое омический материал.
- Опишите простую схему.
Что движет током? Мы можем думать о различных устройствах, таких как батареи, генераторы, розетки и т. Д., Которые необходимы для поддержания тока. Все такие устройства создают разность потенциалов и условно называются источниками напряжения. Когда источник напряжения подключен к проводнику, он прикладывает разность потенциалов В , которая создает электрическое поле. Электрическое поле, в свою очередь, воздействует на заряды, вызывая ток.
Ток, протекающий через большинство веществ, прямо пропорционален приложенному к нему напряжению В. . Немецкий физик Георг Симон Ом (1787–1854) первым экспериментально продемонстрировал, что ток в металлической проволоке прямо пропорционален приложенному напряжению :
[латекс] I \ propto {V} \\ [/ латекс].
Это важное соотношение известно как закон Ома . Его можно рассматривать как причинно-следственную связь, в которой напряжение является причиной, а ток — следствием.Это эмпирический закон, подобный закону трения — явление, наблюдаемое экспериментально. Такая линейная взаимосвязь возникает не всегда.
Сопротивление и простые схемы
Если напряжение увеличивает ток, что ему мешает? Электрическое свойство, препятствующее току (примерно такое же, как трение и сопротивление воздуха), называется сопротивлением R . Столкновения движущихся зарядов с атомами и молекулами вещества передают энергию веществу и ограничивают ток.Сопротивление обратно пропорционально току, или
[латекс] I \ propto \ frac {1} {R} \\ [/ latex].
Так, например, при удвоении сопротивления ток уменьшается вдвое. Комбинируя отношения тока к напряжению и тока к сопротивлению, получаем
[латекс] I = \ frac {V} {R} \\ [/ латекс].
Это соотношение также называется законом Ома. Закон Ома в такой форме действительно определяет сопротивление определенных материалов. Закон Ома (как и закон Гука) не универсален.Многие вещества, для которых действует закон Ома, называются омическими . К ним относятся хорошие проводники, такие как медь и алюминий, и некоторые плохие проводники при определенных обстоятельствах. Омические материалы имеют сопротивление R , которое не зависит от напряжения В и тока I . Объект с простым сопротивлением называется резистором , даже если его сопротивление невелико. Единицей измерения сопротивления является Ом и обозначается символом Ω (заглавная греческая омега).Перестановка I = V / R дает R = V / I , поэтому единицы сопротивления равны 1 Ом = 1 вольт на ампер:
[латекс] 1 \ Omega = 1 \ frac {V} {A} \\ [/ latex].
На рисунке 1 показана схема простой схемы. Простая схема имеет один источник напряжения и один резистор. Можно предположить, что провода, соединяющие источник напряжения с резистором, имеют незначительное сопротивление, или их сопротивление можно включить в R .
Рисунок 1.Простая электрическая цепь, в которой замкнутый путь для прохождения тока обеспечивается проводниками (обычно металлическими проводами), соединяющими нагрузку с выводами батареи, представленными красными параллельными линиями. Зигзагообразный символ представляет собой единственный резистор и включает любое сопротивление в соединениях с источником напряжения.
Пример 1. Расчет сопротивления: автомобильная фара
Каково сопротивление автомобильной фары, через которую проходит 2,50 А при 12.0 В к нему приложено?
СтратегияМы можем изменить закон Ома в соответствии с формулой I = V / R и использовать его для определения сопротивления.
РешениеПерестановка I = V / R и замена известных значений дает
[латекс] R = \ frac {V} {I} = \ frac {\ text {12} \ text {.} \ Text {0 V}} {2 \ text {.} \ Text {50 A}} = \ text {4} \ text {.} \ text {80 \ Omega} \\ [/ latex].
ОбсуждениеЭто относительно небольшое сопротивление, но оно больше, чем хладостойкость фары.Как мы увидим в разделе «Сопротивление и удельное сопротивление», сопротивление обычно увеличивается с температурой, поэтому лампа имеет меньшее сопротивление при первом включении и потребляет значительно больший ток во время короткого периода прогрева.
Сопротивление может быть разным. Некоторые керамические изоляторы, например те, которые используются для поддержки линий электропередач, имеют сопротивление 10 12 Ом или более. Сопротивление сухого человека может составлять 10 5 Ом, в то время как сопротивление человеческого сердца составляет примерно 10 3 Ом.Кусок медного провода большого диаметра длиной в метр может иметь сопротивление 10 −5 Ом, а сверхпроводники вообще не имеют сопротивления (они неомичны). Сопротивление связано с формой объекта и материалом, из которого он состоит, как будет показано в разделе «Сопротивление и удельное сопротивление». Дополнительное понимание можно получить, решив I = V / R для V , что дает
В = ИК
Это выражение для В можно интерпретировать как падение напряжения на резисторе, вызванное протеканием тока I .Фраза IR drop часто используется для этого напряжения. Например, фара в Примере 1 выше имеет падение IR на 12,0 В. Если напряжение измеряется в различных точках цепи, будет видно, что оно увеличивается на источнике напряжения и падает на резисторе. Напряжение аналогично давлению жидкости. Источник напряжения подобен насосу, создающему перепад давления, вызывающему ток — поток заряда. Резистор похож на трубу, которая снижает давление и ограничивает поток из-за своего сопротивления.Здесь сохранение энергии имеет важные последствия. Источник напряжения подает энергию (вызывая электрическое поле и ток), а резистор преобразует ее в другую форму (например, тепловую энергию). В простой схеме (с одним простым резистором) напряжение, подаваемое источником, равно падению напряжения на резисторе, так как PE = q Δ V , и через каждую из них протекает то же самое q . Таким образом, энергия, подаваемая источником напряжения, и энергия, преобразуемая резистором, равны.(См. Рисунок 2.)
Рис. 2. Падение напряжения на резисторе в простой цепи равно выходному напряжению батареи.
Подключение: сохранение энергииВ простой электрической цепи единственный резистор преобразует энергию, поступающую от источника, в другую форму. Здесь о сохранении энергии свидетельствует тот факт, что вся энергия, подаваемая источником, преобразуется в другую форму одним резистором. Мы обнаружим, что сохранение энергии имеет другие важные применения в схемах и является мощным инструментом анализа схем.
Исследования PhET: закон ОмаПосмотрите, как уравнение закона Ома соотносится с простой схемой. Отрегулируйте напряжение и сопротивление и посмотрите, как изменяется ток по закону Ома. Размеры символов в уравнении изменяются в соответствии с принципиальной схемой.
Щелкните, чтобы запустить моделирование.
Сводка раздела
- Простая схема — это схема , в которой есть один источник напряжения и одно сопротивление.
- Одно из утверждений закона Ома дает соотношение между током I , напряжением В и сопротивлением R в простой схеме как [латекс] I = \ frac {V} {R} \\ [/ latex] .
- Сопротивление выражается в единицах Ом (Ом), относящихся к вольтам и амперам на 1 Ом = 1 В / А.
- Имеется падение напряжения IR на резисторе, вызванное протекающим через него током, равным V = IR .
Концептуальные вопросы
- Падение напряжения IR на резисторе означает изменение потенциала или напряжения на резисторе.Изменится ли ток при прохождении через резистор? Объяснять.
- Как падение IR в резисторе похоже на падение давления в жидкости, протекающей по трубе?
Задачи и упражнения
1. Какой ток протекает через лампочку фонаря на 3,00 В, когда ее горячее сопротивление составляет 3,60 Ом?
2. Рассчитайте эффективное сопротивление карманного калькулятора с батареей на 1,35 В, через которую протекает ток 0,200 мА.
3.Каково эффективное сопротивление стартера автомобиля, когда через него проходит 150 А, когда автомобильный аккумулятор подает на двигатель 11,0 В?
4. Сколько вольт подается для работы светового индикатора DVD-плеера с сопротивлением 140 Ом при прохождении через него 25,0 мА?
5. (a) Найдите падение напряжения на удлинителе с сопротивлением 0,0600 Ом, через который проходит ток 5,00 А. (b) Более дешевый шнур использует более тонкую проволоку и имеет сопротивление 0.300 Ом. Какое в нем падение напряжения при протекании 5.00 А? (c) Почему напряжение на любом используемом приборе снижается на эту величину? Как это повлияет на прибор?
6. ЛЭП подвешена к металлическим опорам со стеклянными изоляторами, имеющими сопротивление 1,00 × 10 9 Ом. Какой ток протекает через изолятор при напряжении 200 кВ? (Некоторые линии высокого напряжения — постоянного тока.)
Глоссарий
- Закон Ома:
- эмпирическое соотношение, указывающее, что ток I пропорционален разности потенциалов V , V ; часто записывается как I = V / R , где R — сопротивление
- сопротивление:
- электрическое свойство, препятствующее току; для омических материалов это отношение напряжения к току, R = V / I
- Ом:
- единица сопротивления, равная 1Ω = 1 В / A
- омическое:
- вид материала, для которого действует закон Ома
- простая схема:
- схема с одним источником напряжения и одним резистором
Избранные решения проблем и упражнения
1.0,833 А
3. 7,33 × 10 −2 Ом
5. (а) 0,300 В
(б) 1,50 В
(c) Напряжение, подаваемое на любой используемый прибор, снижается, поскольку общее падение напряжения от стены до конечной мощности прибора является фиксированным. Таким образом, если падение напряжения на удлинителе велико, падение напряжения на приборе значительно уменьшается, поэтому выходная мощность прибора может быть значительно уменьшена, что снижает способность прибора работать должным образом.
10.5 RC Circuits — University Physics Volume 2
Задачи обучения
По окончании раздела вы сможете:- Опишите процесс зарядки конденсатора
- Опишите процесс разрядки конденсатора
- Перечислите некоторые применения RC-цепей
Когда вы используете камеру со вспышкой, для зарядки конденсатора, питающего вспышку, требуется несколько секунд. Световая вспышка разряжает конденсатор за крошечные доли секунды.Почему зарядка занимает больше времени, чем разрядка? Этот вопрос и несколько других явлений, связанных с зарядкой и разрядкой конденсаторов, обсуждаются в этом модуле.
Цепи с сопротивлением и емкостью
Цепь RC — это цепь, содержащая сопротивление и емкость. Как показано в разделе «Емкость», конденсатор — это электрический компонент, который накапливает электрический заряд, накапливая энергию в электрическом поле.
На рис. 10.38 (a) показана простая схема RC , в которой используется источник постоянного напряжения εε, резистор R , конденсатор C и двухпозиционный переключатель.Схема позволяет конденсатору заряжаться или разряжаться в зависимости от положения переключателя. Когда переключатель перемещается в положение A , конденсатор заряжается, в результате чего возникает цепь в части (b). Когда переключатель перемещается в положение B , конденсатор разряжается через резистор.
Рисунок 10.38 (a) Схема RC с двухполюсным переключателем, который можно использовать для зарядки и разрядки конденсатора. (b) Когда переключатель перемещается в положение A , схема сводится к простому последовательному соединению источника напряжения, резистора, конденсатора и переключателя.(c) Когда переключатель перемещается в положение B , схема сводится к простому последовательному соединению резистора, конденсатора и переключателя. Источник напряжения снят с цепи.
Зарядка конденсатора
Мы можем использовать правило петли Кирхгофа, чтобы понять заряд конденсатора. Это приводит к уравнению ε − VR − Vc = 0. ε − VR − Vc = 0. Это уравнение можно использовать для моделирования заряда как функции времени при зарядке конденсатора. Емкость определяется как C = q / V, C = q / V, поэтому напряжение на конденсаторе равно VC = qCVC = qC.Согласно закону Ома падение потенциала на резисторе VR = IRVR = IR, а ток определяется как I = dq / dt.I = dq / dt.
ε − VR − Vc = 0, ε − IR − qC = 0, ε − Rdqdt − qC = 0. ε − VR − Vc = 0, ε − IR − qC = 0, ε − Rdqdt − qC = 0.Это дифференциальное уравнение можно проинтегрировать, чтобы найти уравнение для заряда конденсатора как функции времени.
ε − Rdqdt − qC = 0, dqdt = εC − qRC, ∫0qdqεC − q = 1RC∫0tdt.ε − Rdqdt − qC = 0, dqdt = εC − qRC, ∫0qdqεC − q = 1RC∫0tdt.Пусть u = εC − qu = εC − q, тогда du = −dq.du = −dq. Результат
−∫0qduu = 1RC∫0tdt, ln (εC − qεC) = — 1RCt, εC − qεC = e − tRC.−∫0qduu = 1RC∫0tdt, ln (εC − qεC) = — 1RCt, εC − qεC = e − tRC.В результате упрощения получается уравнение для заряда зарядного конденсатора как функции времени:
q (t) = Cε (1 − e − tRC) = Q (1 − e − tτ). q (t) = Cε (1 − e − tRC) = Q (1 − e − tτ).10,8
График зависимости заряда конденсатора от времени показан на рис. 10.39 (а). Во-первых, обратите внимание, что по мере приближения времени к бесконечности экспонента стремится к нулю, поэтому заряд приближается к максимальному заряду Q = CεQ = Cε и имеет единицы кулонов. Единицы измерения RC — секунды, единицы времени.Эта величина известна как постоянная времени:
.В момент времени t = τ = RCt = τ = RC заряд равен 1 − e − 1 = 1−0,368 = 0,6321 − e − 1 = 1−0,368 = 0,632 от максимального заряда Q = CεQ = Cε. Обратите внимание, что изменение скорости заряда во времени представляет собой наклон в точке графика зависимости заряда от времени. Наклон графика большой в момент времени t = 0,0st = 0,0 с и приближается к нулю с увеличением времени.
По мере увеличения заряда конденсатора ток через резистор уменьшается, как показано на Рисунке 10.39 (b). Ток через резистор можно найти, взяв производную заряда по времени.
I (t) = dqdt = ddt [Cε (1 − e − tRC)], I (t) = Cε (1RC) e − tRC = εRe − tRC = Ioe − tRC, I (t) = dqdt = ddt [Cε (1 − e − tRC)], I (t) = Cε (1RC) e − tRC = εRe − tRC = Ioe − tRC, I (t) = I0e − t / τ. I (t) = I0e − t / τ.10,10
В момент времени t = 0,00 с, t = 0,00 с ток через резистор равен I0 = εRI0 = εR. Когда время приближается к бесконечности, ток приближается к нулю. В момент времени t = τt = τ ток через резистор равен I (t = τ) = I0e − 1 = 0,368I0.I (t = τ) = I0e − 1 = 0,368I0.
Рис. 10.39 (a) Заряд конденсатора в зависимости от времени по мере заряда конденсатора.(б) Ток через резистор в зависимости от времени. (c) Разность напряжений на конденсаторе. (d) Разность напряжений на резисторе.
На рисунках 10.39 (c) и 10.39 (d) показаны разности напряжений на конденсаторе и резисторе соответственно. По мере увеличения заряда конденсатора ток уменьшается, как и разница напряжений на резисторе VR (t) = (I0R) e − t / τ = εe − t / τ. VR (t) = (I0R) e − t / τ = εe − t / τ. Разность напряжений на конденсаторе увеличивается как VC (t) = ε (1-e-t / τ).VC (t) = ε (1 − e − t / τ).
Разряд конденсатора
Когда переключатель на Рисунке 10.38 (a) перемещается в положение B , схема сокращается до схемы в части (c), и заряженному конденсатору позволяют разрядиться через резистор. График зависимости заряда конденсатора от времени показан на Рисунке 10.40 (а). Использование правила петли Кирхгофа для анализа цепи при разряде конденсатора приводит к уравнению -VR-Vc = 0-VR-Vc = 0, которое упрощается до IR + qC = 0IR + qC = 0.Используя определение тока dqdtR = −qCdqdtR = −qC и интегрируя уравнение контура, получаем уравнение для заряда конденсатора как функции времени:
q (t) = Qe − t / τ.q (t) = Qe − t / τ.10,11
Здесь Q — начальный заряд конденсатора, а τ = RCτ = RC — постоянная времени цепи. Как показано на графике, заряд экспоненциально уменьшается от начального заряда, приближаясь к нулю, когда время приближается к бесконечности.
Ток как функцию времени можно найти, взяв производную заряда по времени:
I (t) = — QRCe − t / τ.I (t) = — QRCe − t / τ.10,12
Отрицательный знак показывает, что ток течет в направлении, противоположном току, наблюдаемому при зарядке конденсатора. На рис. 10.40 (b) показан пример графика зависимости заряда от времени и тока от времени. График зависимости разности напряжений на конденсаторе и разницы напряжений на резисторе от времени показан в частях (c) и (d) рисунка. Обратите внимание, что величины заряда, тока и напряжения экспоненциально уменьшаются, приближаясь к нулю с увеличением времени.
Рис. 10.40 (a) Заряд конденсатора в зависимости от времени при разрядке конденсатора. (б) Ток через резистор в зависимости от времени. (c) Разность напряжений на конденсаторе. (d) Разность напряжений на резисторе.
Теперь мы можем объяснить, почему упомянутой в начале этого раздела фотовспышке требуется гораздо больше времени для зарядки, чем для разрядки: сопротивление во время зарядки значительно больше, чем во время разрядки. Внутреннее сопротивление батареи составляет большую часть сопротивления во время зарядки.По мере старения аккумулятора возрастающее внутреннее сопротивление делает процесс зарядки еще медленнее.
Пример 10,8
Осциллятор релаксации
Одним из применений схемы RC является релаксационный генератор, как показано ниже. Релаксационный генератор состоит из источника напряжения, резистора, конденсатора и неоновой лампы. Неоновая лампа действует как разомкнутая цепь (бесконечное сопротивление), пока разность потенциалов на неоновой лампе не достигнет определенного напряжения.При таком напряжении лампа действует как короткое замыкание (нулевое сопротивление), и конденсатор разряжается через неоновую лампу и производит свет. В показанном релаксационном генераторе источник напряжения заряжает конденсатор до тех пор, пока напряжение на конденсаторе не станет 80 В. Когда это происходит, неон в лампе выходит из строя и позволяет конденсатору разряжаться через лампу, создавая яркую вспышку. После того, как конденсатор полностью разрядится через неоновую лампу, он снова начинает заряжаться, и процесс повторяется.Если предположить, что время, необходимое для разряда конденсатора, незначительно, каков временной интервал между вспышками?Стратегия
Период времени можно найти, рассматривая уравнение VC (t) = ε (1 − e − t / τ), VC (t) = ε (1 − e − t / τ), где τ = (R + r) C .τ = (R + r) C.Решение
Неоновая лампа мигает, когда напряжение на конденсаторе достигает 80 В. Постоянная времени RC равна τ = (R + r) C = (101 Ом) (50 × 10−3F) = 5,05 с. Τ = (R + r) C = (101 Ом) (50 × 10−3F) = 5,05 с. Мы можем решить уравнение напряжения для времени, за которое конденсатор достигает 80 В: VC (t) = ε (1 − e − t / τ), e − t / τ = 1 − VC (t) ε, ln (e − t / τ) = ln (1 − VC (t) ε), t = −τln (1 − VC (t) ε) = — 5.05s · ln (1−80V100V) = 8.13s.VC (t) = ε (1 − e − t / τ), e − t / τ = 1 − VC (t) ε, ln (e − t / τ) = ln (1 − VC (t) ε), t = −τln (1 − VC (t) ε) = — 5,05 с · ln (1−80V100V) = 8,13 с.Значение
Одним из применений генератора релаксации является управление световыми индикаторами, которые мигают с частотой, определяемой значениями для R и C . В этом примере неоновая лампа будет мигать каждые 8,13 секунды, частота f = 1T = 18,13 с = 0,123 Гц. F = 1T = 18,13 с = 0,123 Гц. Осциллятор релаксации имеет много других практических применений. Он часто используется в электронных схемах, где неоновая лампа заменяется транзистором или устройством, известным как туннельный диод.Описание транзистора и туннельного диода выходит за рамки этой главы, но вы можете рассматривать их как переключатели, управляемые напряжением. Обычно это разомкнутые переключатели, но при подаче правильного напряжения переключатель замыкается и проводит ток. «Выключатель» можно использовать для включения другой цепи, включения света или запуска небольшого двигателя. Осциллятор релаксации можно использовать, чтобы заставить мигать указатели поворота вашего автомобиля или вибрировать мобильный телефон.Цепи RC имеют множество применений.Их можно эффективно использовать в качестве таймеров для таких приложений, как стеклоочистители прерывистого действия, кардиостимуляторы и стробоскопы. В некоторых моделях стеклоочистителей прерывистого действия используется переменный резистор для регулировки интервала между движениями стеклоочистителя. Увеличение сопротивления увеличивает постоянную времени RC , что увеличивает время между срабатываниями дворников.
Еще одно приложение — кардиостимулятор. Частота сердечных сокращений обычно контролируется электрическими сигналами, которые заставляют мышцы сердца сокращаться и перекачивать кровь.Если сердечный ритм ненормален (сердцебиение слишком высокое или слишком низкое), для исправления этого нарушения можно использовать кардиостимуляторы. У кардиостимуляторов есть датчики, которые обнаруживают движение тела и дыхание, чтобы увеличить частоту сердечных сокращений во время физических нагрузок, таким образом удовлетворяя повышенную потребность в крови и кислороде, а схема синхронизации RC может использоваться для управления временем между сигналами напряжения, подаваемыми на сердце.
Забегая вперед к изучению цепей переменного тока (цепей переменного тока), переменные напряжения изменяются как синусоидальные функции с определенными частотами.Ученые часто регистрируют периодические изменения напряжения или электрических сигналов. Эти сигналы напряжения могут исходить от музыки, записанной с помощью микрофона, или от атмосферных данных, собранных радаром. Иногда эти сигналы могут содержать нежелательные частоты, известные как «шум». Фильтры RC могут использоваться для фильтрации нежелательных частот.
В области изучения электроники популярное устройство, известное как таймер 555, выдает синхронизированные импульсы напряжения. Время между импульсами контролируется схемой RC .Это лишь некоторые из бесчисленных применений схем RC .
Пример 10.9
Стеклоочистители с прерывистым режимом работы
Осциллятор релаксации используется для управления парой дворников. Релаксационный генератор состоит из конденсатора емкостью 10,00 мФ и переменного резистора 10,00 кОм и 10,00 кОм, известного как реостат. Ручка, подключенная к переменному резистору, позволяет регулировать сопротивление от 0,00 Ом до 10,00 кОм. Выход конденсатора используется для управления переключателем, управляемым напряжением.Переключатель обычно открыт, но когда выходное напряжение достигает 10,00 В, переключатель замыкается, запитывая электродвигатель и разряжая конденсатор. Двигатель заставляет дворники один раз подметать лобовое стекло, и конденсатор снова начинает заряжаться. На какое сопротивление нужно настроить реостат, чтобы время работы щеток стеклоочистителя составляло 10,00 секунд?Стратегия
Сопротивление учитывает уравнение Vout (t) = V (1 − e − t / τ), Vout (t) = V (1 − e − t / τ), где τ = RC.τ = RC. Приведены емкость, выходное напряжение и напряжение батареи.Нам нужно решить это уравнение для сопротивления.Решение
Выходное напряжение будет 10,00 В, а напряжение батареи 12,00 В. Емкость задана как 10,00 мФ. Решение для сопротивления дает Vout (t) = V (1 − e − t / τ), e − t / RC = 1 − Vout (t) V, ln (e − t / RC) = ln (1 − Vout (t) V), −tRC = ln (1 − Vout (t) V), R = −tCln (1 − VC (t) V) = — 10,00 с10 × 10−3Fln (1−10V12V) = 558,11 Ом. Vout (t) = V (1 − e − t / τ), e − t / RC = 1 − Vout (t) V, ln (e − t / RC) = ln (1 − Vout (t) V), — tRC = ln (1 −Vout (t) V), R = −tCln (1 − VC (t) V) = — 10,00s10 × 10−3Fln (1−10V12V) = 558,11 Ом.Значение
Увеличение сопротивления увеличивает временную задержку между срабатываниями дворников.Когда сопротивление равно нулю, дворники работают постоянно. При максимальном сопротивлении период работы дворников составляет: t = −RCln (1 − Vout (t) V) = — (10 × 10−3F) (10 × 103Ω) ln (1−10V12V) = 179,18s = 2,98 мин. t = −RCln (1 − Vout (t ) V) = — (10 × 10−3F) (10 × 103Ω) ln (1−10V12V) = 179,18 с = 2,98 мин.Схема RC имеет тысячи применений и является очень важной схемой для изучения. Его можно не только использовать для измерения времени в цепях, но и для фильтрации нежелательных частот в цепи и использовать в источниках питания, например в вашем компьютере, чтобы преобразовать переменное напряжение в постоянное.
SmartLearner
Вопросы по электричеству
Щелкните вопрос, чтобы получить решения, включая видео.Март 2013
9 Схема, представленная ниже, используется для исследования взаимосвязи между ток через резистор и разность потенциалов на резисторе P.
Полученные результаты используются для построения графика ниже.
9.1.1 Запишите независимую переменную. (1)
9.1.1 Возможная разница9.1.2 Запишите переменную, которой необходимо управлять. (1)
9.1.2 ТемператураСопротивление
9.1.3 Запишите вывод, который можно получить из графика. (2)
9.1.3 Ток прямо пропорционален разности потенциалов.OR
Отношение разности потенциалов к току постоянно.
9.1.4 Используя градиент графика, рассчитайте сопротивление резистор П. (4)
9.1.49,2 В схеме, представленной ниже, батарея с ЭДС 30 В и неизвестным внутренним сопротивлением r подключена к резисторам, как показано. Игнорируйте сопротивление амперметр и соединительные провода.
Ток, проходящий через резистор 10 Ом, равен 0,6 А.
Вычислите:
9.2.1 Эквивалентное сопротивление двух резисторов, включенных параллельно (3)
9.2.19.2.2 Ток через резистор 8 Ом (4)
9.2.29.2.3 Внутреннее сопротивление аккумулятора (4)
9.2.3ноя 2013
9 Учащийся хочет использовать аккумулятор 12 В с внутренним сопротивлением 1 Ом для работы электрическое устройство.Он использует схему ниже, чтобы получить желаемую разность потенциалов для устройство для работы. Сопротивление устройства 5 Ом. Когда переключатель S замкнут, как показано, устройство работает с максимальной мощностью 5 Вт.
9,1 Объясните словами значение ЭДС 12 В. (2)
9,1 & nbsp 12 Дж энергии передается (работа выполняется) на каждый кулон заряда (на C) заряда, проходящего через батарею.
9.2 Рассчитайте ток, проходящий через электрическое устройство. (3)
9,29,3 Рассчитайте сопротивление резистора R x . (7)
9,39,4 Переключатель S теперь разомкнут. Будет ли устройство работать на максимальной мощности? Запишите ДА или НЕТ. Объясните ответ, не производя вычислений. (4)
9.4 №
Общее сопротивление (R) увеличивается.
Ток (I) уменьшается
(При постоянном R) мощность (P = I 2 R) уменьшается.
Мощность уменьшается
март 2012
9 Учащиеся используют закон Ома, чтобы определить, какой из двух резисторов A и B имеет большее сопротивление. Для каждого резистора они измеряют ток через резистор для разных потенциальные различия на концах.На приведенном ниже графике показаны результаты их расследования. 9.1.1 Учащимся предоставляется следующая аппаратура:
• Аккумулятор 6 В
• Вольтметр
• Амперметр
• Реостат
• Резисторы А и В
• Проводящие провода
Нарисуйте принципиальную схему, чтобы показать, как учащиеся должны использовать вышеуказанное оборудование для получения каждого из приведенных выше графиков. (4)
9.1.19.1.2 Запишите ОДНУ переменную, которая должна оставаться постоянной во время этого исследования.(1)
9.1.2 Температура
9.1.3 Какой из A или B имеет более высокое сопротивление?
Дайте пояснение к ответу. (3)
Соотношение больше, чем у А.
Обратите внимание, что по оси Y отображается ток, а по оси X — напряжение.
Сопротивление В / I . Следовательно, сопротивление — это обратный градиент. B более пологий, поэтому градиент меньше.Следовательно, при инвертировании это будет большее значение.
Возможно, что ось Y — это напряжение в другом вопросе. Тогда градиент будет сопротивлением.
9,2 На схеме ниже аккумулятор имеет ЭДС 12 В и внутреннее сопротивление 0,8 Ом. Сопротивлением амперметра и соединительных проводов можно пренебречь.
Рассчитайте:
9.2.1 Эффективное сопротивление цепи (4)
9.2,19.2.2 Показания амперметра (3)
9.2.29.2.3 Показания вольтметра (4)
9.2.3ноя 2012
9,1 В схеме, представленной ниже, два резистора 60 Ом, подключенных параллельно, соединены последовательно с резистором 25 Ом. Аккумулятор имеет ЭДС 12 В и внутреннее сопротивление 1,5 Ом.
Рассчитайте:
9.1.1 Эквивалентное сопротивление параллельной комбинации (3)
9.1.19.1.2 Полный ток в цепи (5)
9.1.29.1.3 Разность потенциалов на параллельных резисторах (3)
9.1.3 9,2 Учащиеся проводят исследование, чтобы определить ЭДС и внутреннее сопротивление (r) батареи.
Они создают схему, как показано на схеме ниже, и измеряют разность потенциалов с помощью вольтметра для разных токов в цепи.
Полученные результаты показаны на графике ниже.
9.2.1 Используйте график, чтобы определить ЭДС аккумулятора. (1)
9.2.1 & nbsp 1,5 В
9.2.2 Рассчитайте градиент графика.(3)
9.2.29.2.3 Какая физическая величина представлена величиной градиент графика? (2)
9.2.3 Внутреннее сопротивление
9.2.4 Как изменяется показание вольтметра при увеличении показания амперметра? Запишите УВЕЛИЧЕНИЕ, УМЕНЬШЕНИЕ или ОСТАВЛЕНИЕ ОДИНАКОВЫЙ. Используйте формулу ЭДС = IR + Ir, чтобы объяснить ответ. (3)
Уменьшается
Когда я увеличиваю
«Потерянное напряжение» / Ir увеличивается.
Vext = ЭДС — Ir уменьшается.
март 2011
9 Схема ниже представляет комбинацию резисторов, включенных последовательно и параллельно. Аккумулятор имеет ЭДС 12 В и неизвестное внутреннее сопротивление r.
Когда переключатель S ОТКРЫТ, амперметр A дает показание 1,2 А.
9,1 Вычислите полное сопротивление цепи. (3)
9,19.2 Рассчитайте внутреннее сопротивление аккумулятора. (4)
9,29,3 Рассчитайте энергию, рассеиваемую в резисторе 6 Ом за 3 минуты. (3)
9,3Переключатель S теперь ЗАКРЫТ.
9,4 Как повлияет на КАЖДЫЙ из следующего?
Запишите ТОЛЬКО УВЕЛИЧИВАЕТ, УМЕНЬШАЕТСЯ или ОСТАЕТСЯ ТО ЖЕ.
9.4.1 Суммарное сопротивление цепи (1)
9.4.1 Уменьшение
9.4.2 Показания амперметра А (1)
9.4.2 Увеличивает
9,5 Между точками P и Q теперь подключен провод с незначительным сопротивлением. Как это повлияет на температуру батареи?
Записывайте только УВЕЛИЧИВАЕТ, УМЕНЬШАЕТСЯ или ОСТАЕТСЯ ТО ЖЕ.
Объясните, как вы пришли к ответу. (4)
9.5 Увеличений
R ext уменьшается (значительно).
У меня через батарею увеличивается (существенно).
W = I 2 Rt / Передача энергии батарее / работа, выполняемая батареей, увеличивается
(существенный).
ноя 2011
9 Учащиеся проводят расследование для проверки закона Ома. Они измеряют ток через проводящий провод при различных разностях потенциалов на его концах. Результаты, достижения полученные показаны на графике ниже.
9,1 Какая из измеряемых величин является зависимой переменной? (1)
9.1 Ток (I)
9,2 График в какой-то момент отклоняется от закона Ома.
9.2.1 Запишите координаты нанесенной на график точки, за пределами которой закон Ома не выполняется. (2)
9.2.1 & nbsp (4,03; 0,64)
9.2.2 Укажите возможную причину отклонения от закона Ома, как показано на графике. Предположим, что все измерения верны. (2)
9.2.2 Температура не поддерживалась постоянной.
9,3 Рассчитайте градиент графика для участка, где соблюдается закон Ома. Используйте это, чтобы рассчитать сопротивление проводящего провода. (4)
9,310 Фара и два ИДЕНТИЧНЫХ задних фонаря скутера подключены параллельно к батарее с неизвестным внутренним сопротивлением, как показано на упрощенной принципиальной схеме. ниже.Фара имеет сопротивление 2,4 Ом и управляется переключателем S1. Задние фонари управляются переключателем S2. Сопротивлением соединительных проводов можно пренебречь.
На приведенном рядом графике показана разность потенциалов на клеммах батареи до и после замыкания переключателя S1 (пока переключатель S2 разомкнут). Переключатель S1 замкнут в момент t1.
10,1 Используйте график, чтобы определить ЭДС аккумулятора. (1)
10.1 и 12 В
10.2 ПРИ ТОЛЬКО ЗАКРЫТОМ ПЕРЕКЛЮЧАТЕЛЯ S1 вычислите следующее:
10.2.1 Ток через фару (3)
10.2.110.2.2 Внутреннее сопротивление r батареи (3)
10.2.210,3 ОБЕ ВЫКЛЮЧАТЕЛИ S1 И S2 ТЕПЕРЬ ЗАКРЫТЫ. Батарея в это время выдает ток 6А. Рассчитайте сопротивление каждого заднего фонаря.(5)
10,3 10,4 Как повлияет на показания вольтметра, если фара перегорит?
(Оба переключателя S1 и S2 все еще замкнуты.)
Записывайте только УВЕЛИЧИВАЕТ, УМЕНЬШАЕТСЯ или ОСТАЕТСЯ ТО ЖЕ.
Дайте объяснение. (3)
10.4 Увеличивает
Сопротивление увеличивается, ток уменьшается
Ir (потерянное напряжение) уменьшается
Март 2010
11 На принципиальной схеме ниже показана батарея с внутренним сопротивлением r, подключенная к трем резисторам M, N и Y.Сопротивление N составляет 2 Ом, а показания на вольтметр V составляет 14В. Показание амперметра A1 составляет 2 А, а показание амперметра A2 — 1 А. (Сопротивлением амперметра и соединительных проводов можно пренебречь.)
11,1 Закон Ома словами. (2)
11.1 Ток через проводник прямо пропорционален разности потенциалов на его концах при постоянной температуре.
11.2 Как сопротивление M по сравнению с сопротивлением N?
Объясните, как вы пришли к ответу. (2)
11.2 Равно
Ток 2А делится поровну при Т (и, поскольку I M = 1A, следует, что I N = 1 A)
11,3 Если ЭДС батареи составляет 17 В, рассчитайте внутреннее сопротивление батареи. (5)
11,311.4 Рассчитайте разность потенциалов на резисторе N. (3)
11,411,5 Рассчитайте сопротивление Y. (4)
11,5ноя 2010
10 Фары автомобиля подключаются параллельно к аккумулятору 12 В, как показано на упрощенная принципиальная схема ниже. Внутреннее сопротивление батареи 0,1 Ом и каждая фара имеет сопротивление 1,4 Ом.Стартер подключен параллельно с фарами и управляется замком зажигания, S2. Сопротивление соединительные провода можно игнорировать.
10,1 Закон Ома словами. (2)
10.1 Ток в проводнике прямо пропорционален разности потенциалов на его концах при постоянной температуре.OR
Отношение разности потенциалов к току постоянно при постоянной температуре
10.2 Если замкнут только переключатель S1, рассчитайте следующее:
10.2.1 Эффективное сопротивление двух фар (3)
10.2.110.2.2 Разница потенциалов между двумя фарами (4)
10.2.210.2.3 Мощность, рассеиваемая одной из фар (3)
10.2.3 10,3 Выключатель зажигания S2 замкнут (в то время как S1 также замкнут) на короткое время, и стартер с ОЧЕНЬ НИЗКИМ СОПРОТИВЛЕНИЕМ вращается.
Как повлияет на яркость фар при замкнутом переключателе S2? Записывайте только УВЕЛИЧИВАЕТ, УМЕНЬШАЕТСЯ или ОСТАЕТСЯ ТО ЖЕ.
Полностью объясните, как вы пришли к ответу. (4)
Уменьшается
(Эффективное / общее) сопротивление уменьшается.
(Всего) ток увеличивается.
«Потерянное вольт», то есть увеличение V (внутреннего),
таким образом уменьшается разность потенциалов V на фарах.
март 2009
12 Батарея в схеме ниже имеет ЭДС 12 В и внутреннее сопротивление 0,2 Ом.Сопротивлением соединительных проводов можно пренебречь.
12,1 Рассчитайте ток I, протекающий через батарею. (6)
12,112,2 Как повлияет на показания вольтметра, если резистор 9 Ом будет удален и заменен проводящим проводом с незначительным сопротивлением? Поясните свой ответ. (4)
12.2 Уменьшение
• Эффективное сопротивление цепи уменьшается
(Нет тока через сопротивления 15 Ом и 8 Ом)
• Общий ток увеличивается на
• Ir (потерянное напряжение) увеличивается
• V внешний уменьшается
Ноябрь 2009 Не используется
12.1 Аккумулятор на схеме ниже имеет ЭДС 12 В и неизвестное внутреннее сопротивление r. Вольтметр В 1 подключается через аккумулятор и вольтметр V 2 подключен к переключателю S. Сопротивлением соединительных проводов и амперметра можно пренебречь.
12.1.1 Запишите соответствующие показания вольтметров V 1 и V 2 , когда переключатель S разомкнут. (2)
12.1.1 & nbsp V 1 = 12 В
& nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp V 2 = 12 В
Переключатель S замкнут. Показание вольтметра V 1 изменится на 9 В.
12.1.2 Каким будет новое чтение V 2 ? (1)
12.1.2 В 2 = 0 ВКогда переключатель замкнут, возникает короткое замыкание. V 2 ничего не измеряет.Резистора там нет.
12.1.3 Вычислите общее внешнее сопротивление цепи. (4)
12.1.312.1.4 Вычислите внутреннее сопротивление батареи r. (5)
12.1.42,2 На схеме ниже показаны две лампочки X и Y, подключенные параллельно к аккумулятор с незначительным внутренним сопротивлением.
Лампочки имеют маркировку 40 Вт и 60 Вт соответственно. Лампа Y светится ярче лампы X.
12.2.1 Как сопротивление лампы Y по сравнению с сопротивлением лампы X? Используйте соответствующее уравнение (или соотношение), чтобы объяснить свой ответ. (3)
12.2.1Во время эксперимента ученик подключает эти две лампочки последовательно к одному источнику питания, как показано ниже. Он замечает, что лампочка X теперь светится ярче лампы Y.
12.2.2 Используйте соответствующее уравнение (или соотношение), чтобы объяснить, почему лампа X теперь светится ярче, чем лампа Y. (3)
12.2.2ноя 2009
11 Три резистора, R 1 , R 2 и R 3 , подключены к батарее, как показано на схеме диаграмма ниже. Внутреннее сопротивление батареи 0,3 Ом. Сопротивление R 2 и R 3 равно.Сопротивление R 1 вдвое меньше сопротивления R 2 . Когда оба переключателя разомкнуты, вольтметр на батарее показывает 9 В.
11,1 Какое значение эдс АКБ? Обоснуйте свой ответ. (2)
11.1 & nbsp 9VПотенциальная разница, измеренная при:
• выключатель разомкнут
• нет тока
• цепь разомкнута
• во внешней цепи не выполняются никакие работы.
Вольтметр включен последовательно с батареей и показывает 9В.Следовательно, ЭДС батареи должна быть 9В.
11,2 Когда только переключатель S 1 замкнут , показание амперметра составляет 3А.
Рассчитайте сопротивление R 1 . (5)
11,3 Оба переключателя S 1 и S 2 теперь замкнуты.
11.3.1 Как изменится сопротивление цепи? Записывайте только УВЕЛИЧИВАЕТ, УМЕНЬШАЕТСЯ или ОСТАЕТСЯ ТО ЖЕ.(1)
11.3.1 Уменьшение
11.3.2 Проводящий провод с незначительным сопротивлением подключен между точками Q и N. Как это повлияет на «потерянные вольт»? Объясни ответ. (3)
11.3.2 Увеличивает• Сопротивление снижается на
• Текущее увеличение
• Ir увеличивает
ИЛИ
увеличивает
• Ток проходит через провод QN
• Провод QN закорачивает параллельную комбинацию резисторов R 2 и R 3
• Весь ток проходит через R1, а также через батарею,
• таким образом Ir увеличивается
ноя 2008
11 Учащиеся исследуют проводящую способность двух металлических проводов P и Q, изготовленных из разных материалов.Они подключают ОДИН провод за раз в цепи, как показано ниже.
Разность потенциалов на каждом проводе увеличивается с равными приращениями, и измеряется результирующий ток через эти провода. Используя измерения, учащиеся получили следующие графические схемы для каждого из проводов.
11,1 Назовите ДВЕ переменные, которые учащиеся могли бы контролировать в каждой из эксперименты. (2)
11.1 Любые два
• Температура
• Площадь поперечного сечения (толщина) материала
• Длина
11,2 Какой провод (P или Q) лучше? Поясните свой ответ. (4)
11.2 Проводник QНаклон графика для провода Q больше, чем для провода P.
Более низкое сопротивление Q делает его лучшим проводником.
12 Схема подключена, как показано ниже.Сопротивление резистора R, подключенного параллельно резистору 10 Ом, неизвестно. При замкнутом переключателе S показание на вольтметр V уменьшается с 45В до 43,5В. Внутреннее сопротивление батареи 0,5 Ом.
12,1 Вычислите показание амперметра A. Покажите ВСЕ свои расчеты. (8)
12,112,2 Определите сопротивление резистора R. (3)
12,212.3 Как изменится показание вольтметра V, если резистор R перегорит? Дать причина вашего ответа. (4)
12.3 Увеличивает
• Общее сопротивление увеличивается, следовательно, ток уменьшается
• поэтому V внутренний уменьшение
• поэтому значение V увеличивается
Prep Paper 2008
Рассмотрите электрическую схему ниже и ответьте на следующие вопросы.
10.1 Рассчитайте величину тока. (6)
10.2 Вычислите разность потенциалов на резисторе 15 Ом. (3)
10,2Образец бумаги 2008
11 Группе учащихся предлагается изучить взаимосвязь между электрическими ток и разность потенциалов. Перед проведением расследования они должны спланировать и разработайте подходящий эксперимент.
Учащиеся подходят к вам, чтобы помочь им в планировании и разработке изучение. Используйте приведенный ниже макет, чтобы помочь им в планировании и дизайне. расследования.
11,1 Планирование
11.1.1 Каков следственный вопрос для этого расследования? (2)
11.1.1 ПримерыКакая связь между электрическим током и разностью потенциалов?
OR
Как изменяется электрический ток при изменении разности потенциалов?
11.1.2 Запишите возможную гипотезу для этого исследования. (2)
(Любое предсказание, которое отвечает на следственный вопрос)Электрический ток прямо пропорционален разности потенциалов
OR
Электрический ток увеличивается с увеличением разности потенциалов.
OR
Электрический ток уменьшается с уменьшением разности потенциалов.
11.1.3 Запишите ОДНУ переменную, которую учащиеся должны контролировать во время этого исследования.(1)
11.1.3 Температура
11,2 Конструкция
11.2.1 Перечислите ВСЕ оборудование, которое потребуется учащимся для этого исследования. (3)
Метод 1Батарейки для фонарей, амперметр, вольтметр, резистор, например нихромовая проволока (не лампочка), соединительные провода
ИЛИ
Способ 2
Источник питания, реостат, амперметр, вольтметр, резистор, например нихромовый провод (не лампочка), соединительные провода
11.2.2 Нарисуйте принципиальную схему, которую они могут использовать для сборки устройства. (3)
11.2.2 Метод 1 Метод 2
11.2.3 Опишите не более чем в четырех строках, как учащиеся должны использовать этот прибор для выполнения требуемых измерений. (3)
11.2.3 С помощью одной батареи измерьте показания вольтметра и амперметра.• Добавьте еще одну батарею последовательно с первой и повторите измерения.
• Добавьте третью батарею последовательно с первыми двумя и повторите измерения.
OR
Отрегулируйте реостат, подключенный последовательно к источнику питания, и снимите показания амперметра и вольтметра.
• Увеличьте / уменьшите сопротивление реостата и снимите второй набор показаний.
• Увеличьте / уменьшите сопротивление реостата, чтобы снять третий набор показаний.
Дополнительная статья с образцами 2008
11 Четыре резистора с разным сопротивлением соединены в схему, как показано ниже.Аккумулятор имеет ЭДС 30 В и внутреннее сопротивление 2 Ом. Сопротивление соединительные провода незначительны.
11,1 Определите понятие ЭДС батареи. (2)
11.1 Максимальный объем работы на единицу заряда
11,2 Рассчитайте разность потенциалов между точками X и Y. (7)
11,2Решения для дополнительной викторины
Две лампочки, одна мощностью 60 Вт при 120 В, а другая — 100 Вт при 120 В, объединены в две разные цепи.
1. Рассчитайте сопротивление каждой лампочки.
Ответ:
, т. Е.
для лампы мощностью 60 Вт.
для лампы мощностью 100 Вт.
2. Объясните, что означают значения 60 Вт и 100 Вт.
Ответ: Лампы предназначены для непосредственного подключения к источнику 120 В. Когда вы эксплуатируете лампы по назначению, они будут рассеивать номинальную мощность. Если они рассеивают больше номинальной мощности, они могут сгореть.
3. Какая из следующих величин определяет яркость лампочки?
Ответ: c. Мощность
4. Какие из следующих величин должны быть одинаковыми для каждой лампы в последовательной цепи?
Ответ: а. Текущий
5. Если обе лампочки подключены параллельно к источнику 120 В, какая яркость ярче? Кратко объясните свой ответ.
Ответ: Лампа мощностью 100 Вт будет ярче.Когда обе лампы подключены к номинальному напряжению, они будут рассеивать номинальную мощность. Яркость лампы зависит от рассеиваемой мощности, поэтому лампа мощностью 100 Вт будет ярче, чем лампа мощностью 60 Вт.
6. Если обе лампочки подключены параллельно к источнику 50 В, какая яркость ярче? Объяснять.
Ответ: Теперь лампы будут тусклее, чем при подключении к напряжению 120 В. Но лампа на 100 Вт все равно будет ярче. Независимо от того, к чему подключена лампочка, ее сопротивление является свойством.Параллельные лампы должны иметь одинаковое напряжение. Согласно уравнению мощности, лампа с меньшим сопротивлением будет рассеивать больше энергии. Лампа 100 Вт имеет меньшее сопротивление, поэтому она будет более яркой.
7. Если обе лампочки последовательно подключены к источнику 120 В, какой из них ярче? Объяснять.
Ответ: Лампочки, соединенные последовательно, потребляют одинаковый ток. Мощность также задается уравнением P = I 2 R . При том же токе лампа с сопротивлением больше будет рассеивать больше энергии.Так как лампа 60 Вт имеет большее сопротивление, она будет ярче.
8. Оцените яркость следующих лампочек: 1 — самая яркая, а 4 — самая тусклая. Обоснуйте свой ответ объяснением и / или расчетом в свободном месте ниже.
Рассчитайте мощность, рассеиваемую каждой лампочкой.
Ответ: Лампочка ___ 60 Вт подключена к источнику 50 В
___ Лампа мощностью 100 Вт, подключенная к источнику 50 В
В серии: Эквивалентное сопротивление двух последовательно включенных ламп составляет 380 Вт.При подключении к 120 В ток в цепи. Этот же ток течет через обе лампочки.
___ Лампа 60 Вт последовательно с лампой 100 Вт и источником 120 В
___ Лампа 100 Вт последовательно с лампой 60 Вт и источником 120 В
Теперь ранг в зависимости от рассеиваемой мощности:
4 (10 Вт) Лампа 60 Вт, подключенная к источнику 50 В
2 (18 Вт) Лампа 100 Вт, подключенная к источнику 50 В
1 (25 Вт) Лампа 60 Вт, соединенная последовательно с лампой 100 Вт и Источник 120 В
3 (14 Вт) Лампа 100 Вт последовательно с лампой 60 Вт и источником 120 В
9.Кратко объясните, почему в вашем доме лампа мощностью 100 Вт всегда будет ярче лампы мощностью 60 Вт.
Ответ: В доме все электрические розетки подключены параллельно к напряжению 120 В. Лампочки, которые вы покупаете в магазине, рассчитаны на использование в стандартной домашней сети на 120 В. Поэтому, если вы подключаете лампы к стандартной розетке, вы всегда используете лампы с их номинальным напряжением и, следовательно, с их номинальной мощностью. Домашняя лампа мощностью 100 Вт всегда будет рассеивать больше энергии, чем лампа мощностью 60 Вт, и поэтому всегда будет ярче.
Омметр Дизайн | Цепи измерения постоянного тока
Хотя механические омметры (измерители сопротивления) сегодня используются редко, в значительной степени вытесненные цифровыми приборами, их работа, тем не менее, интригует и заслуживает изучения.
Назначение омметра
Конечно, омметр предназначен для измерения сопротивления между его выводами. Это показание сопротивления отображается с помощью механического счетчика, работающего от электрического тока.В этом случае омметр должен иметь внутренний источник напряжения для создания необходимого тока для управления движением, а также иметь соответствующие резисторы для измерения диапазона, чтобы пропускать только нужное количество тока через движение при любом заданном сопротивлении.
Как работает омметр?
Начнем с простого механизма и схемы батареи, давайте посмотрим, как он будет работать как омметр:
При бесконечном сопротивлении (отсутствие непрерывности между измерительными проводами) через движение измерителя проходит нулевой ток, а стрелка указывает в крайний левый угол шкалы.В этом отношении показание омметра «назад», потому что максимальное показание (бесконечность) находится слева от шкалы, в то время как измерители напряжения и тока имеют ноль слева от шкалы.
Если измерительные провода этого омметра напрямую закорочены (при измерении ноль Ом), через движение измерителя будет проходить максимальный ток, ограниченный только напряжением батареи и внутренним сопротивлением механизма:
При напряжении аккумулятора 9 В и сопротивлении движению всего 500 Ом ток в нашей цепи составит 18 мА, что намного превышает номинальные характеристики механизма.Такое превышение тока может повредить счетчик.
Не только это, но наличие такого состояния ограничивает полезность устройства. Если крайняя левая шкала на циферблате измерителя представляет собой бесконечное сопротивление, тогда полная правая шкала должна представлять ноль. В настоящее время наша конструкция «фиксирует» движение счетчика вправо, когда между выводами приложено нулевое сопротивление. Нам нужен способ сделать так, чтобы движение просто регистрировалось в полном масштабе, когда тестовые провода замкнуты вместе.Это достигается добавлением последовательного сопротивления к цепи счетчика:
.Чтобы определить правильное значение для R, мы вычисляем полное сопротивление цепи, необходимое для ограничения тока до 1 мА (полное отклонение движения) с напряжением 9 В от батареи, а затем вычитаем внутреннее сопротивление механизма из этого числа:
Теперь, когда правильное значение R рассчитано, у нас все еще осталась проблема с диапазоном измерения. В левой части шкалы находится «бесконечность», а в правой части — ноль.Помимо того, что эта шкала «отстает» от шкал вольтметров и амперметров, эта шкала странная, потому что она идет от ничего ко всему, а не от ничего к конечному значению (например, 10 вольт, 1 ампер и т. Д.).
Можно сделать паузу, чтобы спросить: «Что означает середина шкалы? Какая фигура лежит точно между нулем и бесконечностью? » Бесконечность — это больше, чем просто очень большое количество : это неисчислимая величина, больше, чем может быть любое определенное число. Если показание половины шкалы на любом другом типе измерителя представляет 1/2 значения полной шкалы, то что такое половина бесконечности на шкале омметра?
Логарифмическая шкала омметра
Ответом на этот парадокс является нелинейная шкала .Проще говоря, шкала омметра не движется плавно от нуля до бесконечности, когда стрелка движется справа налево. Скорее, шкала начинает «расширяться» с правой стороны, а последовательные значения сопротивления растут все ближе и ближе друг к другу по направлению к левой части шкалы:
Бесконечность не может быть приближена линейным (четным) способом, потому что шкала никогда не достигнет ! При нелинейной шкале величина сопротивления, охватываемого для любого заданного расстояния на шкале, увеличивается по мере того, как шкала приближается к бесконечности, что делает бесконечность достижимой целью.
Однако у нас все еще есть вопрос о диапазоне для нашего омметра. Какое значение сопротивления между измерительными проводами вызовет отклонение стрелки ровно на 1/2 шкалы? Если мы знаем, что у механизма номинальный диапазон полной шкалы 1 мА, то 0,5 мА (500 мкА) должно быть значением, необходимым для отклонения на половину шкалы. Следуя нашему проекту с батареей на 9 В в качестве источника, мы получаем:
При внутреннем сопротивлении перемещению 500 Ом и резисторе последовательного диапазона 8,5 кОм остается 9 кОм для внешнего (между выводами) испытательного сопротивления по шкале 1/2.Другими словами, испытательное сопротивление, дающее 1/2 отклонения шкалы в омметре, равно по величине (внутреннему) последовательному полному сопротивлению цепи измерителя.
Используя закон Ома еще несколько раз, мы можем определить значение испытательного сопротивления для отклонения шкалы 1/4 и 3/4:
Отклонение шкалы 1/4 (0,25 мА тока счетчика):
Отклонение шкалы на 3/4 (0,75 мА тока счетчика):
Итак, шкала этого омметра выглядит примерно так:
Одной из основных проблем этой конструкции является то, что она полагается на стабильное напряжение батареи для точного измерения сопротивления.Если напряжение батареи снизится (как и все химические батареи с возрастом и использованием), шкала омметра потеряет точность. При постоянном значении резистора последовательного диапазона 8,5 кОм и снижении напряжения батареи измеритель больше не будет отклоняться на полную шкалу вправо, когда измерительные провода замкнуты вместе (0 Ом). Точно так же испытательное сопротивление 9 кОм не сможет отклонить стрелку точно до 1/2 шкалы при меньшем напряжении батареи.
Существуют методы проектирования, используемые для компенсации изменения напряжения батареи, но они не решают проблему полностью, и их следует рассматривать в лучшем случае как приблизительные.По этой причине, а также из-за наличия нелинейной шкалы омметры этого типа никогда не считались прецизионными.
Следует упомянуть еще одно последнее предостережение относительно омметров: они работают правильно только при измерении сопротивления, которое не питается от источника напряжения или тока. Другими словами, вы не можете измерить сопротивление омметром в «живой» цепи! Причина этого проста: точные показания омметра зависят от того, что единственным источником напряжения является его внутренняя батарея.Наличие любого напряжения на измеряемом компоненте будет мешать работе омметра. Если напряжение достаточно велико, это может даже повредить омметр.
ОБЗОР:
- Омметры содержат внутренние источники напряжения для питания при измерении сопротивления.
- Аналоговая шкала омметра находится «в обратном направлении» от шкалы вольтметра или амперметра: стрелка движения показывает нулевое сопротивление при полной шкале и бесконечное сопротивление в состоянии покоя.
- Аналоговые омметры также имеют нелинейную шкалу, «расширенную» на нижнем конце шкалы и «сжатую» на верхнем конце, чтобы можно было охватить диапазон от нуля до бесконечного сопротивления.
- Аналоговые омметры не являются точными приборами.
- Омметры никогда не следует подключать к цепи под напряжением (т. Е. Цепи с собственным источником напряжения). Любое напряжение, приложенное к измерительным проводам омметра, приведет к недействительности его показаний.
СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:
Схема моста Уитстона| Теория, примеры и приложения
В этом руководстве мы узнаем о мосте Уитстона.Мы увидим принцип работы моста Уитстона, несколько примеров схем и некоторые важные приложения.
Введение в мост Уитстона
В реальном мире мы сталкиваемся с различными сигналами, некоторые из которых измеряются изменениями сопротивления, а некоторые — индуктивностью и емкостью.
Если мы рассмотрим сопротивление, большинство промышленных датчиков, таких как температура, деформация, влажность, смещение, уровень жидкости и т. Д., Производят изменение значения сопротивления для переменного изменения.Следовательно, существует потребность в формировании сигнала для каждого датчика сопротивления.
Обычно измерение сопротивления делится на три типа: измерение низкого сопротивления, измерение среднего сопротивления и измерение высокого сопротивления. Если измерение сопротивления составляет от нескольких миллиом до микроом, то это считается измерением низкого сопротивления.
Это измерение фактически используется в исследовательских целях. Если измерение составляет от 1 Ом до 100 кОм, это обычно считается измерением сопротивления среды.Измерения потенциометров, термисторов и т. Д. Подпадают под эту категорию.
При этом считается измерением очень высокое сопротивление от 100 кОм до более 100 мегаом. Для определения среднего значения сопротивления используются разные методы, но в основном используется мост Уитстона.
Что такое мост Уитстона?Самая распространенная и простая мостовая сеть для определения сопротивления — это мост Уитстона постоянного тока. Этот мост используется там, где необходимо измерять небольшие изменения сопротивления, например, в сенсорных приложениях.Это используется для преобразования изменения сопротивления в изменение напряжения преобразователя.
Комбинация этого моста с операционным усилителем широко используется в промышленности для различных преобразователей и датчиков. Мост Уитстона состоит из четырех резисторов, которые в форме ромба соединены с источником питания и индикаторными приборами, как показано на рисунке.
Этот мост используется для очень точного определения неизвестного сопротивления путем его сравнения с известным значением сопротивлений.В этом мосту для определения сопротивления используется нулевое или сбалансированное состояние.
Для этого моста в сбалансированном состоянии напряжение в точках C и D должно быть одинаковым. Следовательно, ток через гальванометр не течет. Для сбалансированного состояния один из резисторов должен быть переменным.
На рисунке
Напряжение в точке D = V × R X / (R 3 + R X )
Напряжение в точке C = V × R 2 / (R 1 + R 2 )
Напряжение (В) на гальванометре или между C и D составляет,
V CD = V × R X / (R 3 + R X ) — V R 2 / (R 1 + R 2 )
Когда мост сбалансирован V CD = 0,
Итак,
V × R X / (R 3 + R X ) = V R 2 / (R 1 + R 2 )
R X R 1 + R X R 2 = R 2 R 3 + R 2 R X
R 1 R X = R 2 R 3
R 2 / R 1 = R X / R 3
Это условие балансировки моста.И для нахождения неизвестного значения сопротивления
R X = R 3 × (R 2 / R 1 )
Из приведенного выше уравнения R4 или Rx могут быть вычислены из известного значения сопротивления R3 и отношения R2 / R1. Следовательно, в большинстве случаев значения R2 и R1 являются фиксированными, а значение R3 является переменным, так что достигается нулевое значение и мост балансируется.
Принцип работыБез гальванометра мостовая схема выглядит как схема делителя напряжения, как показано на рисунке ниже.Рассмотрим R 1 = 20 Ом, R 2 = 40 Ом для одного плеча, а для другого рассмотрим те же значения R 3 и R 4 соответственно.
Текущий поток в первом плече
I 1 = V / (R 1 + R 2 )
I 1 = 12 В / (20 + 40)
I 1 = 0,2 А
А напряжение в точке C равно падению напряжения на резисторе R 2 ,
V R2 = I 1 × R 2 = 0.2 × 40 = 8 В
Аналогично, напряжение на R 1 составляет 4 В (0,2 × 20). Из-за тех же значений сопротивления напряжения на R 4 и R 3 будут такими же, как у R 1 и R 2 соответственно. Следовательно, в точках A и B напряжения одинаковы, поэтому гальванометр показывает нулевое значение, поскольку разность потенциалов равна нулю. В этом случае считается, что мост находится в сбалансированном состоянии.
Предположим, что если мы поменяем местами резисторы во втором плече, ток останется таким же из-за последовательной цепи.Но напряжение на резисторе R 4 меняется, т.е. 0,2 * 20 = 4В. Таким образом, в этом состоянии напряжения в точках A и B различны и существует разность потенциалов 8 — 4 = 4 В. Это неуравновешенное состояние моста.
Пример моста УитстонаСверху мост Уитстона неуравновешен, когда показание вольтметра не равно нулю. Это показание может быть положительным или отрицательным, в зависимости от величин напряжений на выводах счетчика.Давайте рассмотрим приведенную ниже схему моста Уитстона, который подключен для нахождения неизвестного значения сопротивления с использованием декадной коробки резисторов, чтобы получить переменное сопротивление R 3 .
Мы знаем, что условие баланса моста —
R 4 = R 3 × R 2 / R 1
R x = R КОРОБКА × (10 x 10 3 ) / (10 x 10 3 )
R x = R КОРОБКА
В данном случае мост Уитстона уравновешивается регулировкой декадного сопротивления до тех пор, пока вольтметр не покажет нулевое значение.И соответствующее значение сопротивления в коробке равно неизвестному сопротивлению. Предположим, что если условие нулевого напряжения возникает на 250 Ом декадной ячейки сопротивления, то неизвестное сопротивление также равно 250 Ом.
Мост Уитстона для измерения деформацииЧаще всего для измерения деформации используются тензодатчики, электрическое сопротивление которых изменяется пропорционально деформации в устройстве. На практике диапазон сопротивления тензодатчика составляет от 30 Ом до 3000 Ом.Для данной деформации изменение сопротивления может составлять лишь часть полного диапазона. Поэтому для измерения очень небольшой части изменений сопротивления с высокой точностью используется конфигурация моста Уитстона. На рисунке ниже показан мост Уитстона, в котором неизвестный резистор заменен тензодатчиком.
В приведенной выше схеме два резистора R 1 и R 2 равны друг другу, а R 3 — переменный резистор. Без приложения силы к тензодатчику реостат изменяют и, наконец, устанавливают так, чтобы вольтметр показывал нулевое отклонение.Это называется условием балансировки моста. Это состояние означает, что датчик не подвергается деформации.
Если тензодатчик либо растянут, либо сжимается, сопротивление может увеличиваться или уменьшаться. Следовательно, это вызывает разбалансировку моста. Это дает показание напряжения на вольтметре, соответствующее изменению деформации. Если напряжение, приложенное к тензодатчику, больше, то разница напряжений на выводах измерителя больше. Если деформация равна нулю, мост уравновешивается, и счетчик показывает нулевое значение.
Речь идет об измерении сопротивления с помощью моста Уитстона для точного измерения. Из-за дробного измерения сопротивления мосты Уитстона в основном используются при измерениях тензодатчиков и термометров.
Приложения- Мост Уитстона используется для точного измерения очень низких значений сопротивления. Мост
- Уитстона вместе с операционным усилителем используется для измерения физических параметров, таких как температура, деформация, свет и т. Д.
- Мы также можем измерить емкости, индуктивность и импеданс, используя вариации моста Уитстона.

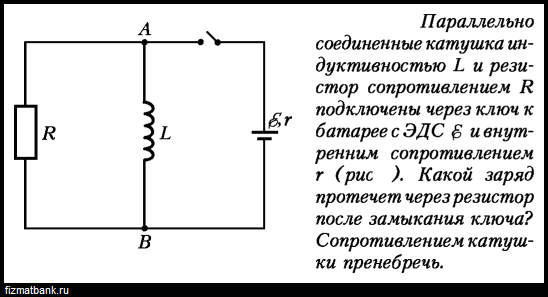

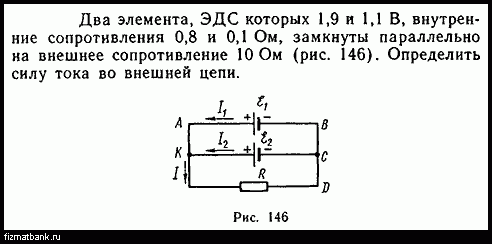 Дополнительно к
ним можно выполнить задания высокого
уровня, тем самым повысив оценку на 1
балл (до «4», до «5»).
Дополнительно к
ним можно выполнить задания высокого
уровня, тем самым повысив оценку на 1
балл (до «4», до «5»). Найти силу тока в цепи и напряжение на
зажимах батареи.
Найти силу тока в цепи и напряжение на
зажимах батареи. Определите
напряжение на зажимах источника тока.
Определите
напряжение на зажимах источника тока.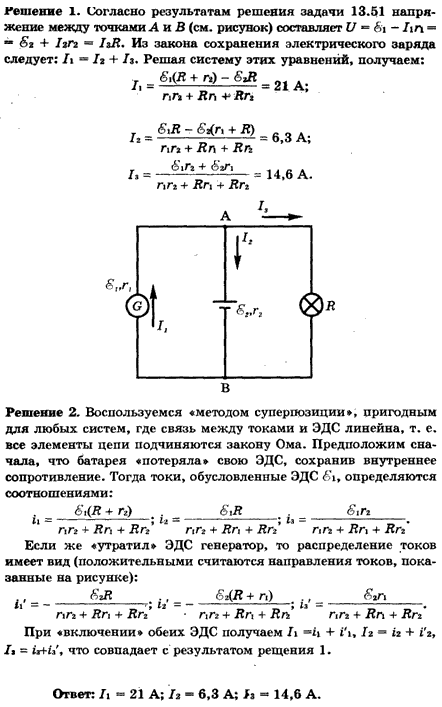 Какой ток даст элемент, если его замкнуть
накоротко?
Какой ток даст элемент, если его замкнуть
накоротко? Второй имеет ЭДС 1,5 В и внутреннее сопротивление 0,4 Ом.
Определите напряжение на зажимах
батареи.
Второй имеет ЭДС 1,5 В и внутреннее сопротивление 0,4 Ом.
Определите напряжение на зажимах
батареи.
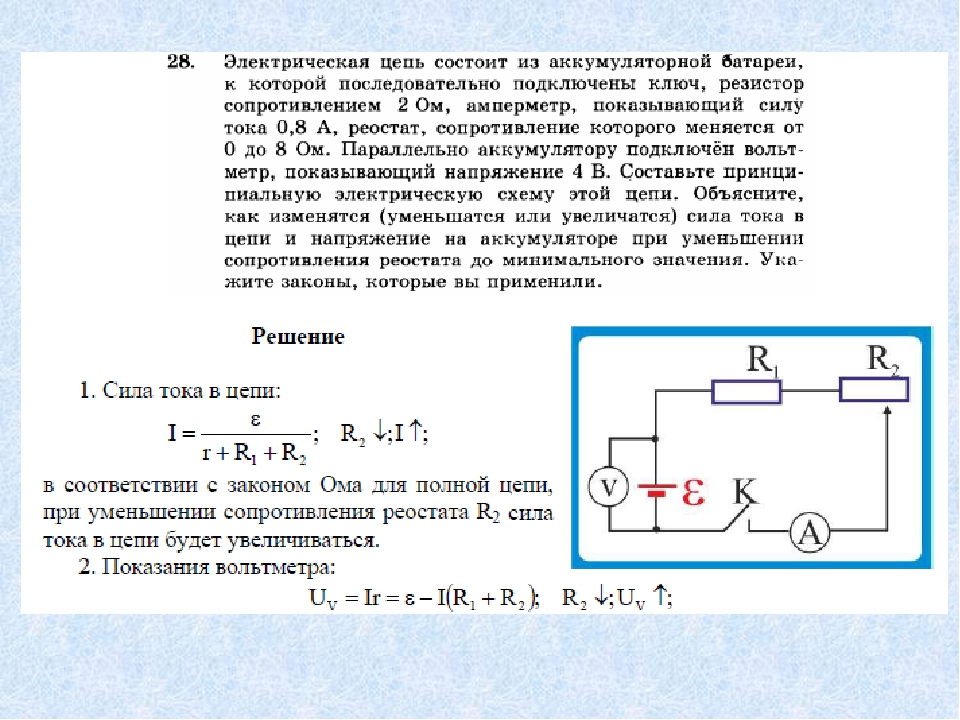
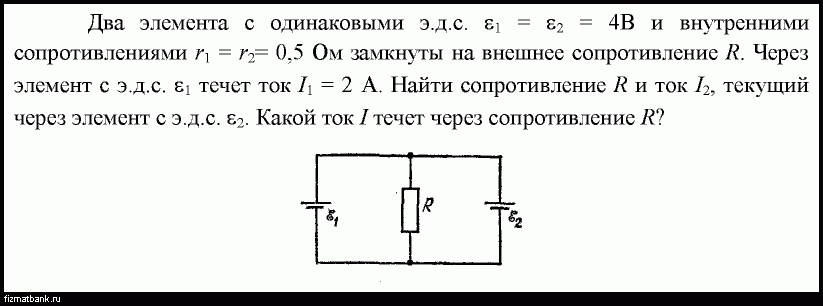

Leave A Comment