152. Известно, что а и b — положительные числа, а х и у — отрицательные. Математика Мордкович 6 класс ГДЗ – Рамблер/класс
152. Известно, что а и b — положительные числа, а х и у — отрицательные. Математика Мордкович 6 класс ГДЗ – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
152. Известно, что а и b — положительные числа, а х и у — отрица-
Известно, что а и b — положительные числа, а х и у — отрица-
а) 0 и х; а и 0; -b и 0; 0 и -х;
б) а и х; у и b; -у и х; -а и b;
в) |х| и х; -|у| и у; а и |а|; b и |-b|;
г) |х| и а; |х| и -х; |х| и -|y|; а и |-b|.
ответы
решение такое
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Психология
3 класс
5 класс
Репетитор
похожие вопросы 5
10. При каких значениях р уравнение -х 2 + 6х — 2 = р:
а) не имеет корней;
б) имеет один корень; (Подробнее. ..)
..)
ГДЗМордкович А.Г.Алгебра8 класс
Приветик! Кто решил? № 411 Математика 6 класс Виленкин.
Выполните вычисления с помощью микрокалькулятора и резуль-
тат округлите до тысячных:
3,281 ∙ 0,57 + 4,356 ∙ 0,278 — 13,758 (Подробнее…)
ГДЗМатематика6 классВиленкин Н.Я.
Помогите установить соответствие между неравенствами. Математика базовый уровень ЕГЭ — 2017. Вар.№1. Зад.№17. Под руководством Ященко И.В.
Здравствуйте! Помогите установить соответствие между неравенствами и их решениями: (Подробнее…)
ЕГЭЭкзаменыМатематикаЯщенко И.В.
Помогите выбрать утверждения. Математика базовый уровень ЕГЭ — 2017. Вар.№1. Зад.№18. Под руководством Ященко И.В.
Здравствуйте! Перед волейбольным турниром измерили рост игроков волейбольной команды города N. Оказалось, что рост каждого из (Подробнее…)
ЕГЭЭкзаменыМатематикаЯщенко И.В.
 Выпишите слово, в котором на месте пропуска пишется буква Е. Русский язык ЕГЭ-2017 Цыбулько И. П. ГДЗ. Вариант 12.
Выпишите слово, в котором на месте пропуска пишется буква Е. Русский язык ЕГЭ-2017 Цыбулько И. П. ГДЗ. Вариант 12.11.
Выпишите слово, в котором на месте пропуска пишется буква Е.
произнос., шь (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
Числовые неравенства и их свойства. Сложение и умножение числовых неравенств 8 класс онлайн-подготовка на Ростелеком
Тема 8: Неравенства
- Видео
- Тренажер
- Теория
Заметили ошибку?
Числовые неравенства и их свойства. Сложение и умножение числовых неравенств.
Мы можем сравнить любые числа а и b и результат сравнения записать в виде равенства или неравенства, используя знаки =, <, >. Для произвольных чисел а и b выполняется одно и только одно из соотношений: a=b, a<b, a>b.
Пример 1. Сравним обыкновенные дроби 58 и 47.
Для этого приведем их к общему знаменателю: 58=3556; 47=3256.
Так как 35>32, то 58>47.
Пример 2. Сравним десятичные дроби 3,6748 и 3,675.
Цифры в разрядах единиц, десятых и сотых совпадают, а в разряде тысячных в первой дроби стоит цифра 4, а во второй – цифра 5. Так как 4<5, то 3,6748<3,675.
Пример 3. Сравним обыкновенную дробь 920 и десятичную дробь 0,45. Обратив дробь 920 в десятичную, получим, что 920=0,45.
Пример 4. Сравним отрицательные числа -15 и -23. Модуль первого числа меньше модуля второго. Значит, первое число больше второго, -15>-23.
В зависимости от вида числа мы использовали тот или иной способ сравнения. Но есть универсальный способ сравнения, который охватывает все случаи.
Число а больше числа b, если разность а-b – положительное число; число а меньше числа b, если разность a-b – отрицательное число. Если разность а-b = 0, то числа а и b равны.
На координатной прямой большее число изображается точкой, лежащей правее, а меньшее – точкой, лежащей левее.
Рассмотрим некоторые свойства числовых неравенств.
-
Если a>b, то b<a, если a<b, то b>a.
Действительно, если разность a-b – положительное число, то разность b-a – отрицательное число, и наоборот.
-
Если a<b и b<c, то а<c.
Докажем, что разность а-с – отрицательное число. Прибавим к этой разности числа b и –b и сгруппируем слагаемые:
а-с = а-с+b-b = (а-b)+(b+c).
По условию а<b и b<c. Поэтому слагаемые а-b и b-c – отрицательные числа. Значит, и их сумма является отрицательным числом. Следовательно, а<c.
-
Если a<b и c – любое число, то а+с<b+c.
Преобразуем разность (а+с)-(b+c) = а-b
По условию а<b, поэтому a-b – отрицательное число. Значит, и разность (а+с)-(b+c) отрицательна. Следовательно, a+c<b+c.
Если к обеим частям верного неравенства прибавить одно и то же число, то получится верное неравенство.

-
Если a<b и c – положительное число, то aс<bс. Если a<b и c – отрицательное число, то aс>bc.
Представим разность ас-bc в виде произведения: ас-bc = с(а-b).
Так как a<b, то a-b – отрицательное число. Если с>0, то произведение с(а-b) отрицательно, и, следовательно, ас<bc. Если с<0, то произведение с(а-b) положительно, и, следовательно, ас>bc.
Так как деление можно заменить умножением на число, обратное делителю, то аналогичное свойство справедливо и для деления.
Если обе части верного неравенства умножить или разделить на одно и то же положительное число, то получится верное неравенство.
s -
Если а и b – положительные числа и а<b, то 1a>1b.

Разделим обе части неравенства a<b на положительное число ab: aab<bab. Сократив дроби, получим, что 1b<1a, т.е. 1а>1b.
Приведем пример использования рассмотренных свойств неравенств.
Пример 5. Оценим периметр равностороннего треугольника со стороной а мм, если известно, что 54,2<a и a<54,3, и запишем результат в виде двойного неравенства.
54,2·3 < 3a < 54,3·3,
162,6 < 3a < 162,9.
Значит, периметр Р данного треугольника больше 162,6 мм, но меньше 162,9 мм.
Рассмотрим теперь, как выполняется сложение и умножение числовых неравенств.
-
Если a<b и c<d, то a+c<b+d.
Прибавив к обеим частям неравенства a<b число с, получим а+с<b+с. Прибавив к обеим частям неравенства с<d число b, получим b+c<b+d.
То есть а+с<b+с<b+d. Из этого следует, что a+c<b+d.

Если почленно сложить верные неравенства одного знака, то получится верное неравенство.
-
Если a<b и c<d, где а,b,c,d – положительные числа, то ac<bd.
Умножим обе части неравенства a<b на положительное число с, получим ac<bс. Умножив обе части неравенства c<d на положительное число b, получим bc<bd. Получим ac<bс<bd. Следовательно ac<bd.
Если почленно перемножить верные неравенства одного знака, левые и правые части которых – положительные числа, то получится верное неравенство.
Из этой теоремы следует, что
Если числа а и b положительны и a<b, то a
Доказанные свойства используют для оценки суммы, разности, произведения и частного.
Пример 6. Известно, что 15<x<16 и 2<y<3.
 Требуется оценить сумму х+у, разность х-у, произведение ху и частное х/у.
Требуется оценить сумму х+у, разность х-у, произведение ху и частное х/у.Сложим почленно неравенства 15<x<16 и 2<y<3, получим 17<x+y<19.
Оценим разность. Для этого умножим 2<y<3 почленно на (-1). Получим -3<-y<-2.
Теперь сложим почленно неравенства 15<x<16 и -3<-y<-2. Получим 12<x-y<14.
Оценим произведение ху. Перемножим почленно неравенства 15<x<16 и 2<y<3. Получим 30<xy<48.
Оценим частное. Для этого сначала запишем неравенство для 1у. Получится 13<1y<12. Теперь перемножим почленно 15<x<16 и 13<1y<12. Получим 5<xy<8.
Заметили ошибку?
Расскажите нам об ошибке, и мы ее исправим.положительных и отрицательных чисел | SkillsYouNeed
Стандартные числа, большие нуля, описываются как «положительные» числа. Мы не ставим перед ними знак плюс (+), потому что нам это не нужно, так как общее понимание таково, что числа без знака положительны.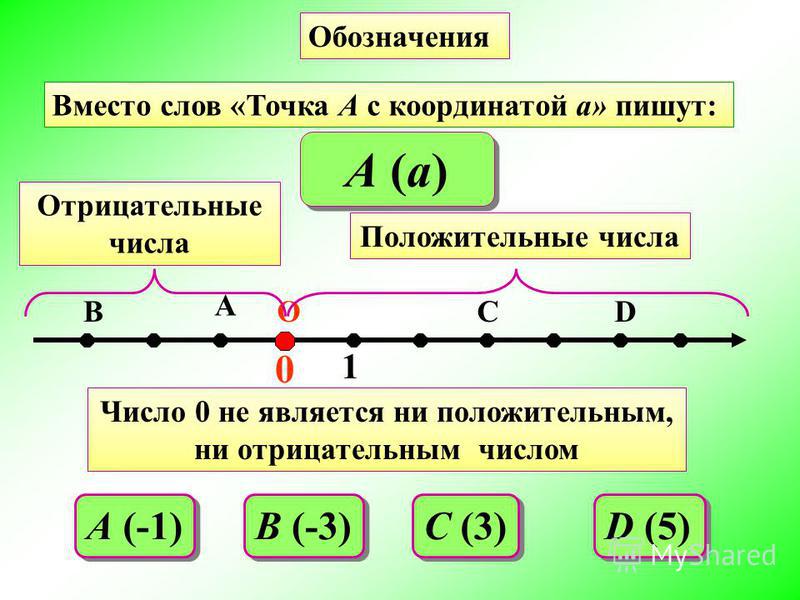
Числа меньше нуля называются «отрицательными». Перед ними стоит знак минус (-), указывающий, что они меньше нуля (например, -10 или ‘ минус 10 ‘).
Визуализация отрицательных и положительных чисел
Вероятно, самый простой способ визуализировать отрицательные и положительные числа — использовать числовую прямую, инструмент, с которым вы, возможно, хорошо знакомы, особенно если ваши дети учатся в начальной школе.
Это выглядит примерно так:
Числовая линия может помочь вам визуализировать как положительные, так и отрицательные числа, а также операции (сложение и вычитание), которые вы можете с ними выполнять.
Когда вам нужно вычислить сложение или вычитание, вы начинаете с первого числа и перемещаете второе число разрядов вправо (для сложения) или влево (для вычитания).
Эта числовая линия является упрощенной версией, но вы можете нарисовать их, включив в них все числа, если хотите. Большим преимуществом числовой линии является то, что ее очень легко нарисовать самому себе на обратной стороне конверта или на клочке бумаги, а также очень сложно ошибиться в расчетах. Пока вы внимательно подсчитываете количество мест, которые вы перемещаете, вы получите правильный ответ.
Большим преимуществом числовой линии является то, что ее очень легко нарисовать самому себе на обратной стороне конверта или на клочке бумаги, а также очень сложно ошибиться в расчетах. Пока вы внимательно подсчитываете количество мест, которые вы перемещаете, вы получите правильный ответ.
Вычитание отрицательных чисел
Если вы вычитаете отрицательное число, два отрицательных числа объединяются, чтобы получить положительное.
−10−(−10) не равно −20. Вместо этого вы можете думать об этом как о повороте одного из отрицательных знаков вертикально, чтобы пересечь другой и сделать плюс. Тогда сумма будет равна −10+10 = 0.
Краткое примечание о скобках
Для ясности: вы никогда не будете писать два отрицательных знака рядом без скобок.
Таким образом, если вас попросят вычесть отрицательное число, оно всегда будет заключено в скобки, чтобы вы могли видеть, что использование двух отрицательных знаков было преднамеренным.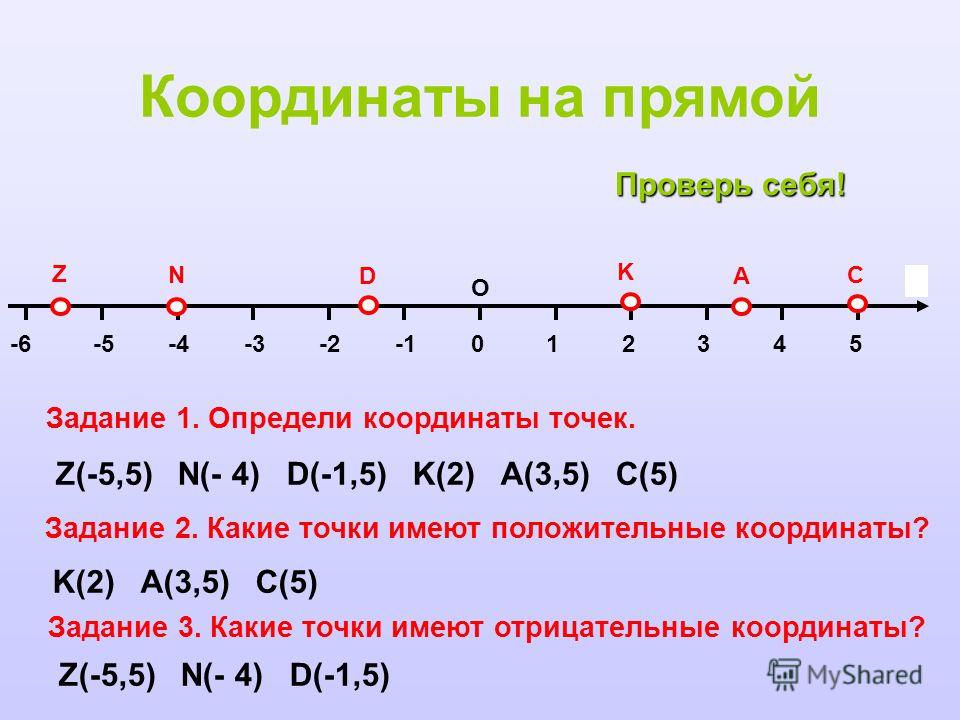
-10—10 неверно (и сбивает с толку)
-10-(-10) правильно (и более ясно)
Умножение и деление с положительными и отрицательными числами
положительные и отрицательные числа, вы можете упростить процесс, сначала игнорируя знаки (+/-) и просто умножая или разделяя числа, как если бы они оба были положительными. Получив числовой ответ, вы можете применить очень простое правило для определения знака ответа:
- Когда знаки двух чисел совпадают с , ответ будет положительным .
- Когда знаки двух чисел отличаются , ответ будет отрицательным .
Итак:
(положительное число) × (положительное число) = положительное число
(отрицательное число) × (отрицательное число) = положительное число
Но:
× (положительное число) число) = отрицательное число
В качестве побочного вопроса, это каким-то образом объясняет, почему вы не можете получить квадратный корень из отрицательного числа (подробнее об этом читайте на нашей странице Специальные числа и концепции ). Квадратный корень — это число, которое нужно умножить само на себя, чтобы получить число. Нельзя умножать число само на себя, чтобы получить отрицательное число. Чтобы получить отрицательное число, вам нужно одно отрицательное и одно положительное число.
Квадратный корень — это число, которое нужно умножить само на себя, чтобы получить число. Нельзя умножать число само на себя, чтобы получить отрицательное число. Чтобы получить отрицательное число, вам нужно одно отрицательное и одно положительное число.
Правило работает так же, когда у вас есть более двух чисел для умножения или деления. Четное количество отрицательных чисел даст положительный ответ. Нечетное количество отрицательных чисел даст отрицательный ответ.
Почему умножение двух отрицательных чисел дает положительный ответ?
Тот факт, что отрицательное число, умноженное на другое отрицательное число, дает положительный результат, часто сбивает с толку и кажется нелогичным.
Чтобы объяснить, почему это так, вернитесь к числовым линиям, использованным ранее в этой статье, поскольку они помогают объяснить это визуально.
- Во-первых, представьте, что вы стоите на числовой прямой в нулевой точке и смотрите в положительном направлении, то есть в сторону 1, 2 и так далее.
 Вы делаете два шага вперед, останавливаетесь, затем делаете еще два шага. Вы прошли 2 × 2 шага = 4 шага.
Вы делаете два шага вперед, останавливаетесь, затем делаете еще два шага. Вы прошли 2 × 2 шага = 4 шага.
Следовательно, положительный × положительный = положительный - Теперь вернитесь к нулю и повернитесь лицом в отрицательном направлении, то есть к −1, −2 и т. д. Сделайте два шага вперед, затем еще два. Теперь вы стоите на −4. Вы переместились на 2 × -2 шага = -4 шага.
Отсюда минус × плюс = минус
В обоих этих примерах вы двигались вперед (т. е. в том направлении, в котором вы смотрели), положительное движение.
- Снова вернитесь к нулю, но на этот раз вы пойдете назад (негативное движение). Снова повернитесь лицом в положительном направлении и сделайте два шага назад. Теперь вы стоите на −2. Положительное (направление, в котором вы смотрите) и отрицательное (направление, в котором вы движетесь) приводят к отрицательному движению.
Отсюда положительный × отрицательный = отрицательный - Наконец, снова вернитесь к нулю, повернитесь лицом в отрицательном направлении.
 Теперь сделайте два шага назад , а затем еще два назад. Вы стоите на +4. Повернувшись лицом в отрицательном направлении и пройдя назад ( два отрицания ), вы достигли положительного результата.
Теперь сделайте два шага назад , а затем еще два назад. Вы стоите на +4. Повернувшись лицом в отрицательном направлении и пройдя назад ( два отрицания ), вы достигли положительного результата.
Отсюда минус × минус = плюс
- Два отрицательных числа компенсируют друг друга. Вы можете увидеть это в речи:
- «Просто сделай это!» позитивное побуждение к действию.
- «Не делай этого!» просит кого-то не делать что-то. Это минус.
- «Не делай этого» означает «пожалуйста, сделай это». Два отрицания компенсируются и дают положительный результат как в математике, так и в речи.
- Знаки складываются физически. Когда у вас есть два отрицательных знака, один переворачивается, и они складываются вместе, чтобы получить положительный. Если у вас есть положительный и отрицательный, остается одна черточка, и ответ отрицательный. Это простая и наглядная памятка, несмотря на то, что она не обязательно удовлетворит тех, кто хочет понять правило.

Заключение
Отрицательные знаки могут показаться немного пугающими, но правила их использования просты и понятны. Помните об этом, и у вас не будет проблем.
Отрицательные числа — PSAT Math
Все математические ресурсы PSAT
10 диагностических тестов 421 практический тест Вопрос дня Карточки Learn by Concept
← Предыдущий 1 2 Далее →
Справка по математике PSAT » Арифметика » Целые числа » Отрицательные числа
Сколько элементов набора меньше ?
Возможные ответы:
Четыре
Три
Один
Два
Нет
Правильный ответ:33 3 Четыре
Объяснение: Абсолютное значение отрицательного числа можно вычислить, просто удалив отрицательный символ. Все четыре (отрицательных) числа в наборе меньше этого положительного числа. Сообщить об ошибке a, b, c — целые числа. abc < 0 ab > 0 bc > 0 Что из следующего должно быть правдой? Возможные ответы: A + B <0 AC <0 A — B> 0 A> 0 B> 0 Правильный ответ:  Следовательно,
Следовательно,
Объяснение:
Давайте редуктивно рассмотрим, что говорят нам эти данные.
Рассмотрим каждую группу (a,b,c) как группу знаков.
Из abc < 0 мы знаем, что возможно следующее:
(–, +, +), (+, –, +), (+, +, –), (–, –, –)
Из ab > 0 мы знаем, что мы должны исключить (–, +, +) и (+, –, +)
Из bc > 0 мы знаем, что мы должны исключить (+, +, –)
Следовательно, любой из наших ответов должен выполняться для (–, –, –)
Это немедленно исключает a > 0, b > 0
Точно так же исключает a – b > 0, потому что мы не знаем относительных размеров a и b.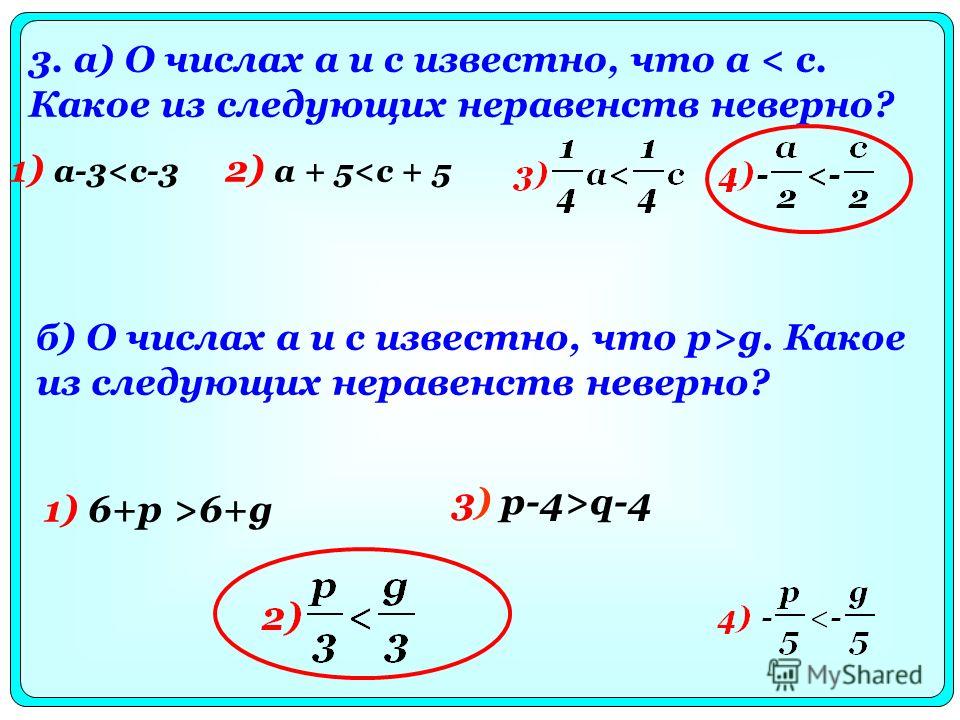 Следовательно, это может быть положительным или отрицательным.
Следовательно, это может быть положительным или отрицательным.
Наконец, ac является произведением отрицаний и, следовательно, положителен. Следовательно, ac < 0 не выполняется.
У нас остается a + b < 0, что верно, так как сложение двух минусов должно быть отрицательным.
Сообщить об ошибке
Что такое ?
Возможные ответы:
Правильный ответ:
Объяснение:
Отрицательное число, деленное на отрицательное число, всегда дает положительное число. разделить на равно . Поскольку ответ положительный, ответ не может быть или любым другим отрицательным числом.
Сообщить об ошибке. Объяснение:
Начните с выделения вашей переменной.
Вычтите из обеих частей:
или
Затем вычтите из обеих частей:
или
Затем разделите обе части на:
Вспомните, что деление отрицательного числа на , следовательно:
или
Сообщить об ошибке
Если является положительным числом, а также является положительным числом, какое возможное значение для ?
Возможные ответы:
Правильный ответ:
Объяснение:
Поскольку число положительное, оно должно быть отрицательным, так как произведение двух отрицательных чисел положительно.
Поскольку значение тоже положительное, оно также должно быть отрицательным, чтобы производить положительный продукт.
Чтобы проверить свой ответ, вы можете попробовать подставить любое отрицательное число для .
Сообщить об ошибке
, , и все отрицательные нечетные целые числа. Какое из следующих трех выражений должно быть положительным?
I)
II)
III)
Possible Answers:
All of these
III only
II only
I only
None of these
Correct answer:
Все эти
Объяснение:
Отрицательное целое число, возведенное в целую степень, положительно тогда и только тогда, когда абсолютное значение показателя степени четно. Поскольку сумма или разность двух нечетных целых чисел всегда является четным целым числом, это имеет место во всех трех выражениях. Правильный ответ — все это.
Правильный ответ — все это.
Сообщить об ошибке
– положительное целое число; и являются отрицательными целыми числами. Какое из следующих трех выражений должно быть отрицательным?
I)
II)
III)
Возможные ответы:
Ни один из I, II или III
I, II и III
I и III только
II и III III, II и III
I и III III.
Только I и II
Правильный ответ:
Ни один из I, II или III
Объяснение:
Отрицательное целое число, возведенное в целую степень, положительно тогда и только тогда, когда абсолютное значение показателя степени четно; оно отрицательно тогда и только тогда, когда абсолютное значение показателя степени нечетно. Следовательно, все три выражения имеют знаки, зависящие от четности/нечетности и , которые не заданы в задаче.
Ни один из этих ответов не является правильным.
Сообщить об ошибке
, , и все отрицательные числа. Что из следующего должно быть положительным?
Возможные ответы:
Правильный ответ:
Объяснение:
Ключ в том, чтобы знать, что отрицательное число, возведенное в нечетную степень, дает отрицательный результат, а отрицательное число, возведенное в четную степень, дает положительный результат.
: и положительны, принося положительный дивиденд; является отрицательным делителем; этот результат отрицательный.
: и отрицательны, что дает положительный дивиденд; является отрицательным делителем; этот результат отрицательный.
: является положительным и отрицательным, что дает отрицательный дивиденд; положительный делитель; этот результат отрицательный.
: отрицательно и положительно, что дает отрицательный дивиденд; положительный делитель; этот результат отрицательный.
: является положительным и отрицательным, что дает отрицательный дивиденд; является отрицательным делителем; этот результат положительный.
Правильный выбор .
Сообщить об ошибке
и являются положительными числами; является отрицательным числом. Все следующие должен быть положительным, кроме:
Возможные ответы:
Правильный ответ:
Объяснение:
Поскольку и положительны, все степени и будут положительными; также в каждом из выражений добавляются степени и . Подсказка, которую нужно искать, — это сила и знак перед ней.
В случаях и , поскольку отрицательное число возводится в четную степень, каждое выражение составляет сумму трех положительных чисел, что является положительным.
В случаях и , поскольку отрицательное число возводится в нечетную степень, средняя степень отрицательна, но поскольку оно вычитается, это то же самое, как если бы положительное число складывалось. Следовательно, каждое из них по существу является суммой трех положительных чисел, что, опять же, положительно.
Следовательно, каждое из них по существу является суммой трех положительных чисел, что, опять же, положительно.
Однако в случае , поскольку отрицательное число возводится в нечетную степень, средняя степень снова будет отрицательной. На этот раз это в основном то же самое, что и вычитание положительного числа. Как видно из этого примера, это может быть равно отрицательному числу:
:
Таким образом это правильный выбор.
Сообщить об ошибке
Пусть – отрицательное целое число и – ненулевое целое число. Какой из следующих должен быть отрицательным независимо от того, является ли он положительным или отрицательным?
Возможные ответы:
Ни один из других ответов не является правильным.
Правильный ответ:
Объяснение:
Поскольку положительное значение, произведение отрицательного числа на положительное число также должно быть отрицательным.


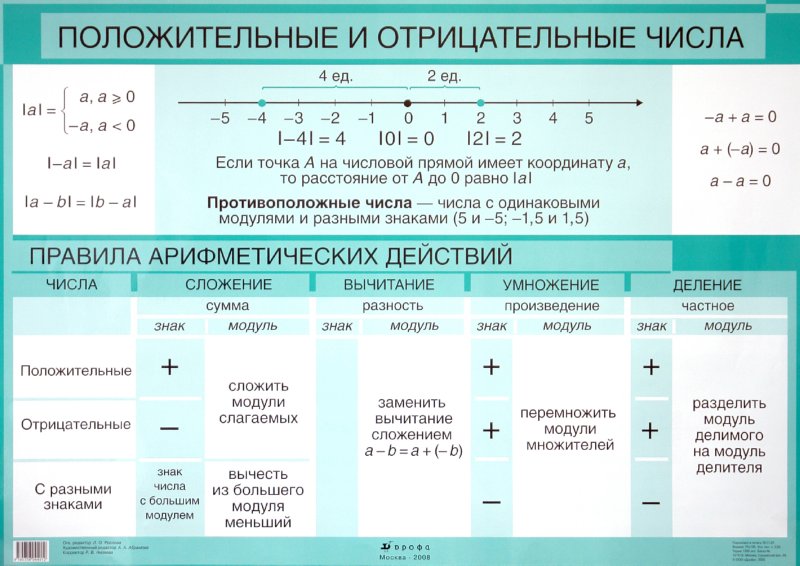

 Требуется оценить сумму х+у, разность х-у, произведение ху и частное х/у.
Требуется оценить сумму х+у, разность х-у, произведение ху и частное х/у. Вы делаете два шага вперед, останавливаетесь, затем делаете еще два шага. Вы прошли 2 × 2 шага = 4 шага.
Вы делаете два шага вперед, останавливаетесь, затем делаете еще два шага. Вы прошли 2 × 2 шага = 4 шага.  Теперь сделайте два шага назад , а затем еще два назад. Вы стоите на +4. Повернувшись лицом в отрицательном направлении и пройдя назад ( два отрицания ), вы достигли положительного результата.
Теперь сделайте два шага назад , а затем еще два назад. Вы стоите на +4. Повернувшись лицом в отрицательном направлении и пройдя назад ( два отрицания ), вы достигли положительного результата. 
Leave A Comment