Х умножить на 2 меньше 20: conf__edu_age }) }) edu_group = edu_age_conf.groups[conf__edu_age] edu_ad = edu_age_conf.ads[edu_group] } $(document).ready(() => { if (typeof KrApi != ‘undefined’) { edu_group = edu_age_conf.pods[KrApi.settings.base_pod] if (typeof edu_group != ‘undefined’) { edu_ad = edu_age_conf.ads[edu_group] } } })

Mathway | Популярные задачи

1	Найти объем	сфера (5)	
2	Найти площадь	окружность (5)	
3	Найти площадь поверхности	сфера (5)	
4	Найти площадь	окружность (7)	
5	Найти площадь	окружность (2)	
6	Найти площадь	окружность (4)	
7	Найти площадь	окружность (6)	
8	Найти объем	сфера (4)	
9	Найти площадь	окружность (3)	
10	Вычислить	(5/4(424333-10220^2))^(1/2)
11	Разложить на простые множители	741
12	Найти объем	сфера (3)	
13	Вычислить	3 квадратный корень из 8*3 квадратный корень из 10
14	Найти площадь	окружность (10)	
15	Найти площадь	окружность (8)	
16	Найти площадь поверхности	сфера (6)	
17	Разложить на простые множители	1162
18	Найти площадь	окружность (1)	
19	Найти длину окружности	окружность (5)	
20	Найти объем	сфера (2)	
21	Найти объем	сфера (6)	
22	Найти площадь поверхности	сфера (4)	
23	Найти объем	сфера (7)	
24	Вычислить	квадратный корень из -121
25	Разложить на простые множители	513
26	Вычислить	квадратный корень из 3/16* квадратный корень из 3/9
27	Найти объем	прямоугольный параллелепипед (2)(2)(2)	
28	Найти длину окружности	окружность (6)	
29	Найти длину окружности	окружность (3)	
30	Найти площадь поверхности	сфера (2)	
31	Вычислить	2 1/2÷22000000
32	Найти объем	прямоугольный параллелепипед (5)(5)(5)	
33	Найти объем	прямоугольный параллелепипед (10)(10)(10)	
34	Найти длину окружности	окружность (4)	
35	Перевести в процентное соотношение	1. 2-4*-1+2
45	Разложить на простые множители	228
46	Вычислить	0+0
47	Найти площадь	окружность (9)	
48	Найти длину окружности	окружность (8)	
49	Найти длину окружности	окружность (7)	
50	Найти объем	сфера (10)	
51	Найти площадь поверхности	сфера (10)	
52	Найти площадь поверхности	сфера (7)	
53	Определить, простое число или составное	5
54	Перевести в процентное соотношение	3/9
55	Найти возможные множители	8
56	Вычислить	(-2)^3*(-2)^9
57	Вычислить	35÷0. 2
60	Преобразовать в упрощенную дробь	2 1/4
61	Найти площадь поверхности	сфера (12)	
62	Найти объем	сфера (1)	
63	Найти длину окружности	окружность (2)	
64	Найти объем	прямоугольный параллелепипед (12)(12)(12)	
65	Сложение	2+2=
66	Найти площадь поверхности	прямоугольный параллелепипед (3)(3)(3)	
67	Вычислить	корень пятой степени из 6* корень шестой степени из 7
68	Вычислить	7/40+17/50
69	Разложить на простые множители	1617
70	Вычислить	27-( квадратный корень из 89)/32
71	Вычислить	9÷4
72	Вычислить	2+ квадратный корень из 21
73	Вычислить	-2^2-9^2
74	Вычислить	1-(1-15/16)
75	Преобразовать в упрощенную дробь	8
76	Оценка	656-521
77	Вычислить	3 1/2
78	Вычислить	-5^-2
79	Вычислить	4-(6)/-5
80	Вычислить	3-3*6+2
81	Найти площадь поверхности	прямоугольный параллелепипед (5)(5)(5)	
82	Найти площадь поверхности	сфера (8)	
83	Найти площадь	окружность (14)	
84	Преобразовать в десятичную форму	11/5
85	Вычислить	3 квадратный корень из 12*3 квадратный корень из 6
86	Вычислить	(11/-7)^4
87	Вычислить	(4/3)^-2
88	Вычислить	1/2*3*9
89	Вычислить	12/4-17/-4
90	Вычислить	2/11+17/19
91	Вычислить	3/5+3/10
92	Вычислить	4/5*3/8
93	Вычислить	6/(2(2+1))
94	Упростить	квадратный корень из 144
95	Преобразовать в упрощенную дробь	725%
96	Преобразовать в упрощенную дробь	6 1/4
97	Вычислить	7/10-2/5
98	Вычислить	6÷3
99	Вычислить	5+4
100	Вычислить	квадратный корень из 12- квадратный корень из 192

Введение в задачи с параметром: решение уравнений с параметром

На этой странице вы узнаете

• Игра в прятки: как значение одной переменной может помочь найти другую?
• Парадокс: как стоять на месте и бежать с любой скоростью одновременно? 
• Решаем параметры осторожно: как не совершить ошибку в квадратном уравнении с параметром? 

Мы привыкли, что в уравнении коэффициенты не меняются. Но возможно ли из одного уравнения составить бесконечное множество различных его вариантов? Узнаем об этом в статье. 

Что такое параметр 

Утром на термометре было некоторое количество градусов, которое мы обозначим за х. В обед температура воздуха изменилась в несколько раз. Во сколько раз должна была измениться температура воздуха, чтобы на термометре было 20 градусов? 

Такие задачи достаточно легко решаются. Если бы изначально было пять градусов, то искомое число было бы равно \(\frac{20}{5} = 4\). А если было 10 градусов, то искомое число было бы равно \(\frac{20}{10} = 2\). 

Но не все так просто. Мы не знаем, какой изначально была температура. Также мы не знаем, во сколько раз она изменилась. То есть мы получили уравнение с двумя неизвестными переменными. 

Обозначим вторую переменную a, у нас получится уравнение вида ax=20. Только что введенная нами переменная “a”  называется параметр. 

Параметр — это условная буква, вместо которой можно подставить число.  

То есть параметр — это еще одна переменная, которая может принять несколько значений. 

Как решать уравнения с параметром, если у нас целых две (а то и больше) неизвестных переменных? Нужен иной подход, чем при решении обычного уравнения.

Решить уравнение с параметром — это найти такие числовые значения параметра, при которых условие выполняется. 

Мы ищем не единственное значение параметра, а все возможные его значения для заданного условия.

Игра в прятки: как значение одной переменной может помочь найти другую? Поскольку параметр — переменная в уравнении, которая является коэффициентом, его значение задает и корни уравнения. То есть переменные а и х зависят друг от друга так же, как и зависят корни обычного уравнения от его коэффициентов.

Линейные уравнения с параметром

Вернемся к нашей погоде. У нас получилось уравнение ax = 20. Как найти, сколько градусов было изначально? Разделить все уравнение на число a. 

\(x = \frac{20}{a}\)

Какие значения может принимать параметр? Любые. Например, при a = 1 x = 20.
При a = 2 x = 10.
При a = 40 x = 0,5 

Что, если a=0? Мы получаем уравнение \(x = \frac{20}{0}\), у которого нет решения, поскольку на 0 делить нельзя. 

Если мы не будем преобразовывать изначальное уравнение, то получится 0*x=20, то есть уравнение не будет выполняться: какое бы число мы ни умножили на 0, получится 0. 

Получается, решение есть при любых значениях a, кроме 0. Таким образом, мы и нашли ответ: при a = 0 решений нет, при a \(\neq\) 0 — x = 20a. 

Добавим немного теории. Представим наше уравнение в виде ax = b, где a, b — действительные числа. Рассмотрим несколько случаев. 

1) b \(\neq\) 0. 

Предположим, Пете необходимо в несколько раз увеличить скорость х, пробежать дистанцию и поставить рекорд. Чтобы поставить рекорд, он должен бежать со скоростью 15 км/ч — это и будет коэффициент b. 

Получаем уравнение ax = 15. Как найти начальную скорость Пети? \(x = \frac{15}{a}\). 

Такое уравнение мы уже решали выше. Получаем два случая: 

• Если a = 0 — решений нет. 
• Если a \(\neq\) 0, то изначальная скорость Пети была равна \(x = \frac{15}{a}\). 

Парадокс: как стоять на месте и бежать с любой скоростью одновременно? Когда Пете нужно увеличить скорость в 0 раз, получается парадокс.  С какой бы скоростью ни бежал Петя, он все равно будет стоять на месте, поскольку 0 * x = 0. Даже если он изначально бегал со скоростью света, его скорость останется равна 0, а не 15 км/ч.

2) b = 0. 

Мы получаем уравнение ax = 0. Также разберем два случая значений параметра: 

• a = 0. Мы получаем уравнение 0 * x = 0. Какое значение х нужно подставить, чтобы уравнение выполнялось? 

Какое бы число мы ни умножили на 0, получим 0. Получаем бесконечное множество решений. 

• a \(\neq\) 0. Здесь получается, что равен 0 уже х: \(x = \frac{0}{a} = 0\). 

Подведем итог. Как можно решить уравнение вида ax = b?

• Если a = 0, b = 0 — бесконечное множество решений. 
• Если a = 0, b \(\neq\) 0 — решений нет. 
• Если a \(\neq\) 0, b \(\neq\) 0 — решением будет \(x = \frac{b}{a}\). 

Квадратные уравнения с параметром

Прежде чем приступать к изучению следующего материала, рекомендуем ознакомиться с понятием квадратного уравнения в статье «Линейные, квадратные и кубические уравнения». Также важно ориентироваться в графиках параболы из статьи «Основные элементарные функции». 

Квадратное уравнение имеет вид ax² + bx + c = 0, а графиком функции y = ax² + bx + c будет парабола. 

Как работать с такими уравнениями, если в них присутствует параметр? В первую очередь, важны рассуждения. Любое задание с параметром можно решить, проанализировав функцию.  

Решение квадратного уравнения опирается на понятие дискриминанта. В зависимости от его значений может получиться разное количество корней: 

• При D > 0 уравнение имеет два корня. 
• При D = 0 уравнение имеет один корень. 
• При D < 0 уравнение не имеет корней. 

Как это проверить на графике? Корни уравнения — это точки, в которых парабола пересекает ось абсцисс, то есть ось х. 

Рассмотрим три уравнения. 

1) x² — x — 2 = 0
Решим уравнение с помощью дискриминанта. 
D = 1² — 4 * 1 * (-2) = 1 + 8 = 9
Поскольку дискриминант больше 0, то уравнение имеет два корня. 

\(x_1 = \frac{1 + 3}{2} = 2\)
\(x_2 = \frac{1 — 3}{2} = -1\)

Проверим с помощью графика функции. Построим параболу и заметим, что она действительно дважды пересекает ось абсцисс, а координаты этих точек равны (−1; 0) и (2; 0) . 

2) x² -4x + 4 = 0
Решим уравнение с помощью дискриминанта.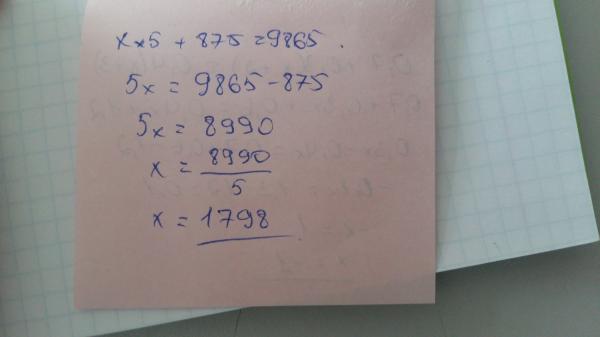  
D = 16 — 4 * 1 * 4 = 16 — 16 = 0
Поскольку дискриминант равен 0, у уравнения всего один корень. 

\(x = \frac{4}{2} = 2\)

Проверим на графике. И действительно, парабола касается оси х только один раз в вершине, координаты которой (2; 0). 

3) x² — 5x + 7 = 0
Решим уравнение с помощью дискриминанта. 
D = 25 — 4 * 1 * 7 = 25 — 28 = -3

Поскольку дискриминант отрицательный, у уравнения нет корней. И это отлично видно, если посмотреть на график функции: парабола лежит выше оси х и никогда ее не пересечет. 

Где можно применить эти знания, решая параметры? 

Пример 1. Найдите все значения параметра a, при которых уравнение x² + (3a + 11)x + 18,25 + a = 0 имеет два различных решения. 

Решение. Перед нами квадратное уравнение с коэффициентами b = 3a + 11, c = a + 18,25. В каких случаях это уравнение будет иметь два различных корня?

Квадратное уравнение имеет два корня, если D > 0. Нужно найти все значения параметра, при которых дискриминант будет положительным. 

1. Для начала найдем сам дискриминант. 

D = (3a + 11)² — 4 * 1 * (a + 18,25) = 9a² + 66a + 121 — 4a — 73 = 9a² + 62a + 48

2. Поскольку дискриминант должен быть больше 0, то получаем неравенство 9a² + 62a + 48 > 0

3. Решим его «Методом интервалов».

9a² + 62a + 48 = 0
D = 3844 — 1728 = 2116
\(a_1 = \frac{-62 + 46}{18} = -\frac{16}{18} = -89\)
\(a_2 = \frac{-62 — 46}{18} = -\frac{108}{18} = -6\)

4. Дискриминант будет положительным при \(a \in (-\infty; -6) \cup (-\frac{8}{9}; +\infty)\). Это и будет ответ. 

Ответ: \(a \in (-\infty; -6) \cup (-\frac{8}{9}; +\infty)\).

Важно: в уравнении мы указываем не сами решения уравнения, а значения параметра, при которых уравнение имеет два решения. 

Пример 2. При каких значениях параметра a уравнение (2a + 1)x² — ax + 3a + 1 = 0 имеет два различных решения? 

Решение. Этот пример похож на предыдущий, однако здесь есть одна важная особенность. Что произойдет с уравнением, если 2a+1 = 0? 

Мы получим уравнение 0,5x — 0,5 = 0, то есть линейное уравнение. У уравнения будет всего одно решение, что уже не подходит под условие задачи. 

Решаем параметры осторожно: как не совершить ошибку в квадратном уравнении с параметром?  Если перед x2 стоит коэффициент, обязательно проверить, чтобы он не был равен 0. В противном случае уравнение из квадратного превращается в линейное, а это уже совершенно другой алгоритм решений уравнений.

1. Поскольку по условию должно быть 2 решения, мы получаем, что a \(\neq\) -0,5. 

2. Найдем дискриминант уравнения. Он должен быть строго больше 0, чтобы у уравнения было два решения. 

D = a² — 4 * (2a + 1) * (3a + 1) = a² — 24a² — 20a -4 = -23a² — 20a — 4

3. Составим неравенство и решим его:

-23a² — 20a — 4 > 0
23a² + 20a + 4 < 0
23a² + 20a + 4 = 0
D = 400 — 4 * 23 * 4 = 400 — 368 = 32
\(a_1 = \frac{-20 + 4 \sqrt{2}}{46} = \frac{2\sqrt{2} — 10}{23}\)
\(a_2 = \frac{-20 — 4\sqrt{2}}{46} = \frac{-2\sqrt{2} — 10}{23}\)

4. 2 + 20a + 4 = 23(a — \frac{2\sqrt{2} — 10}{23})(a — \frac{-2\sqrt{2} — 10}{23})\)

5. Получаем неравенство:

\(23(a — \frac{2\sqrt{2} — 10}{23})(a — \frac{-2\sqrt{2} — 10}{23} < 0\)

6.Тогда  \(a \in (\frac{-2\sqrt{2} — 10}{23}; \frac{2\sqrt{2} — 10}{23})\). Вспомним, что a \(\neq\) -0,5, следовательно, мы получаем ответ \(a \in (\frac{-2\sqrt{2} — 10}{23}; -0,5) \cup (-0,5; \frac{2\sqrt{2} — 10}{23})\).

Ответ: \(a \in (\frac{-2\sqrt{2} — 10}{23}; -0,5) \cup (-0,5; \frac{2\sqrt{2} — 10}{23})\)

Теорема Виета 

Дискриминант — не единственный способ решить квадратное уравнение. Обратимся к теореме Виета. Если нам дано уравнение ax² + bx + c = 0, то его корни можно найти с помощью следующей системы: 

Теорему Виета удобно использовать, если на корни уравнения наложены дополнительные ограничения. 

Пример 3. При каких значениях параметра a корни уравнения x² — 3ax — a(a — 1) = 0 удовлетворяют условию x₁ = 5x₂. 2 — 4a = 0 \rightarrow a(9a — 4) = 0 \rightarrow a = 0, a = \frac{4}{9}\)

5. Мы нашли значения параметра, при которых выполняется условие. Осталось проверить, чтобы при этих значениях у уравнения было два корня. 

a = 0 не подходит, поскольку ограничение \(a \in (-\infty; 0) \cup (\frac{4}{13}; +\infty)\) не включает точку 0. 

\(a = \frac{4}{9}\) подходит, поскольку \(\frac{4}{9} > \frac{4}{13}\). 

Ответ: \(a = \frac{4}{9}\)

Условия на корни квадратного трехчлена 

Однако могут встретиться еще более сложные задания с параметрами. Рассмотрим каждый из этих случаев. 

1. Корни квадратного трехчлена меньше, чем число N. 

Построим параболу. Вспомним, что ветви параболы могут быть направлены или вверх, или вниз. 

Если ветви параболы направлены вверх. Отметим на оси х точку N так, чтобы она лежала правее обоих корней уравнения. Так мы зададим условие, что корни уравнения меньше, чем число N.  

Представим, что мы идем по холмистой местности, и у нас есть ее карта. Имея перед собой плоскую картинку, мы понимаем, как относительно друг друга располагаются точки в пространстве. Но посмотрев на рельеф сбоку, заметим, что точки имеют разную высоту. 

Пусть в точках, где парабола пересекает ось х, будут привалы на экскурсионном маршруте, а в точке N будет смотровая площадка. 

Что можно сказать про смотровую площадку на этой карте? Она находится выше, чем привалы, и лежит правее, чем самая низкая точка рельефа. 

Рассмотрим эти условия на графике. В точке N значение функции f(x) больше, чем в корнях уравнения. Более того, она лежит правее, чем вершина параболы, то есть ее абсцисса больше абсциссы параболы. 

Почему эти условия так важны? Пусть точка N будет лежать левее вершины параболы. Тогда не выполняется условие, что корни меньше, чем N. 

В этом случае на нашем экскурсионном маршруте смотровая площадка будет лежать до привалов.  

А если значение функции в точке N будет меньше, чем в корнях уравнения? Точка N будет лежать между ними. 

В этом случае смотровая площадка окажется между привалами. 

Аналогичным способом можно проследить изменение условий при любом положении точки N на графике. 

Для того чтобы оба корня квадратного трехчлена ax² + bx + c были меньше, чем число N, необходимо и достаточно выполнение следующих условий: 

Что произойдет, если ветви параболы будут направлены вниз? Наш экскурсионный маршрут немного поменяется: появится гора, а не овраг. 

Где теперь располагается смотровая площадка? Она будет ниже, чем привалы, и дальше, чем самая высокая точка горы. 

Мы можем сделать вывод, что точка N на графике будет лежать правее вершины параболы, а значение функции в ней будет меньше, чем значение функции в корнях уравнения. 

Для того чтобы оба корня квадратного трехчлена ax² + bx + c были меньше, чем число N, необходимо и достаточно выполнение следующих условий: 

2. Корни квадратного трехчлена больше, чем число N. 

Рассуждаем так же, как и в предыдущей функции, однако теперь точка N перемещается левее параболы. 

Если ветви параболы направлены вверх, то функция в точке N принимает большее значение, чем в корнях уравнения, а сама точка N будет лежать левее параболы. 

Для того чтобы оба корня квадратного трехчлена ax² + bx + c были больше, чем число N, необходимо и достаточно выполнение следующих условий: 

Теперь направим ветви параболы вниз. Значение функции в точке N будет меньше, чем в корнях уравнения. 

Для того чтобы оба корня квадратного трехчлена ax² + bx + c были больше, чем число N, необходимо и достаточно выполнение следующих условий: 

С помощью анализа расположения точек на графике функций можно задать условия для любой ситуации, даже если точек будет несколько. 

Алгоритм: как задать любые условия для корней квадратных уравнений с помощью графика?  Достаточно начертить примерный график функции и расставить на оси х нужные точки. Чтобы составить систему, необходимо:  1. Определить, куда направлены ветви параболы и задать условие для коэффициента перед x2. 2. Определить, сколько корней имеет уравнение и задать условие для дискриминанта. 3. Определить расположение вершины параболы относительно точек на графике и задать условие для их абсцисс. 4. Определить, какое значение принимает функция в данных точках относительно корней уравнения.

В итоге должна получиться система, с помощью которой можно решить задачу.

Фактчек

• Параметр — это буква a, вместо которой можно подставить число. Решить уравнение с параметром — это найти такие числовые значения параметра, при которых условие выполняется. 
• При решении линейного уравнения ax=b в зависимости от значения коэффициентов может получиться несколько вариантов решений. Если a = 0, b = 0 — бесконечное множество решений. Если a = 0, b \(\neq\) 0 — решений нет. Если a \(\neq\) 0, b \(\neq\) 0 — решением будет \(x = \frac{b}{a}\). 
• При решении квадратного уравнения обязательно проверять коэффициент перед x². Если коэффициент будет равен 0, то уравнение станет линейным.
• При решении квадратного уравнения важно учитывать значение дискриминанта: если он строго больше 0, то корней у уравнения два, если дискриминант равен 0, то у уравнения один корень, если дискриминант меньше 0, то у уравнения нет корней. 
• Решить квадратное уравнение можно и с помощью теоремы Виета. 
• Если в задаче даны дополнительные условия на корни уравнения (например, они должны быть больше или меньше определенного числа), то задать их можно с помощью системы. Неравенства в системе можно составить с помощью анализа примерного графика функций. 

Проверь себя

Задание 1. 
Что такое параметр?

1. Это буква a, вместо которой можно подставить число.
2. Это коэффициент перед x² в квадратном уравнении.
3. Это переменная х.
4. Это значение функции в определенной точке. 

Задание 2. 
Дано уравнение ax = b. Сколько решений оно имеет, если a = 0 и b = 0?

1. Решений нет.
2. Одно решение.
3. Бесконечное множество решений.
4. Невозможно определить количество решений. 

Задание 3. 
При каких значениях дискриминанта уравнение будет иметь корни?

1. D > 0
2. D = 0
3. D < 0
4. D \(\neq\) 0

Задание 4. 
Корни квадратного уравнения меньше числа А. Где будет лежать вершина параболы относительно точки А?

1. Справа.
2. Слева.
3. Совпадать с точкой А.
4. Невозможно определить расположение вершины. 

Задание 5. 
Меньший корень квадратного уравнения больше числа А, но меньше числа В. Ветви параболы направлены вниз. Чему будет равно значение функции в точке В?

1. Значение функции в точке В будет меньше 0.
2. Значение функции в точке В будет равно 0.
3. Значение функции в точке В будет больше 0.
4. Невозможно определить значение функции. 

Ответы: 1. — 1 2. — 3 3. — 4 4. — 2 5. — 3.

Запишите предложение в виде неравенства. 8 меньше 6 более чем в 3 раза больше числа x

Алгебра 1

Джослин М.

спросил 04.09.20

Подписаться І 1

Подробнее

Отчет

3 ответа от опытных наставников

Лучший Новейшие Самый старый

Автор: Лучшие новыеСамые старые

Уильям В. ответил 04.09.20

Репетитор

5,0 (840)

Математика и естественные науки стали проще — учитесь у инженера на пенсии

Об этом репетиторе ›

Об этом репетиторе ›

Голосовать за 0 голос против

Подробнее

Отчет

Трейси Д. ответил 04.09.20

Репетитор

5,0 (126)

жизнерадостный, терпеливый репетитор по математике, вкладывающий средства в успех учащихся

смотрите таких репетиторов

Смотрите таких репетиторов

Иногда вам приходится думать немного не по порядку, чтобы решить такую ​​задачу…. но вот объяснение.

8 меньше, чем выглядит так: 8 <

6 больше, чем выглядит так: +6

3 раза число x равно: 3x

Итак,

8 < 3x+6 соответствует критерию

Голосовать за 0 голос против

Подробнее

Отчет

Раймонд Б. ответил 04.09.20

Репетитор

5 (2)

Математика, микроэкономика или уголовное правосудие

См. таких репетиторов

Смотрите таких репетиторов

8<6+3x

вычесть 6 с обеих сторон, чтобы получить

2<3x

разделить на 3

2/3 < x или

x> 2/3

Голосовать за 0 голос против

Подробнее

Отчет

Все еще ищете помощи? Получите правильный ответ, быстро.

Задайте вопрос бесплатно

Получите бесплатный ответ на быстрый вопрос.
Ответы на большинство вопросов в течение 4 часов.

ИЛИ

Найдите онлайн-репетитора сейчас

Выберите эксперта и встретьтесь онлайн. Никаких пакетов или подписок, платите только за то время, которое вам нужно.

Три меньше, чем удвоенное число равно числу. Какой номер?

Решение проблем

Ширли А.

спросил 05.07.13

Не могу решить. Не знаю, как это написать.

Подписаться І 4

Подробнее

Отчет

4 ответа от опытных наставников

Лучший Новейшие Самый старый

Автор: Лучшие новыеСамые старые

Майк С. ответил 06.07.13

Репетитор

4,8 (82)

Увлеченный репетитор для учащихся средних и старших классов

Смотрите таких репетиторов

Смотрите таких репетиторов

2х — 3 = х;

х — 3 = 0;

х = 3.

Голосовать за 1 голос против

Подробнее

Отчет

Кайл М. ответил 05.07.13

Репетитор

Новое в Византе

Студент компьютерных наук, специализирующийся на репетиторстве по математике в старших классах!

Смотрите таких репетиторов

Смотрите таких репетиторов

Ответ: 3.

Х=2Х-3

Х+3=2Х

3=2Х-Х

3=Х

Голосовать за 3 голос против

Подробнее

Отчет

Мартин С. ответил 05.07.13

Репетитор

Новое в Византе

Репетитор по математике и физике напрокат

Смотрите таких репетиторов

Смотрите таких репетиторов

Число: n

Дважды число: 2n

Три Меньше: из 2n вычесть 3.

n = 2n — 3

 

Голосовать за 1 голос против

Подробнее

Отчет

Брайан Г. ответил 05.07.13

Репетитор

4.9 (38)

Базовая математика, Предварительная алгебра, Алгебра 1, 2, Геометрия

См. таких репетиторов

Смотрите таких репетиторов

x = 3. 3 умножить на 2 равно 6. 6 минус 3 равно 3, поэтому ответ равен 3. 

Голосовать за 0 голос против

Подробнее

Отчет

Все еще ищете помощи? Получите правильный ответ, быстро.

Задайте вопрос бесплатно

Получите бесплатный ответ на быстрый вопрос.