Ответ: 0,01
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Анна Александровна Хохлова
Репетитор по математике
Стаж (лет)
Образование:
Уральский федеральный университет имени первого Президента России Б.Н. Ельцина
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Елена Александровна Дворянинова
Репетитор по математике
Стаж (лет)
Образование:
Северо-Казахстанский Государственный Университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Екатерина Витальевна Турец
Репетитор по математике
Стаж (лет)
Образование:
Минский государственный лингвистический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Предметы
- Математика
- Репетитор по физике
- Репетитор по химии
- Репетитор по русскому языку
- Репетитор по английскому языку
- Репетитор по обществознанию
- Репетитор по истории России
- Репетитор по биологии
- Репетитор по географии
- Репетитор по информатике
Специализации
- Репетитор для подготовки к ОГЭ по физике
- Репетитор для подготовки к сочинению ЕГЭ по русскому
- Подготовка к олимпиадам по английскому языку
- Репетитор по английскому для взрослых
- ВПР по математике
- Репетитор для подготовки к ВПР по английскому языку
- ВПР по физике
- Репетитор для подготовки к ВПР по обществознанию
- Репетитор по биологии для подготовки к ОГЭ
- Программирование Pascal
Похожие статьи
- Как легко умножить на 0,5
- МФТИ (ФБМФ): Биоинформатика
- Задачи по финансовой математике
- ЕГЭ по математике, профильный уровень.
 Уравнения
Уравнения - Решаем олимпиадные задачи. 5 класс
- Советы школьникам для продуктивного начала дня
- Ребенок хочет уйти из дома: как вести себя родителям и что говорить
- Умные по-разному: 8 видов интеллекта, о которых должен знать каждый родитель
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Текст с ошибкой:
Расскажите, что не так
Решутест. Продвинутый тренажёр тестов
Решутест. Продвинутый тренажёр тестов- Главная
- ЕГЭ
- Математика профильная
- Тригонометрические уравнения и неравенства
Решил заданий
Не решил заданий
Осталось заданий
История решения
9779 — не приступал 1154 — не приступал 3455 — не приступал 6343 — не приступал 8295 — не приступал 6392 — не приступалФормат ответа: цифра или несколько цифр, слово или несколько слов. {-3}$ Дж. Ответ выразите десятичной дробью, если нужно округлите до сотых.
{-3}$ Дж. Ответ выразите десятичной дробью, если нужно округлите до сотых.
Очень лёгкий заряженный металлический шарик зарядом q = 2 ∙ 10-6 Кл скатывается по гладкой наклонной плоскости. В момент, когда его скорость составляет v = 5 м/с, на него начинает действовать постоянное магнитное поле, вектор индукции B которого лежит в той же плоскости и составляет угол α с направлением движения шарика. Значение индукции поля B = 4 ∙ 10-3
Небольшой мячик бросают под острым углом α к плоской горизонтальной поверхности земли. 2}{g}$sin2α (м), где ʋ0 = 20 м/с — начальная скорость мячика, а g — ускорение свободного падения (считайте
2}{g}$sin2α (м), где ʋ0 = 20 м/с — начальная скорость мячика, а g — ускорение свободного падения (считайте
Трактор тащит сани с силой F = 80 кН, направленной под острым углом к горизонту. Работа трактора (в килоджоулях) на участке длиной S = 50м вычисляется по формуле A = FScosα. При каком максимальном угле α (в градусах) совершённая работа будет не менее 2000 кДж.
Так твой прогресс будет сохраняться.
Регистрация
Мы отправили код на:
ИзменитьПолучить код повторно через 00:00
Я прочитал(-а) Политику конфиденциальности и согласен(-на) с правилами использования моих персональных данных
Ништяк!
Решено верно
Браво!
Решено верно
Крутяк!
Решено верно
Зачёт!
Решено верно
Чётко!
Решено верно
Бомбезно!
Решено верно
Огонь!
Решено верно
Юхууу!
Решено верно
Отпад!
Решено верно
Шикарно!
Решено верно
Блестяще!
Решено верно
Волшебно!
Решено верно
Движение массы на пружине
В предыдущей части этого урока движение массы, прикрепленной к пружине, было описано на примере колебательной системы.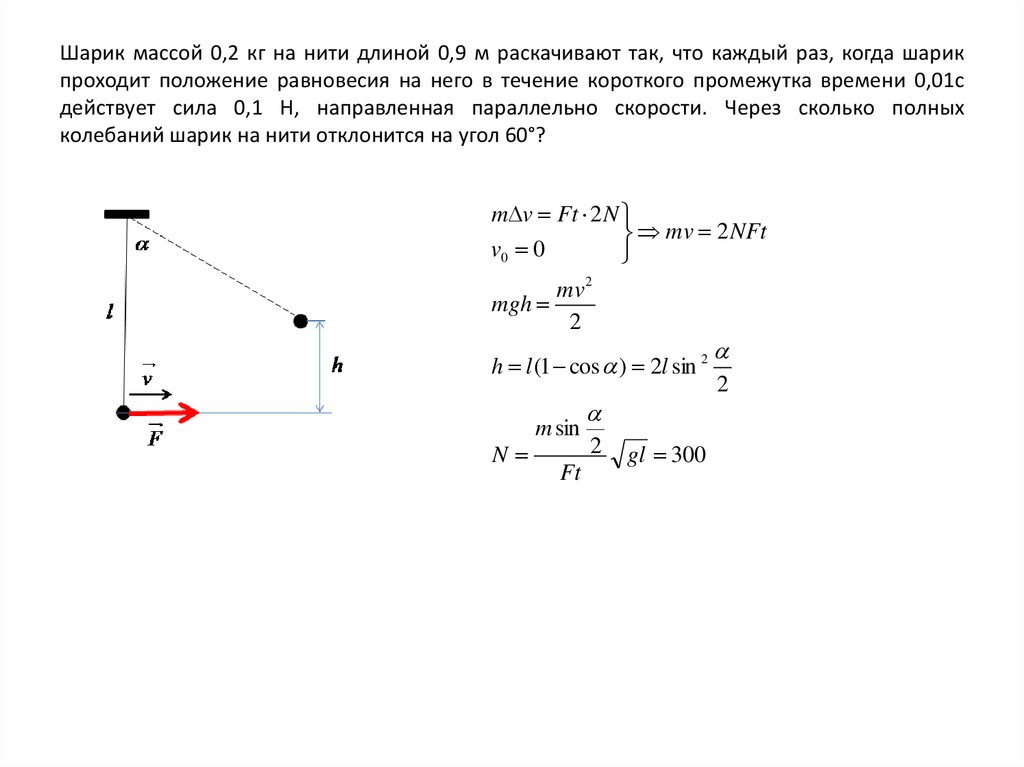 Масса при пружинном движении обсуждалась более подробно, поскольку мы стремились понять математические свойства объектов, находящихся в периодическом движении. Теперь мы исследуем движение массы на пружине еще более подробно, сосредоточившись на том, как различные величины изменяются с течением времени. Такие величины будут включать в себя силы, положение, скорость и энергию — как кинетическую, так и потенциальную энергию.
Масса при пружинном движении обсуждалась более подробно, поскольку мы стремились понять математические свойства объектов, находящихся в периодическом движении. Теперь мы исследуем движение массы на пружине еще более подробно, сосредоточившись на том, как различные величины изменяются с течением времени. Такие величины будут включать в себя силы, положение, скорость и энергию — как кинетическую, так и потенциальную энергию.
Закон Гука
Мы начнем наше обсуждение с исследования сил, действующих пружиной на подвешенный груз. Рассмотрим систему, показанную справа, с пружиной, прикрепленной к опоре. Пружина висит в расслабленном, нерастянутом положении. Если бы вы взялись за нижнюю часть пружины и потянули вниз, пружина растянулась бы. Если бы вы потянули с небольшим усилием, пружина немного растянулась бы. И если бы вы тянули с гораздо большей силой, пружина растянулась бы в гораздо большей степени. Какова именно количественная связь между силой тяги и степенью растяжения?
Чтобы определить это количественное соотношение между величиной силы и величиной растяжения, к пружине можно прикрепить предметы известной массы. Для каждого добавленного объекта можно измерить величину растяжения. Сила, приложенная в каждом случае, будет весом объекта. Можно провести регрессионный анализ данных силы-растяжения, чтобы определить количественную взаимосвязь между силой и степенью растяжения. В приведенной ниже таблице данных показаны некоторые репрезентативные данные для такого эксперимента.
Для каждого добавленного объекта можно измерить величину растяжения. Сила, приложенная в каждом случае, будет весом объекта. Можно провести регрессионный анализ данных силы-растяжения, чтобы определить количественную взаимосвязь между силой и степенью растяжения. В приведенной ниже таблице данных показаны некоторые репрезентативные данные для такого эксперимента.
Масса (кг) | Усилие на пружине (Н) | Величина растяжения (м) |
0,000 | 0,000 | 0,0000 |
0,050 | 0,490 | 0,0021 |
0,100 | 0,980 | 0,0040 |
0,150 | 1.470 | 0,0063 |
0,200 | 1,960 | 0,0081 |
0,250 | 2. | 0,0099 |
0,300 | 2,940 | 0,0123 |
0,400 | 3,920 | 0,0160 |
0,500 | 4.900 | 0,0199 |
Построив график данных силы-растяжения и выполнив линейный регрессионный анализ, можно определить количественное соотношение или уравнение. Сюжет показан ниже.
Линейный регрессионный анализ дает следующую статистику:
уклон = 0,00406 м/с
y-перехват = 3,43 x 10 -5 ( на почти близко к 0,000)
константа регрессии = 0,999
Уравнение для этой линии:
Растяжение = 0,00406• Сила + 3,43×10 -5
Тот факт, что константа регрессии очень близка к 1,000, указывает на то, что существует сильное соответствие между уравнением и точками данных. Эта сильная посадка придает достоверность результатам эксперимента.
Эта сильная посадка придает достоверность результатам эксперимента.
Эта связь между силой, приложенной к пружине, и величиной растяжения была впервые обнаружена в 1678 году английским ученым Робертом Гуком. Как выразился Гук: Ut tensio, sic vis . В переводе с латыни это означает «Как протяженность, так и сила». Другими словами, величина растяжения пружины пропорциональна величине силы, с которой она тянет. Если бы мы завершили это исследование около 350 лет назад (и если бы мы знали немного латыни), мы были бы знамениты! Сегодня это количественное соотношение между силой и растяжением называется законом Гука и часто упоминается в учебниках как 9.0003
F пружина = -k•x
где Fspring — сила, действующая на пружину, x — степень растяжения пружины относительно ее расслабленного положения, а k — константа пропорциональности, часто называемая пружиной. постоянный. Постоянная пружины — это положительная константа, значение которой зависит от исследуемой пружины. Жесткая пружина будет иметь высокую жесткость пружины. Это означает, что потребуется относительно большое количество силы, чтобы вызвать небольшое смещение. Единицами жесткости пружины являются ньютон/метр (Н/м). Знак минус в приведенном выше уравнении указывает на то, что направление растяжения пружины противоположно направлению силы, действующей на пружину. Например, когда пружина была растянута ниже своего расслабленного положения, x равно 9.0171 вниз . Пружина реагирует на это растяжение приложением силы вверх . X и F находятся в противоположных направлениях. Последнее замечание относительно этого уравнения заключается в том, что оно работает для пружины, растянутой по вертикали, и для пружины, растянутой по горизонтали (такой, которая будет обсуждаться ниже).
Жесткая пружина будет иметь высокую жесткость пружины. Это означает, что потребуется относительно большое количество силы, чтобы вызвать небольшое смещение. Единицами жесткости пружины являются ньютон/метр (Н/м). Знак минус в приведенном выше уравнении указывает на то, что направление растяжения пружины противоположно направлению силы, действующей на пружину. Например, когда пружина была растянута ниже своего расслабленного положения, x равно 9.0171 вниз . Пружина реагирует на это растяжение приложением силы вверх . X и F находятся в противоположных направлениях. Последнее замечание относительно этого уравнения заключается в том, что оно работает для пружины, растянутой по вертикали, и для пружины, растянутой по горизонтали (такой, которая будет обсуждаться ниже).
Силовой анализ массы на пружине
Ранее в этом уроке мы узнали, что на вибрирующий объект действует восстанавливающая сила. Возвращающая сила заставляет вибрирующий объект замедляться по мере удаления от положения равновесия и ускоряться по мере приближения к положению равновесия. Именно эта возвращающая сила отвечает за вибрацию. Так какова возвращающая сила массы на пружине?
Именно эта возвращающая сила отвечает за вибрацию. Так какова возвращающая сила массы на пружине?
Мы начнем обсуждение этого вопроса с рассмотрения системы на диаграмме ниже.
На схеме показаны воздушная трасса и планер. Планер крепится пружиной к вертикальной опоре. Трение между планером и воздушной гусеницей незначительно. Таким образом, на планер действуют три доминирующие силы. Эти три силы показаны на диаграмме свободного тела справа. Сила гравитации (Fgrav) довольно предсказуема — как по величине, так и по направлению. Сила тяжести всегда действует вниз; его величина может быть найдена как произведение массы на ускорение свободного падения (m•90,8 Н/кг). Опорная сила (Fsupport) уравновешивает силу тяжести. Он питается воздухом от воздушной дорожки, в результате чего планер левитирует над поверхностью гусеницы. Конечная сила – это сила пружины (Fspring). Как обсуждалось выше, сила пружины изменяется по величине и направлению. Его величину можно найти с помощью закона Гука. Его направление всегда противоположно направлению растяжения и к положению равновесия. Как планер на воздушной гусенице делает движение вперед и назад сила пружины (Fspring) действует как восстанавливающая сила. Он действует на планер влево, когда он расположен справа от положения равновесия; и он действует на планер вправо, когда он расположен слева от положения равновесия.
Его направление всегда противоположно направлению растяжения и к положению равновесия. Как планер на воздушной гусенице делает движение вперед и назад сила пружины (Fspring) действует как восстанавливающая сила. Он действует на планер влево, когда он расположен справа от положения равновесия; и он действует на планер вправо, когда он расположен слева от положения равновесия.
Предположим, что планер оттягивается вправо от положения равновесия и выходит из состояния покоя. На приведенной ниже диаграмме показано направление силы пружины в пяти различных положениях на протяжении пути параплана. Когда планер перемещается из положения А (точка освобождения) в положение В, а затем в положение С, сила пружины действует влево на движущийся влево планер. Когда планер приближается к положению C, степень растяжения пружины уменьшается, а сила пружины уменьшается в соответствии с законом Гука. Несмотря на это уменьшение силы пружины, все еще существует ускорение, вызванное восстанавливающей силой, для всего размаха от положения А до положения С. В положении С планер достиг максимальной скорости. Как только планер проходит влево от положения C, сила пружины действует вправо. Во время этой фазы цикла планера пружина сжимается. Чем дальше от положения С перемещается планер, тем больше степень сжатия и больше сила пружины. Эта сила пружины действует как восстанавливающая сила, замедляя планер при его перемещении из положения C в положение D и в положение E. К тому времени, когда планер достигает положения E, он замедляется до положения мгновенного покоя, прежде чем изменить свое направление и возвращаясь к положению равновесия. Во время движения планера из положения E в положение C степень сжатия пружины уменьшается, и сила пружины уменьшается. На протяжении всего расстояния от положения Е до положения С сохраняется ускорение. В положении С планер достиг максимальной скорости. Теперь планер начинает двигаться вправо от точки C. При этом сила пружины действует влево на планер, движущийся вправо. Эта восстанавливающая сила заставляет планер замедляться на всем пути от положения C до положения D и положения E.
В положении С планер достиг максимальной скорости. Как только планер проходит влево от положения C, сила пружины действует вправо. Во время этой фазы цикла планера пружина сжимается. Чем дальше от положения С перемещается планер, тем больше степень сжатия и больше сила пружины. Эта сила пружины действует как восстанавливающая сила, замедляя планер при его перемещении из положения C в положение D и в положение E. К тому времени, когда планер достигает положения E, он замедляется до положения мгновенного покоя, прежде чем изменить свое направление и возвращаясь к положению равновесия. Во время движения планера из положения E в положение C степень сжатия пружины уменьшается, и сила пружины уменьшается. На протяжении всего расстояния от положения Е до положения С сохраняется ускорение. В положении С планер достиг максимальной скорости. Теперь планер начинает двигаться вправо от точки C. При этом сила пружины действует влево на планер, движущийся вправо. Эта восстанавливающая сила заставляет планер замедляться на всем пути от положения C до положения D и положения E.
Ранее на этом уроке обсуждались изменения положения массы на пружине во времени. В то время было показано, что положение груза на пружине зависит от синуса времени. Обсуждение относилось к массе, которая колебалась вверх и вниз, будучи подвешенной к пружине. Обсуждение было бы в равной степени применимо и к нашему планеру, движущемуся по воздушной трассе. Если бы детектор движения был размещен в правом конце воздушной дорожки для сбора данных для графика зависимости положения от времени, график выглядел бы так, как показано ниже. Положение А — это крайнее правое положение на воздушной дорожке, когда планер находится ближе всего к детектору.
Обозначенные положения на приведенной выше диаграмме — это те же положения, которые использовались при рассмотрении восстанавливающей силы выше. Вы могли вспомнить из этого обсуждения, что положения А и Е были положениями, в которых масса имела нулевую скорость. Положение С было положением равновесия и было положением максимальной скорости. Если бы тот же детектор движения, который собирал данные о положении и времени, использовался для сбора данных о скорости и времени, то данные на графике выглядели бы так, как показано на графике ниже.
Положение С было положением равновесия и было положением максимальной скорости. Если бы тот же детектор движения, который собирал данные о положении и времени, использовался для сбора данных о скорости и времени, то данные на графике выглядели бы так, как показано на графике ниже.
Обратите внимание, что график зависимости скорости от времени для массы на пружине также имеет синусоидальную форму. Единственная разница между графиками положение-время и скорость-время состоит в том, что один смещен на одну четверть колебательного цикла от другого. Также обратите внимание на графики, что абсолютное значение скорости наибольшее в положении C (соответствующем положению равновесия). Скорость любого движущегося объекта, независимо от того, вибрирует он или нет, — это скорость с направлением. Величина скорости есть скорость. Направление часто выражается как положительный или отрицательный знак. В некоторых случаях скорость имеет отрицательное направление (планер движется влево) и ее скорость откладывается под осью времени. В остальных случаях скорость имеет положительное направление (планер движется вправо) и ее скорость отложена над осью времени. Вы также заметите, что скорость равна нулю всякий раз, когда положение находится в экстремальном положении. Это происходит в положениях А и Е, когда планер начинает менять направление. Так же, как и в случае маятникового движения, скорость наибольшая, когда смещение массы относительно ее положения равновесия наименьшее. И скорость наименьшая, когда смещение массы относительно ее положения равновесия наибольшее.
В остальных случаях скорость имеет положительное направление (планер движется вправо) и ее скорость отложена над осью времени. Вы также заметите, что скорость равна нулю всякий раз, когда положение находится в экстремальном положении. Это происходит в положениях А и Е, когда планер начинает менять направление. Так же, как и в случае маятникового движения, скорость наибольшая, когда смещение массы относительно ее положения равновесия наименьшее. И скорость наименьшая, когда смещение массы относительно ее положения равновесия наибольшее.
Энергетический анализ массы на пружине
На предыдущей странице обсуждался энергетический анализ вибрации маятника. Здесь мы проведем аналогичный анализ для движения массы на пружине. В нашем обсуждении мы будем ссылаться на движение планера без трения по воздушной дорожке, которое было введено выше. Планер потянет вправо от положения равновесия и выйдет из состояния покоя (положение А). Как уже упоминалось, планер затем ускоряется к положению C (положение равновесия). Как только планер проходит положение равновесия, он начинает замедляться, поскольку сила пружины тянет его назад против движения. К тому времени, когда он достигает положения E, планер замедляется до мгновенной паузы, прежде чем изменить направление и снова разогнаться до положения C. Еще раз, после того, как планер пройдет точку C, он начинает замедляться по мере приближения к позиции A. в положении А цикл начинается сначала… и снова… и снова.
Как только планер проходит положение равновесия, он начинает замедляться, поскольку сила пружины тянет его назад против движения. К тому времени, когда он достигает положения E, планер замедляется до мгновенной паузы, прежде чем изменить направление и снова разогнаться до положения C. Еще раз, после того, как планер пройдет точку C, он начинает замедляться по мере приближения к позиции A. в положении А цикл начинается сначала… и снова… и снова.
Кинетическая энергия, которой обладает объект, — это энергия, которой он обладает благодаря своему движению. Это величина, которая зависит как от массы, так и от скорости. Уравнение, которое связывает кинетическую энергию (KE) с массой (m) и скоростью (v), выглядит следующим образом:
KE = ½•m•v 2
Чем быстрее движется объект, тем большей кинетической энергией он обладает. Мы можем объединить эту концепцию с приведенным выше обсуждением того, как скорость изменяется в процессе движения. Это смешение концепций привело бы нас к выводу, что кинетическая энергия массы на пружине увеличивается по мере ее приближения к положению равновесия; и уменьшается по мере удаления от положения равновесия.
Эта информация представлена в таблице ниже:
Стадия цикла | Изменение скорости | Изменение кинетической энергии |
от А до В до С | Увеличение | Увеличение |
C-D-E | По убыванию | По убыванию |
E-D-C | Увеличение | Увеличение |
С до В до А | По убыванию | По убыванию |
Кинетическая энергия — это только одна из форм механической энергии. Другая форма – потенциальная энергия. Потенциальная энергия — это накопленная энергия положения, которым обладает объект. Потенциальная энергия может быть гравитационной потенциальной энергией, и в этом случае положение относится к высоте над землей. Или потенциальная энергия может быть упругой потенциальной энергией, и в этом случае положение относится к положению массы на пружине относительно положения равновесия. Для нашего планера с вибрирующей воздушной гусеницей нет изменения высоты. Поэтому гравитационная потенциальная энергия не меняется. Эта форма потенциальной энергии не представляет большого интереса для нашего анализа изменений энергии. Однако происходит изменение положения массы относительно ее положения равновесия. Каждый раз, когда пружина сжимается или растягивается относительно ее расслабленного положения, происходит увеличение упругой потенциальной энергии. Количество упругой потенциальной энергии зависит от степени растяжения или сжатия пружины. Уравнение, связывающее величину потенциальной энергии упругости (PEspring) с величиной сжатия или растяжения (x), имеет вид 9.
Другая форма – потенциальная энергия. Потенциальная энергия — это накопленная энергия положения, которым обладает объект. Потенциальная энергия может быть гравитационной потенциальной энергией, и в этом случае положение относится к высоте над землей. Или потенциальная энергия может быть упругой потенциальной энергией, и в этом случае положение относится к положению массы на пружине относительно положения равновесия. Для нашего планера с вибрирующей воздушной гусеницей нет изменения высоты. Поэтому гравитационная потенциальная энергия не меняется. Эта форма потенциальной энергии не представляет большого интереса для нашего анализа изменений энергии. Однако происходит изменение положения массы относительно ее положения равновесия. Каждый раз, когда пружина сжимается или растягивается относительно ее расслабленного положения, происходит увеличение упругой потенциальной энергии. Количество упругой потенциальной энергии зависит от степени растяжения или сжатия пружины. Уравнение, связывающее величину потенциальной энергии упругости (PEspring) с величиной сжатия или растяжения (x), имеет вид 9. 0003
0003
PE пружина = ½ • k•x 2
где k — жесткость пружины (в Н/м), а x — расстояние, на которое пружина растягивается или сжимается относительно расслабленного, нерастянутого положения.
Когда планер с воздушной гусеницей находится в положении равновесия (положение C), он движется с наибольшей скоростью (как обсуждалось выше). В этой позиции значение x равно 0 метру. Таким образом, количество упругой потенциальной энергии (PEspring) равно 0 Дж. Это положение, при котором потенциальная энергия минимальна. Когда планер находится в положении А, пружина растягивается на максимальное расстояние и потенциальная энергия упругости максимальна. Аналогичное утверждение можно сделать и для положения E. В положении E пружина сжата больше всего, и упругая потенциальная энергия в этом месте также максимальна. Поскольку пружина растягивается столько же, сколько и сжимается, упругая потенциальная энергия в положении А ( растянутое положение ) такое же, как и в положении E ( сжатое положение ). В этих двух положениях — А и Е — скорость равна 0 м/с, а кинетическая энергия равна 0 Дж. Таким образом, как и в случае вибрирующего маятника, колеблющаяся масса на пружине имеет наибольшую потенциальную энергию, когда она имеет наименьшую кинетическая энергия. И он также имеет наименьшую потенциальную энергию (положение C), когда он имеет наибольшую кинетическую энергию. Эти принципы показаны на анимации ниже.
В этих двух положениях — А и Е — скорость равна 0 м/с, а кинетическая энергия равна 0 Дж. Таким образом, как и в случае вибрирующего маятника, колеблющаяся масса на пружине имеет наибольшую потенциальную энергию, когда она имеет наименьшую кинетическая энергия. И он также имеет наименьшую потенциальную энергию (положение C), когда он имеет наибольшую кинетическую энергию. Эти принципы показаны на анимации ниже.
При проведении анализа энергопотребления обычно используется гистограмма энергопотребления. Гистограмма энергии использует гистограмму для представления относительного количества и формы энергии, которой обладает движущийся объект. Это полезный концептуальный инструмент для демонстрации того, какая форма энергии присутствует и как она меняется с течением времени. На приведенной ниже диаграмме представлена гистограмма энергии для планера с воздушной гусеницей и пружинной системы.
Гистограмма показывает, что по мере того, как масса на пружине перемещается от A к B и C, кинетическая энергия увеличивается, а потенциальная энергия упругости уменьшается. Однако общее количество этих двух форм механической энергии остается постоянным. Механическая энергия переходит из потенциальной формы в кинетическую; а общая сумма законсервировано . Аналогичное явление сохранения энергии происходит, когда масса перемещается от C к D и E. Когда пружина сжимается, а масса замедляется, ее кинетическая энергия преобразуется в упругую потенциальную энергию. При этом преобразовании общее количество механической энергии сохраняется. Этот самый принцип сохранения энергии был объяснен в предыдущей главе — главе «Энергия» — учебника по физике.
Однако общее количество этих двух форм механической энергии остается постоянным. Механическая энергия переходит из потенциальной формы в кинетическую; а общая сумма законсервировано . Аналогичное явление сохранения энергии происходит, когда масса перемещается от C к D и E. Когда пружина сжимается, а масса замедляется, ее кинетическая энергия преобразуется в упругую потенциальную энергию. При этом преобразовании общее количество механической энергии сохраняется. Этот самый принцип сохранения энергии был объяснен в предыдущей главе — главе «Энергия» — учебника по физике.
Очевидно, не все пружины одинаковы. И не все пружинно-массовые системы одинаковы. Одной измеряемой величиной, которую можно использовать для отличия одной системы массы пружины от другой, является период. Как обсуждалось ранее в этом уроке, период — это время, за которое вибрирующий объект совершает один полный цикл вибрации. Переменными, влияющими на период системы пружина-масса, являются масса и постоянная пружины. Уравнение, связывающее эти переменные, напоминает уравнение для периода маятника. Уравнение
Уравнение, связывающее эти переменные, напоминает уравнение для периода маятника. Уравнение
T = 2•Π•(m/k) ,5
где T — период, m — масса объекта, прикрепленного к пружине, а k — жесткость пружины. Уравнение можно интерпретировать так, что более массивные объекты будут вибрировать с более длительным периодом. Их большая инерция означает, что для завершения цикла требуется больше времени. А пружины с большей жесткостью (более жесткие пружины) имеют меньший период; массам, прикрепленным к этим пружинам, требуется меньше времени для завершения цикла. Их более высокая жесткость пружины означает, что они оказывают более сильное восстанавливающее усилие на прикрепленную массу. Эта большая сила сокращает время, необходимое для завершения одного цикла вибрации.
Ожидание урока 2
Как мы видели в этом уроке, вибрирующие объекты покачиваются на месте . Они колеблются взад и вперед вокруг фиксированного положения. Простой маятник и груз на пружине — классические примеры такого колебательного движения. Хотя это и не очевидно при простом наблюдении, использование детекторов движения показывает, что колебания этих объектов имеют синусоидальный характер. Существует тонкое волнообразное поведение, связанное с тем, как положение и скорость изменяются во времени. На следующем уроке мы будем исследовать волны. Как мы скоро узнаем, если масса пружины равна покачивания во времени , тогда волна представляет собой совокупность шевелений, разбросанных по пространству . Когда мы начнем изучение волн в Уроке 2, понятия частоты, длины волны и амплитуды останутся важными.
Простой маятник и груз на пружине — классические примеры такого колебательного движения. Хотя это и не очевидно при простом наблюдении, использование детекторов движения показывает, что колебания этих объектов имеют синусоидальный характер. Существует тонкое волнообразное поведение, связанное с тем, как положение и скорость изменяются во времени. На следующем уроке мы будем исследовать волны. Как мы скоро узнаем, если масса пружины равна покачивания во времени , тогда волна представляет собой совокупность шевелений, разбросанных по пространству . Когда мы начнем изучение волн в Уроке 2, понятия частоты, длины волны и амплитуды останутся важными.
Мы хотели бы предложить …
Зачем просто читать об этом и когда вы могли бы взаимодействовать с ним? Взаимодействие — это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашей мессы в Spring Interactive. Вы можете найти его в разделе Physics Interactives на нашем сайте. Интерактивная масса на пружине предоставляет учащимся простую среду для изучения влияния массы, жесткости пружины и продолжительности движения на период и амплитуду вертикально вибрирующей массы.
Вы можете найти его в разделе Physics Interactives на нашем сайте. Интерактивная масса на пружине предоставляет учащимся простую среду для изучения влияния массы, жесткости пружины и продолжительности движения на период и амплитуду вертикально вибрирующей массы.
Посетите: месса на весенней интерактивной
1. Требуется усилие 16 Н, чтобы растянуть пружину на расстояние 40 см от исходного положения. Какая сила (в ньютонах) нужна, чтобы растянуть ту же пружину…
а. … в два раза больше?
б. … в три раза больше?
в. …половина дистанции?
2. Постоянно обеспокоенный привычкой белок на заднем дворе нападать на его кормушки для птиц, мистер Х. решает использовать немного физики для лучшей жизни. Его текущий план включает в себя оснащение кормушки для птиц пружинной системой, которая растягивается и колеблется, когда масса белки приземляется на кормушку. Он желает иметь максимально возможную амплитуду вибрации. Должен ли он использовать пружину с большой жесткостью пружины или с малой жесткостью пружины?
Он желает иметь максимально возможную амплитуду вибрации. Должен ли он использовать пружину с большой жесткостью пружины или с малой жесткостью пружины?
3. Ссылаясь на предыдущий вопрос. Если г-н Х хочет, чтобы его кормушка для птиц (и прикрепленная к ней белка) вибрировала с максимально возможной частотой, должен ли он использовать пружину с большой жесткостью пружины или с малой жесткостью пружины?
4. Используйте энергосбережение, чтобы заполнить пропуски на следующей диаграмме.
5. Какая из следующих систем масса-пружина будет иметь самую высокую частоту вибрации?
Случай A: Пружина с k = 300 Н/м и массой 200 г подвешена к ней.
Случай B: Пружина с k = 400 Н/м и массой 200 г подвешена к ней.
6. Какая из следующих систем масса-пружина будет иметь самую высокую частоту вибрации?
Случай A: Пружина с k = 300 Н/м и массой 200 г подвешена к ней.

Случай B: Пружина с k = 300 Н/м и массой 100 г подвешена к ней.
Перейти к следующему уроку:
2.5: Осциллятор пружины-массы — Physics LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 19098
Эта страница является черновиком и находится в активной разработке.
- Дина Жабинская
- Калифорнийский университет в Дэвисе
Взгляните на три сценария, изображенные ниже, для горизонтальной пружинно-массовой системы. На рисунке A) масса пружины находится в положении равновесия (x=0), что означает, что на нее не действует результирующая сила. Положение равновесия — это то место, где система «пружина-масса» «хочет» находиться естественным образом. Когда масса смещена от равновесия, сила, известная как , восстанавливающая сила , всегда будет указывать назад, к равновесию. На картинке Б) пружина сжимается и сила толкает массу обратно к равновесию, а на картинке В) пружина растягивается, и восстанавливающая сила тянет массу обратно влево.
Положение равновесия — это то место, где система «пружина-масса» «хочет» находиться естественным образом. Когда масса смещена от равновесия, сила, известная как , восстанавливающая сила , всегда будет указывать назад, к равновесию. На картинке Б) пружина сжимается и сила толкает массу обратно к равновесию, а на картинке В) пружина растягивается, и восстанавливающая сила тянет массу обратно влево.
Рис. 2.5.1: Силы, действующие на систему пружины-массы.
Сила, с которой пружина оттягивается при растяжении (или отталкивается при сжатии), пропорциональна величине растяжения от равновесия, при условии, что пружина не растянута слишком сильно. Исторически сложилось так, что эта линейная пропорциональность между силой и величиной растяжения упоминается как поведение Закона Гука , что верно, если массой пружины можно пренебречь. Мы пишем восстанавливающая сила как:
\[F = -k x\]
, где k — «постоянная пружины» или «силовая постоянная» (и зависит от жесткости конкретной пружины), а x — отклонение от положения равновесия. Знак минус указывает, что сила является направлением, противоположным направлению растяжения или сжатия пружины. Другими словами, если вы прикладываете к пружине силу, выводящую ее из равновесия, восстанавливающая сила будет действовать в направлении, противоположном приложенной силе. Важно отметить, что в выражении для силы пружины x измеряется от нерастянутого положения свободного конца пружины.
Знак минус указывает, что сила является направлением, противоположным направлению растяжения или сжатия пружины. Другими словами, если вы прикладываете к пружине силу, выводящую ее из равновесия, восстанавливающая сила будет действовать в направлении, противоположном приложенной силе. Важно отметить, что в выражении для силы пружины x измеряется от нерастянутого положения свободного конца пружины.
Для того, чтобы сила была выражена в ньютонах, единицами измерения k должны быть ньютоны на метр ( Н/м ). Сила, которую вы (внешний агент) должны приложить к пружине, чтобы растянуть ее на расстояние \(x\), направлена в сторону, противоположную восстанавливающей силе, и равна \(F_{приложено}=+k x\).
Закон Гука нарушается в крайних точках движения пружины. Например, при растяжении до точки разрыва или остаточной деформации поведение пружины начнет существенно отклоняться от линейного ожидаемого. Кроме того, при сжатии до такой степени, что он начинает касаться самого себя, действующие силы меняются. По этим причинам обычно предполагается, что пружины растягиваются только в пределах небольшой части их максимальной деформации.
По этим причинам обычно предполагается, что пружины растягиваются только в пределах небольшой части их максимальной деформации.
Потенциальная энергия пружины-массы
Вернемся к рис. 2.3.4. Работа совершается, когда масса выводится из положения равновесия. Предполагая, что кинетическая энергия остается постоянной (пружинная масса неподвижна в состоянии равновесия и удерживается на месте при растяжении), выполненная работа способствует только увеличению потенциальной энергии системы пружина-масса. Мы называем этот тип энергии потенциальной энергией пружины-массы , \(P_{sm}\). Изменение потенциальной энергии зависит от количества выполненной работы. Работа пропорциональна силе, которая зависит от расстояния до точки равновесия. Это говорит о том, что показатель для \(P_{sm}\) равен смещение от равновесия , обозначаемое d или |x| или иногда |y| для вертикально висящих пружин. Обратите внимание, знак абсолютного значения вокруг «|x|» подразумевает, что потенциальная энергия не зависит от того, сжата или растянута пружина, поскольку Закон Гука симметричен относительно положения равновесия. Если предположить, что масса пружины растянута на расстояние 90 171 d 90 172 от точки равновесия, диаграмма энергии-взаимодействия для интервала, изображенного на рис. 2.3.4, будет следующей:
Если предположить, что масса пружины растянута на расстояние 90 171 d 90 172 от точки равновесия, диаграмма энергии-взаимодействия для интервала, изображенного на рис. 2.3.4, будет следующей:
Рисунок 2.5.2: Диаграмма взаимодействия энергии для растяжения системы пружина-масса.
Возвращающая сила \(F = -kx\) непостоянна, так как зависит от перемещения x . То есть сила пропорциональна расстоянию, на которое пружина была нажата или натянута. Таким образом, мы больше не можем использовать упрощенную версию работы, а будем использовать общее уравнение 2.3.1 для работы. Приложенная сила работает, когда пружина растягивается от нуля до максимум 9{2}\]
, где x — смещение от равновесия. При растяжении пружины энергия накапливается в связях пружин в виде потенциальной энергии. Эта потенциальная энергия высвобождается, когда пружине позволяют колебаться. Максимальная скорость достигается, когда пружина возвращается в положение равновесия ( PE см =0 ), а вся энергия является кинетической.
Пример \(\PageIndex{1}\)
Пружина незначительной массы и жесткости 120 Н/м закреплена на стене и может свободно колебаться. На другом конце прикреплен мяч массой 1,5 кг. Затем пружинная масса растягивается на 0,4 м и освобождается.
а) Какова максимальная скорость прикрепленного мяча? Эффектами трения пренебречь.
б) Пружинная масса теряет 2 Джоуля энергии за одно колебание. Найдите максимальное перемещение груза после 4 колебаний.
- Раствор
а) Давайте сосредоточимся на интервале после того, как мяч будет выпущен, пока он не будет находиться в равновесии, когда скорость максимальна. Система пружины-массы замкнута, так как она не взаимодействует с другими системами в этом интервале. Поскольку потенциал пружины колеблется, а кинетическая энергия изменяется, \(\Delta E_{tot}= \Delta PE_{sm}+\Delta KE=0\). 92-0)=0\номер\]
и найдя \(v_f\), получим \(v_f=3,58 м/с\).
б) За 4 колебания пружинная масса потеряет 8 Дж.
 Выберем интервал от начального максимального смещения 0,4 м до конечного максимального смещения после 4 колебаний. Поскольку при максимальном смещении скорость равна нулю, кинетическая энергия на этом интервале не изменится. Диаграмма взаимодействия энергии для этого процесса показана ниже: 92)=-8 Дж\номер\]
Выберем интервал от начального максимального смещения 0,4 м до конечного максимального смещения после 4 колебаний. Поскольку при максимальном смещении скорость равна нулю, кинетическая энергия на этом интервале не изменится. Диаграмма взаимодействия энергии для этого процесса показана ниже: 92)=-8 Дж\номер\] Решая \(d_{max}\), мы находим максимальное перемещение после 4 колебаний равным 0,16 м.
Вертикальные пружинно-массовые системы
Пружина со свисающим вниз грузом действует точно так же, как горизонтальная пружина, за исключением того, что конец пружины находится в другом положении равновесия. Для вертикально подвешенной пружинной массы на колеблющуюся массу действуют две силы: сила пружины, тянущая вверх или толкающая вниз, и сила Земли, всегда тянущая вниз. Рассмотрим подробнее, почему горизонтальную и вертикальную системы упругих масс можно рассматривать одинаково.
Для вертикальной пружины (как и для горизонтальной) сила, с которой масса-пружина оттягивается при растяжении (или отталкивается при сжатии), пропорциональна величине растяжения от положения равновесия, определяемого с присоединенной массой (при условии пружина не сильно растянута). Для вертикальной пружины мы обычно будем записывать восстанавливающую силу, используя символ «y» вместо «x», но это всего лишь соглашение:
Для вертикальной пружины мы обычно будем записывать восстанавливающую силу, используя символ «y» вместо «x», но это всего лишь соглашение:
\[F = -k y\]
Аналогично горизонтально прикрепленной пружины в примере 2.5.1, проанализируем ситуацию нахождения максимальной скорости массы в состоянии равновесия. В этом примере мы нашли следующее общее уравнение для интервала, когда масса перемещается от максимального смещения до положения равновесия, предполагая, что рассеивание тепла незначительно: 92\label{energy.SM}\]
Теперь посмотрим, что мы получим для вертикальной пружины с тем же интервалом. Мы начнем с измерения потенциальной энергии этой системы из ( y=0 ) на рисунке ниже, положения равновесия пружины без прикрепленной массы.
Рисунок 2.5.3: Вертикальная пружинно-массовая система.
Когда масса изначально прикреплена, она растягивается на расстояние \(d_1\) до нового равновесия пружины-массы. В этом положении пружинная масса неподвижна, поэтому действующие на нее силы должны быть уравновешены. То есть сила тяжести должна быть равна и противоположна восстанавливающей силе пружинной массы:
То есть сила тяжести должна быть равна и противоположна восстанавливающей силе пружинной массы:
\[mg=kd_1\label{forces.vertical.SM}\]
Затем пружинная масса растягивается еще на одно расстояние \(d_2\), освобождается и позволяется колебаться. Напомним, что все высоты по вертикали, использованные при расчете PE g , измеряются от точки y=0, указанной на рис. 2.5.3. Таким образом, значения y для положений равновесия и растяжения (центральная и правая конфигурации на рисунке) будут отрицательными. Диаграмма взаимодействия энергии для расчета максимальной скорости, когда масса пружины возвращается в равновесие после отпускания, показана на рисунке ниже. 92=0\]
Приведенное выше уравнение идентично горизонтальной массе пружины, полученной в уравнении \ref{energy.SM}, при условии, что смещение для вертикальной массы пружины измеряется из нового положения равновесия после того, как масса крепится к пружине.
Предупреждение
Приведенный выше результат показывает, что при вертикальном прикреплении пружинной массы влияние силы гравитации учитывается автоматически, если новое положение равновесия определяется в положении пружины с прикрепленной массой.

 Уравнения
Уравнения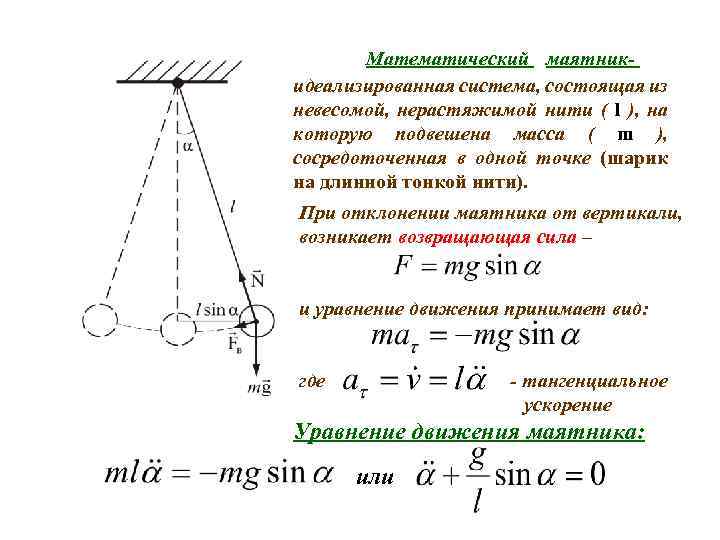 450
450
 Выберем интервал от начального максимального смещения 0,4 м до конечного максимального смещения после 4 колебаний. Поскольку при максимальном смещении скорость равна нулю, кинетическая энергия на этом интервале не изменится. Диаграмма взаимодействия энергии для этого процесса показана ниже: 92)=-8 Дж\номер\]
Выберем интервал от начального максимального смещения 0,4 м до конечного максимального смещения после 4 колебаний. Поскольку при максимальном смещении скорость равна нулю, кинетическая энергия на этом интервале не изменится. Диаграмма взаимодействия энергии для этого процесса показана ниже: 92)=-8 Дж\номер\]
Leave A Comment