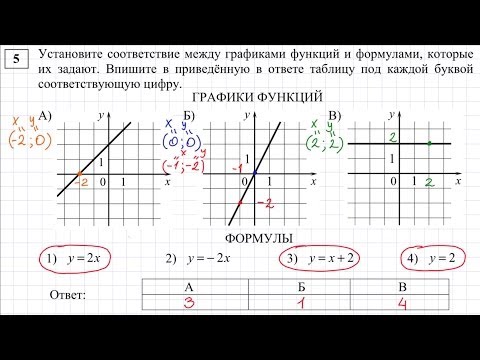
Раздел недели: Скоропись физического, математического, химического и, в целом, научного текста, математические обозначения. Математический, Физический алфавит, Научный алфавит. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Математический справочник / / Математика для самых маленьких. Поделиться:
 Введите свой запрос: Введите свой запрос: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Раздел недели: Скоропись физического, математического, химического и, в целом, научного текста, математические обозначения. Математический, Физический алфавит, Научный алфавит. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа. / / Графики простейших функций — линейная, параболы, гиперболы, экспоненты, показательные, степенные, логарифмическая, синус, косинус, тангенс, котангенс изучаемых в школе Справочная таблица. Поделиться:
 Введите свой запрос: Введите свой запрос: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Графики общих функций: список, типы и рабочий лист
Графики общих функций представляют собой графические представления функций, которые часто используются в математике.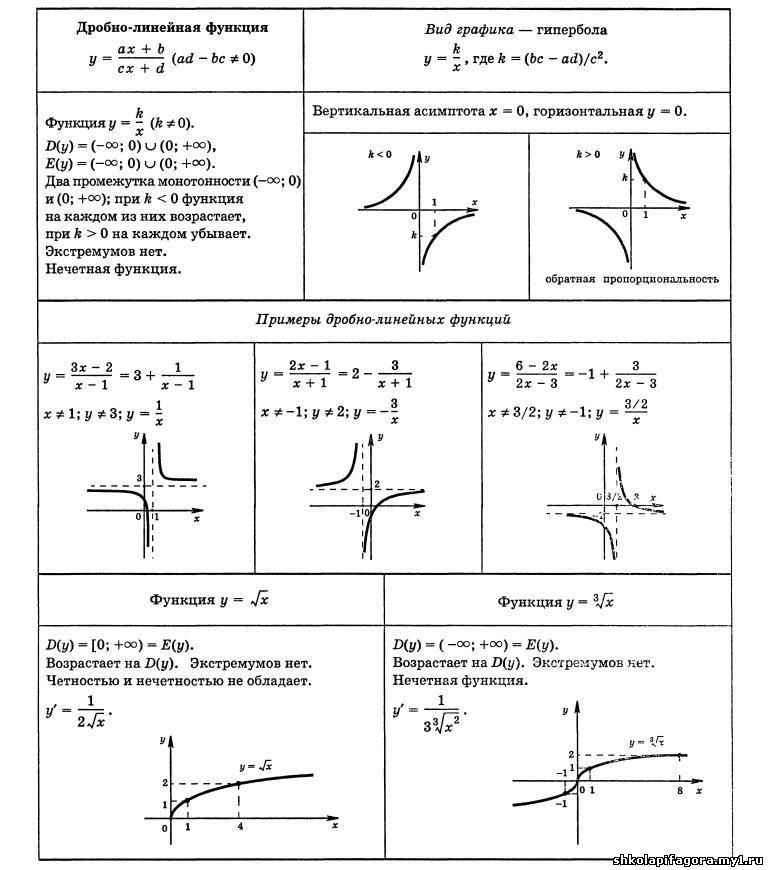
Помните, что функция — это математическая конструкция, которая принимает значения x в качестве входных данных и выводит значения y в соответствии один к одному или многие к одному. Функции представляют отношения между независимой переменной x и зависимой переменной y.
Представление функции, Марилу Гарсия Де Тейлор — StudySmarter Originals
Типы графиков функций
Некоторые из наиболее распространенных функций , которые вы найдете в математике, перечислены ниже:
1. Константа: f(x)=c, где c — константа. Форма графика постоянных функций представляет собой прямую линию, параллельную оси x, пересекающую ось y, где y = c.
График постоянной функции, Марилу Гарсиа Де Тейлор — StudySmarter Originals
2. Линейный (тождественный) f(x)=x. Форма линейных графиков также представляет собой прямую линию. В этом случае линия имеет наклон, который может быть пологим или крутым в зависимости от ее значения.
График функции идентичности, Марилу Гарсия Де Тейлор — StudySmarter Originals
3. Квадратичный: f(x)=x2. Форма графика квадратичных функций – парабола.
График квадратичной функции, Марилу Гарсия Де Тейлор — StudySmarter Originals
4. Кубический: f(x)=x3. Кубические графики представляют собой непрерывные и гладкие линии, которые могут иметь максимальные или минимальные точки, в которых они меняют направление в средней части кривой, а на любом конце кривой они стремятся уйти в положительную или отрицательную бесконечность.
График кубической функции, Марилу Гарсия Де Тейлор — StudySmarter Originals
5. Квадратный корень: f(x)=x. График функции квадратного корня имеет характерную форму из-за ограниченной области определения (id=»2853741″ role=»math» x≥0). Это потому, что квадратный корень из отрицательного числа не имеет действительного решения. Поэтому в этом типе графика используются только положительные числа.
График функции квадратного корня, Марилу Гарсия Де Тейлор — StudySmarter Originals
6. Кубический корень: f(x)=x3. Графы кубического корня отличаются от графов квадратного корня тем, что кубический корень из отрицательных чисел имеет действительные решения. Следовательно, функции кубического корня не имеют ограниченной области определения, x может принимать как отрицательные, так и положительные значения, что видно из формы его графика.
График функции кубического корня, Марилу Гарсия Де Тейлор — StudySmarter Originals
7. Модуль или абсолютное значение: f(x)=|x|. График модульных функций имеет характерную v-образную форму. Это то же самое, что f (x) = x, но отрицательные значения y отражаются на оси x. Это потому, что модуль числа x — это то же число, но положительное.
График функции модуля или абсолютного значения, Марилу Гарсиа Де Тейлор — StudySmarter Originals
8. Обратное: f(x)=1x. На графике обратных функций есть асимптоты — линии, к которым кривая подходит очень близко, но никогда их не касается. График f(x)=1x имеет асимптоты при x = 0 и y = 0.
На графике обратных функций есть асимптоты — линии, к которым кривая подходит очень близко, но никогда их не касается. График f(x)=1x имеет асимптоты при x = 0 и y = 0.
График обратной функции, Марилу Гарсия Де Тейлор — StudySmarter Originals
9. Квадрат обратной функции: f(x)=1×2. Форма графика функции обратного квадрата меняется по сравнению с предыдущей, потому что наличие x2 в знаменателе означает, что все значения y будут положительными.
x2 График функции обратного квадрата, Марилу Гарсиа Де Тейлор — StudySmarter Originals
10. Экспоненциальная функция: f(x)=ex. График показательной функции имеет горизонтальную асимптоту при y = 0 и пересекает ось y в точке (0, 1). После этого он быстро увеличивается.
График экспоненциальной функции, Марилу Гарсия Де Тейлор — StudySmarter Originals
11. Логарифмический: f(x)=ln(x). Логарифмическая функция является обратной экспоненциальной функции, поэтому график логарифмической функции будет отражением экспоненциального графика, к которому она относится, по линии y = x.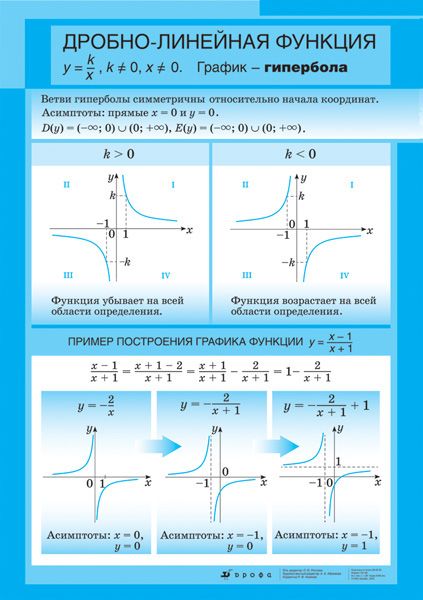 График логарифмической функции имеет вертикальную асимптоту при x = 0 и пересекает ось x в точке (1, 0).
График логарифмической функции имеет вертикальную асимптоту при x = 0 и пересекает ось x в точке (1, 0).
График логарифмической функции, Марилу Гарсия Де Тейлор — StudySmarter Originals
12. Тригонометрические функции : Графики тригонометрических функций (синуса, косинуса и тангенса) имеют характерную форму, поскольку они периодические, а это означает, что они повторяются. после определенного интервала.
а) Синус: f(x)=sin(x). График для синуса имеет максимальное значение 1 и минимальное значение -1, и он повторяется каждые 2π. График синуса пересекает ось Y в начале координат (0, 0).
2π радиан = 360 °
График тригонометрической функции — sin (x), Марилу Гарсия Де Тейлор — StudySmarter Originals
b) Косинус: f(x)=cos(x). График косинуса также имеет максимальное значение 1 и минимальное значение -1 и повторяется каждые 2π. Вы можете отличить его от графика синуса, потому что график косинуса пересекает ось Y в точке (0, 1).
График тригонометрической функции — cos (x), Марилу Гарсия Де Тейлор — StudySmarter Originals
c) Тангенс: f(x)=tan(x). Касательный граф не имеет точек максимума или минимума и повторяется через каждые π. Следовательно, он имеет вертикальные асимптоты при -π2, π2, 3π2 и т. д.
График тригонометрической функции — tan (x), Марилу Гарсия Де Тейлор — StudySmarter Originals
Как найти общую функцию графика?
Чтобы определить общую функцию графика, очень полезно изучить формы их графиков. Сосредоточьтесь на их характеристиках и формулах (например, на форме кривой), чтобы вы могли быстро определить, какой тип функции представляет график. Запоминание предыдущего списка графиков общих функций поможет вам приобрести этот важный навык на тот случай, если они понадобятся вам для решения конкретных задач.
Определение того, является ли график функцией
Если вам дан график, и вас просят проверить, представляет ли график функцию или нет, вы можете действовать следующим образом:
Проверка вертикальной линии: Этот тест покажет вам, представляет ли график функцию.
 Вам нужно провести вертикальные линии, пересекающие график. Если в какой-либо точке вертикальная линия пересекает график более одного раза, то график не является функцией (x имеет более одного выхода). Например:
Вам нужно провести вертикальные линии, пересекающие график. Если в какой-либо точке вертикальная линия пересекает график более одного раза, то график не является функцией (x имеет более одного выхода). Например:
Пример теста с вертикальной линией, Марилу Гарсия Де Тейлор — StudySmarter Originals
Этот график не является функцией, поскольку вертикальная линия пересекает две точки на графике.
Тест горизонтальной линии: Этот тест показывает, является ли функция взаимно однозначной или нет. Если вы рисуете горизонтальную линию, и она пересекает график более одного раза, то это , а не однозначная функция . Например:
Пример теста горизонтальной линии, Марилу Гарсиа Де Тейлор — StudySmarter Originals
Этот график является функцией, поскольку он проходит тест вертикальной линии, но не является взаимно однозначной функцией, поскольку горизонтальная линия пересекает график дважды.
Графики общих функций — основные выводы
Функция — это математическая конструкция, которая принимает значения x в качестве входных данных и выводит значения y в соответствии один к одному или многие к одному.
Графики общих функций — это графическое представление функций, которые часто используются в математике.
Изучение форм различных типов графиков функций, их особенностей и формул помогает быстро определить, какой тип функции представляет график, глядя на форму кривой.
Проверка вертикальной линии используется для определения того, представляет ли график функцию.
Проверка горизонтальной линии используется для определения того, является ли функция взаимно однозначной или нет.
Шпаргалка по предварительному исчислению для чайников
Авторы: Ян Куанг и Эллейн Касе и
Обновлено: 24. 07.2021 Манекены
07.2021 Манекены
Предварительно -Исчисление для чайников
Исследуйте книгу Купить на Amazon
Когда вы изучаете предварительное исчисление, вы пересекаете мост от алгебры II к исчислению. Предварительное исчисление включает в себя построение графиков, работу с углами и геометрическими фигурами, такими как круги и треугольники, и нахождение абсолютных значений. Вы открываете новые способы записи решений с помощью интервальной нотации и включаете тождества триггеров в свои уравнения.Единичный круг предварительного исчисления
В предварительном исчислении единичный круг похож на единичные улицы, это очень маленький круг на графике, который охватывает координаты 0,0. Его радиус равен 1, следовательно, единица измерения. На рисунке показаны все измерения единичного круга:
Прямоугольные треугольники и триггерные функции для предварительного исчисления
Если вы изучаете предварительное исчисление, вы столкнетесь с треугольниками и, конечно же, с теоремой Пифагора.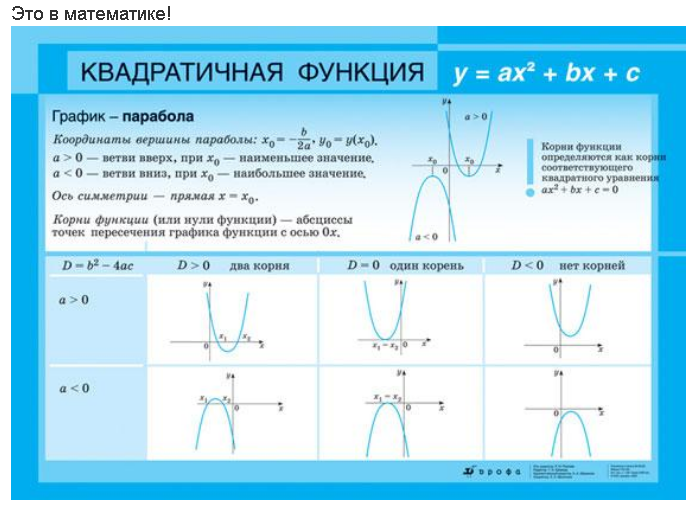 Теорема и то, как она применяется к специальным прямоугольным треугольникам, изложены здесь:
Теорема и то, как она применяется к специальным прямоугольным треугольникам, изложены здесь:
Как отформатировать обозначение интервала в предварительном исчислении
В предварительном исчислении вы имеете дело с неравенствами и используете представление интервала для выражения набора решений неравенства. Следующие формулы показывают, как форматировать наборы решений в интервальной нотации.
Формулы абсолютных значений для предварительного исчисления
Несмотря на то, что вы занимаетесь предварительным исчислением, вы помните свою старую любовь, алгебру и тот факт, что абсолютные значения тогда обычно имели два возможных решения. Теперь, когда вы занимаетесь предварительным исчислением, вы понимаете, что с абсолютными значениями немного сложнее, когда вы добавляете неравенства в смесь. Не бойтесь, следующие формулы покажут вам, как работать с абсолютными значениями в предварительном исчислении.

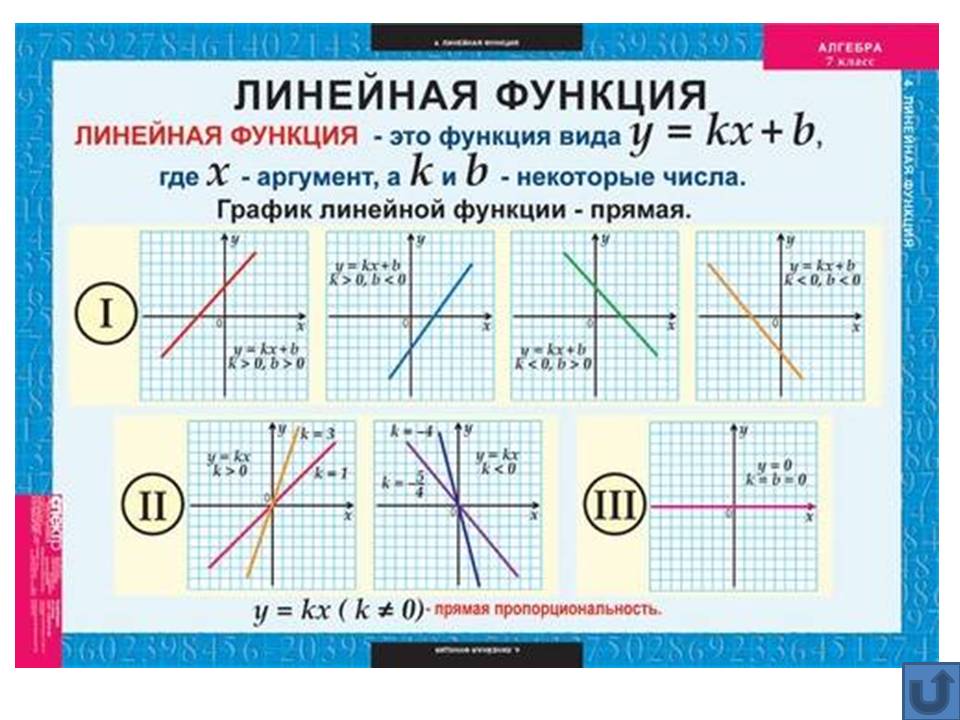
 Шпаргалки. Детский сад, Школа. / / Графики простейших функций — линейная, параболы, гиперболы, экспоненты, показательные, степенные, логарифмическая, синус, косинус, тангенс, котангенс изучаемых в школе Справочная таблица. Примерно 7-9 класс (13-15 лет)
Шпаргалки. Детский сад, Школа. / / Графики простейших функций — линейная, параболы, гиперболы, экспоненты, показательные, степенные, логарифмическая, синус, косинус, тангенс, котангенс изучаемых в школе Справочная таблица. Примерно 7-9 класс (13-15 лет) На рисунке пример для
На рисунке пример для 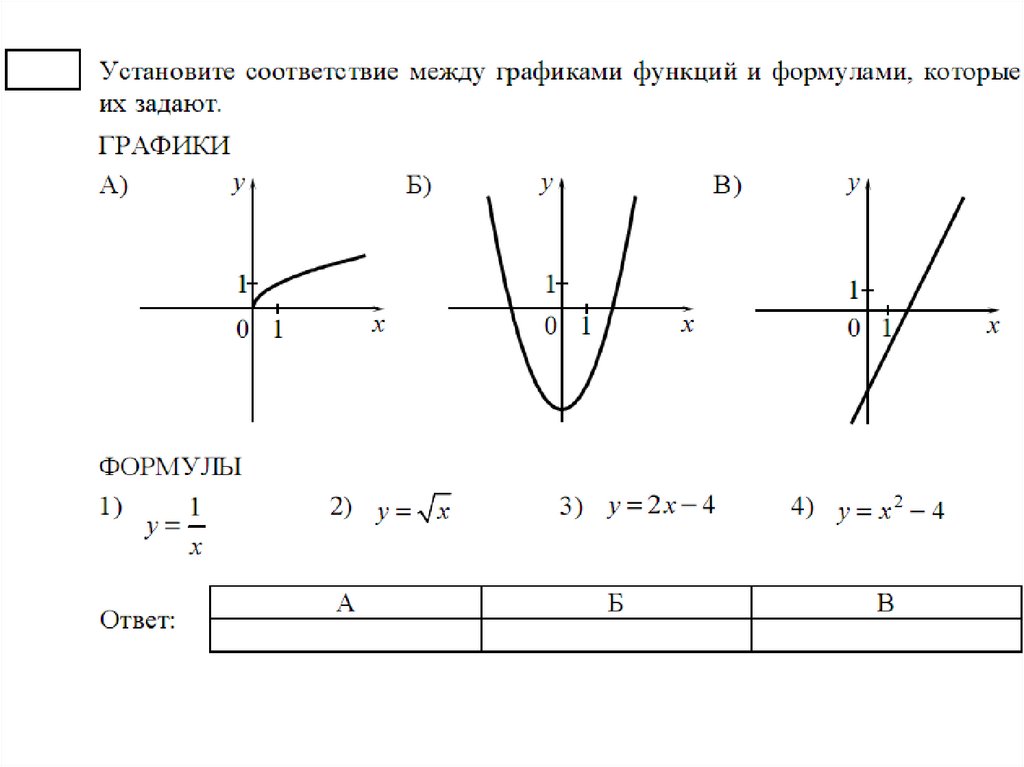
 ..
..

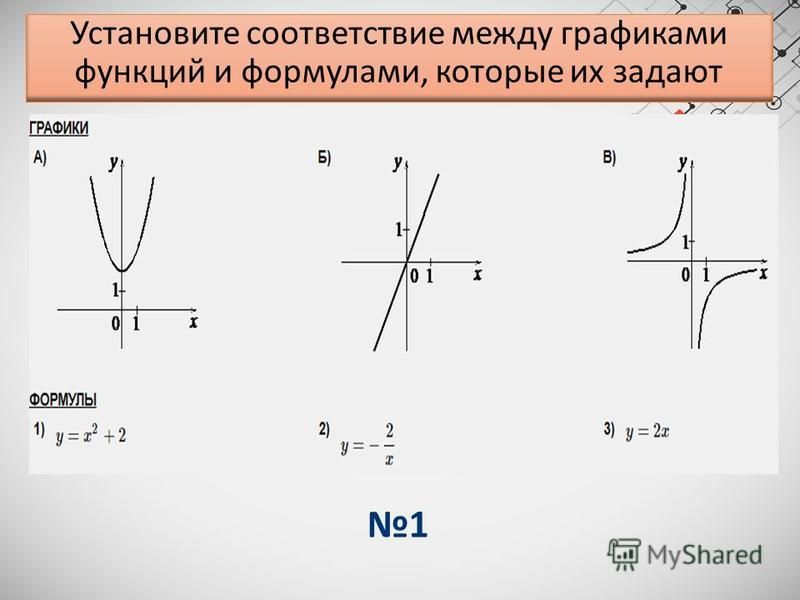 Примерно 7-9 класс (13-15 лет)
Примерно 7-9 класс (13-15 лет) Примерно 7-9 класс (13-15 лет)
Примерно 7-9 класс (13-15 лет)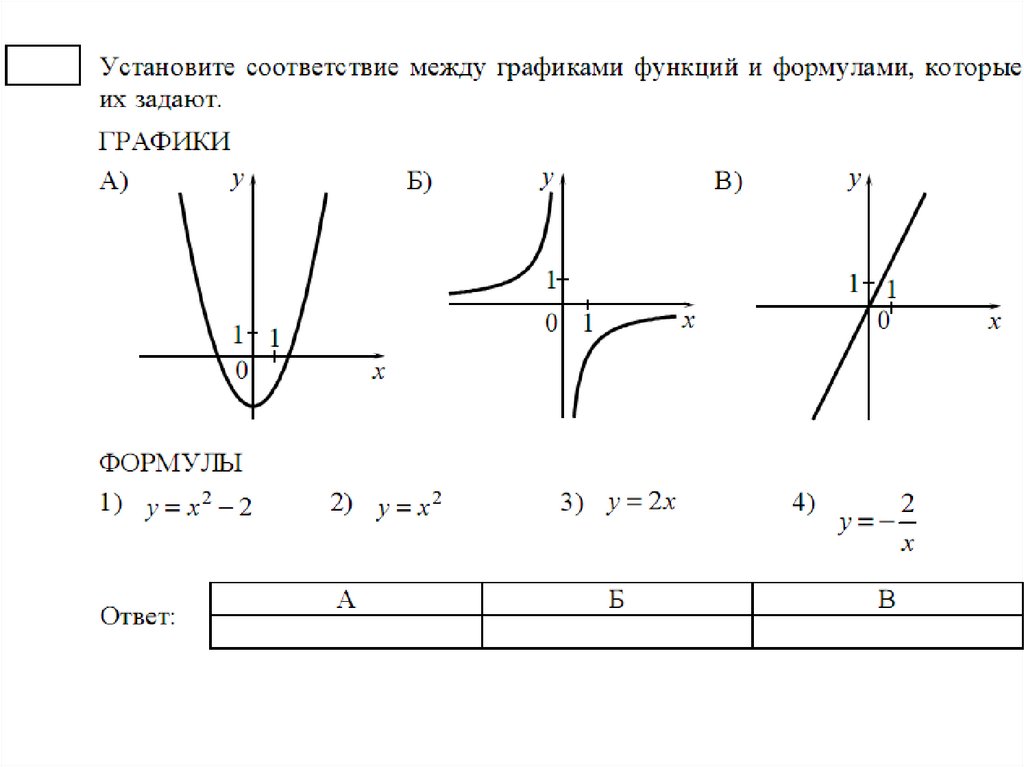 На рисунке пример для k = 1, т.е. фактически приведенный график иллюстрирует функциональную зависимость, которая задаёт равенство значения функции значению аргумента.
На рисунке пример для k = 1, т.е. фактически приведенный график иллюстрирует функциональную зависимость, которая задаёт равенство значения функции значению аргумента.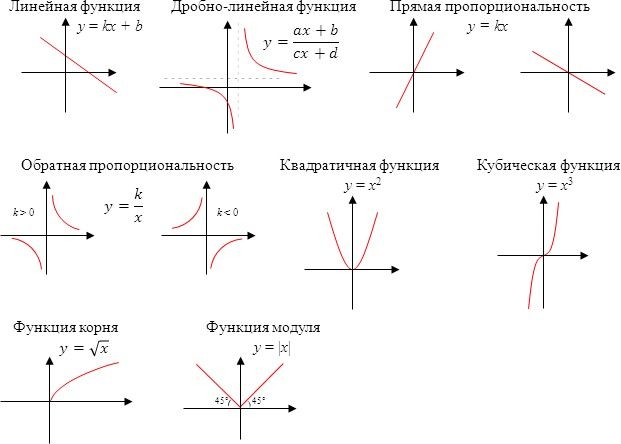 Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций».
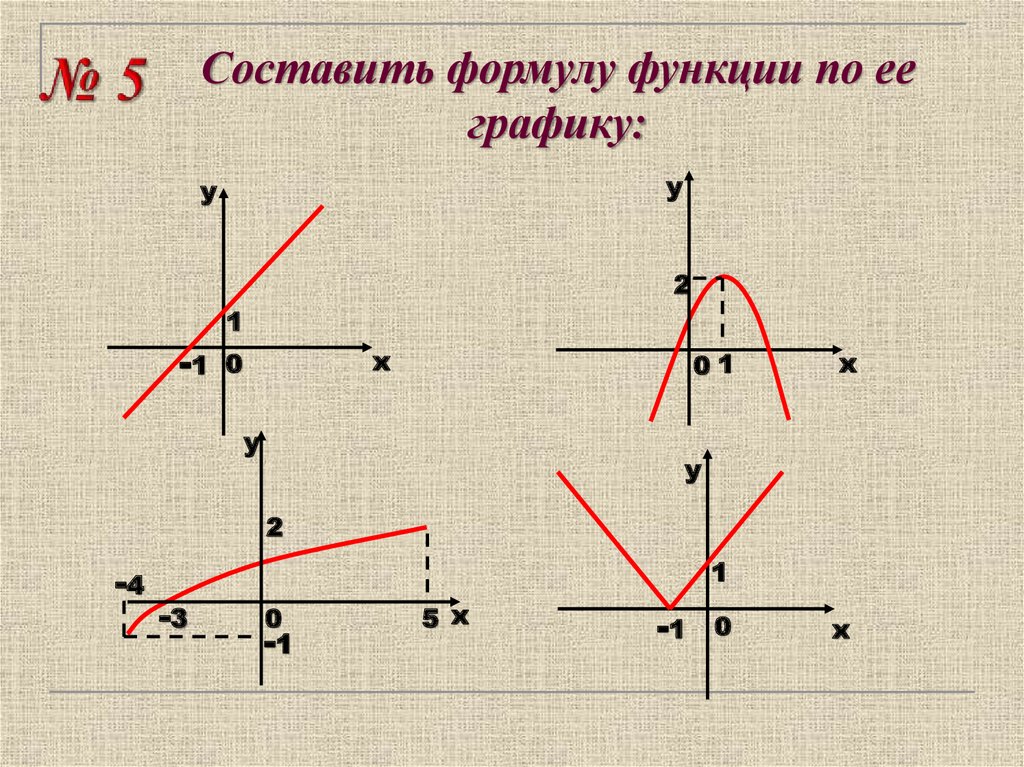
Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций».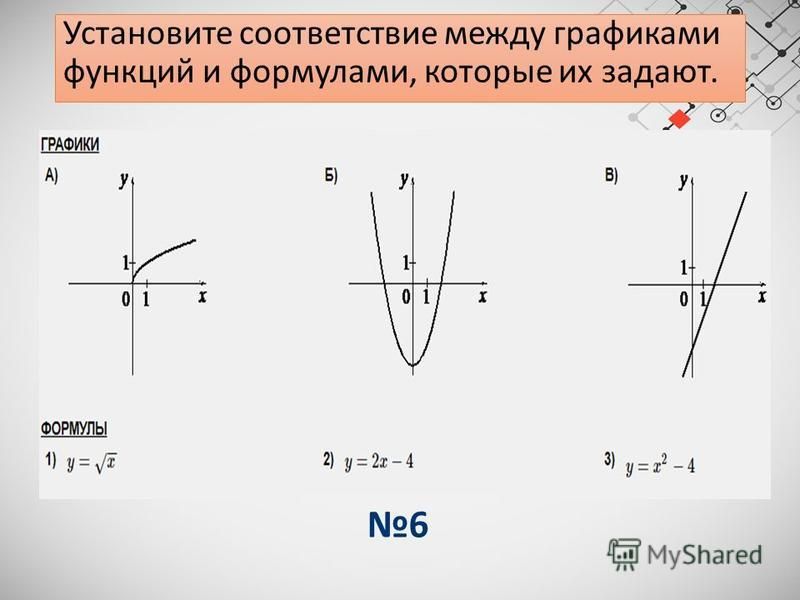 ..
..
 Вам нужно провести вертикальные линии, пересекающие график. Если в какой-либо точке вертикальная линия пересекает график более одного раза, то график не является функцией (x имеет более одного выхода). Например:
Вам нужно провести вертикальные линии, пересекающие график. Если в какой-либо точке вертикальная линия пересекает график более одного раза, то график не является функцией (x имеет более одного выхода). Например:
Leave A Comment