Функция состоит из трех квадратных трехчленов. разложим их на множители по формуле
ax2 + bx + c = a(x — x1)(x — x2), где х1 и х2 — корни квадратных уравнений.
Все три квадратных уравнения приведенные. Это значит, что можно найти их корни по теореме Виета. Именно поэтому я сразу напишу разложения этих трехчленов на множители. Конечно, решать через дискриминант никто не запрещал и ошибкой это не будет.
Итак, после разложения на множители функция примет такой вид:
Видно невооруженным глазом, что скобки из знаменателя сокращаются со скобками из числителя. Это просто супер-пупер! Но надо обязательно оговориться, что знаменатель не может быть равен нулю, а значит, что x ≠ -1 и x ≠ 3. Эти исключения подразумевают выколотые точки на нашем будущем графике.
После сокращения раскрываем оставшиеся скобки.
О, чудо! Это квадратичная функция! График — парабола!
Ищем ее вершину О (m; n).
Первая координата m, которую мы будем отмечать на оси Ох, находится по формуле.
А чтобы найти вторую координату надо m подставить в упрощенную ранее функцию и посчитать.
В общем, вершина параболы имеет координаты (-0,5; -2,25).
Чертим координатную плоскость и отмечаем вершину.
Мастера по рисованию парабол могут ее начертить, не прибегая к таблице по нахождению координат других точек. А вот тем, кто не в очень теплых отношениях с параболами, придется ее рисовать.
Поскольку я мастер — обойдусь без таблицы 🙂
Не забываем про выколотые точки!
В условии задачи сказано, что некоторая прямая y = m должна иметь одну общую точку с параболой. Эта прямая будет параллельна оси Ох и одну общую точку она будет иметь в выколотых точках и вершине параболы.
Ответ: 10; -2; -2,25.
P.S. Бывает так, что график нарисован очень криво. Как не ошибиться в координатах выколотых точек? Очень просто. В нашей задаче x ≠ -1 и x ≠ 3. Подставь эти числа в функцию (упрощенную, разумеется), посчитай и найдешь, чему должны быть не равны координаты по игреку (у ≠ -2 и у ≠ 10).
Как не ошибиться в координатах выколотых точек? Очень просто. В нашей задаче x ≠ -1 и x ≠ 3. Подставь эти числа в функцию (упрощенную, разумеется), посчитай и найдешь, чему должны быть не равны координаты по игреку (у ≠ -2 и у ≠ 10).
2 х 4 график
Вы искали 2 х 4 график? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и 4 x 2 функция, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «2 х 4 график».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как 2 х 4 график,4 x 2 функция,x 2 4x y график,y 2 х 4,y 4x 2 2x,y 4x x2 график,y x 2 2x 4,y x 2 4x построить график,y x 4 x 2,y x 4x 2,y x2 4x график,график 2x 4,график y x 2 4x,график функции 2 x 4,график функции 4x x 2,график функции y 2x 4,график функции y x 2 4,график функции y x2 4,график функции у 4х2,график функции х 2 4,график х 2 4,постройте график x 2 y 4,постройте график функции y x 2 4 x 2,у 2 4х,у 2 х 4,у 2х 4,у х2 4х,функция 4 x 2,функция 4 х 2. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и 2 х 4 график. Просто введите задачу в окошко и нажмите «решить» здесь (например, x 2 4x y график).
Где можно решить любую задачу по математике, а так же 2 х 4 график Онлайн?
Решить задачу 2 х 4 график вы можете на нашем сайте https://pocketteacher. ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.
ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.
Построение графика квадратичной функций: алгоритм и примеры 9 класс онлайн-подготовка на Ростелеком Лицей
Тема 5.
Построение графика квадратичной функции с помощью преобразований.
Рассмотрим частные случаи
y = ax2 + n и y = a(x – m)2.
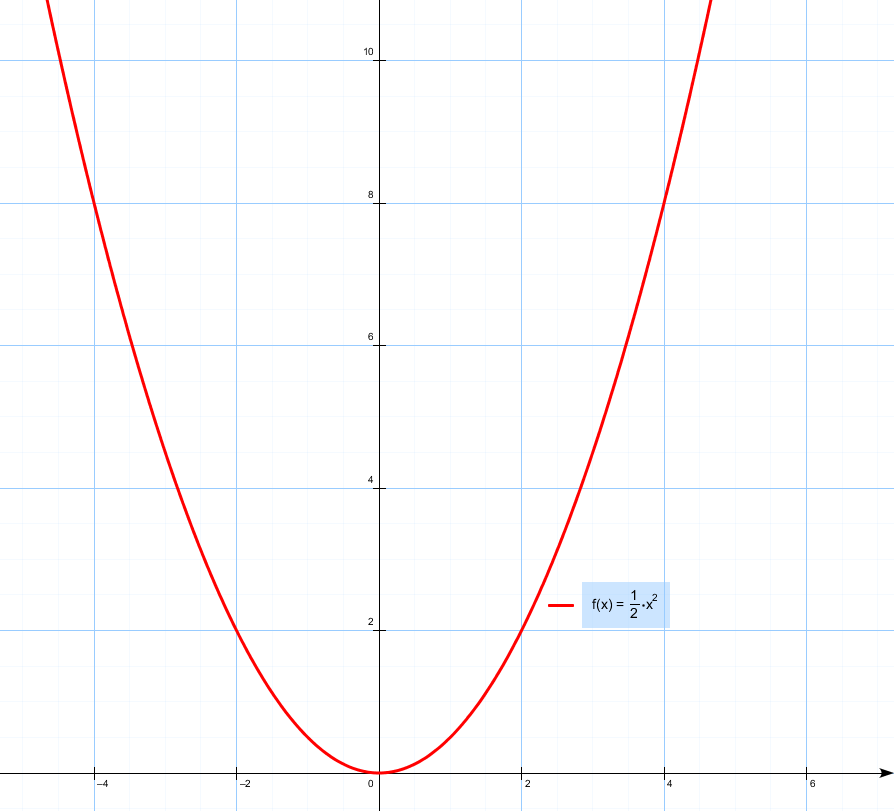
В одной системе координат построим графики функцийy=12×2 и y=12×2+5.
Составим таблицу значений функции: y=12×2
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
y |
4,5 |
2 |
0,5 |
0 |
0,5 |
2 |
4,5 |
Чтобы получить таблицу значений для функции y=12×2+5 для тех же значений аргумента, необходимо к найденным значениям функции y=12×2 прибавить 5.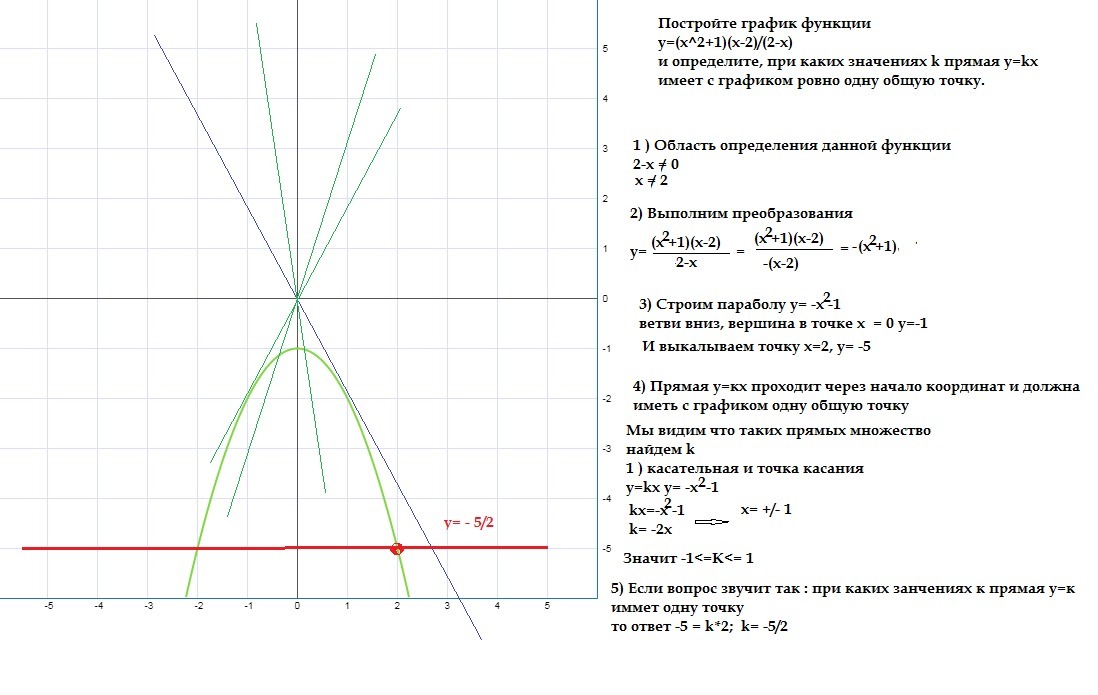
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
y |
9,5 |
7 |
5,5 |
5 |
5,5 |
7 |
9,5 |
Получается, что каждую точку второго графика можно получить из некоторой точки первого графика с помощью параллельного переноса на 5 единиц вверх вдоль оси y.
График функции y=12×2+5 – парабола, полученная в результате сдвига вверх графика функции y=12×2.
График функции y = ax2 + n – парабола, которую можно получить из графика функции y = ax2 с помощью параллельного переноса вдоль оси y на n единиц вверх, если n > 0 или на –
В одной системе координат построим графики функций y=12×2 и y=12x-52. Составим таблицы значений для этих функций.
y=12×2
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
|
4,5 |
2 |
0,5 |
0 |
0,5 |
2 |
4,5 |
y=12x-52
|
x |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
y |
4,5 |
2 |
0,5 |
0 |
0,5 |
2 |
4,5 |
Значит, если переместить каждую точку графика y=12×2 вправо на 5 единиц, то получим соответствующую точку графика функции y=12x-52. Иначе говоря, каждую точку второго графика можно получить из соответствующей точки первого графика с помощью параллельного переноса на 5 единиц вправо вдоль оси x.
Иначе говоря, каждую точку второго графика можно получить из соответствующей точки первого графика с помощью параллельного переноса на 5 единиц вправо вдоль оси x.
График функции y=12x-52 – парабола, полученная y=12x-52 в результате сдвига вправо графика функции y=12×2.
График функции y = a(x — m)2 – парабола, которую можно получить из графика функции y = ax2 с помощью параллельного переноса вдоль оси x на на m единиц вправо, если m > 0 или на – m единиц влево, если m
Полученные выводы позволяют понять, что представляет собой график функции y = a(x — m)2. Например, график функции y=12x-52+3 можно получить из графика функции y=12×2 с помощью двух параллельных переносов – сдвига вдоль оси x на 5 единиц вправо и вдоль оси y на 3 единицы вверх.
Таким образом, график функции y = a(x — m)2 можно получить из параболы y = ax2 с помощью двух параллельных переносов: сдвига вдоль x на m единиц вправо, если m > 0 или на – m единиц влево, если m n единиц вверх, если n > 0 или на – n единиц вниз, если n
Заметим, что данные преобразования можно производить в любом порядке: сначала выполнить параллельный перенос вдоль оси x, а затем вдоль оси y или наоборот.
Преобразования, которые мы рассмотрели применимы для любых функций.
Рассмотрим пример.
Построим график функции y = x2 — 4x двумя способами: с помощью преобразований, которые мы сегодня рассмотрели и с помощью таблицы значений функции.
Для того, чтобы построить график функции с помощью преобразований, необходимо его представить в виде y = a(x — m)2. Для этого надо выделить полный квадрат. Итак, в нашу функцию y = x2 — 4x добавим 4 и вычтем 4. Получим:
Для этого надо выделить полный квадрат. Итак, в нашу функцию y = x2 — 4x добавим 4 и вычтем 4. Получим:
y=x2-4x+4-4=x-22-4
График данной функции можно получить из графика функции y = x2 с помощью двух параллельных переносов: сдвига вдоль оси x на 2 единицы вправо, и сдвига вдоль оси y на 4 единицы вниз.
Чтобы построить график функции вторым способом, составим таблицу ее значений. Возьми нечетное количество точек, например, пять и семь. В центре поставь координаты вершины параболы.
xв=-b2a=—42∙1=2
yв=22-4∙2=-4
График квадратичной функции симметричен относительно прямой, параллельной оси y, проходящей через вершину параболы. В данном случае прямая x = 2 является осью симметрии.
|
x |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
|
y |
5 |
0 |
-3 |
-4 |
-3 |
0 |
5 |
График x 2 2x 3. Квадратичная и кубическая функции
Урок на тему: «График и свойства функции $y=x^3$.
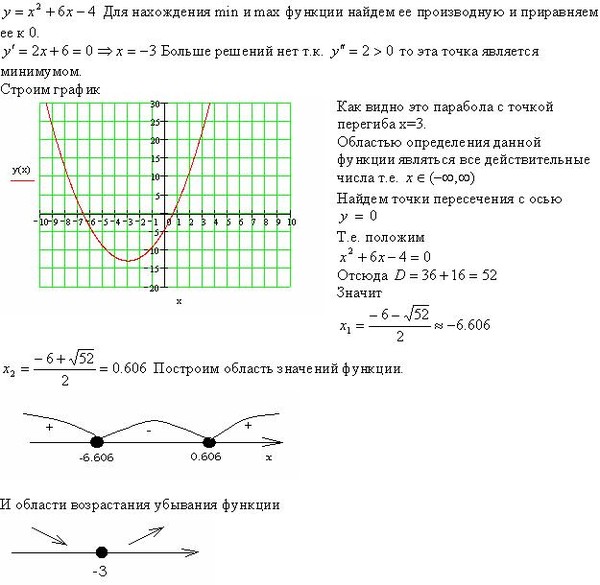 3$.
3$.2. Найдем точку А, координата x, которой равна 1,5. Мы видим, что координата функции находится между значениями 3 и 4 (см. рис. 2). Значит надо заказать 4 куба.
Как построить параболу? Существует несколько способов построения графика квадратичной функции. Каждый из них имеет свои плюсы и минусы. Рассмотрим два способа.
Начнём с построения графика квадратичной функции вида y=x²+bx+c и y= -x²+bx+c.
Пример.
Построить график функции y=x²+2x-3.
Решение:
y=x²+2x-3 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы
От вершины (-1;-4) строим график параболы y=x²(как от начала координат. Вместо (0;0) — вершина (-1;-4). От (-1;-4) идём вправо на 1 единицу и вверх на 1 единицу, затем влево на 1 и вверх на 1; далее: 2 — вправо, 4 — вверх, 2- влево, 4 — вверх; 3 — вправо, 9 — вверх, 3 — влево, 9 — вверх. Если этих 7 точек недостаточно, далее — 4 вправо, 16 — вверх и т. д.).
График квадратичной функции y= -x²+bx+c — парабола, ветви которой направлены вниз. Для построения графика ищем координаты вершины и от неё строим параболу y= -x².
Пример.
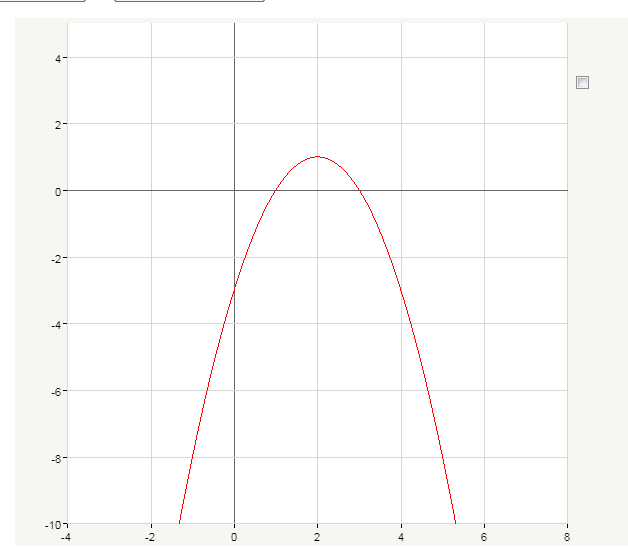
Построить график функции y= -x²+2x+8.
Решение:
y= -x²+2x+8 — квадратичная функция. График — парабола ветвями вниз. Координаты вершины параболы
От вершины строим параболу y= -x² (1 — вправо, 1- вниз; 1 — влево, 1 — вниз; 2 — вправо, 4 — вниз; 2 — влево, 4 — вниз и т. д.):
Этот способ позволяет построить параболу быстро и не вызывает затруднений, если вы умеете строить графики функций y=x² и y= -x². Недостаток: если координаты вершины — дробные числа, строить график не очень удобно. Если требуется знать точные значения точек пересечения графика с осью Ох, придется дополнительно решить уравнение x²+bx+c=0 (или —x²+bx+c=0), даже если эти точки непосредственно можно определить по рисунку.
Другой способ построения параболы — по точкам, то есть можно найти несколько точек графика и через них провести параболу (с учетом того, что прямая x=хₒ является её осью симметрии). Обычно для этого берут вершину параболы, точки пересечения графика с осями координат и 1-2 дополнительные точки.
Обычно для этого берут вершину параболы, точки пересечения графика с осями координат и 1-2 дополнительные точки.
Построить график функции y=x²+5x+4.
Решение:
y=x²+5x+4 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы
то есть вершина параболы — точка (-2,5; -2,25).
Ищем . В точке пересечения с осью Ох y=0: x²+5x+4=0. Корни квадратного уравнения х1=-1, х2=-4, то есть получили две точки графике (-1; 0) и (-4; 0).
В точке пересечения графика с осью Оy х=0: y=0²+5∙0+4=4. Получили точку (0; 4).
Для уточнения графика можно найти дополнительную точку. Возьмем х=1, тогда y=1²+5∙1+4=10, то есть еще одна точка графика — (1; 10). Отмечаем эти точки на координатной плоскости. С учетом симметрии параболы относительно прямой, проходящей через её вершину, отметим еще две точки: (-5; 6) и (-6; 10) и проведем через них параболу:
Построить график функции y= -x²-3x.
Решение:
y= -x²-3x — квадратичная функция. График — парабола ветвями вниз. Координаты вершины параболы
Вершина (-1,5; 2,25) — первая точка параболы.
В точках пересечения графика с осью абсцисс y=0, то есть решаем уравнение -x²-3x=0. Его корни — х=0 и х=-3, то есть (0;0) и (-3; 0) — еще две точки графика. Точка (о; 0) является также точкой пересечения параболы с осью ординат.
При х=1 y=-1²-3∙1=-4, то есть (1; -4) — дополнительная точка для построения графика.
Построение параболы по точкам — более трудоёмкий, по сравнению с первым, способ. Если парабола не пересекает ось Oх, дополнительных точек потребуется больше.
Прежде чем продолжить построение графиков квадратичных функций вида y=ax²+bx+c, рассмотрим построение графиков функций с помощью геометрических преобразований. Графики функций вида y=x²+c также удобнее всего строить, используя одно из таких преобразований — параллельный перенос.
Рубрика: |Построение графиков функций, содержащих модули, обычно вызывает немалые затруднения у школьников. Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции. Давайте разберемся, что же это за алгоритмы.
Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции. Давайте разберемся, что же это за алгоритмы.
1. Построение графика функции y = |f(x)|
Заметим, что множество значений функций y = |f(x)| : y ≥ 0. Таким образом, графики таких функций всегда расположены полностью в верхней полуплоскости.
Построение графика функции y = |f(x)| состоит из следующих простых четырех этапов.
1) Построить аккуратно и внимательно график функции y = f(x).
2) Оставить без изменения все точки графика, которые находятся выше оси 0x или на ней.
3) Часть графика, которая лежит ниже оси 0x, отобразить симметрично относительно оси 0x.
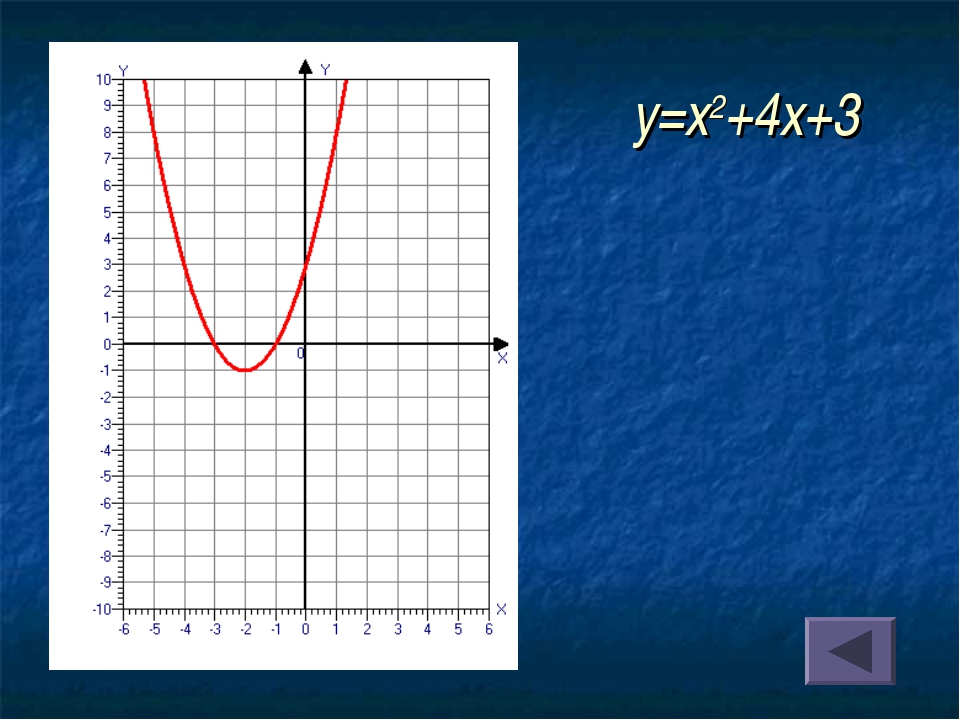
Пример 1. Изобразить график функции y = |x 2 – 4x + 3|
1) Строим график функции y = x 2 – 4x + 3. Очевидно, что график данной функции – парабола. Найдем координаты всех точек пересечения параболы с осями координат и координаты вершины параболы.
x 2 – 4x + 3 = 0.
x 1 = 3, x 2 = 1.
Следовательно, парабола пересекает ось 0x в точках (3, 0) и (1, 0).
y = 0 2 – 4 · 0 + 3 = 3.
Следовательно, парабола пересекает ось 0y в точке (0, 3).
Координаты вершины параболы:
x в = -(-4/2) = 2, y в = 2 2 – 4 · 2 + 3 = -1.
Следовательно, точка (2, -1) является вершиной данной параболы.
Рисуем параболу, используя полученные данные (рис. 1)
2) Часть графика, лежащую ниже оси 0x, отображаем симметрично относительно оси 0x.
3) Получаем график исходной функции (рис. 2 , изображен пунктиром).
2. Построение графика функции y = f(|x|)
Заметим, что функции вида y = f(|x|) являются четными:
y(-x) = f(|-x|) = f(|x|) = y(x). Значит, графики таких функций симметричны относительно оси 0y.
Построение графика функции y = f(|x|) состоит из следующей несложной цепочки действий.
1) Построить график функции y = f(x).
2) Оставить ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отобразить указанную в пункте (2) часть графика симметрично оси 0y.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 2. Изобразить график функции y = x 2 – 4 · |x| + 3
Так как x 2 = |x| 2 , то исходную функцию можно переписать в следующем виде: y = |x| 2 – 4 · |x| + 3. А теперь можем применять предложенный выше алгоритм.
1) Строим аккуратно и внимательно график функции y = x 2 – 4 · x + 3 (см. также рис. 1 ).
2) Оставляем ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отображаем правую часть графика симметрично оси 0y.
(рис. 3) .
Пример 3. Изобразить график функции y = log 2 |x|
Применяем схему, данную выше.
1) Строим график функции y = log 2 x (рис. 4) .
3. Построение графика функции y = |f(|x|)|
Заметим, что функции вида y = |f(|x|)| тоже являются четными. Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому, их графики симметричны относительно оси 0y. Множество значений таких функций: y ≥ 0. Значит, графики таких функций расположены полностью в верхней полуплоскости.
Чтобы построить график функции y = |f(|x|)|, необходимо:
1) Построить аккуратно график функции y = f(|x|).
2) Оставить без изменений ту часть графика, которая находится выше оси 0x или на ней.
3) Часть графика, расположенную ниже оси 0x, отобразить симметрично относительно оси 0x.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 4. Изобразить график функции y = |-x 2 + 2|x| – 1|.
1) Заметим, что x 2 = |x| 2 . Значит, вместо исходной функции y = -x 2 + 2|x| – 1
можно использовать функцию y = -|x| 2 + 2|x| – 1, так как их графики совпадают.
Строим график y = -|x| 2 + 2|x| – 1. Для этого применяем алгоритм 2.
a) Строим график функции y = -x 2 + 2x – 1 (рис. 6) .
b) Оставляем ту часть графика, которая расположена в правой полуплоскости.
c) Отображаем полученную часть графика симметрично оси 0y.
d) Полученный график изображен на рисунке пунктиром (рис. 7) .
2) Выше оси 0х точек нет, точки на оси 0х оставляем без изменения.
3) Часть графика, расположенную ниже оси 0x, отображаем симметрично относительно 0x.
4) Полученный график изображен на рисунке пунктиром (рис. 8) .
Пример 5. Построить график функции y = |(2|x| – 4) / (|x| + 3)|
1) Сначала необходимо построить график функции y = (2|x| – 4) / (|x| + 3). Для этого возвращаемся к алгоритму 2.
a) Аккуратно строим график функции y = (2x – 4) / (x + 3) (рис. 9) .
Заметим, что данная функция является дробно-линейной и ее график есть гипербола. Для построения кривой сначала необходимо найти асимптоты графика. Горизонтальная – y = 2/1 (отношение коэффициентов при x в числителе и знаменателе дроби), вертикальная – x = -3.
2) Ту часть графика, которая находится выше оси 0x или на ней, оставим без изменений.
3) Часть графика, расположенную ниже оси 0x, отобразим симметрично относительно 0x.
4) Окончательный график изображен на рисунке (рис. 11) .
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Разберем как строить график с модулем.
Найдем точки при переходе которых знак модулей меняется.
Каждое выражения, которое под модулем приравниваем к 0. У нас их два x-3 и x+3.
x-3=0 и x+3=0
x=3 и x=-3
У нас числовая прямая разделится на три интервала (-∞;-3)U(-3;3)U(3;+∞). На каждом интервале нужно определить знак под модульных выражений.
1. Это сделать очень просто, рассмотрим первый интервал (-∞;-3). Возьмем с этого отрезка любое значение, например, -4 и подставим в каждое под модульное уравнение вместо значения х.
Возьмем с этого отрезка любое значение, например, -4 и подставим в каждое под модульное уравнение вместо значения х.
х=-4
x-3=-4-3=-7 и x+3=-4+3=-1
У обоих выражений знаки отрицательный, значит перед знаком модуля в уравнении ставим минус, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (-∞;-3).
y=— (x-3)-(— (x+3))=-х+3+х+3=6
На интервале (-∞;-3) получился график линейной функции (прямой) у=6
2. Рассмотрим второй интервал (-3;3). Найдем как будет выглядеть уравнение графика на этом отрезке. Возьмем любое число от -3 до 3, например, 0. Подставим вместо значения х значение 0.
х=0
x-3=0-3=-3 и x+3=0+3=3
У первого выражения x-3 знак отрицательный получился, а у второго выражения x+3 положительный. Следовательно, перед выражением x-3 запишем знак минус, а перед вторым выражением знак плюс.
y=— (x-3)-(+ (x+3))=-х+3-х-3=-2x
На интервале (-3;3) получился график линейной функции (прямой) у=-2х
3.Рассмотрим третий интервал (3;+∞). Возьмем с этого отрезка любое значение, например 5, и подставим в каждое под модульное уравнение вместо значения х.
х=5
x-3=5-3=2 и x+3=5+3=8
У обоих выражений знаки получились положительными, значит перед знаком модуля в уравнении ставим плюс, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (3;+∞).
y=+ (x-3)-(+ (x+3))=х-3-х-3=-6
На интервале (3;+∞) получился график линейной функции (прямой) у=-6
4. Теперь подведем итог.Постоим график y=|x-3|-|x+3|.
На интервале (-∞;-3) строим график линейной функции (прямой) у=6.
На интервале (-3;3) строим график линейной функции (прямой) у=-2х.
Чтобы построить график у=-2х подберем несколько точек.
x=-3 y=-2*(-3)=6 получилась точка (-3;6)
x=0 y=-2*0=0 получилась точка (0;0)
x=3 y=-2*(3)=-6 получилась точка (3;-6)
На интервале (3;+∞) строим график линейной функции (прямой) у=-6.
5. Теперь проанализируем результат и ответим на вопрос задания найдем значение k, при которых прямая y=kx имеет с графиком y=|x-3|-|x+3| данной функции ровно одну общую точку.
Прямая y=kx при любом значении k всегда будет проходить через точку (0;0). Поэтому мы можем изменить только наклон данной прямой y=kx, а за наклон у нас отвечает коэффициент k.
Если k будет любое положительное число, то будет одно пересечение прямой y=kx с графиком y=|x-3|-|x+3|. Этот вариант нам подходит.
Если k будет принимать значение (-2;0), то пересечений прямой y=kx с графиком y=|x-3|-|x+3| будет три.Этот вариант нам не подходит.
Если k=-2, решений будет множество [-2;2], потому что прямая y=kx будет совпадать с графиком y=|x-3|-|x+3| на данном участке. Этот вариант нам не подходит.
Если k будет меньше -2, то прямая y=kx с графиком y=|x-3|-|x+3| будет иметь одно пересечение.Этот вариант нам подходит.
Если k=0, то пересечений прямой y=kx с графиком y=|x-3|-|x+3| также будет одно.Этот вариант нам подходит.
Ответ: при k принадлежащей интервалу (-∞;-2)U и возрастает на промежутке }
Построение графиков содержащих знак модуля построение графика функции содержащей переменную или функцию под знаком модуля согласно определению модуля
Построение графиков, содержащих знак модуля
Построение графика функции, содержащей переменную
или функцию под знаком модуля согласно определению модуля:
x, если х>=0 f(x), если f(x)>=0
|x| = ; |f(x) | =
-x, если x
Пример:
Построить график функции у=|2x-3|-х.
Рассмотрим два случая.
2х-3>=0 2х-3
y=2x-3-x или y=-2x+3-x
x>= xSUB>
y=x-3 y= -3x+3
Таким образом, чтобы построить график функции у=|2x-3|-x, надо построить графики функций, заданными различными выражениями на различных промежутках.
х-3, х>=
у=
— 3х+3, хSUB>
График изображен ниже:
y=|2x-3|-x
Построить график:
Y=|X|+X
Y=|X| · (X-2)
Y=|X+4| · X
Y=
Y=
Y=2–1)
Y=2+4X+3)
Y=
Y=
Y=X — 1 — |X-1|
Y=|3X-4|-X
Y=
13. Y=
Y=
Y=
Y=
Y=X2 — 2|X+1|-1
Y=X+
Y=|X2-4X+3|+2X
Y=
Y=|X2-4|+4X
Y=
Элементарные преобразования графика функции у=f(x)
Если формула зависимости имеют вид |y| = f(x):
Надо построить график у = f(x)
Часть графика, расположенную выше оси Ох (и на самой оси) оставить без изменения
Часть графика расположенную ниже оси Ох стереть
Для оставленной части построить симметричную относительно оси Ох
Пример:
Построить график |y| = 2х-1
Построить график:
Y|=5X-4
|Y|=9-X2
|Y|=
|Y|=(X+4)2-5
|Y|=
|Y|=X+2
|Y|=X2-6X+8
|Y|=X2-4X
X|Y|=2
|Y|=
|Y| · (X+1)=1
|Y|=1-
|Y|=|2X-X2|
Y2=-2X
|Y|=8+2X-X2
Y2=0,5X
Элементарные преобразования графика функции у=f(x)
Если формула зависимости у = f(|x|):
Надо построить график функции у = f(x), часть графика расположенную правее оси Оу(и на самой оси) оставить без изменения
Часть графика расположенную левее оси Оу стереть
Построить для оставленной части симметричную относительно оси Оу
Пример:
Построить график у=2|x|-1
Построить график:
Y=5|X|-5
Y=9-|X|2
Y=
Y=
Y=
Y=(|X|+4)2-5
Y=
Y=
Y=|X|-1
Y=
Y=X2-|X|-6
Y=-X2+6|X|-8
Постройте график.
 С его помощью укажите пути функции, интервалы знакопостоянства, промежутки монотонности, наибольшее и наименьшее значения функции, область значений функции:
С его помощью укажите пути функции, интервалы знакопостоянства, промежутки монотонности, наибольшее и наименьшее значения функции, область значений функции:
2-, если |X|
у= , если |X|>4
Y=X2-|X|-2
Решите уравнение X2+3|X|-18=0 графически.
Y=|X|-X2
Y=
Элементарные преобразования графика функции у=f(x)
Если формула зависимости имеет вид у = |f(x)|,
График функции у = f(x) выше оси Ох (и на самой оси Ох) оставить без изменения
Для части графика расположенной ниже оси Ох строят симметричную относительно
оси Ох
Часть графика расположенная ниже оси Ох стирается.
Пример:
Построить график функции у=|2x-1|
Построить график:
Y=|5X-4|
Y=|9 -X2|
Y=
Y=|(X-4)2-5)|
Y=|X+2|
Y=|X-1|
Y=|X2+2X|
Y=
Y=||
Y=||X2-3|-1|
Y=|X2-1|
Y=|X+1|-2
Y=4+|X-3|
Y=3 ∙ |X-2|
Найдите наибольшее и наименьшее значение функции Y=:
а)на отрезке [-2;2]
б)на луче [0;+ )
в)на луче (- ;3]
г)на отрезке [-5;0]
16.Найдите наименьшее и наибольшее значение функции Y=:
а)на луче (- ;5]
б)на отрезке [4;7]
в)на луче [2;+ )
г)на полуинтервале [-1;6]
17.Решите уравнение графически:
а)|X2-9|=5 б)|X-2|=X2 в)|X+1|= -2X2
г)|X2-1|=|X2-X+1| д)|X-3|=X2+1 е)|X+5|=-X-1
ё) -2(X+2)2 ж) з)(X+3)2
и)-X
Построение графиков уравнений, содержащих несколько модулей
Пример: построить график функции
1). Найти те значения переменной, при которых выражение, стоящее под знаком модуля, равно нулю. ; ; .
Найти те значения переменной, при которых выражение, стоящее под знаком модуля, равно нулю. ; ; .
2). Числовую прямую разбивают на промежутки точками, соответствующими найденным значениям переменной
0 1
3). На каждом промежутке определяют знак выражения, стоящего под знаком модуля (берут числа из промежутка и ставят в под модульное выражение). Определяют знак выражения стоящего под знаком модуля
− 0 − 1 +
− + +
4). Берут промежуток, раскрывают модуль (пользуясь определением модуля) на данном промежутке и упрощают
Составляют формулу кусочной функции
y
Строят график кусочной функции
1
x
0 1
1). Найдите промежутки убывания функции и ее наибольшее значение на отрезке . Ответ: , .
2). Найдите множество значений функции и ее наименьшее значение на отрезке . Ответ: , .
3). Найдите множество значений функции и значения, которые функция принимает ровно три раза. Ответ: ; ; .
4). Найдите все значения , при которых значения функции положительны и значения, принимаемые функцией ровно 2 раза. Ответ: ; , .
5). Постройте график функции и для каждого укажите количество общих точек этого графика и прямой .
а). . Ответ: Общих точек нет при ;
При , одна точка;
При и , две точки;
При , бесконечное множество точек.
б). . Ответ: Общих точек нет при ;
При , одна точка;
При и , две точки;
При ,, три точки;
При , четыре точки.
6). Найдите наибольшее и наименьшее значения функции на отрезке . Ответ: ; .
7). Найдите наименьшее значение функции
а). .Ответ: при .
б). .Ответ: при .
9). Докажите, что если , то наименьшее значение функции равно .
10). Исследуйте функцию на промежутки монотонности
а). . Ответ: На промежутках ; функция убывает. На промежутках возрастает.
б). . Ответ: На промежутках ; функция убывает. На промежутках и возрастает. На промежутках и функция постоянна.
11). Постройте графики функций
1). 2).
3). 4).
Решение неравенств, содержащих знак модуля
Неравенства вида
> , где > 0
Если выражение, стоящее под знаком модуля , обозначить через t (f(x) = t), то данное неравенство примет вид > . Используя геометрический смысл модуля (модуль на числовой прямой представляет собой расстояние от точки, которая изображает данное число, до точки ноль). Изображаем на числовой прямой все точки, расстояние от которых до ноля больше .
———∙——————∙—————∙————►t
—0
t или t >
Решаем совокупность неравенств
Пример:
Решите неравенство > 11
Решение: > 11
Пусть , >11
———∙——————∙—————∙————►t
-11 0 11
; ;
Ответ: ; ;
Неравенство вида > , гдеB>0 верно при всех из области допустимых значений неравенства.
Решите неравенства
1). > 11. Ответ:
2). . Ответ:
3). . Ответ: : .
4). . Ответ: . .
5). . Ответ: .
6). . Ответ: .
7). . Ответ: .
8). . Ответ: .
9). . Ответ: .
10). >2. Ответ: .
Неравенства вида
>
Учитывая свойство модуля =
и свойство неравенства: если обе части неравенства неотрицательны, то при возведении в квадрат получаем неравенство равносильное данному .
Неравенство > можно заменить равносильным неравенством > это — >0 (—) ∙ (+) >0
Далее решать методом интервалов или заменить совокупностью систем
Аналогично решаются неравенства вида .
Решите неравенства
1). . Ответ: .
2). Найти целочисленные решения неравенства .
Ответ: -8; -7; -6; … -1;0.
3). . Ответ: .
4). . Ответ: .
5). . Ответ: .
6). . Ответ: .
7). . Ответ: .
8). . Ответ: .
9). . Ответ: .
10). . Ответ: .
11). . Ответ: .
Ответ: .
12). . Ответ: .
13). . Ответ: .
14). . Ответ: .
15). . Ответ: .
16). . Ответ: .
17). . Ответ: .
18). . Ответ: .
19). . Ответ: .
20). . Ответ: .
21). . Ответ: .
22). . Ответ: .
23). . Ответ: .
Решение неравенств вида
;
Неравенство
Доказательство:
.
Неравенство
Доказательство:
.
.
Решите неравенства
1). . Ответ: .
2). . Ответ: .
3). . Ответ: .
4). . Ответ: .
5). . Ответ: .
6). . Ответ: или .
7). . Ответ: .
8). . Ответ: ; .
9). . Ответ: .
10). . Ответ: .
11). . Ответ: .
12). . Ответ: или .
13). . Ответ: ; .
14). . Ответ: или .
15). . Ответ: .
16). . Ответ: .
17). . Ответ: .
18). . Ответ: .
19). . Ответ: .
20). . Ответ: ; .
Решение неравенств, содержащих несколько модулей методом интервалов
Суть метода состоит в следующем:
Пример:
1). Находят те значения переменной при которых выражения, стоящие под знаком модуля равно нулю.
Находят те значения переменной при которых выражения, стоящие под знаком модуля равно нулю.
2). Числовую ось разбивают на промежутки точками, соответствующими значениям переменной
1
3). На каждом промежутке, определяют знак выражения, стоящего под знаком модуля (берут число из промежутка, ставят в подмодульное выражение, определяют знак выражения, стоящего под знаком модуля)
— 0 + 1 +
-1 — — +
4). Берут промежуток, раскрывают каждый модуль, пользуясь определением модуля на данном промежутке, и решают неравенство
5). Проверяют, принадлежат ли найденные решения неравенства рассматриваемому промежутку; если принадлежат, то их включают в ответ
0
2
Если нет – отбрасывают. Так поступают с каждым промежутком.
6). Объединяют все решения исходного неравенства, найденные на всех промежутках, и учитывая область допустимых значений первоначального неравенства, выписывают ответ.
Ответ: -2SUB>
Решите неравенство
1). Ответ:
2). Ответ:
3). Ответ:
4). Ответ:
5).Укажите целочисленные решения неравенства Ответ: 3;4
6). Ответ:
7). Ответ:
8). Ответ:
9). Ответ:
10). Ответ:
11). Ответ:
12). Ответ:
13). Ответ:
14). Ответ:
15). Ответ:
16). Ответ:
Решение неравенств, содержащих знак модуля, методом введения новой переменной.
1). Найти область значений переменной, входящей в неравенство.
2). Если в уравнении неоднократно встречается фиксированное выражение, зависящее от неизвестной величины, то имеет смысл обозначить это выражение, какой либо буквой. Когда вводится обозначение желательно сразу отбросить все или некоторые значения при которых уравнение = не имеет решений , т.е. полезно сразу указать область значений функции = .
3). Решить неравенство относительно введенной неизвестной.
4). Решить неравенство относительно исходной переменной.
5). Учитывая область допустимых значений исходного неравенства записать ответ.
Пример:
Учитывая свойство модулей имеем Пусть = , , тогда неравенство примет вид =1; =-3. f
Учитывая, что имеем
Учитывая область допустимых значений исходного неравенства Ответ:
Решите неравенства
1). Ответ:
2). Ответ:
3). Ответ:
4). Ответ:
5). Ответ:
6). Ответ:
7). Ответ:
8). Ответ:
9). Ответ:
10). Ответ:
Изображение на координатной плоскости множества точек, координаты которых удовлетворяют данному неравенству
Чтобы на координатной плоскости изобразить множество точек, координаты которых удовлетворяют неравенству надо:
1). Построить множество точек, координаты которых удовлетворяют уравнению (если неравенство строгое, то линия изображается пунктирной, если не строгое, то сплошной).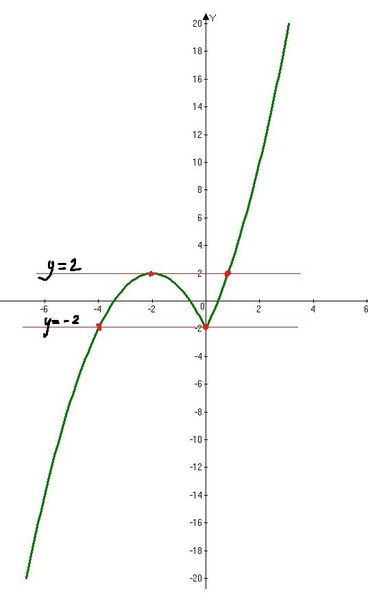
2). График или графики уравнений разбивают координатную плоскость на части.
3). Взять координаты точки, принадлежащей каждой части по очереди и поставить в неравенство. Если координаты точки удовлетворяют неравенству, то эту часть координатной плоскости заштриховать.
Пример: Изобразить на координатной плоскости множество точек, координаты которых удовлетворяют неравенству .
1). Построим график уравнения .
или
III II I
-1 0 1
Прямые и изображаем сплошными линиями, так как неравенство не строгое. Прямые разбивают координатную плоскость на три области. Неравенству удовлетворяют координаты точек, принадлежащих II части, поэтому заштриховываем II часть.
Изобразите на координатной плоскости множество точек, координаты которых удовлетворяют неравенству.
1). .
2). .
3). .
4). .
5). .
6). .
7). .
8). .
9). .
10). .
11). .
12). .
13). .
14). .
15). .
16). .
17). .
18). .
19).
20). .
21). .
22). .
23. .
24). .
Изобразите на координатной плоскости множество точек, удовлетворяющих условию
а) . б).
в) г)
д) е) .
Системы неравенств с параметрами, содержащие знак модуля
1). Найдите все значения параметра , при которых система неравенств имеет единственное решение.
а). Ответ: При .
б). Ответ: При .
2). При каких значениях параметра система неравенств имеет ровно одно решение?. Для всех таких найдите это решение.
а). Ответ: При , ;
При , .
б). Ответ: При , ;
При , .
3). При каких значениях параметра система не имеет решения.
а). Ответ: При .
б). Ответ: При .
4). Для каждого значения параметра решите систему неравенств.
а). Ответ: При , ;
При , ;
При , ;
При , .
б). Ответ: При и , ;
При , ;
При , ;
При , ;
При , .
Нестандартные уравнения и неравенства, содержащие знак модуля
К нестандартным ,обычно относятся такие уравнения и неравенства, где традиционные алгоритмы решения не проходят. Во многих случаях, решение таких уравнений и неравенств осуществляется на функциональном уровне, т.е с помощью графиков, или за счет сопоставления некоторых свойств функций, содержащихся в левой и правой частях уравнения или неравенства.
Если, например, наименьшее значение одной из функций совпадает с наибольшим значением функции , то уравнение = заменяют равносильной системой , где — наименьшее значение или наибольшее значение .
Решение системы является решением уравнения = .
1). Решите уравнение
Уравнение необходимо решить графически. Ответ:
2). Решите неравенство
. Применить метод оценки. Ответ:
3). Решите уравнение
Решите уравнение
. Решить уравнение графически. Ответ:
4). Решите уравнение
. Применить свойство: сумма неотрицательных функций равна нулю тогда и только тогда, когда все функции одновременно равны нулю. Ответ:
5). Решите уравнение
.Область допустимых значений (ОДЗ) уравнения состоит из конечного числа значений. Для решения достаточно проверить все эти значения. Ответ:
Применение свойства = для любого
при нахождении значения выражения
Вычислите:
1). Ответ: -6
2). , если t = -10; t = 127. Ответ: -8; 127
3). ∙ . Ответ: 0,125
4). −. Ответ: -6
5). − . Ответ: 2
6). − . Ответ: 8
7). + . Ответ: 2
8). + . Ответ: 6
9). + . Ответ: 2
10). + . Ответ: 10
11). − . Ответ: -3
12). − . Ответ: -6
13). − − 0,5. Ответ: 0
14). + . Ответ:1
15). + Ответ: 1
16). . Ответ: 8
17). Найти и , если = — . Ответ: 28; -2
18). Найти и , если = — . Ответ: 40; -2
19). Сравните значение выражения
с числом . Ответ:
20). Сравните значение выражения
с числом . Ответ:
Ответ:
21). Докажите, что выражение ∙ является корнем уравнения = 1.
22). Докажите, что выражение является корнем уравнения = 1.
23). Удовлетворяет ли число − неравенству 7+58+13>0 .
Ответ: нет
24). Удовлетворяет ли число − неравенству 11+26-730 .
Ответ: да
Л и т е р а т у р а
1). Алгебра: 8; 9; 10 – 11 класс.
Авторы: А.Г.Мордкович, Т.Н. Мишустина, Е.Е. Тульчинская.
2). Задания по математике для подготовки к письменному экзамену в 9 классе.
Авторы: Л.И. Звавич, Д.И.Аверьянов, Б.П. Пигарёв, Т.Н. Грушанина.
3). Сборник задач по алгебре 8 – 9 класс.
Авторы: М.Л. Галицкий,А.М. Гольдман, Л.И. Звавич.
4). Сборник для проведения письменного экзамена за курс средней школы 11 класс.
Авторы: Г.В. Дорофеев, Г.К.Муравин, Е.А.Седова.
5). Алгебраический тренажер.
Авторы: А.Г. Мерзляк,В.Б.Полонский, М.С.Якир
6). Материалы ЦТ и ЭГЭ за 2002 – 2005 годы.
7). Математика. Самостоятельные и контрольные работы 8; 9; 10 – 11 классы.
Авторы: А.П. Ершова, В.В. Голобородько.
8). Различные сборники для поступающих в В У З Ы.
График квадратичной функции | Формулы с примерами
Графики квадратичной функции 9 класс
ПравилоЛюбую квадратичную функцию можно представить в виде , где
Примеры, свойства, правила
Правила1) y = 2x2 — 4x + 3.
I способ — выделение полного квадрата:
y = 2x2 — 4x + 3 = 2(x2 — 2x) + 3 =
= 2(x2 — 2 • x • 1 + 12) — 2 • 12 + 3 = 2(x — 1)2 + 1;
II способ — по формулам:
x0 = -4 2 • 2 = 1, y0 = y(1) = 2 • 12 — 4 • 1 + 3 = 1, значит y = 2(x — 1)2 + 1.
2) y = 2 — 3x2 + x = 2 — 3(x2 — 13x) =
= 2 — 3(x2 — 2 • 16 • x + (16)2 + 3 • (16)2) = -3 (x — 16)2 + 2 1 12.
График квадратичной функции, рисунок
ПравилоГрафик функции — y = a(x — x0)2 + y0 — парабола, которую можно получить из параболы y = ax2 с помощью двух параллельных переносов (сдвигов:
1) вдоль оси OX на X0 вправо, если x0 > 0,
или на |x0| влево, если x0
2) вдоль оси OY на y0 вверх, если y0 > 0,
или на |y0| вниз, если y0
Порядок выполнения сдвигов — любой.
ПравилоВершина параболы y = a(x — x0)2 + y0— точка O1(x0,y0).
Ось симметрии — прямая x = x0.
Область значений — интервал [y0, +?), если a > 0, или (-?, y0], если a
Пример 11) y = 2x2 — 4x + 3 y = 2(x -1)2 + 1 Пример 2
2) y = 1 — 12x2 — 2x y = -(x + 2)2 + 3
Формулы по алфавиту:
© 2021 Все права защищеныПри использовании материалов данного сайта обязательно указывать ссылку на источник
Пошаговое руководство построение графика квадратичной функции
Для того, чтобы начертить график функции в Прямоугольной системе координат, нам необходимы две перпендикулярные прямые xOy (где O это точка пресечения x и y), которые называются «координатными осями», и нужна единица измерения. 2-\frac{\Delta}{4a}$
2-\frac{\Delta}{4a}$
где Δ = b2 — 4ac
Если a > 0, то минимальным значением f(x) будет $-\frac{\Delta}{4a}$ , которое получается, если $x=-\frac{b}{2a}$. Графиком будет выпуклая парабола, вершина которой (точка, в которой она меняет направление) это $V(-\frac{b}{2a};-\frac{\Delta}{4a})$.
Если a < 0, то минимальное значение f(x) будет $-\frac{\Delta}{4a}$ , которое получается, если $x=-\frac{b}{2a}$. Графиком будет вогнутая парабола, вершина которой это$V(-\frac{b}{2a};-\frac{\Delta}{4a})$.
Парабола симметрична относительно прямой, которую она пересекает $x=-\frac{b}{2a}$ и которая называется «осью симметрии».
Именно поэтому, когда мы присваиваем знаячения x, то вибираем их симметричными относительно $-\frac{b}{2a}$.
При построении графика, точки пересечения с осями координат очень важны.
|. Точка, расположенная на оси Ox имеет форму P(x, 0), потому что расстояние от неё до Ox равно 0. Если точка находиться и на Ox и на графике функции,то она также имеет вид P(x, f(x)) ⇒ f(x) = 0.
Таким образом, для того чтобы найти координаты точки пересечения с осью Ox, мы должны решить уравнение f(x)=0. Мы получаем уравнение a2 + bx + c = 0.
Решение уравнения зависит от знака Δ = b2 — 4ac.
Иммем следующие варианты:
1) Δ < 0,
тогда у уравнения нет решений в R (множестве действительных чисел) и график не пересекает Ox. Форма графика будет:
или
2) Δ = 0,
тогда у уравнения два решения $x_1=x_2=-\frac{b}{2a}$
График касается оси Ox в вершине параболы. Форма графика будет:
или
3) Δ > 0,
тогда у уравнения два разных решения.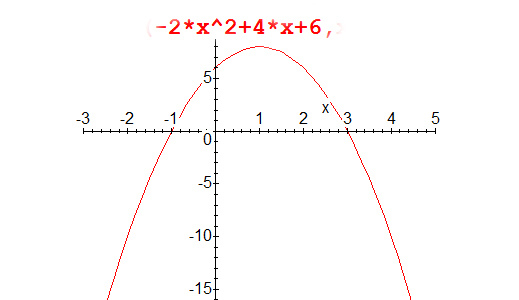
$x_1=\frac{-b-\sqrt{\Delta}}{2a}$ и $x_2=\frac{-b+\sqrt{\Delta}}{2a}$
График функции будет пересекать ось Ox в точках M(x1 и Ox. Форма графика будет:
или
||. Точка, находящаяся на оси Oy имеет форму R(0, y), потому что расстояние от Oy равно 0. Если точка находиться и на Oy и на графике функции, то она также имеет форму R(x, f(x)) ⇒ x = 0 ⇒ R(0, f(0)).
В случае квадратичной функции,
f(0) = a×02 + b×0 + c ⇒ R(0, c).
Необходимые шаги для построения графика квадратичной функции
f: R → R
f(x) = ax2 + bx + c
1. Составляем таблицу переменных, куда заносим некоторые важные значения x.
2. Вычисляем координаты вершины$V(-\frac{b}{2a};-\frac{\Delta}{4a})$.
3. Также записываем 0 в таблицу и нулевые значения симметричные $-\frac{b}{2a}$.
или
4. Мы определяем точку пересечения с осью Ox,решая уравнение f(x)=0 и записываем корни x1 и x2 в таблице.
Δ > 0 ⇒
Δ < 0 ⇒ точек пересечения нет. В этом случае мы выберем два удобных значения, которые симметричны $-\frac{b}{2a}$
Δ = 0 ⇒ график касается Ox прямо в вершине параболы. Мы снова выберем два удобных значения, симметричных $-\frac{b}{2a}$. Для лучшего определения формы графика мы может выбрать другие пары значений для x, но они должны быть симметричны $-\frac{b}{2a}$.
5. Мы наносим эти значения на систему координат и строим график, соединяя эти точки.
Пример 1
f: R → R
f(x) = x2 — 2x — 3
a = 1, b = -2, c = -3
Δ = b2 — 4×a×c = (-2)2 — 4×1×(-3) = 16
$-\frac{b}{2a}=\frac{2}{2}=1$
⇒ V(1; -4)
1. $-\frac{\Delta}{4a}=-\frac{16}{4}=-4$
2. f(0) = -3
Симметричное 0 значение относительно 1 равно 2.
f(2) = -3
Δ = 16 > 0
$x_1=\frac{-b-\sqrt{\Delta}}{2a}=\frac{2-4}{2}=-1$
$x_1=\frac{2+4}{2}=3$
Мы нашли точки:
A(-1; 0)
B(0; -3)
V(1; -4)
C(2; -3)
D(3; 0)
График будет иметь вид:
Пример 2
f: R → R
f(x) = -x2 — 2x + 8
a = -1, b = -2, c = 8
Δ = b2 — 4×a×c = (-2)2 — 4×(-1)×8 = 36
$-\frac{b}{2a}=\frac{2}{-2}=-1$
⇒ V(-1; 9)
1. $-\frac{\Delta}{4a}=-\frac{-36}{-4}=9$
2. f(0) = 8
f(-2) = 8 (симметричное 0 значение относительно -1 равно -2)
3. f(x) = 0 ⇒ -x2 — 2x + 8 = 0
Δ = 36
x1 = 2 и x2 = -4
A(-4; 0)
B(-2; 8)
V(-1; 9)
C(0; 8)
D(2; 0)
Пример 3
f: R → R
f(x) = x2 — 4x + 4
a = 1, b = -4, c = 4
Δ = b2 — 4×a×c = (-4)2 — 4×1×4 = 0
$-\frac{b}{2a}=\frac{4}{2}=2$
⇒ V(2; 0)
1. $-\frac{\Delta}{4a}=0$
2. f(0) = 4
f(4) = 4 (симметричное 0 значение относительно 2 равно 4)
3. f(x) = 0 ⇒ x2 — 4x + 4 = 0
Δ = 0
x1 = x2 = $-\frac{b}{2a}$ = 2
A(-2; 9)
B(0; 4)
V(2; 0)
C(4; 4)
D(5; 9)
Пример 4
f: R → R
f(x) = -x2 + 4x — 5
a = -1, b = 4, c = -5
Δ = b2 — 4×a×c = 42 — 4×(-1)×(-5) = 16 — 20 = -4
$-\frac{b}{2a}=\frac{-4}{-2}=2$
⇒ V(2; -1)
1. $-\frac{\Delta}{4a}=-\frac{-4}{-4}=-1$
2. f(0) = -5
f(4) = -5 (симметричное 0 значение относительно 2 равно 4)
3. f(x) = 0 ⇒ -x2 + 4x — 5 = 0,
Δ < 0
У этого уравнения нет решений.
Мы выбрали симметричные значения вокруг 2
A(-1; -10)
B(0; 5)
V(2; -1)
C(4; -5)
D(5; -10)
Если область определения не R (множество действительных чисел), а какой-то интервал, то мы стираем часть графика, которая соответствует тем значениям x, которые не находятся в данном интервале. Необходимо записать конечные точки интервала в таблице.
Необходимо записать конечные точки интервала в таблице.
Пример 5
f: [0; +∞) → R
f(x) = x2 — 2x — 3
a = 1, b = -2, c = -3
Δ = b2 — 4×a×c = (-2)2 — 4×1×(-3) = 16
$-\frac{b}{2a}=1$
⇒ V(1; -4)
1. $-\frac{\Delta}{4a}=-4$
2. f(0) = -3
f(2) = -3 симметричное 0 значение относительно 1 равно 2)
3. f(x) = 0 ⇒ x2 — 2x — 3 = 0,
Δ = 16
x1 = -1 ∉ [0; ∞)
x2 = 3
A(0; -3)
V(1; -4)
B(2; -3)
C(3; 0)
Графические квадратичные функции: больше примеров
Графики Квадратичные функции: примеры (стр. 4 из 4)
Разделы: Введение, Значение старшего коэффициента / Вершина, Примеры
- Найдите перехваты x и вершина y = x 2 4 x + 2.
Так как это так просто найти перехват и (и в любом случае это будет точка на моей Т-диаграмме), они всего лишь просят перехватить x этот раз. Чтобы найти перехват x , Ставил у равно 0 и решаем:
0 = x 2 4 х + 2
х 2 + 4 x 2 = 0
Для построения графиков
точки перехвата находятся примерно на (4.4,
0) и (0,4,
0). (Когда я пишу
ниже, я, конечно, буду использовать «точную» форму с
квадратные корни; десятичные приближения моего калькулятора предназначены только для
Помогая мне график.)
Чтобы найти вершину, я
посмотрите на коэффициенты: a = 1 и b = 4. Тогда:
Тогда:
Найти k , Подключаю х = 2 дюйма для x через у = х 2 4 x + 2, и упростить:
Сейчас найду дополнительные точек на графике, которые помогут мне заполнить график:
Обратите внимание, что я выбрал значения x . которые были сосредоточены вокруг координаты x вершины.Теперь построю параболу:
Вершина в (2, 6), и перехваты на следующие точки:
(0, 2),, и
- Найдите перехваты x и вершина y = x 2 + 2 x 4.
Чтобы найти вершину, я посмотрите на коэффициенты: a = 1 и b = 2. Тогда:
Найти k , Подключу ч дюйм для x и упростить:
Вершина находится ниже x — ось, и, поскольку это отрицательная квадратичная величина, я знаю, что парабола равна будет перевернутым.Так может ли моя линия пересечь ось x ? Могут ли быть какие-нибудь перехваты x ? Конечно, нет! Поэтому я ожидаю получить «нет (реального) решения», когда Я пытаюсь найти перехваты x , но мне все равно нужно показать свою работу. Чтобы найти перехват x , Ставил у равно 0 и решаем:
0 = x 2 + 2 х 4
х 2 2 х + 4 = 0
Как только я получаю отрицательный
внутри квадратного корня, я знаю, что не могу получить наглядное решение. Итак, как и ожидалось, перехватов x нет.
Теперь я найду несколько дополнительных точек, чтобы заполнить свой график:
Итак, как и ожидалось, перехватов x нет.
Теперь я найду несколько дополнительных точек, чтобы заполнить свой график:
Обратите внимание, что я выбрал значения x . которые были сосредоточены вокруг координаты x вершины. Теперь построю параболу: авторское право Элизабет Стапель 2002-2011 Все права защищены
Вершина в (1, 3), и единственный перехват находится в (0, 4).
Это последнее упражнение иллюстрирует таким образом вы можете немного сократить свою работу. Если вы решите для вершины сначала вы можете легко определить, нужно ли вам продолжить и искать x -перехват, или если вы можете сразу перейти к нанесению некоторых точек и построению графика. Если вершина ниже оси x (то есть, если y -значение отрицательна), а квадратичная отрицательна (поэтому парабола открывается вниз), тогда не будет х -перехватов.Аналогично, если вершина находится выше оси x (то есть, если y -значение положительна), а квадратичная положительна (парабола открывается вверх), тогда не будет х -перехватов.
На большинстве графиков
Я сделал (правда, не первый), так уж получилось, что баллы
на Т-диаграмме были симметричны относительно вершины; то есть, что точки
«совпадают» по обе стороны от вершины.Пока парабола
всегда симметрично относительно вертикальной линии, проходящей через вершину (параболы
«ось»), точки Т-диаграммы могут быть несимметричными. В частности,
точки Т-диаграммы не будут «совпадать», если координата x вершины не является целым числом или половинным числом
(например, «3,5»).
Предупреждение: не ожидайте, что сюжетные точки всегда будут «совпадать» на
обе стороны от вершины; в частности, не делайте половину баллов на
ваш T-график, а затем «заполните» остальную часть вашего T-графика,
предполагая симметрию, которая может не существовать.
Другие советы по построению графиков: Если парабола будет «тощей», то ожидайте, что вы получат очень большие значения на вашем Т-графике. Вы либо закончите с действительно высоким графиком или довольно коротким T-графиком. Если парабола будет «толстым», тогда ожидайте, что у вас, вероятно, будет для построения точек с дробями в качестве координат. В любом случае, когда вы иди, чтобы соединить точки, чтобы нарисовать параболу, это может оказаться полезным повернуть бумагу на бок и сначала прорисовать действительно изогнутую часть вершину, убедившись, что она выглядит красивой и круглой.Затем переверните бумагу спиной правой стороной вверх и нарисуйте «стороны» параболы.
Предупреждение: нарисуйте свои графики достаточно большой, чтобы его хорошо видел ваш инструктор. Если вы подходите больше чем два или, может быть, три графика на одной стороне стандартного листа бумаги, тогда вы рисуете свои графики слишком маленькими.
<< Предыдущая Вверх | 1 | 2 | 3 | 4 | Вернуться к индексу

 С его помощью укажите пути функции, интервалы знакопостоянства, промежутки монотонности, наибольшее и наименьшее значения функции, область значений функции:
С его помощью укажите пути функции, интервалы знакопостоянства, промежутки монотонности, наибольшее и наименьшее значения функции, область значений функции: 2-4x-6 = 0 Tiger Algebra Solver
2-4x-6 = 0 Tiger Algebra Solver По этой причине мы хотим иметь возможность найти координаты вершины.
По этой причине мы хотим иметь возможность найти координаты вершины.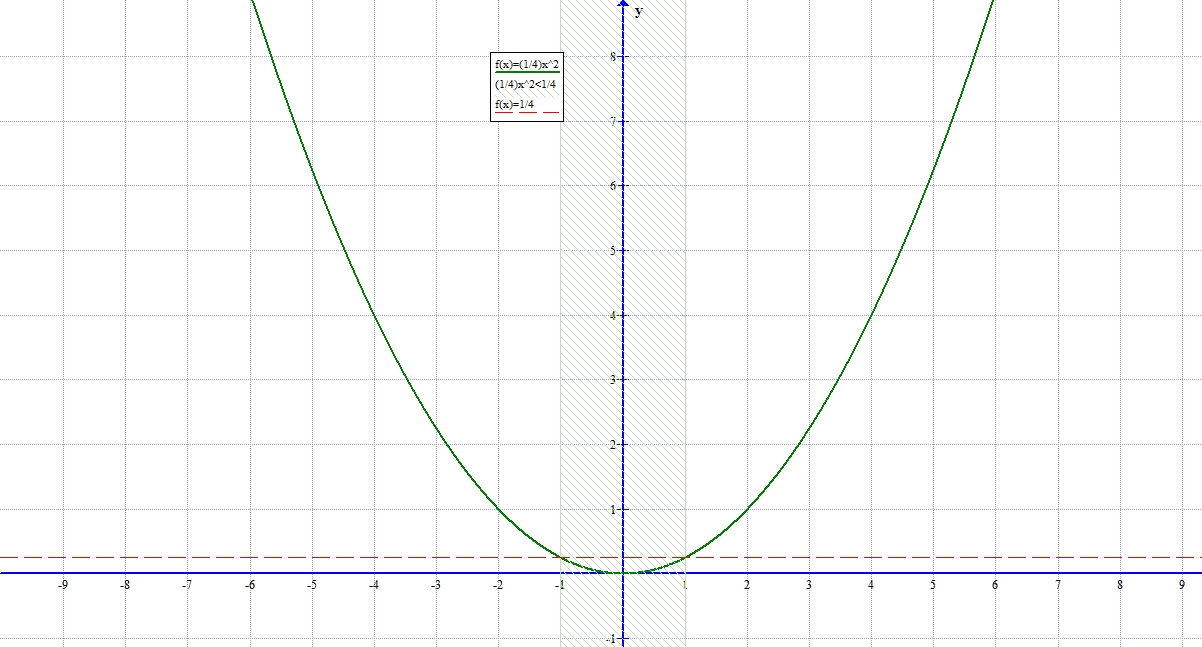 # 2.2.1 получаем:
# 2.2.1 получаем: 


 {2} + bx + c [/ латекс]
{2} + bx + c [/ латекс]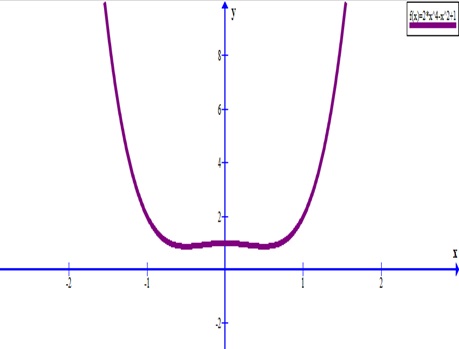 {2} + k [/ latex] с положительным [латексом] a [/ latex] значение равно [latex] f \ left (x \ right) \ ge k [/ latex]; диапазон квадратичной функции, записанной в стандартной форме с отрицательным значением [latex] a [/ latex], равен [latex] f \ left (x \ right) \ le k [/ latex].
{2} + k [/ latex] с положительным [латексом] a [/ latex] значение равно [latex] f \ left (x \ right) \ ge k [/ latex]; диапазон квадратичной функции, записанной в стандартной форме с отрицательным значением [latex] a [/ latex], равен [latex] f \ left (x \ right) \ le k [/ latex]. Церемония проходит в храме Геры в Олимпии, Греция, и уходит своими корнями в греческую мифологию, отдавая дань уважения Прометею, который украл огонь у Зевса, чтобы раздать его всем людям. Одна из одиннадцати действующих жриц помещает факел в фокус параболического зеркала (рис. \ (\ PageIndex {1} \)), которое фокусирует световые лучи от солнца, чтобы зажечь пламя.
Церемония проходит в храме Геры в Олимпии, Греция, и уходит своими корнями в греческую мифологию, отдавая дань уважения Прометею, который украл огонь у Зевса, чтобы раздать его всем людям. Одна из одиннадцати действующих жриц помещает факел в фокус параболического зеркала (рис. \ (\ PageIndex {1} \)), которое фокусирует световые лучи от солнца, чтобы зажечь пламя.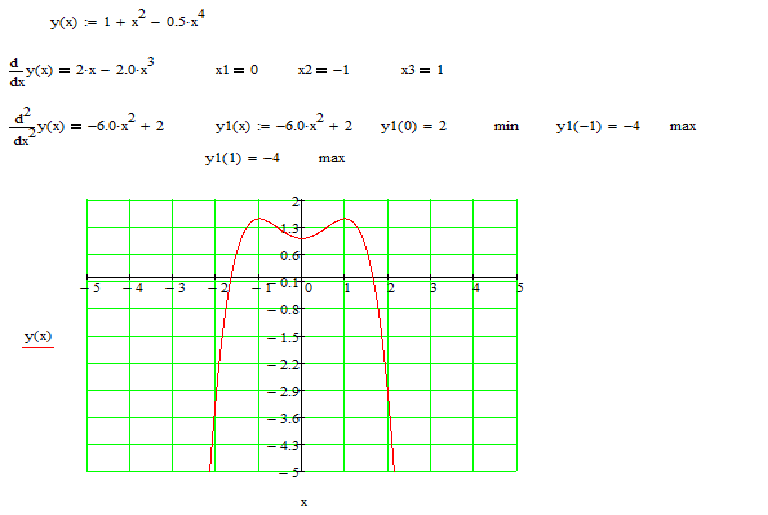 2 = 4py \)
2 = 4py \) 2 = 4 пикс \). Таким образом, осью симметрии является ось x . Отсюда следует, что:
2 = 4 пикс \). Таким образом, осью симметрии является ось x . Отсюда следует, что: 2 = 4p (y − k) \), то:
2 = 4p (y − k) \), то: 2−8x − 28y − 208 = 0 \).2 & = 4⋅7⋅ (y + 8) \ end {align *} \]
2−8x − 28y − 208 = 0 \).2 & = 4⋅7⋅ (y + 8) \ end {align *} \]
Leave A Comment