Функция y = ∛x, её свойства и график 9 класс онлайн-подготовка на Ростелеком Лицей
Определение кубического корня, его запись и назначение
Практическая задача
Необходимо сконструировать кубический резервуар, объем которого равен (). Как отмерить величину ребра?
Решение:
Предположим, что ребро куба имеет длину (м). В этом случае объем будет равен (). Получается, что необходимо подобрать такое число , куб которого равен ().
Например: если объем равен , то длина ребра будет равна 2 м ().
На основании этого примера можно сделать вывод, что необходимо уметь находить число, если известен его куб.
На данном этапе эту задачу можно сравнить с квадратным корнем. И нахождение искомого числа будет происходить по аналогии.
Определение:
Число называется кубическим корнем или корнем третьей степени числа , если выполняется соотношение . Это можно записать как, в этом случае – подкоренное выражение, 3 – показатель корня.
Это можно записать как, в этом случае – подкоренное выражение, 3 – показатель корня.
Таким образом, выражения эквивалентны, то есть выражают одну и ту же зависимость между действительными числами и .
Например:
Кубический корень из существует для любого действительного числа .
Как и в случае квадратного корня, при извлечении кубического корня из рационального числа часто будет появляться иррациональный результат.
Доказательство иррациональности
Построим доказательство методом от противного. Предположим, что – рациональное число, то есть его можно представить в виде , где чисто целое, – натуральное. Причем – это несократимая обыкновенная дробь. Тогда по определению: , откуда следует, что . Последнее равенство означает, что пятерка является делителем числа , то есть натуральное число делится на пять без остатка. Однако это возможно тогда и только тогда, когда пятерка является делителем самого числа , то есть , где – некоторое натуральное число.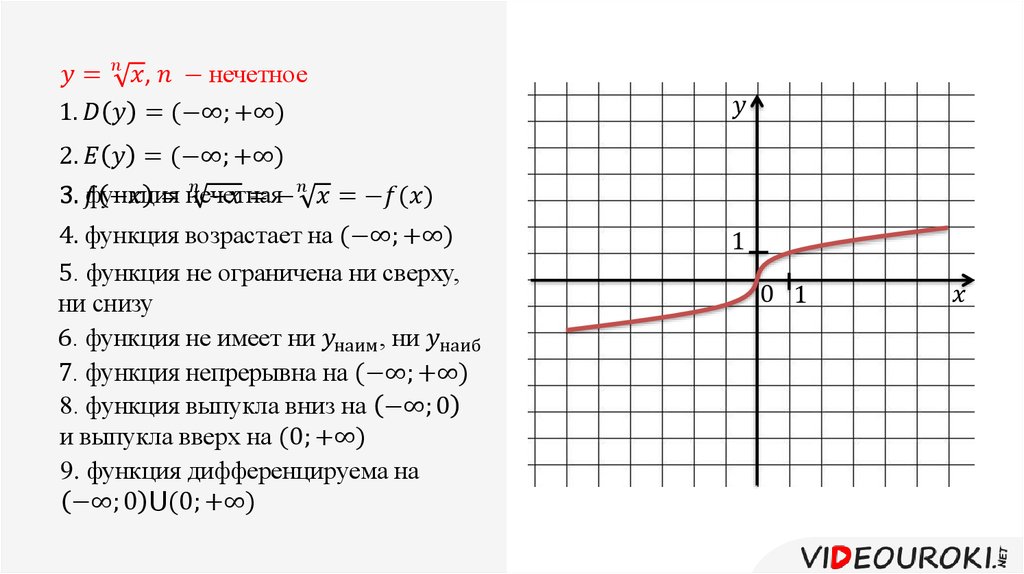
Подставим значение из последнего равенства в начальное:
Последнее равенство означает, что двадцать пять является делителем числа и тем более, что делится на пять, тогда и число делится без остатка на пять.
Таким образом, мы получили, что и делятся на пять, а это значит, что – сократимая дробь, так как и числитель и знаменатель можно сократить на пять, но это противоречит нашему предположению. Значит, – иррациональное число.
Результат возведения в куб отрицательного числа будет числом отрицательным, следовательно, и корень кубический из отрицательного числа будет отрицательным числом.
Доказать:
Доказательство:
Пусть , , тогда, по определению кубического корня, , . Отсюда следует, что или . Из последнего равенства следует, что , а значит, справедливо исходное тождество .
Задача о проектировании кубического резервуара
Необходимо автоматизировать процесс сварки. На вход поступает число – объем куба – автомат должен сам посчитать длину ребра.
На вход поступает число – объем куба – автомат должен сам посчитать длину ребра.
Как научить автомат извлекать корень кубический из любого действительного числа? Для этого введем понятие функции, область определения которой – все действительные числа.
Свойства функции
Рассмотрим функцию , выясним ее свойства и постоим график.
1. Область определения функции – множество действительных чисел ().
2. Данная функция является нечетной.
3. Функция возрастает на луче от нуля до плюс бесконечности ( при ).
Доказательство
Возьмем два значения аргумента, расположенные следующим образом: . Необходимо доказать: .
Построим доказательство методом от противного. Предположим, что , тогда, по свойству числовых неравенств, при возведении левую и правую часть в куб знак неравенства сохраняется . Таким образом, , что противоречит условию задачи. Исходя из этого, можно сделать вывод, что наше предположение неверно и .
В силу нечетности функции, свойство можно обобщить на всю область определения ( при ).
4. Функция не ограничена сверху на луче от нуля до плюс бесконечности ()
Доказательство
Дано: .
Доказать: .
Построим доказательство методом от противного. Предположим, что существует такое положительное число , что для любого выполняется неравенство . Возьмем на луче от нуля до плюс бесконечности некую точку . Тогда значение функции в этой точке будет равно , а это больше . Значит, мы нашли точку, такую, что что противоречит нашему предположению.
Функция монотонно возрастает на всей области определения и не ограничена ни сверху, ни снизу.
Не ограничена сверху при , не ограничена снизу при .
Доказывается это аналогично приведенным доказательствам для положительной полуоси .
5. Функция ограничена снизу ()
Построим график функции на луче от нуля до плюс бесконечности (). Для этого сперва составим таблицу значений:
|
X |
0 |
1 |
8 |
|
|
Y |
0 |
1 |
2 |
Построим четыре точки на координатной плоскости, координаты которых возьмем из таблицы.
Рис. 1. Построение графика функции по точкам
С помощью этого графика и уже установленных свойств функции легко определить оставшиеся свойства функции.
6. Функция непрерывна на всей числовой прямой.
7. Область значений функции – это все действительные числа ().
8. Функция выпукла вниз на луче и выпукла вверх на луче .
Решение задач по теме
Задача
Имеется помещение кубической формы, в которое необходимо подобрать подходящий обогреватель. Теплоизоляция стен имеет фиксированную теплопроводность для всех возможных размеров помещений.
Решение
Пусть длина, ширина и высота равны , так как в кубе все эти величины равны.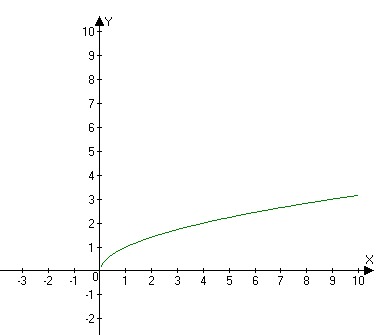 Количество теплоты, потребляемое помещением в единице времени от обогревателя, пропорционально объему помещения, то есть равно , где – некоторый коэффициент пропорциональности. Количество теплоты, отдаваемое сквозь стены в окружающее пространство, пропорционально площади стен, то есть равно , где – некоторый коэффициент пропорциональности. Конкретный смысл и значение этих коэффициентов нас интересовать не будут. Обозначим как отношение потребляемого и отдаваемого количества теплоты: . Поскольку , где – объем помещения, то имеем: . Без вреда для понимания решения задачи мы можем принять . Тогда мы имеем в точности нашу изучаемую функцию. Таким образом, мощность нагревателя зависит от объема помещения как корень кубический из этого объема. Это может быть полезно при проектировании систем обогрева.
Количество теплоты, потребляемое помещением в единице времени от обогревателя, пропорционально объему помещения, то есть равно , где – некоторый коэффициент пропорциональности. Количество теплоты, отдаваемое сквозь стены в окружающее пространство, пропорционально площади стен, то есть равно , где – некоторый коэффициент пропорциональности. Конкретный смысл и значение этих коэффициентов нас интересовать не будут. Обозначим как отношение потребляемого и отдаваемого количества теплоты: . Поскольку , где – объем помещения, то имеем: . Без вреда для понимания решения задачи мы можем принять . Тогда мы имеем в точности нашу изучаемую функцию. Таким образом, мощность нагревателя зависит от объема помещения как корень кубический из этого объема. Это может быть полезно при проектировании систем обогрева.
Задача
Решить уравнение .
Воспользуемся графическим способом решения: построим графики функций и (рис. 2).
Рис. 2. Графическое решение уравнения
Найдем точки пересечения двух графиков.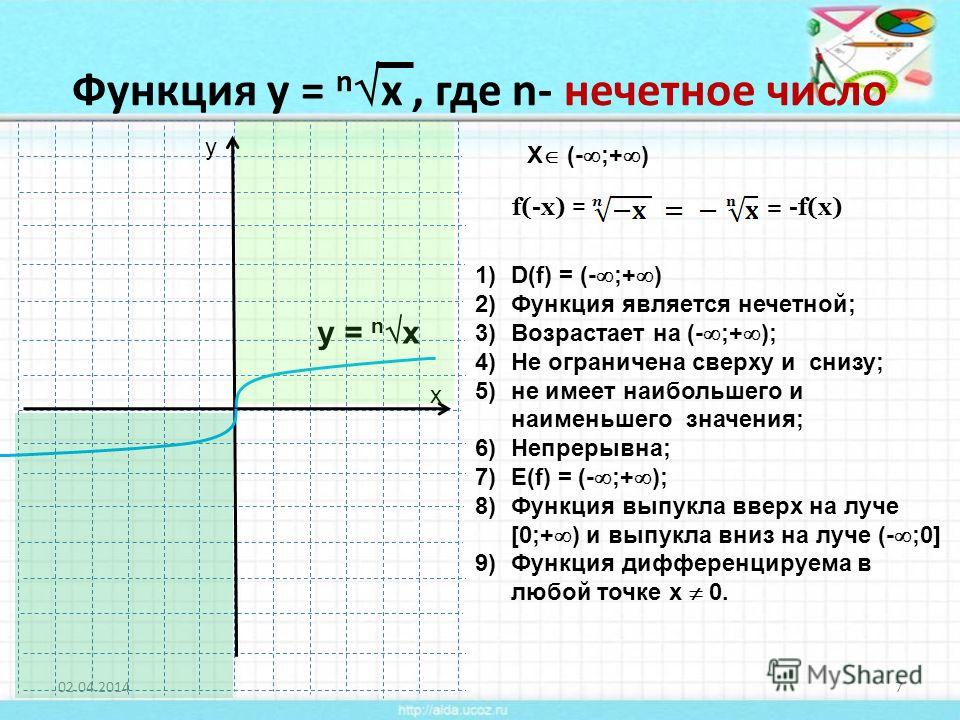 Как видно из рисунка, графики пересекаются лишь в одной точке с координатами .
Как видно из рисунка, графики пересекаются лишь в одной точке с координатами .
Ответ: исходное уравнение имеет один корень .
Задача
Построить график функции .
Решение
Для того чтобы решить данную задачу, вспомним тему «Преобразование графиков функций».
Рис. 3. Построение графика функции .
Вначале построим график функции , затем сместим этот график параллельным переносом влево на единицу (), затем сместим параллельным переносом график вниз на две единицы (). Таким образом, мы получили график требуемой функции (рис. 3).
Выводы
На данном уроке мы ознакомились с понятием кубического корня из действительного числа и изучили соответствующую функцию.
Список литературы
- Башмаков М.И. Алгебра 8 класс. – М.: Просвещение, 2004.
- Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – изд. 5. – М.: Просвещение, 2010.
- Никольский С.
 М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2006.
М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2006.
Домашнее задание
- Что такое кубический корень?
- Чем отличается четная функция от нечетной?
- Доказать, что функция не ограничена сверху при .
- На одном рисунке построить графики двух функций и . Сделать выводы.
- Решить уравнение .
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал Yaklass.ru (Источник).
- Интернет-портал Mathematics-tests.com (Источник).
- Интернет-портал School.xvatit.com (Источник).
3-8
Функция извлечения квадратного корня — график, домен, диапазон, примеры
Функция извлечения квадратного корня включает символ квадратного корня √ (который читается как «квадратный корень из»).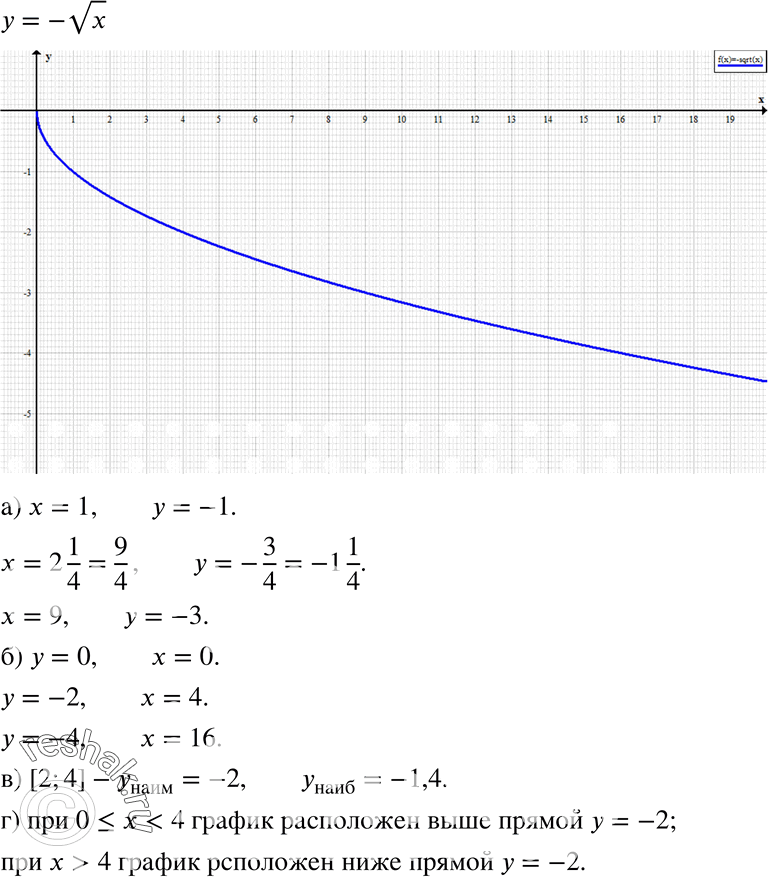 Квадратный корень числа «x» — это число «y», такое что y 2 = x. т. е. если y 2 = x ⇒ y = √x. т. е. если «x» — это квадрат «y», то «y» — это квадратный корень из «x». Некоторые примеры:
Квадратный корень числа «x» — это число «y», такое что y 2 = x. т. е. если y 2 = x ⇒ y = √x. т. е. если «x» — это квадрат «y», то «y» — это квадратный корень из «x». Некоторые примеры:
- 2 2 = 4 ⇒ √4 = 2
- 4 2 = 16 ⇒ √16 = 4
Мы знаем, что квадратный корень из числа может быть как положительным, так и отрицательным. т. е. √ 4 = ± 2. Но при определении функции квадратного корня мы ограничиваем ее диапазон множеством всех положительных действительных чисел (иначе она вообще не станет функцией), и, следовательно, в случае функции квадратного корня результат всегда положительный. . Давайте воспользуемся всеми этими фактами, чтобы понять функцию квадратного корня.
| 1. | Что такое функция извлечения квадратного корня? |
| 2. | Домен и диапазон функции квадратного корня |
3. | График квадратного корня |
| 4. | График любой функции квадратного корня |
| 5. | Свойства функции квадратного корня |
| 6. | Часто задаваемые вопросы о функции извлечения квадратного корня |
Что такое функция извлечения квадратного корня?
Функция квадратного корня в основном имеет вид f(x) = √x. т. е. родительская функция квадратного корня есть f(x) = √x. Это обратная функция квадрата g(x) = x 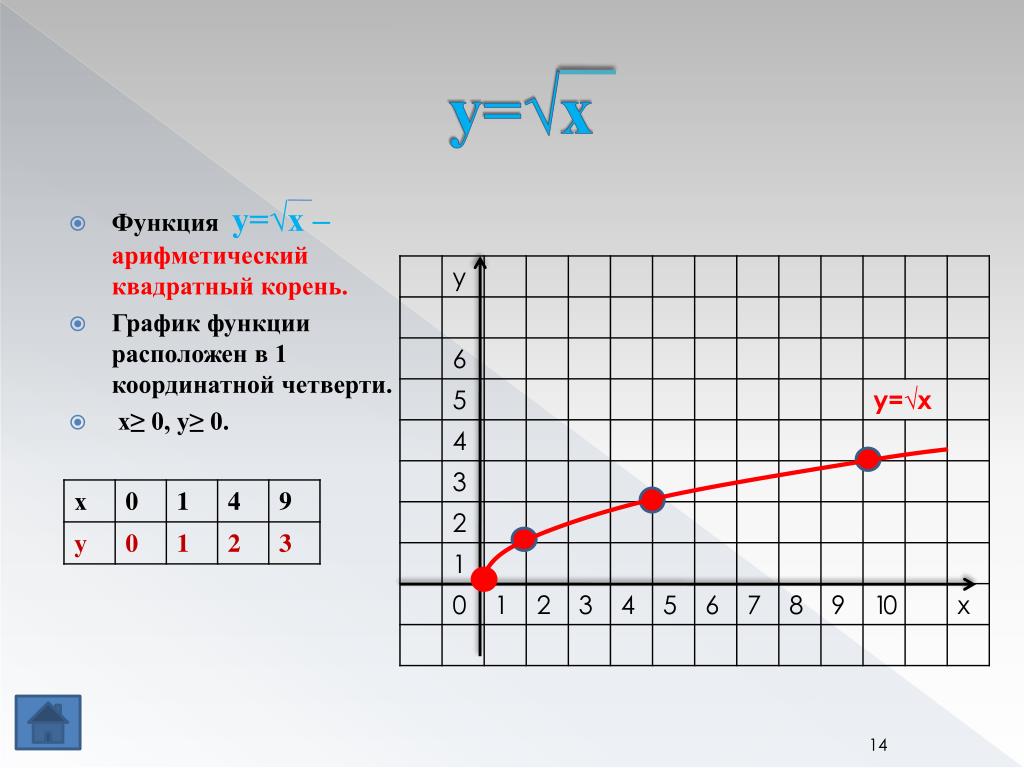
f(x) = √x является исходной функцией квадратного корня, но когда к ней применяются преобразования, она может выглядеть как f(x) = a√(b(x — h)) + k, где a , b, h и k — такие числа, что
- ‘a’ — вертикальное расширение
- ‘b’ — горизонтальное расширение
- ‘h’ — горизонтальный перевод
- ‘k’ — вертикальный перевод
Домен и диапазон функции квадратного корня
Квадратный корень из отрицательного числа НЕ является действительным числом. т. е. функция квадратного корня не может принимать отрицательные числа в качестве входных данных. т. е.
- Область определения функции извлечения квадратного корня f(x) = √x — это множество всех неотрицательных действительных чисел. т. е. область определения функции квадратного корня равна [0, ∞). Обратите внимание, что он также включает 0 в домене.
В общем случае квадратный корень из числа может быть как положительным, так и отрицательным. т. е. √25 = 5 или -5, поскольку 5 2 = 25 и (-5) 2 = 25. Но диапазон функции квадратного корня (т. е. ее значения y) ограничен только положительными числами, потому что в противном случае он не пройдет тест вертикальной линии и не будет функцией, если вход имеет два выхода. Таким образом,
т. е. √25 = 5 или -5, поскольку 5 2 = 25 и (-5) 2 = 25. Но диапазон функции квадратного корня (т. е. ее значения y) ограничен только положительными числами, потому что в противном случае он не пройдет тест вертикальной линии и не будет функцией, если вход имеет два выхода. Таким образом,
- Область значений функции квадратного корня f(x) = √x совпадает с ее областью определения [0, ∞). Обратите внимание, что он также включает 0 в диапазоне.
График квадратного корня
Мы уже видели, как выглядит граф квадратного корня. Но теперь мы увидим, как построить график квадратного корня из x. Мы уже видели, что область определения и область значений исходной функции квадратного корня f(x) = √x — это множество всех неотрицательных действительных чисел. Таким образом, график квадратного корня функции f(x) = √x лежит только в первом квадранте. Мы можем нарисовать его график, построив таблицу значений с некоторыми случайными значениями x (из области [0, ∞), а затем вычислив соответствующие значения y, подставив каждое x в y = √x.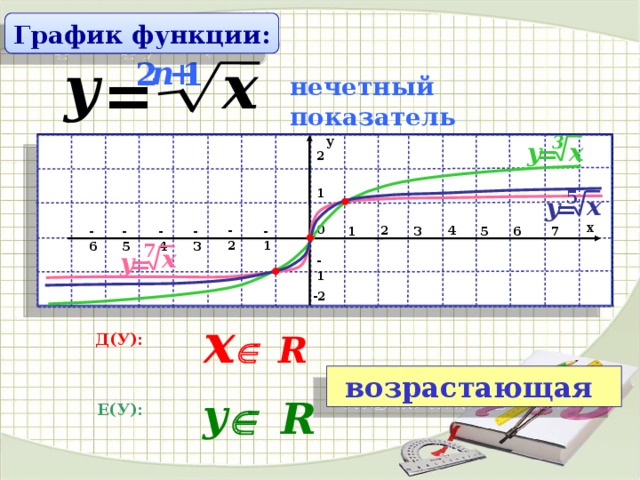 Затем мы можем получить несколько точек, которые мы нанесем на координатную плоскость, и соединим их все кривой.
Затем мы можем получить несколько точек, которые мы нанесем на координатную плоскость, и соединим их все кривой.
| х | и |
|---|---|
| 0 | √0 = 0 |
| 1 | √1 = 1 |
| 4 | √4 = 2 |
Обратите внимание, что когда к графику применяются некоторые преобразования, сам график может не лежать в первом квадранте.
График любой функции квадратного корня
Мы видели, как построить график родительской функции квадратного корня f(x) = √x. Вот шаги, которые полезны при построении графика любой функции квадратного корня, имеющей форму f (x) = a √ (b (x — h)) + k в целом.
- Шаг 1: Определите область определения функции, установив «выражение внутри квадратного корня» больше или равное 0 и найдя x.
- Шаг 2: Диапазон любой функции квадратного корня всегда равен y ≥ k, где k — вертикальный сдвиг функции f(x) = a√(b(x — h)) + k.

- Шаг 3: Построить таблицу значений с двумя столбцами x и y, взять несколько случайных чисел для x (только из домена), начиная с первого значения домена, подставить их в заданную функцию и найти соответствующие значения у.
- Шаг 4: Нанесите все точки на плоскость и соедините их кривой, а также продлите кривую в том же направлении.
Примечание: Вычисление точек пересечения по осям x и y также может помочь в построении графика функции квадратного корня.
Пример: Постройте график функции квадратного корня f(x) = √(x — 2) + 3.
Решение:
Чтобы найти ее область определения, x — 2 ≥ 0 ⇒ x ≥ 2.
Его вертикальный сдвиг равен 3, и, следовательно, его диапазон равен y ≥ 3.
Теперь мы построим таблицу с некоторыми значениями больше 2 (поскольку область определения x ≥ 2). Выберите некоторые значения для x так, чтобы √(x — 2) был правильным квадратом, чтобы упростить вычисление.
| х | г |
|---|---|
| 2 | √(2 — 2) + 3 = 0 + 3 = 3 |
| 3 | √(3 — 2) + 3 = 1 + 3 = 4 |
| 6 | √(6 — 2) + 3 = 2 + 3 = 5 |
| 11 | √(11 — 2) + 3 = 3 + 3 = 6 |
Теперь постройте эти точки и соедините их кривой.
Мы также можем построить график функции квадратного корня, применив преобразования к родительскому графику квадратного корня f(x) = √x.
Свойства функции извлечения квадратного корня
Вот важные моменты/свойства, которые следует отметить в отношении функции квадратного корня f(x) = √x.
- Его домен [0, ∞).
- Диапазон: [0, ∞).
- Не имеет относительных максимумов, но имеет минимум в точке (0, 0).
- Функция квадратного корня не имеет асимптот.
- Это возрастающая функция во всей области определения [0, ∞).

- Функция квадратного корня f(x) = √x имеет критическую точку в точке (0, 0) и не имеет точек перегиба.
Часто задаваемые вопросы о функции извлечения квадратного корня
Что такое родительская функция извлечения квадратного корня?
Родительская функция квадратного корня имеет вид f(x) = √x. Эту функцию можно транслировать/расширять/отражать и приводить к виду f(x) = a√(b(x — h)) + k.
Что такое формула функции квадратного корня?
Формула для функции квадратного корня: f(x) = √x. Это означает, что вывод каждого входного значения равен квадратному корню из входного значения. Например, f(25) = √25 = 5. Обратите внимание, что все входы и выходы функции квадратного корня всегда неотрицательны.
Что такое производная функции квадратного корня?
Производная функции квадратного корня f(x) = √x вычисляется по степенному правилу дифференцирования, d(x n )/dx = nx n-1 .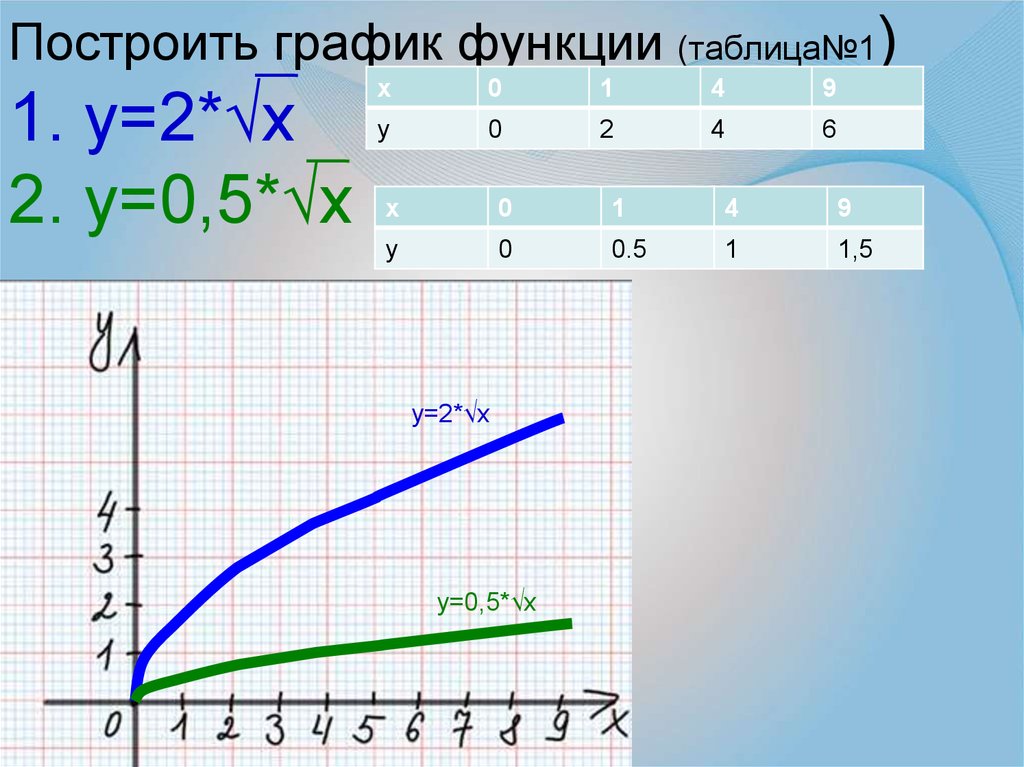 По этому правилу d(√x)/dx = d(x 1/2 )/dx = (1/2) x (1/2) — 1 = (1/2) x -1/ 2 = 1/(2√x). Таким образом, производная от √x равна 1/(2√x).
По этому правилу d(√x)/dx = d(x 1/2 )/dx = (1/2) x (1/2) — 1 = (1/2) x -1/ 2 = 1/(2√x). Таким образом, производная от √x равна 1/(2√x).
Как построить график квадратного корня из x?
Чтобы построить график квадратного корня из x, просто заметьте, что все его входы и выходы неотрицательны и, следовательно, его график лежит в первом квадранте. Далее, чтобы получить четкую форму графика, вычислите на нем несколько точек, взяв несколько случайных чисел за x и вычислив для них соответствующие значения y.
Что такое область функции квадратного корня?
Функция квадратного корня не может быть вычислена для отрицательных входных данных. Попробуйте ввести √(-2) в калькуляторе, он показывает ошибку. Таким образом, функция квадратного корня f(x) = √x принимает только неотрицательные значения и, следовательно, ее областью определения является множество всех неотрицательных действительных чисел, [0, ∞). В дальнейшем, если функция похожа на f (x) = a√ (b (x — h)) + k, то ее область определения равна x ≥ h.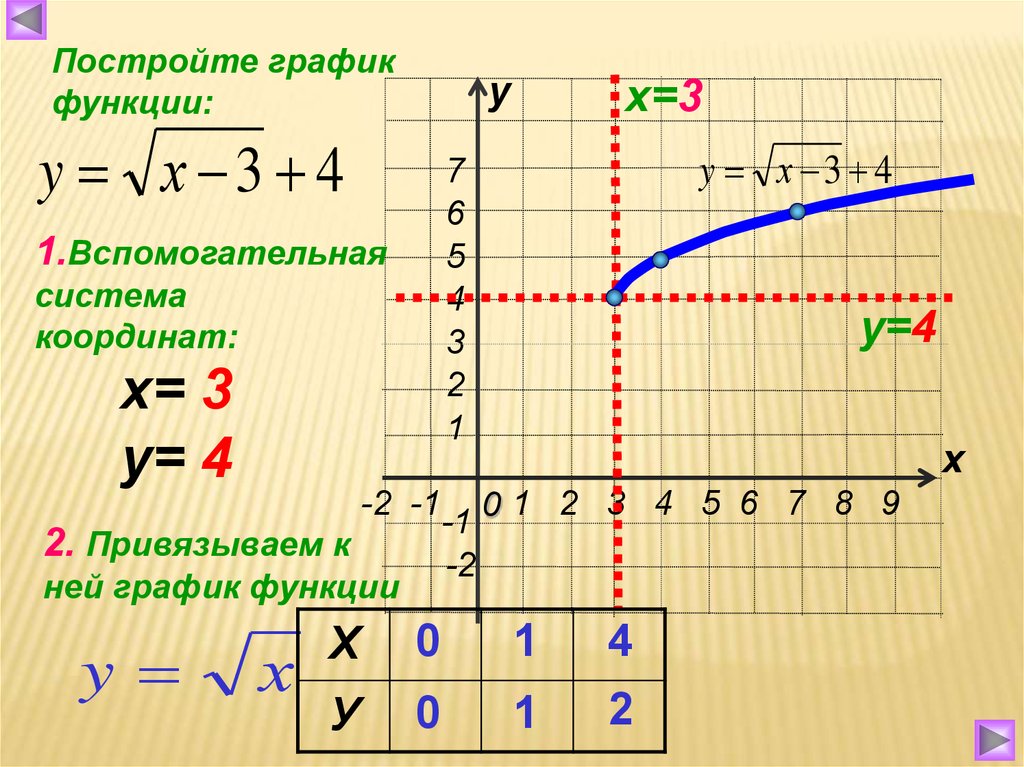

 М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2006.
М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2006.
Leave A Comment