Равнобедренный треугольник


Определение равнобедренного треугольника

Равнобедренный треугольник — это треугольник, в котором длины двух его сторон равны между собой.

Примечание. Из определения равнобедренного треугольника следует, что правильный треугольник также является равнобедренным. Однако, необходимо помнить, что обратное утверждение — неверно.



Свойства равнобедренного треугольника

Свойства, приведенные ниже, используются при решении задач. Поскольку они широко известны, то подразумевается, что они не нуждаются в пояснении. Поэтому в текстах задач ссылка на них опущена.
  • Углы, противолежащие равным сторонам равнобедренного треугольника, равны между собой.
  • Биссектрисы, медианы и высоты, проведённые из углов, противолежащих равным сторонам треугольника, равны между собой.
  • Биссектриса, медиана и высота
    , проведенные к основанию, совпадают между собой.
  • Центры вписанной и описанной окружностей лежат на высоте, биссектрисе и медиане (они совпадают) проведенных к основанию.
  • Углы, противолежащие равным сторонам равнобедренного треугольника, всегда острые.

Стороны в равнобедренном треугольнике могут быть вычислены с помощью формул, выражающих их длину через другие стороны и углы, величина которых известна.

Боковая сторона равнобедренного треугольника равна частному от деления основания на двойной косинус угла при основании (Формула 1). Данное тождество может быть получено путем несложных преобразований из теоремы косинусов.

Основание равнобедренного треугольника равно произведению боковой стороны на квадратный корень из удвоенной разности единицы и косинуса угла при вершине (Формула 2)

Основание равнобедренного треугольника равно удвоенному произведению боковой стороны на синус половины угла при вершине.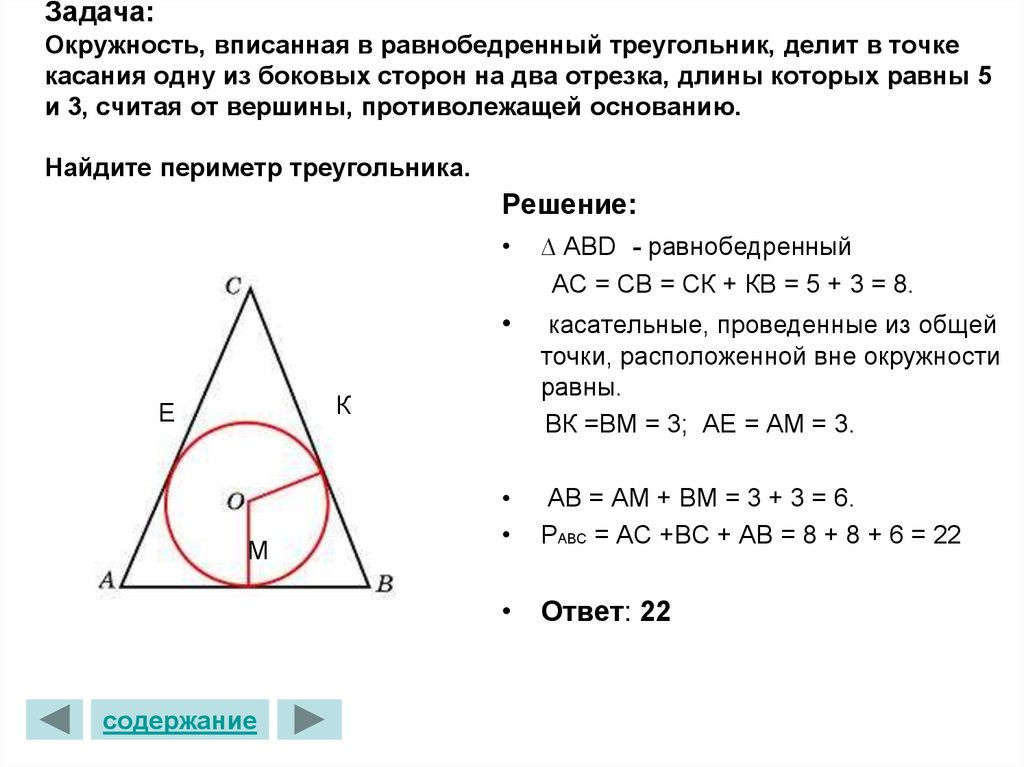 (Формула 3)

Основание равнобедренного треугольника равно удвоенному произведению боковой стороны на косинус угла при его основании (Формула 4).

    Радиус вписанной окружности в равнобедренный треугольник

          Обозначения в формулах, можно посмотреть на рисунке выше.

    Радиус вписанной окружности для равнобедренного треугольника можно найти, исходя из величин основания и каждой стороны. (Формула 1)

    Радиус вписанной окружности для равнобедренного треугольника можно определить,исходя из величин основания  и высоты, проведенной к этому основанию (Формула 2)

    Радиус вписанной в равнобедренный треугольник окружности можно также вычислить через длину боковой стороны и высоту, проведенную к основанию треугольника (Формула 3)

    Знание величины угла между боковыми сторонами и длины основания также позволяет определить радиус вписанной окружности (Формула 4)

    Аналогичная формула (5) позволяет определить радиус вписанной окружности через боковые стороны и угол между ними

    Признаки равнобедренного треугольника

    Треугольник, у которого присутствуют перечисленные ниже признаки, является равнобедренным.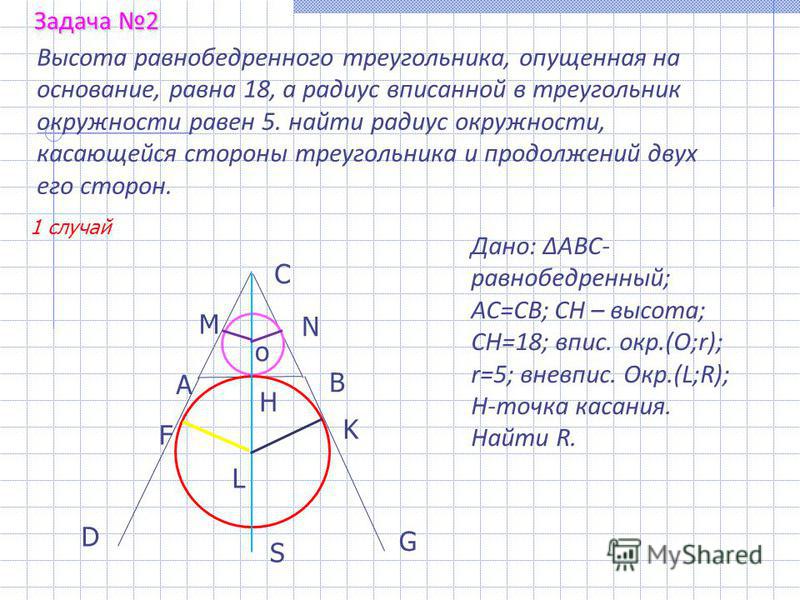
    • Два угла треугольника равны
    • Высота совпадает с медианой
    • Высота совпадает с биссектрисой
    • Биссектриса совпадает с медианой
    • Две высоты равны
    • Две медианы равны
    • Две биссектрисы равны

    Площадь равнобедренного треугольника

    Площадь равнобедренного треугольника находится по следующим формулам:

    ,
     где
    a — длина одной из двух равных сторон треугольника
    b — длина основания
    α — величина одного из двух равных углов при основании

    β — величина угла между равными сторонами треугольника и противолежащего его основанию.

    См. также «Площадь треугольника».

    Содержание главы:

    • Равнобедренный треугольник
    • Рівнобедрений трикутник
    • Площадь равнобедренного треугольника
    • Площа рівнобедреного трикутника
    • Углы равнобедренного треугольника
    • Высота равнобедренного треугольника
    • Окружность, вписанная в равнобедренный треугольник

    0  

     Перпендикуляр к плоскости прямоугольного треугольника | Описание курса | Равнобедренный треугольник 

       

    треугольник, радиус вписанной и описанной окружностей

    Все формулы для треугольника, как найти сторону, биссектрису, медиану, высоту, угол. ..

    Найти длину биссектрисы в треугольнике

    L — биссектриса, отрезок |OB|, который делит угол ABC пополам

    a, b — стороны треугольника

    с — сторона на которую опущена биссектриса

    d, e — отрезки полученные делением биссектрисы

    γ — угол ABC, разделенный биссектрисой пополам

    p — полупериметр, p=(a+b+c)/2

     

     

    Длина биссектрисы через две стороны и угол, (L):

     

    Длина биссектрисы через полупериметр и стороны, (L):

     

    Длина биссектрисы через три стороны, (L):

     

    Длина биссектрисы через стороны и отрезки d, e, (L):

     

     

     

    Точка пересечения всех трех биссектрис треугольника ABC, совпадает с центром О, вписанной окружности.

     

     

     

     

     

     

     

    Биссектриса прямоугольного треугольника

     

    1.  Найти по формулам длину биссектрисы из прямого угла на гипотенузу:

     

    L — биссектриса, отрезок ME ,  исходящий из прямого угла (90 град)

    a, b — катеты прямоугольного треугольника

    с — гипотенуза

    α — угол прилежащий к гипотенузе

     

     

    Формула длины биссектрисы через катеты, ( L):

     

    Формула длины биссектрисы через гипотенузу и угол, ( L):

     

     

     

    2. Найти по формулам длину биссектрисы из острого угла на катет:

     

    L — биссектриса, отрезок ME ,  исходящий из острого угла

    a, b — катеты прямоугольного треугольника

    с — гипотенуза

    α, β — углы прилежащие к гипотенузе

     

     

    Формулы длины биссектрисы через катет и угол, (L):

     

    Формула длины биссектрисы через катет и гипотенузу, (L):

     

    Длина биссектрисы равнобедренного треугольника

    Формулы для вычисления высоты, биссектрисы и медианы.

    В равнобедренном треугольнике: высота, биссектриса и медиана, исходящие из угла образованного равными сторонами, один и тот же отрезок.

     

    L — высота=биссектриса=медиана

    a — одинаковые стороны треугольника

    b — основание

    α — равные углы при основании

    β — угол вершины

     

     

    Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):

     

     

     

    Формула высоты, биссектрисы и медианы, через стороны, (L):

    Найти медиану=биссектрису=высоту равностороннего треугольника

    Формула для вычисления высоты= биссектрисы= медианы.

    В равностороннем треугольнике: все высоты, биссектрисы и медианы, равны. Точка их пересечения, является центром вписанной окружности.

     

     

    L — высота=биссектриса=медиана

    a —  стороны треугольника

     

     

     

    Формула длины высоты, биссектрисы и медианы равностороннего треугольника, (L):

     

     

    Найти длину медианы треугольника по формулам

    Медиана — отрезок |AO|, который выходит из вершины A и делит противолежащею сторону  c пополам.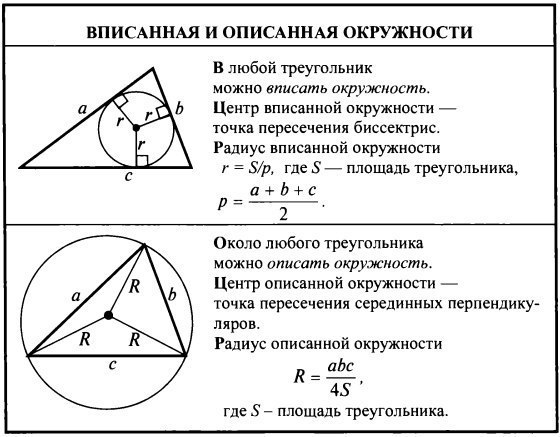  Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.

     

     

    M — медиана, отрезок |AO|

    c — сторона на которую ложится медиана

    a , b — стороны треугольника

    γ — угол CAB

     

     

    Формула длины медианы через три стороны, (M):

     

    Формула длины медианы через две стороны и угол между ними, (M):

     

     

    Длина медианы прямоугольного треугольника

    Медиана, отрезок |CO|, исходящий из вершины прямого угла BCA и делящий гипотенузу c, пополам. Медиана в прямоугольном треугольнике (M), равна, радиусу описанной окружности (R).

    M — медиана

    R — радиус описанной окружности

    O — центр описанной окружности

    с — гипотенуза

    a, b — катеты

    α — острый угол CAB

     

    Медиана равна радиусу и половине гипотенузы, (M):

     

    Формула длины через катеты, (M):

     

    Формула длины через катет и острый угол, (M):

     

     

    Найти длину высоты треугольника

    Высота— перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).  Высоты треугольника пересекаются в одной точке, которая называется — ортоцентр.

     

    H — высота треугольника

    a — сторона, основание

    b. c — стороны

    β, γ — углы при основании

    p — полупериметр, p=(a+b+c)/2

    R — радиус описанной окружности

    S — площадь треугольника

     

     

    Формула длины высоты через стороны, (H):

     

    Формула длины высоты через сторону и угол, (H):

     

    Формула длины высоты через сторону и площадь, (H):

     

    Формула длины высоты через стороны и радиус, (H):

     

     

    Формулы высоты прямого угла в прямоугольном треугольнике

     

    В прямоугольном треугольнике катеты, являются высотами. Ортоцентр — точка пересечения высот, совпадает с вершиной прямого угла.

     

    H — высота из прямого угла

    a, b — катеты

    с — гипотенуза

    c1 , c2 — отрезки полученные от деления гипотенузы, высотой

    α, β — углы при гипотенузе

     

     

    Формула длины высоты через стороны, (H):

     

    Формула длины высоты через гипотенузу и острые углы, (H):

     

    Формула длины высоты через катет и угол, (H):

     

    Формула длины высоты через составные отрезки гипотенузы , (H):

     

     

    Как найти неизвестную сторону треугольника

    Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.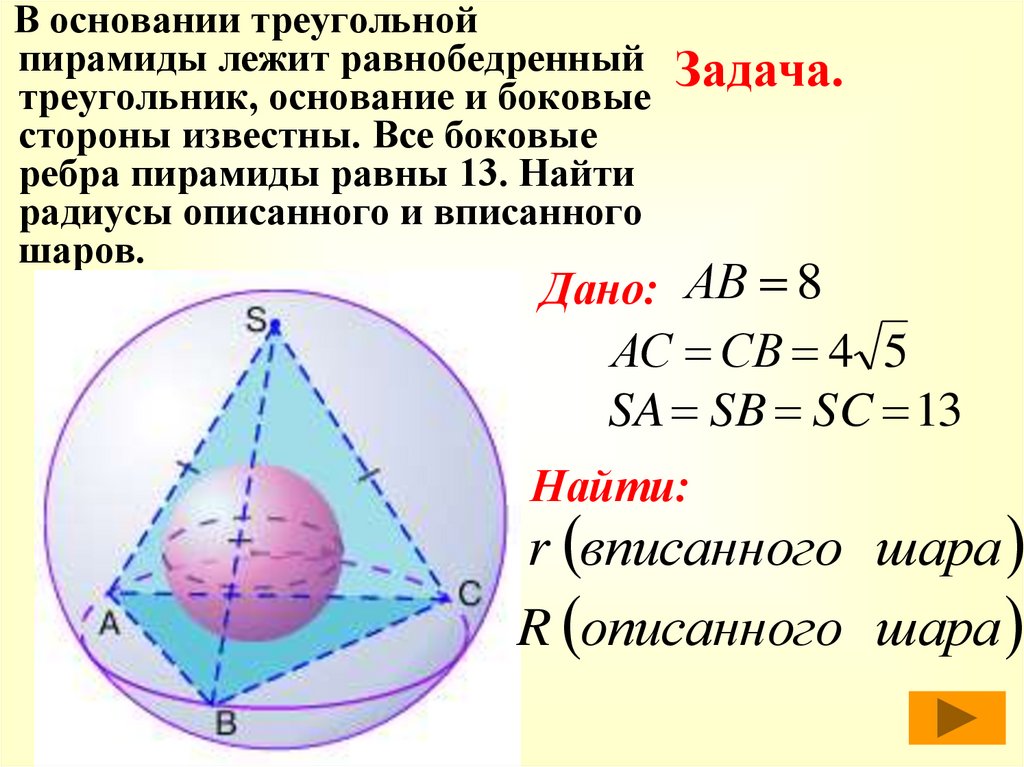

     

     

    a, b, c — стороны произвольного треугольника

    α, β, γ — противоположные углы

     

     

     

    Формула  длины через две стороны и угол (по теореме косинусов), (a):

    *Внимательно, при подстановке в формулу, для тупого угла ( α90), сosα,принимает отрицательное значение

     

    Формула  длины через сторону и два угла (по теореме синусов), (a):

     

    Формулы сторон равнобедренного треугольника

    Вычислить длину неизвестной стороны через любые стороны и углы

    b — сторона (основание)

    a — равные стороны

    α — углы при основании

    β — угол образованный равными сторонами

     

     

     

    Формулы длины стороны (основания), (b):

     

    Формулы длины равных сторон , (a):

     

    Как узнать сторону прямоугольного треугольника

    Есть следующие формулы для определения катета или гипотенузы

     

     

    a, b — катеты

    c — гипотенуза

    α, β — острые углы

     

     

    Формулы для катета, (a):

     

    Формулы для катета, (b):

     

    Формулы для гипотенузы, (c):

     

    Формулы сторон по теореме Пифагора, (c, a, b):

     

     

    Все формулы радиуса описанной окружности

    Радиус описанной окружности трапеции по сторонам и диагонали

    a — боковые стороны трапеции

    c — нижнее основание

    b — верхнее основание

    d — диагональ

    h — высота

    p = (a+d+c)/2

    Формула радиуса описанной окружности трапеции, (R)

     

     

    Радиус описанной окружности правильного многоугольника

     

    a — сторона многоугольника

    N — количество сторон многоугольника

     

     

     

    Радиус  описанной  окружности  правильного  многоугольника, (R):

     

    Радиус описанной окружности правильного шестиугольника

     

     

    a — сторона шестиугольника

    d — диагональ шестиугольника

     

     

     

    Радиус  описанной  окружности  правильного  шестиугольника (R):

     

     

     

    Радиус описанной окружности прямоугольника по стороне

     

     

    a, b — стороны прямоугольника

    d — диагональ

     

     

     

    Радиус описанной окружности прямоугольника (R):

     

     

     

    Найти радиус описанной окружности около квадрата

     

     

     

    a — сторона квадрата

    d — диагональ

     

     

    Радиус описанной окружности квадрата (R):

     

    Найти радиус описанной окружности треугольника, формула

     

     

    a, b, c — стороны треугольника

    p — полупериметр,

    p= (a+b+c)/2

     

     

    Формула радиуса описанной окружности треугольника, (R):

     

    Найти радиус описанной окружности равностороннего треугольника по стороне

     

     

     

     

    a — сторона треугольника

     

     

    Радиус  описанной  окружности  равностороннего  треугольника (R):

     

    найти радиус описанной окружности равнобедренного треугольника по сторонам

     

    Зная стороны равнобедренного треугольника, можно по формуле, найти, радиус описанной окружности около этого треугольника.

    a, b — стороны треугольника

     

     

     

    Радиус  описанной  окружности  равнобедренного  треугольника (R):

     

    Найти радиус описанной окружности прямоугольного треугольника по катетам

     

    a, b — катеты прямоугольного треугольника

    c — гипотенуза

     

     

     

    Радиус описанной окружности прямоугольного треугольника (R):

    Все формулы радиуса вписанной окружности

    Радиус вписанной окружности в шестиугольник

     

     

     

    a — сторона шестиугольника

     

     

     

    Радиус вписанной окружности в шестиугольник, (r):

     

     

     

    Радиус вписанной окружности в правильный многоугольник

     

     

    a — сторона многоугольника

    N — количество сторон многоугольника

     

     

     

    Радиус вписанной окружности в правильный многоугольник, (r):

     

    Радиус вписанной окружности в ромб

    r — радиус вписанной окружности

    a — сторона ромба

    D, d — диагонали

    h — высота ромба

     

     

     

    Формула радиуса вписанной окружности в ромб, (r):

     

    Радиус вписанной окружности в квадрат

     

     

     

     

    a — сторона квадрата

     

     

    Радиус вписанной окружности в квадрат (r):

     

    Радиус вписанной окружности в равнобочную трапецию

    с — нижнее основание

    b — верхнее основание

    a — боковые стороны

    h — высота

     

     

     

    Радиус вписанной окружности равнобочной трапеции (r):

     

    Радиус вписанной окружности в прямоугольный треугольник

     

     

    a, b — катеты треугольника

    с — гипотенуза

     

     

     

    Радиус вписанной окружности в прямоугольный треугольник (r):

     

    Радиус вписанной окружности в равнобедренный треугольник

     

     

     

    a, b — стороны треугольника

     

     

     

    Радиус вписанной окружности в равнобедренный треугольник (r):

     

    Радиус вписанной окружности в равносторонний треугольник

     

     

     

    a — сторона треугольника

     

     

     

    Радиус вписанной окружности в равносторонний треугольник (r):

     

     

    Радиус вписанной окружности в треугольник

     

     

    a, b, c — стороны треугольника

    p — полупериметр, p=(a+b+c)/2

     

     

     

    Радиус вписанной окружности в треугольник (r):

    Уравнения равнобедренного треугольника Калькулятор формул

    Изменить уравнение
    Выберите, чтобы найти другое неизвестное

    Разносторонний треугольник:
    Нет сторон одинаковой длины
    Нет равных углов

    Уравнения разностороннего треугольника
    Эти уравнения применимы к любому типу треугольника.

    Сокращенные
    уравнений для равностороннего, прямого и равнобедренного треугольников приведены ниже.

    Периметр
    Полупериметр
    Area
    Area
    Base
    Height
    Angle Bisector of side a
    Angle Bisector of side b
    Биссектриса угла c
    Медиана стороны a
    Медиана стороны b
    Median of side c
    Altitude of side a
    Altitude of side b
    Altitude of side c
    Circumscribed Circle Radius
    Радиус вписанной окружности

    Закон косинусов

    угол A 91018

    018

    длина стороны a

    Equilateral Triangle:
    All three sides have equal length
    All three angles are equal to 60 degrees

    Equilateral Triangle Equations

    8
    Perimeter
    Semiperimeter
    Area
    Высота
    Медиана
    Биссектриса угла
    0016 Circumscribed Circle Radius
    Inscribed Circle Radius

    Right Triangle:
    One angle is equal to 90 degrees

    Right Triangle Equations

    Pythagorean Theorem
    Периметр
    Полупериметр
    Площадь
    Высота над уровнем моря0018
    Altitude of b
    Altitude of c
    Angle Bisector of a
    Angle Bisector of b
    Angle Bisector of c
    Медиана A
    Медиана B
    Медиана C
    внедорожник
    . 0018
    Circumscribed Circle Radius

    Isosceles Triangle:
    Two sides have equal length
    Two angles are equal

    Isosceles Triangle Equations

    Perimeter
    Semiperimeter
    Площадь
    Высота сторон a и c
    Высота стороны b
    Median of sides a and c
    Median of side b
    Angle Bisector of sides a and c
    Angle Bisector of side b
    Радиус описанной окружности
    Радиус вписанной окружности

    Где

    P Периметр0021
    S = Semiperimeter
    A =. side c
    h = Altitude
    m = Median
    A = Angle A
    B = Angle B
    C = Angle C
    t = Angle bisector
    R = Circumscribed Circle Radius
    r = Радиус вписанной окружности

    Справочник — Книги: 1) Макс А. Собель и Норберт Лернер. 1991. Предварительная математика. Прентис Холл. 4-е изд.

    ABC — равнобедренный треугольник, вписанный в окружность Если стороны AB AC равны 125 см, а BC 24 см, найдите радиус…

    Перейти к

    • Круговое упражнение 15.1
    • Круговое упражнение 15. 2
    • Рациональные и иррациональные числа
    • Сложные проценты
    • Расширения
    • Факторизация
    • Одновременные линейные уравнения
    • Задачи на одновременные линейные уравнения
    • Квадратные уравнения
    • Индексы
    • Логарифмы
    • Треугольники
    • Теорема о средней точке
    • Теорема Пифагора
    • Прямолинейные фигуры
    • Теоремы о площади
    • Круг
    • Измерение
    • Тригонометрические отношения
    • Тригонометрические отношения и стандартные углы
    • Координатная геометрия
    • Статистика

    Главная > ML Aggarwal Solutions Класс 9 Математика > Глава 15 — Круг > Круговое упражнение 15.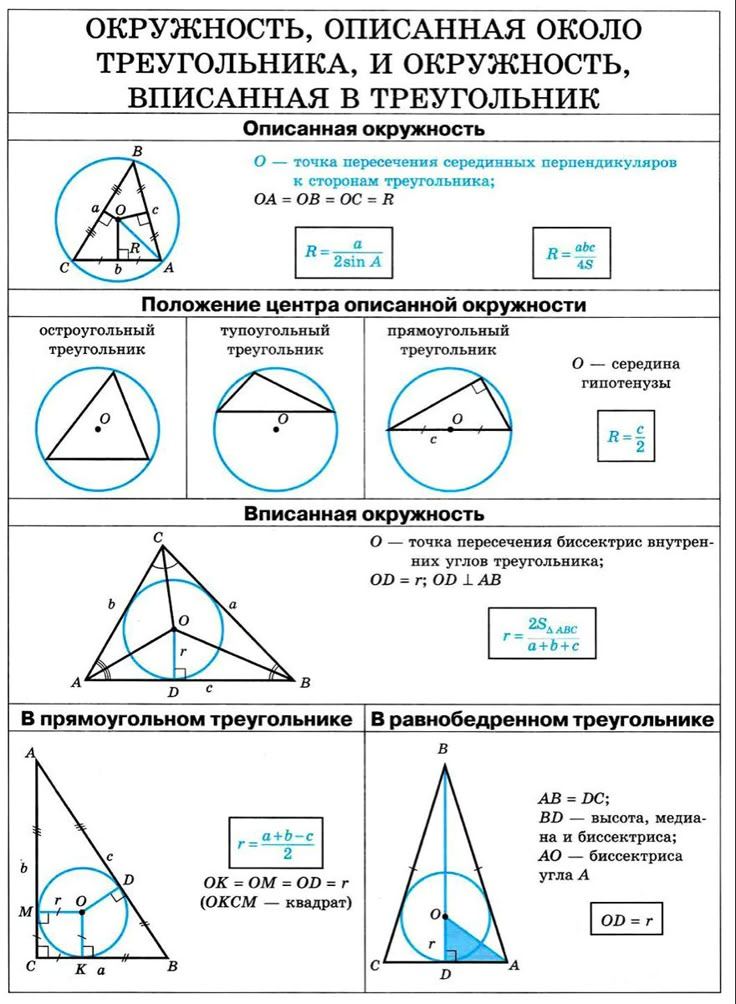 1 > Вопрос 7

    Вопрос 7 Круговое упражнение 15.1

    ABC — равнобедренный треугольник, вписанный в окружность. Если AB = AC = 12√5 см и BC = 24

    см, найдите радиус окружности.

    Ответ:

    АВ = АС 12√5 и ВС = 24 см.

    Связанные вопросы

    Вычислите длину хорды, которая находится на расстоянии 12 см от центра окружности радиуса…

    Хорда длиной 8 см проходит на расстоянии 3 см от центра окружности. Вычислите радиус…

    Вычислите длину хорды, которая проходит на расстоянии 6 см от центра окружности диаметром…

    Хорда длиной 16 см проходит на расстоянии 6 см от центра окружности. Найдите длину т…

    В окружности радиусом 5 см AB и CD проходят две параллельные хорды длиной 8 см и 6 см соответственно….

    а) На приведенном ниже рисунке О — центр окружности. AB и CD — две хорды окружности…

    Фейсбук WhatsApp

    Копировать ссылку

    Было ли это полезно?

    Упражнения

    Circle Degins 15.1

    Упражнение по кругу 15.2

    Главы

    Рациональные и иррациональные номера

    Соединенные проценты

    Расширение

    . Индексы

    Логарифмы

    Треугольники

    Теорема средней точки

    Теорема Pythagoras

    Прямолинейные рисунки

    Теорема

    Trigersistry Angelios

    Delistriclic

    96666666667.