Равномерное прямолинейное движение
Равномерное движение – это движение с постоянной скоростью, то есть когда скорость не изменяется (v = const) и ускорения или замедления не происходит (а = 0).
Прямолинейное движение – это движение по прямой линии, то есть траектория прямолинейного движения – это прямая линия.
Равномерное прямолинейное движение – это движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. Например, если мы разобьём какой-то временной интервал на отрезки по одной секунде, то при равномерном движении тело будет перемещаться на одинаковое расстояние за каждый из этих отрезков времени.
Скорость равномерного прямолинейного движения не зависит от времени и в каждой точке траектории направлена также, как и перемещение тела. То есть вектор перемещения совпадает по направлению с вектором скорости. При этом средняя скорость за любой промежуток времени равна мгновенной скорости:
vcp = v
Скорость равномерного прямолинейного движения – это физическая векторная величина, равная отношению перемещения тела за любой промежуток времени к значению этого промежутка t:
= / t
Таким образом, скорость равномерного прямолинейного движения показывает,
какое перемещение совершает материальная точка за единицу времени.
Перемещение при равномерном прямолинейном движении определяется формулой:
= • t
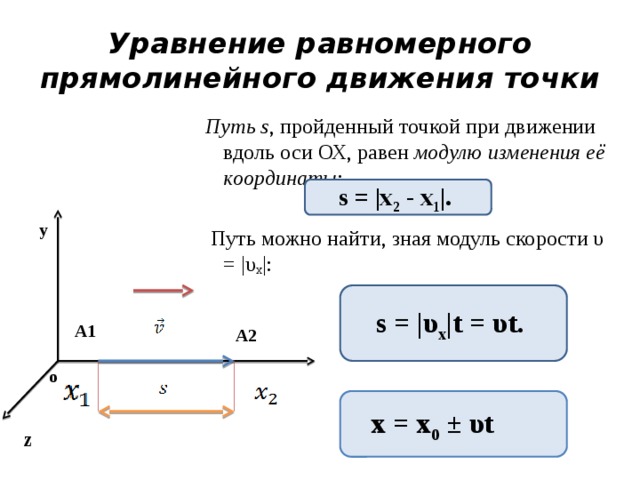
Пройденный путь при прямолинейном движении равен модулю перемещения. Если положительное направление оси ОХ совпадает с направлением движения, то проекция скорости на ось ОХ равна величине скорости и положительна:
vx = v, то есть v > 0
Проекция перемещения на ось ОХ равна:
s = vt = x – x0
где x0 – начальная координата тела, х – конечная координата тела (или координата тела в любой момент времени)
Уравнение движения, то есть зависимость координаты тела от времени х = х(t), принимает вид:
х = x0 + vt
Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v < 0), и тогда уравнение движения принимает вид:
х = x0 - vt
Зависимость проекции скорости тела от времени показана на рис.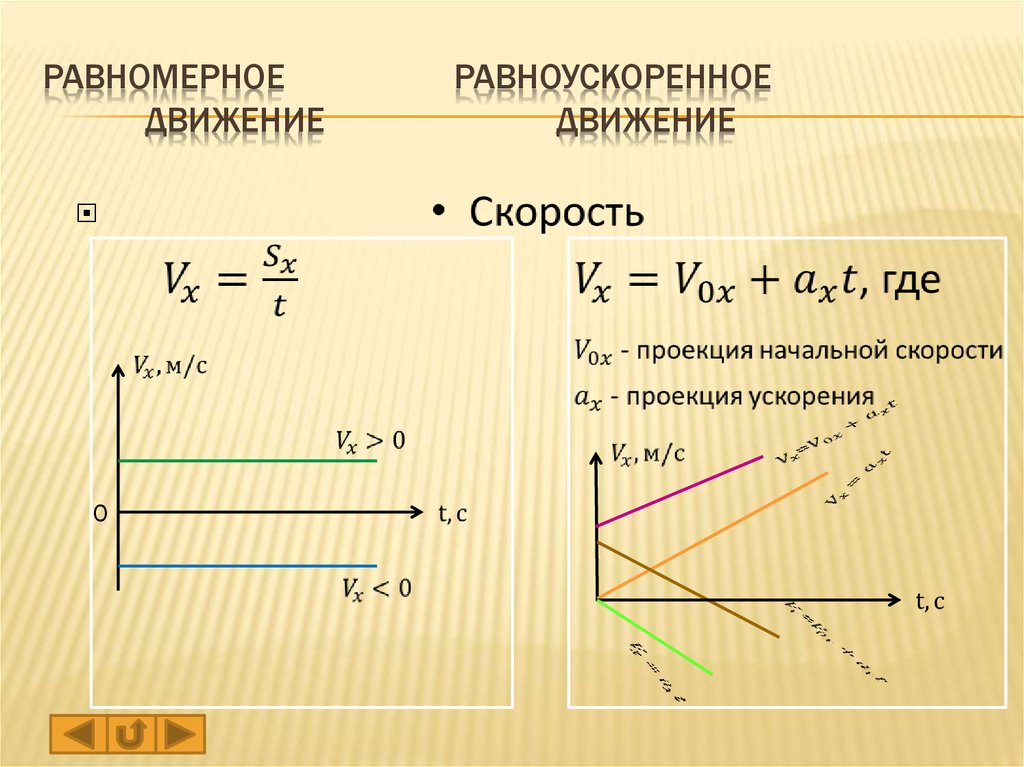 1.11.
Так как скорость постоянна (v = const), то графиком скорости является прямая линия,
параллельная оси времени Ot.
1.11.
Так как скорость постоянна (v = const), то графиком скорости является прямая линия,
параллельная оси времени Ot.
Рис. 1.11. Зависимость проекции скорости тела от времени при равномерном прямолинейном движении.
Проекция перемещения на координатную ось численно равна площади прямоугольника ОАВС (рис. 1.12), так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.
Рис. 1.12. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.
График зависимости перемещения от времени показан на рис. 1.13. Из графика видно, что проекция скорости равна
v = s1 / t1 = tg α
где α – угол наклона графика к оси времени. Чем больше угол α, тем быстрее движется тело, то есть тем больше его скорость (больший путь тело проходит за меньшее время). Тангенс угла наклона касательной к графику зависимости координаты от времени равен скорости:
tg α = v
Рис. 1.13. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.
1.13. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.
Зависимость координаты от времени показана на рис. 1.14. Из рисунка видно, что
tg α1 > tg α2
следовательно, скорость тела 1 выше скорости тела 2 (v1 > v2).
tg α3 = v3 < 0
Если тело покоится, то графиком координаты является прямая, параллельная оси времени, то есть
х = х0
Рис. 1.14. Зависимость координаты тела от времени при равномерном прямолинейном движении.
Равномерное прямолинейное движение | СПАДИЛО
ОпределениеРавномерное прямолинейное движение — это такое движение, при котором тело совершает за любые равные промежутки времени равные перемещения.
Скорость при прямолинейном равномерном движении
Если тело движется равномерно и прямолинейно, его скорость остается постоянной как по модулю, так и по направлению. Ускорение при этом равно нулю.
Ускорение при этом равно нулю.
Векторный способ записи скорости при равномерном прямолинейном движении:
Основная единица измерения скорости — 1 метр в секунду. Сокращенно — 1 м/с.
Дополнительные единицы измерения- 1 км/ч (километр в час) = 1000 м/3600 с.
- 1 км/мин (километр в минуту) = 1000 м/60 с.
- 1 км/с (километр в секунду) = 1000 м/с.
- 1 м/мин (метр в минуту) = 1 м/60 с.
- 1 см/с (сантиметр в секунду) = 0,01 м/с.
Спидометр — прибор для измерения модули скорости тела.
График зависимости скорости от времени представляет собой прямую линию, перпендикулярную оси скорости и параллельную оси времени.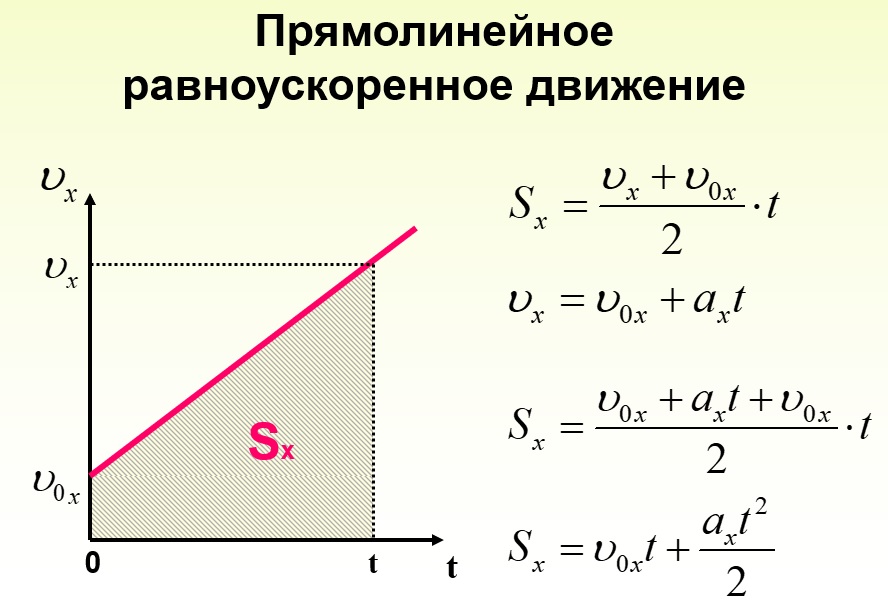 Выглядит он так:
Выглядит он так:
- Если график скорости лежит выше оси времени, тело движется в направлении оси ОХ.
- Если график скорости лежит ниже оси времени, тело движется против оси ОХ.
Чтобы сравнить модули скоростей на графике, нужно оценить их удаленность от оси времени. Чем дальше график от оси, тем больше модуль.
Пример №1. Найти модуль скорости и направление движения тела относительно оси ОХ. Выразить скорость в км/ч.
График скорости пересекает ось в точке со значением 10. Единица измерения — м/с. Поэтому модуль скорости равен 10 м/с. График лежит выше оси времени. Это значит, что тело движется по направлению оси ОХ. Чтобы выразить скорость в км/ч, нужно перевести 10 м в километры и 1 с в часы:
Теперь нужно разделить километры на часы:
Перемещение и координаты тела при равномерном прямолинейном движении
Геометрический смысл перемещения заключается в том, что его модуль равен площади фигуры, ограниченной графиком скорости, осями скорости и времени, а также линией, проведенной перпендикулярно оси времени.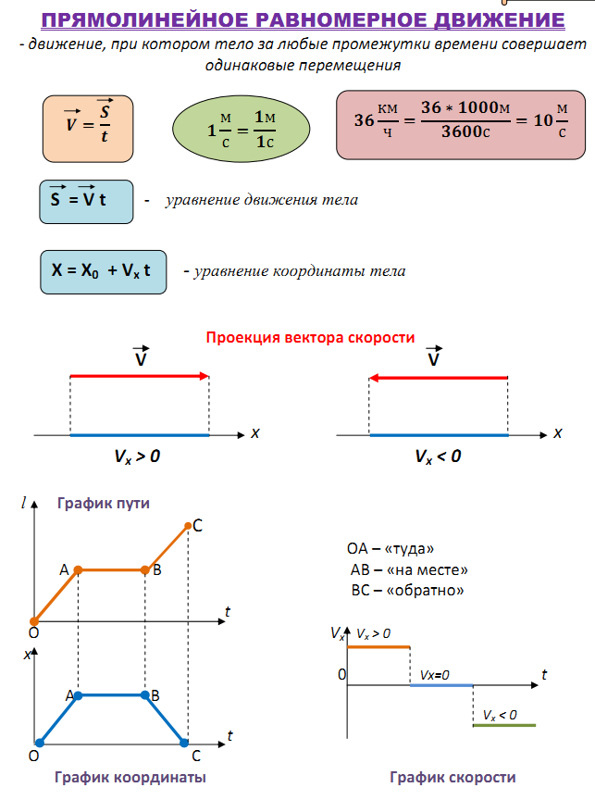
При прямолинейном равномерном движении эта фигура представляет собой прямоугольник. Поэтому модуль перемещения вычисляется по следующей формуле:
Вектор перемещения равен произведению вектора скорости на время движения:
Внимание!При равномерном прямолинейном движении путь и перемещение совпадают. Поэтому путь, пройденный телом, можно найти по этим же формулам.
Формула проекции перемещения:
График проекции перемещения
График проекции перемещения показывает зависимость этой проекции от времени. При прямолинейном равномерном движении он представляет собой луч, исходящий из начала координат. Выглядит он так:
Определение направления движения по графику проекции перемещения- Если луч лежит выше оси времени, тело движется в направлении оси ОХ.
- Если луч лежит ниже оси времени, тело движется против оси ОХ.
- Если луч совпадает с этой осью, тело покоится.

Чтобы по графику проекции перемещения сравнить модули скоростей, нужно сравнить углы их наклона к оси sx.Чем меньше угол, тем больше модуль. Согласно рисунку выше, модули скорости тел, которым соответствуют графики 1 и 3, равны. Они превосходят модуль скорости тела 2, так как их угол наклона к оси sx меньше.
График координаты
График координаты представляет собой график зависимости координаты от времени. Выглядит он так:
Так как график координаты представляет собой график линейной функции, уравнение координаты принимает вид:
Определение направления движения тела по графику координаты- Если с течением времени координата увеличивается (график идет снизу вверх), тело движется в направлении оси ОХ. На картинке выше этому соответствуют графики тел 1 и 2.
- Если с течением времени координата уменьшается (график идет сверху вниз), тело движется противоположно направлению оси ОХ.
 На картинке выше этому соответствует график тела 3.
На картинке выше этому соответствует график тела 3. - Если координата не изменяется, тело покоится.
Чтобы сравнить модули скоростей тел по графику координат, нужно сравнить углы наклона графика к оси координат. Чем меньше угол, тем больше модуль скорости. На картинке выше наибольший модуль скорости соответствует графику 1. У графиков 2 и 3 модули равны.
Чтобы по графику координат найти время встречи двух тел, нужно из точки пересечения их графиков провести перпендикуляр к оси времени.
Пример №2. График зависимости координаты тела от времени имеет вид:
Изучите график и на его основании выберите два верных утверждения:
- На участке 1 скорость тела постоянна, а на участке 2 равна нулю.
- Проекция ускорения тела на участке 1 положительна, а на участке 2 — отрицательна.
- На участке 1 тело движется равномерно, а на участке 2 оно покоится.
- На участке 1 тело движется равноускорено, а на участке 2 оно движется равномерно.

- Проекция ускорения тела на участке 1 отрицательна, а на участке 2 — положительна.
На участке 1 координата растет, и ее график представляет собой прямую. Это значит, что на этом участке тело движется равномерно (с постоянной скоростью). На участке 2 координата с течением времени не меняется, что говорит о том, что тело покоится. Исходя из этого, верными утверждениями являются номера 1 и 3.
Пример №3. На рисунке изображен график движения автомобиля из пункта А (х=0 км) в пункт В (х=30 км). Чему равна минимальная скорость автомобиля на всем пути движения туда и обратно?
Согласно графику, с начала движения до прибытия автомобиля в пункт 2 прошло 0,5 часа. А с начала движения до возвращения в пункт А прошло 1,5 часа. Поэтому время, в течение которого тело возвращалось из пункта В в пункт А, равно:
1,5 – 0,5 = 1 (час).
Туда и обратно автомобиль проходил равные пути, каждый из которых равен 30 км. Поэтому скорость во время движения от А к В равна:
Скорость во время движения от В к А равна:
Минимальная скорость автомобиля на всем пути движения составляет 30 км/ч.
На рисунке представлены графики зависимости пройденного пути от времени для двух тел. Скорость второго тела v2 больше скорости первого тела v1 в n раз, где n равно…
Алгоритм решения
- Выбрать любой временной интервал.
- Выбрать для временного интервала начальные и конечные пути для каждого из графиков.
- Записать формулу скорости и вычислить ее для 1 и 2 тела.
- Найти n — отношение скорости второго тела к скорости первого тела
Решение
Рассмотрим графики во временном интервале от 0 до 4 с. Ему соответствуют следующие данные:
- Для графика 1: начальный путь s10 = 0 м. Конечный путь равен s1 = 80 м.
- Для графика 2: начальный путь s20 = 0 м. Конечный путь равен s2 = 120 м.
Скорость определяется формулой:
Так как начальный момент времени и скорость для обоих тел нулевые, формула примет вид:
Скорость первого тела:
Скорость второго тела:
Отношение скорости второго тела к скорости первого тела:
Ответ: 1,5pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18768На рисунке приведён график зависимости координаты тела от времени при прямолинейном движении тела по оси Ox.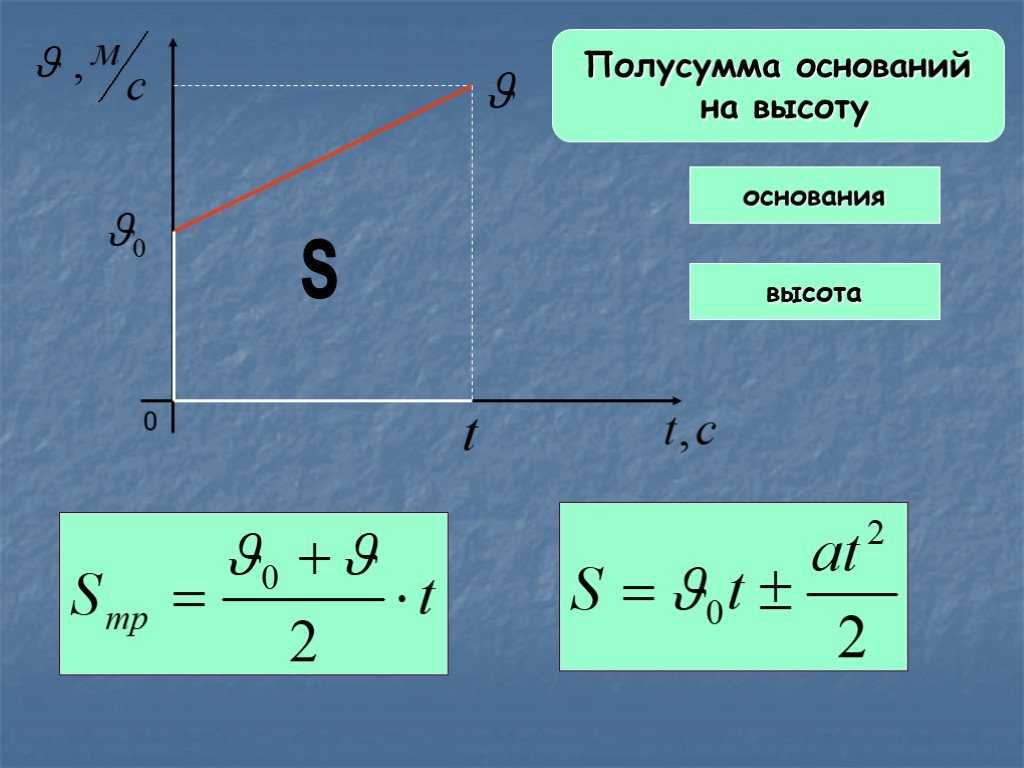
Какой из графиков соответствует зависимости от времени для проекции υx скорости этого тела на ось Ox?
Алгоритм решения
- Записать уравнение координаты при равномерном прямолинейном движении.
- Выразить из уравнения проекцию скорости.
- Определить начальную и конечную координаты, а также время, в течение которого двигалось тело.
- Вычислить проекцию скорости.
- Выбрать соответствующий график.
Уравнение координаты при равномерном прямолинейном движении имеет вид:
Отсюда проекция скорости равна:
Начальная координата xo = 10 м, конечная x = –10 м. Общее время, в течение которого двигалось тело, равно 40 с.
Вычисляем проекцию скорости:
Этому значению соответствует график «в».
Ответ: вpазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18831 На рисунке представлен график зависимости модуля скорости υ автомобиля от времени t.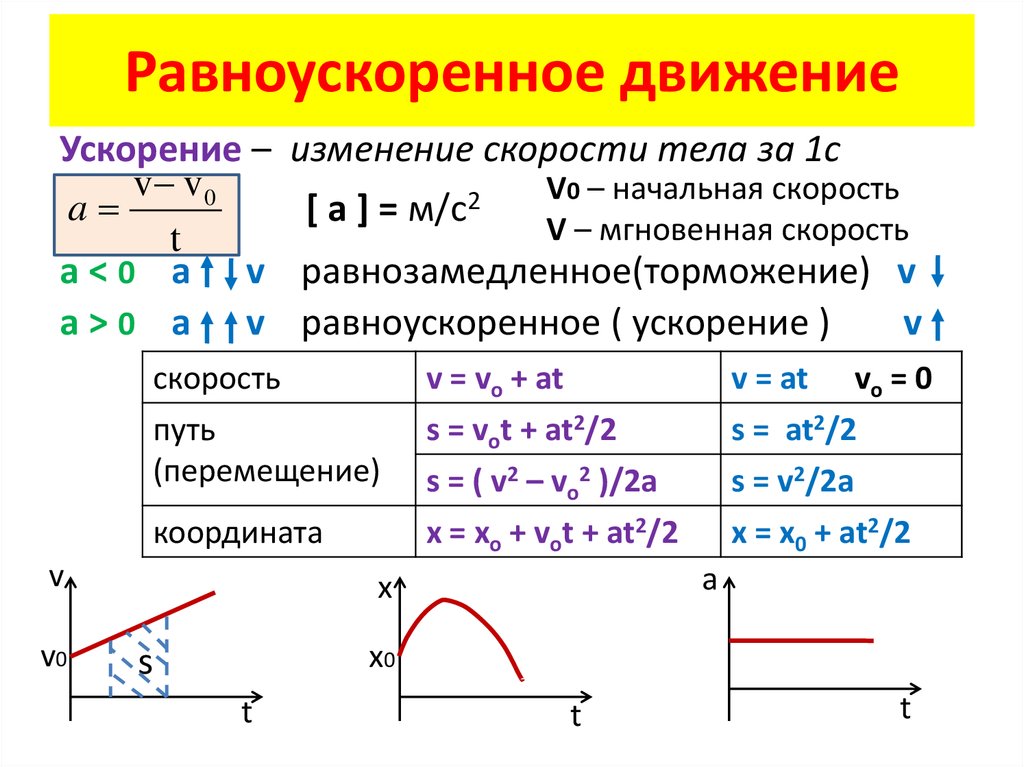 Определите по графику путь, пройденный автомобилем в интервале времени от t1=20 с до t2=50 с.
Определите по графику путь, пройденный автомобилем в интервале времени от t1=20 с до t2=50 с.
Алгоритм решения
- Охарактеризовать движение тела на различных участках графика.
- Выделить участки движения, над которыми нужно работать по условию задачи.
- Записать исходные данные.
- Записать формулу определения искомой величины.
- Произвести вычисления.
Решение
Весь график можно поделить на 3 участка:
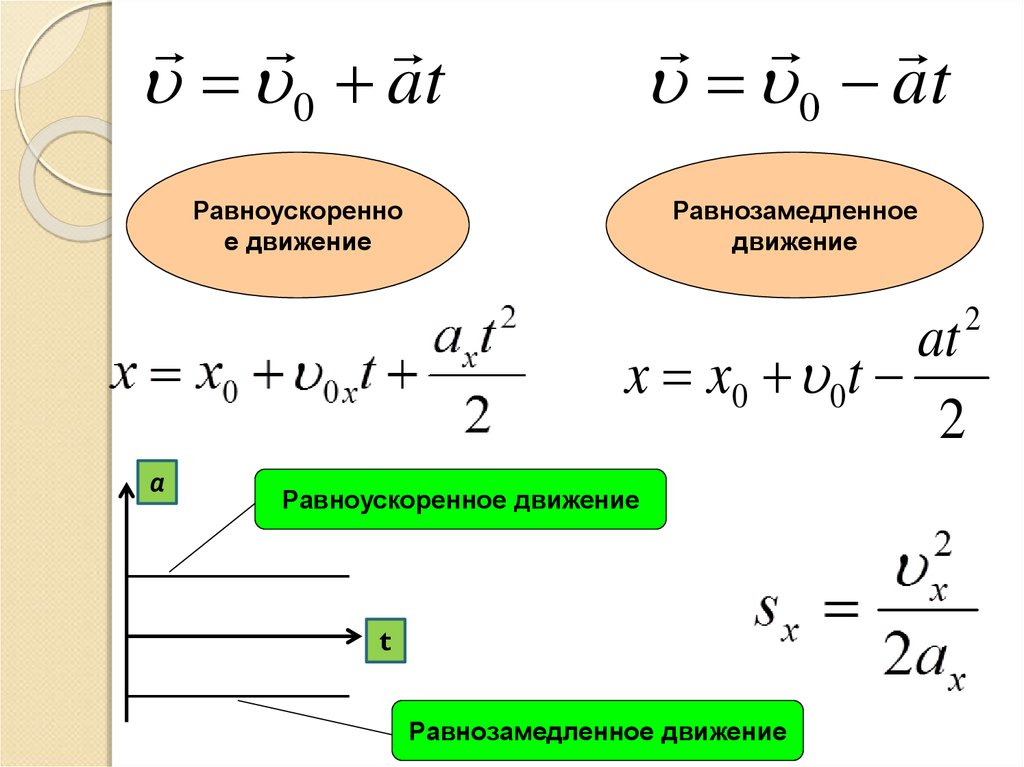
- От t1 = 0 c до t2 = 10 с. В это время тело двигалось равноускоренно (с положительным ускорением).
- От t1 = 10 c до t2 = 30 с. В это время тело двигалось равномерно (с нулевым ускорением).
- От t1 = 30 c до t2 = 50 с. В это время тело двигалось равнозамедленно (с отрицательным ускорением).
По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t1 = 20 c до t2 = 50 с. Этому времени соответствуют два участка:
Этому времени соответствуют два участка:
- От t1 = 20 c до t2 = 30 с — с равномерным движением.
- От t1 = 30 c до t2 = 50 с — с равнозамедленным движением.
Исходные данные:
- Для первого участка. Начальный момент времени t1 = 20 c. Конечный момент времени t2 = 30 с. Скорость (определяем по графику) — 10 м/с.
- Для второго участка. Начальный момент времени t1 = 30 c. Конечный момент времени t2 = 50 с. Скорость определяем по графику. Начальная скорость — 10 м/с, конечная — 0 м/с.
Записываем формулу искомой величины:
s = s1 + s2
s1 — путь тела, пройденный на первом участке, s2 — путь тела, пройденный на втором участке.
s1и s2 можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:
Теперь рассчитаем пути s1и s2, а затем сложим их:
s1+ s2= 100 + 100 = 200 (м)
Ответ: 200pазбирался: Алиса Никитина | обсудить разбор | оценить
Алиса Никитина | Просмотров: 13. 2k
2k
Движение снаряда — Формулы | Решенные проблемы
Движение снаряда — это движение объекта, который проецируется в воздух, а затем подвергается силе тяжести. Это тип двумерного движения. Горизонтальное движение является равномерным (постоянная скорость), а вертикальное движение равномерно ускорено (свободное падение под действием силы тяжести). Путь, по которому следует снаряд, известен как траектория и представляет собой параболическую кривую. Ключевыми факторами, влияющими на движение снаряда, являются начальная скорость $u$ и угол проекции $\theta$.
Формулы снарядов
Пусть из начала координат вылетает частица со скоростью $u$, составляющей угол $\theta$ с горизонтом. Ось $x$ расположена в горизонтальной плоскости (по направлению проекции), ось $y$ – вертикально вверх.
Параболическая траектория снаряда Начальная скорость частицы
\начать{выравнивать}
u_x &=u\cos\тета,\\
u_y &=u\sin\тета.
\end{выравнивание}
Ускорение частицы равно
\начать{выравнивать}
а_х&=0, \\
a_y &=-g\шляпа\jmath. 2\sin2\theta}{g}. \номер
\end{выравнивание}
9\circ+\theta)}{g}=\frac{\sqrt{2}u}{g}\left(\cos\theta+\sin\theta\right),\nonumber
\end{выравнивание}
Легко показать, что $T_1T_2=2R/g$.
2\sin2\theta}{g}. \номер
\end{выравнивание}
9\circ+\theta)}{g}=\frac{\sqrt{2}u}{g}\left(\cos\theta+\sin\theta\right),\nonumber
\end{выравнивание}
Легко показать, что $T_1T_2=2R/g$.
Задача о максимальной высоте снаряда
Мяч брошен с земли со скоростью 15 м/с под углом $\theta$ к горизонту так, что его дальность полета и максимальная высота равны, тогда $\tan\theta$ будет равно (JEE Mains 2022)
- 1/4
- 1/2
- 2
- 4
92/г}.\номер \end{выравнивание}
Снаряд на наклонной плоскости
Наклонная плоскость без трения составляет угол 45 градусов с горизонтом. Частица брошена на наклон из точки O под углом $\theta$ к горизонту. Одновременно ящик подбрасывается вверх по склону из точки O. Если частица приземляется в ящике, когда ящик достигает максимальной высоты, то значение $\theta$ равно?
Проецирование на наклонную плоскостьНаводящая на размышления задача на снаряд
Вопрос 1 Частица вылетает из точки со скоростью 2 м/с под углом 30 градусов к горизонту.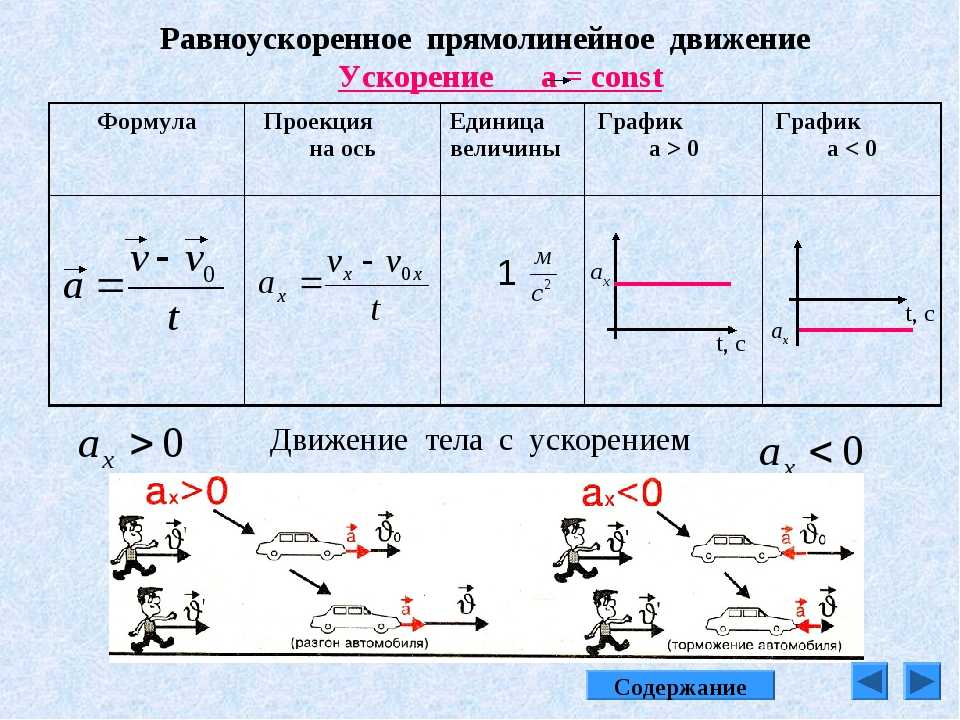 График зависимости высоты $h$ в метрах от времени в секундах показан на рисунке. Каким будет угол $\theta$, изображенный на рисунке. Сопротивлением воздуха пренебречь.
График зависимости высоты $h$ в метрах от времени в секундах показан на рисунке. Каким будет угол $\theta$, изображенный на рисунке. Сопротивлением воздуха пренебречь.
Вопрос 2 Предположим, что частица имеет положительный заряд $q$ и в пространстве существует очень малое электрическое поле $E$ направленное вверх. Нарисуйте график зависимости $h$ от $t$ (покажите пунктиром) в этой ситуации на том же рисунке, что и выше.
Вопрос 3 Траектория снаряда при отсутствии сопротивления воздуха показана на рисунке пунктирной линией. Путь того же снаряда при наличии сопротивления воздуха определяется как
Влияние сопротивления на траекторию снаряда- 1
- 2
- 3
- 4
Больше задач на снаряд
- IIT JEE 2011: Снаряд на разгоняющемся поезде
- Угловой момент снаряда
Связанные
- Угловой момент снаряда
- Движение в плоскости (общее)
- Реактивно-линейное движение
Избранные видеоролики о снаряде
Ваши конструктивные комментарии
Объяснение урока: Вертикальное движение под действием силы тяжести к гравитации.
Вблизи поверхности Земли тело, на которое не действует результирующая вертикальная сила, отличная от собственного веса, будет равномерно ускоряться вертикально вниз. Ускорение свободного падения представлено 𝑔 и имеет величину примерно 9.8 м/с 2 . Ускорение силы тяжести зависит от расстояния от центра масс Земли, но изменение 𝑔 с высотой мало у поверхности Земли и рассматривается как постоянное значение.
Важно различать ускорение свободного падения вблизи поверхности Земли и чистое ускорение тела вблизи поверхности Земли. Тело вблизи поверхности Земли не обязательно движется вертикально вниз со скоростью 9,8 м/с 2 . Например, тело в состоянии покоя или движущееся параллельно поверхности Земли (моделируя Землю как сферу) имеет нулевое вертикальное ускорение. Это связано с тем, что вес тела, находящегося в контакте с поверхностью Земли, не является единственной силой, действующей на тело.
Этот объяснитель рассматривает исключительно тела, на которые действует только сила их веса, поэтому мы пренебрежем силами сопротивления, действующими на тела со стороны воздуха. Движение таких тел можно смоделировать с помощью кинематических уравнений движения с равномерным ускорением, таких как
𝑣=𝑢+𝑎𝑡,𝑣=𝑢+2𝑎𝑠,𝑠=𝑢𝑡+12𝑎𝑡,
где 𝑢 — начальная скорость частицы, 𝑣 — конечная скорость частицы, 𝑎 — ускорение частицы, а 𝑠 — смещение частицы.
Движение таких тел можно смоделировать с помощью кинематических уравнений движения с равномерным ускорением, таких как
𝑣=𝑢+𝑎𝑡,𝑣=𝑢+2𝑎𝑠,𝑠=𝑢𝑡+12𝑎𝑡,
где 𝑢 — начальная скорость частицы, 𝑣 — конечная скорость частицы, 𝑎 — ускорение частицы, а 𝑠 — смещение частицы.
Рассмотрим пример свободно движущегося тела, на которое действует только его вес.
Пример 1. Определение начальной скорости частицы, брошенной вертикально вверх
Частица была брошена вертикально вверх от земли. Учитывая, что максимальная высота, на которую поднялась частица, была 62,5 м, найти скорость, с которой она была отброшена. Примите ускорение свободного падения 𝑔=9,8/мс.
Ответ
Движение частицы можно смоделировать с помощью уравнения 𝑣=𝑢+2𝑎𝑠.
Ускорение частицы обусловлено только силой тяжести, поэтому величина ускорения составляет 9,8 м/с 2 . Ускорение направлено вертикально вниз. Частица летит вертикально вверх, поэтому ускорение силы тяжести направлено в сторону, противоположную начальной скорости частицы. Если направление начальной скорости частицы принять за положительное, то ускорение отрицательно; следовательно, мы имеем это
𝑣=𝑢−2(9,8)(𝑠)=𝑢−19,6(𝑠).
Если направление начальной скорости частицы принять за положительное, то ускорение отрицательно; следовательно, мы имеем это
𝑣=𝑢−2(9,8)(𝑠)=𝑢−19,6(𝑠).
Это уравнение можно изменить так, чтобы 𝑢 стало предметом: 𝑢=𝑣+19.6(𝑠).
Частица мгновенно покоится, когда достигает максимальной высоты, поэтому в этот момент ее скорость равна нулю. Мы видим тогда, что 𝑢=0+19,6(62,5)=1225,
Извлекая положительный корень из 𝑢, получаем 𝑢=√1225=35/.ms
Отрицательным корнем пренебрегаем, так как это соответствует вертикально нисходящей скорости частицы, а частица не может изначально иметь вертикально нисходящую скорость, поскольку она проецируется вертикально вверх.
Равномерно ускоренное тело имеет непрерывно изменяющуюся скорость, но среднее значение этой скорости равно среднему значению его скоростей до и после ускорения, определяемому формулой 𝑣=𝑣+𝑢2.среднее
Рассмотрим пример определения средней скорости тела, ускоренного только силой тяжести.
Пример 2.
 Определение средней скорости падающего тела
Определение средней скорости падающего телаЕсли тело, упавшее со здания, достигло земли за 3 секунды, найдите его среднюю скорость в момент падения. Пусть ускорение свободного падения 𝑔=9,8/мс.
Ответ
Ускорение тела, движущегося с равномерным ускорением, равно 𝑎=𝑣−𝑢𝑡.
Это выражение можно преобразовать для определения средней скорости следующим образом: 𝑣−𝑢=𝑎𝑡𝑣=𝑢+𝑎𝑡.
Подставив известные значения 𝑡 и 𝑎 и предположив, что 𝑢 равно нулю, поскольку тело было сброшено, а не спроецировано вертикально, мы имеем, что 𝑣=9,8(3)=29,4/.мс
Средняя скорость объекта – это среднее значение его скоростей до и после ускорения, определяемое выражением 𝑣=𝑣+𝑢2.average
Мы уже видели, что 𝑢 равно нулю, поэтому имеем 𝑣=29,42=14,7/.averagems
Теперь давайте рассмотрим пример, в котором мы определяем перемещение тела, брошенного вертикально с известной скоростью.
Пример 3. Определение максимальной высоты, на которую попадает мяч, брошенный вертикально вверх
Частица брошена вертикально вверх со скоростью 7 м/с из точки на высоте 38,7 м над землей. Найдите максимальную высоту, на которую может подняться частица. Считайте, что ускорение свободного падения равно 𝑔=9,8/мс.
Найдите максимальную высоту, на которую может подняться частица. Считайте, что ускорение свободного падения равно 𝑔=9,8/мс.
Ответ
Частица достигает максимальной высоты в тот момент, когда она мгновенно находится в покое и вот-вот начнет падать обратно к точке, из которой она была спроецирована.
В этом примере нам даны начальная скорость частицы, начальное вертикальное смещение частицы и вертикальное ускорение частицы. Скорость частицы при ее наибольшем вертикальном смещении будет мгновенно равна нулю.
Смещение частицы из точки, в которую она была спроецирована в данный момент, можно определить по формуле, содержащей эти члены; следовательно, мы можем использовать формулу 𝑣=𝑢+2𝑎𝑠, где 𝑣=0/мс, 𝑢=7/мс и 𝑎=-9,8/мс. Преобразовывая уравнение, чтобы сделать 𝑠 предметом, мы получаем 𝑠=𝑣−𝑢2𝑎.
Подставляя известные значения, находим 𝑠=0−72(−9,8)=2,5.м
Начальное вертикальное смещение частицы составляло 38,7 м, поэтому наибольшее вертикальное смещение частицы определяется выражением
38,7+2,5=41,2. м
м
Рассмотрим еще один такой пример.
Пример 4: Использование уравнений движения для решения вертикальной проекции Вопрос
Заполните пропуск: Если тело брошено вертикально вверх со скоростью 𝑉 чтобы достичь максимальной высоты ℎ, то скорость, с которой тело должно быть отброшено, чтобы достичь высоты 4ℎ, равна .
Ответ
Частица достигает максимальной высоты в тот момент, когда она мгновенно находится в покое и вот-вот начнет падать обратно к точке, из которой она была спроецирована. Смещение частицы из точки, в которую она была спроецирована в этот момент, можно определить по формуле 𝑣=𝑢+2𝑎𝑠.
Преобразуя уравнение, чтобы сделать 𝑠 субъектом, и отметив, что 𝑣 равно нулю, и что, поскольку вертикальное направление вниз считается отрицательным, 𝑢 и 𝑎 отрицательны, мы получаем 𝑠=−𝑢−2𝑔.
Числитель и знаменатель правой части выражения отрицательны, поэтому оно эквивалентно выражению 𝑠=𝑢2𝑔.
Для значения 𝑢, равного 𝑉, значение 𝑠 равно ℎ. Важно отметить, что мы не должны путать значение начальной скорости 𝑉 с символом, используемым для термина конечной скорости, 𝑣.
Важно отметить, что мы не должны путать значение начальной скорости 𝑉 с символом, используемым для термина конечной скорости, 𝑣.
Используя значения 𝑉 и ℎ, мы имеем, что ℎ=𝑉2𝑔.
Нам нужно определить, как начальная скорость, обозначаемая 𝑉, соответствующая значению 𝑠, равному 4ℎ, сравнивается с начальной скоростью 𝑉.
Мы знаем, что частица, запущенная вертикально вверх со скоростью 𝑉, имеет нулевую скорость, когда ее вертикальное перемещение равно 4ℎ.
Мы можем использовать уравнение 𝑣=𝑢+2𝑎𝑠 и подставьте значения 𝑉 для начальной скорости, 𝑔 для ускорения и 4ℎ для смещения. Отметив, что 𝑣 равно нулю и что 𝑔 отрицательно, когда 𝑉 положительно, мы имеем, что 0=𝑉−2𝑔(4ℎ).
Замена ℎ=𝑉2𝑔, у нас есть это 0=𝑉−2𝑔(4)𝑉2𝑔0=𝑉−8𝑔𝑉2𝑔0=𝑉−4𝑉.
Мы можем преобразовать это выражение, чтобы получить выражение, которое связывает 𝑨 : 4𝑉=𝑉.
Взяв квадратный корень из обеих частей, мы находим, что √4𝑉=𝑉2𝑉=𝑉.
Мы видим, что 𝑉 имеет вдвое большее значение, чем 𝑉.
Рассмотрим пример, когда тело брошено вертикально с неизвестной скоростью и конечная скорость тела также неизвестна.
Пример 5. Определение времени, за которое тело достигает основания башни
Тело было брошено вертикально вниз с вершины башни высотой 80 м. Учитывая, что за 1-ю секунду своего движения он прошел 35,9 м, найдите время, за которое он достиг земли, округленное до двух знаков после запятой. Пусть ускорение свободного падения 𝑔=90,8/мс.
Ответ
Ни начальная скорость тела, ни его скорость в какой-либо точке во время его движения не могут быть определены из информации, данной в вопросе, и поэтому ответ не может быть определен путем сравнения начальной и конечной скоростей тела.
Может показаться, что конечная скорость тела равна нулю, так как тело в конце концов достигает земли, но в момент, когда тело достигает земли, его мгновенная скорость не равна нулю. Если тело не отскакивает, то скорость тела вскоре после того, как оно достигнет земли, будет равна нулю, но оно не достигает земли с нулевой скоростью.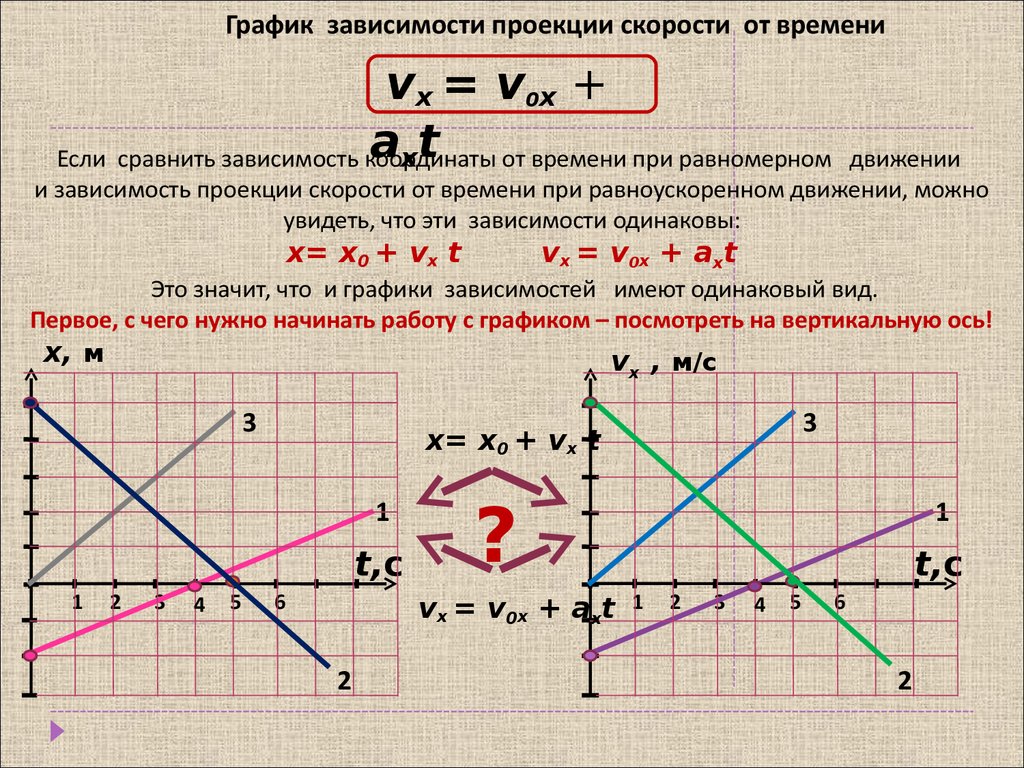

 На картинке выше этому соответствует график тела 3.
На картинке выше этому соответствует график тела 3.
Leave A Comment