Формулы площади треугольника через синус

Определение и формула площади треугольника через синус

ОПРЕДЕЛЕНИЕ

Треугольником называется фигура, состоящая из трех вершин и трех сторон.

Существует много формул для вычисления площади треугольника. Если известны длины двух сторон треугольника и угол между этими сторонами, то для вычисления площади треугольника удобно пользоваться следующей формулой

   

где – стороны треугольника, – угол между сторонами и .

Примеры решения задач

ПРИМЕР 1
Задание Найти площадь треугольника со сторонами см и см, если угол между этими сторонами равен .
Решение Площадь треугольника будем искать как полупроизведение сторон треугольника на синус угла между ними:

   

Ответ см
ПРИМЕР 2
Задание В треугольнике угол , а сторона на см больше стороны . Найти длины сторон и треугольника, если его площадь равна .
Решение Обозначим сторону через , тогда сторона будет равна . Запишем формулу для площади треугольника

   

и подставим в нее известные данные:

   

Преобразуем последнее уравнение и получим квадратное уравнение

   

Корнями полученного уравнения будут и . По смыслу задачи подходит только первый корень. Тогда см, а см.
Ответ см, см.

ru.solverbook.com

Площадь треугольника через синус и косинус

I. Площадь треугольника через синус

Если в задаче даны длины двух сторон треугольника и угол между ними, то можно применить формулу площади треугольника через синус.

Пример расчета площади треугольника через синус. Даны стороны a = 3, b = 4, и угол γ= 30°. По таблице синусов синус угла в 30° равен 0.5

Площадь треугольника будет равна 3 кв. см.
Также могут быть и другие условия. Если дана длина одной стороны и углы, то для начала нужно вычислить недостающий угол. Т.к. сумма всех углов треугольника равняется 180°, то:

Площадь будет равна половине квадрата стороны, умноженной на дробь. В ее числителе находится произведение синусов прилегающих углов, а в знаменателе синус противолежащего угла. Теперь рассчитываем площадь по следующим формулам:

Например, дан треугольник со стороной a=3 и углами γ=60°, β=60°. Вычисляем третий угол:
Подставляем данные в формулу
Получаем, что площадь треугольника равняется 3,87 кв. см.

II. Площадь треугольника через косинус

Чтобы найти площадь треугольника, нужно знать длины всех сторон. По теореме косинусов можно найти не известные стороны, а уже потом использовать формулу Герона.

По теореме косинусов квадрат неизвестной стороны треугольника равняется сумме квадратов остальных сторон минус удвоенное произведение этих сторон на косинус угла, находящегося между ними.

Из теоремы выводим формулы для поиска длины неизвестной стороны:

Зная как найти недостающую сторону, имея две стороны и угол между ними можно легко посчитать площадь. Формула площади треугольника через косинус помогает легко и быстро найти решение различных задач.

2mb.ru

Теорема о площади треугольника. Формулы для нахождения площадей параллелограмма и треугольника

На этом уроке мы выведем формулу площади треугольника через синус его угла.

Сформулируем, проанализируем и докажем теорему о площади треугольника.

Теорема звучит так:

Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.

Запишем данную теорему в стандартных для треугольника обозначениях.

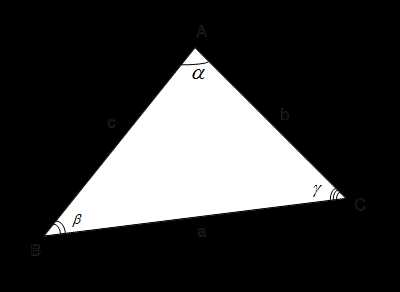
Рис. 1. Площадь треугольника

Формула площади треугольника (рис. 1) имеет такой вид:

 

Докажем данную теорему.

Дано: (рис. 2)

Доказать:

Доказательство:

Любой треугольник АВС имеет не менее двух острых углов, так как сумма углов треугольника равна 180 градусов. Пусть острыми являются угол  и угол . Тогда высота АН= находится внутри треугольника АВС, потому что иначе сумма углов в треугольнике  (рис. 2) превышала бы 180 градусов (угол  прямой, так как  – высота; а угол при вершине В тупой, так как угол  (по условию).

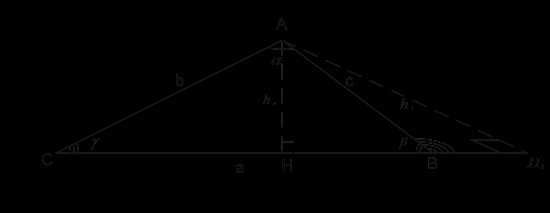
Рис. 2. Иллюстрация к теореме

Получили два прямоугольных треугольника общим катетом АН=. Для нахождения данного катета мы используем свойство сторон и углов прямоугольного треугольника: гипотенузу умножаем на синус противолежащего угла:     

 

Подставим данное значение в формулу площади треугольника:

 

Получаем:

 

Мы доказали две формулы из трёх через острые углы . Если угол α острый, доказательство будет аналогичное. Если угол α будет прямым, доказательство очевидное (. При  высота С= находится вне треугольника АВС (рис. 3).

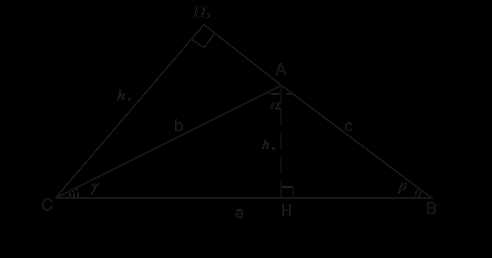
Рис. 3. Иллюстрация к теореме

Рассмотрим треугольник  . В нём угол . Чтобы найти катет , нужно гипотенузу умножить на синус противолежащего угла:

 

 

          

Подставляем в формулу для площади треугольника  () значение катета :

 

Мы доказали и третью формулу. Следовательно, доказали теорему.

Также эту теорему можно доказать координатным методом (рис. 4).

Дано: треугольник АВС, ,

Доказать:

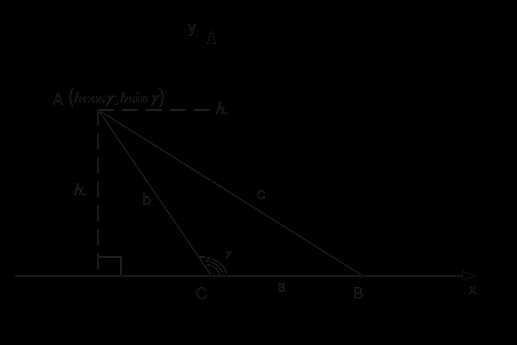
Рис. 4. Иллюстрация к теореме

Координаты вершины А определяются через длину АС=b и угол γ. В предыдущих уроках мы выяснили, что координаты точки А будут . А  – это высота , то есть ордината точки А.

   

Подставляем в формулу площади треугольника:

 

Формула доказана независимо от величины углов треугольника – за начало координат была взята точка С. Остальные 2 формулы получаются аналогично, если за начало координат взять точку А или В.

Полученные формулы можно использовать во многих задачах.

Дано: треугольник АВС, АВ= см, АС=4 см, ⦟А=(рис. 5)

Найти: площадь треугольника АВС

Решение:

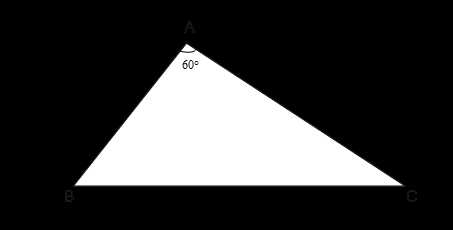
Рис. 5. Иллюстрация к задаче

Для решения данной задачи воспользуемся ранее доказанной теоремой.

 

Подставляем известные значения:

 

 

Докажите, что площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними.

Доказательство:

Для доказательства воспользуемся свойствами параллелограмма. Диагональ BD рассекает параллелограмм на два треугольника.  (рис. 6) по трём равным сторонам (противоположные стороны в параллелограмме равны, следовательно, АВ=CD, AD=BC. Сторона BD – общая для двух треугольников.). Отсюда следует, что площади этих двух треугольников тоже равны.

Площадь параллелограмма

 

Согласно теореме о площади треугольника

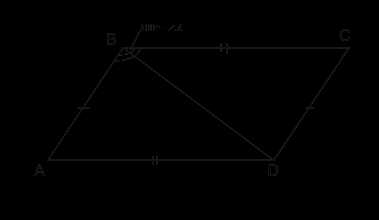
Рис. 6. Иллюстрация к задаче

 

Значит, площадь параллелограмма равна

 =

Можно рассмотреть и угол В. Он равен , следовательно, . Поэтому площадь параллелограмма можно рассчитать через :

 

Формула для площади параллелограмма доказана.

Треугольники ADB и ADC параллелограмма ABCD . Доказать, что площади этих треугольников равны.

Доказательство:

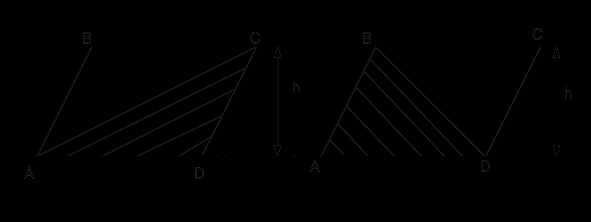Рис. 7. Иллюстрация к задаче

Площади первого и второго треугольника есть произведение половины основания на высоту (рис. 7). Основание у них одинаковое (AD), высота, опущенное на это основание, также одинаковая, следовательно:

 

Дано:, АС15 см,

Найти: сторону АВ (рис. 8)

Решение:

Рис. 8. Иллюстрация к задаче

Найдём сторону АВ через формулу площади треугольника

 

Подставляем известные величины:

 

 см

 

Докажите, что площадь параллелограмма равна половине произведения длин его диагоналей на синус угла между ними.

Дано:

ABCD – параллелограмм (рис. 9)

Доказать:

Доказательство: первый способ:

Учтём, что угол α и угол  имеют один и тот же синус:

 

Площадь треугольника АОВ (согласно теореме о площади треугольника):

 

Площадь треугольника ВОС: 

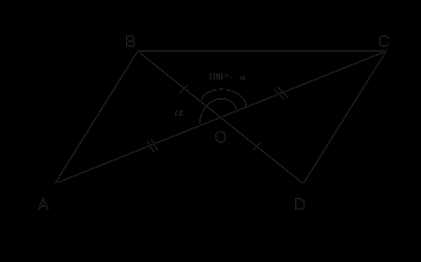
Рис. 9. Иллюстрация к задаче

 

Так как синусы равны, то и . Учитывая, что , а , мы доказали, что диагонали параллелограмма делят его на 4 равновеликих треугольника.

Поэтому для нахождения площади параллелограмма достаточно найти площадь одного из треугольников и умножить на 4.

   

Так как , то

Что и требовалось доказать.

 

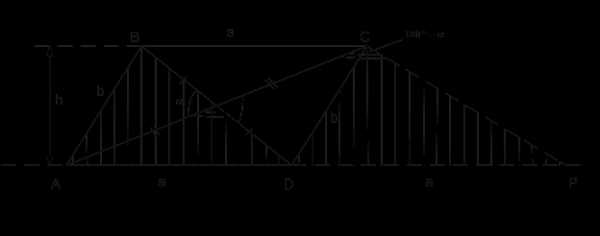
Рис. 10. Иллюстрация к задаче

Из точки С диагонали АС проводим прямую CР, параллельную другой диагонали (BD). Получаем параллелограмм BDPC, треугольник ABD равновелик треугольнику DCP, так как

Основания и высота у них одинаковы.

Таким образом, отнимая от параллелограмма ABCD треугольник ABD и прибавляя треугольник DCP, получаем треугольник АСР с такой же площадью, как у исходного параллелограмма. И площадь этого треугольника равна:

 

 

    

Так как СРBD и  , то

  

Что и требовалось доказать.

Дано:

, , высота ВН=h

Найти: площадь треугольника АВС (рис. 11)

Решение:

                                           

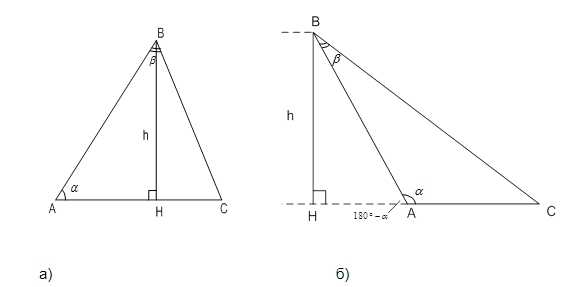
Рис. 11. Иллюстрация к задаче

Согласно теореме о площади треугольника

 

Выражаем АВ и ВС через h и другие известные величины. АВ является

гипотенузой в прямоугольном треугольнике АВН, поэтому:

, при  (рис. 11 а)

, при  (рис. 11 б)

Аналогично находим ВС (). В обоих случаях:

Подставляем данные значения в формулу площади треугольника:

 

На данном уроке мы доказали теорему о площади треугольника через синус его

угла и решили задачи по данной теме.

           

Список литературы

  1. Атанасян Л. С. и др. Геометрия 7–9 классы. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2010.
  2. Фарков А. В. Тесты по геометрии: 9 класс. К учебнику Л. С. Атанасяна и др. – М.: Экзамен, 2010.
  3. Погорелов А. В. Геометрия, уч. для 7–11 кл. общеобр. учрежд. – М.: Просвещение, 1995.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

  1. E-science.ru (Источник).
  2. 2mb.ru (Источник).
  3. Festival.1september.ru (Источник).

 

Домашнее задание

  1. В треугольнике ABC AB = 1 см, BC = 2 см, , . Найдите площадь треугольника. 
  2. Для определения площади треугольника АВС измерили две его стороны a и b и угол между ними γ. Вычислить площадь (a= 125 мм, b= 160 мм, γ = 52).
  3. Площадь треугольника АВС равна 18. АС = ВС = 3. Найдите сторону АВ.

interneturok.ru

Площадь треугольника через синус угла

Площадь треугольника через синус угла
Рассматривать возможные формулы будем на примере построенного произвольного треугольника с обозначенными сторонами и углами.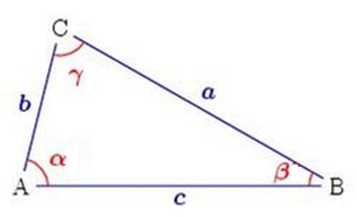

Если по условию задачи заданы две стороны треугольника и угол между этими же сторонами, то удобно использовать следующие формулы площади треугольника:

   

   

   

Рассмотрим пример расчета с помощью этой формулы.

Задача.
Известны стороны треугольника 3 см и 4 см, а также угол между ними 30 градусов. Найти площадь этого треугольника.

Решение.
Используем одну из выше рассмотренных формул:

   

   

Чтобы найти синус 30 градусов, можно воспользоваться таблицей синусов. Получим:
(кв. см)

Ответ. 3 кв. см.

Если же по условию задана одна из сторон и два угла, то изначально необходимо вычислить третий угол, используя свойство углов треуг-ника:

   

   

   

В таком случае площадь треуг-ника можно найти как 1/2 от квадрата стороны, умноженного на дробь, c перемноженными sin-ми прилежащих к стороне углов в числителе и sin-ом третьего угла — в знаменателе. Формулы будут выглядеть следующим образом:

   

   

   

ru.solverbook.com

Площадь треугольника по двум сторонам

Выясним, как найти площадь треугольника по двум сторонам.

Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.

Формула площади треугольника по двум сторонам:

 

   

 

 

 

 

Дано:

∆ ABC.

 

Доказать:

   

Доказательство:

 

Проведем в треугольнике ABC высоту BD.

Площадь треугольника

равна половине произведения его стороны на высоту, проведенную к этой стороне:

   

Рассмотрим треугольник ABD — прямоугольный (так как BD — высота по построению).

По определению синуса острого угла в прямоугольном треугольнике,

   

Отсюда

   

Таким образом,

   

 

Если в треугольнике ABC

угол A тупой,

 

 

 

 

 

 

 

то в треугольнике ABD

 

 

 

   

(как смежные).

По формуле

   

имеем:

   

   

То есть, и в случае тупого угла A выполняется равенство

   

а значит, верна формула

   

Что и требовалось доказать.

www.treugolniki.ru

Площадь треугольника | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU

Площадь любого треугольника можно найти, зная основание и высоту. Вся простота схемы заключается в том, что высота делит основание a на две части a1 и a2, а сам треугольник – на два прямоугольных треугольника, площадь которых получается и . Тогда площадь всего треугольника будет суммой двух указанных площадей, и если мы вынесем одну вторую высоты за скобку, то в сумме мы получим обратно основание:

Более сложный для расчетов способ – это формула Герона, для которой необходимо знать все три стороны. Для этой формулы нужно вычислить сначала полупериметр треугольника: Сама формула Герона подразумевает квадратный корень из полупериметра, умноженного поочередно на разность его с каждой из сторон.

Следующий способ, также актуальный для любого треугольника, позволяет найти площадь треугольника через две стороны и угол между ними. Доказательство этому проистекает из формулы с высотой – проводим высоту на любую из известных сторон и через синус угла α получаем, что h=a⋅sinα . Для вычисления площади умножим половину высоты на вторую сторону.

Другой способ – найти площадь треугольника, зная 2 угла и сторону между ними. Доказательство этой формулы достаточно простое, и наглядно видно из схемы.

Опускаем из вершины третьего угла высоту на известную сторону и называем полученные отрезки x соответственно. Из прямоугольных треугольников видно, что первый отрезок x равен произведению котангенса угла α на высоту, а второй отрезок y – произведению котангенса угла β на эту же высоту. Дальше соединяем это вместе:



geleot.ru

Площадь треугольника

Площадь треугольника — это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной тремя отрезками (сторонами), которые соединяют три точки (вершины), не лежащие на одной прямой.

Для вычисления площади треугольника применяются различные формулы, в зависимости от известных исходных данных. Ниже приведены формулы и калькулятор, который поможет вычислить площадь треугольника или проверить уже выполненные вычисления. Приведены общие формулы для всех типов треугольников, частные случаи для равносторонних, равнобедренных и прямоугольных треугольников.


Для всех треугольников


1

Площадь треугольника по основанию и высоте

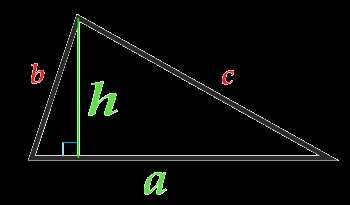
Площадь треугольника равна половине произведения основания треугольника на высоту, опущенную на это основание: . Основанием треугольника может быть выбрана любая из сторон треугольника.

Сторона a

Высота h




2

Площадь треугольника по двум сторонам и углу между ними

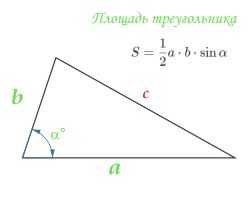
Площадь треугольника равна половине произведения двух любых его сторон на синус угла между этими сторонами: . Угол α между сторонами может быть любым: тупым, острым, прямым.

Сторона a

Сторона b

Угол α° между сторонами a и b




3

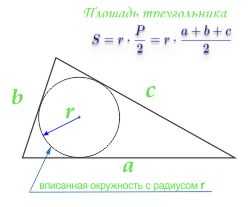
Площадь треугольника по радиусу вписанной окружности и трем сторонам

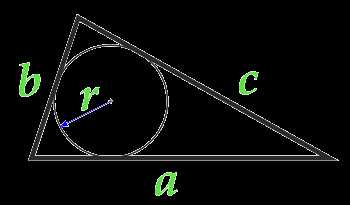
Площадь треугольника равна половине суммы всех трех сторон треугольника умноженной на радиус вписанной окружности.  или по-другому можно сказать: «Площадь треугольника равна половине периметра треугольника, умноженного на радиус вписанной окружности.»

Сторона a

Сторона b

Сторона c

Радиус r вписанной окружности




4

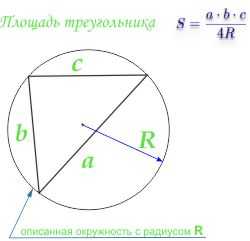
Площадь треугольника по радиусу описанной окружности и трем сторонам

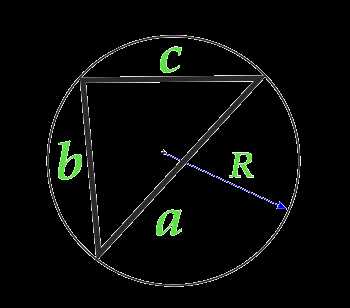
Площадь треугольника равна произведению трех сторон треугольника, деленных на четыре радиуса описанной окружности:

Сторона a

Сторона b

Сторона c

Радиус R описанной окружности




5

Площадь треугольника по формуле Герона

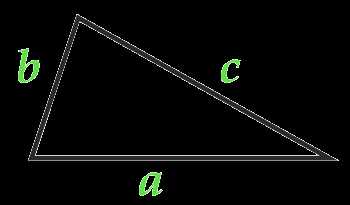
Если известны все три стороны треугольника, можно вычислить его площадь используя формулу Герона: , где p – это полупериметр треугольника, вычисляемый по формуле

Сторона a

Сторона b

Сторона c

Полупериметр:



Для равнобедренных треугольников


6

Площадь равнобедренного треугольника по боковым сторонам и углу между ними

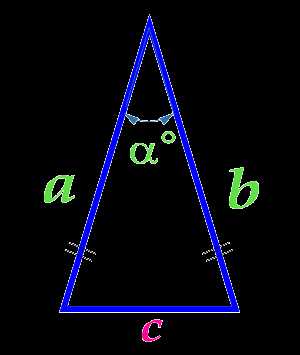
Вычислить площадь:

Боковая сторона a (a = b)

Угол α° между боковыми сторонами




7

Площадь равнобедренного треугольника по боковым сторонам и углу между ними

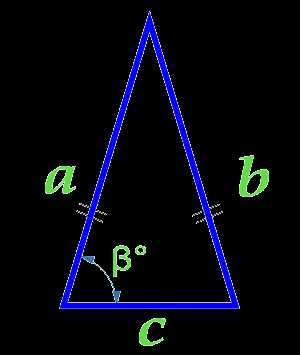
Вычислить площадь:

Боковая сторона a (a = b)

Основание треугольника c

Угол β° между основанием и стороной




8

Площадь равнобедренного треугольника по основанию и углу между боковыми сторонами

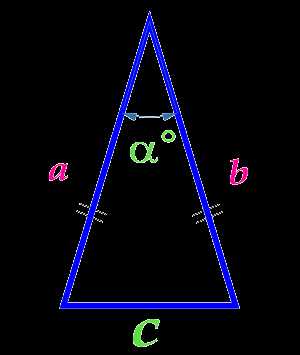
Вычислить площадь:

Основание треугольника c

Угол α° между боковыми сторонами



Для равносторонних треугольников


9

Площадь равностороннего треугольника по стороне

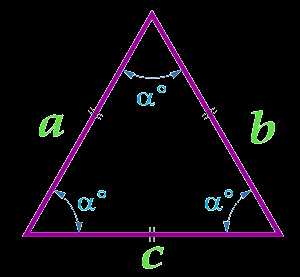
Вычислить площадь:

Сторона a (a = b = c)




10

Площадь равностороннего треугольника по высоте

Вычислить площадь:

Высота h




11

Площадь равностороннего треугольника по радиусу вписанной окружности

Вычислить площадь:

Радиус r вписанной окружности




12

Площадь равностороннего треугольника по радиусу описанной окружности

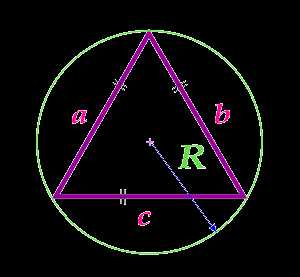
Вычислить площадь:

Радиус R описанной окружности



Для прямоугольных треугольников


13

Площадь прямоугольного треугольника по двум катетам

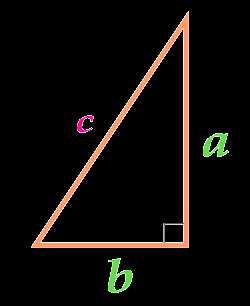
Вычислить площадь:

Катет a

Катет b




14

Площадь прямоугольного треугольника по отрезкам, на которые делит гипотенузу вписанная окружность

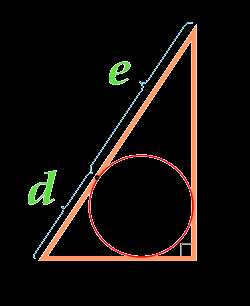
Вычислить площадь:

Отрезок d

Отрезок e




15

Площадь прямоугольного треугольника по формуле Герона

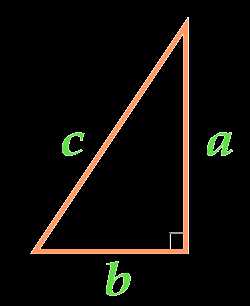
Формула Герона для прямоугольного треугольника , где p – это полупериметр треугольника, вычисляемый по формуле

Вычислить площадь:

Сторона a

Сторона b

Сторона c

Полупериметр:


Определения

Треугольник – это геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Отрезки называют сторонами треугольника, а точки – вершинами треугольника.

Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.

Площадь измеряется в единицах измерения в квадрате: км2, м2, см2, мм2 и т.д.

В зависимости от вида треугольника и его известных исходных данных, площадь треугольника можно вычислить:

Для всех треугольников

  1. по основанию и высоте
  2. по двум сторонам и углу между ними
  3. по радиусу вписанной окружности и трем сторонам
  4. по радиусу описанной окружности и трем сторонам
  5. по формуле Герона

Для равнобедренных треугольников

  1. по боковым сторонам и углу между ними
  2. по боковой стороне, основанию и углу между боковыми сторонами и основанием
  3. по основанию и углу между боковыми сторонами

Для равносторонних треугольников

  1. по стороне
  2. по высоте
  3. по радиусу вписанной окружности
  4. по радиусу описанной окружности

Для прямоугольных треугольников

  1. по двум катетам
  2. по отрезкам, на которые делит гипотенузу вписанная окружность
  3. по формуле Герона

doza.pro