Радиус описанной около треугольника окружности

Радиус описанной около треугольника окружности можно найти по одной из двух общих формул.

Кроме того, для правильного и прямоугольного треугольников существуют дополнительные формулы.

Радиус описанной около произвольного треугольника окружности

Формула I (следствие из теоремы синусов)

   

 

То есть радиус описанной окружности равен отношению длины стороны треугольника к удвоенному синусу противолежащего этой стороне угла.

В общем виде эту формулу записывают так:

   

 

Формула II.

   

в общем виде —

   

То есть чтобы найти радиус описанной около треугольника окружности, надо произведения длин сторон треугольника разделить на четыре площади треугольника.

Если площадь треугольника находить по формуле Герона

   

где p — полупериметр,

   

то получим формулу радиуса описанной около треугольника окружности через длины сторон:

   

Обе эти формулы можно применить к треугольнику любого вида. Следует только учесть положение центра.

Центр описанной около прямоугольного треугольника окружности лежит на середине гипотенузы.

Центр описанной около тупоугольного треугольника окружности лежит вне треугольника, напротив тупого угла.

 

Радиус окружности, описанной около прямоугольного треугольника

Формула:

   

То есть в прямоугольном треугольнике радиус описанной окружности равен половине гипотенузы.

Обычно гипотенузу обозначают через c (AB=c) и формулу записывают так:

   

 

Радиус окружности, описанной около правильного треугольника

Формула:

   

Если без иррациональности в знаменателе, то

   

В равностороннем треугольнике радиус описанной окружности в два раза больше радиуса вписанной окружности:

   

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — ПланиметрияОписанная окружность центр радиус серединный перпендикуляр свойства теорема синусов

Серединный перпендикуляр к отрезку

      Определение 1. Серединным перпендикуляром к отрезку называют, прямую, перпендикулярную к этому отрезку и проходящую через его середину (рис. 1).

Серединный перпендикуляр свойства

Рис.1

      Теорема 1. Каждая точка серединного перпендикуляра к отрезку находится на одном и том же расстоянии от концов этого отрезка.

      Доказательство. Рассмотрим произвольную точку   D,   лежащую на серединном перпендикуляре к отрезку   AB   (рис.2), и докажем, что треугольники   ADC   и   BDC   равны.

Серединный перпендикуляр свойства

Рис.2

      Действительно, эти треугольники являются прямоугольными треугольниками, у которых катеты   AC   и   BC   равны, а катет   DC   является общим. Из равенства треугольников   ADC   и   BDC   вытекает равенство отрезков   AD   и   DB.   Теорема 1 доказана.

      Теорема 2 (Обратная  к теореме 1). Если точка находится на одном и том же расстоянии от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку.

      Доказательство. Докажем теорему 2 методом «от противного». С этой целью предположим, что некоторая точка   E   находится на одном и том же расстоянии от концов отрезка, но не лежит на серединном перпендикуляре к этому отрезку. Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точки   E   и   A   лежат по разные стороны от серединного перпендикуляра (рис.3). В этом случае отрезок   EA   пересекает серединный перпендикуляр в некоторой точке, которую мы обозначим буквой   D.

Серединный перпендикуляр свойства

Рис.3

      Докажем, что отрезок   AE   длиннее отрезка   EB.   Действительно,

Серединный перпендикуляр свойства
Серединный перпендикуляр свойства

      Таким образом, в случае, когда точки   E   и   A   лежат по разные стороны от серединного перпендикуляра, мы получили противоречие.

Серединный перпендикуляр свойства

Рис.4

      Теперь рассмотрим случай, когда точки   E   и   A   лежат по одну сторону от серединного перпендикуляра (рис.4). Докажем, что отрезок   EB   длиннее отрезка   AE.   Действительно,

Серединный перпендикуляр свойства
Серединный перпендикуляр свойства

      Полученное противоречие и завершает доказательство теоремы 2

Окружность, описанная около треугольника

      Определение 2. Окружностью, описанной около треугольника, называют окружность, проходящую через все три вершины треугольника (рис.5). В этом случае треугольник называют треугольником, вписанным в окружность, или вписанным треугольником.

Описанная около треугольника окружность треугольник вписанный в окружность

Рис.5

Свойства описанной около треугольника окружности. Теорема синусов

ФигураРисунокСвойство
Серединные перпендикуляры
к сторонам треугольника		Серединный перпендикуляр свойства
Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.
Посмотреть доказательство
Окружность, описанная около треугольникаОписанная около треугольника окружность треугольник вписанный в окружностьОколо любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.
Посмотреть доказательство
Центр описанной около остроугольного треугольника окружностиЦентр описанной около остроугольного треугольника окружности лежит внутри треугольника.
Центр описанной около прямоугольного треугольника окружностиОписанная около прямоугольного треугольника окружностьЦентром описанной около прямоугольного треугольника окружности является середина гипотенузы.
Посмотреть доказательство
Центр
 описанной около тупоугольного треугольника окружности		Описанная около треугольника окружность центр радиус свойстваЦентр описанной около тупоугольного треугольника окружности лежит вне треугольника.
Теорема синусовТеорема синусов

Для любого треугольника справедливы равенства (теорема синусов):

Теорема синусов,

где   a , b , c   – стороны треугольника,   A , B , С   – углы треугольника,   R   – радиус описанной окружности.

Посмотреть доказательство

Площадь треугольника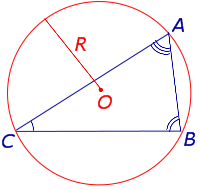Формула площади треугольника через радиус описанной окружности

Для любого треугольника справедливо равенство:

S = 2R2 sin A sin B sin C ,

где   A , B , С   – углы треугольника,   S   – площадь треугольника,   R   – радиус описанной окружности.

Посмотреть доказательство

Радиус описанной окружностиФормула для радиуса описанной окружности

Для любого треугольника справедливо равенство:

Формула для радиуса описанной окружности

где   a , b , c   – стороны треугольника,   S   – площадь треугольника,   R   – радиус описанной окружности.

Посмотреть доказательство

Серединные перпендикуляры к сторонам треугольника
Серединный перпендикуляр свойства

Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.

Посмотреть доказательство

Окружность, описанная около треугольника
Описанная около треугольника окружность треугольник вписанный в окружность

Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.

Посмотреть доказательство

Центр описанной около остроугольного треугольника окружности
Описанная около треугольника окружность треугольник вписанный в окружность

Центр описанной около остроугольного треугольника окружности лежит внутри треугольника.

Центр описанной около прямоугольного треугольника окружности
Описанная около прямоугольного треугольника окружность

Центром описанной около прямоугольного треугольника окружности является середина гипотенузы.

Посмотреть доказательство

Центр описанной около тупоугольного треугольника окружности
Описанная около треугольника окружность центр радиус свойства

Центр описанной около тупоугольного треугольника окружности лежит вне треугольника.

Теорема синусов
Теорема синусов

Для любого треугольника справедливы равенства (теорема синусов):

Теорема синусов,

где   a , b , c   – стороны треугольника,   A , B , С   – углы треугольника,   R   – радиус описанной окружности.

Посмотреть доказательство

Площадь треугольника
Формула площади треугольника через радиус описанной окружности

Для любого треугольника справедливо равенство:

S = 2R2 sin A sin B sin C ,

где   A , B , С   – углы треугольника,   S   – площадь треугольника,   R   – радиус описанной окружности.

Посмотреть доказательство

Радиус описанной окружности
Формула для радиуса описанной окружности

Для любого треугольника справедливо равенство:

Формула для радиуса описанной окружности

где   a , b , c   – стороны треугольника,   S   – площадь треугольника,   R   – радиус описанной окружности.

Посмотреть доказательство

Доказательства теорем о свойствах описанной около треугольника окружности

      Теорема 3. Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.

      Доказательство. Рассмотрим два серединных перпендикуляра, проведённых к сторонам   AC   и   AB   треугольника   ABC,   и обозначим точку их пересечения буквой   O   (рис. 6).

Описанная около треугольника окружность серединный перпендикуляр свойства доказательства

Рис.6

      Поскольку точка   O   лежит на серединном перпендикуляре к отрезку   AC,   то в силу теоремы 1 справедливо равенство:

CO = AO .

      Поскольку точка O лежит на серединном перпендикуляре к отрезку   AB,   то в силу теоремы 1 справедливо равенство:

AO = BO .

      Следовательно, справедливо равенство:

CO = BO ,

откуда с помощью теоремы 2 заключаем, что точка O лежит на серединном перпендикуляре к отрезку   BC. Таким образом, все три серединных перпендикуляра проходят через одну и ту же точку, что и требовалось доказать.

      Следствие. Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.

      Доказательство. Рассмотрим точку   O,   в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника   ABC   (рис. 6).

      При доказательстве теоремы 3 было получено равенство:

AO = OB = OC ,

из которого вытекает, что окружность с центром в точке   O   и радиусами   OA,   OB,   OC   проходит через все три вершины треугольника   ABC,   что и требовалось доказать.

      Теорема 4 (теорема синусов). Для любого треугольника (рис. 7)

Теорема синусов

Рис.7

справедливы равенства:

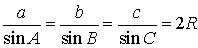Теорема синусов.

      Доказательство. Докажем сначала, что длина хорды окружности радиуса   R хорды окружности радиуса   R,   на которую опирается вписанный угол величины   φ ,   вычисляется по формуле:

      Рассмотрим сначала случай, когда одна из сторон вписанного угла является диаметром окружности (рис.8).

Описанная около треугольника окружность серединный перпендикуляр свойства доказательства

Рис.8

      Угол   MPN,   как угол,опирающийся на диаметр, является прямым угломугол,опирающийся на диаметр, является прямым углом, и равенство (1) вытекает из определения синуса угла прямоугольного треугольника.

      Поскольку все вписанные углы, опирающиеся на одну и ту же дугу, равны, то для произвольного вписанного угла всегда найдется равный ему вписанный угол, у которого одна из сторон является диаметром окружности.

      Формула (1) доказана.

      Из формулы (1) для вписанного треугольника   ABC   получаем (рис.7):

Теорема синусов доказательствоТеорема синусов доказательство

      Теорема синусов доказана.

Подготовка к ЕГЭ и ОГЭ в учебном центре Резольвента

      На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Радиус описанной окружности равностороннего треугольника

радиус описанной окружности равностороннего треугольника

 

сторона — сторона треугольника

высота — высота

радиус — радиус описанной окружности

 

 

Формула радиуса  описанной  окружности  равностороннего  треугольника через его сторону:

Формула радиуса описанной окружности равностороннего треугольника через сторону

Калькулятор — вычислить, найти радиус описанной окружности равностороннего треугольника по стороне

 

 

Формула радиуса  описанной  окружности  равностороннего  треугольника через высоту:

Формула радиуса описанной окружности равностороннего треугольника через высоту

 

Калькулятор — вычислить, найти радиус описанной окружности равностороннего треугольника по стороне

 

 

Подробности
Автор: Administrator logo

Как найти радиус окружности — Лайфхакер

Выбирайте формулу в зависимости от известных величин.

Через площадь круга

  1. Разделите площадь круга на число пи.
  2. Найдите корень из результата.
Как найти радиус окружности через площадь кругаИллюстрация: Лайфхакер
  • R — искомый радиус окружности.
  • S — площадь круга. Напомним, кругом называют плоскость внутри окружности.
  • π (пи) — константа, равная 3,14.

Сейчас читают 🔥

Через длину окружности

  1. Умножьте число пи на два.
  2. Разделите длину окружности на результат.
Как найти радиус круга через длину окружностиИллюстрация: Лайфхакер
  • R — искомый радиус окружности.
  • P — длина окружности (периметр круга).
  • π (пи) — константа, равная 3,14.

Через диаметр окружности

Если вы вдруг забыли, радиус равняется половине диаметра. Поэтому, если диаметр известен, просто разделите его на два.

Как найти радиус окружности через диаметрИллюстрация: Лайфхакер
  • R — искомый радиус окружности.
  • D — диаметр.

Через диагональ вписанного прямоугольника

Диагональ прямоугольника является диаметром окружности, в которую он вписан. А диаметр, как мы уже вспомнили, в два раза больше радиуса. Поэтому достаточно разделить диагональ на два.

Как вычислить радиус окружности через диагональ вписанного прямоугольникаИллюстрация: Лайфхакер
  • R — искомый радиус окружности.
  • d — диагональ вписанного прямоугольника. Напомним, она делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Поэтому, если диагональ неизвестна, её можно найти через соседние стороны прямоугольника с помощью теоремы Пифагора.
  • a, b — стороны вписанного прямоугольника.

Через сторону описанного квадрата

Сторона описанного квадрата равна диаметру окружности. А диаметр — повторимся — равен двум радиусам. Поэтому разделите сторону квадрата на два.

Как найти радиус круга через сторону описанного квадратаИллюстрация: Лайфхакер
  • r — искомый радиус окружности.
  • a — сторона описанного квадрата.

Через стороны и площадь вписанного треугольника

  1. Перемножьте три стороны треугольника.
  2. Разделите результат на четыре площади треугольника.
Как найти радиус окружности через стороны и площадь вписанного треугольникаИллюстрация: Лайфхакер

Через площадь и полупериметр описанного треугольника

Разделите площадь описанного треугольника на его полупериметр.

Как найти радиус окружности через площадь и полупериметр описанного треугольникаИллюстрация: Лайфхакер
  • r — искомый радиус окружности.
  • S — площадь треугольника.
  • p — полупериметр треугольника (равен половине от суммы всех сторон).

Через площадь сектора и его центральный угол

  1. Умножьте площадь сектора на 360 градусов.
  2. Разделите результат на произведение пи и центрального угла.
  3. Найдите корень из полученного числа.
Как найти радиус окружности через площадь сектора и его центральный уголИллюстрация: Лайфхакер
  • R — искомый радиус окружности.
  • S — площадь сектора круга.
  • α — центральный угол.
  • π (пи) — константа, равная 3,14.

Через сторону вписанного правильного многоугольника

  1. Разделите 180 градусов на количество сторон многоугольника.
  2. Найдите синус полученного числа.
  3. Умножьте результат на два.
  4. Разделите сторону многоугольника на результат всех предыдущих действий.
Как вычислить радиус круга через сторону вписанного правильного многоугольникаИллюстрация: Лайфхакер
  • R — искомый радиус окружности.
  • a — сторона правильного многоугольника. Напомним, в правильном многоугольнике все стороны равны.
  • N — количество сторон многоугольника. К примеру, если в задаче фигурирует пятиугольник, как на изображении выше, N будет равняться 5.

Читайте также 📐✂️📌

Радиус окружности — что такое, формула, как найти ⚪

Основные понятия

Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.

Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.

Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.

Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.

Формула радиуса окружности

Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.

Если известна площадь круга

R = √ S : π, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

Если известна длина

R = P : 2 * π, где P — длина (периметр круга).

Если известен диаметр окружности

R = D : 2, где D — диаметр.

Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.

Если известна диагональ вписанного прямоугольника

R = d : 2, где d — диагональ.

Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:

d = √ a2 + b2, где a, b — стороны вписанного прямоугольника.

Если известна сторона описанного квадрата

R = a : 2, где a — сторона.

Сторона описанного квадрата равна диаметру окружности.

Если известны стороны и площадь вписанного треугольника

R = (a * b * c) : (4 * S), где a, b, с — стороны, S — площадь треугольника.

Если известна площадь и полупериметр описанного треугольника

R = S : p, где S — площадь треугольника, p — полупериметр треугольника.

Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.

Если известна площадь сектора и его центральный угол

R = √ (360° * S) : (π * α), где S — площадь сектора круга, α — центральный угол.

Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.

Если известна сторона вписанного правильного многоугольника

R = a : (2 * sin (180 : N)), где a — сторона правильного многоугольника, N — количество сторон.

В правильном многоугольнике все стороны равны.

Скачать онлайн таблицу

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики в детскую школу Skysmart. Вместо скучных учебников ученики проходят интерактивные задания с автоматической проверкой, рисуют вместе с учителем на онлайн-доске и задают вопросы, которые бывает неловко спросить перед всем классом.

 

Радиус вписанной и описанной окружности: полезные формулы. Задание С4

В этой статье я хочу привести несколько полезных формул, которые помогают легко найти радиус вписанной и описанной окружности, и показать решение задачи из задания С4 с использованием этих формул.

1. Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности:

 S=pr. где p={a+b+c}/2, r — радиус вписанной окружности.

Отсюда: r=S/p

То есть радиус вписанной окружности равен отношению площади треугольника к его полупериметру.

Для прямоугольного треугольника p={a+b+c}/2, S={ab}/2, тогда

r={ab}/{a+b+c}

где a и b — катеты треугольника, а c — гипотенуза.

2. Площадь треугольника равна отношению произведения его сторон к учетверенному радиусу описанной окружности:

c

S={abc}/{4R}

Отсюда:

R={abc}/{4S}

Радиус  окружности, описанной около треугольника, равен отношению произведения сторон треугольника к его учетверенной площади.

3. По теореме синусов, отношение стороны треугольника к синусу противолежащего угла равно двум радиусам описанной окружности:

a/{sinA}=b/{sinB}=c/{sinC}=2R

Отсюда:

R=a/{2sinA}=b/{2sinB}=c/{2sinC}

Радиус  окружности, описанной около треугольника, равен отношению стороны треугольника к удвоенному синусу противолежащего угла.

Предлагаю вам посмотреть ВИДЕОРЕШЕНИЕ задачи:

Угол при основании равнобедренного треугольника  равен varphi. Найдите отношение радиуса вписанной в этот треугольник окружности к радиусу описанной окружности:

 

 

И.В. Фельдман, репетитор по математике.

Описанная окружность — YouClever.org

Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».

Первый вопрос, который может возникнуть: описанная – вокруг чего?

Ну, вообще-то иногда бывает и вокруг чего угодно, а мы будем рассуждать об окружности, описанной вокруг (иногда ещё говорят «около») треугольника. Что же это такое?

Описанная окружность – такая окружность, что проходит через все три вершины треугольника, около которого она описана.

Вот так:

Описанная окружность рис. 1

И вот, представь себе, имеет место удивительный факт:

Вокруг всякого треугольника можно описать окружность.

Почему этот факт удивительный?

Но ведь треугольники – то бывают разные!

Описанная окружность рис. 2

И для всякого найдётся окружность, которая пройдёт через все три вершины, то есть описанная окружность.

Доказательство этого удивительного факта можешь найти в следующих уровнях теории, а здесь заметим только, что если взять, к примеру, четырехугольник, то уже вовсе не для всякого найдётся окружность, проходящая через четыре вершины. Вот, скажем, параллелограмм – отличный четырехугольник, а окружности, проходящей через все его четыре вершины – нет!

Описанная окружность рис. 3

А есть только для прямоугольника:

Описанная окружность рис. 4

Ну вот, а треугольник всякий и всегда имеет собственную описанную окружность! И даже всегда довольно просто найти центр этой окружности.

Центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к сторонам этого треугольника.

Знаешь ли ты, что такое серединный перпендикуляр?

Прямая, проходящая через середину отрезка и перпендикулярная ему Это прямая, проходящая через середину отрезка и перпендикулярная ему.Прямая   – это серединный перпендикуляр к отрезку  .

А теперь посмотрим, что получится, если мы рассмотрим целых три серединных перпендикуляра к сторонам треугольника.

Вот оказывается (и это как раз и нужно доказывать, хотя мы и не будем), что все три перпендикуляра пересекутся в одной точке. Смотри на рисунок – все три серединных перпендикуляра пересекаются в одной точке  .

Три серединных перпендикуляра к сторонам треугольника Это и есть центр описанной около (вокруг) треугольника   окружности.

Как ты думаешь, всегда ли центр описанной окружности лежит внутри треугольника? Представь себе – вовсе не всегда!

Если треугольник тупоугольный, то центр его описанной окружности лежит снаружи!

Вот так:

Если треугольник тупоугольный, то центр его описанной окружности лежит снаружи

А вот если остроугольный, то – внутри:

Если треугольник остроугольный, то центр его описанной окружности лежит внутри

Что же делать с прямоугольным треугольником?

В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы.
В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы. Правда, здорово?Если треугольник – прямоугольный, то не надо строить аж три перпендикуляра, а можно просто найти середину гипотенузы – и центр описанной окружности готов!

Да ещё с дополнительным бонусом:

в прямоугольном треугольнике радиус описанной окружности равен половине гипотенузы

Раз уж заговорили о радиусе описанной окружности: чему он равен для произвольного треугольника? И есть ответ на этот вопрос: так называемая теорема синусов.

А именно:

В прямоугольном треугольнике радиус описанной окружности равен половине гипотенузы

В произвольном треугольнике:
 

Ну и, конечно,

Так что ты теперь всегда сможешь найти и центр , и радиус окружности, описанной вокруг треугольника.То есть чтобы найти радиус описанной окружности, нужно знать одну (!) сторону и один (!) противолежащий ей угол. Хорошая формула? По-моему, просто отличная!

ОПИСАННАЯ ОКРУЖНОСТЬ. СРЕДНИЙ УРОВЕНЬ

В этой части мы обсудим окружность, описанную вокруг (часто говорят «около») треугольника. Прежде всего дадим определение.

Окружность, описанная около треугольника – такая окружность, что происходит через все три вершины этого треугольника.

1. Существование и центр описанной окружности

Тут возникает вопрос: а для всякого ли треугольника существует такая окружность? Вот оказывается, что да, для всякого. И более того, мы сейчас сформулируем теорему, которая ещё и отвечает на вопрос, где же находится центр описанной окружности.

Теорема.Вокруг всякого треугольника можно описать окружность, при том единственным образом.

Центр этой окружности – точка пересечения серединных перпендикуляров к сторонам треугольника.

Смотри, вот так:

Теорема. Вокруг всякого треугольника можно описать окружность, при том единственным образом. Центр этой окружности – точка пересечения серединных перпендикуляров к сторонам треугольника.

Давай наберёмся мужества и докажем эту теорему. Если ты читал уже тему «Биссектриса» разбирался в том, почему же три биссектрисы пересекаются в одной точке, то тебе будет легче, но и если не читал – не переживай: сейчас во всём разберёмся.

Доказательство будем проводить, используя понятие геометрического места точек (ГМТ).

Геометрическое место точек, обладающих свойством « » — такое множество точек, что все они обладают свойством « » и никакие другие точки этим свойством не обладают.

Ну вот, например, является ли множество мячей – «геометрическим местом» круглых предметов? Нет, конечно, потому что бывают круглые …арбузы. А является ли множество людей, «геометрическим местом», умеющих говорить? Тоже нет, потому что есть младенцы, которые говорить не умеют. В жизни вообще сложно найти пример настоящего «геометрического места точек». В геометрии проще. Вот, к примеру, как раз то, что нам нужно:

Серединный перпендикуляр к отрезку является геометрическим местом точек, равноудалённых от концов отрезка.

Тут множество – это серединный перпендикуляр, а свойство « » — это «быть равноудаленной (точкой) от концов отрезка».

Проверим? Итак, нужно удостовериться в двух вещах:

  1. Всякая точка на серединном перпендикуляре находится на одинаковом расстоянии от концов отрезка
  2. Всякая точка, которая равноудалена от концов отрезка – находится на серединном перпендикуляре к ему.
Всякая точка на серединном перпендикуляре находится на одинаковом расстоянии от концов отрезка Проверим 1. Пусть точка   лежит на серединном перпендикуляре к отрезку  .

Соединим   с   и с  .Тогда линия   является медианой и высотой в  . Значит,   – равнобедренный,   – убедились, что любая точка  , лежащая на серединном перпендикуляре, одинаково удалена от точек   и  .

Всякая точка, которая равноудалена от концов отрезка – находится на серединном перпендикуляре к ему. Теперь 2. Почти точно так же, но в другую сторону. Пусть точка   равноудалена от точек   и  , то есть  .

Возьмём   – середину   и соединим   и  . Получилась медиана  . Но   – равнобедренный по условию   не только медиана, но и высота, то есть – серединный перпендикуляр. Значит, точка   — точно лежит на серединном перпендикуляре.

Всё! Полностью проверили тот факт, что серединный перпендикуляр к отрезку является геометрическим местом точек, равноудаленных от концов отрезка.

Это все хорошо, но не забыли ли мы об описанной окружности? Вовсе нет, мы как раз подготовили себе «плацдарм для нападения».

Серединный перпендикуляр к отрезку является геометрическим местом точек, равноудаленных от концов отрезка.

Рассмотрим треугольник  . Проведём два серединных перпендикуляра   и  , скажем, к отрезкам   и  . Они пересекутся в какой-то точке, которую мы назовем  .

А теперь, внимание!

Точка   лежит на серединном перпендикуляре  ;
точка   лежит на серединном перпендикуляре  .
И значит,   и  .

Отсюда следует сразу несколько вещей:

Во – первых,   точка   обязана лежать на третьем серединном перпендикуляре, к отрезку  .

Серединный перпендикуляр к отрезку является геометрическим местом точек, равноудаленных от концов отрезка.

То есть серединный перпендикуляр   тоже обязан пройти через точку  , и   все три серединных перпендикуляра пересеклись в одной точке.

Во – вторых:   если мы проведём окружность с центром в точке   и радиусом  , то эта окружность также пройдёт и через точку  , и через точку  , то есть будет описанной окружностью  . Значит, уже есть, что пересечение трёх серединных перпендикуляров – центр описанной окружности для любого треугольника.

И последнее: о единственности. Ясно (почти), что точку   можно получить единственным образом, поэтому и окружность – единственная. Ну, а «почти» — оставим на твоё размышление. Вот и доказали теорему. Можно кричать «Ура!».

2. Радиус описанной окружности.

А если в задаче стоит вопрос «найдите радиус описанной окружности»? Или наоборот, радиус дан, а требуется найти что – то другое? Есть ли формула, связывающая радиус описанной окружность с другими элементами треугольника?

Радиус описанной окружности Есть, конечно! И эта формула называется «Теорема синусов» (доказательство смотри именно в этой теме). 

То есть:

Обрати внимание: теорема синусов сообщает, что для того чтобы найти радиус описанной окружности, тебе нужна одна сторона (любая!) и противолежащий ей угол. И всё!

3. Центр окружности – внутри или снаружи

А теперь вопрос: может ли центр описанной окружности лежать снаружи треугольника.
Ответ: ещё как может. Более того, так всегда бывает в тупоугольном треугольнике.

И вообще:

В остроугольном треугольнике центр описанной окружности всегда лежит внутри треугольника В остроугольном треугольнике центр описанной окружности всегда лежит внутри треугольника.
В тупоугольном треугольнике центр описанной окружности всегда лежит вне треугольника В тупоугольном треугольнике центр описанной окружности всегда лежит вне треугольника
В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы, а радиус равен половине гипотенузы. В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы, а радиус равен половине гипотенузы.

ОПИСАННАЯ ОКРУЖНОСТЬ. КОРОТКО О ГЛАВНОМ

1. Окружность, описанная около треугольника 

– это окружность, которая проходит через все три вершины этого треугольника.

В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы, а радиус равен половине гипотенузы.
  • Вокруг всякого треугольника можно описать окружность.

2. Существование и центр описанной окружности

В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы, а радиус равен половине гипотенузы.
  • Вокруг всякого треугольника можно описать окружность, при том единственным образом.
  • Центр этой окружности – точка пересечения серединных перпендикуляров к сторонам треугольника.

3. Радиус описанной окружности

В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы, а радиус равен половине гипотенузы.  

Обрати внимание: теорема синусов сообщает, что для того чтобы найти радиус описанной окружности, нужна одна сторона (любая!) и противолежащий ей угол.

4. Центр окружности – внутри или снаружи

В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы, а радиус равен половине гипотенузы.
  • В остроугольном треугольнике центр описанной окружности всегда лежит внутри треугольника
В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы, а радиус равен половине гипотенузы.
  • В тупоугольном треугольнике центр описанной окружности всегда лежит вне треугольника
В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы, а радиус равен половине гипотенузы.
  • В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы, а радиус равен половине гипотенузы.

ОСТАВШИЕСЯ 2/3 СТАТЬИ ДОСТУПНЫ ТОЛЬКО УЧЕНИКАМ YOUCLEVER!

Стать учеником YouClever,

Подготовиться к ОГЭ или ЕГЭ по математике по цене «чашка кофе в месяц», 

А также получить бессрочный доступ к учебнику «YouClever», Программе подготовки (решебнику) «100gia», неограниченному пробному ЕГЭ и ОГЭ, 6000 задач с разбором решений и к другим сервисам YouClever и 100gia.

можно кликнув по этой ссылке.

 

 

 

 

Методы калькулятора

для кругов и треугольников в плоской геометрии

Вписанные и описанные круги

Круг может быть вписан или ограничен. Круг, описывающий треугольник, проходит через вершины треугольника, в то время как круг, вписанный в треугольник, касается трех сторон треугольника. Третье соединение, связывающее круги и треугольники, представляет собой круг, обозначенный около треугольника. Эта комбинация происходит, когда часть кривой касается одной стороны, и существует воображаемая касательная, идущая от двух сторон треугольника.Учитывая, что A, B и C являются сторонами треугольника, а A — площадью, формула для радиуса окружности, описывающей треугольник, имеет вид r = ABC / 4A, а для окружности, вписанной в треугольник, — r = A / S. где S = (A + B + C) / 2.

Методы калькулятора для кругов и треугольников

Методы калькулятора для задач, связанных с кругами и треугольниками, больше по алгебре, тригонометрии и геометрии. Запоминание формул — это то, что нужно. Вот содержание статьи.

  • Круг, вписанный в треугольник
  • Круг, описывающий треугольник
  • Три окружности, которые касаются друг друга
  • Площадь сектора
  • Круг вписан в сектор
  • Биссектриса треугольника
  • Боковые размеры треугольника
  • Аккорд круга
  • Точка вне треугольника

Задача 1. Круг, вписанный в треугольник

Стороны треугольника 8 см, 10 см и 14 см.Определите радиус вписанной окружности.

Калькулятор Техника

а. Используя формулу Герона, решите для области треугольника.

б. Решите по периметру треугольника.

c. Решите для радиуса вписанной окружности.

Окончательный ответ: Радиус вписанного круга составляет 2,45 сантиметра.

Задача 2: окружность, описывающая равносторонний треугольник

Площадь круга, описывающего равносторонний треугольник, равна 250.45 кв. Какова площадь треугольника?

Калькулятор Техника

а. Учитывая площадь круга, решите для радиуса.

б. Решите для стороны равностороннего треугольника.

c. Решите для области равностороннего треугольника.

Окончательный ответ: Площадь равностороннего треугольника, вписанного в круг, составляет 103,59 кв.

Задача 3: Три Взаимно Касательных

Расстояние между центрами трех окружностей, которые взаимно касаются друг друга, составляет 10, 12 и 14 единиц.Какова площадь самого большого круга?

Калькулятор Техника

а. Сформируйте три уравнения для трех неизвестных.

б. Расположите уравнения в форме системы.

c. Решите область самого большого круга, используя самый большой радиус из шага 2.

Окончательный ответ: Площадь самого большого круга составляет 201,06 квадратных единиц.

Задача 4: Треугольник, вписанный в круг

Площадь треугольника, вписанного в круг, составляет 39.19 квадратных сантиметров, а радиус описанного круга составляет 7,14 сантиметра. Если две стороны вписанного треугольника составляют 8 сантиметров и 10 сантиметров соответственно, найдите третью сторону.

Калькулятор Техника

а. Решить для третьей стороны C.

Окончательный ответ: Длина третьей стороны составляет 14,00 сантиметра.

Задача 5: Площадь сектора

Угол сектора круга составляет 300 градусов, а радиус — 15 сантиметров.Найдите площадь в квадратных сантиметрах.

Калькулятор Техника

а. Используйте формулу для нахождения площади сектора.

б. Перейти в радиан режим. В радианном режиме введите Shift Answer и выберите знак градуса.

Окончательный ответ: Площадь сектора составляет 598,05 квадратных сантиметров.

Задача 6: Круг, вписанный в сектор

Сектор окружает круг с радиусом 8,00 сантиметров. Если центральный угол сектора составляет 80 градусов, какова площадь?

Калькулятор Техника

а.Решите для радиуса сектора.

б. Решите для области сектора.

c. Перейти в радиан режим. В радианном режиме введите Shift Answer и выберите знак градуса.

Окончательный ответ: Площадь сектора составляет 291,83 квадратных сантиметров.

Задача 7: Биссектриса треугольника

Дан треугольник ABC со сторонами AB = 30 сантиметров, BC = 36 сантиметров и AC = 48 сантиметров. Найти расстояние от точки пересечения перпендикулярных биссектрис до стороны BC.

Калькулятор Техника

а. Точка пересечения перпендикулярных биссектрис является радиусом описанной окружности. Решите для области треугольника, используя формулу Герона.

б. Решите для радиуса описанной окружности.

c. Используя теорему Пифагора, найдите недостающее значение x.

Окончательный ответ: Расстояние от точки пересечения перпендикулярных биссектрис до стороны BC составляет 15.92 сантиметра.

Задача 8: Мера сторон треугольника

Периметр треугольника ABC составляет 400 сантиметров. Если угол A составляет 30 градусов, а угол B составляет 58 градусов, найдите меру стороны AC.

Калькулятор Техника

а. Предположим, что AC = 1, затем используйте технику закона синуса при решении для сторон AB и BC. Установите калькулятор в режим уравнения и введите следующие значения.

б. Решите для длины стороны переменного тока.

Окончательный ответ: Длина стороны AC составляет 170.31 сантиметр.

Задача 9: Аккорд круга

Круг, дающий площадь 1018 квадратных сантиметров, разрезается на два сегмента хордой в 8 сантиметрах от центра. Найти отношение площади меньшей части к большей?

Калькулятор Техника

а. Решите для радиуса круга.

c. Найдите площадь маленького сегмента.

д. Решите для большего сегмента.

эл. Решите для отношения между двумя сегментами.

Окончательный ответ: Соотношение между двумя сегментами составляет 0,293.

Задача 10: Точка вне треугольника

От точки вне равностороннего треугольника расстояния до вершин составляют 10 сантиметров, 18 сантиметров и 10 сантиметров соответственно. Какова длина одной стороны треугольника?

Калькулятор Техника

а. Решите для длины одной стороны X, используя закон косинуса.

Окончательный ответ: Длина одной стороны треугольника составляет 19.95 сантиметров.

,

Уравнения окружности

Круг легко сделать:

Нарисуйте кривую, которая находится в радиусе
от центральной точки.

И так:

Все точки находятся на одинаковом расстоянии
от центра.

На самом деле определение круга

Круг на графике

Поместим круг радиуса 5 на график:

Теперь давайте отработаем , точно , где все точки.

Делаем прямоугольный треугольник:

А затем использовать Пифагор:

x 2 + y 2 = 5 2

Таких точек бесконечное множество, вот несколько примеров:

x и x 2 + y 2
5 0 5 2 + 0 2 = 25 + 0 = 25
3 4 3 2 + 4 2 = 9 + 16 = 25
0 5 0 2 + 5 2 = 0 + 25 = 25
−4 −3 (−4) 2 + (−3) 2 = 16 + 9 = 25
0 −5 0 2 + (−5) 2 = 0 + 25 = 25

Во всех случаях точка на окружности следует правилу x 2 + y 2 = радиус 2

Мы можем использовать эту идею, чтобы найти пропущенное значение

Пример: x значение 2 и радиус 5

Начать с: x 2 + y 2 = r 2

Известные нам значения: 2 2 + y 2 = 5 2

Перегруппировать: y 2 = 5 2 — 2 2

Квадратный корень с обеих сторон: y = ± √ (5 2 — 2 2 )

Решить: у = ± √21

г. ≈ ± 4.58 …

( ± означает, что есть два возможных значения: одно с + , другое с — )

И вот две точки:

Более общий случай

Теперь давайте поместим центр в (а, б)

Таким образом, круг равен , все точки (x, y) , которые находятся на расстоянии «r» от центра (a, b) .

Теперь давайте выясним, где находятся точки (используя прямоугольный треугольник и Пифагора):

Это та же идея, что и раньше, но нам нужно вычесть а и б :

И это «Стандартная форма» для уравнения круга!

Показывает всю важную информацию с одного взгляда: центр (a, b) и радиус r .

Пример: круг с центром в (3,4) и радиусом 6:

Начать с:

(x-a) 2 + (y-b) 2 = r 2

положить в (a, b) и r:

(x − 3) 2 + (y − 4) 2 = 6 2

Затем мы можем использовать наши навыки алгебры, чтобы упростить и перестроить это уравнение в зависимости от того, для чего оно нам нужно.

Попробуй сам

«Общая форма»

Но вы можете увидеть уравнение окружности, а — не знать !

Потому что это может быть не в аккуратной «Стандартной форме» выше.

В качестве примера, давайте поместим некоторые значения в a, b и r, а затем расширим их

Начать с: (x-a) 2 + (y-b) 2 = r 2

Пример: a = 1, b = 2, r = 3: (x − 1) 2 + (y − 2) 2 = 3 2

Расширить: x 2 — 2x + 1 + y 2 — 4y + 4 = 9

Соберите одинаковые термины: x 2 + y 2 — 2x — 4y + 1 + 4 — 9 = 0

И мы в конечном итоге с этим:

x 2 + y 2 — 2x — 4y — 4 = 0

Это круговое уравнение, но «замаскированное»!

Итак, когда вы видите что-то подобное, подумайте «хмм…. что может быть кругом! «

Фактически мы можем записать это в «Общая форма» , поместив константы вместо чисел:

x 2 + y 2 + Axe + By + C = 0

Примечание. Общая форма всегда имеет x 2 + y 2 для первых двух слагаемых .

Переход от общей формы к стандартной форме

Теперь представьте, что у нас есть уравнение в Общая форма :

x 2 + y 2 + Axe + By + C = 0

Как мы можем получить это в Стандартной Форме , как это?

(x-a) 2 + (y-b) 2 = r 2

Ответ состоит в том, чтобы завершить квадрат (читайте об этом) дважды… один раз за x и один раз за y :

Пример: x 2 + y 2 — 2x — 4y — 4 = 0

Начать с: x 2 + y 2 — 2x — 4y — 4 = 0

Соедините x с и y с: (x 2 — 2x) + (y 2 — 4y) — 4 = 0

Константа справа: (x 2 — 2x) + (y 2 — 4y) = 4

Теперь завершите квадрат для x (возьмите половину -2, возведите в квадрат и добавьте к обеим сторонам):

(x 2 — 2x + (-1) 2 ) + (y 2 — 4y) = 4 + (-1) 2

И завершите квадрат для y (возьмите половину −4, возведите в квадрат и добавьте к обеим сторонам):

(x 2 — 2x + (-1) 2 ) + (y 2 — 4y + (-2) 2 ) = 4 + (-1) 2 + (-2) 2

Убирать:

Упростить: (x 2 — 2x + 1) + (y 2 — 4y + 4) = 9

Наконец: (x — 1) 2 + (y — 2) 2 = 3 2

И у нас это есть в стандартной форме!

(Примечание: здесь использовался пример a = 1, b = 2, r = 3, поэтому мы правильно поняли!)

Unit Circle

Если мы поместим центр круга в (0,0) и установим радиус в 1, мы получим:

(x-a) 2 + (y-b) 2 = r 2

(x − 0) 2 + (y − 0) 2 = 1 2

x 2 + y 2 = 1

Что является уравнением единичного круга

Как построить круг вручную

1.Участок центр (а, б)

2. Нанесите 4 точки «радиуса» от центра в направлении вверх, вниз, влево и вправо

3. Сделайте набросок!

Пример: участок (x − 4) 2 + (y − 2) 2 = 25

Формула для круга: (x-a) 2 + (y-b) 2 = r 2

Таким образом, центр находится в (4,2)

А р 2 составляет 25 , поэтому радиус составляет √25 = 5

Таким образом, мы можем построить:

  • Центр: (4,2)
  • Up: (4,2 + 5) = (4,7)
  • Вниз: (4,2−5) = (4, −3)
  • Слева: (4-5,2) = (-1,2)
  • Справа: (4 + 5,2) = (9,2)

Теперь просто нарисуйте в круге как можно лучше!

Как построить круг на компьютере

Нам нужно изменить формулу, чтобы мы получили «у =».

Мы должны получить два уравнения (верх и низ круга), которые затем можно построить.

Пример: участок (x − 4) 2 + (y − 2) 2 = 25

Таким образом, центр находится в (4,2), а радиус √25 = 5

Переставь, чтобы получить «y =»:

Начните с: (x − 4) 2 + (y − 2) 2 = 25

Переместить (x − 4) 2 вправо: (y − 2) 2 = 25 — (x − 4) 2

Возьмем квадратный корень: (y − 2) = ± √ [25 — (x − 4) 2 ]

(обратите внимание на ± «плюс / минус»…
может быть два квадратных корня!)

Переместите «−2» вправо: y = 2 ± √ [25 — (x − 4) 2 ]

Итак, когда мы строим эти два уравнения, у нас должен быть круг:

  • y = 2 + √ [25 — (x − 4) 2 ]
  • y = 2 — √ [25 — (x − 4) 2 ]

Попробуйте нанести эти функции на график функций.

Также возможно использовать уравнение уравнений, чтобы сделать все это за один раз.

,
Вокруг многоугольника — Математика Открытая ссылка Incircle of the Polygon — Math Открытая ссылка

Определение: самый большой круг будет помещаться внутри многоугольника, который касается каждой стороны

Попробуй это Отрегулируйте правильный многоугольник ниже, перетаскивая любую оранжевую точку или измените количество сторон. Обратите внимание на поведение окружности многоугольника.

Окружность правильного многоугольника — это самый большой круг, который будет помещаться внутри многоугольника и касаться каждой стороны. только в одном месте (см. рисунок выше), и поэтому каждая из сторон является касательная к вписанной.Если количество сторон 3, это равносторонний треугольник и его вписанный точно такой же, как тот, что описан в «Круге треугольника».

Инрадиус правильного многоугольника точно такой же, как и его апофема. Приведенные ниже формулы такие же, как для апофема. Используйте формулу, которая использует факты, которые вам даны, чтобы начать.

Inradius с учетом длины стороны

По определению все стороны правильного многоугольника равны по длине. Если вы знаете длину одной из сторон, интрадиус определяется по формуле:

где
с — длина любой стороны
n — количество сторон
tan — функция тангенса, рассчитанная в градусах (см. Обзор тригонометрии)

Инрадиусу дан радиус (окрадиус)

Если вы знаете радиус (расстояние от центра до вершины):

где
r — радиус (окружность)
n — количество сторон
cos — функция косинуса, рассчитанная в градусах (см. Обзор тригонометрии)

неправильных полигонов

Нерегулярные многоугольники не считаются имеющими вкрапления или даже центры.Если вы должны были нарисовать многоугольник случайным образом, это маловероятно, что существует круг, у которого каждая сторона является касательной. Исключением является 3-сторонний многоугольник (треугольник). Все треугольники всегда имеют вкрапления. (См. Вкрапление треугольника)

Однако это может произойти в обратном порядке. Вы можете начать с круга и нарисовать неправильный многоугольник вокруг него, как показано на рисунке справа. Это будет называться ограниченным многоугольником.

Некоторые математики считают, что окружность является самым большим кругом, который поместится внутри многоугольника, без требования, что это касается всех сторон.Понятно, что под этим определением всегда можно нарисовать такой круг.

Другие темы многоугольника

Общие

Типы полигонов

Площадь различных типов полигонов

Периметр различных типов многоугольников

Углы, связанные с полигонами

названных полигонов

(C) 2011 Copyright Math Открытая ссылка.
Все права защищены

,2 $$ где r — радиус круга.

Диаграмма 1

Площадь Круг Концепции

Площадь круга — это все пространство внутри окружности круга. На диаграмме 1 площадь круга обозначена синим цветом.

Область на самом деле не является частью круга. Помните, что круг — это просто локус точек. Область заключена внутри этого локуса точек.

Интересный факт об окружности и площади

Исследуйте и откройте для себя связь между формулой площади, радиусом круга и его графиком с помощью нашего интерактивного апплета.

Задача 1

Какая площадь круга на картинке?

Округлите свой ответ до десятых.

Покажи ответ

Помните формулу:

$$ Площадь = \ pi \ cdot r ^ 2 \\ A = \ pi \ cdot (22 ‘) ^ 2 \\ A = \ pi \ cdot 484 \\ A = \ pi \ cdot 1520.2 \\ \ sqrt {114.59155902616465} = r \\ r = 10.704744696916627 \ text {дюймов} \\ $$

Теперь, когда мы нашли радиус, как нам найти диаметр?

Ответ

$$ диаметр = 2 \ радиус cdot \\ = 2 \ cdot 10.704744696916627 \\ = +21,409489393833255 \\ \ boxed {диаметр = 21,41} \\ \ text {дюймов, округлено до ближайшей сотой} $$

Задачи Проблемы

Круг имеет диаметр 12 дюймов. Какова его площадь с точки зрения $$ \ pi $$.2 \\ A = 36 \ pi $$

Задача 7

Если радиус круга удвоится, то насколько увеличилась его площадь?

Покажи ответ

Поскольку формула для площади круга возводит в квадрат радиус , площадь большего круга всегда в 4 (или 2 2 ) раз меньше круга. Подумайте об этом: вы удваиваете число (что означает × 2) и затем возводите его в квадрат (то есть возводите в квадрат 2), что приводит к новой области, которая в четыре раза меньше.

Вы можете увидеть, что это соотношение верно, если вы выберете некоторые фактические значения для радиуса круга.2 $$ A = $$ 9 \ pi $$ A = $$ 36 \ pi $$

$$ A_ {больше} = \ colo

.

Related Posts

Leave A Comment