Равномерное движение по окружности. Скорость, ускорение
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: движение по окружности с постоянной по модулю скоростью, центростремительное ускорение.
Равномерное движение по окружности — это достаточно простой пример движения с вектором ускорения, зависящим от времени.
Пусть точка вращается по окружности радиуса . Скорость точки постоянна по модулю и равна . Скорость называется линейной скоростью точки.
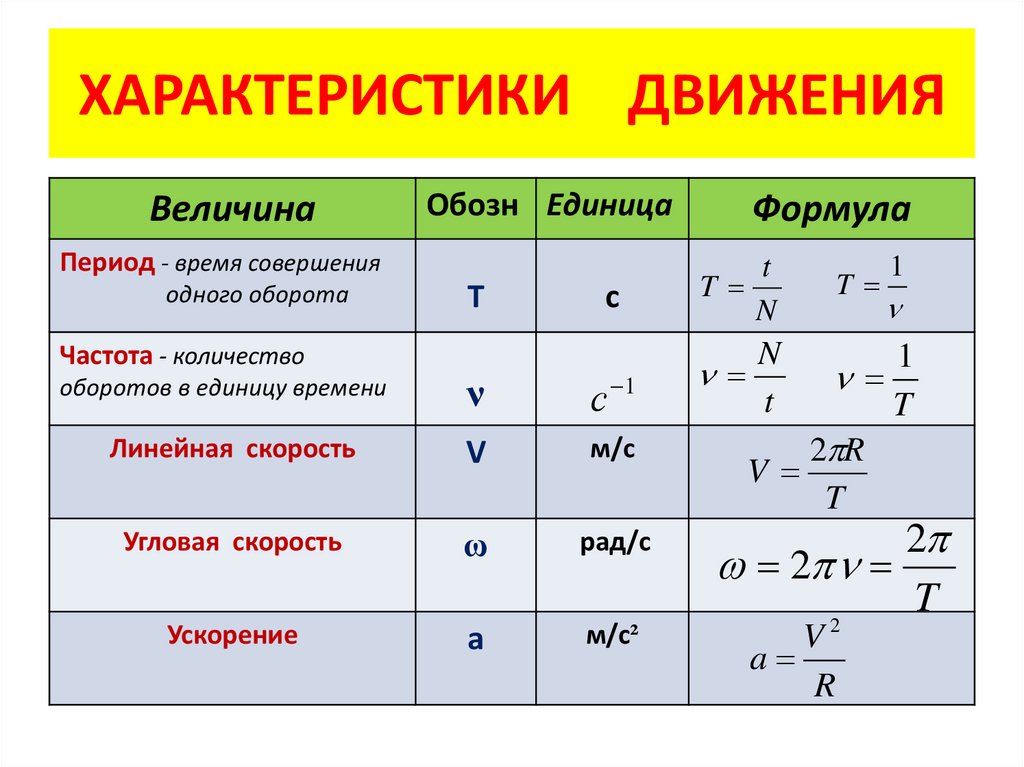
Период обращения — это время одного полного оборота. Для периода имеем очевидную формулу:
. (1)
Частота обращения — это величина, обратная периоду:
.
Частота показывает, сколько полных оборотов точка совершает за секунду. Измеряется частота в об/с (обороты в секунду).
Пусть, например, . Это означает, что за время точка совершает один полный
оборот. Частота при этом получается равна: об/с; за секунду точка совершает 10 полных оборотов.
Частота при этом получается равна: об/с; за секунду точка совершает 10 полных оборотов.
Угловая скорость.
Рассмотрим равномерное вращение точки в декартовой системе координат. Поместим начало координат в центре окружности (рис. 1).
| Рис. 1. Равномерное движение по окружности |
Пусть — начальное положение точки; иными словами, при точка имела координаты . Пусть за время точка повернулась на угол и заняла положение .
Отношение угла поворота ко времени называется угловой скоростью вращения точки:
. (2)
Угол , как правило, измеряется в радианах, поэтому угловая скорость измеряется в рад/с. За время, равное периоду вращения, точка поворачивается на угол . Поэтому
. (3)
Сопоставляя формулы (1) и (3), получаем связь линейной и угловой скоростей:
.
Закон движения.
Найдём теперь зависимость координат вращающейся точки от времени. Видим из рис. 1, что
.
Но из формулы (2) имеем: . Следовательно,
. (5)
Формулы (5) являются решением основной задачи механики для равномерного движения точки по окружности.
Центростремительное ускорение.
Теперь нас интересует ускорение вращающейся точки. Его можно найти, дважды продифференцировав соотношения (5):
С учётом формул (5) имеем:
(6)
Полученные формулы (6) можно записать в виде одного векторного равенства:
(7)
где — радиус-вектор вращающейся точки.
Мы видим, что вектор ускорения направлен противоположно радиус-вектору, т. е. к центру окружности (см. рис. 1). Поэтому ускорение точки, равномерно движущейся по окружности, называется центростремительным.
Кроме того, из формулы (7) мы получаем выражение для модуля центростремительного ускорения:
(8)
Выразим угловую скорость из (4)
и подставим в (8). Получим ещё одну формулу для центростремительного ускорения:
Получим ещё одну формулу для центростремительного ускорения:
.
Спасибо за то, что пользуйтесь нашими публикациями. Информация на странице «Равномерное движение по окружности.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам. Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена: 07.02.2023
Движение по окружности
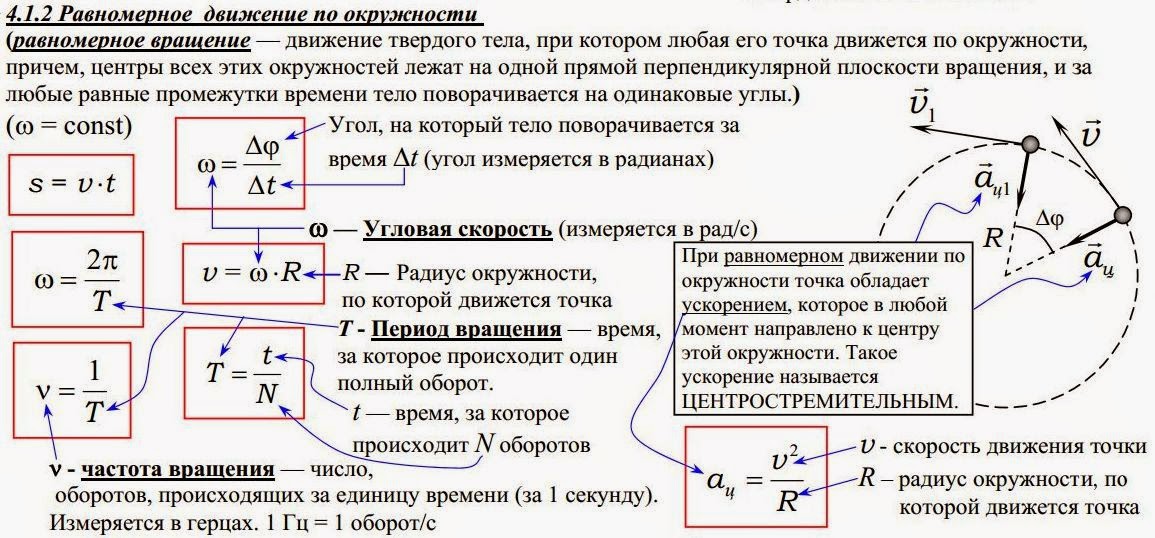
Движение по окружности — простейший случай криволинейного движения тела. Когда тело движется вокруг некоторой точки, наряду с вектором перемещения удобно ввести угловое перемещение ∆φ (угол поворота относительно центра окружности), измеряемое в радианах.
Зная угловое перемещение, можно вычислить длину дуги окружности (путь), которую прошло тело.
∆l=R∆φ
Если угол поворота мал, то ∆l≈∆s.
Проиллюстрируем сказанное:
Угловая скорость
При криволинейном движении вводится понятие угловой скорости ω, то есть скорости изменения угла поворота.
Определение. Угловая скоростьУгловая скорость в данной точке траектории — предел отношения углового перемещения ∆φ к промежутку времени ∆t, за которое оно произошло. ∆t→0.
ω=∆φ∆t, ∆t→0.
Единица измерения угловой скорости — радиан в секунду (радс).
Существует связь между угловой и линейной скоростями тела при движении по окружности. Формула для нахождения угловой скорости:
ω=vR
Нормальное ускорение
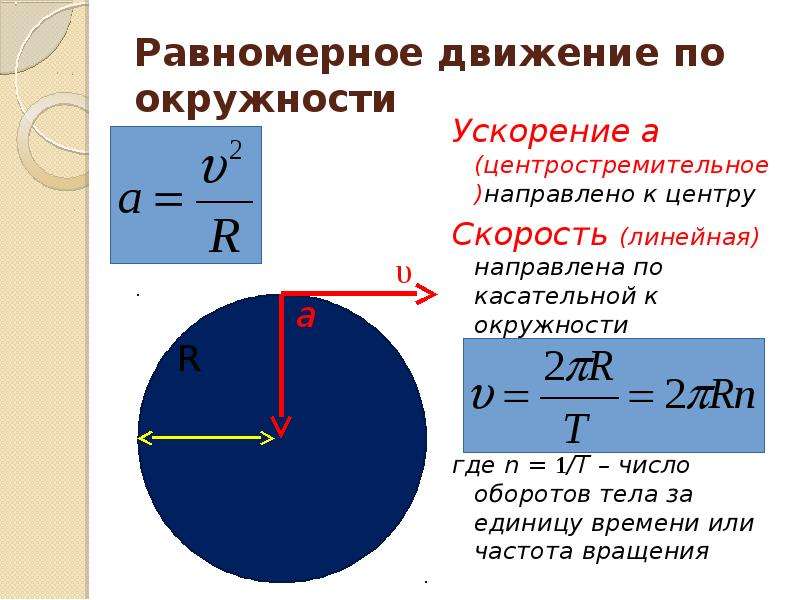
При равномерном движении по окружности, скорости v и ω остаются неизменными. Меняется только направление вектора линейной скорости.
При этом равномерное движение по окружности на тело действует центростремительное, или нормальное ускорение, направленное по радиусу окружности к ее центру.
an=∆v→∆t, ∆t→0
Модуль центростремительного ускорения можно вычислить по формуле:
an=v2R=ω2R
Докажем эти соотношения.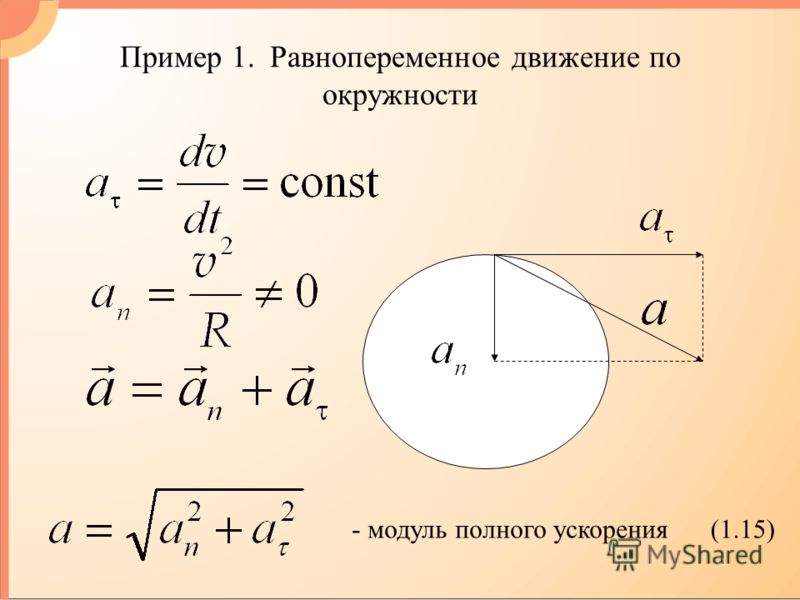
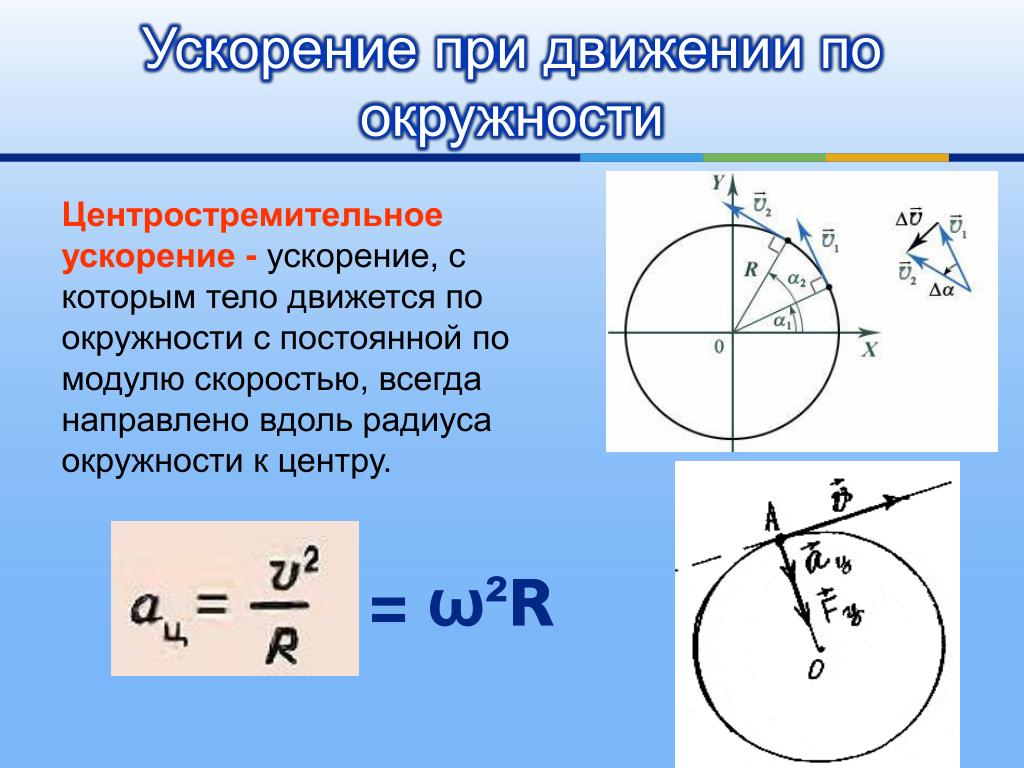
Рассмотрим, как изменяется вектор v→ за малый промежуток времени ∆t. ∆v→=vB→-vA→.
В точках А и В вектор скорости направлен по касательной к окружности, при этом модули скоростей в обеих точках одинаковы.
По определению ускорения:
a→=∆v→∆t, ∆t→0
Взглянем на рисунок:
Треугольники OAB и BCD подобны. Из этого следует, что OAAB=BCCD.
Если значение угла ∆φ мало, расстояние AB=∆s≈v·∆t. Принимая во внимание, что OA=R и CD=∆v для рассмотренных выше подобных треугольников получим:
Rv∆t=v∆v или ∆v∆t=v2R
При ∆φ→0, направление вектора ∆v→=vB→-vA→ приближается к направлению на центр окружности. Принимая, что ∆t→0, получаем:
a→=an→=∆v→∆t; ∆t→0; an→=v2R.
При равномерном движении по окружности модуль ускорения остается постоянным, а направление вектора изменяется со временем, сохраняя ориентацию на центр окружности. Именно поэтому это ускорение называется центростремительным: вектор в любой момент времени направлен к центру окружности.
Запись центростремительного ускорения в векторной форме выглядит следующим образом:
an→=-ω2R→.
Здесь R→ — радиус вектор точки на окружности с началом в ее центре.
Тангенциальное ускорение
В общем случае ускорение при движении по окружности состоит из двух компонентов — нормальное, и тангенциальное.
Рассмотрим случай, когда тело движется по окружности неравномерно. Введем понятие тангенциального (касательного) ускорения. Его направление совпадает с направлением линейной скорости тела и в каждой точке окружности направлено по касательной к ней.
aτ=∆vτ∆t; ∆t→0
Здесь ∆vτ=v2-v1 — изменение модуля скорости за промежуток ∆t
Направление полного ускорения определяется векторной суммой нормального и тангенциального ускорений.
Движение по окружности в плоскости можно описывать при помощи двух координат: x и y. В каждый момент времени скорость тела можно разложить на составляющие vx и vy.
Если движение равномерное, величины vx и vy а также соответствующие координаты будут изменяться во времени по гармоническому закону с периодом T=2πRv=2πω
Математика кругового движения
Существуют три математические величины, которые будут представлять для нас основной интерес при анализе движения объектов по окружности.
Ускорение объекта, движущегося по окружности, можно определить с помощью любого из двух следующих уравнений.
Уравнение справа (выше) получено из уравнения слева заменой выражения для скорости.
Суммарная сила ( F сеть ), действующая на объект, движущийся по кругу, направлена внутрь. Хотя на объект может действовать более одной силы, векторная сумма всех их должна составлять результирующую силу. В общем, внутренняя сила больше, чем внешняя сила (если она есть), так что внешняя сила уравновешивается, а неуравновешенная сила направлена в центр круга. Суммарная сила связана с ускорением объекта (как всегда) и, таким образом, определяется следующими тремя уравнениями:0003
Уравнения в середине (вверху) и справа (вверху) получаются из уравнения слева заменой выражений для ускорения.
Этот набор уравнений кругового движения можно использовать двумя способами:
- как «рецепт» для решения алгебраических задач для решения неизвестной величины.
- как руководство к размышлению о том, как изменение одной величины повлияет на другую величину.
Эти два способа показаны ниже.
Уравнение выражает математическую связь между величинами, присутствующими в этом уравнении. Например, уравнение для второго закона Ньютона определяет, как ускорение связано с результирующей силой и массой объекта.
Связь, выраженная уравнением, заключается в том, что ускорение объекта прямо пропорционально действующей на него чистой силе. Другими словами, чем больше значение чистой силы, тем больше будет значение ускорения. По мере увеличения чистой силы ускорение увеличивается.
Уравнение второго закона Ньютона также раскрывает связь между ускорением и массой. Согласно уравнению, ускорение объекта обратно пропорционально массе объекта. Другими словами, чем больше значение массы, тем меньше значение ускорения. С увеличением массы ускорение уменьшается. На самом деле, если бы масса увеличилась в 2 раза, уравнение предсказало бы, что ускорение уменьшится в 2 раза. Точно так же, если бы масса уменьшилась в 2 раза, уравнение предсказало бы, что ускорение уменьшится. увеличить в 2,9 раза0003

Это уравнение показывает, что результирующая сила, необходимая для движения объекта по кругу, прямо пропорциональна квадрату скорости объекта. Для постоянной массы и радиуса F сеть пропорциональна скорости 2 .
Коэффициент изменения чистой силы равен квадрату коэффициента изменения скорости. Следовательно, если скорость объекта удваивается, чистая сила, необходимая для кругового движения этого объекта, увеличивается в четыре раза. А если скорость объекта уменьшится вдвое (уменьшится в 2 раза), необходимая результирующая сила уменьшится в 4 раза.0003
Приведенные выше математические уравнения движения объектов по окружностям можно использовать для решения задач о движении по окружности, в которых необходимо определить неизвестную величину.
Автомобиль массой 900 кг, движущийся со скоростью 10 м/с, совершает поворот по окружности радиусом 25,0 м. Определить ускорение и результирующую силу, действующую на автомобиль. |
Решение этой задачи начинается с идентификации известной и запрашиваемой информации.
Известная информация: м = 900 кг | Запрашиваемая информация: а = ???? |
Для определения ускорения автомобиля используйте уравнение a = v 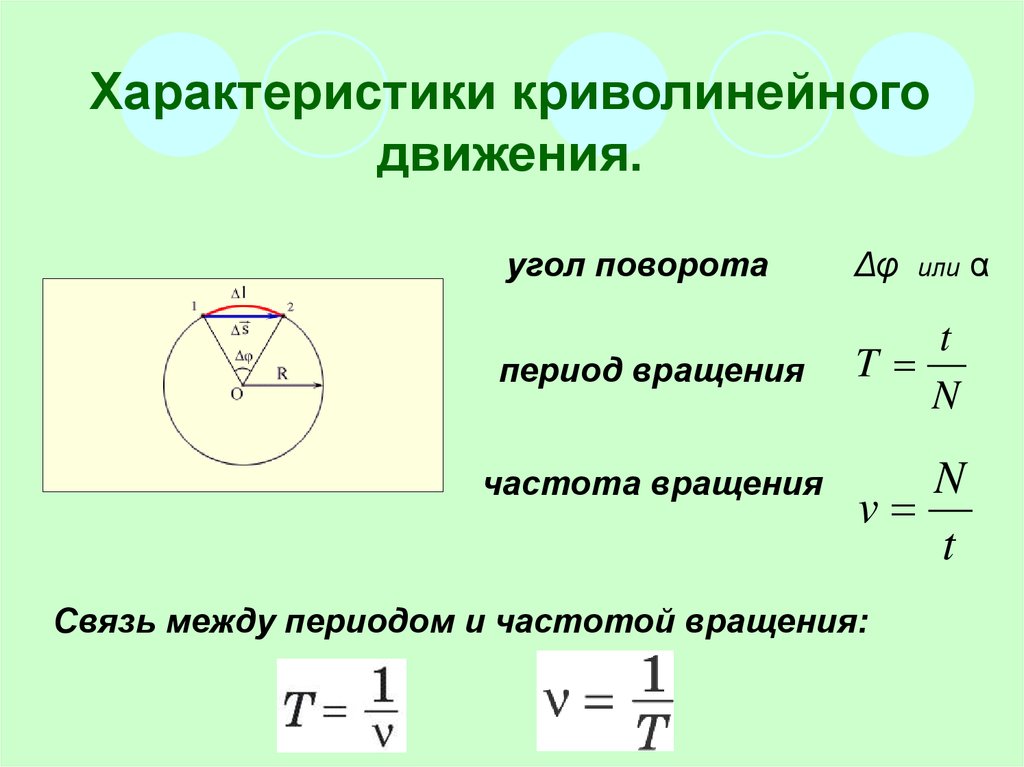 Решение выглядит следующим образом:
Решение выглядит следующим образом:
а = (10,0 м/с) 2 / (25,0 м)
а = (100 м 2 /с 2 ) / (25,0 м)
а = 4 м/с 2
Чтобы определить результирующую силу, действующую на автомобиль, используйте уравнение F net = m•a. Решение заключается в следующем.
F нетто = (900 кг) • (4 м/с 2 )
F нетто = 3600 Н
Полузащитник весом 95 кг делает разворот на футбольном поле. Полузащитник прокладывает путь, который представляет собой часть круга радиусом 12 метров. Полузащитник делает четверть оборота по кругу за 2,1 секунды. Определить скорость, ускорение и чистую силу, действующую на полузащитника. |
Решение этой задачи начинается с идентификации известной и запрашиваемой информации.
Известная информация: м = 95,0 кг | Запрашиваемая информация: v = ???? |
Чтобы определить скорость полузащитника, используйте уравнение v = d / t, где d — одна четвертая длины окружности, а время — 2,1 с. Решение выглядит следующим образом:
v = (0,25 • 2 • пи • R) / t
v = (0,25 • 2 • 3,14 • 12,0 м) / (2,1 с)
v = 8,97 м/с
Для определения ускорения полузащитника воспользуемся уравнением a = v 2 /R.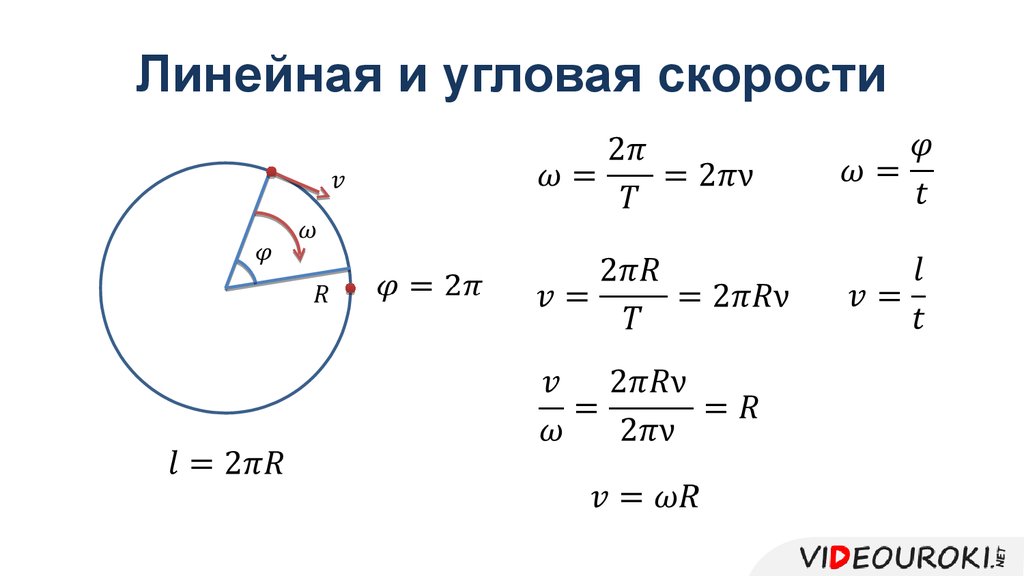 Решение будет следующим:
Решение будет следующим:
а = (8,97 м/с) 2 / (12,0 м)
а = (80,5 м 2 /с 2 ) / (12,0 м)
а = 6,71 м/с 2
Чтобы определить результирующую силу, действующую на полузащитника, используйте уравнение F нетто = м•а. Решение заключается в следующем.
F нетто = (95,0 кг)*(6,71 м/с 2 )
F нетто = 637 Н
В уроке 2 этого модуля принципы кругового движения и приведенные выше математические уравнения будут объединены для объяснения и анализа различных реальных сценариев движения, включая аттракционы в парке развлечений и круговые движения в легкой атлетике.
Мы хотели бы предложить…
Иногда недостаточно просто прочитать об этом. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием либо нашего интерактивного равномерного кругового движения, либо нашего моделирования горизонтального круга. Вы можете найти их в разделе Physics Interactives на нашем сайте. Интерактивное приложение «Равномерное круговое движение» позволяет учащимся в интерактивном режиме исследовать взаимосвязь между скоростью, ускорением и силой для объекта, движущегося по кругу. Наше моделирование горизонтального круга моделирует движение трех разных объектов, движущихся по горизонтальному кругу, при этом анализируя влияние, которое изменения переменной могут оказать на движение.
Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием либо нашего интерактивного равномерного кругового движения, либо нашего моделирования горизонтального круга. Вы можете найти их в разделе Physics Interactives на нашем сайте. Интерактивное приложение «Равномерное круговое движение» позволяет учащимся в интерактивном режиме исследовать взаимосвязь между скоростью, ускорением и силой для объекта, движущегося по кругу. Наше моделирование горизонтального круга моделирует движение трех разных объектов, движущихся по горизонтальному кругу, при этом анализируя влияние, которое изменения переменной могут оказать на движение.
Посетите: Интерактивное равномерное круговое движение || Моделирование горизонтального круга
1. Анна Литикал тренируется дома с демонстрацией центростремительной силы. Она наполняет ведро водой, привязывает его к прочной веревке и раскручивает по кругу. Анна крутит ведро, когда оно наполовину наполнено водой и когда оно на четверть. В каком случае требуется большее усилие, чтобы вращать ведро по кругу? Объясните, используя уравнение как «руководство к мышлению».
Она наполняет ведро водой, привязывает его к прочной веревке и раскручивает по кругу. Анна крутит ведро, когда оно наполовину наполнено водой и когда оно на четверть. В каком случае требуется большее усилие, чтобы вращать ведро по кругу? Объясните, используя уравнение как «руководство к мышлению».
2. Линкольн Континенталь и Юго делают поворот. Lincoln в четыре раза массивнее Yugo. Если они совершают поворот с одинаковой скоростью, то как соотносятся центростремительные силы, действующие на два автомобиля? Объяснять.
3. Cajun Cliffhanger в Great America – это аттракцион, в котором участники выстраиваются вдоль периметра цилиндра и вращаются по кругу с высокой скоростью. Когда цилиндр начинает вращаться очень быстро, пол убирается из-под ног гонщиков. Как влияет удвоение скорости на центростремительную силу? Объяснять.
4.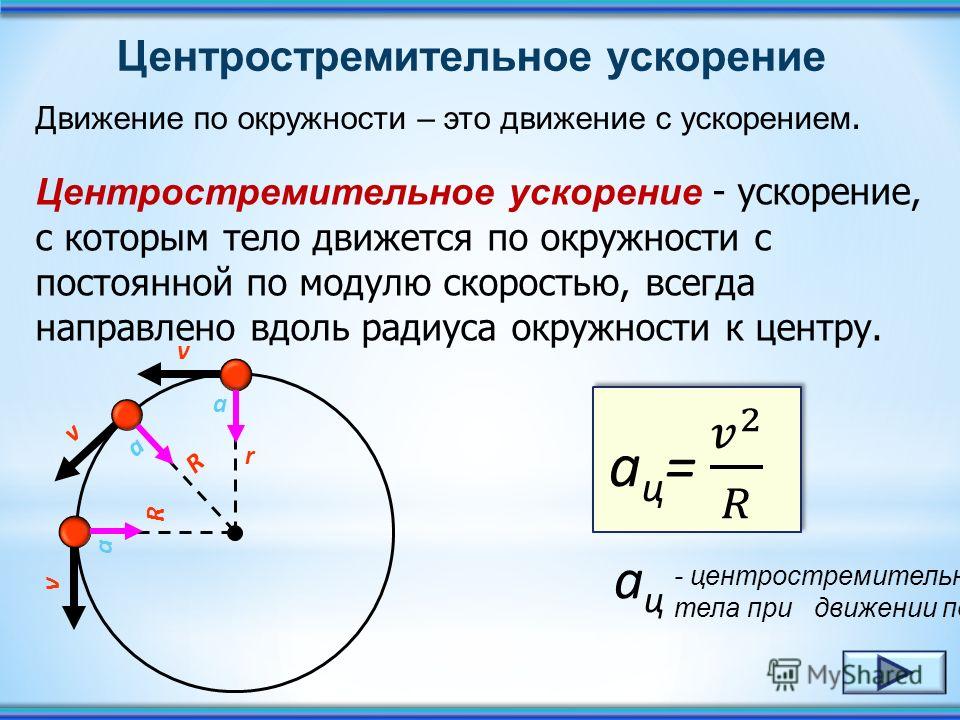 Определить центростремительную силу, действующую на ребенка массой 40 кг, который делает 10 оборотов вокруг скалодрома за 29,3 секунды. Радиус ствола составляет 2,90 метра.
Определить центростремительную силу, действующую на ребенка массой 40 кг, который делает 10 оборотов вокруг скалодрома за 29,3 секунды. Радиус ствола составляет 2,90 метра.
Перейти к следующему уроку:
6.2 Равномерное движение по окружности — физика
Раздел Цели обучения
К концу этого раздела вы сможете делать следующее:
- Описать центростремительное ускорение и связать его с линейным ускорением
- Опишите центростремительную силу и свяжите ее с линейной силой
- Решение задач на центростремительное ускорение и центростремительную силу
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим учащимся освоить следующие стандарты:
- (4) Научные концепции. Учащийся знает и применяет законы, управляющие движением, в различных ситуациях.
 Ожидается, что студент:
Ожидается, что студент:- (C) анализировать и описывать ускоренное движение в двух измерениях, используя уравнения, включая примеры снарядов и окружностей.
- (D) рассчитать действие сил на объекты, включая закон инерции, связь между силой и ускорением и природу пар сил между объектами.
Кроме того, руководство по физике для старших классов рассматривает содержание этого раздела лабораторной работы под названием «Круговое и вращательное движение», а также следующие стандарты:
- (4) Научные концепции. Учащийся знает и применяет законы, управляющие движением, в различных ситуациях. Ожидается, что студент:
- (C) анализировать и описывать ускоренное движение в двух измерениях, используя уравнения, включая примеры снарядов и окружностей.
Основные термины раздела
| центробежная сила | центростремительное ускорение | центростремительная сила | равномерное круговое движение |
Центростремительное ускорение
Поддержка учителей
Поддержка учителей
[BL][OL] Проверьте равномерное круговое движение. Попросите учащихся привести примеры кругового движения. Просмотрите линейное ускорение.
Попросите учащихся привести примеры кругового движения. Просмотрите линейное ускорение.
В предыдущем разделе мы определили круговое движение. Простейшим случаем кругового движения является равномерное круговое движение, когда объект движется по круговому пути с постоянной скоростью . Обратите внимание, что, в отличие от скорости, линейная скорость объекта в круговом движении постоянно меняется, потому что он всегда меняет направление. Из кинематики мы знаем, что ускорение есть изменение скорости либо по величине, либо по направлению, либо по тому и другому. Следовательно, объект, совершающий равномерное круговое движение, всегда ускоряется, даже если величина его скорости постоянна.
Вы сами испытываете это ускорение каждый раз, когда едете в машине, когда она поворачивает за угол. Если вы держите руль неподвижно во время поворота и двигаетесь с постоянной скоростью, вы выполняете равномерное круговое движение. Что вы заметите, так это ощущение скольжения (или отбрасывания, в зависимости от скорости) от центра поворота.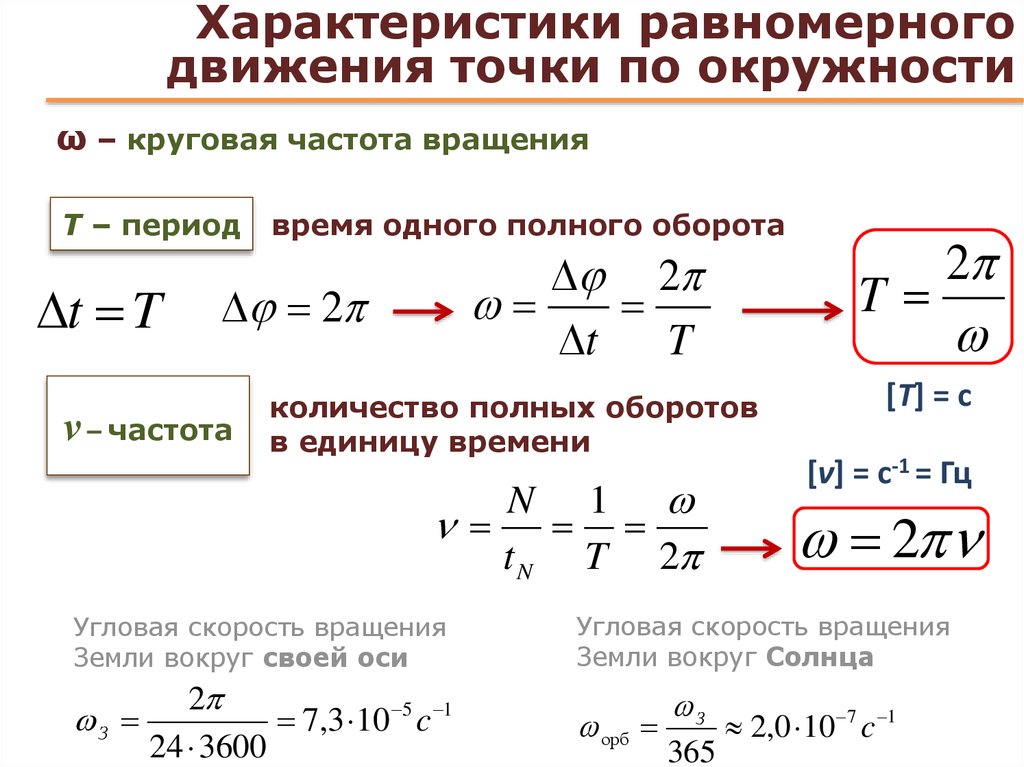 Это не реальная сила, действующая на вас — это происходит только потому, что ваше тело хочет продолжать движение по прямой линии (согласно первому закону Ньютона), в то время как автомобиль сворачивает с этой прямолинейной траектории. Внутри машины создается впечатление, что вас выталкивает из центра поворота. Эта фиктивная сила известна как центробежная сила. Чем круче кривая и чем больше ваша скорость, тем заметнее становится этот эффект.
Это не реальная сила, действующая на вас — это происходит только потому, что ваше тело хочет продолжать движение по прямой линии (согласно первому закону Ньютона), в то время как автомобиль сворачивает с этой прямолинейной траектории. Внутри машины создается впечатление, что вас выталкивает из центра поворота. Эта фиктивная сила известна как центробежная сила. Чем круче кривая и чем больше ваша скорость, тем заметнее становится этот эффект.
Поддержка учителей
Поддержка учителей
[BL][OL][AL] Продемонстрируйте круговое движение, привязав груз к веревке и вращая ее. Спросите учащихся, что произойдет, если вы внезапно перережете веревку? В каком направлении будет двигаться объект? Почему? Что это говорит о направлении ускорения? Попросите учащихся привести примеры случаев, когда они столкнулись с центростремительным ускорением.
На рис. 6.7 показан объект, движущийся по круговой траектории с постоянной скоростью.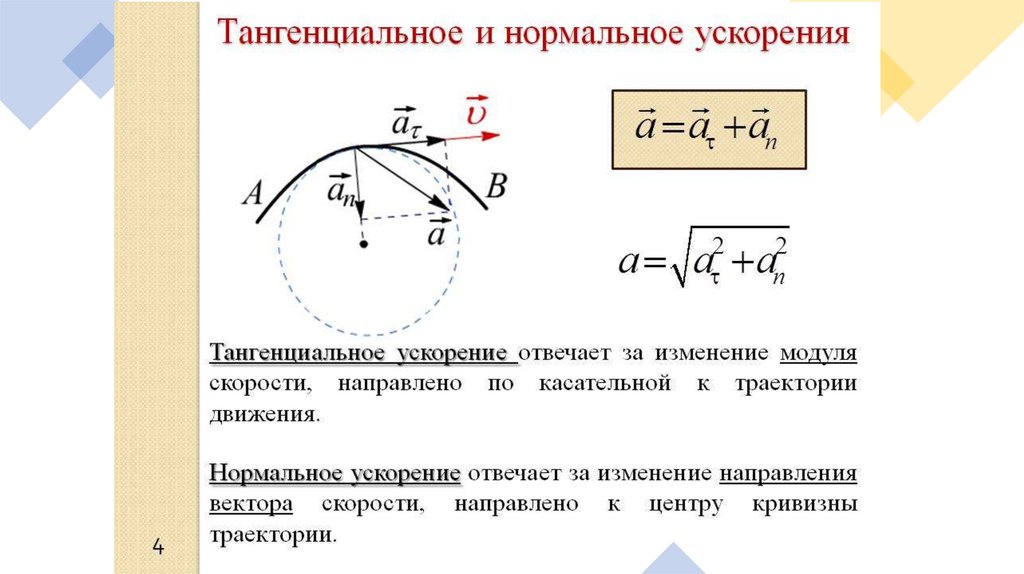 Направление мгновенной тангенциальной скорости показано в двух точках вдоль траектории. Ускорение направлено в сторону изменения скорости; в этом случае он указывает примерно на центр вращения. (Центр вращения находится в центре кругового пути). Если представить, что ΔsΔs становится все меньше и меньше, то ускорение будет равно точно к центру вращения, но этот случай сложно нарисовать. Мы называем ускорение объекта, движущегося в равномерном круговом движении, центростремительным ускорением a c , потому что центростремительное означает поиск центра .
Направление мгновенной тангенциальной скорости показано в двух точках вдоль траектории. Ускорение направлено в сторону изменения скорости; в этом случае он указывает примерно на центр вращения. (Центр вращения находится в центре кругового пути). Если представить, что ΔsΔs становится все меньше и меньше, то ускорение будет равно точно к центру вращения, но этот случай сложно нарисовать. Мы называем ускорение объекта, движущегося в равномерном круговом движении, центростремительным ускорением a c , потому что центростремительное означает поиск центра .
Рисунок
6.7
Показаны направления скорости объекта в двух разных точках, и видно, что изменение скорости ΔvΔv указывает примерно на центр кривизны (см. маленькую вставку). Для чрезвычайно малого значения ΔsΔs ΔvΔv указывает точно на центр круга (но это трудно нарисовать). Поскольку ac=Δv/Δtac=Δv/Δt, ускорение также направлено к центру, поэтому a c называется центростремительным ускорением.
Поддержка учителей
Поддержка учителей
См. рис. 6.7. На рисунке изображен объект, движущийся по круговой траектории с постоянной скоростью и направлением мгновенной скорости двух точек по траектории. Ускорение направлено в сторону изменения скорости и указывает на центр вращения. Это строго верно только тогда, когда ΔsΔs стремится к нулю.
Теперь, когда мы знаем, что направление центростремительного ускорения направлено к центру вращения, давайте обсудим величину центростремительного ускорения. Для объекта, движущегося со скоростью v по круговой траектории с радиусом r , модуль центростремительного ускорения равен
ac=v2r.ac=v2r.
Центростремительное ускорение больше на высоких скоростях и в крутых поворотах (меньший радиус), как вы, возможно, заметили, управляя автомобилем, потому что автомобиль фактически толкает вас к центру поворота. Но немного удивительно, что a c пропорционально квадрату скорости. Это означает, например, что ускорение в четыре раза больше при движении по кривой на скорости 100 км/ч, чем на скорости 50 км/ч.
Но немного удивительно, что a c пропорционально квадрату скорости. Это означает, например, что ускорение в четыре раза больше при движении по кривой на скорости 100 км/ч, чем на скорости 50 км/ч.
Мы также можем выразить a c через величину угловой скорости. Подставляя v=rωv=rω в приведенное выше уравнение, мы получаем ac=(rω)2r=rω2ac=(rω)2r=rω2 . Следовательно, величина центростремительного ускорения через величину угловой скорости равна
ac=rω2.ac=rω2.
6,9
Советы для успеха
Уравнение, выраженное в форме a c = rω 2 , полезно для решения задач, где вы знаете угловую скорость, а не тангенциальную скорость.
Виртуальная физика
Божья коровка в 2D
В этой симуляции вы экспериментируете с положением, скоростью и ускорением божьей коровки в круговом и эллиптическом движении.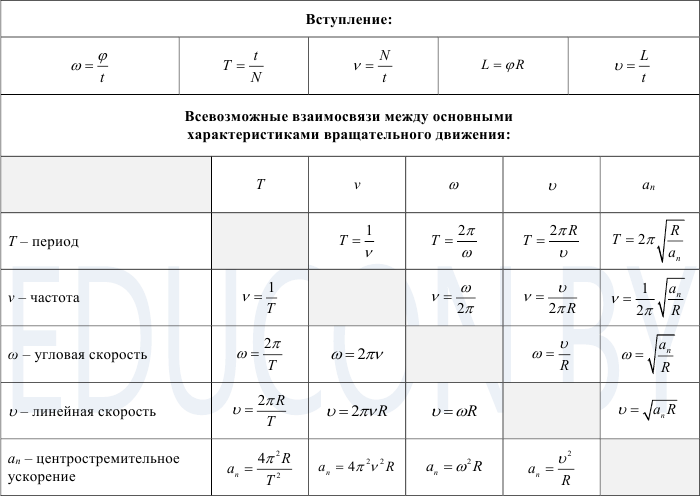 Переключите тип движения с линейного на круговой и наблюдайте за векторами скорости и ускорения. Затем попробуйте эллиптическое движение и обратите внимание, как векторы скорости и ускорения отличаются от векторов кругового движения.
Переключите тип движения с линейного на круговой и наблюдайте за векторами скорости и ускорения. Затем попробуйте эллиптическое движение и обратите внимание, как векторы скорости и ускорения отличаются от векторов кругового движения.
Проверка захвата
Каков угол между ускорением и скоростью при равномерном круговом движении? Какое ускорение испытывает тело при равномерном движении по окружности?
- Угол между ускорением и скоростью равен 0°, и тело испытывает линейное ускорение.
- Угол между ускорением и скоростью равен 0°, и тело испытывает центростремительное ускорение.
- Угол между ускорением и скоростью равен 90°, и тело испытывает линейное ускорение.
- Угол между ускорением и скоростью равен 90°, и тело испытывает центростремительное ускорение.
Центростремительная сила
Поддержка учителей
Поддержка учителей
[BL][OL][AL] Используя ту же демонстрацию, что и раньше, попросите учащихся предсказать отношения между величинами угловой скорости, центростремительного ускорения, массы и центростремительной силы. Предложите учащимся поэкспериментировать, используя веревки разной длины и разного веса.
Предложите учащимся поэкспериментировать, используя веревки разной длины и разного веса.
Поскольку объект в равномерном круговом движении претерпевает ускорение (за счет изменения направления движения, но не скорости), мы знаем из второго закона Ньютона, что на объект должна действовать результирующая внешняя сила. Поскольку величина ускорения постоянна, постоянна и величина результирующей силы, а поскольку ускорение направлено к центру вращения, то же самое и результирующая сила.
Любая сила или комбинация сил может вызвать центростремительное ускорение. Всего несколько примеров: натяжение веревки на шаре, сила земного притяжения на Луне, трение между дорогой и шинами автомобиля, когда он движется по кривой, или нормальная сила американских горок. след на тележке во время петли.
Компонент любой результирующей силы, вызывающей круговое движение, называется центростремительной силой. Когда результирующая сила равна центростремительной силе, а ее величина постоянна, возникает равномерное круговое движение.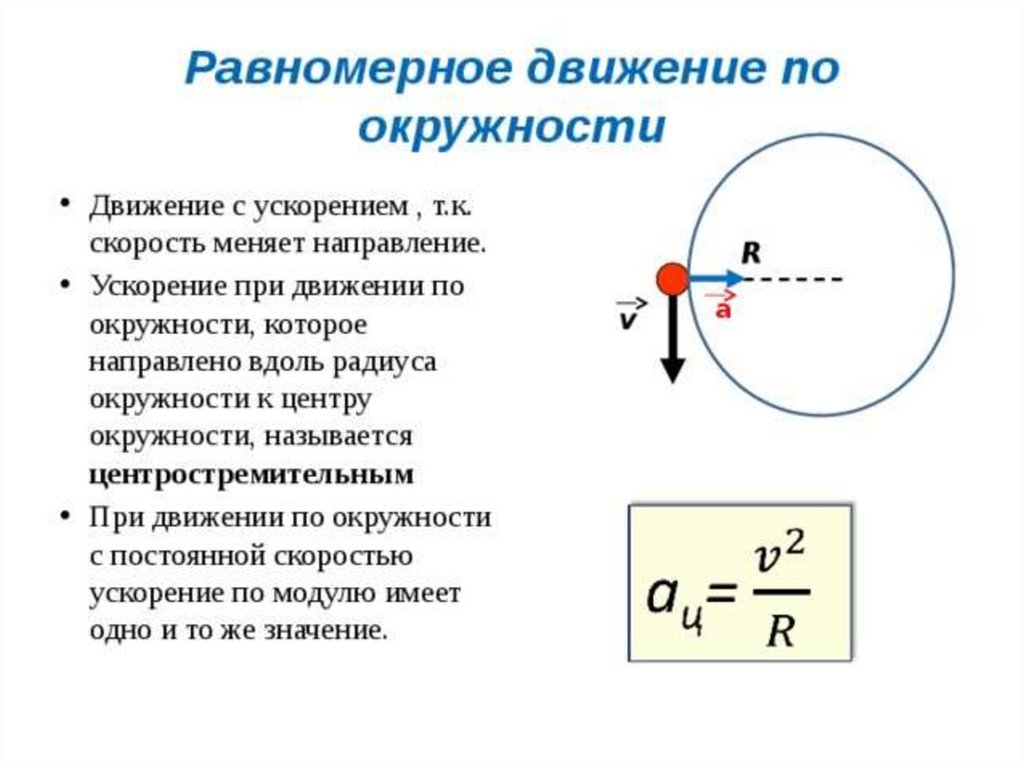 Центростремительная сила направлена к центру вращения, как и центростремительное ускорение. Согласно второму закону движения Ньютона, результирующая сила вызывает ускорение массы в соответствии с F нетто = м a . Для равномерного кругового движения ускорение равно центростремительному ускорению: a = a c . Следовательно, величина центростремительной силы F c равна Fc=macFc=mac .
Центростремительная сила направлена к центру вращения, как и центростремительное ускорение. Согласно второму закону движения Ньютона, результирующая сила вызывает ускорение массы в соответствии с F нетто = м a . Для равномерного кругового движения ускорение равно центростремительному ускорению: a = a c . Следовательно, величина центростремительной силы F c равна Fc=macFc=mac .
Используя две разные формы уравнения для величины центростремительного ускорения, ac=v2/rac=v2/r и ac=rω2ac=rω2, мы получаем два выражения, включающие величину центростремительной силы FcFc. Первое выражение в терминах тангенциальной скорости, второе в терминах угловой скорости: Fc=mv2rFc=mv2r и Fc=mrω2Fc=mrω2.
Обе формы уравнения зависят от массы, скорости и радиуса кругового пути. Вы можете использовать любое более удобное выражение для центростремительной силы.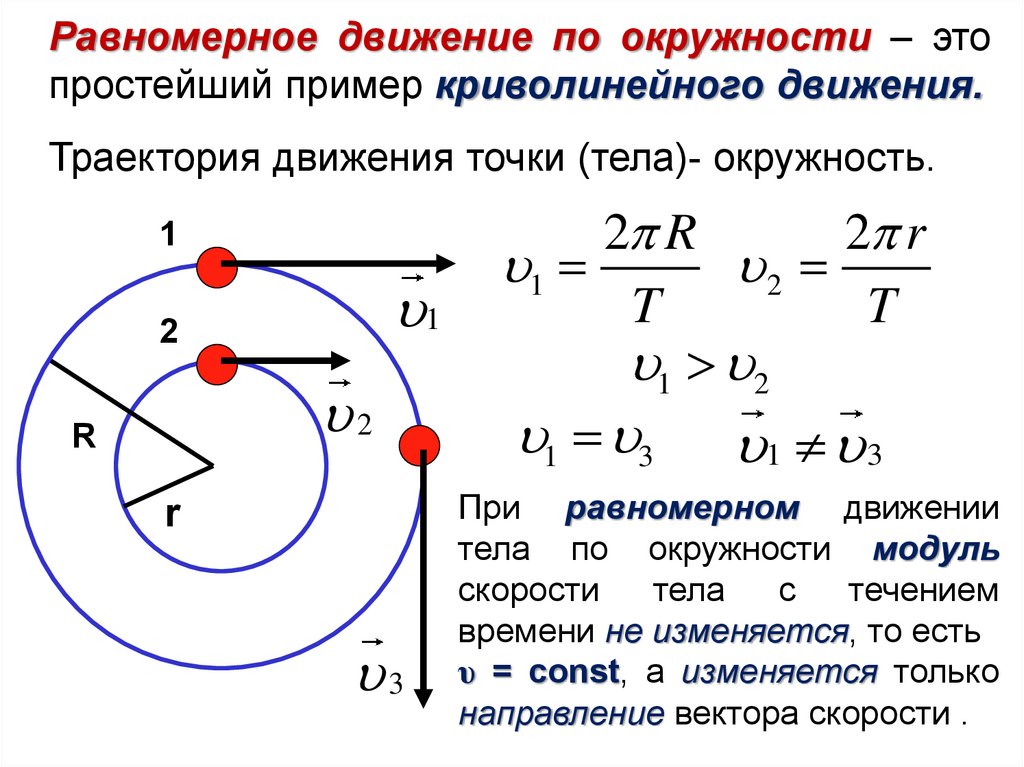 Второй закон Ньютона также гласит, что объект будет ускоряться в том же направлении, что и результирующая сила. По определению центростремительная сила направлена к центру вращения, поэтому объект также будет ускоряться по направлению к центру. Прямая линия, проведенная от кругового пути к центру круга, всегда будет перпендикулярна тангенциальной скорости. Обратите внимание, что если вы решите первое выражение для р , получается
Второй закон Ньютона также гласит, что объект будет ускоряться в том же направлении, что и результирующая сила. По определению центростремительная сила направлена к центру вращения, поэтому объект также будет ускоряться по направлению к центру. Прямая линия, проведенная от кругового пути к центру круга, всегда будет перпендикулярна тангенциальной скорости. Обратите внимание, что если вы решите первое выражение для р , получается
r=mv2Fc.r=mv2Fc.
Из этого выражения мы видим, что при данной массе и скорости большая центростремительная сила вызывает малый радиус кривизны, то есть крутую кривую.
Рисунок
6,8
На этом рисунке сила трения f служит центростремительной силой F c . Центростремительная сила перпендикулярна тангенциальной скорости и вызывает равномерное круговое движение. Чем больше центростремительная сила F c , тем меньше радиус кривизны r и тем острее кривая.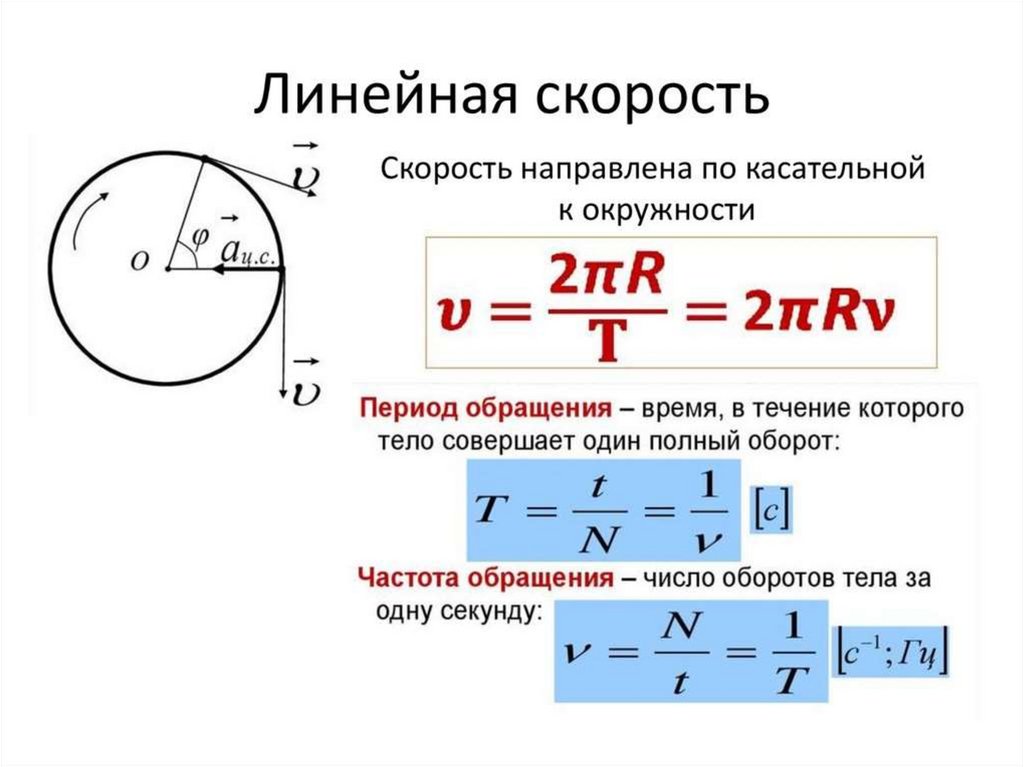 Нижняя кривая имеет ту же скорость v , но большая центростремительная сила F c создает меньший радиус r′r′ .
Нижняя кривая имеет ту же скорость v , но большая центростремительная сила F c создает меньший радиус r′r′ .
Смотреть физику
Центростремительная сила и интуиция ускорения
Это видео объясняет, почему центростремительная сила, когда она равна чистой силе и имеет постоянную величину, создает центростремительное ускорение и равномерное круговое движение.
Поддержка учителей
Поддержка учителей
Предупреждение о заблуждении
Некоторые студенты могут путать центростремительную силу и центробежную силу. Центробежная сила — это не реальная сила, а результат ускоряющейся системы отсчета, такой как вращающаяся машина или вращающаяся Земля. Центробежная сила относится к вымышленному центру , убегающему от силы .
com/embed/vZOk8NnjILg» data-media=»screen»>Представьте, что вы раскачиваете йойо по вертикали по часовой стрелке перед собой, перпендикулярно направлению взгляда. Если струна порвется, как только йо-йо достигнет крайнего нижнего положения, ближайшего к полу. Что будет с йойо после того, как порвется струна?
Йо-йо полетит внутрь в направлении действия центростремительной силы.
Йо-йо будет лететь наружу в направлении действия центростремительной силы.
Йо-йо полетит влево в направлении тангенциальной скорости.
Йо-йо полетит вправо в направлении тангенциальной скорости.

Решение задач центростремительного ускорения и центростремительной силы
Чтобы получить представление о типичных величинах центростремительного ускорения, мы проведем лабораторную работу, оценив центростремительное ускорение теннисной ракетки, а затем в нашем первом рабочем примере сравним центростремительное ускорение автомобиля, совершающего поворот, с ускорением свободного падения. Для второго рабочего примера мы рассчитаем силу, необходимую для поворота автомобиля по кривой.
Снап Лаборатория
Оценка центростремительного ускорения
В этом упражнении вы измерите замах клюшки для гольфа или теннисной ракетки, чтобы оценить центростремительное ускорение конца клюшки или ракетки. Вы можете сделать это в замедленном темпе. Напомним, что уравнение для центростремительного ускорения имеет вид ac=v2rac=v2r или ac=rω2ac=rω2.
- Одна теннисная ракетка или клюшка для гольфа
- Один таймер
- Одна линейка или рулетка
Процедура
- Работа с партнером.
 Стойте на безопасном расстоянии от партнера, когда он или она размахивает клюшкой для гольфа или теннисной ракеткой.
Стойте на безопасном расстоянии от партнера, когда он или она размахивает клюшкой для гольфа или теннисной ракеткой. - Опишите движение качелей — это равномерное круговое движение? Почему или почему нет?
- Постарайтесь, чтобы качание было как можно ближе к равномерному круговому движению. Какие коррективы должен был внести ваш партнер?
- Измерьте радиус кривизны. Что вы измеряли физически?
- Используя таймер, найдите либо линейную, либо угловую скорость, в зависимости от того, какое уравнение вы решите использовать.
- Каково приблизительное центростремительное ускорение на основе этих измерений? Как вы думаете, насколько они точны? Почему? Как вы и ваш партнер можете сделать эти измерения более точными?
Поддержка учителей
Поддержка учителей
Замах клюшки для гольфа или ракетки можно сделать очень близким к равномерному круговому движению. Для этого человек должен был бы перемещать его с постоянной скоростью, не сгибая руки.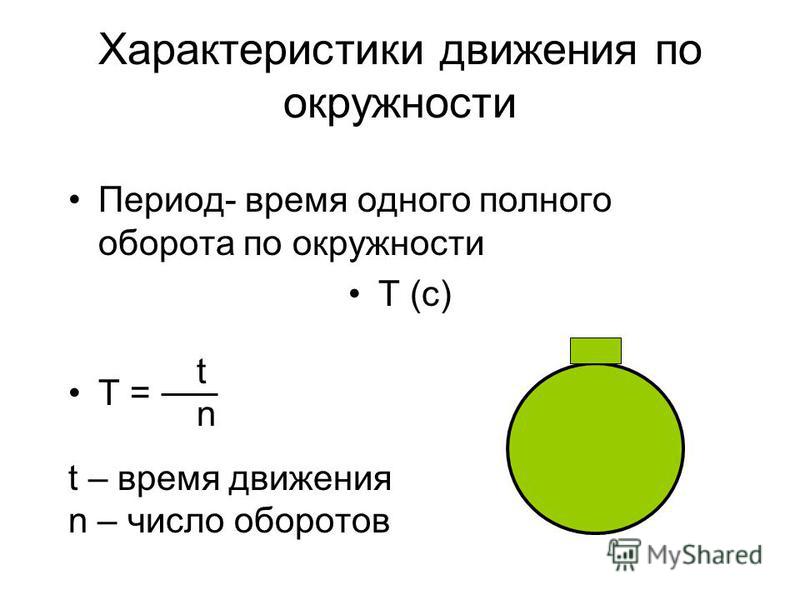 Длина руки плюс длина клюшки или ракетки – это радиус кривизны. Точность измерений угловой скорости и углового ускорения будет зависеть от разрешающей способности используемого таймера и ошибки человеческого наблюдения. Замах клюшки для гольфа или ракетки можно сделать очень близким к равномерному круговому движению. Для этого человек должен был бы перемещать его с постоянной скоростью, не сгибая руки. Длина руки плюс длина клюшки или ракетки – это радиус кривизны. Точность измерений угловой скорости и углового ускорения будет зависеть от разрешающей способности используемого таймера и ошибки человеческого наблюдения.
Длина руки плюс длина клюшки или ракетки – это радиус кривизны. Точность измерений угловой скорости и углового ускорения будет зависеть от разрешающей способности используемого таймера и ошибки человеческого наблюдения. Замах клюшки для гольфа или ракетки можно сделать очень близким к равномерному круговому движению. Для этого человек должен был бы перемещать его с постоянной скоростью, не сгибая руки. Длина руки плюс длина клюшки или ракетки – это радиус кривизны. Точность измерений угловой скорости и углового ускорения будет зависеть от разрешающей способности используемого таймера и ошибки человеческого наблюдения.
Проверка захвата
Было ли полезнее использовать уравнение ac=v2rac=v2r или ac=rω2ac=rω2 в этом упражнении? Почему?
- Должно быть проще использовать ac=rω2ac=rω2, потому что измерение угловой скорости путем наблюдения было бы проще.
- Должно быть проще использовать ac=v2rac=v2r, поскольку было бы проще измерить тангенциальную скорость посредством наблюдения.

- Должно быть проще использовать ac=rω2ac=rω2, потому что измерение угловой скорости путем наблюдения будет затруднено.
- Должно быть проще использовать ac=v2rac=v2r, потому что измерение тангенциальной скорости путем наблюдения будет затруднено.
Рабочий пример
Сравнение центростремительного ускорения автомобиля, огибающего кривую, с ускорением под действием силы тяжести
Автомобиль следует по кривой радиусом 500 м со скоростью 25,0 м/с (около 90 км/ч). Чему равно центростремительное ускорение автомобиля? Сравните центростремительное ускорение для этой довольно плавной кривой, снятой на скорости шоссе, с ускорением под действием силы тяжести ( г ).
Стратегия
Поскольку дана линейная, а не угловая скорость, наиболее удобно использовать выражение ac=v2rac=v2r для нахождения величины центростремительного ускорения.
Solution
Ввод данных значений v = 25,0 м/с и r = 500 м в выражение для a c дает
ac=v2r=(25,20 м/с) м/с2.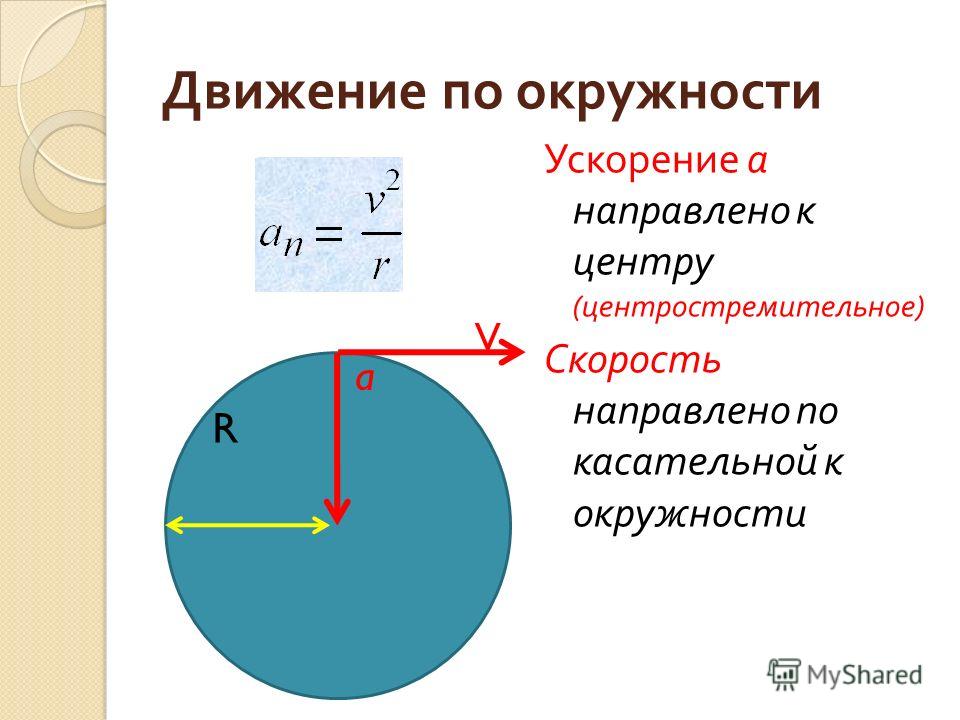 ac=v2r=(25,0 м/с)2500 м=1,25 м/с2.
ac=v2r=(25,0 м/с)2500 м=1,25 м/с2.
Обсуждение
Чтобы сравнить это с ускорением свободного падения ( г = 9,80 м/с 2 ), возьмем отношение ac/g=(1,25 м/с2)/(9,80 м/с2)=0,128ac/ g=(1,25 м/с2)/(9,80 м/с2)=0,128 . Следовательно, ac=0,128gac=0,128g, что означает, что центростремительное ускорение составляет примерно одну десятую ускорения свободного падения.
Рабочий пример
Сила трения на автомобильных шинах, огибающих кривую
- Рассчитайте центростремительную силу, действующую на автомобиль массой 900 кг, который движется по кривой радиусом 600 м на горизонтальной поверхности со скоростью 25,0 м/с.
- Статическое трение предотвращает скольжение автомобиля. Найдите величину силы трения между шинами и дорогой, которая позволяет автомобилю пройти поворот без соскальзывания по прямой.

- Если бы автомобиль скользил, если бы он двигался еще быстрее, каков коэффициент статического трения между шинами и дорогой? Могли бы мы сделать какие-либо выводы о коэффициенте трения покоя, если бы не знали, может ли автомобиль двигаться быстрее по кривой без проскальзывания?
Стратегия и решение для (а)
Мы знаем, что Fc=mv2rFc=mv2r . Следовательно,
Fc=mv2r=(900кг)(25,0м/с)2600м=938Н.Fc=mv2r=(900кг)(25,0м/с)2600м=938Н.
Стратегия и решение для (б)
На изображении выше показаны силы, действующие на автомобиль при движении по кривой. На этой диаграмме автомобиль въезжает на страницу, как показано, и поворачивает налево. Трение действует влево, ускоряя автомобиль к центру кривой. Поскольку трение является единственной горизонтальной силой, действующей на автомобиль, в данном случае оно обеспечивает всю центростремительную силу. Следовательно, сила трения является центростремительной силой в этой ситуации и направлена к центру кривой.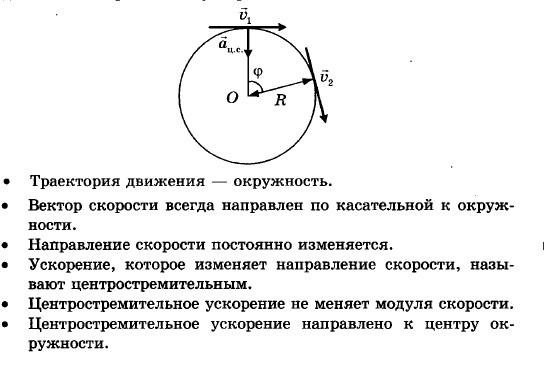
f=Fc=938Nf=Fc=938N
Стратегия и решение для (c)
Если автомобиль вот-вот начнет скользить, трение покоя достигнет максимального значения и f=µsN=µsmgf=µsN=µsmg. Решая для мксмкс, получаем мкс=938900×9,8=0,11 мкс=938900×9,8=0,11. Независимо от того, знаем ли мы максимально допустимую скорость для скругления кривой, мы можем сделать вывод, что это минимальное значение коэффициента.
Обсуждение
Поскольку мы нашли силу трения в части (b), мы могли также найти коэффициент трения, поскольку f=µsN=µsmgf=µsN=µsmg. Трение покоя равно только µsNµsN, когда оно имеет максимально возможное значение. Если бы автомобиль мог двигаться быстрее, трение при заданной скорости было бы таким же, как мы рассчитали, но коэффициент статического трения был бы больше.
Практические задачи
9.
Какое центростремительное ускорение испытывают пассажиры автомобиля, движущегося со скоростью 12 м/с по кривой радиусом 2,0 м?
3 м/с 2
6 м/с 2
36 м/с 2
72 м/с 2
10.
Рассчитайте центростремительное ускорение объекта, следующего по пути с радиусом кривизны 0,2 м и с угловой скоростью 5 рад/с.
- 1 м/с
- 5 м/с
- 1 м/с 2
- 5 м/с 2
Проверьте свое понимание
11.
Что такое равномерное круговое движение?
Равномерное круговое движение — это когда объект ускоряется по круговой траектории с постоянно увеличивающейся скоростью.
Равномерное круговое движение — это когда объект движется по круговой траектории с переменным ускорением.
Равномерное круговое движение — это когда объект движется по круговой траектории с постоянной скоростью.

Равномерное круговое движение — это когда объект движется по круговой траектории с переменной скоростью.
12.
Что из следующего является центростремительным ускорением?
- Ускорение объекта, движущегося по круговой траектории и направленного радиально к центру круговой орбиты
- Ускорение объекта, движущегося по круговой траектории и направленного по касательной по круговой траектории
- Ускорение объекта, движущегося по прямолинейному пути и направленного в направлении движения объекта
- Ускорение объекта, движущегося по прямолинейному пути и направленного в сторону, противоположную движению объекта
13.
Есть ли результирующая сила, действующая на объект при равномерном круговом движении?
Да, объект ускоряется, поэтому на него должна действовать результирующая сила.

Да потому что разгона нет.
Нет, потому что есть ускорение.
Нет, потому что нет ускорения.
14.
Приведите два примера сил, которые могут вызвать центростремительное ускорение.
- Сила земного притяжения на Луне и нормальная сила
- Сила земного притяжения на Луне и натяжение веревки на орбитальном шаре
- Нормальная сила и сила трения, действующие на движущийся автомобиль
- Нормальная сила и натяжение веревки на шаре
Поддержка учителей
Поддержка учителей
Используйте вопросы «Проверьте свое понимание», чтобы оценить, справляются ли учащиеся с целями обучения этого раздела.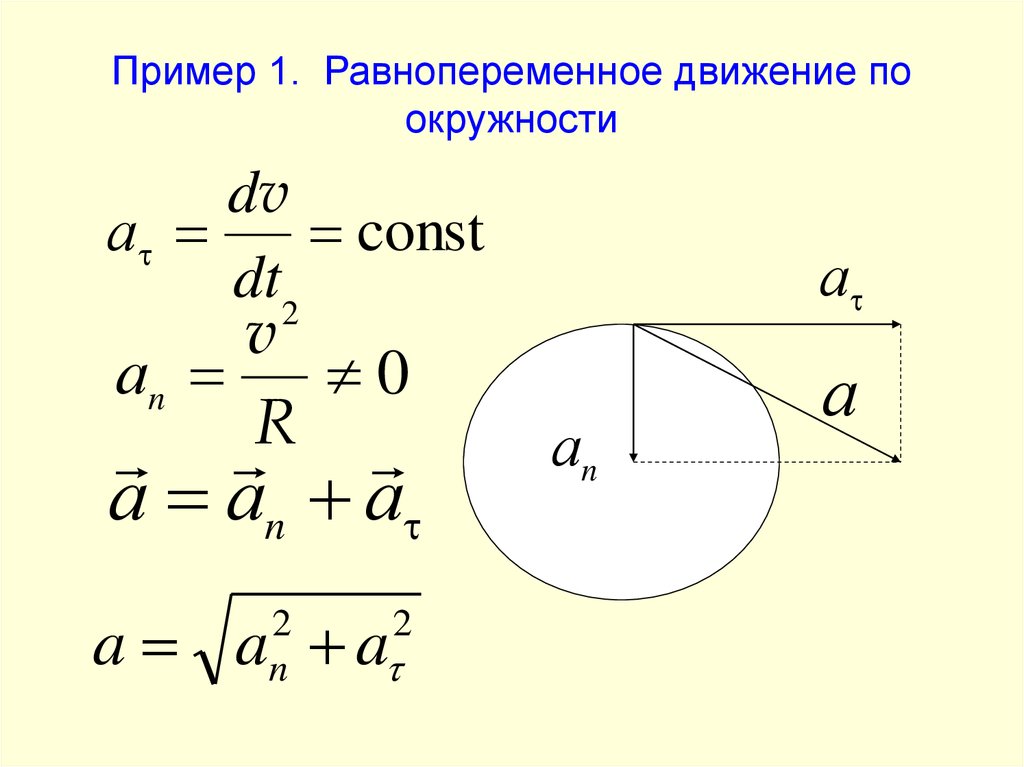

 Ожидается, что студент:
Ожидается, что студент: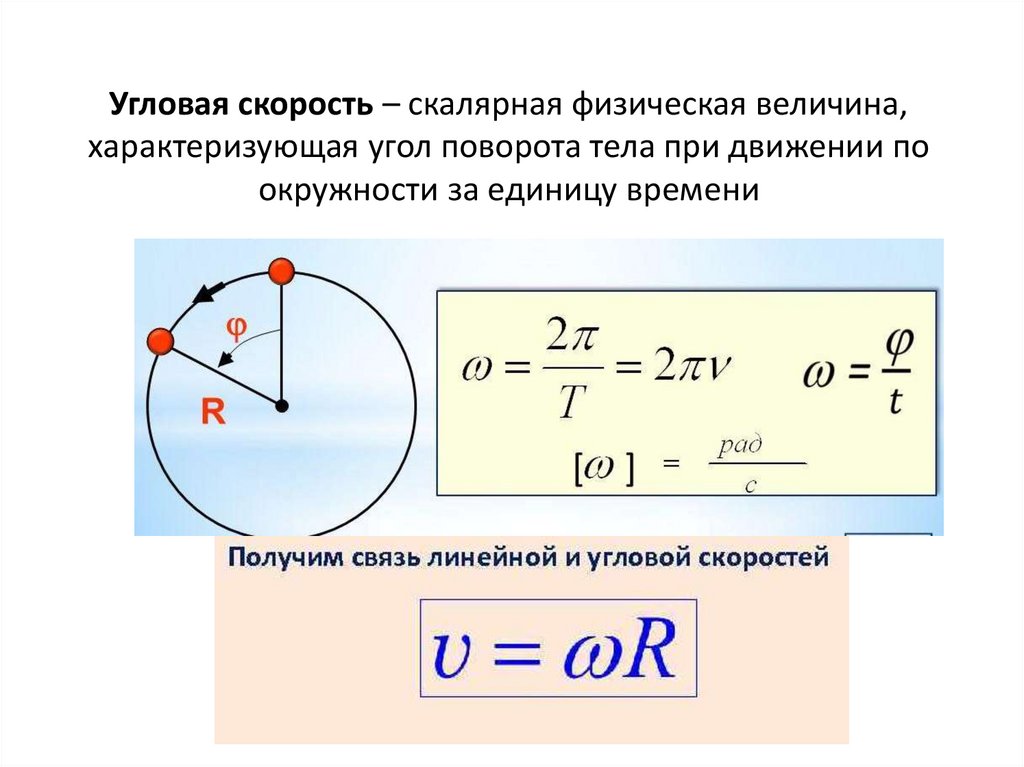
 Стойте на безопасном расстоянии от партнера, когда он или она размахивает клюшкой для гольфа или теннисной ракеткой.
Стойте на безопасном расстоянии от партнера, когда он или она размахивает клюшкой для гольфа или теннисной ракеткой.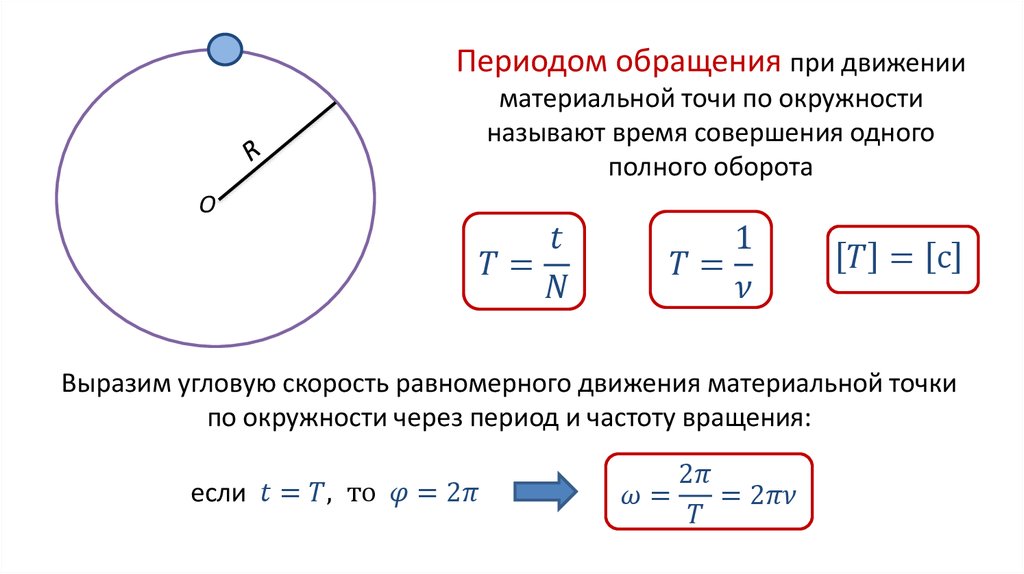

Leave A Comment