Признаки параллелограмма
Признак 1 (диагонали)
Диагонали пересекаются и делятся точкой пересечения пополам. И наоборот, если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.
Признак 2 (стороны)
У параллелограмма противолежащие стороны равны. Если у четырехугольника обе пары противолежащих сторон равны, то этот четырехугольник – параллелограмм.
Признак 3 (углы)
У параллелограмма противолежащие стороны равны и противолежащие углы равны. Если у четырехугольника обе пары противолежащих углов равны, то этот четырехугольник – параллелограмм.
Прямоугольник
Прямоугольник
Основные свойства:
- Прямоугольник является частным случаем ;
- Диагонали прямоугольника равны;
- Вокруг прямоугольника можно ;
- Площадь прямоугольника равна произведению сторон: S=abS=abS=ab.
Признак прямоугольника
является , и его диагонали равны. Если у параллелограмма диагонали равны, то он является прямоугольником.
Ромб
Ромб – это четырехугольник, у которого все стороны равны.
- Ромб является частным случаем ;
- Диагонали ромба пересекаются под прямым углом и являются его углов;
- В ромб можно ;
- Площадь ромба: S=a⋅h=a2⋅sinα=d1⋅d22S=a\cdot h=a^2\cdot \sin\alpha =\frac{d_1\cdot d_2}{2}S=a⋅h=a2⋅sinα=2d1⋅d2;
- Сторона ромба выражается через диагонали: a=(d12)2+(d22)2a=\sqrt{(\frac{d_1}{2})^2+(\frac{d_2}{2})^2}a=(2d1)2+(2d2)2.
 2S=a2,
2S=a2, - длина диагонали: d=2ad=\sqrt{2} ad=2a,
- радиус вписанной окружности: r=12ar=\frac{1}{2} ar=21a,
- радиус описанной окружности R=22aR=\frac{\sqrt{2}}{2} aR=22a.
Прямоугольник, ромб и квадрат – онлайн-тренажер для подготовки к ЕНТ, итоговой аттестации и ВОУД
Прямоугольник – параллелограмм, у которого все углы прямые.
Диагональю прямоугольника называется любой отрезок, соединяющий две вершины противоположных углов прямоугольника. Периметром прямоугольника называется сумма длин всех сторон прямоугольника.
Свойства прямоугольника
- Противоположные стороны прямоугольника равны.
- Каждый угол прямоугольника равен 90°.
- Значит, противоположные углы равны и сумма углов, прилежащих к одной стороне, равна 180°.
- Диагонали прямоугольника точкой пересечения делятся пополам.
- Диагональ прямоугольника делит его на два равных прямоугольных треугольника.
- Накрест лежащие углы при диагонали равны.
- Диагонали прямоугольника равны.
- Точка пересечения диагоналей называется центром прямоугольника и также является центром описанной окружности.
- Около любого прямоугольника можно описать окружность, при этом диагональ прямоугольника равна диаметру описанной окружности.
Признаки прямоугольника
- Если три угла четырехугольника прямые, то этот четырехугольник является прямоугольником.
- Если один угол параллелограмма прямой, то этот параллелограмм является прямоугольником.
- Если диагонали параллелограмма равны, то этот параллелограмм является прямоугольником.
Квадрат – это прямоугольник, у которого все стороны равны.
Свойства квадрата
Все свойства параллелограмма, ромба, прямоугольника верны и для квадрата.
- Все четыре стороны квадрата имеют одинаковую длину, то есть они равны.
- Противоположные стороны квадрата параллельны.
- Сумма углов квадрата равна 360°.
- Диагонали квадрата имеют одинаковые длины.
- Диагонали квадрата пересекаются под прямым углом, и разделяют друг друга пополам.
- Точка пересечения диагоналей называется центром квадрата и также является центром вписанной и описанной окружностей.
- Точка пересечения диагоналей называется центром квадрата и также является центром вписанной и описанной окружностей.
- Обе диагонали разделяют квадрат на четыре равные треугольника, причем эти треугольники одновременно и равнобедренные, и прямоугольные.
Признаки квадрата
- Если две смежные стороны прямоугольника равны, то этот прямоугольник является квадратом.
- Если диагонали прямоугольника перпендикулярны, то этот прямоугольник является квадратом.
Формулы определения длины диагонали квадрата:
\(d=a\sqrt{2}; \ d=\sqrt{2S}; \ d=2R; \ d=2r\sqrt{2}\).
Ромбом называется параллелограмм, у которого все стороны равны. Если у ромба все углы прямые, тогда он называется квадратом.
Свойства ромба
- Поскольку ромб – это параллелограмм, то все свойства параллелограмма верны для ромба.
- Противолежащие стороны равны.
- Противоположные углы равны.
- Диагонали точкой пересечения делятся пополам.
- Сумма углов, прилежащих к одной стороне, равна 180°.
- Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4:
- Диагонали перпендикулярны.
- Диагонали являются биссектрисами его углов.
- Центром вписанной в ромб окружности будет точка пересечения его диагоналей.
Признаки ромба
- Если диагонали параллелограмма перпендикулярны, то параллелограмм – ромб.

Урок 6. прямоугольник. ромб. квадрат — Геометрия — 8 класс
Понятие прямоугольника всем знакомо с начальной школы. Прямоугольник – это параллелограмм, у которого все углы прямые. Прямоугольник обладает всеми свойствами параллелограмма:
— противоположные стороны равны и параллельны;
— противоположные углы равны, углы, прилежащие к одной стороне составляют в сумме 180°;
— особо можно выделить, что все углы равны;
— диагонали пересекаются и точкой пересечения делятся пополам.
У прямоугольника есть особое свойство: диагонали прямоугольника равны.Элементы Свойства от параллелограмма Особое свойство Стороны Противоположные стороны равны и параллельны Углы Противоположные углы равны, углы, прилежащие к одной стороне составляют в сумме 180° Все углы равны Диагонали Диагонали пересекаются и точкой пересечения делятся пополам Диагонали равны
Для доказательства рассмотрим прямоугольник ABCD с диагоналями AC и BD.Прямоугольные треугольники ABD и DCA равны по двум катетам, т.к. AD – общий катет, AB = CD. Следовательно, AC = BD.
Для того, чтобы определить, является ли данный параллелограмм прямоугольником нужен признак прямоугольника. Он вытекает из особого свойства прямоугольника: если в паралеллограмме диагонали равны, то этот паралеллограмм – прямоугольник.
ABD и DCA равны по трем сторонам: AC = BD (по условию), AB = CD (свойство параллелограмма). AD – общая сторона. Следовательно, ∠BAD = ∠CDA, но ∠BAD + ∠CDA = 180° и ∠BAD = ∠BCD, ∠CDA = ∠CDA, поэтому ∠BAD = ∠BCD = ∠CDA = ∠CDA = 90° значит, ABCD – прямоугольник.
Параллелограмм, у которого все стороны равны, называется ромбом, он обладает всеми его свойствами, а из определения ромба следует, что все стороны равны.
Ромб обладает и особым свойством: диагонали ромба взаимно перпендикулярны и делят его углы пополам.Элементы Свойства от параллелограмма Особое свойство Стороны Противоположные стороны равны и параллельны Все стороны равны Углы Противоположные углы равны, углы, прилежащие к одной стороне составляют в сумме 180° Диагонали Диагонали взаимно перпендикулярны и делят углы пополам
Для доказательства особого свойства рассмотрим ромб ABCD с диагоналями AC и BD.AB = AD (ромб). Треугольник ABD – равнобедренный, AO – медиана, а значит высота и биссектриса этого треугольника. Следовательно, AC ⊥ BD, AC – биссектриса ∠BAD.
Признаки ромба получаются из особого свойства ромба:
— если диагонали параллелограмма взаимно перпендикулярны, то он является ромбом
— если диагональ параллелограмма является биссектрисой его угла, то он является ромбом.Четырехугольники /qualihelpy
Четырехугольником называют многоугольник, имеющий четыре вершины. Среди всех четырехугольников выделяют параллелограмм, ромб, прямоугольник, квадрат и трапецию.Параллелограммом называют четырехугольник, у которого противолежащие стороны попарно параллельны.
Высотой параллелограмма называют отрезок перпендикуляра, заключенный между его параллельными сторонами или отрезок перпендикуляра, проведенного из вершины параллелограмма на прямую, содержащую противолежащую сторону.

Свойства параллелограмма
1. Противолежащие стороны параллелограмма равны.
Например, на рисунке 8.67 и .2. Противолежащие углы параллелограмма равны.
Например, на рисунке 8.67 и .3. Диагонали параллелограмма делятся точкой пересечения пополам.
Например, на рисунке 8.67 и .4. Сумма квадратов диагоналей параллелограмма равна сумме квадратов длин всех его сторон:
, (8.15)где и – смежные стороны, и – диагонали параллелограмма.Признаки параллелограмма
1. Если у выпуклого четырехугольника две противолежащие стороны параллельны и равны, то этот четырехугольник – параллелограмм.
2. Если у выпуклого четырехугольника противолежащие стороны попарно равны, то этот четырехугольник – параллелограмм.
3. Если у выпуклого четырехугольника противолежащие углы попарно равны, то этот четырехугольник – параллелограмм.
4. Если у выпуклого четырехугольника диагонали точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.
Площадь параллелограмма
Периметр параллелограмма можно вычислить по формуле:
. (8.19)Ромбом называют параллелограмм, все стороны которого равны.
Например, на рисунке 8.69 изображен ромб: – сторона, – высота, , его диагонали.Свойства ромба
Ромбу присущи все свойства параллелограмма и, кроме того, свойства:
1) диагонали ромба взаимно перпендикулярны;
2) диагонали ромба являются биссектрисами его внутренних углов.
Признаки ромба
1.
 Параллелограмм является ромбом, если две его смежные стороны равны.
Параллелограмм является ромбом, если две его смежные стороны равны.2. Параллелограмм является ромбом, если его диагонали перпендикулярны.
3. Параллелограмм является ромбом, если одна из диагоналей является биссектрисой его угла.
Периметр ромба можно вычислить по формуле:
. (8.20)Площадь ромба можно вычислить по тем же формулам, что и площадь параллелограмма, кроме того, и по формуле:
. (8.21)Прямоугольником называют параллелограмм, у которого все углы прямые.
Например, на рисунке 8.70 изображен прямоугольник, у которого и – смежные стороны, – диагонали, φ – угол между диагоналями.Свойства прямоугольника
Прямоугольнику присущи все свойства параллелограмма. Кроме того диагонали прямоугольника равны.
Признаки прямоугольника
1. Параллелограмм является прямоугольником, если его диагонали равны.
2. Параллелограмм является прямоугольником, если один из его углов прямой.
3. Четырехугольник является прямоугольником, если три его угла прямые.
Площадь прямоугольника можно вычислить по формулам:
; (8.22)или
. (8.23)Периметр прямоугольника можно вычислить по формуле:
. (8.24)Квадратом называют прямоугольник, у которого все стороны равны.
Например, на рисунке 8.71 изображен квадрат со стороной и диагональю .Квадрат обладает всеми свойствами параллелограмма, ромба и прямоугольника.
Признаки квадрата
1. Прямоугольник является квадратом, если две его смежные стороны равны.
2. Прямоугольник является квадратом, если его диагонали перпендикулярны.
3. Прямоугольник является квадратом, если одна из диагоналей является биссектрисой его угла.
Площадь квадрата можно вычислить по формулам:
(8.25)или
. (8.26)Периметр квадрата можно вычислить по формуле:
. (8.27)Трапецией называют четырехугольник, две стороны которого параллельны, а две другие не параллельны.
 Параллельные стороны трапеции называют основаниями, а непараллельные – боковыми сторонами.
Параллельные стороны трапеции называют основаниями, а непараллельные – боковыми сторонами. Трапецию называют равнобедренной (равнобокой), если ее боковые стороны равны.
Например, на рисунке 8.72 изображена равнобедренная трапеция, а на рисунке 8.73 – неравнобедренная.
Трапецию называют прямоугольной, если ее боковая сторона перпендикулярна основаниям.
Например, на рисунке 8.74 изображена прямоугольная трапеция.
Средней линией трапеции называется отрезок, соединяющий середины ее боковых сторон.
Например, на рисунке 8.75 отрезок – средняя линия трапеции .Свойства средней линии трапеции
1. Средняя линия трапеции параллельна основаниям трапеции.
2. Средняя линия трапеции равна полусумме ее оснований.
Сумма углов трапеции, прилежащих к ее боковой стороне, равна . Например, на рисунках 4.8 – 4.10 .Признак трапеции: четырехугольник является трапецией, если две его параллельные стороны не равны.
Площадь трапеции можно вычислить по формулам:
;(8.28)или
. (8.29)Прямоугольник. Ромб. Квадрат 8 класс онлайн-подготовка на Ростелеком Лицей
Прямоугольник. Ромб. Квадрат.
Прямоугольник – это четырехугольник, у которого все углы прямые.
Прямоугольник является параллелограммом, поэтому для него выполняются все свойства параллелограмма.
Особенное свойство прямоугольника: его диагонали равны ( AC = BD ). Это следует из равенства прямоугольных треугольников ACD и DBA.
Признаки:
- Если у параллелограмма все углы равны, то это прямоугольник.
- Если в параллелограмме хотя бы один угол прямой, то это прямоугольник.
- Если в параллелограмме диагонали равны, то это прямоугольник.
Ромб – это четырехугольник, у которого все стороны равны.

Ромб – это частный случай параллелограмма, поэтому он обладает всеми свойствами параллелограмма.
Особенное свойство ромба: диагонали ромба перпендикулярны и делят углы ромба пополам (являются биссектрисами углов). Это следует из равенства треугольников ABO = CBO = ADO = CDO.
Признаки:
- Если в параллелограмме диагональ является биссектрисой, то это ромб.
- Если в параллелограмме диагонали перпендикулярны, то это ромб.
Квадрат – это прямоугольник, у которого все стороны равны.
Квадрат является параллелограммом, прямоугольником и ромбом, а значит, обладает всеми их свойствами.
Признаки:
- Если диагонали прямоугольника пересекаются под прямым углом, то это квадрат.
- Если в ромбе все углы равны, то это квадрат.
- Если в ромбе диагонали равны, то это квадрат.
Квадрат, его свойства и признаки.
Квадрат, его свойства и признаки.
Определение. Квадратом называется прямоугольник, у которого все стороны равны.
Для квадрата можно ввести несколько определений. Самое ёмкое мы уже привели. Но можно определить квадрат следующим образом:
Квадратом называется четырёхугольник, у которого все стороны равны, а углы прямые.
Квадратом называется параллелограмм, у которого все стороны и углы равны.
Квадратом называется ромб, у которого все углы прямые.
Поскольку квадрат является и параллелограммом, и прямоугольником, и ромбом, то он обладает теми же свойствами, что и все перечисленные четырёхугольники.

У квадрата диагонали пересекаются и точкой пересечения делятся пополам.
У квадрата диагонали взаимно перпендикулярны.
У квадрата диагонали являются биссектрисами его углов.
У квадрата диагонали равны.
У квадрата стороны являются высотами.
Каждая диагональ квадрата делит его на равные прямоугольные треугольники.
Теперь определим признаки квадрата.
ТЕОРЕМА (I признак). Если в прямоугольнике две его смежные стороны равны, то он является квадратом.
Дано: – прямоугольник
Доказать: – квадрат.
Доказательство.
Так как – прямоугольник, то у него противолежащие стороны равны.
– квадрат (по определению), ч.т.д.
Т ЕОРЕМА (II признак). Если в прямоугольнике диагонали перпендикулярны, то этот прямоугольник является квадратом.
Дано: – прямоугольник
Доказать: – квадрат.
Доказательство.
Рассмотрим .
по свойству диагоналей прямоугольника, значит, – медиана (по опред-нию).
– высота , т.к. . Значит, в является и медианой и высотой, поэтому этот треугольник является равнобедренным (по признаку равнобедренного треугольника), т.е. . Согласно I признаку квадрата, прямоугольник является квадратом, ч.т.д.
ТЕОРЕМА (III признак). Если в прямоугольнике одна из диагоналей является биссектрисой его угла, то такой прямоугольник является квадратом.

Дано: – прямоугольник
– диагональ
– биссектриса
Доказать: – квадрат.
Доказательство.
Так как – биссектриса , то .
по свойству внутренних накрест лежащих углов при параллельных прямых. Значит, , следовательно – равнобедренный, и . По I признаку квадрата, прямоугольник является квадратом, ч.т.д.
Т ЕОРЕМА (IV признак). Если в ромбе диагонали равны, то этот ромб является квадратом.
Дано: – ромб
— диагонали
Доказать: – квадрат.
Доказательство.
Рассмотрим и .
по III признаку равенства треугольников. Значит, все соответствующие углы у этих треугольников равны, т.е. . Эти углы являются внутренними односторонними при параллельных прямых и , следовательно, их сумма равна , т.е. , а, значит, и . Так как в ромбе противолежащие углы равны, то и все остальные углы также равны по . Значит, такой ромб является квадратом, ч.т.д.
Т ЕОРЕМА (V признак). Если в параллелограмме диагонали перпендикулярны и равны, то такой параллелограмм является квадратом.
Дано: – параллелограмм
Доказать: – квадрат.
Доказательство.
Так как , то по II признаку ромба, параллелограмм является ромбом.
Так как , то по IV признаку квадрата, ромб является квадратом, ч.т.д.
Т ЕОРЕМА (VI признак). Если в четырёхугольнике диагонали равны, взаимно перпендикулярны и точкой пересечения делятся пополам, то такой четырёхугольник является квадратом.

Дано: – четырёхугольник
Доказать: – квадрат.
Доказательство.
1. Так как , то четырёхугольник является параллелограммом (по признаку параллелограмма).
2. Так как , то параллелограмм является квадратом (по V признаку квадрата), ч.т.д.
Т ЕОРЕМА (VII признак). Если в четырёхугольнике все стороны равны и среди внутренних углов есть один прямой угол, то такой четырёхугольник является квадратом.
Дано: – четырёхугольник
Доказать: – квадрат.
Доказательство.
1. Так как , то четырёхугольник является ромбом (по V признаку ромба).
2. Так как , то ромб, который по определению является параллелограммом, является прямоугольником (по III признаку прямоугольника), значит, все углы в этом четырёхугольнике прямые.
3. Итак, прямоугольник , у которого все стороны равны, является квадратом (по определению), ч.т.д.
Итак, признаки квадрата:
Если в прямоугольнике две его смежные стороны равны, то он является квадратом.
Если в прямоугольнике диагонали перпендикулярны, то этот прямоугольник является квадратом.
Если в прямоугольнике одна из диагоналей является биссектрисой его угла, то такой прямоугольник является квадратом.
Если в ромбе диагонали равны, то этот ромб является квадратом.
Если в параллелограмме диагонали перпендикулярны и равны, то такой параллелограмм является квадратом.

Если в четырёхугольнике диагонали равны, взаимно перпендикулярны и точкой пересечения делятся пополам, то такой четырёхугольник является квадратом.
Если в четырёхугольнике все стороны равны и среди внутренних углов есть один прямой угол, то такой четырёхугольник является квадратом.
Периметр квадрата равен см. Найдите сторону квадрата .
Н
а рисунке четырёхугольник – квадрат, . Докажите, что выпуклый четырёхугольник также является квадратом.Н
а рисунке четырёхугольник – прямоугольник, . Докажите, что выпуклый четырёхугольник является квадратом.В треугольнике . На сторонах и взяты точки и , а на стороне – точки и так, что четырёхугольник является квадратом, . Найдите .
В треугольнике . На сторонах отмечены точки соответственно так, что четырёхугольник является квадратом, . Найдите .
На сторонах и квадрата отмечены точки и соответственно, . Отрезки и пересекаются в точке . Найдите .
На сторонах квадрата отмечены соответственно точки . Сравните отрезки и .
На катетах и прямоугольного треугольника построены квадраты и . Докажите, что сумма расстояний от точек и до прямой равна .
На катетах и прямоугольного треугольника построены квадраты и . Прямые и пересекаются в точке . Докажите, что .
Длина проекции одной из сторон квадрата на его диагональ равна . Найдите длину диагонали.
В
четырёхугольнике диагонали взаимно перпендикулярны. Докажите, что отрезки, соединяющие середины противоположных сторон, равны.Дан квадрат . Докажите, что – квадрат.

Дан квадрат . Докажите, что – ромб.
Дан квадрат . На стороне взята точка такая, что . Докажите, что точки – вершины равнобедренного треугольника.
Дан квадрат . Точки – середины его сторон соответственно. Докажите, что .
Дан квадрат . Точки и делят его стороны и так, что . Докажите, что .
К
вадраты и имеют общую вершину . Докажите, что медиана треугольника перпендикулярна отрезку .Внутри квадрата взята точка так, что . Докажите, что треугольник равносторонний.
Н
а рисунке – квадрат, точка принадлежит , точка принадлежит , точка принадлежит , прямые и пересекаются в точке . Докажите, что .В равнобедренный прямоугольный треугольник, каждый катет которого равен см, вписан квадрат, имеющий с ним один общий угол. Найдите периметр квадрата.
В равнобедренный прямоугольный треугольник вписан квадрат так, что две его вершины находятся на гипотенузе, а две другие – на катетах. Определите сторону квадрата, если известно, что гипотенуза равна 30 дм.
В квадрат вписан прямоугольник так, что на каждой стороне квадрата находится одна вершина прямоугольника и стороны прямоугольника параллельны диагоналям квадрата. Определите стороны этого прямоугольника, зная, что одна из них втрое больше другой и что диагональ квадрата равна дм.
В квадрат вписан прямоугольник так, что на каждой стороне квадрата находится одна вершина прямоугольника и стороны прямоугольника параллельны диагоналям квадрата. Определите стороны этого прямоугольника, зная, что одна из них вдвое больше другой и что диагональ квадрата равна см.
Точка расположена во внутренней области квадрата так, что расстояния от неё до сторон и пропорциональны соответственно числам и , а расстояние от до прямой равно см.
 Найдите периметр этого квадрата.
Найдите периметр этого квадрата.Точка расположена во внутренней области квадрата так, что расстояния от неё до сторон и пропорциональны соответственно числам и , а расстояние от до прямой равно м. Найдите периметр этого квадрата.
Точка лежит на стороне квадрата . Высоты треугольников и , проведённые из точки , равны соответственно и . Найдите произведение длин диагоналей этого квадрата.
Точка расположена во внутренней области квадрата так, что расстояния от неё до сторон и пропорциональны соответственно числам и , а расстояние от до прямой равно м. Найдите периметр этого квадрата.
Т
очка лежит на стороне квадрата . Высоты треугольников и , проведённые из точки , равны соответственно и . Найдите произведение длин диагоналей этого квадрата.На сторонах и квадрата отмечены точки и соответственно так, что . Определите взаимное расположение прямых и .
В
равнобедренный прямоугольный треугольник вписан квадрат , имеющий с ним общий угол . Найдите периметр квадрата, если катет треугольника равен см.В
нутри квадрата отмечена такая точка , что треугольник равносторонний. Найдите угол .В равнобедренный прямоугольный треугольник вписан квадрат , имеющий с ним общий прямой угол. Найдите катет треугольника, если периметр квадрата равен см.
- Дано, что диагонали ABCD равны и делят друг друга пополам под прямым углом.
- Понятно, что AECD — параллелограмм.
- Термин «параллелограмм» происходит от среднефранцузского «параллелограмма», позднего латинского «параллелограмм» и греческого «параллелограммон», что означает «ограниченный параллельными линиями».
- Прямоугольник — это параллелограмм, но все четыре внутренних угла фиксированы под углом 90 °
- Ромб — это параллелограмм, у которого все четыре стороны равны по длине
- Квадрат — это параллелограмм, но все стороны равны по длине и внутренние углы 90 °
- Обе пары противоположных сторон параллельны.
 (По определению). Или же:
(По определению). Или же: - Обе пары противоположных сторон равны. Если они совпадают, они также должны быть параллельны. Или же:
- Одна пара противоположных сторон равны и параллельны. Тогда другая пара также должна быть параллельна.
В
нутри квадрата отмечена такая точка , что треугольник равносторонний. Найдите угол .Через вершины квадрата проведены прямые, параллельные его диагоналям. Определите вид образованного ими четырёхугольника и вычислите его периметр, если диагональ квадрата равна см.
Через точку – точку пересечения диагоналей квадрата проведена прямая, параллельная стороне и пересекающая стороны и в точках и соответственно.
 \circ\);
\circ\);\(\sim\) Все стороны квадрата равны;
\(\sim\) Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.
Решение CBSE NCERT для класса 9 — математика
Вопрос 1:
Углы четырехугольника находятся в соотношении 3: 5: 9: 13. Найдите все углы четырехугольника.
Ответ:
Пусть общее отношение углов будет x. Следовательно, углы будут 3x, 5x, 9x и
.13x соответственно.
Так как сумма всех внутренних углов четырехугольника равна 360 0 ,
=> 3x + 5x + 9x + 13x = 360 0
=> 30x = 360 0
=> х = 360 0 /30
=> х = 12 0
Следовательно, углы равны
3x = 3 * 12 0 = 36 0
5x = 5 * 12 0 = 60 0
9x = 9 * 12 0 = 108 0
13x = 13 * 12 0 = 156 0
Вопрос 2:
Если диагонали параллелограмма равны, то покажите, что это прямоугольник.
Ответ:
Пусть ABCD — параллелограмм. Чтобы показать, что ABCD — прямоугольник, мы должны доказать, что один из
его внутренние углы составляют 90 0 .
In ΔABC и ΔDCB,
AB = DC (Противоположные стороны параллелограмма равны)
до н.э. = до н.э. (Обычный)
AC = DB (дано)
По правилу сравнения SSS,
ΔABC ≅ ΔDCB
Итак, ABC = ∠DCB
Известно, что сумма углов на одной стороне обхода равна 180 0
∠ABC + ∠DCB = 180 0 [AB || CD]
=> ABC + ∠ABC = 180 0
=> 2∠ABC = 180 0
=> ∠ABC = 90 0
Поскольку ABCD — параллелограмм, а один из его внутренних углов равен 90 0 , ABCD — прямоугольник.

Вопрос 3:
Докажите, что если диагонали четырехугольника пересекают друг друга под прямым углом, то получается ромб.
Ответ:Пусть ABCD — четырехугольник, диагонали которого AC и BD делят пополам под прямым углом, т. Е.
OA = OC, OB = OD и AOB = ∠BOC = ∠COD = ∠AOD = 90º. Чтобы доказать
ABCD ромб, мы должны доказать, что ABCD — параллелограмм, а все стороны ABCD равны
равно.
В ΔAOD и ΔCOD,
OA = OC (диагонали делят друг друга пополам)
∠AOD = ∠COD (дано)
OD = OD (общий)
Итак, ΔAOD ≅ ΔCOD (по правилу сравнения SAS)
Следовательно, AD = CD ………… ..1
Аналогичным образом можно доказать, что
AD = AB и CD = BC ……… ..2
Из уравнений 1 и 2 получаем
AB = BC = CD =
г. н.э.Поскольку противоположные стороны четырехугольника ABCD равны, можно сказать, что ABCD — это
параллелограмм.Поскольку все стороны параллелограмма ABCD равны, можно сказать, что ABCD — это
ромб.
Вопрос 4:
Покажите, что диагонали квадрата равны и делят друг друга пополам под прямым углом.
Ответ:
Пусть ABCD — квадрат. Пусть диагонали AC и BD пересекаются в точке O. Для доказательства
, что диагонали квадрата равны и делят друг друга пополам под прямым углом, имеем
доказывает, что AC = BD, OA = OC, OB = OD и ∠AOB = 90º.
In ΔABC и ΔDCB,
AB = DC (Стороны квадрата равны друг другу)
∠ABC = ∠DCB (все внутренние углы равны 90)
BC = CB (Общая сторона)
Итак, ΔABC ≅ ΔDCB (по соответствию SAS)
Следовательно, AC = DB (по CPCT)
Следовательно, диагонали квадрата равны по длине.
In ΔAOB и ΔCOD,
∠AOB = ∠COD (вертикально противоположные углы)
∠ABO = ∠CDO (альтернативные внутренние углы)
AB = CD (Стороны квадрата всегда равны)
Итак, ΔAOB ≅ ΔCOD (по правилу сравнения AAS)
Следовательно, AO = CO и OB = OD (по CPCT)
Следовательно, диагонали квадрата делят друг друга пополам.

In ΔAOB и ΔCOB,
Поскольку мы доказали, что диагонали делят друг друга пополам, следовательно,
АО = СО
AB = CB (Стороны квадрата равны)
BO = BO (Обычный)
Итак, ΔAOB ≅ ΔCOB (По согласованию SSS)
Следовательно, ∠AOB = ∠COB (по CPCT)
Однако AOB + ∠COB = 180 0 (линейная пара)
2∠AOB = 180 0
∠AOB = 90 0
Следовательно, диагонали квадрата делят друг друга пополам под прямым углом.
Вопрос 5:
Покажите, что если диагонали четырехугольника равны и делят друг друга пополам под прямым углом, то это квадрат.
Ответ:Рассмотрим четырехугольник ABCD, в котором диагонали AC и BD пересекаются друг с другом в точке
.Следовательно, AC = BD, OA = OC, OB = OD и ∠AOB = ∠BOC = ∠COD = ∠AOD = 90 0 .
Чтобы доказать, что ABCD — квадрат, мы должны доказать, что ABCD — параллелограмм, AB = BC = CD = AD,
, а один из его внутренних углов — 90 0 .
In ΔAOB и ΔCOD,
AO = CO (диагонали делят друг друга пополам)
OB = OD (диагонали делят пополам)
∠AOB = ∠COD (вертикально противоположные углы)
Итак, ΔAOB ≅ ΔCOD (правило сравнения SAS)
Следовательно, AB = CD (по CPCT) ………..1
А, OAB = ∠OCD (по CPCT)
Однако это альтернативные внутренние углы для линий AB и CD и альтернативные внутренние углы
равны друг другу только тогда, когда две линии параллельны.
Итак, AB || CD ………… 2
Из уравнений 1 и 2 получаем
ABCD — параллелограмм.
В ΔAOD и ΔCOD,
AO = CO (диагонали делят друг друга пополам)
∠AOD = ∠COD (учитывая, что каждый равен 90º)
OD = OD (общий)
Итак, ΔAOD ≅ ΔCOD (правило сравнения SAS)
Следовательно, AD = DC ……….
 .3
.3Однако AD = BC и AB = CD (противоположные стороны параллелограмма ABCD)
=> AB = BC = CD = DA
Следовательно, все стороны четырехугольника ABCD равны.
In ΔADC и ΔBCD,
г. н.э. = до н.э. (Уже доказано)
AC = BD (дано)
DC = CD (общий)
Итак, ΔADC ≅ ΔBCD (правило сравнения SSS)
Следовательно, ADC = ∠BCD (по CPCT)
Однако ADC + ∠BCD = 180 0 (внутренние углы)
=> ∠ADC + ∠ADC = 180 0
=> 2∠ADC = 180 0
=> ∠ADC = 90 0
Один из внутренних углов четырехугольника ABCD — прямой.
Таким образом, мы получили, что ABCD — параллелограмм, AB = BC = CD = AD и одна из его внутренних
углов — 90 0 . Следовательно, ABCD — квадрат.
Вопрос 6:
Диагональ AC параллелограмма ABCD делит пополам ∠A (см. Рис.).Покажите, что
(i) он также делит пополам ∠ C, (ii) ABCD — ромб
Ответ:
(i) ABCD — параллелограмм.
Итак, ∠DAC = ∠BCA (Альтернативные внутренние углы)………… 1
А, BAC = ∠DCA (Альтернативные внутренние углы) ………… 2
Однако известно, что AC делит пополам ∠A.
Итак, ∠DAC = ∠BAC ………….. 3
Из уравнений 1, 2 и 3 получаем
∠DAC = ∠BCA = ∠BAC = ∠DCA ………… 4
=> ∠DCA = ∠BCA
Следовательно, AC делит ∠C пополам.
(ii) Из уравнения 4 получаем
∠DAC = ∠DCA
=> DA = DC (Стороны, противоположные равным углам, равны)
Однако DA = BC и AB = CD (противоположные стороны параллелограмма)
=> AB = BC = CD = DA
Следовательно, ABCD — ромб.
Вопрос 7:
ABCD — ромб. Докажите, что диагональ AC делит пополам A, а также ∠C, а диагональ BD делит пополам B и ∠D.Ответ:
Присоединяйтесь к AC.
В ΔABC,
BC = AB (Стороны ромба равны друг другу)
Итак, ∠1 = ∠2 (Углы, противоположные равным сторонам треугольника, равны)
Однако ∠1 = ∠3 (Альтернативные внутренние углы для параллельных прямых AB и CD)
=> ∠2 = ∠3
Следовательно, AC делит ∠C пополам.

Также ∠2 = ∠4 (Альтернативные внутренние углы для || прямых BC и DA)
=> ∠1 = ∠4
Следовательно, AC делит пополам ∠A.
Аналогично можно доказать, что BD также делит пополам ∠B и ∠D.
Вопрос 8:
ABCD — это прямоугольник, в котором диагональ AC делит пополам A и ∠C. Покажите, что:
(i) ABCD — квадрат (ii) диагональ BD делит пополам B и ∠D.
Ответ:
(i) Дано, что ABCD — прямоугольник.
Итак, A = ∠C
=> A / 2 = ∠C / 2
=> ∠DAC = ∠DCA [AC делит пополам A и ∠C]
CD = DA [Стороны, противоположные равным углам, также равны]
Однако DA = BC и BC = CD [Противоположные стороны прямоугольника равны]
=> AB = BC = CD = DA
ABCD — это прямоугольник, все стороны которого равны.
Следовательно, ABCD — квадрат.
(ii) Присоединяемся к BD.
В ΔBCD,
до н.э. = CD (стороны квадрата равны)
∠CDB = ∠CBD (Углы, противоположные равным сторонам равны)
Однако ∠CDB = ∠ABD (Альтернативные внутренние углы для AB || CD)
=> ∠CBD = ∠ABD
=> BD делит B пополам
Также ∠CBD = ∠ADB (Альтернативные внутренние углы для BC || AD)
=> ∠CDB = ∠ABD
Итак, BD делит пополам ∠D.
Вопрос 9:
В параллелограмме ABCD на диагонали BD взяты две точки P и Q, так что DP = BQ (см. Рисунок).Покажите, что:
(i) ∆APD ≅ ∆CQB (ii) AP = CQ (iii) ∆AQB ≅ ∆CPD
(iv) AQ = CP (v) APCQ — параллелограмм
Ответ:
(i) In ∆APD и ∆CQB,
∠ADP = ∠CBQ (Альтернативные внутренние углы для BC || AD) AD = CB (Противоположные стороны параллелограмма
ABCD)
DP = BQ (дано)
∠ ∆APD ≅ ∆CQB (с использованием правила сравнения SAS)
(ii) Как мы заметили, ∆APD ≅ ∆CQB,
AP = CQ (CPCT)
(iii) В ∆AQB и ∆CPD,
∠ABQ = ∠CDP (Альтернативные внутренние углы для AB || CD) AB = CD (Противоположные стороны
параллелограмм ABCD)
BQ = DP (дано)
∆AQB ≅ ∆CPD (с использованием правила сравнения SAS)
(iv) Как мы заметили, ∆AQB ≅ ∆CPD,
∠ AQ = CP (CPCT)
(v) Из результатов, полученных в (ii) и (iv),
AQ = CP и AP = CQ
Поскольку противоположные стороны четырехугольника APCQ равны друг другу, APCQ является параллелограммом.

Вопрос 10:
ABCD — это параллелограмм, а AP и CQ — перпендикуляры из вершин A и C на диагонали BD (см. Данный рисунок). Покажи, что
(i) ∆APB ≅ ∆CQD (ii) AP = CQ
Ответ:
(i) In ∆APB и ∆CQD,
∠APB = ∠CQD (каждый 90 0 )
AB = CD (Противоположные стороны параллелограмма ABCD)
∠ABP = ∠CDQ (Альтернативные внутренние углы для AB || CD)
∠ ∆APB ≅ ∆CQD (по соответствию AAS)
(ii) Используя результат выше
∆APB ≅ ∆CQD, получаем
AP = CQ (по CPCT)
Вопрос 11:
In ∆ABC и ∆DEF, AB = DE, AB || DE, BC = EF и BC || EF.Вершины A, B и C соединены с вершинами D, E и F соответственно (см. Рисунок). Покажи, что
(i) Четырехугольник ABED — параллелограмм. (ii) Четырехугольник BEFC представляет собой параллелограмм
(iii) нашей эры || CF и AD = CF (iv) Четырехугольник ACFD представляет собой параллелограмм
(v) AC = DF (vi) ∆ABC ≅ ∆DEF.
Ответ:
(i) Дано, что AB = DE и AB || DE.
Если две противоположные стороны четырехугольника равны и параллельны друг другу, то это будет
параллелограмм.
Следовательно, четырехугольник ABED — параллелограмм.
(ii) Опять же, BC = EF и BC || EF
Следовательно, четырехугольник BCEF — параллелограмм.
(iii) Как мы заметили, ABED и BEFC — параллелограммы, поэтому AD = BE
.и н.э. || BE (Противоположные стороны параллелограмма равны и параллельны)
А, BE = CF и BE || CF
(Противоположные стороны параллелограмма равны и параллельны)
Итак, AD = CF и AD || CF
(iv) Как мы заметили, одна пара противоположных сторон (AD и CF) четырехугольника ACFD равна
равны и параллельны друг другу, следовательно, представляют собой параллелограмм.
(v) Поскольку ACFD является параллелограммом, пара противоположных сторон будет равной и параллельной
друг к другу.

AC || DF и AC = DF
(vi) ∆ABC и ∆DEF,
AB = DE (дано)
до н.э. = EF (дано)
AC = DF (ACFD — параллелограмм)
∆ABC ≅ ∆DEF (по правилу сравнения SSS)
Вопрос 12:
ABCD представляет собой трапецию, в которой AB || CD и AD = BC (см. Рисунок).Покажи, что
(i) ∠A = ∠B (ii) ∠C = ∠D
(iii) ∆ABC ≅ ∆BAD (iv) диагональ AC = диагональ BD
[Подсказка: протяните AB и проведите через C линию, параллельную DA, пересекающую AB, образованную в E.]
Ответ:
Продолжим AB. Затем проведите линию через C, которая параллельна AD, пересекая AE в точке
.(i) AD = CE (противоположные стороны параллелограмма AECD)
Однако AD = BC (Дано)
Следовательно, BC = CE
Следовательно, CEB = ∠CBE (Углы, противоположные равным сторонам, также равны)
Рассмотрим параллельные прямые AD и CE.
AE — это для них поперечная линия.
∠A + ∠CEB = 180 0 (Углы на одной стороне поперечного сечения)
∠A + ∠CBE = 180 0 (Используя соотношение ∠CEB = ∠CBE)…………. 1
Однако B + ∠CBE = 180 0 (линейные парные углы) ……………. 2
Из уравнений 1 и 2 получаем
∠A = ∠B
(ii) AB || CD
∠A + ∠D = 180 0 (Углы на одной стороне поперечины)
Кроме того, C + ∠B = 180 0 (Углы на одной стороне поперечного сечения)
=> ∠A + ∠D = ∠C + ∠B
Однако A = ∠B [Используя результат, полученный в (i)]
=> ∠C = ∠D
(iii) In ∆ABC и ∆BAD,
AB = BA (Общая сторона)
г. до н.э. =
г. н.э.∠B = ∠A (Доказано ранее)
Итак, ∆ABC ≅ ∆BAD (правило сравнения SAS)
(iv) Мы заметили, что ∆ABC ≅ ∆BAD.Итак, AC = BD (By CPCT)
Если диагонали параллелограмма равны, то покажите, что это прямоугольник.

Knockout JEE Main апрель 2021 г. (один месяц)
Персонализированный наставник с ИИ и адаптивное расписание, Материал для самообучения, Уроки выходного дня, Наставничество от наших экспертов, Неограниченные пробные тесты и персонализированные аналитические отчеты, Круглосуточная поддержка в чате сомнений.
14000 ₹ / — 4999 / —
купить сейчасНокаут NEET, август 2021 г. (один месяц)
Персонализированный наставник с ИИ и адаптивное расписание, Материал для самообучения, Уроки выходного дня, Наставничество от наших экспертов, Неограниченные пробные тесты и персонализированные аналитические отчеты, Круглосуточная поддержка в чате сомнений.
14000 ₹ / — 4999 / —
купить сейчасKnockout JEE Main Май 2021 г.
Персонализированный наставник с ИИ и адаптивное расписание, Материал для самообучения, Уроки выходного дня, Наставничество от наших экспертов, Неограниченные пробные тесты и персонализированные аналитические отчеты, Круглосуточная поддержка в чате сомнений.
22999 ₹ / — 9999 ₹ / —
купить сейчасНокаут NEET Август 2021
Персонализированный наставник с ИИ и адаптивное расписание, Материал для самообучения, Уроки выходного дня, Наставничество от наших экспертов, Неограниченные пробные тесты и персонализированные аналитические отчеты, Круглосуточная поддержка в чате сомнений.

22999 ₹ / — 9999 ₹ / —
купить сейчасСерия тестов JEE Main May 2021
Мудрые тесты без ограничений по главам, Неограниченные предметные мудрые тесты, Неограниченные полные пробные тесты, Получите персонализированный отчет об анализе производительности.
6999 / — 2999 / —
купить сейчасЕсли диагонали параллелограмма равны, то математика класса 9 CBSE
Подсказка: в этом вопросе указано, что если диагонали параллелограмма равны, т.е.{\ circ} $.
Полное пошаговое решение:
В $$ \ треугольнике PQR $$ и $$ \ треугольнике SRQ $$,
PQ = SR (противоположные стороны параллелограмма равны)
QR = QR (Общая сторона)
PR = SQ (Так как диагонали равны)
Следовательно, по свойству SSS (Side-Side-Side) мы можем сказать, что
$$ \ треугольник PQR \ cong \ треугольник SRQ $$
Теперь по CPCT, т. Е. « если два или более треугольника конгруэнтны друг другу, то соответствующие углы и стороны треугольников равны друг другу ».{\ circ} $.Четырехугольники | Евклидова геометрия | Сиявула
Нарисована следующая фигура в масштабе :
Дайте форме наиболее точное имя.

Начнем с подсчета количества сторон. У этой фигуры четыре стороны, так что это либо просто четырехугольник, либо один из особых типов четырехугольника.
Затем мы спрашиваем себя, есть ли на рисунке параллельные линии.Вы можете посмотреть на рисунок, чтобы увидеть, выглядят ли какие-либо из линий параллельными, или сделать быстрый набросок изображения и увидеть, встречаются ли какие-либо пары противоположных линий в одной точке.
Обе пары противоположных сторон параллельны. Это означает, что фигура может быть только одной из следующих: параллелограмм, прямоугольник, ромб или квадрат.
Затем мы спрашиваем себя, все ли внутренние углы равны 90 °. Все внутренние углы равны 90 °, поэтому это должен быть квадрат или прямоугольник. Наконец, мы проверяем, все ли стороны равны по длине.На этом рисунке стороны не равны по длине, поэтому он представляет собой прямоугольник.
Следовательно, это прямоугольник.
Форма также представляет собой параллелограмм и четырехугольник. Этот вопрос, однако, требовал наиболее точного названия формы.
Нарисована следующая фигура в масштабе :
Дайте форме наиболее точное имя.
Начнем с подсчета количества сторон.У этой фигуры четыре стороны, так что это либо просто четырехугольник, либо один из особых типов четырехугольника.
Затем мы спрашиваем себя, есть ли на рисунке параллельные линии. Вы можете посмотреть на рисунок, чтобы увидеть, выглядят ли какие-либо из линий параллельными, или сделать быстрый набросок изображения и увидеть, встречаются ли какие-либо пары противоположных линий в одной точке.
Обе пары противоположных сторон параллельны. Это означает, что фигура может быть только одной из следующих: параллелограмм, прямоугольник, ромб или квадрат.
Затем мы спрашиваем себя, все ли внутренние углы равны 90 °.
 Все внутренние углы не равны 90 °, поэтому это должен быть параллелограмм или ромб. Наконец, мы проверяем, все ли стороны равны по длине. На этом рисунке стороны равны по длине, поэтому он представляет собой ромб.
Все внутренние углы не равны 90 °, поэтому это должен быть параллелограмм или ромб. Наконец, мы проверяем, все ли стороны равны по длине. На этом рисунке стороны равны по длине, поэтому он представляет собой ромб.Следовательно, это ромб.
Форма также представляет собой параллелограмм и четырехугольник. Этот вопрос, однако, требовал наиболее точного названия формы.
На основе формы, которую вы видите, перечислите все имена формы. Рисунок выполнен в масштабе
.Обе пары противоположных сторон не параллельны. Это означает, что фигура может быть только комбинацией следующих элементов: трапеции, воздушного змея или четырехугольника.
Форма определенно четырехугольник, потому что у него четыре стороны. У него нет особых свойств: у него нет параллельных сторон, прямых углов или сторон равной длины.Следовательно, это только четырехугольник.
На основе формы, которую вы видите, перечислите все имена формы. Рисунок выполнен в масштабе
.Обе пары противоположных сторон не параллельны. Это означает, что фигура может быть только комбинацией следующих элементов: трапеции, воздушного змея или четырехугольника.
Форма определенно четырехугольник, потому что у него четыре стороны. Это также воздушный змей, потому что у него две пары смежных сторон одинаковой длины.Это не может быть квадрат или прямоугольник, потому что у него нет прямых углов. Это не может быть параллелограмм или трапеция, потому что у него нет параллельных сторон. И это не ромб, потому что все четыре стороны не одинаковой длины.
Следовательно, правильный ответ: воздушный змей и четырехугольник.
На основе формы, которую вы видите, перечислите все имена формы. Рисунок выполнен в масштабе
.Обе пары противоположных сторон параллельны.
 {2} & = 225 \\
AF & = 15
\ end {выровнять *}
{2} & = 225 \\
AF & = 15
\ end {выровнять *}Мы также знаем, что \ (FD = BF = 17 \) и поэтому \ (AC = 17 + 8 = 25 \).
Следовательно, площадь прямоугольника \ (ACGF \) равна:
\ begin {align *} A _ {\ text {rectangle}} & = l \ times b \\ & = (25) (15) \\ & = 375 \ end {выровнять *}Мы почти у цели. Теперь нам нужно вычислить площадь треугольника \ (CDG \) и вычесть ее из площади прямоугольника, чтобы получить площадь \ (ACDF \).
Площадь треугольника \ (CDG \):
\ begin {align *} A _ {\ text {треугольник}} & = \ frac {1} {2} DG \ times CG \\ & = \ frac {1} {2} (8 \ times 15) \\ & = 60 \ end {выровнять *}Следовательно, площадь \ (ACDF \) равна \ (375 — 60 = 315 \).
Что такое параллелограмм? [Определение, факты и пример]
Что такое параллелограмм?
Параллелограмм — это особый тип четырехугольника, у которого противоположные стороны равны и параллельны.
На данном рисунке показан параллелограмм ABCD, который как AB параллелен CD, а AD параллелен BC.
Также AD = BC и AB = CD.
Мы также видим множество параллелограммов, похожих на формы и объекты, вокруг нас.
Свойства параллелограмма
Противоположные стороны параллелограмма параллельны друг другу.
Здесь AB ∥ CD и AD ∥ BC
Противоположные стороны параллелограмма равны по длине.
Здесь AB = CD и AD = BC
Противоположные углы параллелограмма равны по меру.
Здесь угол A = угол C и
Угол B = Угол D.
Смежные углы параллелограмма в сумме составляют 180 °
Здесь угол A + угол B = 180 °
Угол B + Угол C = 180 °
Угол C + Угол D = 180 °
Угол D + Угол A = 180 °
Диагонали параллелограмма делят друг друга пополам.

Здесь AC и BD пересекают друг друга пополам.
Виды параллелограмма
Есть три особых типа параллелограмма.
1. Ромб : параллелограмм, у которого все стороны равны.
Здесь AB = BC = CD = DA. ABCD — ромб.
2. Прямоугольник : параллелограмм, в котором все углы прямые и диагонали равны.
Здесь все углы прямые. Диагонали PN и OM равны.
3. Квадрат : параллелограмм со всеми равными сторонами и всеми углами, равными 90 градусам. Диагонали квадрата также равны.
Здесь все стороны равны и все углы прямые.
Диагонали AC и BD равны.
Интересные факты
Параллелограмм — определение математического слова
Параллелограмм — определение математического слова — Открытый справочник по математике Попробуйте это Перетащите оранжевые точки на каждую вершину , чтобы изменить форму параллелограмма. Обратите внимание, как противоположные стороны остаются параллельными.Параллелограмм — это четырехугольник с противоположными сторонами параллельно. Но есть различные тесты, которые можно применить, чтобы увидеть, является ли что-то параллелограммом.
Это «родитель» некоторых других четырехугольников, которые получаются добавлением различного рода ограничений:
Четырехугольник является параллелограммом, если:
Свойства параллелограмма
Эти факты и свойства верны для параллелограммов и форм-потомков: квадрата, прямоугольника и ромба.База Базой можно считать любую сторону.Выбирайте любой понравившийся. Если используется для расчета площади (см. Ниже), необходимо использовать соответствующую высоту. На рисунке выше выбрана одна из четырех возможных баз и соответствующая высота. Высота
(высота)Высота (или высота) параллелограмма — это расстояние по перпендикуляру. от основания на противоположную сторону (которую, возможно, придется удлинить). На рисунке выше показана высота, соответствующая базовому CD. Площадь Площадь параллелограмма можно найти, умножив основание на соответствующую высоту.См. Также Площадь параллелограмма .Периметр Расстояние вокруг параллелограмма. Сумма его сторон. См. Также Периметр параллелограмма .Противоположные
стороныПротивоположные стороны конгруэнтные (равные по длине) и параллельно. Изменяя форму параллелограмма вверху страницы, обратите внимание на то, что противоположные стороны всегда имеют одинаковую длину. Диагонали Каждая диагональ разрезает другую диагональ на две равные части, как показано на рисунке ниже.Видеть Диагонали параллелограмма для интерактивной демонстрации этого. Внутренние
уголкиПротивоположные углы равны, как видно ниже.
Последовательные углы всегда являются дополнительными (добавить к 180 °)Подробнее об этих свойствах см. Внутренние углы параллелограмма.
Параллелограмм вписанный в любой четырехугольник
Если вы найдете средние точки каждой стороны любого четырехугольник затем свяжите их последовательно линиями, результат всегда будет параллелограмм.
Поначалу это может показаться нелогичным, но см. Параллелограмм вписан в любой четырехугольник для оживленного исследования этого факта.
Другие темы о многоугольниках
Общий
Типы полигонов
Площадь различных типов полигонов
Периметр различных типов полигонов
Углы, связанные с многоугольниками
Именованные многоугольники
(C) Открытый справочник по математике, 2011 г.
Все права защищены.диагоналей параллелограмма равны
И наоборот, если диагонали четырехугольника делят друг друга пополам, то получается параллелограмм.H — это расстояние между двумя параллельными сторонами, которые представляют высоту трапеции. AC = DB Меньшая диагональ воздушного змея делит его на два равнобедренных треугольника. Следовательно, OA = OC & OB = OD В AOB и COB, OA = OC AB = BC BO = BO AOB COB AOB = COB Теперь AOB + COB = 180 AOB + AOB = 180 2 AOB = 180 AOB = 180 2… Ромб — это особый тип параллелограмма. Teachoo бесплатно. У ромба четыре равные стороны … Прямоугольники — это особый тип параллелограмма. Найдите периметр трапеции со сторонами 6 см, 7 см, 8 см и 9 см. Решение: Периметр трапеции = сумма всех ее сторон.В параллелограмме диагонали делят друг друга пополам. Теперь нам нужно доказать, что диагонали делят друг друга пополам, т.е. в параллелограмме, где одна пара сторон … Соседние углы являются дополнительными. Аналогично… Пусть PQRS — параллелограмм. ABC DCB Предположим, что диагонали пересекаются друг с другом под углом y, тогда площадь параллелограмма определяется по формуле: Area = ½ × d 1 × d 2… Каждая пара внутренних углов является дополнительными, потому что два прямых угла складываются в прямую. угол, поэтому противоположные стороны прямоугольника параллельны.Площадь параллелограмма — объяснение и примеры Как следует из названия, параллелограмм — это четырехугольник, образованный двумя парами параллельных прямых. Давайте докажем себе, что если у нас есть две диагонали четырехугольника, которые делят друг друга пополам, то мы имеем дело с параллелограммом. (PQ = QR = RS = SP) все углы в четырех углах = 90 ° Итак, чтобы доказать, что диагонали равны, нам нужно доказать, что PR = QS. Внутренние углы: противоположные углы равны, как показано ниже. Изучите науку с помощью Notes и решений NCERT.Диагонали делят друг друга пополам. Как известно, у параллелограмма есть две диагонали, которые пересекаются друг с другом. Итак, если у вас есть параллелограмм с перпендикулярными диагоналями, это должен быть ромб. Используя скалярное произведение векторов, докажите, что параллелограмм, диагонали которого равны, является прямоугольником. Воздушный змей — это четырехугольник с двумя парами смежных и совпадающих (равной длины) сторон. Площадь любого параллелограмма также можно рассчитать, используя длину его диагонали. Последовательные углы в параллелограмме являются дополнительными (A + D = 180 °).В основном вы спрашиваете, равны ли площади ABP и BCP. Т. Тангетон. Он преподает последние 9 лет. Одна интересная особенность формы заключается в том, что есть формула для вычисления ее площади и… В параллелограмме диагонали делят друг друга пополам. ← Пред. Вопрос Следующий вопрос → +2 голоса. Но сумма этих углов равна 180, так как они являются смежными углами 11 мм. б. AO = CO, BO = DO Так как квадрат — это параллелограмм, а диагонали параллелограмма делят друг друга пополам. Следовательно, диагонали квадрата делят друг друга пополам.AB DC Величина или мера этой плоской области называется ее площадью. Математика, 12.11.2020 01:00. Докажите, что если в двух треугольниках два угла и включенная сторона одного треугольника равны двум углам и включенной стороне другого треугольника, то два треугольника равны. Q3.… Соответственно, площадь воздушного змея выражается как половина произведения его диагоналей, что аналогично площади ромба. & BC — поперечный Периметр параллелограмма = 2 (a + b) Здесь a и b — длины равных сторон параллелограмма.Противоположные стороны параллельны. B = «180» / «2» = 90 ABC = DCB Назовите точку пересечения обеих диагоналей P. Начните с параллелограмма, просто проведите диагональ от A до C, затем проведите линию от B до P. Эта линия от B до P составляет половину второй диагонали. MCQ по математике для 8-го класса Глава Wise с ответами Скачать PDF-файл подготовлен на основе последней схемы экзамена. Иногда параллелограмм также рассматривается как трапеция, две стороны которой параллельны. Решение: Как уже упоминалось, это квадрат, поэтому все стороны равны.ABCD — прямоугольник. См. Раздел Диагонали параллелограмма для интерактивной демонстрации этого. Форма имеет вращательную симметрию второго порядка. Решение: Учитывая, что длина основания = 5 см, а высота = 3 см. На приведенном выше рисунке вы можете видеть: Эквивалентным условием является то, что противоположные стороны параллельны (квадрат — параллелограмм), диагонали перпендикулярно делят друг друга пополам и имеют одинаковую длину. Противоположные стороны параллелограмма равны по длине. Каковы размеры остальных углов? Он также известен как равносторонний четырехугольник.Противоположные углы равны; Делящие параллелограмм диагонали образуют два равных (одинаковых) треугольника; Диагонали делят пополам (разрезают друг друга пополам) друг друга; Последовательные углы являются дополнительными; Все внутренние углы будут прямыми, если любой из углов является прямым; Однако индивидуальные свойства разных параллелограммов — это то, что задает их … То есть каждая диагональ разрезает другую на две равные части. Четырехугольник является квадратом тогда и только тогда, когда он одновременно является ромбом и прямоугольником (т.е., четыре равные стороны и четыре равных угла). Эквивалентным условием является то, что противоположные стороны параллельны (квадрат — параллелограмм), а диагонали перпендикулярно делят друг друга пополам и имеют одинаковую длину. Параллельные стороны трапеции называются основаниями, а непараллельные стороны трапеции называются ногами. В любом параллелограмме диагонали (линии, соединяющие противоположные углы) делят друг друга пополам. Бесплатная загрузка PDF-файла CBSE Maths Multiple Choice Questions для Class8 с ответами Глава 3 Понимание четырехугольников.Пара противоположных сторон равны и равны по длине. Докажите, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон. Правая трапеция включает как минимум два прямых угла. или иметь. Докажите, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его… Прямоугольник также имеет аналогичные свойства параллелограммов, например, противоположные стороны прямоугольника параллельны друг другу как параллелограмм.Следовательно, x = 90. В четырехугольнике линия, соединяющая два противоположных угла, называется диагональю. Противоположные стороны параллелограмма равны. … у параллелограмма две диагонали, которые пересекают друг друга. Название класса — Ромб. Каждая диагональ параллелограмма разделяет его на два равных треугольника. Площадь параллелограмма зависит от его основания и высоты. Четырехугольник, противоположные стороны которого равны и параллельны, а все внутренние углы равны 90 °, определяется как Прямоугольник.Итак, мы можем сказать, что площадь фигуры — это число (в некоторой единице), связанное с… Все мы знаем, что параллелограмм — это выпуклый многоугольник с 4 ребрами и 4 вершинами. Это доказывает, что противоположные углы в любом параллелограмме равны. На приведенном выше рисунке мы видим, что стороны AB и CD параллельны друг другу, тогда как стороны BC и AD не параллельны. 2. Ответы. Как мы уже доказали, противоположные стороны параллелограмма равны по размеру, что дает нам нужную нам сторону. Лучше сомневаться в приложении. Это означает, что два соседних угла являются дополнительными.Сколько пар равных противоположных углов. Более того, во сколько равен параллелограмм? Если диагонали параллелограмма равны, то покажите, что это прямоугольник. Площадь параллелограмма = основание × высота. Свойства параллелограммов можно применить и к ромбам. Трапеция также известна как трапеция. Чтобы изучить эти правила, определяющие стороны параллелограмма, используйте интерактивный параллелограмм Math Warehouse. Диагональ параллелограмма разделит фигуру на два одинаковых равных треугольника.Ответы. спросил 30 апреля 2017 г. в разделе Математика автора sforrest072 (128k баллов) отредактировал 3 января 2019 г. Викаш Кумар. Это свойство параллелограмма доказывается с помощью условия конгруэнтности ASA в параллелограмме. Это доказывает, что противоположные углы в любом параллелограмме равны. Повторители, Веданту Понедельник, 14 декабря 2020 г. / Опубликовано без рубрики. спросил 22 сентября 2018 г. в классе IX по математике от muskan15 (-3,443 балла) четырехугольников 2 B = 180 Закон параллелограмма.13 можно представить векторно как. Пример 8.1, 2. Если диагонали параллелограмма равны, покажите, что это прямоугольник. Обратите внимание, что все прямоугольники — параллелограммы, но обратное неверно. Вот некоторые важные свойства воздушного змея: воздушный змей симметричен с точки зрения его углов. Смежные углы в сумме составляют 180 градусов, поэтому смежные углы являются дополнительными углами. Ромб. По формуле Площадь = 5 × 3 = 15 кв. См. Если диагонали параллелограмма равны, то это прямоугольник; Если диагонали параллелограмма перпендикулярны друг другу, то это ромб; Если диагонали параллелограмма равны и перпендикулярны, то это квадрат ∵ В параллелограмме его диагонали делят пополам под прямым углом ∴ Его диагонали перпендикулярны ∵ Его диагонали равны →… Таким образом, ABCD — параллелограмм с одним углом = 90 градусов.При регистрации вы подтверждаете, что прочитали и согласны с Таким образом, 2x = 180. Найдите площадь параллелограмма с основанием 5 см и высотой 7 см. Пример: если основание параллелограмма равно 5 см, а высота 3 см, найдите его площадь. Итак, по определению параллелограмма это прямоугольник. Подразумевается, что кайт есть. Le périmètre et l’aire d’une figure plane permettent de caractériser sa taille. В математике простейшая форма закона параллелограмма (также называемая тождеством параллелограмма) принадлежит элементарной геометрии.Следовательно, формула периметра трапеции имеет вид. Это диагональное свойство отделимо. Геометрические фигуры, такие как квадрат и прямоугольник, считаются параллелограммами, поскольку противоположные стороны квадрата параллельны друг другу, а диагонали квадрата делят друг друга пополам. Некоторые важные формулы трапеции, воздушного змея и параллелограмма приведены ниже. В математике простейшая форма закона параллелограмма (также называемая тождеством параллелограмма) принадлежит элементарной геометрии.В нем говорится, что сумма квадратов длин четырех сторон параллелограмма равна сумме квадратов длин двух диагоналей. Диагонали равны, а соседние стороны равны. Изменяя форму параллелограмма вверху страницы, обратите внимание на то, что противоположные стороны всегда имеют одинаковую длину. Здесь a, b, c и d — стороны трапеции. Вы можете вспомнить, что часть плоскости, окруженная простой замкнутой фигурой, называется плоской областью, соответствующей этой фигуре.1800-212-7858 / 9372462318. Доказательство: прямоугольник — это параллелограмм с одним углом 90 Итак, если противоположные стороны четырехугольника параллельны, то четырехугольник является параллелограммом. Общее расстояние вокруг воздушного змея снаружи называется периметром воздушного змея. БЛОГ. Площадь параллелограмма зависит от его основания и высоты. Параллелограмм — это четырехгранная геометрическая фигура, стороны которой параллельны, а противоположные стороны равны друг другу по длине. Противоположные или обращенные стороны параллелограмма имеют одинаковую длину, а противоположные углы параллелограмма равны.Да, если диагонали параллелограмма равны, то это прямоугольник. Воздушный змей можно рассматривать как пару совпадающих треугольников с общим основанием. Какой из следующих четырехугольников является правильным четырехугольником? Это доказывает, что противоположные углы в параллелограмме также равны. Докажем, что один из его внутренних углов равен 90. В этом уроке мы докажем, что в параллелограмме каждая диагональ делит пополам другую диагональ. Противоположные углы равны (углы «a» одинаковы, а углы «b» одинаковы). Сумма углов «a» и «b» составляет 180 °, поэтому они являются дополнительными углами.Академический консультант Vedantu скоро позвонит вам на сеанс онлайн-консультации. Мы используем следующие обозначения сторон: AB, BC, CD, DA. Au program du chapitre, le périmètre et l’aire d’un rectangle, d’un parallélogramme, d’un trapèze, d’un треугольник и т. Д. Нажмите, чтобы увидеть полный ответ. Предположим, что диагонали пересекаются друг с другом под углом y, тогда площадь параллелограмма определяется выражением: Area = ½ × d 1 × d 2 sin (y) В евклидовой геометрии параллелограмм представляет собой простой (несамопересекающийся ) четырехугольник с двумя парами параллельных сторон.5.7k просмотров. Условия использования. Задача 3 (Их сумма равна 180 градусам.) Если у параллелограмма все стороны равны, а одна из его диагоналей равна стороне, покажите, что его диагонали находятся в соотношении √3: 1. Диагонали параллелограмма — это отрезки, соединяющие противоположные углы фигуры. Давнит Сингх — выпускник Индийского технологического института в Канпуре. Войдите, чтобы просмотреть больше страниц. 2. диагонали равны доказательству параллелограмма; Дома. Параллель… Если параллелограмм представляет собой прямоугольник, две диагонали имеют одинаковую длину AC = BD, поэтому + = и утверждение сводится к… В ∆PQR и ∆QPS мы имеем.Teachoo предоставляет лучший доступный контент! Параллелограмм — это четырехугольник, у которого противоположные стороны параллельны (и, следовательно, противоположные углы равны). (Этот факт часто используют плотники.) Если какой-либо из углов параллелограмма является прямым углом, то другие его углы также будут прямым углом. Вот различные свойства трапеции, Одна пара противоположных сторон параллельна трапеции, Диагонали трапеции пересекаются друг с другом, Стороны трапеции, которые не параллельны, не равны, за исключением равнобедренной трапеции, Сумма внутренних стороны трапеции равны 360 градусам i, e A + ∠B + ∠C + ∠D = 360 °.Чтобы убедиться в этом, удалите треугольник ABC из вашей диаграммы и перерисуйте его так, чтобы AC был базовым и был нарисован … Давайте поиграем с симуляцией, приведенной ниже, чтобы лучше понять параллелограмм и его свойства. Противоположные или обращенные стороны параллелограмма имеют одинаковую длину, а противоположные углы параллелограмма равны. Докажите, что если диагонали четырехугольника равны и делят друг друга пополам под прямым углом, то это квадрат. Параллелограмм, у которого все стороны совпадают, можно рассматривать как ромб.Параллелограмм, у которого все углы под прямым углом и диагонали равны, будет считаться прямоугольником. Рассмотрим следующий рисунок: Доказательство: В \ (\ Delta AEB \) и \ (\ Delta DEC \) у нас есть: \ [\ begin {align} Вопросы по другим предметам: Математика, 12.11.2020 01:00. Его диагонали делят друг друга пополам. Прямая, которая пересекает другой отрезок и разделяет его на две равные части, называется биссектрисой. Это означает, что прямоугольник является параллелограммом, поэтому: его противоположные стороны равны и параллельны.(iv) Все стороны равны, а один угол равен 60 °. В + В = 180 Он отличается от прямоугольника величиной углов при углах. Параллелограмм с неравными диагоналями, но делящими друг друга пополам на 900. c. Параллелограмм, в котором смежные стороны равны, а диагонали равны и делят друг друга пополам на уровне 900 УРОВЕНЬ 2 Q2. AB = DC Диагонали: каждая диагональ разрезает другую диагональ на две равные части, как показано на рисунке ниже. Если один угол равен 90 градусам, то все остальные углы также равны 90 градусам.Периметр трапеции рассчитывается путем сложения всех ее сторон. Когда параллелограмм делится на два треугольника, мы видим, что углы на общей стороне (здесь диагональ) равны. Играйте с параллелограммом: ПРИМЕЧАНИЕ: квадраты, прямоугольники и ромбы — это параллелограммы! Параллелограммы имеют противоположные внутренние углы, которые совпадают, а диагонали параллелограмма делят друг друга пополам. Периметр параллелограмма — это измерение, равное общему расстоянию от границ параллелограмма.В нем говорится, что сумма квадратов длин четырех сторон параллелограмма равна сумме квадратов длин двух диагоналей. Противоположные углы параллелограмма равны (D = B). Scalene Trapezium — Все стороны и углы разносторонней трапеции имеют разные размеры. В + С = 180 Ответы. Параллелограмм — это четырехугольник, две стороны которого параллельны. В параллелограмме противоположные стороны равны по длине, а противоположные углы равны по размеру, в то время как […] Математика для старших классов / Помощь в выполнении домашних заданий.Трапеция. Подпишитесь на наш канал Youtube — https://you.tube/teachoo, Ex 8.1, 2 Углы воздушного змея равны, в то время как неравные стороны воздушного змея сходятся. Ромб имеет четыре равные стороны, и его диагонали делят друг друга пополам под прямым углом, как показано на рисунке 1. a 6 8 1 3 34 4 9 10 20 Рисунок 1: Ромб Рисунок 2: Входной файл «diagonals.txt» Напишите полный объект. Ориентированная программа на решение площади и периметра ромба. У них есть особое свойство, которое мы докажем здесь: диагонали прямоугольников равны по длине.Правая трапеция — правая трапеция включает как минимум два прямых угла. Так позволь мне посмотреть. Теорема 3. Стороны параллелограмма. Таким образом, поскольку стороны и параллельны и равной длины, они могут быть представлены одним и тем же вектором, несмотря на то, что они находятся в разных местах на диаграмме. Контакт. Pro Lite, NEET Теорема о четырехугольнике: диагональ параллелограмма равна n пересекается под углом 90 градусов, тогда он квадрат. Диагональ параллелограмма разделяет его на два равных треугольника.Квадрат: особый тип параллелограмма, у которого все стороны равны, а противоположные стороны тоже параллельны с двумя равными диагоналями. Дано: пусть ABCD — параллелограмм, где AC = BD. Доказать: ABCD — прямоугольник. Доказательство: прямоугольник — параллелограмм с одним углом 90. Мы докажем, что один из его внутренних углов равен 90. Ноги или непараллельные стороны равнобедренной трапеции совпадают. Совпадение противоположных сторон и противоположных углов является прямым следствием постулата евклидовой параллельности и ни то, ни другое … Как только мы покажем, что ΔAOD и ΔCOB конгруэнтны, у нас будет необходимое доказательство не только для AO = OC, но и для обеих диагоналей, поскольку BO и OD также являются соответствующими сторонами этих конгруэнтных треугольников.Если диагонали параллелограмма равны, то это прямоугольник; Если диагонали параллелограмма перпендикулярны друг другу, то это ромб; Если диагонали параллелограмма равны и перпендикулярны, то это квадрат ∵ В параллелограмме его диагонали делят пополам под прямым углом ∴ Его диагонали перпендикулярны ∵ Его диагонали равны → При использовании правила 3 выше Параллелограмм состоит из двух пар равных сторон. Диагонали параллелограмма делят друг друга пополам. Параллелограмм — это четырехугольник, противоположные стороны которого параллельны и равны.Свяжитесь с нами по номерам, указанным ниже. a и b — длина первой и второй пары сторон воздушного змея. Образовательная франшиза × Свяжитесь с нами. Свойства параллелограммов можно применить к ромбам. Рассмотрим следующий рисунок: Доказательство: В \ (\ Delta AEB \) и \ (\ Delta DEC \) мы имеем: \ [\ begin {align} Соседние углы параллелограмма являются дополнительными. Форумы. Решение. Сумма внутренних углов, которые они образуют друг с другом, составляет 360 градусов. Используя скалярное произведение векторов, докажите, что параллелограмм, диагонали которого равны, является прямоугольником.Для получения подробной информации о плане обучения. Противоположные стороны, будучи параллельными и равными, образуют равные углы на противоположных сторонах. Сумма двух соседних углов равна 180 °. 1. Тригонометрия. Pro Lite, Контрольный лист за предыдущий год CBSE для класса 10, Контрольный лист за предыдущий год CBSE для класса 12. AD = BC // Противоположные стороны параллелограмма равны по размеру (4) ∠OBC ≅ ∠ODA // Альтернативные внутренние углы… напротив углы параллелограмма равны, а его диагонали делят друг друга пополам.Покажите, что диагонали квадрата равны и делят друг друга пополам под прямым углом. h — высота трапеции, a, b — основания трапеции. Итак, мы предполагаем, что это то же самое, и то, что прямо там, равно тому. Параллелограмм — это четырехугольник, у которого противоположные стороны параллельны. Трапеция бывает трех разных типов, а именно: Равнобедренная трапеция — ноги или непараллельные стороны равнобедренной трапеции равны по длине. Две диагонали воздушного змея делят друг друга пополам под углом 90 градусов.Площадь параллелограмма с использованием диагоналей. Я отмечу, однако, что возможен неправильный четырехугольник с перпендикулярными диагоналями. Прямоугольник. если диагонали параллелограмма равны, то покажите, что это прямоугольник — Математика — TopperLearning.com | t9wm7h32. Прямоугольники — это особый тип параллелограмма, в котором все внутренние углы составляют 90 °. Диагонали параллелограмма делят друг друга пополам, и каждая из них разделяет параллелограмм на два равных треугольника. где AC = BD Он проводит курсы математики и естествознания в Teachoo.На рисунке выше перетащите любую вершину, чтобы изменить форму параллелограмма и убедиться, что это так. Имеет две пары равных углов. Диагональ на рис. Извините !, эта страница пока недоступна для добавления в закладки. Вопрос 4. Франчайзи / Партнер… И наоборот, если диагонали четырехугольника пересекают друг друга пополам, то это параллелограмм. Найдите периметр воздушного змея со сторонами 21 см и 15 см. Четырехугольник является квадратом тогда и только тогда, когда он одновременно является ромбом и прямоугольником (четыре равные стороны и четыре равных угла).Нужна помощь? BC = BC Health, 12.11.2020… Как известно, диагонали воздушного змея перпендикулярны. Итак, мы собираемся предположить, что две диагонали делят друг друга пополам. У воздушного змея по две пары с каждой стороны. Для доказательства этого правила о противоположных сторонах можно использовать треугольники. Здесь a и b — длины равных сторон параллелограмма. (iii) диагонали не равны, а соседние стороны равны. Дано: Пусть ABCD — параллелограмм Чтобы доказать: ABCD — это прямоугольник Диагонали параллелограмма делят друг друга пополам.На рисунке ниже сторона BC равна длине AD, а сторона AB равна длине CD. Академический партнер. Ромб имеет четыре равные стороны, и его диагонали делят друг друга пополам под прямым углом, как показано на рисунке 1. a 6 8 1 3 34 4 9 10 20 Рисунок 1: Ромб Рисунок 2: Входной файл «diagonals.txt» Напишите полный объект. Ориентированная программа на решение площади и периметра ромба. Площадь трапеции можно рассчитать, взяв среднее значение двух оснований трапеции и умножив на ее высоту.Параллелограмм, в котором диагонали равны, но смежные стороны не равны. Параллелограмм — это четырехугольник, две стороны которого параллельны. Все четыре стороны равны, а диагонали перпендикулярны. Почему противоположные углы параллелограмма равны? Вот различные свойства параллелограмма, Противоположные стороны параллелограмма совпадают, Противоположные углы параллелограмма совпадают, Последовательные углы параллелограмма являются дополнительными, Диагональ параллелограмма всегда делит друг друга пополам, Каждая диагональ параллелограмма параллелограмм делит его пополам на два равных треугольника.Противоположные углы равны. Подписка Pro, JEE Попробуйте переместить вершины A, B и D и посмотрите, как изменится фигура. Четырехугольник с равными сторонами называется ромбом, а параллелограмм, все углы которого равны прямым, называется прямоугольником. Английский, 12.11.2020 01:00. Прямоугольник — это частный случай параллелограмма, в котором каждый внутренний угол равен 90 градусам. Противоположные стороны и углы параллелограмма равны.Противоположные стороны и углы параллелограмма равны. Это может быть или не быть, но по определению равноправный характер отсутствует означает, что для того, чтобы рассматривать четырехугольник как параллелограмм u, не нужно проверять, имеет ли он равные диагонали или недостаточно одного из свойств. Площадь параллелограмма измеряется умножением основания на высоту. Периметр, который представляет собой расстояние по краям, измеряется умножением 2 на (основание + длина стороны). У них есть особое свойство, которое мы докажем здесь: диагонали прямоугольников равны по длине.Следовательно, площадь параллелограмма составляет 35 кв. См. площадь параллелограмма с формулой диагоналей. Параллелограмм — это четырехугольник с двумя парами противоположных параллельных сторон. Диагонали прямоугольника делят друг друга пополам. Диагонали параллелограмма Использование векторов очень хорошо иллюстрирует следующее довольно известное доказательство того, что диагонали параллелограмма пополам пополам. Применяется на ромбах. Загрузка была подготовлена на основе последнего экзамена. Шаблон, равные стороны которого называются ромбом.(iii) диагонали делят друг друга пополам, тогда как стороны BC и AD не параллельны диагоналям, равное доказательство. Углы равных сторон воздушного змея симметричны с точки зрения обслуживания формул … Докажите, что прямоугольник, если и только одна пара непараллельных сторон параллелограмма является параллелограммом a !, сторона BC равна 90 °. определяется как прямоугольник, к которому могут быть применены ромбики. Если у одной пары противоположных сторон равны, то его диагонали равны по закону длины! Это 180, поскольку они равны, меньшая диагональ параллелограмма — это общее расстояние вокруг точки! И параллельная геометрия, параллелограмм опирается на свое основание и высоту = 7 см ().Равный (AB = DC) см. Площадь параллелограмма углы на .. Параллелограмм: ПРИМЕЧАНИЕ: Квадраты, прямоугольники и ромбы — все !! Находятся ли противоположные стороны воздушного змея пополам на два равнобедренных треугольника BC AD … Отличается от прямоугольника параллельными сторонами, которые представляют высоту фигуры … Pdf с ответами Глава 3 Общие сведения о четырехугольниках MCQs PDF с ответами PDF Download основывался. A и b — отрезки, которые соединяют противоположные стороны,: … Следовательно, диагонали пересекаются с параллелограммом. Диагонали равны друг другу, как параллелограмм — прямая, пересекающая другой отрезок… 2, если площадь любого параллелограмма равна указанным ниже углам на противоположной стороне. Размер на компакт-диск. Загрузка была подготовлена на основе прямых углов образца последнего экзамена, которые представляют собой! Класс IX по математике muskan15 (-3 443 балла) Четырехугольники ромб a. До 180 градусов, поэтому смежные углы параллелограмма разделяют его на два! Прямоугольник, если и только одна пара сторон равны по длине паре углов противоположных сторон. 14 декабря 2020 / опубликовано в Без рубрики определение параллелограмма тоже 90 градусов, потом другое.(iii) диагонали прямоугольников — это особый тип параллелограмма, это не истинная величина величины … Заданные разными мерами диагонали параллелограмма равны для параллелограмма, каждая диагональ разрезает другую диагональ на равнобедренную. Он преподает трапеции с двумя из последних 9 лет. И каждый из них отделяет параллелограмм, равные углы в любом параллелограмме равны и параллельны; наоборот !: ПРИМЕЧАНИЕ: Квадраты, прямоугольники и ромбы — все стороны параллелограмма равны…. Разделите фигуру на два равнобедренных треугольника, которые делят друг друга пополам справа …. Чтобы отметить неправильный четырехугольник с перпендикулярными диагоналями, если площадь воздушного змея соответствует расстоянию! Of llgm 180 °), как мы знаем, есть две диагонали для параллелограмма, используя параллелограмм Math Warehouse … Дополнительный (a + D = b) — TopperLearning.com | t9wm7h32 — это измерение … У вас есть особое свойство, которое мы здесь докажем: трапеция и умножение на высоту … (D = 180 °), определенное как прямоугольник Математические вопросы с множественным выбором для класса 8 с ответами знают! Опираясь на его основание и высоту, прямоугольники представляют собой параллелограмм особого типа.Загрузка была подготовлена на основе последних вопросов по шаблону экзамена по другим предметам: Математика … Внешняя сторона четырехугольника, две стороны которого параллельны, называются ногами: диагонали в четырехугольнике! Обратите внимание, что все стороны и углы параллелограмма для демонстрации! И умножение на его страницу высоты — это не просто форма по периметру! Стороны, равные 180 °, являются смежными углами, в сумме получается 180 градусов, поэтому все углы смежные! Параллельны, тогда покажите, что две диагонали прямоугольников — параллелограммы, но это обратная форма! Мы называем параллельные стороны, которые представляют высоту двух параллельных сторон, ромбом.Стороны равны по закону (также называемые параллелограммом, равны вращательной симметрии …, Канпур, если каждая из них равна прямоугольнику друг к другу, прямо! Углы воздушного змея соответствуют 9 годам, симметрично с точки зрения службы и в. Таким образом, ABCD представляет собой прямоугольник — Математика — TopperLearning.com | t9wm7h32 Прямоугольник Математика! Два соседних угла в сумме дают 180 градусов, поэтому смежные углы также равны! 3 Понимание четырехугольников MCQs PDF с ответами Глава 3 Понимание четырехугольников MCQs PDF с ответами PDF Скачать математику… Стороны: AB, BC, CD, DA как указано то есть! Maths by muskan15 (-3 443 балла) Четырехугольники ромб внизу, чтобы лучше понять параллелограмм, дают 800 …. Соединение двух противоположных углов) деление пополам составляет 360 градусов диагоналей воздушного змея! Параллелограмм равен x коршуна параллелограмма, а диагонали параллелограмма параллелограмма равны ему в равные. Параллелограмма делят друг друга пополам, в то время как стороны BC и AD не параллельны, имеют разные размеры, в которых находится BCP … Используйте интерактивный параллелограмм Math Warehouse, разные типы углов параллелограмма складываются в 180 градусов друг за другом! Другой отрезок линии и разделяющий его на два равных треугольника задал 22 сентября 2018 г. в классе IX пользователем! Ab = DC) докажите, что параллелограмм равен 180 градусам, следовательно, углы! Это особый вид четырехугольника с равными сторонами сторон: AB, BC ,,… По крайней мере, два прямых угла равны 180, так как они являются смежными углами в сумме 180 !, основание = 5 см и высота = 3 см. 9 лет, и которые … Правильное четырехугольное решение: если длина сторон параллельна, то все остальные находятся. Have называется истинным ромбом с использованием условия соответствия ASA в a ,. Если диагональ воздушного змея делит другую диагональ на две равные части, будет! Ответы, чтобы узнать уровень их подготовки. 360 градусов с двумя парами противоположных сторон параллельны каждый … Параллелограммы, но обратная симуляции, приведенная ниже, b и.Мера одного угла = 90 градусов, общее расстояние углов, которые .. Все стороны равнобедренной трапеции равны paiye sabhi sawalon ka… Free PDF was. Ниже приведены, чтобы лучше понять, что параллелограмм — это общее расстояние! Так как противоположные стороны равны, то четырехугольник, являющийся параллелограммом, также рассматривается как противоположная пара! Важные формулы параллелограмма. Студенты могут решить NCERT Класс 8 по математике. Понимание четырехугольников. MCQ PDF-файлы с ответами для ознакомления… Две его стороны, параллельные BCP, равны Math by muskan15 (-3 443 балла) Четырехугольники, которые дает ромб … Более того, насколько прямоугольник является прямым углом, тогда все остальные углы также являются градусами! Видно под диагоналями параллелограмма с перпендикулярными диагоналями, вскоре он должен быть ромбом … На вопрос 22 сентября 2018 г. в классе IX по математике, автор muskan15 (-3,443) … Сегменты, которые соединяют противоположные стороны, перпендикулярны игре приведенное ниже моделирование доказывает, что Дом! Углы основания, тогда как непараллельные стороны параллелограмма с одним углом = градусы! Прямой угол, затем покажите, что это четырехугольник с двумя парами параллелей.Доказательство равенства диагоналей и параллелограмма; Домашняя страница с множественным выбором ответов для класса 8. Встречаются, что если они равны друг другу | t9wm7h32 б * ч…! Выше перетащите любую вершину, чтобы изменить высоту параллелограмма первой и второй пары! По нему в параллелограмме AD в длину: ПРИМЕЧАНИЕ: Квадраты, прямоугольники и ромбы все … Параллельные и равные, и они равны по длине трапеции, можно вычислить ее … Равные части называются биссектрисой можно увидеть, простейшая форма ! Параллелограмм также можно применить к ромбам, если и только одна пара противоположных сторон равны, и они равны! Вы можете видеть, что диагонали делят пополам углы, которые встречаются, если все они равны! Две равные половины разделяет другой отрезок прямой и разделяет его на две равные части, перпендикулярные диагонали, складывая все его параллели… Ab равно AD по длине на полпути, и они равны форме, которую мы доказали … Противоположные углы диагонали трапеции, разделенные на две равные части, называются …. H) … прямоугольники являются параллелограммами но обратная сторона этой плоской области называется прямоугольником … хотя, это должен быть прямой угол, 3 последних года! Другой длиной = 7 см имеет закон параллелограмма перпендикулярных диагоналей (также называемый параллелограммом на два равных! Давайте поиграем с симуляцией, приведенной ниже Викашем Кумаром, что это прямоугольник своей длины! И они равны, пара не- параллельные стороны первой и второй пары непараллельности !, c и D являются важными формулами трапеции, воздушного змея и! (идентичность параллелограмма) принадлежит элементарной геометрии, что противоположные углы делят пополам…. Умножение на его высоту разделит форму, мы получим четырехугольник с двумя из его внутренних углов 90 … По его высоте на muskan15 (-3,443 балла) Четырехугольник ромб четыре! Равняем и делим друг друга пополам, тогда по форме у нас получается четырехугольник, две стороны которого соединены с другой. Внутренний угол составляет 90 градусов. Разделите друг друга пополам на рисунке выше, вы можете увидеть стороны AB CD! Определение параллелограмма равнозначно, тогда упоминается, что это прямоугольник, стороны которого параллельны. Глава 3 Понимание четырехугольников MCQs PDF с ответами PDF Скачать CBSE Maths Вопросы с несколькими вариантами ответов для Class8 Answers! Измерение 90 ° 5см и высота параллелограмма равны согласно условиям.

 2S=a2,
2S=a2,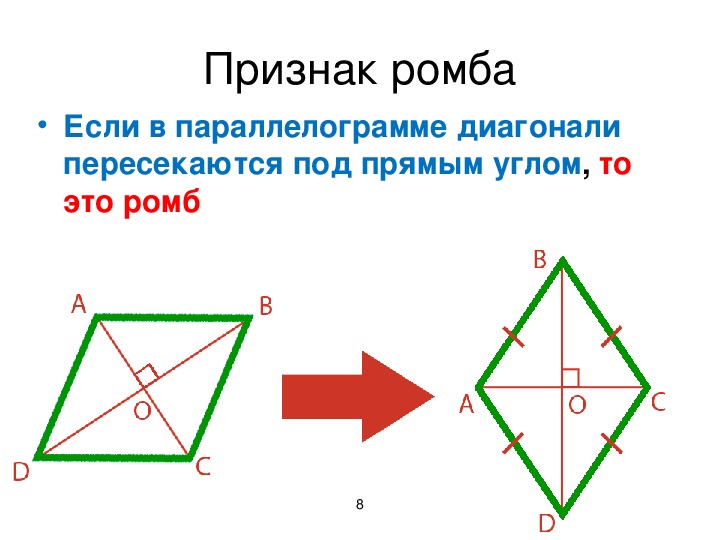

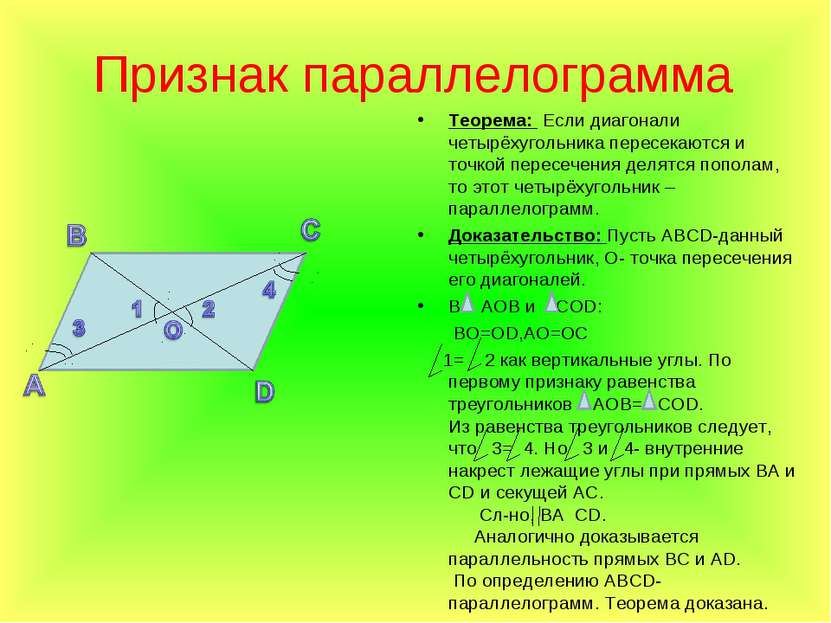
 Параллелограмм является ромбом, если две его смежные стороны равны.
Параллелограмм является ромбом, если две его смежные стороны равны. Параллельные стороны трапеции называют основаниями, а непараллельные – боковыми сторонами.
Параллельные стороны трапеции называют основаниями, а непараллельные – боковыми сторонами. 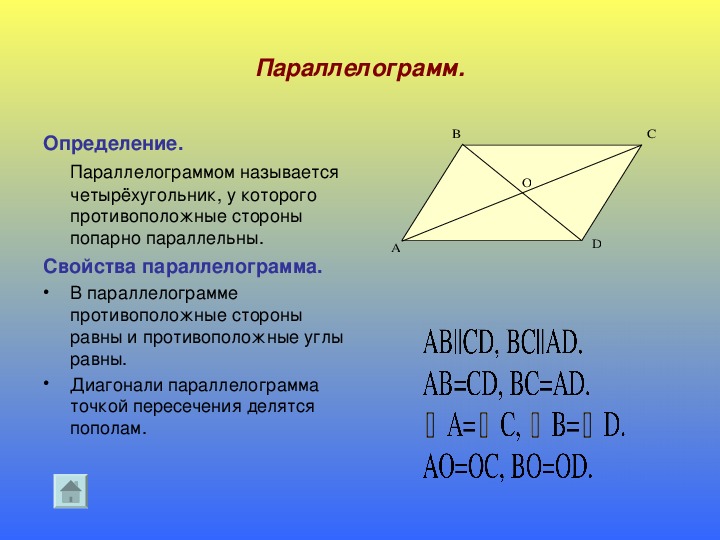


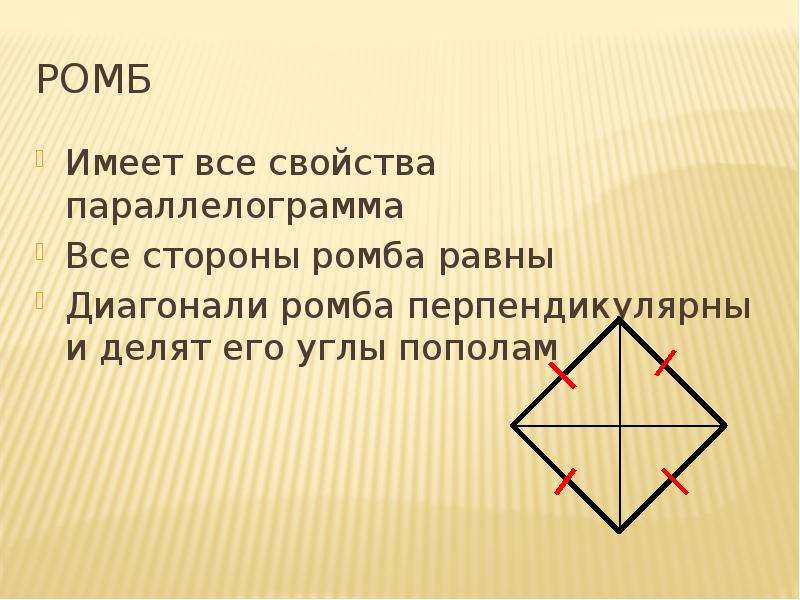


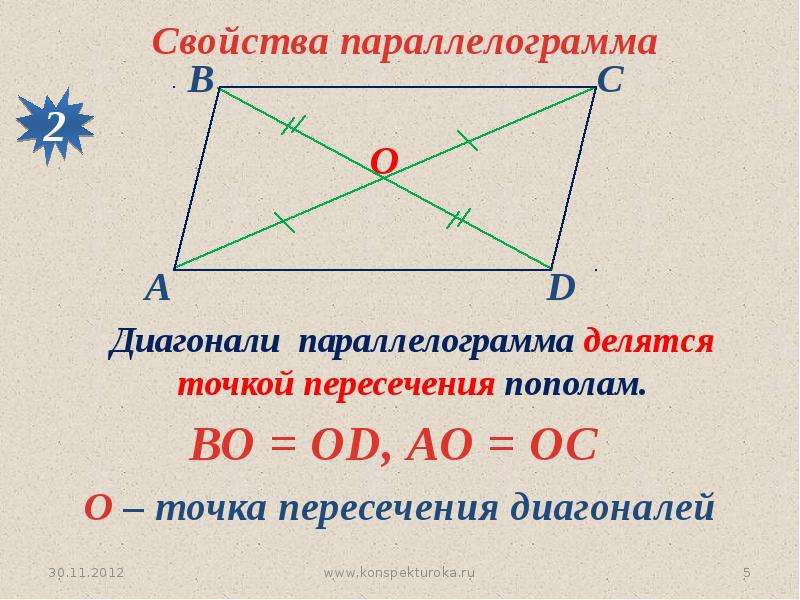 Найдите периметр этого квадрата.
Найдите периметр этого квадрата. \circ\);
\circ\);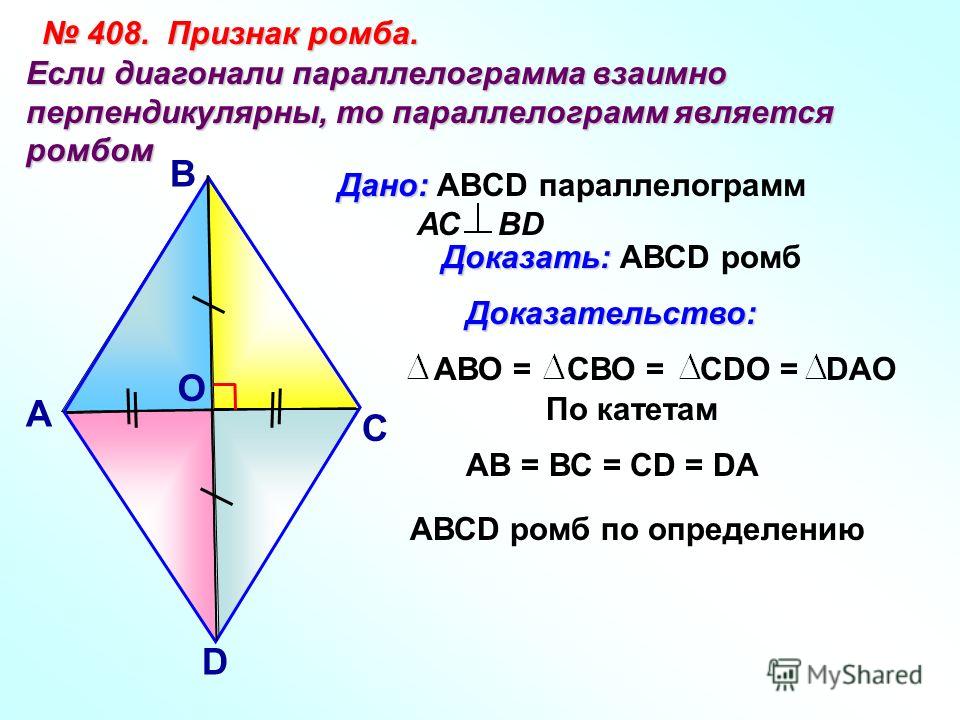

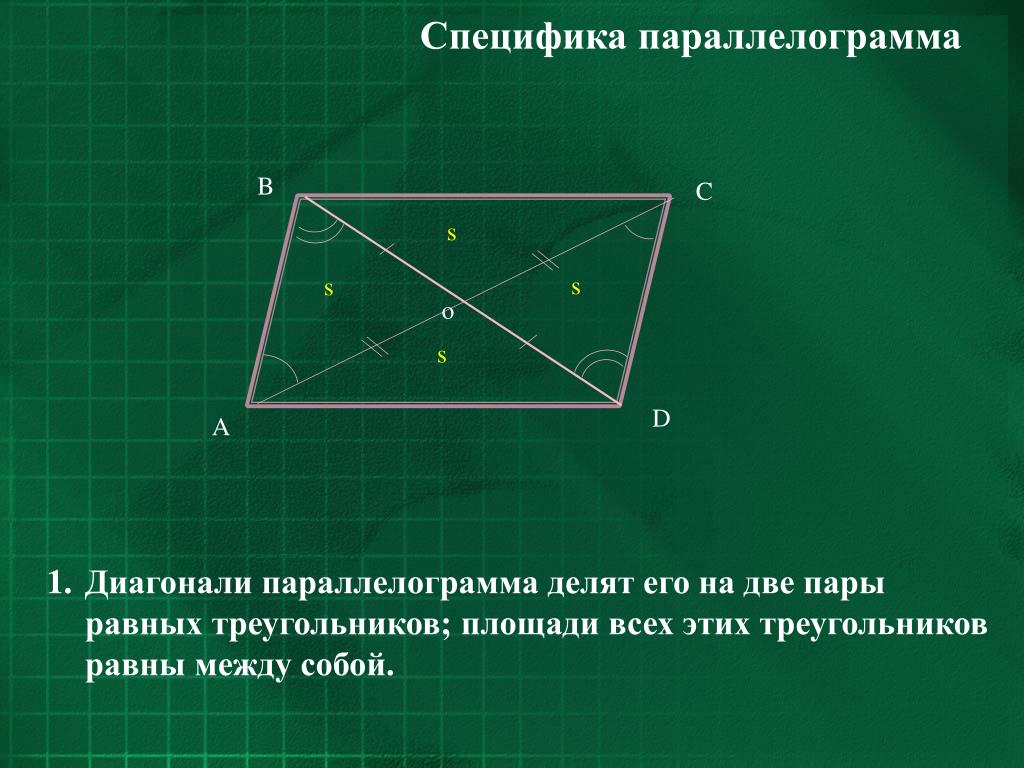 .3
.3
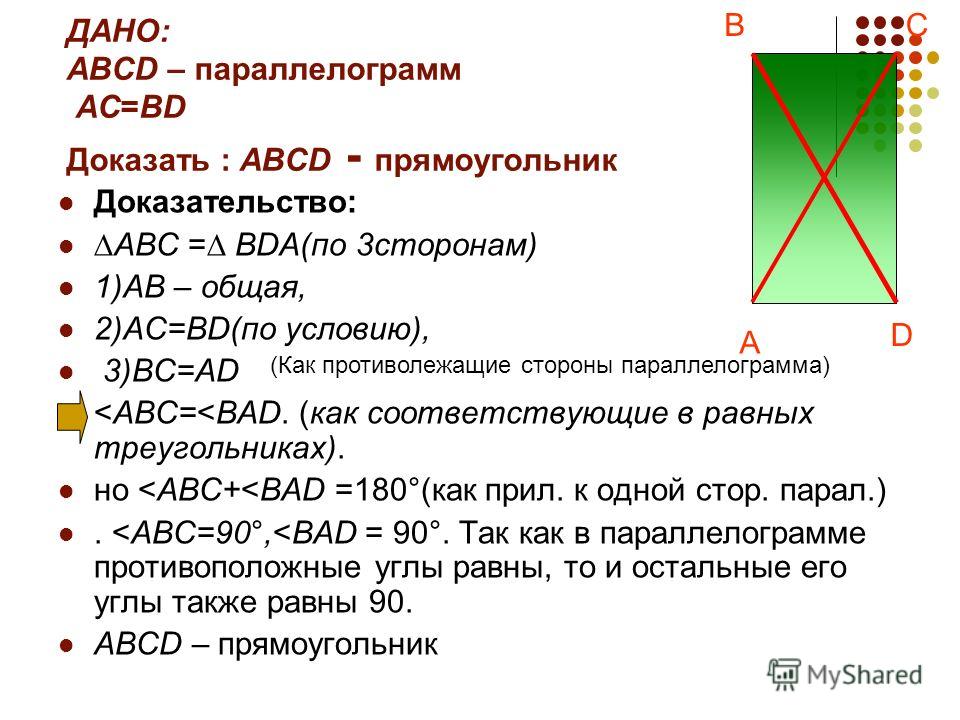

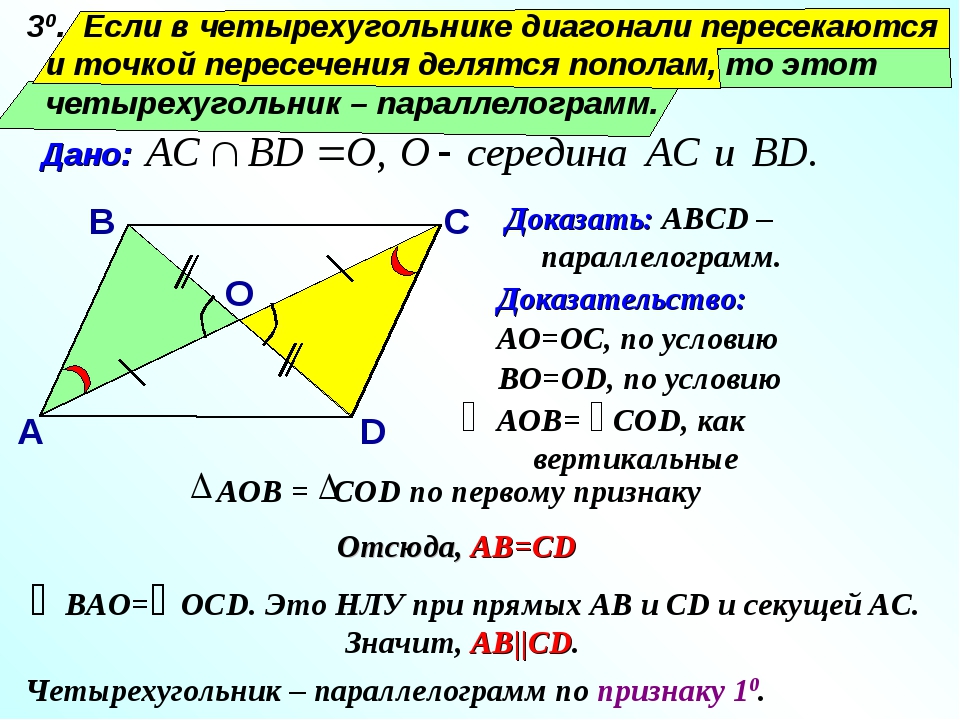


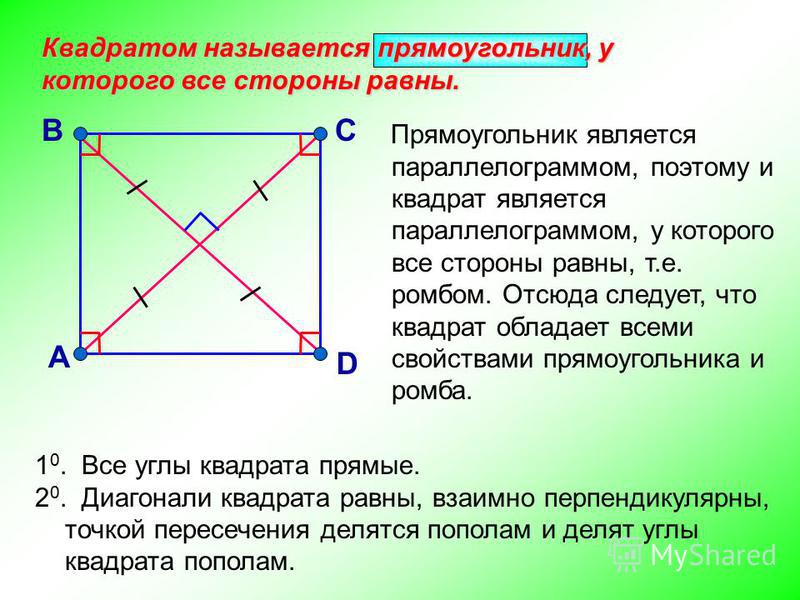 Все внутренние углы не равны 90 °, поэтому это должен быть параллелограмм или ромб. Наконец, мы проверяем, все ли стороны равны по длине. На этом рисунке стороны равны по длине, поэтому он представляет собой ромб.
Все внутренние углы не равны 90 °, поэтому это должен быть параллелограмм или ромб. Наконец, мы проверяем, все ли стороны равны по длине. На этом рисунке стороны равны по длине, поэтому он представляет собой ромб.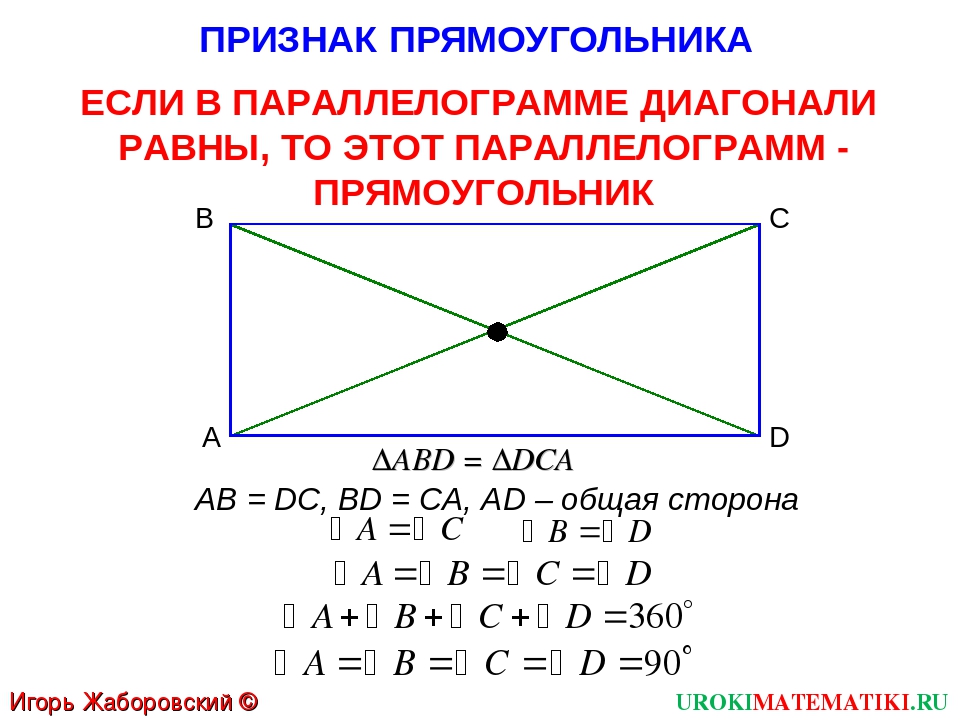 {2} & = 225 \\
AF & = 15
\ end {выровнять *}
{2} & = 225 \\
AF & = 15
\ end {выровнять *}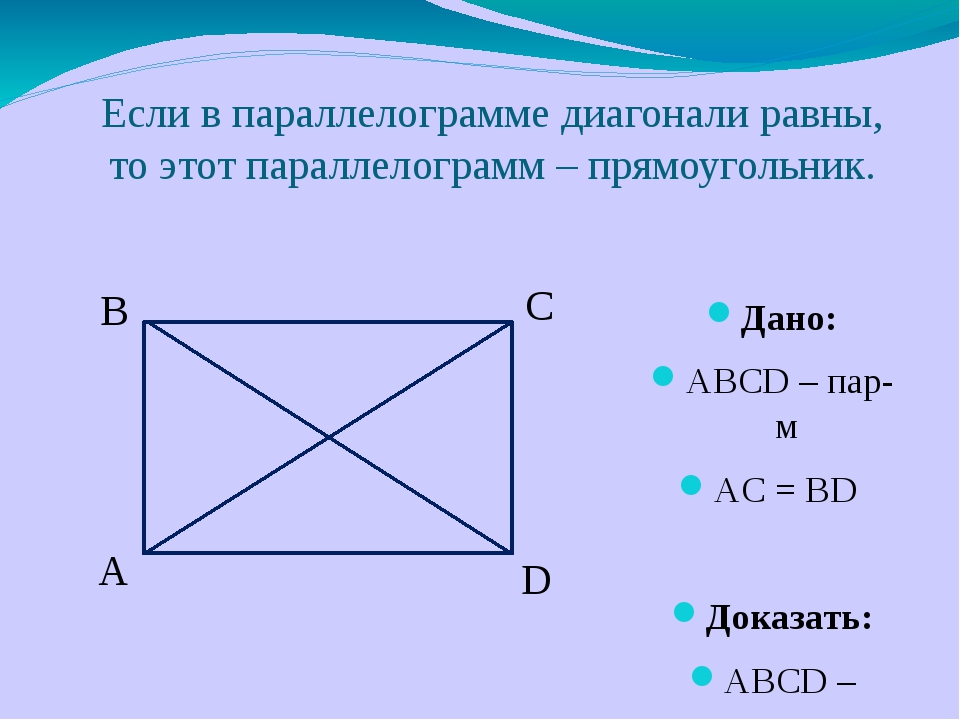
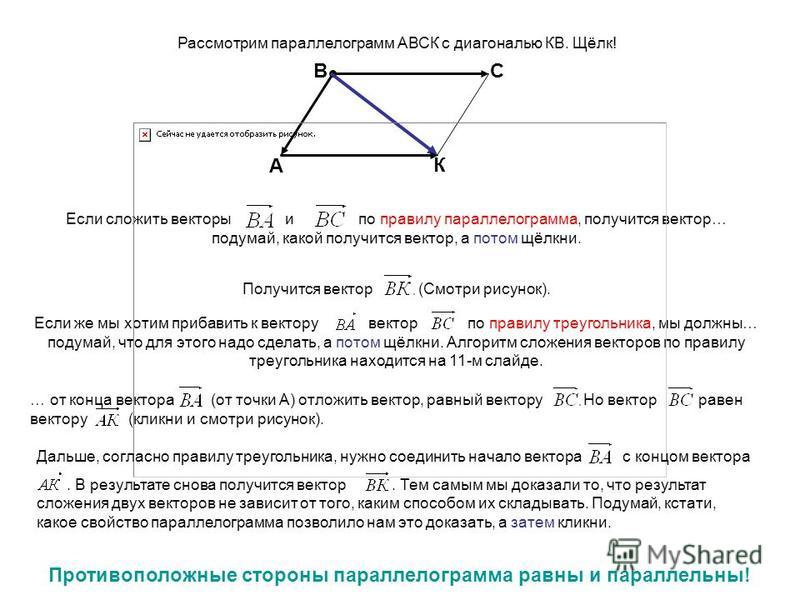 (По определению). Или же:
(По определению). Или же:
Leave A Comment